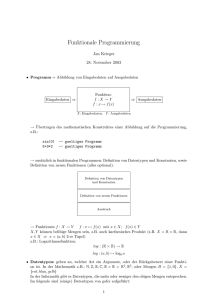
Definition von Funktionen Definition von Funktionen cont. Definition

Funktionen in Haskell:
Definition von Funktionen
• mit Gleichungen
• Funktionen sind in funktionalen
Programmiersprachen ‘Bürger erster Klasse’ (‘first class citizens’)
• dabei bedingte Ausdrücke verwendbar
• sie unterscheiden sich nicht von Daten,
max :: Int -> Int -> Int
max x y = if x >= y then x else y
• sie können Argumente von Funktionen sein,
• gegebenenfalls verschachtelte bedingte Ausdrücke
• sie können Werte von Funktionen sein,
• sie können Elemente in zusammengesetzten Datenstrukturen sein (z.B.
Listen, Tupel, . . . ).
c Prof. Dr. D. Rösner; erstellt: 6. Oktober 2006
WS 2006/2007, Programmierkonzepte und Modellierung (PKM), 37
fib :: Int -> Int
fib x = if x == 0 then 0
else if x == 1 then 1
else fib (x - 1) + fib (x - 2)
c Prof. Dr. D. Rösner; erstellt: 6. Oktober 2006
WS 2006/2007, Programmierkonzepte und Modellierung (PKM), Definition von Funktionen cont.
Definition von Funktionen cont.
• Variante mit ‘Wächtern’ (engl. ‘guards’)
• Beispiele cont.:
• boolesche Ausdrücke für Fälle in einer Definition
fib
fib
|
|
|
• idealerweise disjunkt und vollständig abdeckend
• Beispiele:
max :: Int -> Int -> Int
max x y
| x >= y
| otherwise
:: Int -> Int
x
x == 0
= 0
x == 1
= 1
x > 1
= fib (x - 1) + fib (x - 2)
• Variante:
fib x
| x == 0 || x == 1
| otherwise
= x
= y
c Prof. Dr. D. Rösner; erstellt: 6. Oktober 2006
WS 2006/2007, Programmierkonzepte und Modellierung (PKM), 38
39
= x
= fib (x - 1) + fib (x - 2)
c Prof. Dr. D. Rösner; erstellt: 6. Oktober 2006
WS 2006/2007, Programmierkonzepte und Modellierung (PKM), 40
Definition von Funktionen cont.
Definition von Funktionen cont.
• Variante mit ‘Pattern matching’
• Variante mit ‘Pattern matching’
• Beispiel:
fib :: Int -> Int
fib 0 = 0
fib 1 = 1
fib x = fib (x - 1) + fib (x - 2)
mistery :: Int -> Int -> Int
mistery 0 y = y
mistery x y = x
• ‘guards’ bzw. Gleichungen werden sequentiell ausgewertet
c Prof. Dr. D. Rösner; erstellt: 6. Oktober 2006
WS 2006/2007, Programmierkonzepte und Modellierung (PKM), 41
Definition von Funktionen cont.
42
Operationen mit Funktionen
• Verwendung von ‘wildcards’ in Mustern möglich
• Definition von Funktionen
• Anwendung von Funktionen auf Argumente
mistery :: Int -> Int -> Int
– Argumente können verschachtelt wieder Anwendungen von Funktionen
auf Argumente sein
mistery 0 y = y
mistery x _ = x
• ‘wildcards’ immer dann sinnvoll, wenn beliebige Werte im Muster (auf der
linken Seite) zugelassen werden sollen und auf diese auf der rechten Seite
der Gleichung nicht verwiesen werden muss
c Prof. Dr. D. Rösner; erstellt: 6. Oktober 2006
WS 2006/2007, Programmierkonzepte und Modellierung (PKM), c Prof. Dr. D. Rösner; erstellt: 6. Oktober 2006
WS 2006/2007, Programmierkonzepte und Modellierung (PKM), 43
• partielle Anwendung von Funktionen
• Funktionskomposition
c Prof. Dr. D. Rösner; erstellt: 6. Oktober 2006
WS 2006/2007, Programmierkonzepte und Modellierung (PKM), 44