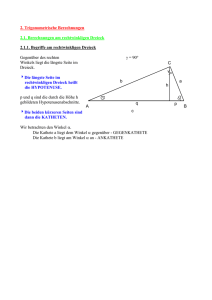
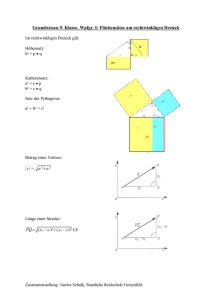
Trigonometrie am rechtwinkligen Dreieck

Klasse 4e 2006/U.Hauser
Trigonometrie am rechtwinkligen Dreieck
1. Geschichtliches
Die Trigonometrie ein Teilgebiet der Geometrie, welches sich mit Dreiecken beschäftigt. Sie entstand vor allem aus der frühen Astronomie1, hat aber neben der
Himmelsvermessung auch zahlreiche
„irdische“ Anwendungen gefunden.
Warum Dreiecke ?
Dreiecke sind in der Geometrie besonders
wichtig, da beliebige durch Strecken oder
Geraden begrenzte ebene Figuren wie
Rechtecke und allgemeine Vielecke, in
Dreiecke zerlegt werden können. Daher
können Methoden der Dreiecksgeometrie zur
Lösung einer Vielzahl komplexer geometrischer
Fragestellungen
angewandt
werden, z.B. bei "Vermessungsaufgaben".
Abb. 1: Winkelmessung mit dem Jakobstab
Abb 2: Jakobstab
Abb 3: Claudius Ptolemäus1
2. Repetition
Die Steigung einer Strecke sagt aus, wie weit man [vertikal] gestiegen/gefallen ist, wenn man eine bestimmte [horizontale] Strecke zurückgelegt hat:
Steigung m =
Höhendifferenz
horizontale Entfernung
Beispiel:
40 m
150 m
1,25 km
100 m
Die Steigung beträgt hier : m = 40 m = 0,4
Die Steigung beträgt hier : m =
=
100 m
oder in Prozent: 40%
oder in Prozent:
3. Der Tangens
Uns interessiert nun die Frage, wie die Steigung mit dem Neigungswinkel α zusammenhängt :
60 m
40 m
α
α
100
m=
80 m
α=
α
100 m
m=
α=
100 m
m=
α=
Je grösser die Steigung m , desto ______________ der Neigungswinkel und umgekehrt.
1
Claudius Ptolemäus (um 140 n. Chr.)
Seite 1
Klasse 4e 2006/U.Hauser
Wir können also sagen, dass zu einer Steigung eindeutig auch ein Neigungswinkel gehört.
Wir werden uns aber nicht nur mit der Steigung befassen, sondern allgemein mit rechtwinkligen Dreiecken
und deren Winkel. Da es sich bei unserem Steigungsdreieck immer um ein rechtwinkliges Dreieck handelt,
kann man die Steigung (also das Streckenverhältnis) nun auch verallgemeinern:
β
α
Dabei nennen wir eine ______________ welche einem Winkel anliegt ______________________ .
Eine _________________ welche einem Winkel gegenüberliegt, heisst _______________________ .
Da wir diese Verhältnis oft brauchen geben wir ihm einen Namen, nämlich :
Tangens =
Im rechtwinkligen Dreieck mit γ = 90° ist:
C
b
tanα =
a
β
α
tanβ =
A
B
Mit dem Taschenrechner :
Winkel Tangens
Tangens Winkel
Beispiel 1:
Seite 2
Klasse 4e 2006/U.Hauser
α = 35°, β = 55° und b=6cm.
Gegeben :
Gesucht :
Dreieck ABC mit
Seite a und c.
Beispiel 2:
Gegeben :
Gesucht :
Dreieck ABC mit a=3cm, b=4cm und c=5cm.
Winkel α und β .
4. Der Sinus
Ein weiteres Verhältnis im rechtwinkligen Dreieck ist :
Sinus =
Im rechtwinkligen Dreieck mit γ = 90° ist:
C
b
sinα =
a
β
α
A
c
B
sinβ =
Mit dem Taschenrechner :
Winkel Sinus
SIN(50) =
Sinus Winkel
2nd SIN (0.5) =
Seite 3
Klasse 4e 2006/U.Hauser
Beispiel 1:
Gegeben :
Gesucht :
Dreieck ABC mit
Seite c.
Beispiel 2:
Gegeben :
Gesucht :
Dreieck ABC mit a=4cm und hc=3cm.
Winkel β und Seite c.
α = 40 und a=3cm.
5. Der Cosinus
Das letzte Verhältnis im rechtwinkligen Dreieck, welches wir betrachten heisst:
Cosinus =
Im rechtwinkligen Dreieck mit γ = 90° ist:
C
b
cosα =
a
β
α
A
c
B
cosβ =
Beispiel:
Gegeben :
Gesucht :
Dreieck ABC mit b=4cm und w α =4.5cm.
Winkel α und Seite a.
Seite 4
Klasse 4e 2006/U.Hauser
6. Anwendungen der trigonometrischen Funktionen
6.1 Berechnen der Baumhöhe
Man kann die Streckenlänge a=20m und den Winkel
α
messen.
Welche Höhe besitzt dann der Baum ?
α
6.2 Berechnen der Flussbreite
Bestimme die Breite des Flusses
zwischen A und B:
A
B
Seite 5
Klasse 4e 2006/U.Hauser
7. Das Bogenmass
Gradmass
Bogenmass
Bogenmass
Gradmass
8. Die Funktionsgraphen von Sinus und Cosinus
Graph von y=sinx :
GRAD α
RAD arc α
− 2π
−1.5π
−π
−0.5π
0
0.5π
π
1.5π
2π
sinx
Seite 6
Klasse 4e 2006/U.Hauser
Graph von y=cosx :
GRAD α
RAD arc α
− 2π
−1.5π
−π
−0.5π
0
0.5π
π
1.5π
2π
sinx
Übungen: Blatt Nr. 3 , 4 , 5 , 6
9. Beziehungen zwischen den Winkelfunktionen
Beweise folgende Beziehungen:
a) „trigonometrischer Pythagoras!“
Beweis:
b) tanα =
(sin α )2 + (cos α )2 = 1
sinα
cosα
Beweis:
c) sinα = cos(90° − α )
cosα = sin(90° − α )
Seite 7
Klasse 4e 2006/U.Hauser
10. Die Flächenformel
C
Behauptung:
Mit zwei Seiten b und c und dem von ihnen eingeschlossenen Winkel α lässt
sich der Flächeninhalt eines beliebigen Dreiecks direkt berechnen.
A
B
Herleitung der Flächenformel:
(stumpfwinkliges Dreieck)
(spitzwinkliges Dreieck)
Seite 8