Aufgabe 7.sxw

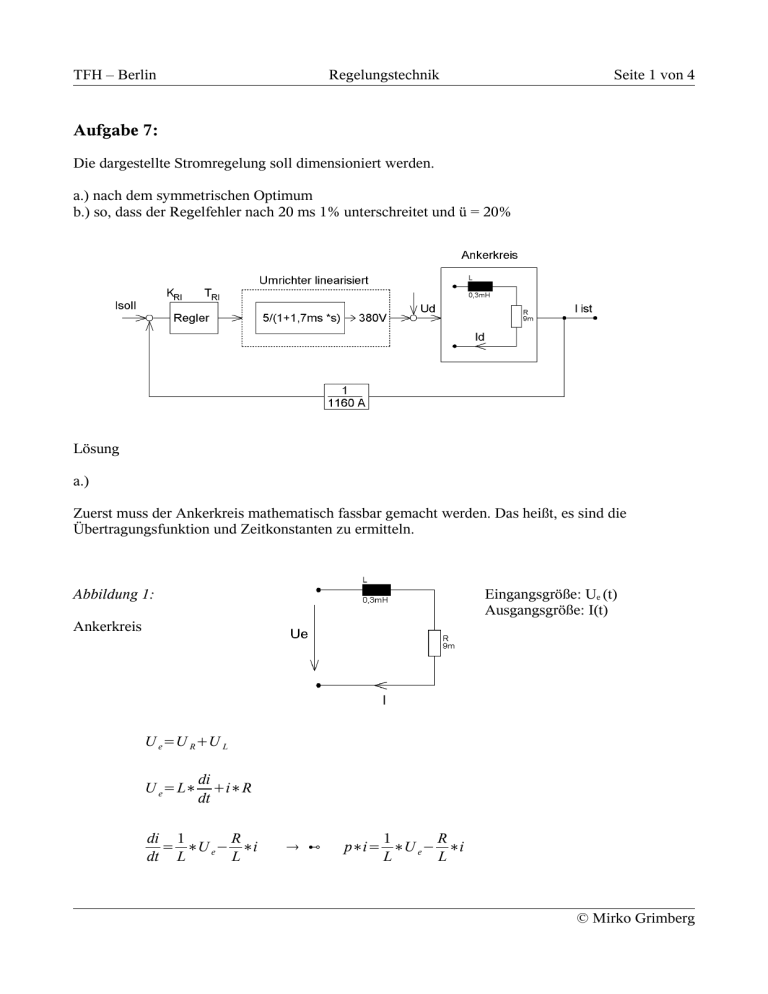
TFH – Berlin
Regelungstechnik
Seite 1 von 4
Aufgabe 7:
Die dargestellte Stromregelung soll dimensioniert werden.
a.) nach dem symmetrischen Optimum
b.) so, dass der Regelfehler nach 20 ms 1% unterschreitet und ü = 20%
Lösung
a.)
Zuerst muss der Ankerkreis mathematisch fassbar gemacht werden. Das heißt, es sind die
Übertragungsfunktion und Zeitkonstanten zu ermitteln.
Eingangsgröße: Ue (t)
Ausgangsgröße: I(t)
Abbildung 1:
Ankerkreis
U e =U R U L
U e =L∗
di
i∗R
dt
di 1
R
= ∗U e − ∗i
dt L
L
 ⊷
1
R
p∗i= ∗U e − ∗i
L
L
© Mirko Grimberg
TFH – Berlin
Regelungstechnik
Seite 2 von 4
R 1
i∗ p = ∗U e
L L
i∗
pLR 1
= ∗U e
L
L
1
L
i= ∗U e∗
L
pLR
i=U e∗
1
pLR
i
1
=
U e pLR

1
L
∗ p1
R

1
Tp1
mit T =
L
R
1
Nach Gleichung 1 handelt es sich bei dem Ankerkreis um ein PT1 – Glied mit der
Zeitkonstante T = L/R. Um die Verstärkung zu ermitteln kann man für Ue eine
Gleichspannungsquelle annehmen. Dann ist nur noch der Ohm'sche Widerstand relevant und der
sich einstellende Strom errechnet sich zu:
I=
Ue
R
=
380 V
9m
=42222,2 A
Erklärung: Gibt man auf den Ankerkreis Ue = 380 V als Eingangsspannung, so wird sich nach
spätestens unendlich langer Zeit (abhängig von der Zeitkonstante) ein Strom von 42,2 kA einstellen.
Hinweis: Diese Rechnung beinhaltet eine Normierung auf 380 V.
Der Regelkreis hat nach der Modellierung des Ankerkreises folgendes Aussehen:
Abbildung 2:
Regelkreis mit
Ankerkreis als
PT1 – Glied
Um den Regelkreis weiter zu vereinfachen, kann die Verstärkung des Ankerkreises mit dem
Übersetzungsverhältnis der Stromistwerterfassung multipliziert werden. So ergibt sich eine
42222,2
=36,3 .
Ankerkreisverstärkung von K A =
1160
© Mirko Grimberg
TFH – Berlin
Regelungstechnik
Seite 3 von 4
Abbildung 3:
Regelstrecke vereinfacht
Zum Dimensionieren des Reglers können nun die Einstellregeln nach dem symetrischen Optimum
verwendet werden.
T T =Stromrichtertotzeit=1,7 ms
K T =Stromrichterverstärkung=5
T A = Ankerzeitkonstante=33,3 ms
K A = Ankerkreisverstärkung=36,3
K 1 und K 2=Korrekturfaktoren
K 1=
1
3∗T T
1
TA
K 2=
1
K2
T RI = K 1∗4∗T T
1 T
1
K RI =K 2∗ ∗ A ∗
2 T T K A∗K T
T RI =
1
∗4∗1,7 ms =5,896
1,7 ms
13∗
33,3 ms
K RI =

1
1
1,7 ms
13∗
33,3 ms
∗0,5∗
1
33,3 ms
∗
1,7 ms 5∗36,3
=0,0058
Eine Simulation des geschossenen Regelkreises muss nun zeigen, ob die gewählten
Reglerparameter die Kriterien des symmetrischen Optimum einhalten. Sind die Reglerparameter
korrekt gewählt, schwingt die Sprungantwort um 40% über.
© Mirko Grimberg
TFH – Berlin
Regelungstechnik
Seite 4 von 4
Abbildung 4:
Sprungantwort des
geschlossenen Regelkreises
Abbildung 4 zeigt deutlich, dass der Strom bei sprungförmiger Änderung der Führungsgröße
ca. 40% überschwingt.
Hinweis zur Lösung: Der Regler enthält noch keinerlei Strommaximalwertbegrenungen für den
Ankerkreis. Gibt man diesem Regler am Eingang einen Sollwert von 1
(normiert) vor, so wird er die Spannung am Ausgang des Stromrichters
380 V
=42 KA fließen. Sollte ein
so lange erhöhen bis im Ankerkreis
9m
Maximalwert für den Strom erkennbar sein, so empfiehlt es sich auf diesen
Strom zu normieren.
KA ergibt sich dann:
Ue
380V
∗Messwanderübersetzungsverhältnis
R
9 m ∗1160
=
Ankernennstrom
I A ;N
© Mirko Grimberg