(E1p) Prof. Joachim Rädler Lösung des 2. ¨Ubungsblattes v0

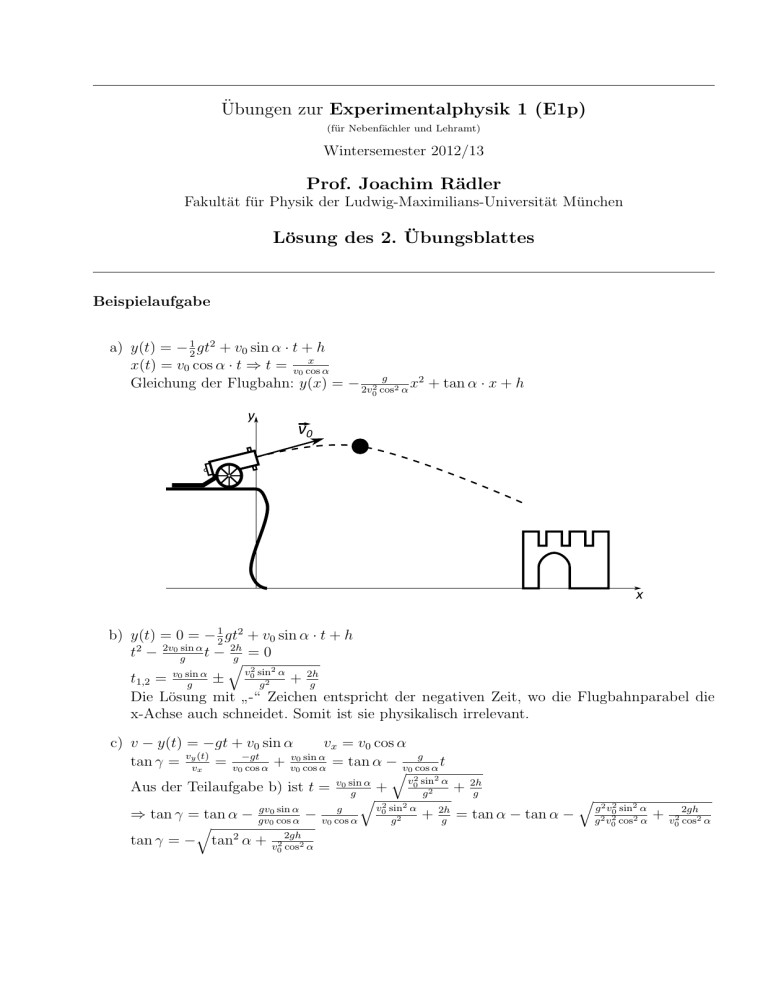
Übungen zur Experimentalphysik 1 (E1p)
(für Nebenfächler und Lehramt)
Wintersemester 2012/13
Prof. Joachim Rädler
Fakultät für Physik der Ludwig-Maximilians-Universität München
Lösung des 2. Übungsblattes
Beispielaufgabe
a) y(t) = − 12 gt2 + v0 sin α · t + h
x
x(t) = v0 cos α · t ⇒ t = v0 cos
α
g
2
Gleichung der Flugbahn: y(x) = − 2v2 cos
2 α x + tan α · x + h
0
y
v0
x
b) y(t) = 0 = − 12 gt2 + v0 sin α · t + h
t2 − 2v0 gsin α t − 2h
=0
g
q
v02 sin2 α
α
t1,2 = v0 sin
±
+ 2h
g
g2
g
Die Lösung mit -“ Zeichen entspricht der negativen Zeit, wo die Flugbahnparabel die
”
x-Achse auch schneidet. Somit ist sie physikalisch irrelevant.
c) v − y(t) = −gt + v0 sin α
vx = v0 cos α
vy (t)
g
−gt
v0 sin α
t
tan γ = vx = v0 cos α + v0 cos α = tan α − v0 cos
q 2 α2
v0 sin α
α
Aus der Teilaufgabe b) ist t = v0 sin
+
+ 2h
2
g
g
q 2 2 g
q 2 2 2
v
sin
α
g v0 sin α
gv0 sin α
g
2h
0
⇒ tan γ = tan α − gv
+
−
+
=
tan
α
−
tan
α
−
2
v0 cos α
g
g
g 2 v02 cos2 α
0 cos α
q
tan γ = − tan2 α + v2 2gh
cos2 α
0
2gh
v02 cos2 α
Aufgabe 1
v0 t
a) ~r(t) =
1 2
gt
2
Die x-Koordinate nach t umstellen und in y(t) einsetzen: y =
g
x2
2v02
Detektionsschirm
x
α
Lot
y
L
9,81 m
b) y = 2vg 2 x2 = 2·(9 ms2)2 · (0,2m)2 = 2,42mm
0
s
tan(α) = vvxy
v0
d~
r
~v = dt =
gt
9,81 m2 ·20cm
gt
gL
gL
s
⇒ tan(α) = v0 = v2 ⇒ α = arctan v2 = arctan
= 1,39◦
2
0
0
(9 ms )
q
q
9,81 m2 ·(20cm)2
gx2 x=L
s
=
= 62,6 ms
c) Aus der Bahngleichung folgt: v0 =
2y
2·50µm
Aufgabe 2
Die wirkenden Kräfte kann man umsortieren, wie es in der Abbildung gezeigt ist. Dabei gilt
F2
φ
F3
F1
F2
F3
φ´
φ
F1
φ′ = 180◦ − φ. Man wendet den Kosinussatz an:
2
2
2
F~3 = F~1 + F~2 − 2F~1 · F~2 cos(φ′ )
2
2
2
Außerdem gilt: F~3 = F~1 + F~2 mit Fi = mi g (einfach Zahlen einsetzen). Aus den beiden
letzten Gleichungen folgt, dass 2F~1 · F~2 cos(φ′ ) = 0 sein muss. ⇒ cos(φ′ ) = 0 ⇒ φ′ = 90◦ ⇒
φ = 180◦ − 90◦ = 90◦
Aufgabe 3
a) Als Parameter bietet sich die x-Koordinate an. Das Koordinatensystem wurde so gewählt,
dass die Parametrisierung möglichst einfach aussieht: y = kx2 mit x ∈ [0, d].
dy
Der Winkel α ist der gleiche wie Steigungswinkel der Bahnkurve. Es gilt also: tan α = dx
.
dy
FH = FG sin α = mg sin arctan dx = mg sin (arctan (2kx)) .
y
h
FN α
FH
FG
x
d
b) Epot (x = d) = Epot (x) + Ekin (x)
p
p
2
⇒ mgh = mgy + mv2 ⇒ v = 2g(h − y) = 2g(h − kx2 )