Prof. Dr. - Bildungsportal Sachsen
Werbung

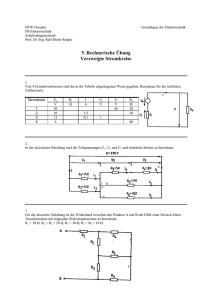
Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 26 Aufgaben 05etu520 5.8 Wechselstromleistung 5.8.01 Gegeben sind die komplexen Scheinleistungen. Berechnen Sie jeweils Wirk- und Blindleistung! a) b) c) d) S = 18kVA 35o S = 18kVA −40o S = 18kVA 55o S = 18kVA −75o 5.8.02 Der Leistungsfaktor eines Wechselstrommotors beträgt bei einer Wirkleistungsaufnahme von Pe.= 1.5kW bei verschiedenen Drehzahlen a) 0.89; c) 0.85; e) 0.75 b) 0.87; d) 0.82; Berechnen Sie die zugehörigen Stromstärken bei einer Netzspannung U = 230V! 5.8.03 An verschiedenen Drosselspulen werden Spannung, Strom und Wirkleistung gemessen. U/V 35 48 19 65 52 I/A 1.1 2.2 0.45 2.4 0.35 P/W 25 79.2 6.67 90.5 10.9 Berechnen Sie die jeweiligen Leistungsfaktoren! 5.8.04 An einer Stromschiene mit der Spannung U = 230V werden drei Wechselstrommotoren (I1 = 2.5A; cos ϕ1 = 0.65; I2 = 3.5A; cos ϕ2 = 0.85;I3 = 6.4A; cos ϕ3 = 0.81) betrieben. Berechnen Sie die Gesamtwerte von Wirkleistung, Blindleistung, Scheinleistung, cosϕ und Strom an der Sammelschiene! 5.8.05 Zwei Motoren entnehmen gemeinsam bei einem cos ϕ = 0.82 eineWirkleistung P = 4.8kW dem Netz. Motor 1 nimmt P1 = 1.5kW Wirkleistung bei einem cos ϕ1 = 0.75 auf. Berechnen Sie den Leistungsfaktor von Motor 2! 5.8.06 Berechnen Sie Wirk-, Blind- und komplexe Scheinleistung bei folgenden Reihenschaltungen an einer Spannung U = 230V; f = 50Hz! a) R = 12Ω; L = 0.03H b) R = 18Ω; L = 0.03H c) R = 200Ω; C = 8µF d) R = 150Ω; L = 0.5H; C = 5µF Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 27 Aufgaben 05etu520 5.8.07 Berechnen Sie die Kapazität C eines Kondensators bei f = 50Hz, der mit einem ohmschen Widerstand R = 300Ω in Reihe geschaltet einen Leistungsfaktor cos ϕ = 0.423 ergibt! 5.8.08 Berechnen Sie Blind- und komplexe Scheinleistung für einen Kondensator C = 0.1µF bei U = 230V und f = 50Hz! 5.8.09 Die Wirkleistung einer Spule (R2; L2) soll mit drei Spannungsmessungen bestimmt werden, indem der bekannte ohmsche Widerstand R1 mit der Spule in Reihe geschaltet wird (Drei-Voltmeter-Methode). Berechnen Sie die Wirkleistung aus den drei Spannungswerten! R2 R1 L2 U1 V V V U2 U 5.8.10 Mit der Drei-Voltmeter-Methode werden Drosselspulen untersucht und folgende Werte gemessen: R1/Ω 15 15 15 U/V 60 60 60 U1/V 24 22 18.3 U2/V 38.2 45.1 52.6 Berechnen Sie Wirkleistung und Leistungsfaktor der drei Spulen! 5.8.11 Mit drei Strommessungen wird die Leistungsaufnahme der Spule (R2; L2) bestimmt, indem der bekannte Widerstand R1 zur Spule parallelgeschaltet wird (Drei-AmperemeterMethode). Berechnen Sie die Wirkleistung der Spule aus den drei Strommessungen! R1 A I1 A U2 L2 A I2 I Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 28 Aufgaben 05etu520 5.8.12 An einer Stromschiene mit der Spannung U = 224V sind Glühlampen mit einer Gesamtstromaufnahme IL = 12.5A und ein Elektromotor, der einen Strom IM = 8.9A aufnimmt, angeschlossen. Der Gesamtstrom beträgt I = 20.6A. Berechnen Sie die Wirkleistungsaufnahme von Motor und Lampen sowie den Leistungsfaktor des Motors! 5.8.13 Zwei Lampen mit den Nennwerten 40W/110V sollen mit passenden Vorschaltwiderständen R v1,R v 2 versehen werden, um sie an der Spannung U = 220V; f = 16.7Hz zu betreiben. Zur Vermeidung von Helligkeitsschwankungen sollen die Stromzeiger I 1 und I 2 um −45o und +45o gegenüber der Netzspannung verschoben sein. a) Berechnen Sie die erforderlichen Werte R1; R2; L; C! b) Berechnen Sie die Wirkleistungsaufnahme der Anlage! c) Berechnen Sie den Gesamtstrom I! 5.8.14 Berechnen Sie die zu kompensierende Blindleistung, wenn bei einer Wirkleistung P = 4.8kW der Leistungsfaktor von 0.6 auf 0.8 erhöht werden soll! 5.8.15 Die Anzeige eines elektrodynamischen Messwerkes ist dem Produkt zweier Ströme II und IU proportional. Die Drehspule wird vom Strom II durchflossen (Stromspule) und hat den Widerstand RMI, der Strom IU baut in der Feldwicklung mit dem Widerstand RMU (Spannungsspule) das Luftspaltfeld des Messwerkes auf. RMU I U II RMI IU RV UB ZB Dimensionieren Sie das Messwerk und die Messschaltung, damit die Anzeige proportional der im Lastwiderstand ZB umgesetzten Wirkleistung P wird! Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 5.8.16 a) b) c) 29 Aufgaben 05etu520 Mit dem elektrodynamischen Messwerk kann auch Blindleistung gemessen werden, wenn durch eine geeignete Schaltung der Strom im Spannungspfad (Spannungsspule) eine Phasenverschiebung von 90o hat. Die Skizze zeigt die dafür geeignete Schaltung nach Hummel. RP RUM = 1kΩ (Spannungsspule) R1 = 200Ω IP R2 = 100Ω I L1 = 4.4H I2 L 2 = 2.2H U f = 50Hz ZB R1 + jXL1 R2 I1 jXL2 Dimensionieren Sie allgemein den Widerstand RP, damit der Strom I 2 gegenüber der Spannung U um 90o phasenverschoben ist! R1;L1 und R2; L2 sind die Werte der Reihenersatzschaltung der Spulen. Berechnen Sie RP für die gegebenen Werte, damit die Schaltung bestimmungsgemäß arbeitet! Zeichnen Sie für IP = 0.1A ein maßstäbliches Zeigerdiagramm der Spannungen und Ströme (mU = 25V/cm; mI = 20mA/cm)! 5.9 5.9.1 Drehstromkreise Schaltungsberechnung 5.9.1.01 An den Klemmen L2 und L3 eines symmetrischen Drehstromanschlusses wird die Spannung U = 370V gemessen. a) Bestimmen Sie die Spannung zwischen L1 und L2! b) Bestimmen Sie die Spannung zwischen L1 und N sowie zwischen L2 und N! 5.9.1.02 Die Strangspannung eines Drehstromgenerators beträgt Ustr = 125V. a) Berechnen Sie die Leiter-Leiter-Spannung bei Sternschaltung der Stränge! b) Berechnen Sie die Leiter-Leiter-Spannung bei Dreieckschaltung der Stränge! 5.9.1.03 Ein Heizofen kann sowohl in Stern- als auch in Dreieckschaltung der Stränge an ein 400-V-Drehstromnetz angeschlossen werden. Der Strangwiderstand beträgt R = 25Ω. Berechnen Sie den Leiterstrom bei beiden Schaltungsarten! Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 30 Aufgaben 05etu520 5.9.1.04 Zwei aus gleich großen Strangwiderständen in Sternschaltung geschaltete Heizöfen sind an ein Drehstromnetz angeschlossen. Berechnen Sie den Gesamtleiterstrom ILYY der angegebenen Schaltung und den Gesamtleiterstrom IL∆Y , wenn einer der beiden Öfen in Dreieckschaltung umgeschaltet wird! 5.9.1.05 Ein in Sternschaltung mit herausgeführtem Sternpunkt geschalteter Drehstromgenerator erzeugt eine Strangspannung Ustr = 225V. a) Berechnen Sie die Leiter-Leiter-Spannung des Generators! b) Berechnen Sie die Leiter-Neutralleiter-Spannung! 5.9.1.06 Drei gleichgroße ohmsche Strangwiderstände eines Drehstromgerätes sind in Sternschaltung geschaltet.Schließt man zunächst zwei und danach alle drei Leiter eines 400-V-Drehstromnetzes an, so nimmt der Leiterstrom um 1A zu. Berechnen Sie den Strangwiderstand Rstr ! 5.9.1.07 Schaltet man die 3 Strangwiderstände von je R = 15Ω eines Heizofens in Dreieck, so fließt der Leiterstrom IL = 43.88A. a) Berechnen Sie die dazu notwenige Spannung des Drehstromnetzes! b) Berechnen Sie den Leiterstrom bei Sternschaltung der Stränge! 5.9.1.08 Drei ohmsche Strangwiderstände von je R = 35Ω sind in Dreieckschaltung an ein 660V-Drehstromnetz geschaltet. a) Berechnen Sie den Leiterstrom! b) Berechnen Sie die Änderung des Leiterstromes, wenn eine der drei Zuleitungen abgeschaltet wird! 5.9.1.09 Drei gleich große Widerstände ergeben an einem 400-V-Drehstromnetz in Sternschaltung einen um 20A kleineren Leiterstrom als in Dreieckschaltung. 'Berechnen Sie den Wert R eines der Widerstände! 5.9.1.10 Legt man an die in Sternschaltung geschalteten Strangwiderstände eines Heizofens nur 2 der 3 Leiter eines Drehstromnetzes, zwischen dessen Leitern eine Spannung von 385 V gemessen wird, so fließt ein Leiterstrom von IL = 15.5A. Berechnen Sie den Leiterstrom beim Anschluss aller drei Leiter! 5.9.1.11 Drei in Dreieck geschaltete Kondensatoren von je C = 8µF werden an ein 380-V-Drehstromnetz bei f = 50Hz angeschlossen. Berechnen Sie Strang- und Leiterstrom! Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 31 Aufgaben 05etu520 5.9.1.12 Schließt man einen Kondensator C = 150µF an die Klemmen L1 und L2 eines Drehstromnetzes an, so ist der Strom 7.59A größer als beim Anschluss an die Klemmen L1 und N. Berechnen Sie die Spannung des Drehstromnetzes bei f = 50Hz! 5.9.1.13 150 Glühlampen mit den Nenndaten 220V/40W werden über eine Leitung von 300m Länge gespeist. Berechnen Sie die Gesamtmasse des notwenigen Kupfers, wenn der prozentuale Spannungsabfall der Leitung 3% der Spannung am Verbraucher betragen soll. Die Spannung am Speisepunkt soll so gewählt werden, dass am Verbraucher Nennspannung gewährleistet ist! a) Drehstromversorgung mit Sternschaltung der Lampen. Die Lampen werden in drei Stränge zu je 50 Lampen geschaltet. b) Drehstromversorgung bei Dreieckschaltung der Stränge c) Es liegt Gleichstromversorgung vor. 5.9.1.14 Zwei symmetrische 400V-Drehstromnetze sind nicht synchronisiert. Sie haben gleiche Frequenz, aber unterschiedliche Phasenlage. Die Spannungen des Netzes A eilen gleichartigen Spannungen des Netzes B um 35o voraus. Die Neutralleiter beider Netze haben gleiches Potenzial. a) Zeichnen Sie ein maßstäbliches Zeigerbild der Spannungen beider Netze! UL1NA = UL1NA 0o Hinweis: b) Zeichnen Sie die Zeiger U1AB ; U2AB ; U3AB , die jeweils zwischen zwei gleichartigen Leitern der Netze liegen, in das Zeigerbild ein! c) Berechnen Sie die Spannungen U1AB ; U2AB ; U3AB 5.9.2 Drehstromleistung 5.9.2.01 Berechnen Sie Wirk-, Blind- und Scheinleistung eines Drehstrommotors am 380-V-Netz bei IL = 16A und cos ϕ = 0.85! 5.9.2.02 Ein in Sternschaltung geschalteter Drehstromverbraucher hat die Strangspannung Ustr = 125 V. Die Leistungsaufnahme beträgt P = 17kW; cos ϕ = 0.65. Berechnen Sie den Leiterstrom! 5.9.2.03 An einem in Dreieckschaltung geschalteten Drehstromverbraucher werden in Strang gemessen: Ustr = 220V, Istr = 12.5A. Berechnen Sie die Leistungsaufnahme bei cos ϕ = 1! einem Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 32 Aufgaben 05etu520 5.9.2.04 Auf dem Leistungsschild eines Drehstrommotors befinden sich folgende Nennangaben: ∆ /Y 220/380V; 65.0/37.6 A; 19.5 kW; cos ϕ = 0.87. Berechnen Sie! a) Leistungsaufnahme bei Stern- und Dreieckschaltung b) Wirkungsgrad bei Nennbelastung! 5.9.2.05 Ein Drehstromverbraucher hat den Strangwiderstand R. Berechnen Sie für Stern- und Dreieckschaltung des Verbrauchers a) Leistungsaufnahme P = f (ULL)! b) Leistungsaufnahme P = f (IL)! 5.9.2.06 Berechnen Sie die Leistungsaufnahme eine Heizofens mit einem Strangwiderstand R = 30Ω am 380-V-Drehstromnetz a) bei Sternschaltung der Stränge! b) bei Dreieckschaltung der Stränge! 5.9.2.07 Unterbricht man eine Zuleitung zu einem in Sternschaltung geschalteten elektrischen Ofen, dessen Strangwiderstände je 10Ω betragen, so verringert sich die Leistungsaufnahme um 7.3kW. Berechnen Sie die Netzspannung! 5.9.2.08 Ein Drehstrommotor hat folgenden Nenndaten: UN = 380V; PN = 4kW; ηN = 0.81; cos ϕN = 0.82. Er wird über ein flexibles Kupferkabel von 250m Länge und einem Aderquerschnitt von 2.5mm2 angeschlossen. a) Berechnen Sie die Verlustleistung des Kabels, wenn der Motor im Nennbetrieb arbeiten soll! b) Geben Sie das Verhältnis Verlustleistung zu Motorleistung in Prozent an! c) Berechnen Sie die am Speisepunkt notwendige Netzspannung! 5.9.2.09 Für eine Drehstromleitung wird je 100 m Streckenlänge bei einer Höchstlast von 29.4kW eine Verlustleistung von 11% angegeben. a) Berechnen Sie die Verlustleistung in beiden Fällen! b) Berechnen Sie die prozentuale Verlustleistung bei einer Belastung von 18kW bei sonst gleichen Verhältnissen! 5.9.2.10 Ein Drehstromgenerator speist 3 Gruppen von Glühlampen, die in Dreieckschaltung geschaltet sind. Die Leitungslänge zwischen Generator und Glühlampen beträgt 500m, der Leiterquerschnitt A = 6mm2, das Leitermaterial ist Kupfer. Der Generator hat eine Klemmenspannung U = 230 V, der Leiterstrom beträgt 25 A. Berechnen Sie! a) Generatorleistung b) Spannungsabfall der Leitung c) Lampenspannung d) Verlustleistung der Leitung! e) Leitungsquerschnitt, damit der Spannungsabfall 3% der Lampennennspannung beträgt! Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 33 Aufgaben 05etu520 5.9.2.11 Berechnen Sie die Klemmenspannung eines Drehstromgenerators, der über eine 400m lange Kupferleitung mit d = 4mm Leiterdurchmesser eine Verbraucherleistung P = 15kW bei der Spannung U = 380V und einem cos ϕ = 0.75 speisen soll! 5.9.2.12 An eine Drehstromleitung Länge s = 500m und Leiterquerschnitt A = 50mm2 Kupfer sind angeschlossen: 1. Motor: 400V Dreieckschaltung; 3kW; η = 0.82; cos ϕ = 0.8 2. Motor: 400V Sternschaltung; 1.5kW; η = 0.75; cos ϕ = 0.75 3. 60 Glühlampen: 230V/75 W in drei Strängen zu 20 Lampen in Sternschaltung. a) Berechnen Sie die Ströme der drei Verbraucher, den Gesamtstrom sowie den cos ϕ! b) Berechnen Sie die notwendige Spannung am Speisepunkt (Transformatorstation), damit an den Verbrauchern die angegebenen Spannungen anliegen! 5.9.2.13 Ein in Dreieck geschalteter Durchlauferhitzer nimmt am 400V-Netz bei cosϕ = 1 die Wirkleistung 15kW auf. a) Berechnen Sie den Leiterstrom! b) Berechnen Sie den Strangwiderstand! c) Berechnen Sie die Leistungsaufnahme bei Sternschaltung der Stränge! 5.9.2.14 Ein Verbraucher mit drei gleichen komplexen Widerständen Z = 62Ω −25o in Dreieckschaltung ist an ein 400V-Drehstromnetz angeschlossen. a) Berechnen Sie den Leiter- und den Strangstrom! b) Berechnen Sie Wirk- und Blindleistung des Verbrauchers! 5.9.2.15 Ein Drehstrommotor mit dem Leistungsfaktor cosϕM = 0.70 hat am 400V-50HzDrehstromnetz den Leiterstrom IL = 7.7A. Der Leistungsfaktor soll durch Kondensatoren auf cosϕ = 0.95 erhöht werden. Berechnen Sie die Kapazität eines Kondensators, wenn die drei Kondensatoren a) in Sternschaltung; b) in Dreieckschaltung geschaltet werden und entscheiden Sie, welche der beiden Schaltungsarten zweckmäßiger ist! Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 5.10 34 Aufgaben 05etu520 Unsymmetrische Drehstromsysteme 5.10.01 Ein Drehstromnetz (ULL = 400V ; f = 50Hz) wird durch einen Motor belastet. Der Strangwiderstand des Motors beträgt Zstr = 10Ω 44o . Berechnen Sie für Stern- und Dreieckschaltung der Stränge a) die Leiterströme! b) die Leiterströme, wenn Leiter L1 unterbrochen wird ! 5.10.02 Gegeben ist nebenstehende Schaltung. ULL =400V R1 = 10Ω R2 = 20Ω R3 = 30Ω R4 = R5 = R6 = 50Ω L1 I1 R1 Bruchstelle R5 R4 L2 I2 R2 R6 L3 I3 R3 N a) b) Berechnen Sie die Leiterströme, wenn alle Verbraucher am Netz angeschlossen sind ! Berechnen Sie die Leiterströme I 1 , I 2 , I 3 , wenn der Leiter L2 an der gekennzeichneten Stelle unterbrochen ist . 5.10.03 Gegeben ist nebenstehende Schaltung. Z1 = 50Ω 0o Z2 = 25Ω 60o Z3 = 25 Ω −60o ULL = 400V f = 50Hz a) b) c) L1 L2 L3 N I1 Z1 I2 Z2 I3 Z3 IN Berechnen Sie die Leiterströme I 1 , I 2 , I 3 ! Berechnen Sie den Neutralleiterstrom I N Zeichnen Sie das Zeigerdiagramm der Ströme! 5.10.04 Berechnen Sie den im Neutralleiter fließenden Strom IN bei folgender unsymmetrischen Belastung eines Drehstromnetzes mit ULL = 400 V ;f = 50 Hz ! Strang 1: P1 = 3 kW cos ϕ1 = 0.866 ind. Strang 2: P2 = 2,5 kW cos ϕ2 = 0,707 kap. Strang 3: P3 = 2,5 kW cos ϕ3 = 1 Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 35 Aufgaben 05etu520 5.10.05 An einem Drehstromnetz ( ULL = 400V ) sind in Sternschaltung angeschlossen. 1. Heizofen, PH = 3 kW 2. 30 Glühlampen UN = 230V; PN = 60W in drei Gruppen zu 10 Lampen. a) Berechnen Sie die Leiterströme, wenn beide Verbraucher angeschlossen sind! b) Berechnen Sie die Leiterströme, wenn der Heizwiderstand im Strang 1 des Ofens abgeschaltet ist! 5.10.06 Gegeben ist nebenstehende Schaltung : ULL = 230V f = 50Hz R1 = 5Ω R2 = 10Ω R3 = 20Ω R4 = 5Ω R5 = 5Ω R6 = 10Ω C1 = 10 µ F C2 = 50 µ F L = 250mH L1 L2 L3 IL1 IL2 IL3 jXL R1 R2 R3 -jXc1 R4 -jXc2 R6 N a) b) Berechnen Sie die Leiterströme ! Berechnen Sie den Strom im Neutralleiter und dessen Phasenverschiebung zur Spannung UL1N ! 5.10.07 Gegeben ist nebenstehendes Drehstromsystem. Der Generator liefert ein symmetrisches Spannungssystem. Za = 110Ω −90o Zb = 110Ω 30o Zc = 110Ω −90o Uu = Uv = Uw = 230 V a) b) c) d) Uu L1 IL1 L2 IL2 UL1N Za Uv UL2N Zb Uw IL3 L3 N IN UL3N Zc Berechnen Sie alle Leiterströme und den Strom im Neutralleiter ! Zeichnen Sie das Zeigerbild aller Ströme und Spannungen am Verbraucher! Berechnen Sie die komplexe Scheinleistung der drei Stränge ! Berechnen Sie die im Verbraucher umgesetzte Wirkleistung! R5 Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 36 Aufgaben 05etu520 5.10.08 Für das skizzierte Drehstromsystem sind folgende Aufgaben durchzuführen: a) Berechnung der Zeiger aller Ströme und Spannungen b) Skizze des Zeigerbildes (mU = 40V/cm ; mI = 2A/cm ) c) Berechnung der komplexen Scheinleistung SL der Leitung d) Berechnung der komplexen Scheinleistung, der Wirk – und der Blindleistung des Verbrauchers UL1N = ZL1 = ZL 1 = Za = Zb = Zc = 230V 0o ZL2 = ZL3 (1+2j)Ω (24 – 2j)Ω (29 – 13j)Ω (24 – 32j)Ω N UL1N IL1 ZL1 Za UL2N IL2 ZL2 Zb UL3N IL3 ZL3 Zc E 5.10.09 Geben Sie den allgemeinen Lösungsweg für die Berechnung der Spannung UNE zwischen dem Sternpunkt N des Generators und dem Sternpunkt E des Verbrauchers der Aufgabe 5.10.08 an für den Fall, dass der Widerstand des Neutralleiters ZN ≠ 0! 5.10.10 Bestimmen Sie mit der 30°-Methode das Mit – und das Gegensystem für folgende Strangströme: a) I a = 0A; I b = − I c = 30A 0o b) I a = 10A 0o ; I b = 10.45A −134o ; I c = 8A 110o 5.10.11 Gegeben ist folgende Schaltung eines Drehstromsystems : a) Berechnen Sie die Sternpunktverlagerungsspannung UNE! b) Berechnen Sie I a; I b; I c ! c) Bestimmen Sie das Mit – und das Gegensystem! UL1N = 230V 0o UL2N = 230V −120o UL3N = 230V 120o Z1 = 100Ω 0o Z2 = 100Ω 45o Z3 = 100Ω −90o Z1 L1 UL1N UNE Ia Z2 L2 N E Ib UL2N UL3N L3 Ic Z3 Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 37 Aufgaben 05etu520 5.10.12 Lösen Sie folgende Aufgaben : a) b) c) d) gegeben : gesucht gegeben : gesucht gegeben : gesucht gegeben : gesucht: I a = 60A 30o ; I b = − j30A; I c = 30A 150o : Mit - , Gegen - , Nullsystem I a = I b = 0; I c = 30A : Mit - , Gegen - , Nullsystem I a = 0A; I b = − I c = 30A : Mit - , Gegen - , Nullsystem I a1= 10A; I c 2 = 20A 60o ; I b0 = 10A I a; I b; I c! 5.10.13 An einem 400V-Vierleiternetz sind drei Verbraucher in Sternschaltung angeschlossen (Sternpunkt ist mit N verbunden): am Leiter L1: Widerstand R = 18.4Ω, am Leiter L3: Einphasenmotor cos ϕ = 0.7 IL = 9A . Bestimmen Sie den notwendigen Widerstand Z2 am Leiter L2, damit der Sternpunktleiterstrom gleich Null wird! 5.10.14 Am Leiter L2 des 400V-Drehstromnetzes (f = 50Hz) ist kein Verbraucher angeschlossen. R1 = 60Ω R2 = 50Ω C = 80µF Bestimmen Sie: Leiterströme I L1; I L3! Strangspannungen Ua ; Ub ; Uc ! L1 L2 L3 I L1 R1 Ua I L3 1 Ub − j ωC Uc R2 5.10.15 An einem 400V-Dreileiternetz (kein N-Leiter) sind drei Verbraucher in Sternschaltung angeschlossen: Z1 = 22Ω 0o ; Z2 = 22Ω 60o ; Z3 = 100Ω −20o . Berechnen Sie die Strangspannungen, die Strangströme und Schein-, Wirk- und Blindleistung der Verbrauchergruppe! 5.10.16 An einem 400V-Dreileiternetz sind drei Verbraucher in Dreieckschaltung angeschlossen: Z12 = 20Ω 0o ; Z23 = 20Ω 60o ; Z31 = 50Ω −20o . Berechnen Sie die Leiterströme! Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 5.10.17 Der Widerstand R = 100Ω sowie die Kondensatoren Ca und Cb sollen am 400VDreileiternetz (f = 50Hz) eine Belastung ergeben, bei der symmetrische Leiterströme fließen. Berechnen Sie a) die Kondensatoren Ca und Cb! b) die Spannung UR! c) den Leiterstrom IL! 38 Aufgaben 05etu520 L1 I L1 −j L2 1 ωC a UR R I L2 −j I L3 1 ωCb L3 5.10.18 Die drei Heizplatten eines Elektroherdes werden von einem symmetrischen Drehstromsystem mit der Leiter-Neutralleiterspannung ULN = 230V gespeist. Infolge einer technischen Störung ist der Neutralleiter unterbrochen. Nennleistungen der Heizplatten: P1N = 500W ; P2N = 1000W ; P3N = 2000 W Berechnen Sie: a) Spannung UNE! b) Leistung der Heizplatten P1; P2; P3! 5.10.19 Ein Drehstromsystem mit der Spannung ULL = 400V wird mit der nebenstehenden Dreieckschaltung belastet. Infolge einer Störung fällt der Leiter L3 verbraucherseitig aus. R1 = 150Ω; R2 = 100Ω R3 = 50Ω XL1 = 200Ω XL3 = 400Ω XC = 200Ω a) b) Berechnen Sie die Leistungen PA und PB der Aron-Schaltung! Berechnen Sie mit den komplexen Scheinleistungen in den zwei Zweigen zwischen den Punkten a und b die Verbraucherleistung und vergleichen Sie das Ergebnis mit dem aus a)! R1 PA L1 UL1N P1 R2 PB L2 UL2N P2 R3 N L3 UL3N P3 UNE PA UL1N L1 I2 a I L1 R1 I1 PB UL 2N L2 E I L2 jXL1 R3 b UL3N L3 R2 − jXC jXL3 Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 5.10.20 Ein symmetrisches Drehstromsystem mit der Spannung ULL = 400V wird mit der nebenstehenden Dreieckschaltung belastet. R1 = 200Ω; XL = 60Ω a) b) c) R3 = 80Ω XC = 100Ω Berechnen Sie die Leistungen PA und PB der Aron-Schaltung! Berechnen Sie mit den komplexen Scheinleistungen in den drei Strängen der Dreieckschaltung die Verbraucherleistung! Zeichnen Sie das Zeigerbild der Leiter- und Strangströme! 5.10.21 Ein symmetrisches Drehstromsystem mit der Spannung ULL = 400V wird mit der nebenstehenden Verbraucherschaltung belastet. R1 = 300Ω R3 = 200Ω R2 = 100Ω XC1 = 300Ω XC2 = 100Ω XL = 200Ω Berechnen Sie die mit der Aron-Schaltung gemessene Leistung! 5.10.22 Ein symmetrisches Drehstromsystem mit der Spannung ULL = 400V wird mit der nebenstehenden Dreieckschaltung symmetrisch belastet. R = 120Ω a) b) c) XL = 90Ω Berechnen Sie: die Verbraucherleistung! die Verbraucherleistung, wenn durch eine Störung der Leiter L3 verbraucherseitig unterbrochen wird! für b) die komplexen Scheinleistungen der Generatorstränge! 39 Aufgaben 05etu520 PA UL1N L1 I L1 Ia R1 UL2N L2 L3 UL3N I L2 PB − jXC I L3 L1 jXL Ib I L1 Ia R1 UL2N L2 L3 UL3N UL1N jXL − jXC1 I L2 PB I b R2 I L3 L1 Ic R3 PA UL1N R3 − jXC2 I L1 Ic Ia R UL2N L2 I L2 jXL R Ib jXL L3 UL3N I L3 R jXL Ic Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 40 Aufgaben 5.10.23 Ein symmetrisches Drehstromsystem mit der Spannung ULL = 400V wird mit der nebenstehenden Dreieckschaltung unsymmetrisch belastet. Die Beträge der drei Lastwiderstände sind gleich groß. UL1N L1 I L1 Ia − jXC UL2N R = XL = XC = 100Ω L2 I L2 L3 Auf welchen Wert RX muss R geändert werden, damit die Leiterströme betragsgleich werden IL1 = IL2 = IL3 ? 5.11 05etu520 UL3N R Ib I L3 jXL Ic Schaltungen bei mehrfrequenter Erregung 5.11.01 An einem Tiefpass liegt am Eingang eine Spannung ue, die neben der Grundwelle auch die 5. und 7. Harmonische enthält ( ue = u1 + u5 + u7 ). Gegeben sind folgende Werte: f1 = 1 kHz; R = 10 kΩ; C = 0.1 µF; U1 = 10 V. Die Amplituden der Eingansspannung verhalten sich zueinander wie ˆ :U ˆ :U ˆ = 1: 1 : 1 U 1 5 7 5 7 Berechnen Sie die Amplituden der Grundschwingung und der Oberschwingungen in der Ausgangsspannung ua sowie deren Verhältnis zueinander! 5.11.02 An einem Einpulsgleichrichter erhält man folgende Ausgangsspannung: ˆ ⋅ cos ωt U u= 0 a) b) −π / 2 ≤ ωt ≤ π / 2 π / 2 ≤ ωt ≤ 3 π / 2 Û = 325V ; f = 50 Hz Skizzieren Sie den zeitlichen Verlauf der Spannung u! Führen Sie eine Fourieranalyse der Spannung u durch und berechnen Sie das Gleichglied sowie die Amplituden der Grundschwingung und der Oberschwingungen bis zur sechsfachen Frequenz der Grundschwingung! 5.11.03 Ein Widerstand R = 15Ω wird vom Strom i durchflossen. i = 1A + 0.25A ⋅ cos ωt + 25mA ⋅ cos(6ωt + π / 3) + 5mA ⋅ cos (10ωt + π / 5 ) Berechnen Sie: a) Spannungsabfall u c) Effektivwert der Spannung U e) Klirrfaktor k, Welligkeit w b) d) f = 50 Hz Effektivwert des Stromes I Wirkleistung P, Blindleistung Q Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 41 Aufgaben 05etu520 5.11.04 Gegeben ist eine periodische Folge rechteckiger Spannungsimpulse der Spannung U = 1V mit der Periodendauer To =20ms und der Breite τ = 0.2 ⋅ T0 nach folgender Funktion: b) c) U −T0 / 2 ≤ t ≤ −τ / 2 0 u = U 0 a) u −τ / 2 ≤ t ≤ +τ / 2 +τ / 2 ≤ t ≤ + T0 / 2 T − o 2 − τ 2 To To τ 2 t 2 Führen Sie eine Fourieranalyse der Funktion durch und bestimmen Sie das Gleichglied und die Oberschwingungen bis zur 15-fachen Frequenz der Grundschwingung! Die Spannung u ist Eingangsspannung eines R-C-Tiefpasses mit R = 100 kΩ und C = 16 nF: Berechnen Sie die Ausgangsspannung unter Verwendung des Ergebnisses der Fourieranalyse der Aufgabe a) Skizzieren Sie die Ausgangsspannung über eine Periode der Grundschwingung To! 5.11.05 Eine Mischspannung besteht aus einem Gleichspannungsanteil U = 5 V, dem eine sinusförmige Wechselspannung mit dem Effektivwert U1 = 1.41 V überlagert ist. a) Mit welcher Passschaltung kann erreicht werden, dass der Gleichspannungsanteil abgetrennt und nur der Wechselspannungsanteil übertragen wird. b) Bestimmen Sie die Grenzfrequenz des Passes, wenn die Ausgangsspannung bei der Frequenz f = 1 kHz 95 % der Eingangsspannung betragen soll! c) Berechnen Sie die Kapazität des Passes, wenn der Widerstand R = 2 kΩ beträgt! 5.11.06 In einer elektroakustischen Schaltung wird das Nutzsignal mit der Frequenz f1 durch ein Signal mit Netzfrequenz f2 gestört. Durch eine R-C-Hochpassschaltung soll das netzfrequente Signal gedämpft werden. Die Skizze zeigt die Ersatzschaltung des Problems. f1 = 10kHz f2 = 50Hz R = 100 kΩ C = 1.6nF u1 C R ua u2 a) b) Berechnen Sie für die beide Frequenzen die Übertragungsfunktionen GU0(ω1) und GU0(ω2)! Berechnen Sie die Verhältnisse Ua/Ue für beide Frequenzen! Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 42 Aufgaben 05etu520 5.11.07 Gegeben ist eine Folge von Spannungsimpulsen u(t) entsprechend Aufgabe 5.11.04 mit U = 10 V; To = 20 ms; τ = 0.2 ⋅ T0 a) b) Berechnen Sie den Effektivwert der Spannung u! Berechnen Sie den Scheitelwert einer sinusförmigen Wechselspannung gleicher Periodendauer und gleichen Effektivwertes! 5.11.08 Eine Spannungsschwingung mit der Periodendauer T = 10ms hat die Fourierkoeffizienten k uak in V ubk in V a) b) 1 4.5 0 2 3.2 1.8 3 2.4 0 4 1.3 -0.8 5 -0.6 -0.4 Bestimmen Sie Frequenzen und Nullphasenwinkel der Teilschwingungen! Zeichnen Sie die Zeitfunktion der Spannung über eine Periode! 5.11.09 Führen Sie eine Fourieranalyse nebenstehender zeitlich periodischer Spannung bis k = 7 durc h! u V 0.2 0.1 20 u V 40 60 80 −0.1 5.11.10 Eine Spannung mit U0 = 15V Gleichspannungsanteil hat folgende Fourierkoeffizienten: k uak in V ubk in V a) b) c) 1 7 4 2 6 -3 3 -3 -1 4 2 0 5 -1 0.5 6 0 0.3 Berechnen Sie Amplituden- und Phasenspektrum sowie die Effektivwerte der Teilschwingungen! Berechnen Sie die Leistung, die die Spannung an einem Widerstand R = 150Ω erzeugt! Bestimmen Sie den Klirrfaktor! t ms Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 5.11.11 An den Klemmen eines Zweipols wird der im Diagramm angegebene Spannungs- und Stromverlauf registriert. a) Formulieren Sie das Spektrum der Teilschwingungen für u und i bis k = 9! b) Bestimmen Sie Wirk-, Blind- und Scheinleistung des Zweipols! 5.11.12 Aus der sinusförmigen Netzspannung uN (230V; 50Hz) wird mittels einer Thyristorschaltung die Spannung u erzeugt, die beim Zündwinkel α der Netzspannung folgt. Berechnen Sie den Effektivwert der Spannung u aus der Fourierreihe für k ≤ 8 sowie durch Integration aus dem Spannungsverlauf! 43 Aufgaben i/ A 0.8 u/ V 100 05etu520 u i 0 0.2 0.1 0.3 −0.8 −100 u π 2π α = 50o 5.11.13 Ein ohmscher Verbraucher RB ist über eine Drosselspule mit der konstanten Induktivität L und dem Wicklungswiderstand Ran eine Zweiweg-GleichrichterSchaltung mit idealen Dioden angeschlossen. i Netzspannung U = 230V; f = 50Hz R L RB = 50Ω L RB L = 0.7H ; R = 2Ω u N a) b) t/s Berechnen Sie das Spektrum der Teilschwingungen für die Spannung u und den Strom i bis k ≤ 8 ! Berechnen Sie die Welligkeit mit und ohne Drosselspule! ωt Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 5.12 44 Aufgaben 05etu520 Vierpolschaltungen Halbglied T - Glied Z1 Z3 Z1 Z2 Z2 π − Glied X - Glied Z2 Z1 Z1 Z3 Z3 Z2 Z2 Z1 5.12.01 Berechnen Sie die Vierpol-Widerstands-Parameter der oben angegebenen Übertragungsglieder! 5.12.02 Berechnen Sie die Vierpol-Leitwert-Parameter der oben angegebenen Übertragungsglieder! 5.12.03 Berechnen Sie die Vierpol-Hybrid-Parameter der oben angegebenen Übertragungsglieder! 5.12.04 Berechnen Sie die Vierpol-Ketten-Parameter der oben angegebenen Übertragungsglieder! 5.12.05 Leiten Sie die Stern-Dreiecks-Umrechnungsbeziehungen von Widerständen unter Verwendung der Widerstands- und Leitwertparameter eines T- und eines π-Gliedes ab! 5.12.06 An einem Vierpol werden folgende Ströme und Spannungen gemessen: Kurzschluss am Ausgangs: Leerlauf am Eingang: U1 = 1 V; I1 = 0.8 A; I2 = −0.12A ; U1 = 0.3 V; U2 = 2 V; I2 = 1.66 A Berechnen Sie die Hybrid-Parameter des Vierpols! Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 45 Aufgaben 05etu520 5.12.07 Ein Einphasentransformator hat auf dem Leistungsschild folgende Angaben für den Nennbetrieb: SN = 167 kVA; U1N = 5.77 kV; f = 50 Hz Messungen am Prüfstand ergaben: Leerlauf: U1 = 5770V; I1 = 1.14A; U2’ = 5770V; P1 = 669W Kurzschluss: U1 = 231V; I1 = 28.94A; I2’ = 28.94A; P1 = 4000W Berechnen Sie die Vierpol-Widerstands-Parameter des Transformators! 5.12.08 Berechnen Sie die Übertragungsfunktion der Phasenkette (Aufgabe 5.7.2.12) mittels Vierpolkettenparameter! 5.12.09 Bestimmen Sie die Leitwert-Parameter eines R-C-Hochpasses mit R = 1 kΩ; C = 10 nF; ω = 104 s-1 ! 5.12.10 a) Bestimmen Sie die Ketten-Parameter der Kettenschaltung eines T- und eines π-Gliedes! b) Wenden Sie das Ergebnis auf eine aus drei R-C-Gliedern bestehende Phasenschieberkette an und bestimmen Sie deren Spannungsübertragungim Leerlauf! 5.12.11 Durch die Parallelschaltung eines Transistors mit einem Widerstand ZK entsteht für den Transistor-Vierpol eine Spannungs-Parallel-Gegenkopplung. H11 H21 H12 H22 Bestimmen Sie die Y- und die H-Parameter der Gesamtschaltung! ZK = 100 kΩ; H11 = 1 kΩ; H12 = 5 ⋅ 10-4; H21 = 50; H22 = 100 µS 5.12.12. Ermitteln Sie für nebenstehendes T-Glied Z1 = 50Ω; Z2 = 40Ω; Z3 = 80Ω a) Leerlauf-Eingangs- und Ausgangswiderstand b) Kurzschluss-Eingangs- und Ausgangswiderstand c) Eingangs- und Ausgangs-Wellenwiderstand d) Vierpol-Wellenwiderstand ZK Z1 Z3 Z2 Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 46 Aufgaben 05etu520 5.12.13. Ermitteln Sie für nebenstehendes T-Glied Z1 = 10Ω; Z2 = 50Ω; Z3 = 25Ω a) Leerlauf-Eingangs- und Ausgangswiderstand b) Kurzschluss-Eingangs- und Ausgangswiderstand c) Eingangs- und Ausgangs-Wellenwiderstand d) Vierpol-Wellenwiderstand Z2 Z1 Z3 5.12.14 Drei gleiche Widerstände bilden ein T-Glied. Bestimmen Sie den Wert eines der Widerstände, wenn der Wellenwiderstand des Gliedes ZL = 75Ω betragen soll! 5.12.15 Drei gleiche Widerstände bilden ein π -Glied. Bestimmen Sie den Wert eines der Widerstände, wenn der Wellenwiderstand des Gliedes ZL = 75Ω betragen soll! 5.12.16 Berechnen Sie für das nebenstehende T-Glied: Z1 = Z3 = 2kΩ Z2 = 4kΩ Spannungsübertragungsfaktor für ZB = 2kΩ Spannungsübertragungsfaktor für Leerlauf Stromübertragungsfaktor für ZB = 2kΩ a) unter Verwendung der Vierpolparameter b) mit Methoden der Stromkreisberechnung Z1 Z3 5.12.17 Bestimmen Sie für nebenstehenden Tiefpass a) b) c) d) ZB Z2 R Z - Matrix Leerlaufspannungsübertragungsfaktor Grenzfrequenz GuL = f(ω / ωg ) und ϕL = f ( ω / ωg ) für C ω / ωg = 0; 0.5; 1; 1.5; 2; 3; 4; 5; 10 e) ωg ; GuL ; ϕL mit R = 100kΩ; C = 1nF für f1 = 800Hz und f2 = 8kHz 5.12.18 a) Bestimmen Sie für den belasteten Tiefpass Gu = f(ω / ωg ) und ϕ = f ( ω / ωg ) b) Untersuchen Sie den Einfluss von RB auf ωg ; Gu ; ϕ c) Bestimmen Sie ωg ; Gu ; ϕ mit R = 100kΩ; C = 1nF; RB = 100kΩ für f1 = 800Hz und f2 = 8kHz R −j 1 ωC RB Prof. Dr.-Ing. Herzig Übung Grundlagen der Elektrotechnik 47 Aufgaben 5.12.19 Bestimmen Sie für nebenstehenden Vierpol: a) Y - Matrix b) GuL und GuL c) Frequenz ω0 , bei der GuL seinen Maximalwert hat d) GuL = f ( ω / ω0 ) für e) 05etu520 R1 U1 −j 1 ωC1 1 −j ωC 2 R2 ω / ω0 = 0.25; 0.5; 1; 1.5; 2; 2.5; 5 mit R1 = R2 = R und C1 = C2 = C ϕL bei ω0 5.12.20 Bestimmen Sie mit Hilfe der Vierpolmatrix GuL und GuL a) R1 U1 1 −j ωC b) R1 R2 U1 U2 c) −j 1 ωC R2 U2 d) R U1 jωL j ωL 1 −j ωC U2 U1 −j 1 ωC R U2 5.12.21 Berechnen Sie die Übertragungsfunktion des Bandpasses (Aufgabe 5.7.2.01) mittels Vierpolkettenparameter! 5.12.22 Aus welchen Einzelwiderständen Z1; Z2; Z3 ist ein T-Glied aufgebaut, wenn folgende Vierpol-Parameter gemessen werden? Z11 = 90 Ω; Z12 = 75 Ω; Z21 = 75 Ω; Z22 = 90 Ω U2