Niedertemperatur- Wärmekraftmaschine mit Gasströmungs

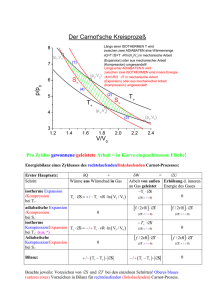
Bild 1
Skizze der vorgeschlagenen Niedertemperatur-Wärmekraftmaschine (oben rechts das pV-Diagramm
des Carnot-Kreisprozesses; angeschrieben die bei den jeweiligen
Einzelprozessen konstant bleibenden Größen). Eingangsstutzen Eu
von Rohrabschnitt Wu und Ausgangsstutzen Eo von Wo zu groß
dargestellt. Wellenförmige Zeichen: Wärmebad; strichförmige
Zeichen: Isolation. Die Doppelpfeile symbolisieren qualitativ mit ihrer
Länge die Gasgeschwindigkeit und
mit ihrer Breite die Gasdichte.
NiedertemperaturWärmekraftmaschine mit
Gasströmungs-Wärmewandler
WÄRMEKRAFTMASCHINE | In dem vorliegenden Beitrag wird eine
neuartige Wärmekraftmaschine vorgeschlagen, die für alle Temperaturen geeignet ist; ihre hervorstechendste Eigenschaft ist jedoch, den
thermodynamisch möglichen Bereich weitgehend auszuschöpfen und
so auch bei niedrigen Temperaturen und geringen Temperaturdifferenzen effektiv und effizient zu arbeiten. Kreisprozess ist der CarnotProzess, Arbeitsmittel ist Gas. Die nötigen Druck- und Temperaturdifferenzen werden durch Gasströmung in einem Rohr hervorgerufen,
dessen Querschnitt und Ummantelung längs der Strömungsrichtung
variieren. Die Wärme wird vorzugsweise von außen zugeführt; Zufuhr
durch innere Verbrennung ist gleichfalls möglich.
Autor
Prof. Dr. Herbert Daniel, Jahrgang 1926,
Studium der Physik an der Universität Heidelberg; Promotion 1954 und Habilitation
1961 ebd.; 1954 bis 1958 Max-Planck-Institut f. Medizinische Forschung, Heidelberg; 1958/59 Iowa State University, Ames,
Iowa, USA; 1959 bis 1965 Max-Planck-Institut f. Kernphysik, Heidelberg; 1966 bis
1968 Cern, Genf, Schweiz; 1968 bis 1994
1
o. Professor und Direktor des Instituts f.
Kernphysik und Nukleare Festkörperphysik
der Technischen Universität München.
i
[email protected].
Danksagung: Herrn PD Dr. F. J. Hartmann
danke ich für Durchsicht und Unterstützung und Prof. S. Paul für sein kollegiales
Interesse.
U
m effektiv und effizient arbeiten
zu können, benötigen Wärmekraftmaschinen, gleich welchen Typs, nach dem zweiten Hauptsatz
eine relativ große Temperaturdifferenz
DT zwischen der Temperatur To der zugeführten Wärme (Speisewärme) Qo und
der Temperatur Tu der abgeführten Wärme (Abwärme) Qu; der maximale Wert
des Wirkungsgrades h ist durch den Carnot-Wert hC gegeben:
η ≤ ηC = ( To − Tu ) / To = ∆T / To .
(1)
Bei den geläufigen Typen ist h für kleine Werte von hC noch erheblich kleiner
als hC. Zudem ist für viele Typen ein hoher Wert von To erforderlich, häufig für
Maschinen mit Phasenumwandlung des
Arbeitsmittels. Andererseits stehen große Mengen Qo an Speisewärme verhältnismäßig niedriger Temperatur To höher
als die Umgebungstemperatur Te zur
Verfügung. Sie lassen sich zum Beispiel
leicht aus der Sonneneinstrahlung gewinnen, auch bei bedecktem Himmel,
BWK Bd. 65 (2013) Nr. 3
Wärmekraftmaschine
wo keine Konzentration durch Spiegel
und ähnliches möglich ist. Te entspricht
in etwa Tu.
Konventionelle Wärmekraftmaschinen mit von außen zugeführter Speisewärme und nach außen abgeführter Abwärme sind nur sehr beschränkt in der
Lage, den Carnot-Prozess ungefähr darzustellen. Es sind hauptsächlich die isothermen Prozesse, die Schwierigkeiten
bereiten. Zum Wärmeaustausch bei geringer Temperaturdifferenz zwischen Arbeitsmittel und wärmeaufnehmendem
bzw. -abgebendem Medium, zum Beispiel einem Reservoir der Temperatur To
bzw. einem Reservoir der Temperatur Tu
oder der Umgebung mit der Temperatur
Te, sind große Austauschflächen notwendig; aus konstruktiven Gründen
kann ein Zylinder einer Dampfmaschine
oder eines Stirling-Motors kann keine
große Oberfläche besitzen.
Im Folgenden wird eine neuartige
Wärmekraftmaschine
vorgeschlagen.
Das Wesentliche ist ein neuartiger Gasströmungs-Wärmewandler, dessen technische Basis die Strömungsmechanik eines Gases in einem Rohr mit Änderung
von Querschnitt und Ummantelung
längs der Strömungsrichtung ist. Diese
Mechanik wird durch die Bernoulli-Gleichung für kompressible Fluide beschrieben; der Einfachheit der Beschreibung
halber wird das Gas als ideal angenommen, obgleich das keine notwendige Bedingung für das Arbeiten der Maschine
ist. Kreisprozess ist der Carnot-Prozess;
die Arbeitsweise ist stationär. Der Gasströmungs-Wärmewandler beruht auf
folgendem Sachverhalt, der im Kapitel
„Allgemeine quantitative Behandlung“
ausführlich behandelt wird: Wird Gas
mit einer gewissen Anfangsgeschwindigkeit in ein Rohr eingelassen, dessen
Querschnitt sich im Verlauf erweitert, so
wird die Strömung abgebremst. Dadurch
erhöht sich der statische Druck, und es
entsteht Kompressionswärme. Speziell
bei einem isothermen Prozess wird diese
Wärme bei gleichzeitiger Druckerhöhung von einem Wärmebad aufgenommen, und speziell bei einem adiabatischen Prozess verbleibt sie im Gas und
führt zu stärkerer Druckerhöhung bei
gleichzeitiger Erwärmung. Verläuft die
Strömung in umgekehrter Richtung,
kehren sich die Effekte entsprechend
um. Die Details dieser Arbeit sind auf eine
Niedertemperatur-Wärmekraftmaschine zugeschnitten. Die Wärmekraftmaschine arbeitet aber bei allen
BWK Bd. 65 (2013) Nr. 3
technisch beherrschbaren Temperaturen, nicht nur niedrigen. Ihre hervorstechende Eigenschaft ist jedoch, dass sie
auch bei niedrigen Temperaturen und
geringer Temperaturdifferenz arbeitet.
Beschreibung
Bild 1 zeigt die vorgeschlagene Niedertemperatur-Wärmekraftmaschine. Sie
besteht vor allem aus einem Wandelrohr W, einem Rückführrohr Z, einer Turbine M und einem Fan F. W ist in drei Abschnitte Wu, Wa und Wo gegliedert. Wu
und Wa erweitern sich in Strömungsrichtung, Wo verengt sich; es mündet in
die Turbine M, die sowohl die kinetische
als auch die thermische Energie des Gases ausnutzt. Vom Turbinenausgang
wird das Gas über Z in Wu geführt, an
dessen Anfang auch der Fan steht (andere Positionen sind möglich, ebenso die
Aufstellung mehrerer Fans an unterschiedlichen Positionen oder die Ausnutzung der Strömung aus der Turbine M
bei entsprechender Turbinenkonstruktion). Die Abschnitte haben die folgenden
Querschnitte am Eingang (zweites Subskript „e“) bzw. am Ausgang (zweites
Subskript „a“) bei Wu, Wa und Wo: Aue,
Aua, Aae, Aaa, Aoe bzw. Aoa. Wu ist in Kontakt mit einem Wärmebad der Temperatur Tu, Wo mit einem Wärmebad der
Temperatur To. Wa ist gegen Wärmeübergang isoliert. Das Arbeitsmittel ist Gas,
der Kreisprozess ist der Carnot-Prozess,
und die Einzelprozesse folgen ohne zeitliche Gliederung aufeinander (ohne Takte).
Die Arbeitsweise ist wie folgt: Der Fan
F erzeugt im Rohr W einen Gasstrom dn/
dt, wobei n die Menge bedeutet. Der jeweilige Prozess in Wu und Wo verläuft
isotherm bei der unteren Temperatur Tu
bzw. der oberen Temperatur To des Carnot-Prozesses sowie adiabatisch in Wa
und M. Die Maschine kann auch als
Durchlaufmaschine gebaut werden (ohne Z), zum Beispiel mit aus der Umgebung entnommener und in die Umgebung abgeführter Luft. Sie kann ferner
als Maschine mit innerer Verbrennung
gebaut werden, dann natürlich nicht als
Niedertemperatur-Wärmekraftmaschine.
Allgemeine quantitative
Behandlung
Die Lösung der Bernoulli-Gleichung
kompressibler Fluide [1] lässt sich im
allgemeinen Fall nicht in geschlossener
Form angeben. Um für das hier zu behandelnde Problem eine einfache Lösung in geschlossener Form zu finden,
behandeln wir die Strömung als laminar; die Reibung wird vernachlässigt.
Wir legen den Energiesatz, die Kontinuitätsgleichung und die Zustandsgleichung des Gases zugrunde. Wir betrachten eine gewisse Menge n des Gases mit
der Masse m. Menge und Masse sind
durch
m = Mt n
(2)
verknüpft, wobei Mt die molare Masse
ist. Das Gas ströme durch die zum Gasstrom senkrechte Querschnittsfläche Ae
in den Rohrabschnitt Wx ein und durch
die ebenfalls zum Gasstrom senkrechte
Querschnittsfläche Aa wieder aus. Der
Energiesatz erfordert
m2e / 2 = mνa2 / 2 + paVa − pe − Ve − Q p
(3)
wobei ne die Eintritts- und na die Austrittsgeschwindigkeit bedeuten; pa und
Va sind Druck bzw. Volumen von n bei
Austritt sowie pe und Ve Druck bzw. Volumen bei Eintritt, und Qp ist die dem Gas
zugeführte Wärme. Die Kontinuitätsgleichung schreibt sich mit
d2n / dt2 = d2m / dt2 = 0,
(4)
Ae ρe νe = Aa ρa νa ,
(5)
wobei pe und pa die Dichte bei Ein- bzw.
Austritt ist. Die Zustandsgleichung für
das Arbeitsmittel, das im in Frage kommenden Temperaturbereich als ideales
Gas behandelt werden soll, ist die allgemeine Gasgleichung
pV = nRT,
(6)
wobei R die allgemeine Gaskonstante
bedeutet. Für adiabatische Prozesse gilt
ferner
pV γ = p0 V0γ = konst.,
(7)
wobei g das Verhältnis der molaren Wärmekapazitäten bei konstantem Druck
und konstantem Volumen bedeutet; das
Subskript 0 kennzeichnet feste Anfangswerte.
2
Wärmekraftmaschine
Isotherme Prozesse
Aus den Gleichungen (2), (3), (5) und (6) ergibt sich für die isothermen Prozesse
(
)
ν2e = 2Q p / Mt Ae2 pe2 / Aa2 pa2 − 1  .


(8)
Diskussion
Beim idealen Gas gilt für die Wärme Qp, die hier für die isotherme Verdrängungsarbeit gebraucht wird,
Q p = −nRT ln ( pe / pa ) .
(9)
Aus den Gleichungen (8) und (9) errechnet man für ein vorgegebenes Druckverhältnis pe/pa
(
)
ν2e = 2RT ln ( pe / pa ) / Mt 1 − pe2 Ae2 / pa2 Aa2  .


(10)
Daraus ergibt sich die Beziehung zwischen Eingangsquerschnitt Ae und Ausgangsquerschnitt Aa zu
(
)
Ae2 / Aa2 = pa2 / pe2 1 − 2RT ln ( pe / pa ) / Mt ν2e  .


(11)
Adiabatische Prozesse
Beim adiabatischen Prozess ist Qp Null. An die Stelle von
Gleichung (10) und (11) treten
(
))
(
ν2e = 2R ( Ta − Te ) / Mt 1 − Ae2Va2Te2 / Aa2Ve2Ta2 


(12)
bzw.
( (
> nae: die Austrittsgeschwindigkeit nua aus dem Abschnitt Wu,
> noa: die Austrittsgeschwindigkeit naa aus dem Rohrabschnitt
Wa.
Die Austrittsgeschwindigkeiten sind durch Gleichung (5) mit
den entsprechenden Eintrittsgeschwindigkeiten verknüpft.
Ae2 / Aa2 = Ta2Ve2 / Te2Va2 1 − 2R / Mt ν2e

))(T
a
− Te )  .

Die Maschine hat einen hohen Wirkungsgrad h; es kann ein
Wert nahe dem Carnot-Wert hC erwartet werden: Der Wärmeübergang bei den isothermen Prozessen ist effizient, weil er
jeweils über großflächige Wände vonstatten geht. Das ist technisch umso leichter zu realisieren, als sich, im Gegensatz zu
bestehenden Maschinen, diese Wände alle in Ruhe befinden.
Überdies können jeweils mehrere Rohre W parallel gelegt werden. Ebenso kann eine hohe Leistung erwartet werden, weil der
Kreisprozess nicht aus Effektivitätsgründen langsam ablaufen
muss. Die beweglichen Teile sind leicht, und es gibt (im Gegensatz zu Kolben) keine Unwucht. Die Verluste bei den mechanischen Teilen (Fan und Turbine) sind verhältnismäßig gering.
Die vorgeschlagene Wärmekraftmaschine ist infolge der
Wärmewandlung durch Gasströmung äußerst einfach im Aufbau, robust und sehr günstig in der Herstellung; auf den Fan F
kann verzichtet werden, wenn man das Gas aus der Turbine M
mit der gemäß Gleichung (10) bis (13) benötigten Geschwindigkeit ausströmen lässt. Mikroanlagen sind nicht notwendig
starr; als Rohr W kann zum Beispiel ein Schlauch dienen. Ein
zusammenlegbares tragbares Gerät („Portable“) kann auf Reisen mitgenommen werden. In Verbindung mit der in [2] beschriebenen Wärmezu- bzw. -abfuhr durch Heat Pipes sowie
der Kurzzeit-Speicherung nutzt die hier beschriebene Wärmekraftmaschine regenerative Energie effektiv und effizient
aus, zum Beispiel über den Temperaturwechsel im Verlauf eines Tages.
Es liegt auf der Hand, den vorgeschlagenen GasströmungsWärmewandler auch als Teil von Wärmepumpen und Kühlaggregaten sowie in der Raumklimatisierung zu verwenden.
(13)
Literatur
Der entsprechende Druck beim Austritt ist
pa = pa ( Va / Ve ) .
γ
(14)
[1] Shaughnessy, E. J.; Katz, I. M.; Schaffer, J. P.: Introduction to fluid mechanics. Oxford
University Press, New York, Oxford, 2005, pp. 474 ff.
[2] Daniel, H.: Aggregat zur effektiven und effizienten Nutzung kleinerer Temperaturdifferenzen. HLH (2003), Nr. 9, S. 67–69.
Die Eintrittsgeschwindigkeiten sind die folgenden:
> nue: die vom Fan F erzeugte Geschwindigkeit,
3
BWK Bd. 65 (2013) Nr. 3