Carnot`scher Kreisprozess

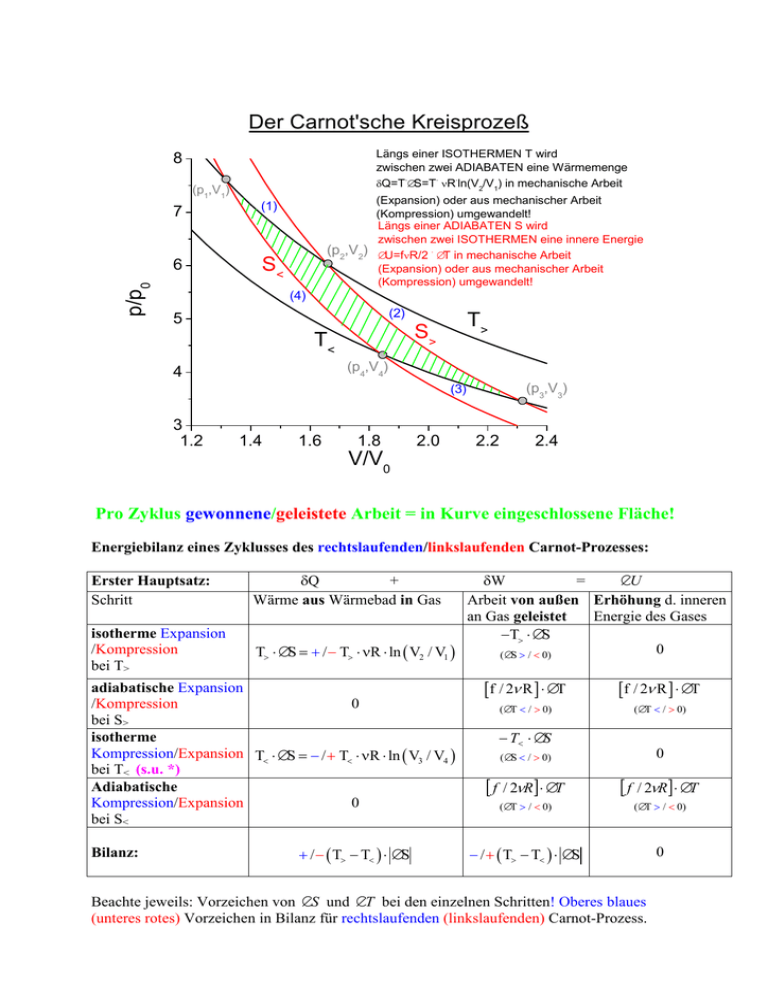
Der Carnot'sche Kreisprozeß
Längs einer ISOTHERMEN T wird
zwischen zwei ADIABATEN eine Wärmemenge
.
.
.
δQ=T ∆S=T νR ln(V2/V1) in mechanische Arbeit
8
(p1,V1)
7
p/p0
6
(1)
(p2,V2)
S<
(Expansion) oder aus mechanischer Arbeit
(Kompression) umgewandelt!
Längs einer ADIABATEN S wird
zwischen zwei ISOTHERMEN eine innere Energie
.
∆U=fνR/2 ∆T in mechanische Arbeit
(Expansion) oder aus mechanischer Arbeit
(Kompression) umgewandelt!
(4)
(2)
5
T>
S>
T<
(p4,V4)
4
(p3,V3)
(3)
3
1.2
1.4
1.6
1.8
2.0
2.2
2.4
V/V0
Pro Zyklus gewonnene/geleistete Arbeit = in Kurve eingeschlossene Fläche!
Energiebilanz eines Zyklusses des rechtslaufenden/linkslaufenden Carnot-Prozesses:
Erster Hauptsatz:
Schritt
δQ
+
Wärme aus Wärmebad in Gas
isotherme Expansion
/Kompression
bei T>
T> ⋅ ∆S = + / − T> ⋅ νR ⋅ ln ( V2 / V1 )
adiabatische Expansion
/Kompression
0
bei S>
isotherme
Kompression/Expansion T< ⋅ ∆S = − / + T< ⋅ νR ⋅ ln ( V3 / V4 )
bei T< (s.u. *)
Adiabatische
Kompression/Expansion
0
bei S<
Bilanz:
+ / − ( T> − T< ) ⋅ ∆S
δW
=
∆U
Arbeit von außen Erhöhung d. inneren
an Gas geleistet
Energie des Gases
−T> ⋅ ∆S
0
( ∆S > / < 0)
[f / 2ν R ] ⋅ ∆T
[f / 2ν R ] ⋅ ∆T
( ∆T < / > 0)
( ∆T < / > 0)
− T< ⋅ ∆S
( ∆S < / > 0)
0
[ f / 2νR] ⋅ ∆T
[ f / 2νR] ⋅ ∆T
( ∆T > / < 0)
( ∆T > / < 0)
− / + ( T> − T< ) ⋅ ∆S
0
Beachte jeweils: Vorzeichen von ∆S und ∆T bei den einzelnen Schritten! Oberes blaues
(unteres rotes) Vorzeichen in Bilanz für rechtslaufenden (linkslaufenden) Carnot-Prozess.
Ideale Wärmekraftmaschine = rechtslaufender Carnot-Prozeß (1)→
→ (2)→
→(3)→
→(4):
T>
Q>
W
Q<
T<
δQ< nicht nutzbar; deswegen ‚ökonomische’ Energiebilanz pro Zyklus:
Netto gewonnene Arbeit (Adiabaten kompensieren sich): δW = ∆S ⋅ ( T> − T< )
Bei T> aufgenommene Wärme:
δ Q > = T> ⋅ ∆S
(Bei T< wieder abgegebene Wärme: (irrelevant für η)
δ Q< = T< ⋅ ∆S )
Ökonomische Bilanz, Wirkungsgrad η (‚Nutzen/Preis’)
η=
T> − T<
T>
stets <1
Ideale Wärmepumpe = linkslaufender Carnot-Prozeß (3)→
→(2)→
→(1)→
→(4):
T>
Q>
W
Q<
T<
δQ< ist umsonst, deswegen ‚ökonomische’ Energiebilanz pro Zyklus:
Netto geleistete Arbeit (Adiabaten kompensieren sich):
δW = ∆S ⋅ ( T> − T< )
(Bei T< aufgenommene Wärme : (irrelevant für η):
δ Q > = T> ⋅ ∆S
Bei T> wieder abgegebene Wärme
δ Q< = T< ⋅ ∆S
Bilanz, Wirkungsgrad η (‚Nutzen/Preis’)
η=
T>
T> − T<
stets >1
Zweiter Hauptsatz der Thermodynamik und ‚perpetuum mobile zweiter Art’
Betrachte:
Hintereinanderschaltung von Carnot’scher Wärmekraftmaschine und
Carnot’scher Wärmepumpe mit gleichen Wärmebädern:
T>
T>
Q>
Q>
W W
Q<
Q<
T<
T<
Nettoresultat: kein Wärmefluß, keine Arbeit!
ABER:
Betrachte:
Hintereinanderschaltung von hypothetischer Wärmekraftmaschine mit
höherem Wirkungsgrad als dem der Carnot’schen und Carnot’scher
Wärmepumpe, wieder mit gleichen Wärmebädern:
T>
T>
Q>
T>
Q>
W
+ Wextra
Q<
Q>
W
W
Wextra
Q<
T<
Q<
T<
T<
Nettoresultat: Maschine, die lediglich durch Wärmeentnahme aus einem Wärmebad
Arbeit leistet = ‚perpetuum mobile zweiter Art’
Zweiter Hauptsatz der Wärmelehre:
Ein ‚perpetuum mobile zweiter Art’ kann nicht realisiert werden!
Oder auch:
Keine Wärmekraftmaschine kann einen höheren Wirkungsgrad als den Carnot’schen haben!
* Ergänzung zum Carnot-Prozess:
Streng genommen muss noch gezeigt werden, dass längs beider Isothermen tatsächlich
ln ( V2 / V1 ) = ln ( V3 / V4 ) ist und damit ∆S1−> 2 = −∆S3 −> 4 . Das ist äquivalent mit dem Beweis
dafür, dass die Entropie sich in einem Kreisprozess nicht ändert, also eine Zustandsgröße ist:
Da die Zustandsänderungen 2 3 und 4 1 adiabatisch sind, gilt jeweils die
Adiabatengleichung (s.o.):
p 2 V2 γ = p3 V3 γ
und
p1V1γ = p 4 V4 γ ;
Kombiniere mit Gasgleichung:
p 2 V2 p 3 V3
=
T>
T<
und
p1V1 p 4 V4
=
;
T>
T<
Dividiere beide Zeilen termweise:
T> V2 γ−1 = T< V3 γ−1
und
T> V1γ−1 = T< V4 γ−1 ;
Dividiere links durch rechts:
 V2 
 
 V1 
γ−1
γ−1
V 
= 3 
;
Bilde Logarithmus auf beiden Seiten
 V4 
V 
V 
ln ( V2 / V1 ) = ln ( V3 / V4 )
wie verlangt.
( γ − 1) ln  2  = ( γ − 1) ln  3  , also
 V1 
 V4 