11. Vorlesung, Di, 29.11.2011 11.1 Joule-Thomson

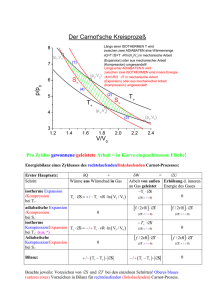
11.
Vorlesung, Di, 29.11.2011
11.1
Joule-Thomson-Expansion
Eine weitere Methode der Gasexpansion, die wie die adiabatische Expansion zur Abkühlung
von Gasen benutzt werden kann ist die Joule-Thomson-Expansion. Ein Gas wird durch einen
Druck PA im Kompartiment A (mit Temperatur TA) durch einen porösen Stopfen in ein
Kompartiment B transportiert (mit Druck pB und Temperatur TB). Das System ist thermisch
isoliert (δQ=0). Der Prozess entspricht keinem Gleichgewichtszustand aber für genügend
langsame Strömung, kann man die beiden Seiten des Stopfens als näherungsweise im
Gleichgewicht betrachten. In einem Zeitintervall wird in bestimmtes Volumen VA und Druck
pA aus dem A-Kompartiment in das B-Kompartiment (mit dann VB unter Druck pB)
verschoben. Die im Kompartiment A geleistete Arbeit ist W=pAVA, im Kompartiment B wird
die Arbeit pBVB an der Umgebung geleistet. D.h. die Arbeitsbilanz ist: δW=pAVA-pBVB.
Aus dem ersten Hauptsatz folgt: ΔU=UB-UA und daraus: UB+pBVB=UA+pAVA
Wir interessieren uns für die Temperaturänderung bei Entspannung des Gases:
 H 
 S 
T   p


V
 T 
 P T    P T
T  1

  
Cp
Cp
 H 
 P  H


 T  P
Für ein ideales Gas (α=1/T) gibt es keinen Effekt. Wenn α >1/T ergibt sich eine Abkühlung
sonst Erwärmung des Gases bei Entspannung. Sowohl adiabatische Expansion als auch JouleThomson-Expansion können zur Erzeugung tiefer Temperaturen benutzt werden.
11.2
Extremaleigenschaften thermodynamischer Potentiale
Das „gerichtete“ Verhalten thermodynamischer Systeme ist eng mit den
Extremaleigenschaften der thermodynamischen Potentiale verbunden. Wir wollen uns die
dafür nötigen Bedingungen vor allem für die Entropie anschauen.
11.2.1 Wir zerlegen ein gegebenes System in zwei gleich große Teilsysteme
U V
U V
S (U ,V )  S1 ( , )  S2 ( , )
2 2
2 2
Wir betrachten „virtuelle“ Änderung δU1, δV1 in System 1 (dementsprechend –δU1, -δV1 im
zweiten System), Änderung der Entropie:
U
V
U
V
 U ,  V )  S2 (  U ,  V )  S (U ,V )
2
2
2
2
 S1 S 2 
 S1 S 2 
1   2 S1  2 S 2  2 1   2 S1  2 S 2  2






U   V  V V  2  U 2  U 2 U  2  V 2  V 2 V

U

U
2 
2 
2 
2 
 1
 1
 1
 1
S  S1 (
  2 S1
 2 S2 
UV ..
 

 V1U1 V2U 2 
Im stationären Gleichgewichtsfall gilt (mit 2tem Hauptsatz), dass lineare Terme (erste
Ableitungen) verschwinden (Maximum der Entropie).
S  0
U
V
U
V
 U ,  V )  S 2 (  U ,  V )  S (U ,V )
2
2
2
2
 S1 S 2 
1 1

  0  

T1 T2
 U1 U 2 
S1 (
 S1 S 2 
P P

  0  1  2

T1 T2
 V1 V2 
Falls auch noch virtuelle Teilchenzahländerungen betrachtet werden folgt auch noch: μ1=μ2
Falls S tatsächlich maximal im Gleichgewicht müssen die folgenden Bedingungen gelten:
 2 S1  2 S 2

0
U12 U 22
 2 S1  2 S1   2 S1 
0

U12 V12  V1U1 
lassen Index weg :
1
 2 S   T 
1

 2
2
 U 
U
T CV

V
 S S 
1 P

,
  , 
 U V    T T  
 (U ,V )
 (U ,V )
1 P
 , 
1
 T T  T ,V    1  P  


3
3
 (T ,V )  (U ,V )
T CV  V T T V CV
Das Resultat drückt die Stabilität des Systems aus: Cv und κτ müssen positiv sein. Bei
Wärmeaufnahme wird System wärmer (nicht kälter) und bei Kompression erhöht sich der
Druck. Prinzip von Le Chatelier: Wenn sich ein System im stabilen Gleichgewicht befindet,
führt jede spontane Änderung seiner Parameter zu einer Reaktion, die das System wieder ins
Gleichgewicht zurückführt. Die Ungleichung Cv >= 0 garantiert thermische Stabilität und κτ
>=0 garantiert mechanische Stabilität.
11.2.2 System bei konstanter Temperatur
Wir betrachten die isotherme Expansion als Beispiel mit Wärmeumsatz ΔQ:
Stot  S system  S reservoir  0 2ter H .S .
 Q
; U  Q  W
T
Q TS  (U  W )
Stot  S system 

T
T
(TS  U )  W )

T
 W  F  0
S reservoir 
 W  F ;
W  F
D.h. die freie Energie definiert die maximale Arbeit, die das Gas bei konstanter Temperatur
verrichten kann. Wir betrachten zusätzlich dV=0 bzw. dW=0 (keine Volumenarbeit, kann aber
auf andere Arten von Arbeit auch übertagen werden).
F  0  F  Fmin
Dies bedeutet F für einen Startzustand muss größer sein, als Fmin (beim Gleichgewicht, dabei
ist noch T, V=const., entspricht kanonischem Ensemble)
11.3
Carnot-Prozess
Der Carnot-Prozess ist ein Spezialfall eines Kreisprozesses und dient als Standardbeispiel
einer periodisch arbeitenden Wärmekraftmaschine. Bei einem Kreisprozess stimmen Anfangsund Endzustand nach einem Prozesszyklus überein.
ΔU=0=ΔQ+ΔW nach einem Zyklus
Die Carnot-Maschine arbeitet durch Expansion/Kontraktion von einem Gas bei verschiedenen
Temperaturen. Für einen reversiblen Kreisprozess im P/V-Diagramm erhält man die netto pro
Zyklus geleistete Arbeit aus einem Kreisintegral in der P/V-Ebene.
11.3.1 Ablauf
Man unterscheidet beim Carnot-Prozess vier Zustände (A, B, C, D: Eckpunkte im P/VDiagramm) und vier Teilprozesse:
A->B isotherme Expansion bei hoher Temperatur T=T2
Volumenausdehnung VA->VB, das System nimmt die Wärmemenge Q2 > 0 auf: die
geleistete Arbeit entspricht bei reversibler Führung (wir vernachlässigen
Reibungsverluste) der aufgenommenen Wärme (ideales Gas)
B->C adiabatische Expansion ΔQ=0,
VC/VB=(T2/T1)y
Weitere Volumensteigerung (VB-VC), die sich aus Adiabatengleichung ergibt. Die
geleistete Arbeit entspricht der Änderung der inneren Energie des Gases, welches sich
dabei abkühlt.
C->D Isotherme Kompression bei niedriger Temperatur T=T1
Es wird Arbeit am System geleistet, die in Form von Wärme an ein Wärmebad (kühl
mit T1) abgegeben wird. VC->VD, Q=-Q1<0
D->A adiabatische Kompression, ΔQ=0
Volumenkomprimierung: Gemäß Adiabatengleichung erwärmt sich das Gas dabei
wieder auf die hohe Temperatur T2,
VD/VA=(T2/T1)y
Bilanz: Die adiabatische Kompression erfordert genauso viel Arbeit wie die adiabatische
Expansion liefert. Ein Teil der bei der isothermen Expansion gewonnenen Arbeit wird bei der
isothermen Kompression wieder benötigt. Daher ist die Arbeitsbilanz:
ΔW=W2-W1=|Q2|-|Q1|
11.3.2 Entropiebilanz:
Wir haben bereits gezeigt, dass bei der reversiblen isothermen Expansion eine
Entropieänderung des Systems von ΔSA->B=ΔQ2/T2 auftritt, beim zweiten isothermen Schritt
tritt eine gleich große Entropieänderung mit umgekehrten Vorzeichen auf während die
adiabatischen Schritte keine Entropieänderung verursachen (siehe T/S-Diagramm). Die
gesamte Entropieänderung ist also, wie zu erwarten, Null.
Je nach Richtung des Ablaufs des Prozesses lassen sich Wärmekraftmaschinen,
Wärmepumpen und Kühlsysteme realisieren.
11.3.3 Wirkungsgrad des Carnot-Prozesses
Wir nehmen an, dass jeder Teilschritt des Carnot-Prozesses reversibel geführt wird, d.h. die
Wärme Q2 (A->B) wird vollständig in Arbeit umgewandelt, ebenso wird die Arbeit W 1 beim
isothermen Komprimieren vollständig in Wärme (Q1) für das Reservoir mit der tieferen
Temperatur umgewandelt. Wir setzen die Wärme Q2 ein, die Wärme Q1 geht verloren. Der
Wirkungsgrad ist definiert als die gewonnene Arbeit pro eingesetzter Wärmeenergie.

W
Q
1 1 ; 0  1
Q2
Q2
Mit dem idealen Gas als Arbeitssubstanz:
Q2  Nk BT2 ln
Q1  Nk BT1 ln
Q1 T1

Q2 T2
ln
VA
VB
VA
VB
VC
VD
V
ln C
VD

T1
T2
Der Wirkungsgrad hängt vom Verhältnis der Temperaturen der Wärmereservoire ab.
Carnot  1 
T1
T2
Der Wirkungsgrad ist umso größer je höher T2 bzw. je kleiner T1. Ein Wirkungsgrad von 1
kann bei T1-> 0 erreicht werden (ist aber physikalisch nicht erreichbar).