Folie 1
Werbung

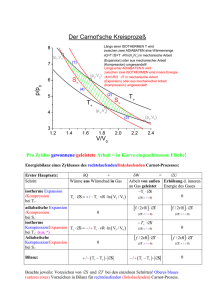
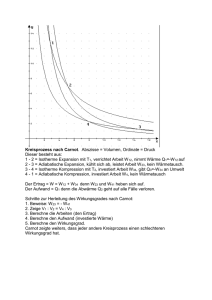
Wärmekraftmaschinen Carnot-Zyklus Stirling-Motor Inhalt • Funktion des Carnot Motors • Vergleich der Funktion von Carnot - und Stirling-Motor • Der optimale Wirkungsgrad für Wärmekraftmaschinen Q p V 2 0 1,5 0,5 1,0 Wärmezähler [J] W p V Isotherme Expansion • Das Wärmebad liefert die Wärme zur Expansion • Das Gegengewicht speichert einen Teil der vom Gas nach außen abgegebenen Arbeit • Zusätzlich wird weitere Arbeit abgeben, z. B. eine Nutzlast angehoben Abgegebene Arbeit 2 W1 Q1 pdV 1 2 V2 dV R T1 R T1 ln V V1 1 Adiabatische Expansion 2 0 1,5 0,5 1,0 Wärmezähler [J] • Der Zylinder wird isoliert • Das expandierende Gas hebt das Gegengewicht weiter, die Innere Energie nimmt ab, die Nutzlast wird nicht weiter angehoben Temperatur Änderung W2 U 2 Cv T2 T1 Q p V 2 0 1,5 0,5 1,0 Wärmezähler [J] Isotherme Kompression • Ein Kühler hält die Temperatur konstant • Das Gegengewicht treibt gegen den Druck den Kolben hoch • Der Kühler führt die bei W p V der Kompression entstehende Wärme ab Abgeführte Wärme 4 W3 Q2 pdV 3 4 V4 dV R T2 R T2 ln V V3 3 Adiabatische Kompression 2 0 1,5 0,5 1,0 Wärmezähler [J] • Der Zylinder wird isoliert • Das Gegengewicht treibt den Kolben gegen den Druck hoch, die innere Energie nimmt zu Temperaturanstieg W4 U 4 Cv (T1 T2 ) W2 Isotherme Expansion 2. Zyklus 2 0 1,5 0,5 1,0 Wärmezähler [J] Adiabatische Expansion 2. Zyklus 2 0 1,5 0,5 1,0 Wärmezähler [J] Isotherme Kompression 2. Zyklus 2 0 1,5 0,5 1,0 Wärmezähler [J] Adiabatische Kompression 2. Zyklus 2 0 1,5 0,5 1,0 Wärmezähler [J] Reversible Prozesse • Der Lauf der Carnot Maschine ist reversibel: In jedem Moment könnte die Maschine angehalten und mit Umkehrung der Vorgänge neu gestartet werden: • Bei der isothermen Kompression kann z. B. durch Einsatz der Nutzlast dem Wärmebad die Wärme wieder zurückgeben werden Definition des Wirkungsgrads im Carnot-Zyklus • Nach einem Zyklus der Carnot Maschine gilt: – Wärme wurde zugeführt – Arbeit wurde verrichtet, z. B. eine Nutzlast angehoben • Der (negative) Quotient zwischen der Nutz-Arbeit und der zugeführten Wärme nennt man Wirkungsgrad einer Wärmekraftmaschine • Ohne Beitrag zum Wirkungsgrad sind – Die während der adiabatischen Vorgänge (z. B. mit Hilfe eines Gegengewichts) gespeicherte und wieder abgerufene Arbeiten, sie sind gleich, aber von entgegengesetzten Vorzeichen und heben sich daher auf – die bei der isothermen Kompression abgeführte Wärme Die Zyklen der Carnot Maschine Weg 1-2 Energiefluss Wärmezufuhr, Arbeit wird gespeichert und abgegeben Zustandsänderung Arbeit 2 Isotherme Expansion W1 Q1 pdV 1 2 R T1 1 2-3 3-4 4-1 Arbeit wird gespeichert Adiabatische Expansion V dV R T1 ln 2 V V1 W2 U 2 Cv T2 T1 4 Kühlung, die gespeicherte Arbeit erzeugt Wärme Isotherme Kompression Die gespeicherte Arbeit erhöht die Temperatur Adiabatische Kompression W3 Q2 pdV 3 4 V4 dV R T2 R T2 ln V V3 3 W4 U 4 Cv (T1 T2 ) W2 Berechnung des Wirkungsgrads W1 W2 W3 W4 Definition des Wirkungsgrad der W Carnot Maschine Q Q1 T ln V2 V1 T2 ln V4 V3 1 T1 ln V2 V1 T1 V2 1 T2 V3 1 T2 V4 T1 V1 1 1 V2 V1 V3 V4 W Q1 Q2 T1 T2 Q Q1 T1 Die Wärmeüberträge werden, nach der Tabelle oben, durch die Volumina und die Temperatur ausgedrückt Die Punkte 2, 3 und 4, 1 sind durch Aiabaten verknüpft, deshalb gilt die Poissongleichung Folgt nach Division beider Gleichungen Wirkungsgrad der Carnot Maschine Zweiter Hauptsatz der Wärmelehre • Es gibt keine periodisch arbeitende Maschine, die nichts anderes bewirkt als Erzeugung mechanischer Arbeit und Abkühlung eines Wärmebehälters Technik des Carnot Motors • Der Carnot-Motor erfordert an seinem Zylinder den unmittelbaren Wechsel von Heizung, Isolation und Kühlung - das ist technisch kaum realisierbar Carnot-Motor 1 2 4 3 Technik des Stirling Motors • Technisch realisierbar ist dagegen die Stirling Maschine mit immer heißem Zylinderkopf und gekühltem Mantel – Allerdings etwas komplizierte Ansteuerung des „Verdränger - Kolbens“ Stirling-Motor 1 2 4 3 Versuch: Stirling Motor • Lauf eines Stirlingmotors • Betrieb als Wärmepumpe Zusammenfassung • Der optimale Wirkungsgrad für Wärmekraftmaschinen ist durch den CarnotZyklus gegeben: η=1-Ttief / Thoch • Der Carnot Prozess ist jederzeit umkehrbar, d.h. die Carnot Maschine kann als Wärmepumpe eingesetzt werden • Der Carnot-Motor erfordert an seinem Zylinder den unmittelbaren Wechsel von Heizung zu Kühlung - das ist technisch kaum realisierbar • Technisch realisierbar ist dagegen die Stirling Maschine mit heißem Zylinderkopf und gekühltem Mantel – Allerdings etwas komplizierte Ansteuerung des „Verdränger - Kolbens“ Finis