Carnot_Prozess

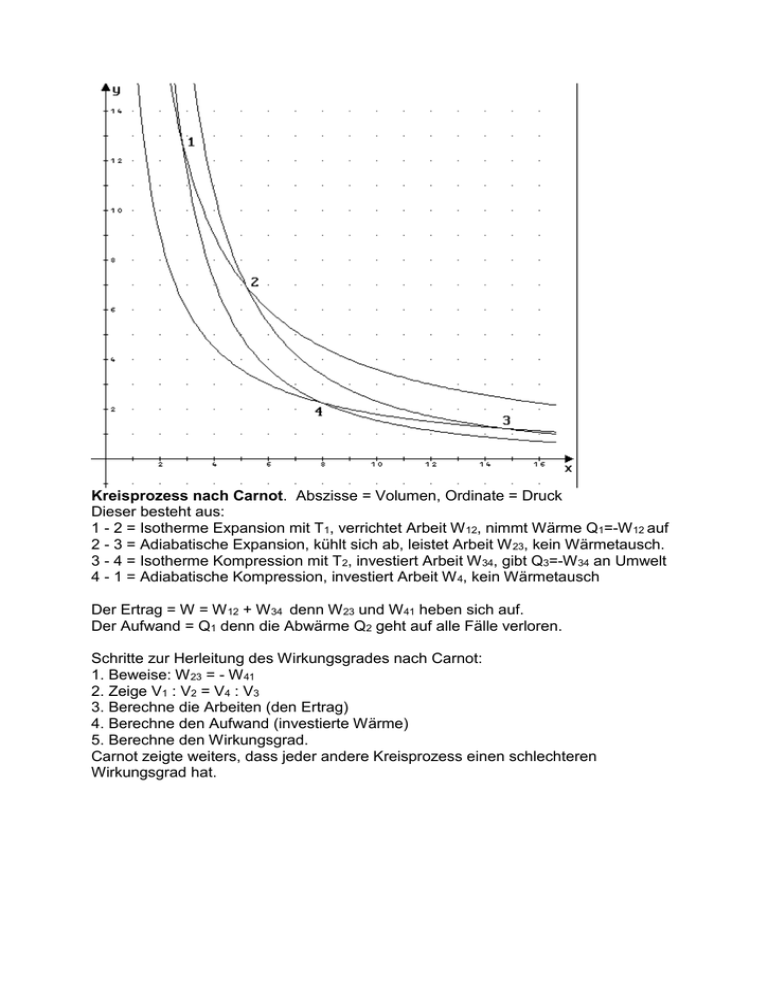
Kreisprozess nach Carnot. Abszisse = Volumen, Ordinate = Druck
Dieser besteht aus:
1 - 2 = Isotherme Expansion mit T1, verrichtet Arbeit W 12, nimmt Wärme Q1=-W 12 auf
2 - 3 = Adiabatische Expansion, kühlt sich ab, leistet Arbeit W 23, kein Wärmetausch.
3 - 4 = Isotherme Kompression mit T2, investiert Arbeit W 34, gibt Q3=-W 34 an Umwelt
4 - 1 = Adiabatische Kompression, investiert Arbeit W 4, kein Wärmetausch
Der Ertrag = W = W 12 + W 34 denn W 23 und W41 heben sich auf.
Der Aufwand = Q1 denn die Abwärme Q2 geht auf alle Fälle verloren.
Schritte zur Herleitung des Wirkungsgrades nach Carnot:
1. Beweise: W 23 = - W 41
2. Zeige V1 : V2 = V4 : V3
3. Berechne die Arbeiten (den Ertrag)
4. Berechne den Aufwand (investierte Wärme)
5. Berechne den Wirkungsgrad.
Carnot zeigte weiters, dass jeder andere Kreisprozess einen schlechteren
Wirkungsgrad hat.
1. Behauptung: W 23 = -W41
beides sind adiabatische Prozesse, Q = 0 J; U = W
W23 = -n Cv (T1- T2)
W41 = -n Cv (T2- T1)
Somit stimmt die Behauptung
2. isotherm sind:
p1V1  p2 V2 ; p4 V4  p3V3
adiabatisch sind:




p 2 V2  p3V3 ; p1V1  p 4 V4


V1 V2
V V
   4  3
V2 V1
V3 V4
1
1
V
V2
 3 1
1
V1
V4
V1 V4

V2 V3
3.
V2
V2
dV
V
 nRT1 ln 2
V
V1
V1
W12    p dV  nRT1 
V1
W34  nRT2 ln
W  nR ln
V3
V
 nRT2 ln 4
V4
V3
V2
(T1  T2 )
V1
4.
Q1   W12  nRT1 ln
V2
V1
5.

W

Q
V2
(T1  T2 )
T T
T
V1
 1 2  1 2
V
T1
T1
nR ln 2  T1
V1
nR ln