Der Carnot`sche Kreisprozess

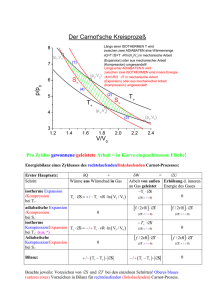
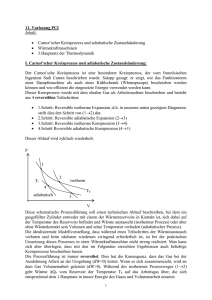
1
Der Carnot'sche Kreisprozess
Man spricht von einem Kreisprozess, wenn ein thermodynamisches System
verschiedene Zustände durchläuft, bevor es schließlich wieder in seinen
ursprünglichen Zustand zurückkehrt. Während dieses Kreisprozesses, kann ein
System Arbeit verrichten und als Wärmemotor fungieren.
Der 1824 von Nicolas Sadi Carnot vorgestellte Zyklus setzt sich aus vier
thermodynamischen Zustandsänderungen zusammen. Zwar ist er nur einer von
vielen möglichen Prozessen, aber er ist der effizienteste, wenn es darum geht eine
gewisse Menge an Wärmeenergie in Arbeit umzuwandeln. Es gibt keinen anderen
Zyklus mit extremen Temperaturen, welcher dieselben Isotherme wie der
Carnot'sche Kreisprozess hat und einen höheren Wirkungsgrad aufweist. Er
beschreibt somit einen idealen Wärmemotor. Alle Wärmemotoren stellen nur eine
sehr unvollkommene Nachbildung dieses idealen und theoretischen
Kreisprozesses dar. Dementsprechend kann kein Wärmemotor ihn perfekt
reproduzieren. Die Bedeutung des Prozesses ist dennoch fundamental für das
Verständnis der Funktionsweise dieser Maschinen, denn er weist das Ziel, das
man anstreben sollte.
Um einen Wärmemotor, egal ob mit Dampf, Verbrennung, heißer Luft o.ä.
angetrieben, zum Laufen zu bringen, benötigt man zwei Wärmereservoirs mit
unterschiedlichen Temperaturen T1 und T2. Das Fluid des Wärmemotors sei in
diesem Fall ein ideales Gas, besser gesagt ein theoretisches Gas, gebildet aus
sich bewegenden, punktförmigen Teilchen, die miteinander interagieren und dem
Gesetz pV=RT folgen (gültig für eine Menge des Gases, wobei p der Druck, V das
Volumen, T die absolute Temperatur und R die allgemeine Gaskonstante ist). Das
Verhalten von realem Gas unterscheidet sich bei den in Wärmemotoren
auftretenden Temperaturen und Druckverhältnissen nicht signifikant von dem
eines idealen Gases.
Grafik einfügen aus dem englischen Text: [Graf]
Dieser Graph zeigt, dass die Isothermen in dem P-V-Diagramm gleichseitige
Hyperbeln sind. Der Carnot'sche Kreisprozess wird in dem Diagramm
wiedergegeben und besteht, wie auch die folgende Abbildung zeigt, aus vier
unterschiedlichen Phasen: zwei isothermen Phasen, in denen die Temperatur von
T1 und T2 konstant bleibt, sowie zwei adiabatischen Phasen, in denen kein
Wärmeaustausch zwischen dem System und der Umgebung statt findet.
Grafiken einfügen:
1. isotherme Expansionsphase A-B
2. adiabatische Expansionsphase B-C
3. isotherme Kompressionsphase C-D
4. adiabatische Kompressionsphase D-A
Ein idealer Carnot'scher Motor besteht aus einem von einem beweglichen Kolben
umschlossenen Zylinder. Während der adiabatischen Phasen muss der Zylinder
völlig wärmeisoliert sein, während bei den isothermen Vorgängen ein
Wärmeaustausch mit den Wärmereservoirs möglich ist.
Grafik einfügen
2
Isotherme Expansion A-B
Der Zylinder wird in Verbindung mit der Temperaturquelle T1 platziert. Das Gas
nimmt die Wärmeenergiemenge Q1 von der heißeren Quelle T1 auf, was zu einer
Vergrößerung seines Volumens und zu einer Druckverminderung führt. Der
Kolben bewegt sich aufwärts und gibt Energie ab. Durch den Einfluss der
Wärmequelle wird der Tendenz des Gases, an Temperatur zu verlieren,
entgegengewirkt und somit bleibt die Temperatur konstant (isotherme Phase).
In diesem Fall ist die Arbeit LA-B, die von der Maschine während der A-B Phase
geliefert wird identisch mit der Wärme Q1, welche vom Reservoir bei der
Temperatur T1 abgegeben wird.
Adiabatische Expansion B-C
Der Zylinder ist nun von der Umgebung isoliert und ein Wärmeaustausch mit dem
Reservoir der Temperatur T1 ist nicht länger möglich. Ein adiabatischer Vorgang
findet statt: sich weiterhin ausdehnend, kühlt das Gas auf die Temperatur T 2 ab
und liefert, unter Einbußen seiner inneren Energie, Arbeit nach außen. Die von der
Maschine bereit gestellte Arbeit ist LB-C= C(T1-T2), wobei C der spezifischen
Wärme des Fluids bei einem konstanten Volumen entspricht.
Isotherme Kommpression C-D
Der Zylinder steht in Verbindung mit der Wärmequelle der Temperatur T2, wobei
diese geringer ist als T1. Nun senkt der Kolben sich. Obwohl das Gas komprimiert
wird, erhitzt es sich nicht, denn es gibt die Wärmemenge Q2 an die Quelle zurück.
Die für den Motor zur Verfügung gestellte Leistung LC-D entspricht der Wärme Q2,
welche mit der Temperatur T2, an das Reservoir abgegeben wird.
Adiabatische Kompression D-A
Der Zylinder ist erneut wärmeisoliert. Durch die von außen geleistete Arbeit wird
das Gas komprimiert und dies wiederum vergrößert die innere Energie des Gases.
Die Temperatur erhöht sich von T2 auf T1 und man kehrt zum Beginn des
Kreislaufes zurück. Die verrichtete Arbeit ist LD-A=C (T1-T2).
Mit dem Ergebnis dieses Kreisprozesses kann man demonstrieren, dass es
möglich ist, Energie zu erhalten und das System auf seine ursprünglichen Zustand
zurück zu versetzen, sofern man einen idealen Carnot’schen Motor, ein perfektes
Fluid und zwei unterschiedlich temperierte Quellen besitzt. Die verfügbare Energie
ergibt sich aus der Differenz zwischen der Energie, welche die Maschine an die
Umgebung abgibt und der Energie, welche der Maschine während des Kreislaufes
von außen zugeführt wird. Der Wirkungsgrad ŋ des Carnot’schen Motors wird
definiert als das Verhältnis zwischen gelieferter Arbeit des Motors und
bereitgestellter Wärme des Reservoirs mit der höchsten Temperatur:
ŋ = (LA-B + LB-C – LC-D – LD-A )/ Q1
Da LB-C gleich ist mit LD-A, LA-B= Q1 und LC-D = Q2 und da in isothermen Prozessen
gilt Q1/ T1 = Q2/ T2, wird der Wirkungsgrad zu
ŋ =(T1-T2)/ T1
Das fundamentale Charakteristikum des Carnot’schen Motors ist, dass er nicht von dem
verwendeten Fluid abhängig ist (z.B. Gas oder Dampf) sondern von dem
Temperaturunterschied der beiden Quellen zwischen denen der Wärmeaustausch
3
stattfindet. Letztlich könnte der hypothetische Wirkungsgrad von 100% nur erreicht
werden, wenn T2 dem absoluten Nullpunkt (0 K) entspräche; etwas, das sich unmöglich
erreichen lässt. Der Wirkungsgrad des Carnot’schen Motors ist daher stets geringer als 1.
´
Es ist weiterhin interessant, dass der Wirkungsgrad des Carnot’schen Kreisprozesses, bei
gleich bleibender Temperaturdifferenz (mit ∆T= T1-T2) umso größer ist, je kleiner die
Werte T1 und T2 sind.
Der Wärmemotor kann ebenso als Kühlschrank fungieren, sofern man den Zyklus
umstellt. In diesem Fall zieht das System Wärme Q2 von der Quelle mit der geringeren
Temperatur T2 (Kühlfach) und liefert Wärme Q1 an die Quelle mit der höheren Temperatur
T1 (Außenumgebung). Da Q1> Q2, muss sämtliche zusätzliche Energie, die für die Quelle
T1 geliefert werden soll, von außen in das System zugeführt werden, um als Kühlschrank
funktionieren zu können.