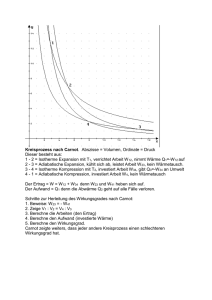
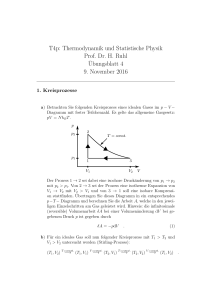
Kreisprozesse

Fachschaft Physik / KSL
Kreisprozesse
Sadi Carnot: 1796-1832
"Réflexions sur la puissance
motrice du feu"
Verfasst von Werner Fuchsberger
James Watt 1736-1819
Erfinder der Dampfmaschine
Thermodynamik
Physikpraktikum Grundlagenfach
Einleitung
Der 2. Hauptsatz der Wärmelehre entstand erst im 19. Jahrhundert vor allem auf
Grund von Arbeiten des Physikers Ludwig Boltzmann (Wien). Dieser Satz ist
Grundlage dafür, dass periodisch arbeitende Wärmekraftmaschinen nie die gesamte
zugeführte Wärme in Arbeit umwandeln können, sondern nur immer einen Teil
davon. Dies ist nicht ein technisches Gebrechen, sondern die Wirkung des 2.
Hauptsatzes der Wärmelehre, eines grundlegenden Naturgesetzes.
Eine erste solche Wärmekraftmaschine war die Dampfmaschine von James Watt.
Diese Maschine war Ausgangspunkt einer revolutionären Wandlung der Gesellschaft
von einer Agrargesellschaft in die Industriegesellschaft.
Knapp 50 Jahre später hat Sadi Carnot (Frankreich) die theoretischen Grundlagen
der Energieumsetzungen in Wärmekraftmaschinen erarbeitet. Er fand und
untersuchte den theoretisch effizientesten Kreisprozess. (Jede Wärmekraftmaschine
kehrt nach einem Zyklus von Vorgängen in die Ausgangsposition zurück, deshalb
Kreisprozess). Er entdeckte damit die Obergrenze für den Wirkungsgrad aller
Wärmekraftmaschinen, die zwischen den Temperaturniveaux T 1 und T2
(T1 > T2, Angabe in Kelvin) arbeiten.
T T
T
  1 2 1 2
T1
T1
Fachschaft Physik / KSL
Versuchsziele






Internet-Recherche zu Sadi Carnot, James Watt, Ludwig Boltzmann
Vorstellen der Ergebnisse der Recherche
Selbständiges Erarbeiten einer physikalischen Grundlage der Technik unter
Benutzung von Unterlagen
Diskussion von Problemen zur Thematik
Studium der Modelle eines Viertakt- und Zweitaktmotors
Übungsaufgaben als Hausaufgabe
Vorbereitung





Vorausgesetzt wird die Kenntnis der Zustandsgleichung idealer Gase, die Kenntnis
der "Isoprozesse": isobar, isochor, istherm, isentropisch (=adiabatisch)
1. Hauptsatz der Wärmelehre: quantitativ
2. Hauptsatz der Wärmelehre: qualitativ
Grundlegendes Vorgehen zur Bestimmung der Wärme
Grundlegendes Vorgehen zur Bestimmung der Arbeit
Material


1 PC / Notebook je Gruppe; Internetzugang
Modell Viertaktmoter, Modell Zweitaktmotor, evtl. Modell Dampfmaschine
Durchführung und Auswertung
1.
2.
3.
4.
5.
Internet-Recherche: 10 min
Je eine Gruppe recherchiert im Internet zu den biographischen Themen (siehe
Versuchsziele) mit folgenden Fragestellungen:
- Umfeld der Person (Familie, soziales Umfeld)
- Ausbildung / Beruf der Person
- Thematik der wichtigsten Arbeit
- Auswirkungen der Ergebnisse und Aussagen der Person für Physik und Gesellschaft.
Mitteilung der Ergebnisse der Internet-Recherche, Diskussion: 10 min
Am gemeinsamen Tisch werden die Ergebnisse mitgeteilt und kurz diskutiert.
Arbeit und Wärme der Iso-Prozesse eines idealen Gases: 20 min
An Hand der im Anhang 1 beigefügten Inhalte zu Wärme und Arbeit der Iso-Prozesse
sind diese zu erarbeiten. Verständnisprobleme sind mit der Lehrperson zu klären.
Der Carnot'sche Kreisprozess: 20 min
An Hand der im Anhang 2 beigefügten Inhalte über den Carnot'schen Kreisprozess sind
die Schritte der Entwicklung nachzuvollziehen. Dabei werden sich wahrscheinlich
Verständnisprobleme ergeben. Diese sind mit der Lehrperson zu besprechen.
Am Ende steht die eingangs geschilderte Idealformel für den thermodynamischen
Wirkungsgrad einer Wärmekraftmaschine.
Beachte, dass Carnot zusätzlich gezeigt hat, dass kein anderer Kreisprozess einen
besseren Wirkungsgrad haben kann. In einer gemeinsamen Diskussionsrunde sollen die
Erkenntnisse nochmals gefestigt werden.
Die Modelle des Viertaktmotors und des Zweitaktmotors: 15 min
Je 2 Gruppen schliessen sich zusammen und studieren die Modelle, sodass der Ablauf
verstanden wird. Das Lehrbuch mit seinen Abbildungen ist sicher hilfreich dafür.
Zusatzaufgaben
Es sind Übungsaufgaben nach Vorgabe der Lehrperson zur Thematik zu lösen.
S 180 / 31 - 34
PS-Praktikum GF
Seite 2/5
Kreisprozesse / Version 1
Fachschaft Physik / KSL
Anhang 1: Arbeit und Wärme der "Iso-Prozesse" eines idealen Gases
Überlege zu den einzelnen Prozessen, welche besonderen Bedingungen der
Zustandsgrössen gelten. Z. B. Isobarer Prozess: Gay-Lussac Gesetz.
Überlege weiter, wie diese Prozesse grafisch in den Diagrammen Vp, TV, Tp
darzustellen sind. Die Richtung (z.B. Kompression oder Expansion) ist von
Bedeutung.
Vorzeichen: Dieses ist positiv, wenn die Transportenergie (Q oder W) dem Gas
zugeführt wird, negativ, wenn sie abgeführt wird.
n = Molzahl, CV, Cp sind spezifische Molwärmen, Temperaturen immer in Kelvin,
Drücke immer in Pascal, Volumen immer in m3. Q = Wärme, W = Arbeit.
Cp
R = universelle Gaskonstante = 8.31 J/(Mol K). Cp  CV  R ,  
CV
p
 const
T
Q  nCV  T2  T1  ; keine Arbeit, weil V = const, also keine Kolbenbewegung
1. Isochorer Prozess: V = const; Amontons Gesetz:
Sofern T2 > T1 ist es eine Erwärmung. Q > 0.
V
 const
T
Q  nCp  T2  T1  , es gilt dabei: Cp  CV  R ; Vorzeichen wie bei 1.
2. Isobarer Prozess: p = const, Gay Lussac Gesetz:
W  p  V2  V1  , Die Arbeit ist negativ, wenn V2 > V1 (Expansion).
3. Isothermer Prozess: T = const, U = const, Boile-Mariotte Gesetz: pV  const
W
V2
V2
V1
V1
 p dV   
V 
nRT
dV  nRT ln  2  Vorzeichen ist negativ bei Expansion
V
 V1 
V 
Weil U = 0 gilt: Q   W  nRT ln  2  Vorzeichen ist positiv bei Expansion
 V1 
Die zugeführte Wärme wird vollständig in Arbeit umgewandelt. In umgekehrter
Richtung wird die zugeführte Arbeit vollständig als Wärme abgeführt
(Umgebungsspeicher)
4. Isentropischer oder adiabatischer Prozess: Q = 0, S = 0.
Poisson Gleichung(en): pV  const , TV k 1  const , T p1  const ,  
Cp
CV
Q=0 (Definition), damit wird U = W (1. Hauptsatz)
W  nCV  T2  T1  Das Vorzeichen ist positiv bei Kompression (Temp.-erhöhung)
PS-Praktikum GF
Seite 3/5
Kreisprozesse / Version 1
Fachschaft Physik / KSL
Anhang 2: Kreisprozess nach Carnot.
Abszisse = Volumen, Ordinate = Druck
Der Prozess besteht aus:
1 - 2 = Isotherme Expansion mit T1, verrichtet Arbeit W 12, nimmt Wärme Q1=-W 12 auf
2 - 3 = Adiabatische Expansion, kühlt sich ab, leistet Arbeit W 23, kein Wärmetausch.
3 - 4 = Isotherme Kompression mit T2, investiert Arbeit W 34, gibt Q3=-W 34 an Umwelt
4 - 1 = Adiabatische Kompression, investiert Arbeit W 4, kein Wärmetausch
Der Ertrag = W = W 12 + W 34 denn W 23 und W41 heben sich auf.
Der Aufwand = Q1 denn die Abwärme Q2 geht auf alle Fälle verloren.
Schritte zur Herleitung des Wirkungsgrades nach Carnot:
1. Beweise: W 23 = - W 41
2. Zeige V1 : V2 = V4 : V3
3. Berechne die Arbeiten (den Ertrag)
4. Berechne den Aufwand (investierte Wärme)
5. Berechne den Wirkungsgrad.
Carnot zeigte weiters, dass jeder andere Kreisprozess einen schlechteren
Wirkungsgrad hat.
PS-Praktikum GF
Seite 4/5
Kreisprozesse / Version 1
Fachschaft Physik / KSL
1. Behauptung: W 23 = -W41
beides sind adiabatische Prozesse, Q = 0 J; U = W
W23 = Cv (T2- T1)
W41 = Cv (T1- T2)
Somit stimmt die Behauptung
2. isotherm sind:
p1V1  p2 V2 ; p4 V4  p3V3
adiabatisch sind:




p 2 V2  p3 V3 ; p1V1  p 4 V4


V1 V2
V V
   4  3
V2 V1
V3 V4
1
1
V
V2
 3 1
1
V1
V4
V1 V4

V2 V3
3.
V2
V2
dV
V
 nRT1 ln 2
V
V1
V1
W12    p dV  nRT1 
V1
W34  nRT2 ln
W  nR ln
V3
V
 nRT2 ln 4
V4
V3
V2
(T1  T2 )
V1
4.
Q1   W12  nRT1 ln
V2
V1
5.

W

Q
PS-Praktikum GF
V2
(T1  T2 )
T T
T
V1
 1 2  1 2
V2
T1
T1
nR ln  T1
V1
nR ln
Seite 5/5
Kreisprozesse / Version 1