Längen berechnen am rechtwinkligen Dreieck!

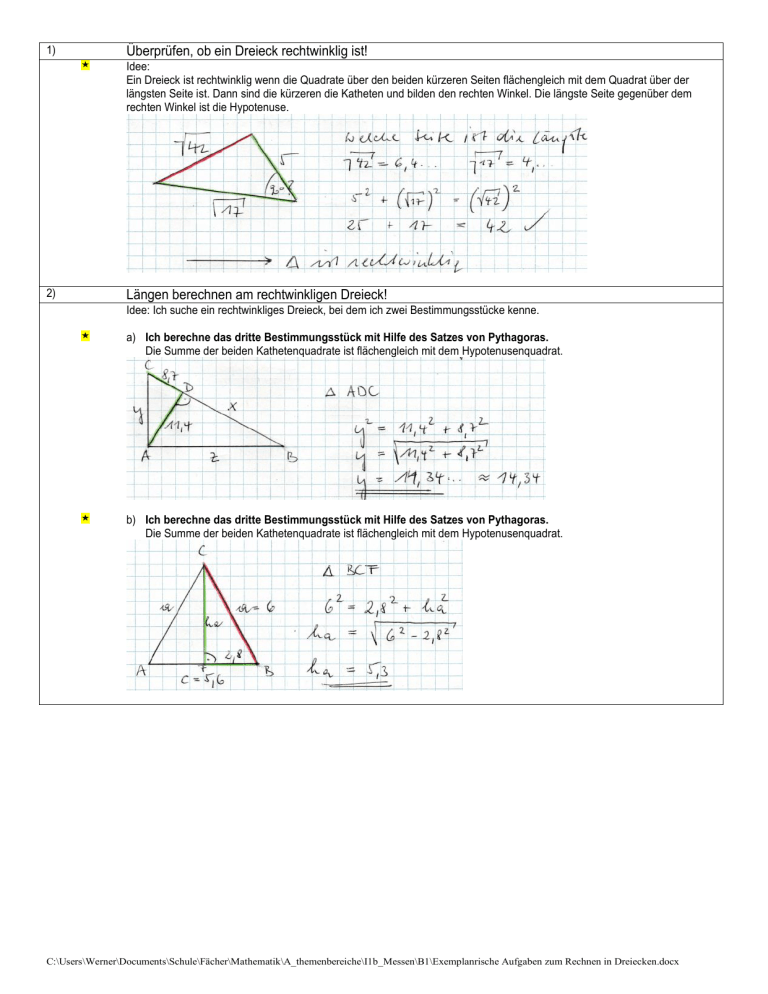
Überprüfen, ob ein Dreieck rechtwinklig ist!
1)
2)

Idee:
Ein Dreieck ist rechtwinklig wenn die Quadrate über den beiden kürzeren Seiten flächengleich mit dem Quadrat über der
längsten Seite ist. Dann sind die kürzeren die Katheten und bilden den rechten Winkel. Die längste Seite gegenüber dem
rechten Winkel ist die Hypotenuse.

Längen berechnen am rechtwinkligen Dreieck!

Idee: Ich suche ein rechtwinkliges Dreieck, bei dem ich zwei Bestimmungsstücke kenne.

a) Ich berechne das dritte Bestimmungsstück mit Hilfe des Satzes von Pythagoras.
Die Summe der beiden Kathetenquadrate ist flächengleich mit dem Hypotenusenquadrat.

b) Ich berechne das dritte Bestimmungsstück mit Hilfe des Satzes von Pythagoras.
Die Summe der beiden Kathetenquadrate ist flächengleich mit dem Hypotenusenquadrat.
C:\Users\Werner\Documents\Schule\Fächer\Mathematik\A_themenbereiche\I1b_Messen\B1\Exemplanrische Aufgaben zum Rechnen in Dreiecken.docx
2)

Längen berechnen am rechtwinkligen Dreieck!

Idee: Ich suche ein rechtwinkliges Dreieck, bei dem ich zwei Bestimmungsstücke kenne.

c) Ich berechne das dritte Bestimmungsstück mit Hilfe des Kathetensatzes.
Ein Kathetenquadrat ist flächengleich dem Produkt aus Hypotenuse und des der Kathete angrenzenden
Hypotenusenabschnittes.

d) Ich berechne das dritte Bestimmungsstück mit Hilfe des Höhensatzes.
Das Höhenquadrat ist flächengleich dem Produkt aus beiden Hypotenusenabschnitten.

e) Ich kann im Dreieck ABD mit Hilfe von Verhältnissen Seitenlängen berechnen, da die Dreiecke ABC, ABD und ADC
ähnlich sind. Das Verhältnis der Seiten im kleinen Dreieck ist dasselbe wie im großen Dreieck.
C:\Users\Werner\Documents\Schule\Fächer\Mathematik\A_themenbereiche\I1b_Messen\B1\Exemplanrische Aufgaben zum Rechnen in Dreiecken.docx