Parallele Systeme - Parallele und verteilte Systeme

> Parallele Systeme
Übung: Das Sieb des Eratosthenes
Philipp Kegel
Wintersemester 2012/2013
Parallele und Verteilte Systeme,
Institut für Informatik
Inhaltsverzeichnis
1 Das Sieb des Eratosthenes
2 Parallelisierung mit MPI
PS, Übung Das Sieb des Eratosthenes
WS 2012/13
Philipp Kegel
2
Das Sieb des Eratosthenes
• Eratosthenes: griechischer Mathematiker (276–194 v. Chr.)
• Das Sieb findet Primzahlen zwischen 2 und einer fest gewählten Zahl n
1
2
3
Erzeuge eine Liste aller natürlichen Zahlen 2, . . . , n;
keine der Zahlen ist markiert
Setze k = 2 (erste nicht markierte Zahl, d. h. Primzahl)
Wiederhole bis k2 > n
a) Markiere alle Vielfachen von k in Interval k 2 , . . . n
b) Finde die kleinste nicht markierte Zahl l > k und setze k = l.
• Komplexität: O(n ln ln n), daher nicht praktikabel für große
Primzahlen mit hunderten Ziffern
PS, Übung Das Sieb des Eratosthenes
WS 2012/13
Philipp Kegel
3
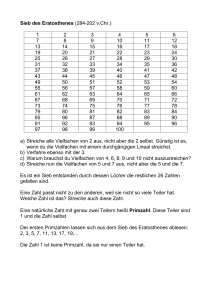
Beispiel: Primzahlen zw. 1, ..., 45
72 = 49 > 45 ⇒ alle verbleibenden nicht markierten Zahlen sind Primzahlen
Primzahlen: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43
PS, Übung Das Sieb des Eratosthenes
WS 2012/13
Philipp Kegel
4
Parallelisierung des Siebs
Idee: jeder Prozess erhält n/p Elemente des Arrays (n: Anzahl Elemente, p:
Anzahl Prozesse) und filtert sequentiell
Beispiel: n = 1024, p = 10
• Problem: da n kein Vielfaches von p (1024/10 = 102, 4), kann das
Array nicht gleichmäßig aufgeteilt werden
• 102 Elemente/Prozess: 4 Elemente werden ignoriert
• 103 Elemente/Prozess: zu wenig oder keine Elemente für letzten
Prozess ⇒ komplexe Programmlogik, Effizienzeinbußen
• Ziel: gleichmäßige Verteilung über alle Prozesse; dabei einfache
Bestimming folgender Werte:
• Welche Elemente besitzt Prozess i
• Welcher Prozess ist für ein bestimmtes Element j zuständig
PS, Übung Das Sieb des Eratosthenes
WS 2012/13
Philipp Kegel
5
Blockzerlegung
Strategie: jeder Prozess erhält ⌊n/p⌋ oder ⌈n/p⌉ Elemente des Arrays;
die größeren Blocke sind gleichmäßig über alle Prozessnummern verteilt
• Erstes Element von Prozess i: ⌊in/p⌋
• Letztes Element von Prozess i: ⌊(i + 1)n/p⌋ − 1
• Anzahl Elemente von Prozess i: ⌊(i + 1)n/p⌋ − ⌊in/p⌋
C-Makros
# define BLOCK_LOW ( id ,p , n )
# define BLOCK_HIGH ( id , p , n )
# define BLOCK_SIZE ( id , p , n )
(( id )*( n )/( p ))
( BLOCK_LOW (( id )+1 , p , n ) -1)
( BLOCK_LOW (( id )+1 , p , n ) \
- BLOCK_LOW (( id ) ,p , n ))
PS, Übung Das Sieb des Eratosthenes
WS 2012/13
Philipp Kegel
6
Eigenschaften der Blockzerlegung
• k muss in jedem Algorithmenschritt bestimmt werden
1 Reduktion um k zu bestimmen
2 Broadcast um neues k an alle Prozesse zu senden
⇒ hoher Kommunikationsaufwand in jedem Algorithmenschritt
√
• Größte verwendete Primzahl, um die Zahlen bis n zu sieben ist n
√
√
• Annahme: p < n ⇔ n/p > n
√
⇒ erster Prozess speichert alle Zahlen von 1, . . . , n
⇒ keine Reduktion erforderlich
PS, Übung Das Sieb des Eratosthenes
WS 2012/13
Philipp Kegel
7
Implementierung (1/3)
MPI_Init (& argc , & argv );
M P I _ C o m m _ r a n k ( MPI_COMM_WORLD , & comm_rank );
M P I _ C o m m _ s i z e ( MPI_COMM_WORLD , & comm_size );
/* abbrechen , falls P r o z e s s 0 nicht alle zum Sieben v e r w e n d e t e n
* P r i m z a h l e n b e s i t z t */
if ((2 + ( n - 1) / comm_size ) < ( int ) sqrt (( double ) n )) {
if ( comm_rank == 0) printf ( " Too many processes .\ n " );
M P I _ F i n a l i z e ();
exit (1); }
/* Teil des Arrays fuer diesen P r o z e s s e r m i t t e l n */
low_value
= 2 + BLOCK_LOW ( comm_rank , comm_size ,n -1);
high_value = 2 + BLOCK_HIGH ( comm_rank , comm_size ,n -1);
size
= BLOCK_SIZE ( comm_rank , comm_size ,n -1);
/* Array und I n d e x v a r i a b l e n i n i t i a l i s i e r e n */
marked = ( char *) calloc ( size , sizeof ( char ));
if ( comm_rank == 0) index = 0; // Index des a k t u e l l e n k
prime = 2; // erste P r i m z a h l ( k )
PS, Übung Das Sieb des Eratosthenes
WS 2012/13
Philipp Kegel
8
Implementierung (2/3)
do {
/* Index des ersten V i e l f a c h e n von k e r m i t t e l n */
if ( prime * prime > low_value ) {
first = prime * prime - low_value ; }
else {
if (( low_value % prime ) == 0) first = 0;
else first = prime - ( low_value % prime ); }
/* 3 a : V i e l f a c h e von k in [ k ^2 , ... , n ] m a r k i e r e n */
for ( i = first ; i < size ; i += prime ) marked [ i ] = 1;
/* 3 b : k l e i n s t e nicht m a r k i e r t e Zahl ( l ) finden und als
*
n a e c h s t e P r i m z a h l ( k ) v e r w e n d e n */
if ( comm_rank == 0) {
while ( marked [++ index ]);
prime = index + 2; }
/* neues k an alle P r o z e s s e senden */
MPI_Bcast (& prime , 1 , MPI_INT , 0 , M P I _ C O M M _ W O R L D );
} while ( prime * prime <= n );
PS, Übung Das Sieb des Eratosthenes
WS 2012/13
Philipp Kegel
9
Implementierung (3/3)
/* Lokale Anzahl P r i m z a h l e n e r m i t t e l n */
count = 0;
for ( i = 0; i < size ; i ++)
if ( marked [ i ] == 0) count ++;
/* Anzahl P r i m z a h l e n aller P r o z e s s e e r m i t t e l n */
MPI_Reduce (& count , & global_count , 1 , MPI_INT , MPI_SUM ,
0 , M P I _ C O M M _ W O R L D );
/* E r g e b n i s in P r o z e s s 0 a u s g e b e n */
if ( comm_rank == 0) {
printf ( " Found % d primes less than or equal to % d .\ n " ,
global_count , n ); }
M P I _ F i n a l i z e (); // MPI b e e n d e n
PS, Übung Das Sieb des Eratosthenes
WS 2012/13
Philipp Kegel
10
Ausführung auf PALMA
• Rechenknoten von PALMA beinhalten mehrere Multicore-Prozessoren
⇒ unterschiedliche Kommunikationsgeschwindigkeit zwischen
MPI-Prozessen auf einer CPU, einem bzw. verschiedenen Knoten
• Idee: nur 1 Prozess je Knoten
• MPI-Implemtierung erlaubt knoten-weise Verteilung der Prozesse nach
Round-Robin-Verfahren:
mpirun -bynode -np <#procs> <application> ...
• Vorteil: gleiche Kommunikationsgeschwindigkeit zwischen allen Knoten
• Weitere Varianten: kern-weise (-bycore, standard), socket-weise
(-bysocket)
• Nachteil: Knoten werden nicht optimal verwendet
⇒ hybride Programmierung mit MPI und Pthreads, OpenMP, etc.
(siehe Vorlesung)
PS, Übung Das Sieb des Eratosthenes
WS 2012/13
Philipp Kegel
11
Laufzeit
• Messung auf PALMA: 8 Knoten, je 1 Prozess; Primzahlen bis 100 Mio.
14
12
runtime (secs)
10
8
6
4
2
0
1
2
3
4
5
#processes
PS, Übung Das Sieb des Eratosthenes
6
7
WS 2012/13
8
Philipp Kegel
12
Optimierungen
• Gerade Zahlen entfernen: 2 ist die einzige gerade Primzahl
• Algorithmus nur auf ungeraden Zahlen arbeiten lassen
⇒ Halbierung des Speicherbedarfs und Verdoppelung der
Markierungsgeschwindigkeit
• Broadcast eliminieren: jeder Prozess ermittelt eigenständig die nächste
Primzahl k
• jeder Prozess erhält ein zusätzlich Array mit 2, . . . ,
√
n und ermittelt
sequentiell die darin enthaltenen Primzahlen
⇒ Broadcast nicht mehr erforderlich
PS, Übung Das Sieb des Eratosthenes
WS 2012/13
Philipp Kegel
13
Zusammenfassung
• Sieb des Eratosthenes: ermittelt Primzahlen zwischen 2 und n
• Gleichmäßige Blockverteilung und einfacher Elementzugriff erhöhen
Effizienz und erleichtern Programmierung
• Optimierung durch Verringerung der Kommunikation aber zusätzliche
Berechnungen
PS, Übung Das Sieb des Eratosthenes
WS 2012/13
Philipp Kegel
14
15
6. Übungsblatt ab sofort im Web
(Bearbeitung bis zum 16.01.2013)
Nächste Übung am 16. Januar 2013
PS, Übung Das Sieb des Eratosthenes
WS 2012/13
Philipp Kegel