Physikalisches Praktikum Universität der Bundeswehr München
Werbung

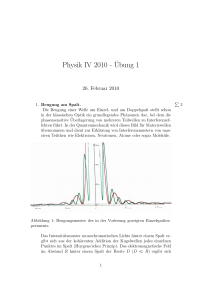
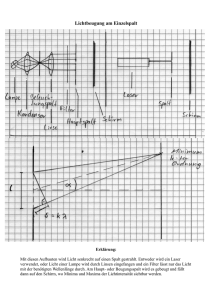
Physikalisches Praktikum Versuch 17: Lichtbeugung Universität der Bundeswehr München Fakultät für Elektrotechnik und Informationstechnik Institut für Physik Oktober 2015 Versuch 17: Lichtbeugung Im Modell der geometrischen Optik breitet sich Licht immer geradlinig aus. Der niederändische Physiker Christiaan Huygens erkannte um 1650, dass die Lichtausbreitung unter gewissen Umständen eben nicht einfach gradlinig verlief. ähnlich wie bei Wasserwellen oder Schallwellen konnte Huygens die Wellenphänomene Beugung und Interferenz von Licht nachweisen. Er begründete das HuygensÂ’sche Prinzip“, welches noch Heute für die Erklärung von Lichtbeugung und Lichtin” terferenz Gültigkeit besitzt. 1. Lernziele dieses Versuchs Die Studierenden sollen... 1.1 ... den Wellencharakter des Lichts (Huygens Prinzip) verstehen. 1.2 ... die daraus resultierenden Phänomene Beugung am Spalt und Interferenzen am Gitter verstehen und sich die Konsequenzen ihrer Überlagerung vergewissern. 1.3 ... die grundsätzliche Funktionsweise eines Lasers beschreiben können. 1.4 ... die Fehler unterschiedlicher Messmethoden sinnvoll abschätzen, miteinander vergleichen und die Konsequenzen interpretieren. 2. Vorraussetzungen Vorlesungsstoff zu den Themen: Beugung und Interferenz allgemein und am Gitter im Speziellen. Selbststudium zu den Themen: Funktionsweise eines He-Ne-Lasers, Huygens Prinzip, Beugung von Licht an einem Spalt (wo entstehen die Maxima und Minima in Abhängigkeit von Wellenlänge, Ordnung und Spaltbreite?), Interferenzen am Gitter (Wo entstehen die Maxima und Minima in Abhängigkeit von Wellenlänge, Ordnung und Spaltabstand?). 3. Literatur Hering, Martin, Stohrer, Physik für Ingenieure, Kapitel 6.4 (als .pdf-Datei über die Uni-Bibliothek downloadbar) Mitschrift zur Vorlesung Physik 1 Wilhelm Walcher: Praktikum der Physik 2 4. Versuchsbeschreibung In diesem Versuch wird die Spaltbreite und der Spaltabstand von Strukturen auf mehreren Dias vermessen. Diese Größen werden mit zwei unterschiedlichen Methoden ermittelt. Die erste Methode verwendet ein Mikroskop mit einem Kalibriermaßstab. Die zweite Methode verwendet einen He-Ne-Laser und macht sich die Welleneigenschaften des Lichts zu nutze. Dazu wird das durch den Spalt bzw. das Gitter erzeugte Beugungs- und Interferenzbild mit einem xy-Schreiber aufgezeichnet. Über die geometrische Anordnung des Versuchsaufbaus lassen sich Spaltabstand und Spaltbreite auf den Dias bestimmen. Abbildung 1: Prinzipskizze des optischen Tisches 5. Versuchsvorbereitung 5.1 Informieren Sie sich über Beugung und Interferenzen am Spalt bzw. Gitter. Fertigen Sie dazu die prinzipiellen Skizzen im Praktikumsprotokoll an. 5.2 Notieren Sie die Formeln für Beugungsmaxima bzw. Beugungsminima. Notieren Sie die Formeln für konstruktive bzw. destruktive Interferenz. 5.3 Der Versuchsaufbau ist in Abbildung 0.2 skizziert. Erklären Sie kurz, wozu jeweils der He-Ne-Laser, das Gitter, der Detektor, der Verschiebeschlitten und der x-y-Schreiber dienen. 5.4 Skizzieren Sie den Aufbau eines He-Ne-Lasers und beschreiben Sie kurz seine Funktionsweise mit Erklärung seiner wichtigsten Bauteile. Welche Funktionen erfüllen diese Bauteile? Erklären Sie anhand des He-Ne-Lasers das Funktionsprinzip eines jeden 3 Lasers. (Pumpe, Besetzungsinversion, stimulierte Emission, Resonator) 5.5 Welche Eigenschaften hat Licht aus einem Laser? Warum sind diese es so wichtig für diesen Versuch? 5.6 Wäre der Versuch auch mit einer Glühlampe oder LED sinnvoll? (Mit Begründung) 6. Versuchsdurchführung Wichtig! Nicht in den Laserstrahl oder den reflektierten Strahl blicken! Der Versuch ist justiert. Bitte keine änderungen vornehmen! 6.1 Kalibrieren Sie die Okularskala des Mikroskops mit dem beiliegenden Kalibriermaßstab (mit Messungenauigkeitsangabe) Bestimmen Sie nun mit dem Mikroskop Spaltbreite und Spaltabstand von Einzel- und Mehrfachspaltanordnungen (4 Diapositive!). 6.2 Bei der Messung der ortsabhängigen Intensität wird ein mit einem Potentiometer versehener Schiebeschlitten, der die Photodiode trägt, verwendet. Die Spannung am Potentiometer ist proportional zum Weg, sie wird vom x-Eingang des Schreibers registriert. Der Schreiberweg entspricht aber nicht direkt dem Schlittenweg, daher ist eine Kalibrierung notwendig (wird in A3 gemacht). Bestimmen Sie den Abstand dDetektor−Linse (mit Messungenauigkeitsangabe). Abbildung 2: Der optische Tisch mit dem Detektor, Linse, Halterung für die Dias, Linse, Laser (von links nach rechts). 4 6.3 Nehmen Sie mit dem Schreiber die Intensitätsverteilung der 4 verschiedenen Spaltanordnungen auf Millimeterpapier auf. Markieren Sie dabei Anfangs- und Endpunkt auf dem Papier. Messen sie anschließend den Maximalweg des Verschiebeschlittens (Messungenauigkeit), um den Schreiberweg kalibrieren zu können. 7. Auswertung 7.1 Bestimmen Sie aus den mit dem Schreiber aufgezeichneten Intensitätsverteilungen die Lage der Maxima bei Zweifach-, Dreifach- und Mehrfachspalt und tragen Sie die gemessenen Abstände mit der zugehörigen Ordnung in Tabellen ein. Zeichnen Sie anschliessend diese Punkte in ein Diagramm ein. Legen Sie dann eine Ausgleichsgerade durch die Punkte und berechnen Sie aus deren Steigung sowie den Werten für dDetektor−Linse und dem Kalibrierfaktor den jeweiligen Spaltabstand a und dessen Messungenauigkeit unter Nutzung der Gaußschen Fehlerfortpflanzung. Bestimmen Sie anschließend aus den Intensitätsverteilungen die jeweilige Position des Minimums erster Ordnung des Beugungsbildes für Einfach-, Zweifach-, Dreifach- und Mehrfachspalt. Berechnen Sie daraus jeweils die Spaltbreite b und deren Messungenauigkeit (Gaußsche Fehlerfortpflanzung). 7.2 Stellen Sie die berechneten Geometrien der Mehrfachspalte mit den Ergebnissen der direkten Messung mit dem Mikroskop in einer Tabelle gegenüber (mit Fehlerangabe). 7.3 Beschreiben sie kurz die Form der aufgezeichneten Intensitätskurven der verschiedenen Spaltkonfigurationen. Sollten sich Abweichungen zu den theoretisch zu erwartenden Kurven ergeben, erläutern sie diese genauer. (Form der Maxima, relative Höhe der Maxima). Wodurch könnten die Abweichungen verursacht werden? 5