Av I (Kontinuitätsgleichung) - dbs-lin

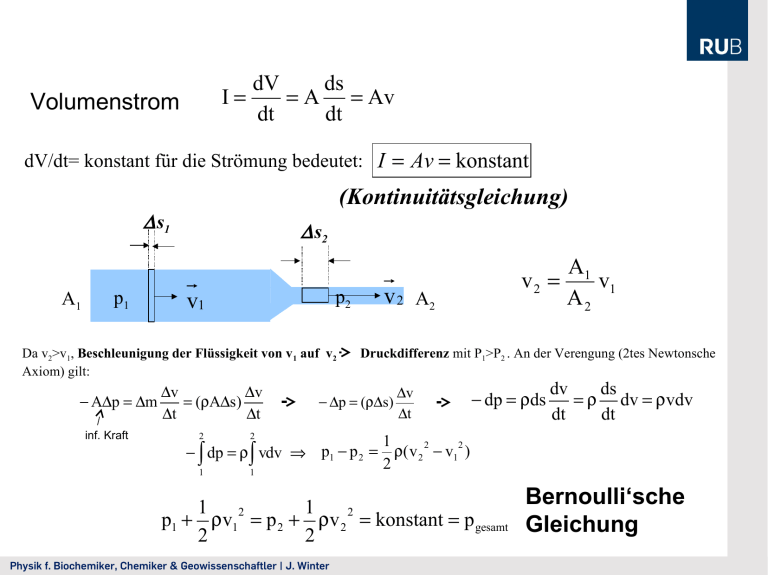
I
Volumenstrom
dV
ds
 A  Av
dt
dt
dV/dt= konstant für die Strömung bedeutet: I  Av  konstant
(Kontinuitätsgleichung)
 s1
A1
p1
 s2
Da v2>v1, Beschleunigung der Flüssigkeit von v 1 auf v2
Axiom) gilt:
 Ap  m
inf. Kraft
v 2 A2
p2
v1
v
v
 (As)
t
t
2
2
1
1
A1
v2 
v1
A2
Druckdifferenz mit P1>P2 . An der Verengung (2tes Newtonsche
 p  (s)
  dp    vdv  p1  p 2 
v
t
 dp  ds
dv
ds
  dv  vdv
dt
dt
1
2
2
( v 2  v1 )
2
Bernoulli‘sche
1
1
2
2
p1  v1  p 2  v 2  konstant  p gesamt Gleichung
2
2
Physik f. Biochemiker, Chemiker & Geowissenschaftler | J. Winter
Prandl‘sches Staurohr
v uft
Die Luft streicht oben am Loch vorbei, es bildet sich
dort ein statischer Druck pi= p0 - 1/2Luftv2 . Am Loch
vorn bildet sich der statische Druck p0
pi
p0
h
 Fl gh 
1
 Luft v 2
2
Messung der Flugzeuggeschwindigkeit
1
p oben  p 0  ( v Luft  r ) 2
2
Es wirkt auf rotierenden Zylinder im Luftstrom
eine Seitenkraft (Flettner-Rotor)
v Luft  r
v Luft

Magnus-Effekt
F  A(p oben  p unten )
v Luft  r
1
p unten  p 0  ( v Luft  r ) 2
2
Physik f. Biochemiker, Chemiker & Geowissenschaftler | J. Winter
Physik f. Biochemiker, Chemiker & Geowissenschaftler | J. Winter
v
2R
F tr  r 2 pe z
z
2r
F tr  FR  0 oder
dv
 r 2 p oder
dr
p
 dv 
rdr
2l
2rl
l
p
Profil durch
Intergration
dv
FR  2rl e z
dr
p r
  dv 
rdr also
v max
2l 0
p 2
v max  v(r ) 
r
4l
v(r )
für v(R) = 0 v max 
Strömungsprofil ist parabelförmig v(r ) 
0
Berechne mittlere Geschwindigkeit
p 2
R
4 l
p 2 2
(R  r )
4l
R
1
1
p 2 2
v
v
(
r
)
dA

(R  r ) 2rdr 

A v max
R 2 0 4l
v
Gesetz von Hagen-Poiseuille
Physik f. Biochemiker, Chemiker & Geowissenschaftler | J. Winter
p 2 1
R  v max
8l
2
I  A v  R 2
p 2  4 p
R 
R
8l
8
l
Zusammenfassung Strömung von Flüssigkeiten
Kontinuitätsgleichung
dV
 Av  konstant
dt
PGesamt  Pstatisch  PStau 
I
Hagen-Poisseuille
1
Pstatisch  v 2  konstant
2
dv
FR  A
dx
 4 p
I
R
8
l
Reibungskraft auf Körper
FR  k R v
Reynoldszahl
Re 
Bernoulli Gleichung
Newtonsches Reibungsgesetz
Physik f. Biochemiker, Chemiker & Geowissenschaftler | J. Winter
lv
