Lösungen zur ¨Ubungen zur Vorlesung Theoretische Chemie, Teil I

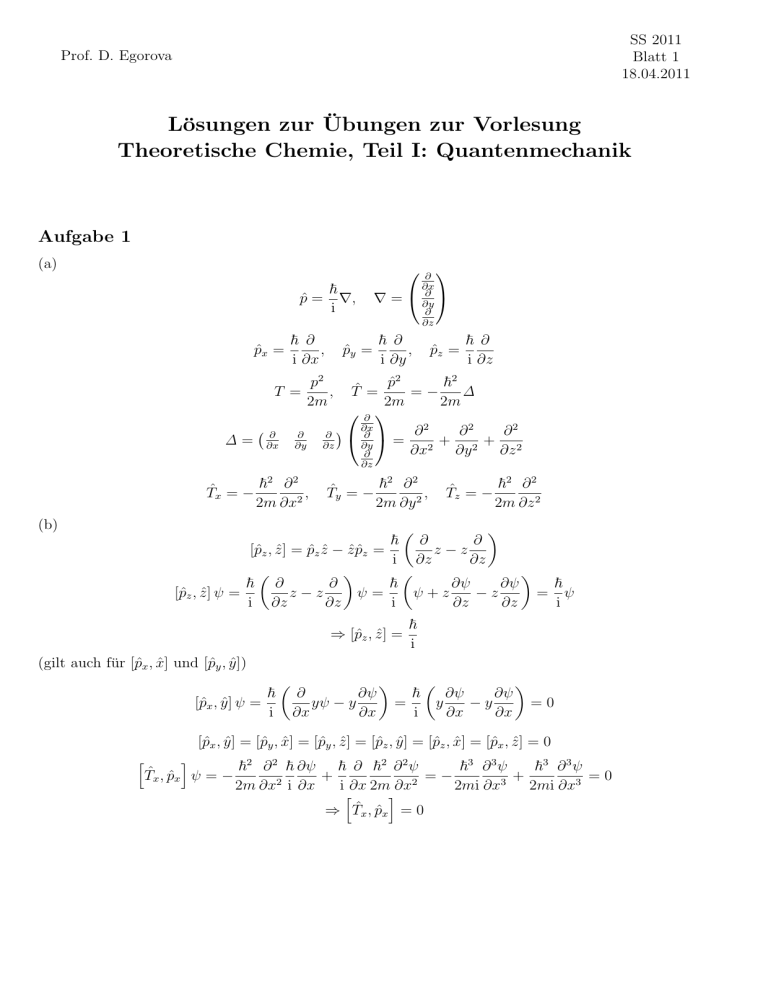
SS 2011
Blatt 1
18.04.2011
Prof. D. Egorova
Lösungen zur Übungen zur Vorlesung
Theoretische Chemie, Teil I: Quantenmechanik
Aufgabe 1
(a)
∂
p̂ =
p̂x =
~ ∂
,
i ∂x
T =
∆=
~
∇,
i
¡∂
∂x
∂
∂y
2
2
∂x
∂ 
∇ =  ∂y
∂
∂z
~ ∂
,
i ∂y
p̂y =
p̂z =
~ ∂
i ∂z
p2
,
2m
p̂2
~2
T̂ =
=−
∆
2m
2m
∂
∂x
¢
∂2
∂2
∂2
∂  ∂ 
=
+
+
∂z
∂y
∂x2 ∂y 2 ∂z 2
∂
∂z
T̂x = −
(b)
~ ∂
,
2m ∂x2
T̂y = −
~2 ∂ 2
,
2m ∂y 2
T̂z = −
~2 ∂ 2
2m ∂z 2
µ
¶
~ ∂
∂
[p̂z , ẑ] = p̂z ẑ − ẑ p̂z =
z−z
i ∂z
∂z
µ
¶
µ
¶
~ ∂
∂
~
∂ψ
∂ψ
~
[p̂z , ẑ] ψ =
z−z
ψ=
ψ+z
−z
= ψ
i ∂z
∂z
i
∂z
∂z
i
⇒ [p̂z , ẑ] =
~
i
(gilt auch für [p̂x , x̂] und [p̂y , ŷ])
~
[p̂x , ŷ] ψ =
i
µ
∂ψ
∂
yψ − y
∂x
∂x
¶
~
=
i
µ
∂ψ
∂ψ
y
−y
∂x
∂x
¶
=0
[p̂x , ŷ] = [p̂y , x̂] = [p̂y , ẑ] = [p̂z , ŷ] = [p̂z , x̂] = [p̂x , ẑ] = 0
h
i
T̂x , p̂x ψ = −
~3 ∂ 3 ψ
~3 ∂ 3 ψ
~2 ∂ 2 ~ ∂ψ ~ ∂ ~2 ∂ 2 ψ
+
=
−
+
=0
2m ∂x2 i ∂x
i ∂x 2m ∂x2
2mi ∂x3
2mi ∂x3
h
i
⇒ T̂x , p̂x = 0
h
i
Â, B̂ = 0 ⇒gleichzeitig meßbar
h
i
³
´
T̂y , ŷ ψ = T̂y ŷ − ŷ T̂y ψ
~2 ∂ 2
~2 ∂ 2
yψ
+
y
ψ
2m ∂y 2
2m ∂y 2
µ
µ
¶
¶
~2
∂
∂ψ
∂2
−
ψ+y
+ y 2ψ
2m
∂y
∂y
∂y
µ
¶
2
2
~
∂ψ ∂ψ
∂ ψ
∂ 2ψ
−
−
−y 2 +y 2
2m
∂y
∂y
∂y
∂y
µ
¶
2
~
∂ψ
−
2
2m
∂y
2
~ ∂ψ
−
m ∂y
h
i
~2 ∂
=⇒
T̂x , x̂ = −
m ∂x
= −
=
=
=
=
Aufgabe 2
(a)
Ĥ = T̂ + V̂ ,
(b)
T̂ = −
~2 ∂ 2
,
2m ∂x2
~2 ∂ 2
Ĥ = −
2m ∂x2
T̂ (x) = −
~2 ∂ 2
,
2m ∂x2
V̂ (x) = 0
kx2
2
V̂ (x) = V (x) =
Ĥ = T̂ + V̂ = −
~2 ∂ 2
kx2
+
2m ∂x2
2
Aufgabe 3
~ ∂
φi = pxi φi
i ∂x
∂
i
φi = pxi φi
∂x
~
ipxi
i
λ = pxi , φi = Ai e ~ x
~
i
freies Teilchen: pxi ∈ {−∞, +∞} ⇒ φ = Ae ~ px x
Aufgabe 4
Orthonormalbasis: hfi | fj i = δij
Orthogonalität: hfi | fj i = 0, i 6= j; Normierung: hfi | fi i = 1
fi = ci Pi
Normierung: i = j,
hfi | fi i = c∗i ci hPi | Pi i = 1
=⇒
¯1
2
x3 ¯¯
=
hP1 | P1 i =
x dx =
¯
3 −1 3
−1
Z
1
2
c∗i ci =
1
hPi | Pi i
r
=⇒
f1 =
3
P1 =
2
r
3
x
2
Z
¡
¢2
1 1
hP2 | P2 i =
dx 3x2 − 1
4 −1
Z
¡
¢
1 1
=
dx 9x4 − 6x2 + 1
4 −1
¯1
¯1
9 x5 ¯¯
6 x3 ¯¯
1
=
−
+ x|1−1
¯
¯
4 5
4 3
4
−1
−1
9
1
=
−1+
10
2
2
=
5
r
=⇒
f2 =
5
P2 =
2
r
¢
5¡ 2
3x − 1
8
Z
¡
¢2
1 1
hP3 | P3 i =
dx 5x3 − 3x
4 −1
Z
¡
¢
1 1
dx 25x6 − 30x4 + 9x2
=
4 −1
¯1
¯1
¯1
25 x7 ¯¯
30 x5 ¯¯
9 x3 ¯¯
=
−
+
4 7¯
4 5¯
4 3¯
−1
−1
3
25
−3+
=
14
2
2
=
7
r
=⇒
Orthogonalität: i 6= j,
Z
−1
f3 =
!
1
¢
1¡
x 3x2 − 1 dx
−1 2
µZ 1
¶
Z 1
1
3
3x dx −
xdx
=
2
−1
−1
¯1
¯1
3 x4 ¯¯
1 x2 ¯¯
=
−
2 4¯
2 2¯
−1
−1
= 0−0
= 0
1
¢
1¡
x 5x3 − 3x dx
−1 2
¯1
¯1
1 x3 ¯¯
1 x5 ¯¯
−
=
2 5 ¯−1 2 3 ¯−1
1
=
(1 + 1 − 1 − 1)
2
= 0
hP1 | P3 i =
r
¢
7¡ 3
5x − 3x
8
!
hf1 | f2 i = hf1 | f3 i = hf2 | f3 i = 0 =⇒ hP1 | P2 i = hP1 | P3 i = hP2 | P3 i = 0
hP1 | P2 i =
Z
7
P3 =
2
Z
1
¢1¡ 3
¢
1¡ 2
3x − 1
5x − 3x dx
2
−1 2
Z 1
Z
Z
Z
15
9 1 3
5 1 3
3 1
5
=
x dx −
x dx −
x dx +
xdx
4 −1
4 −1
4 −1
4 −1
= 0
hP2 | P3 i =
(b)
r µ
¶
´
­
®
® ³√
3
1
3­
3
2
6 − 3 hx | xi − i hx | 1i
hf1 | gi =
5 x |x + i x |x +
2
2
2
r µ
¶
´2
³√
3
=
6−3
− i0
2 + i0 −
2
3
= 2
hf2 | gi =
=
=
=
hf3 | gi =
=
=
=
r µ
´ ­
­
®
® ³√
®
®
3 ­
5
1 ­
5 · 3 x2 | x 3 + i · 3 x2 | x2 +
6 − 3 3 x2 | x − i · 3 x2 | 1
8
2
2
¶
³
´
√
­
®
®
3­
1
−5 1 | x3 − i 1 | x2 +
6 − 3 h1 | xi + i h1 | 1i
2
2
r µ
¶
3
2
1
2
3 2
1
5
0+i ·3· +0−i ·3· −0−i · −0+i ·2
8
2
5
2
3
2 3
2
r µ
¶
5 9
i
−1−1+1
8 5
r
2
i
5
r µ
´ ­
­
®
® ³√
®
®
7
3 ­
1 ­
5 · 5 x3 | x 3 + i · 5 x3 | x2 +
6 − 3 5 x3 | x − i · 5 x3 | 1
8
2
2
¶
³
´
√
­
®
®
3 ­
1
3
2
−5 · 3 x | x − i · 3 x | x +
6 − 3 · 3 hx | xi + i · 3 hx | 1i
2
2
r µ
¶
³√
´
³√
´
7 50
+ i0 +
6 − 3 · 2 − i0 − 6 − i0 −
6 − 3 · 2 + i0
8 7
r
7 8
·
8 7
r
2
2
7
r
r
2
2
g(x) = 2f1 + i
f2 + 2
f3
5
7
Alternativ
√
3
i
g (x) = 5x3 + i x2 + 6x − 3x −
2
2½
¾
©¡ 3
¢ª n√ o
¢
i¡ 2
=
5x − 3x +
6x +
3x − 1
2
√
= 2P3 + 6P1 + iP2
r
r
r
√
2
2
2
=
6
f1 + i
f2 + 2
f3
3
5
7
r
r
2
2
= 2f1 + i
f2 + 2
f3
5
7
Aufgabe 5
Ĥψ = Eψ,
E > 0,
−
−
Ĥ = −
~2 ∂ 2
2m ∂x2
~2 ∂ 2
ψ = Eψ
2m ∂x2
~2 2
λ =E
2m
√
⇒
ψ = A1 ei
2mEx/~
p2
E=
,
2m
√
λ=±
i√
2mE
~
√
+ A2 e−i
2mEx/~
2mE = p;
k=
p
~
ψ = A1 eikx + A2 e−ikx
= (A1 + A2 ) cos kx + i (A1 − A2 ) sin kx
= Ã1 cos kx + Ã2 sin kx
Eigenfunktionen des Impulsoperators:
φ = Aeipx x/~ = Aeikx
falls A2 = 0,
ψ = A1 eikx
ist auch Eigenfunktion von p̂x .
Aufgabe 6
(a)
p=
~ d
i dx
~
~
kf3 , p̂f3 = − kf2
i
i
p11 = 0 p12 = 0
p13 = 0
~
⇒ p21 = 0 p22 = 0 p23 = − i k
p31 = 0 p32 = ~i k
p33 = 0


0 0
0

~ 
p̂ = 0 0 − i k 
0 ~i k
0
p̂f1 = 0,
(b)
p̂f2 =
¯
¯
¯−λ 0
0 ¯¯
¯
¯
~ ¯
det (p̂ − Eλ) = ¯ 0 −λ − i k ¯ = 0
¯
¯
¯ 0 ~ k −λ ¯
i
3
2 2
−λ + ~ k = 0
Eigenwerte:
λ1 = 0,
Eigenvektoren:
zu λ1 = 0:
λ2 = ~k,
λ3 = −~k
   
 
1
0
0
0
x1
x1


0




0
i~k
x2 = 0 ⇒ x2 = 0
x3
x3
0
0 −i~k 0

zu λ2 = ~k:
x1 = 0
i~kx3 = ~kx2
x =i
⇒ 2
−i~kx2 = ~kx3
x3 = 1
 
0

⇒ i
1
zu λ3 = ~k:
x1 = 0
i~kx3 = −~kx2
x = −i
⇒ 2
−i~kx2 = −~kx3
x3 = 1
 
0

⇒ −i
1
Eigenfunktionen:
ψ1 = √
1
2π
1
1
ψ2 = if2 + f3 = √ (i sin kx + cos kx) = √ eikx
π
π
1
ψ3 = −if2 + f3 = √ e−ikx
π
(c) p̂ ist hermitisch, da die Eigenwerte reel sind