Odd Fellows

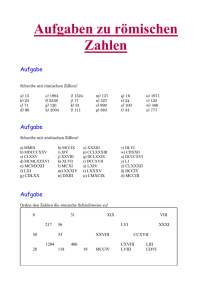
Rituelle Sitzung vom Dienstag, 21. Oktober 2008
XXXVII x LXIII Multiplizieren mit römischen Zahlen
Von Br. Ch. Hug
Ein paar Worte zum römischen Zahlensystem
Das ursprünglich nur auf die 3 Zahlen I, V, X basierende sehr einfache römische
Zahlensystem war letztendlich gerade deswegen schwerfällig und behinderte nicht nur das
Rechnen mit grösseren Zahlen sondern verhinderte geradezu die moderne Mathematik. Mit
dem römischen Zahlensystem, das noch keine Null kannte (obwohl sie schon eine
Bezeichnung für "Nichts" hatten, nämlich "nullum"), konnten nur einfachere
Rechnungsoperationen gemacht werden, wie addieren, subtrahieren, multiplizieren,
dividieren. Schon für Brüche gab es nur ein auf der (allerdings best teilbarsten) Zahl 12
basierendes Teilungssystem. Sehr grosse und sehr kleine Zahlen wie sie heute die
Wissenschaft und die Technik alltäglich benutzen, wären mit den römischen Zahlen und der
römischen Mathematik gar nicht darstellbar. Für Verwaltungsaufgaben jeder Art genügten
aber deren Möglichkeiten. Allerdings haben schon damals die weitgereisten Römer Händler
sehr schnell die vereinfachte "arabische" Rechnungsart für ihre Zwecke eingesetzt,
während die Beamtenschaft weiterhin die römische Zahlenschreibweise weiterführte. Einige
Jahrhunderte lang wurden beide Systeme nebeneinander genutzt. Das ist nicht weiter
erstaunlich, wenn man mit heute vergleicht, denn wir sind auch nicht gescheiter: das
Kilowatt hat im Alltag keine Chance gegen die Pferdestärke; das Joule ersetzt nicht die
Kalorie; in englischsprachigen Ländern gibt es für Masse und Gewichte immer noch kein
Zehnersystem (Gallonen, Yards u.s.w.).
Was Karlchen nicht lernt...... , oder: was der Bauer nicht kennt.....!
Der Übergang zum heutigen Zahlsystem
Während des Zerfalls des römischen Reiches breitete sich der Islam in Richtung Westen
aus. Er beherrschte letztendlich ein Gebiet das von Nordindien bis nach Spanien reichte. So
konnte sich auch "Das Buch über das Rechnen mit indischen Ziffern" von al-Chwarizmi (um
825), einem persischem Mathematiker sowie die Rechenbücher von Ibn Ezra (12. Jhdt) über
ein grosses Gebiet ausbreiten
Leonardo da Pisa genannt Fibonacci (ca. 1170 - 1240) ist der erste grosse Mathematiker
des christlichen Abendlandes, der mit indisch-arabischen Zahlen sowie mit den damit
ermöglichten komplexeren mathematischen Aufgaben vertraut war. Geschöpft hat er dabei
aus den Quellen der arabischen Mathematik, die vom 9. bis ins 12. Jahrhundert ihre
bedeutendsten Werke hervorbrachte. Fibonacci räumt der Null aber nicht den gleichen
Stellenwert wie den übrigen Zahlen ein - er nennt sie Zeichen statt Zahl. Im praktischen
alltäglichen Rechnen setzt sich die Null erst im 17. Jahrhundert durch.
Sehr zur Verbreitung der "arabischen" Zahlen beigetragen hat auch Adam Ries (1492 bis
1559). Er gilt allgemein als „Vater des modernen Rechnens" und hat mit seinen
Forschungen und Werken entscheidend dazu beigetragen, dass die römischen Zahlzeichen
als in der alltäglichen Praxis unhandlich erkannt und weitgehend durch die wesentlich
strukturierteren arabischen Zahlzeichen ersetzt wurden. Bemerkenswert ist, dass Adam
Ries seine Werke nicht – wie damals üblich – in lateinischer, sondern in deutscher Sprache
schrieb. Dadurch erreichte er einen großen Leserkreis. Ries' erstes Buch „Rechenung auff
der linihen (1518)" ist laut dem Vorwort der zweiten Auflage ausdrücklich für Kinder
bestimmt. In „Rechenung auff der linihen und federn... (1522)" beschreibt er das
Ziffernrechnen mit indischen-arabischen Ziffern speziell für Lehrlinge kaufmännischer und
handwerklicher Berufe.
Entwicklung der römischen Ziffern
Zahlensystem basiert auf:
I
V
X
Die später dazugekommenen Ziffern
L (50) C (100) D (500) M (1000)
Vereinfachte Schreibweise durch Subtraktion
40= XL statt XXXX
99= XCIX statt LXXXXVIIII
(falsch = IC)
Grosse Zahlen mit Vinculum und/oder Rahmen
V
5000
X
10.000
I
100.000
Beispiel:
XX
20.000
V
500.000
C
100.000
X
1.000.000
XXVCLDCLII
25’150’652
Brüche
Basiert auf 12er-Teilung
weil12 die meisten Teiler hat: 2,3,4,6
1/12
2/12
3/12
4/12
5/12
6/12
7/12
8/12
9/12
10/12
11/12
Uncia
Sextans
Quadrans
Triens
Quincunx
Semis
Septunx
Bessis
Dodrans
Dextans
Deunx
Beispiel:
1
3
(2 /4) = 2 / = IIQuadrans
II...
12
Praktische Multiplikationsübungen
63 x 37
63 x 37
21 (7 x 3)
420 (7 x 60)
90 (30 x 3)
1800 (30 x 60)
2331
441
189
2331
heute übliche Methode
Fortgesetzte Addition
der Multiplikanden:
entspricht einer römischen
Multiplikationsmethode
“à la Römer”
LXIII
x
XXXVII
DCXXX
DCXXX
DCXXX
CCLLVVV
LXIII
LXIII
(LXIII mal X)
(LXIII mal X)
(LXIII .mal X)
LXIII mal V)
(LXIII .mal..I)
(LXIII .mal..I)
DDD’CCCCC’LLLL’XXXXXXXXXXX’VVV’IIIIII
MMCCCXXXI
2
3
3
(fortgesetzte Addition
der Multiplikanden)
1
(auf einer Linie geschrieben)
(zusammengeführt und vereinfacht)I
Die hier beschriebene Methode ist für Anfänger.
Geübte Römer vereinfachten möglichst viel
schon beim Multiplizieren!
Es gibt noch andere Multiplikationsmethoden
mit römischen Zahlen.