Lineare Algebra - Alexander Stoffel

Mathematik für den Studiengang
Bachelor Technische Informatik
Zug 1TINb“
”
Lineare Algebra
Alexander Stoffel
Institut für Nachrichtentechnik
Fakultät für Informations-, Medien- und Elektrotechnik
Fachhochschule Köln
16. Januar 2014
1
Einleitung
Dieses Skript ist ausschließlich für die Teilnehmer meiner Lehrveranstaltung Mathematik 1
und Mathematik 2 gedacht — neben dem entsprechenden Skript zur Analysis. Es ist noch
fehlerbehaftet, änderungs- und ergänzungsbedürftig. Für entsprechende Hinweise bin ich
sehr dankbar, insbesondere für Hinweise auf Tippfehler und andere Unstimmigkeiten.
Ansonsten sei hier auf das entsprechende Einleitungskapitel im Skript zur Analysis
verwiesen. Was dort gesagt ist, kann entsprechend auch für die Lineare Algebra angewandt
werden und braucht hier nicht nochmal wiedergegeben werden — mit Ausnahme der
Literaturangaben. Auch die hier angegebene Liste stellt nur eine kleine und teilweise
zufällige Auswahl dar:
(1) Papula, Lothar: Mathematik für Ingenieure 2. 6. Auflage, Vieweg, Braunschweig,
1991.
(2) Andrié, Manfred; Meier, Paul: Lineare Algebra und Analytische Geometrie. Eine
anwendungsbezogene Einführung. Bibliographisches Institut, Mannheim, 1977.
(3) Strang, Gilbert: Introduction to linear algebra. Wellesley-Cambridge Press, Wellesley (USA), 1993.
(4) Strang, Gilbert: Linear algebra and its applications. Third edition, Harcourt Brace
Jovanovich, San Diego (USA), 1988
(5) Meyberg, Kurt; Vachenauer, Peter: Höhere Mathematik 1. Springer, Berlin, 1991
(6) Jänich, Klaus: Lineare Algebra. 4. Auflage, Springer, Berlin, 1991
(7) Penney, Richard: Linear Algebra. Wiley-VCH, New York, 1998
(8) Beutelspacher, Albrecht: Lineare Algebra. Eine Einführung in die Wissenschaft der
Vektoren, Abbildungen und Matrizen. 3. Auflage, Vieweg, Braunschweig/Wiesbaden,
1998
2
Inhaltsverzeichnis
1 Grundbegriffe
1.1 Natürliche und ganze Zahlen .
1.2 Summen- und Produktzeichen,
1.2.1 Summenzeichen . . . .
1.2.2 Produktzeichen . . . .
1.2.3 Vollständige Induktion
1.2.4 Binomischer Lehrsatz .
. . . . . . .
vollständige
. . . . . . .
. . . . . . .
. . . . . . .
. . . . . . .
5
. . . . . . . . . . . . . . . . . . 5
Induktion, binomischer Lehrsatz 5
. . . . . . . . . . . . . . . . . . 5
. . . . . . . . . . . . . . . . . . 7
. . . . . . . . . . . . . . . . . . 7
. . . . . . . . . . . . . . . . . . 8
2 Vektorrechnung
2.1 Addition von Vektoren und Multiplikation mit einem Skalar . .
2.2 Komponentendarstellung von Vektoren . . . . . . . . . . . . . .
2.3 Skalarprodukt und Betrag . . . . . . . . . . . . . . . . . . . . .
2.4 Beschreibung von Geraden . . . . . . . . . . . . . . . . . . . . .
2.4.1 Vektorielle Beschreibung . . . . . . . . . . . . . . . . . .
2.4.2 Beschreibung einer Geraden durch einen Normalenvektor
2.5 Vektorprodukt . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.6 Beschreibung von Ebenen im Raum . . . . . . . . . . . . . . . .
2.6.1 Vektorielle Beschreibung . . . . . . . . . . . . . . . . . .
2.6.2 Beschreibung einer Ebene durch einen Normalenvektor .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3 Lineare Gleichungssysteme
3.1 Gauß-Verfahren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.1 Einfaches Beispiel, Rückwärtsauflösen . . . . . . . . . . . . . . . .
3.1.2 Umwandlung in Dreiecksform, einfaches Beispiel . . . . . . . . . .
3.1.3 Weiteres Beispiel zur Umwandlung in Dreiecksform in Kurzschreibweise . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.4 Allgemeines Prinzip des Gauß-Verfahrens . . . . . . . . . . . . . .
3.2 Geometrische Deutung linearer Gleichungssysteme . . . . . . . . . . . . .
3.3 Homogene und inhomogene lineare Gleichungssysteme . . . . . . . . . . .
3.4 Unter- und überbestimmte lineare Gleichungssysteme . . . . . . . . . . .
3.4.1 Unterbestimmte lineare Gleichungssysteme . . . . . . . . . . . . .
3.4.2 Überbestimmte Systeme . . . . . . . . . . . . . . . . . . . . . . .
4 Vektorräume
4.1 Definition des Begriffs Vektorraum“ . . . . .
”
4.2 Der Rn . . . . . . . . . . . . . . . . . . . . . .
4.3 Lineare Abhängigkeit, lineare Unabhängigkeit
4.4 Basis, Dimension . . . . . . . . . . . . . . . .
5 Matrizen
5.1 Matrix als Koeffizientenschema . . . . . . . .
5.2 Lineare Gleichungssysteme und Matrizen . . .
5.3 Lineare Abbildungen und Matrizen . . . . . .
5.4 Matrixmultiplikation und -addition . . . . . .
5.5 Die Umkehrabbildung und die inverse Matrix
5.6 Die transponierte Matrix . . . . . . . . . . . .
5.7 Der Rang einer Matrix . . . . . . . . . . . . .
3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
11
11
12
15
18
18
19
21
24
24
25
26
. 26
. 26
. 28
.
.
.
.
.
.
.
29
31
35
42
43
43
44
.
.
.
.
46
47
50
51
56
.
.
.
.
.
.
.
62
62
63
66
71
81
88
90
6 Endliche Körper und ihre Anwendungen
6.1 Restklassen . . . . . . . . . . . . . . . .
6.2 Endliche Körper . . . . . . . . . . . . . .
6.3 Kanalcodierung: Beispiele . . . . . . . .
bei der
. . . . .
. . . . .
. . . . .
7 Determinanten
7.1 Determinanten für n = 2 und n = 3, Cramersche
7.2 Laplacesche Entwicklung . . . . . . . . . . . . .
7.3 Eigenschaften der Determinante . . . . . . . . .
7.4 Determinanten und Permutationen . . . . . . .
Kodierung
. . . . . . . . . . . . . .
. . . . . . . . . . . . . .
. . . . . . . . . . . . . .
Regel
. . . .
. . . .
. . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
8 Eigenwerte
8.1 Eigenwerte und Eigenvektoren . . . . . . . . . . . . . . . . . . . . . . . .
8.2 Vielfachheit von Eigenwerten . . . . . . . . . . . . . . . . . . . . . . . .
8.3 Diagonalisierung von Matrizen . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
91
91
96
99
104
104
106
108
109
111
. 111
. 118
. 119
9 Weitere Methoden der Algebra in der Nachrichtentechnik: ein Ausblick122
9.1 Polynome und Körpererweiterungen . . . . . . . . . . . . . . . . . . . . . . 122
9.2 Zyklische Codes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126
10 Näherungen
131
10.1 Näherungslösungen für überbestimmte Gleichungssysteme . . . . . . . . . 131
10.2 Beste Näherung durch Vektoren aus einem Unterraum . . . . . . . . . . . 134
A Anhang: Ergänzungen
A.1 Gruppen . . . . . . . .
A.2 Relationen . . . . . . .
A.3 Potenzmenge . . . . .
A.4 Ergänzungen zur Logik
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
143
143
147
151
152
1
1.1
Grundbegriffe
Natürliche und ganze Zahlen
Die Menge der natürlichen Zahlen N wird durch folgende Axiome charakterisiert, die von
dem italienischen Mathematiker Peano stammen:
Axiome 1.1.1
(a) 0 ist eine natürliche Zahl, 0 ∈ N
(b) Jede natürliche Zahl n besitzt genau eine natürliche Zahl als Nachfolger“, der n + 1
”
geschrieben wird.
(c) Wenn die Nachfolger zweier natürlicher Zahlen übereinstimmen, dann stimmen die
urprünglichen Zahlen ebenfalls überein.
(d) 0 ist nicht Nachfolger einer natürlichen Zahl.
(e) Jede Teilmenge M ⊂ N, die die Eigenschaft hat, dass
0∈M
n ∈ M =⇒ n + 1 ∈ M
und
stimmt mit N überein.
Hinweis: Axiom (e) ist die Grundlage der Beweismethode der vollständigen Induktion“,
”
die in Abschnitt 1.2.3 behandelt wird.
Weiterhin vereinbaren wir
N+ := {n ∈ N | n > 0} = N \ {0}
und nennen die Menge der ganzen Zahlen Z, also
Z = {0, +1, −1, +2, −2, +3, −3, +4, −4, +5, −5, . . .}
Leider wird diese Bezeichnungsweise nicht überall verwandt, in einigen Büchern wird von
einer andern Vereinbarung (dies ist auch historisch die ursprüngliche) ausgegangen; dort
gehört die Null nicht zur Menge der natürlichen Zahlen. Die Menge der natürlichen Zahlen
mit der Null wird dort meist mit N0 bezeichnet. Diese Konvention wurde auch bei früheren
Ausgaben dieses Skriptes verwendet. Schauen Sie also beim Benutzen von Büchern nach,
wie der Autor die Menge der natürlichen Zahlen definiert!
1.2
1.2.1
Summen- und Produktzeichen, vollständige Induktion, binomischer Lehrsatz
Summenzeichen
Wir führen hier das Summenzeichen zunächst an Beispielen ein, die allgemeine Definition
wird später gegeben. Nach der Legende wurde der Mathematiker Gauß in seiner Schulzeit
mit der Aufgabe beschäftigt, die ersten 100 Zahlen zu addieren. Wir können diese Aufgabe
mit Pünktchen“ formulieren oder hierzu das Summenzeichen verwenden
”
100
X
1 + 2 + 3 + 4 + · · · + 100 =
k
k=1
5
P
Das Summenzeichen
ist ein großes griechisches Sigma“. Unten steht der Startwert“
”
”
des Summationsindex und oben sein höchster Wert. Der Startwert ist bis zum Erreichen
des Höchstwertes jeweils um 1 zu erhöhen. Wir werden im Abschnitt 1.2.3 eine Formel
beweisen, die es ermöglicht, diese Summe sofort auszurechnen. Weitere Beispiele für die
Verwendung des Summenzeichens:
10
X
1 + 4 + 9 + 16 + 25 + · · · + 100 =
k=1
5
X
13 + 23 + 33 + 43 + 53 =
k2
k 3 = 225
k=1
Auch zur Berechnung dieser Summen werden wir in den Übungen eine einfache Formel
kennenlernen. Beachten Sie, dass die Summe nicht davon abhängt, welchen Buchstaben
wir als Index oder Variable zum Zählen der Summanden verwenden. Es gilt also
5
X
k=1
3
k =
5
X
3
l =
5
X
3
i =
3
m =
m=1
i=1
l=1
5
X
5
X
n3
n=1
Und hier die allgemeine Definition
Definition 1.2.1 ak steht symbolisch für Summanden, die von k abhängen, wobei k ∈ Z
vorausgesetzt wird. Außerdem wird n ≥ m vorausgesetzt. Dann wird definiert
n
X
ak := am + am+1 + am+2 + am+3 + · · · + an−1 + an
k=m
Hinweise:
(a) Die Zahl der Summanden beträgt n − m + 1.
(b) Die Indizes (Mehrzahl von Index) können auch negativ sein, also beispielsweise
2
X
2k = 2−2 + 2−1 + 20 + 21 + 22 =
k=−2
3
1 1
+ +1+2+4=7+
4 2
4
Bei dieser Gelegenheit ein wichtiger Hinweis: In der Mathematik wird vereinbart
(siehe das Skript zur Analysis), dass ein nicht hingeschriebenes Zeichen für eine
Rechenoperation stets als Punkt für die Multiplikation zu interpretieren ist. Bei
Ergebnissen wie 7 + 43 darf also in der Mathematik und in der Nachrichtentechnik
das Plus-Zeichen nicht weggelassen werden, auch wenn dies bei Kartoffelhändlern
üblich ist!
(c) Die Summe ist völlig unabhängig davon, welcher Formelbuchstabe für den Summationsindex verwandt wird, also
n
X
k=m
ak =
n
X
l=m
6
al =
n
X
i=m
ai
1.2.2
Produktzeichen
Das Produktzeichen ist ganz ähnlich zum Summenzeichen definiert, nur dass die auftretenden Zahlen zu multiplizieren sind. Wir haben also beispielsweise
1·2·3·4·5·6 =
1 · 3 · 5 · 7 · 9 · 11 =
6
Y
k
k=1
5
Y
(2k + 1)
k=0
Q
Das Zeichen
ist ein großes griechisches Pi. Auch hier ist unten der Startwert des Index,
der jeweils um 1 zu erhöhen ist, bis der oben angegebene maximale Wert erreicht ist. Die
allgemeine Definition lautet analog zu der des Summenzeichens:
Definition 1.2.2 ak steht symbolisch für Faktoren, die von k abhängen, wobei k ∈ Z
vorausgesetzt wird. Außerdem wird n ≥ m vorausgesetzt. Dann wird definiert
n
Y
ak := am · am+1 · am+2 · am+3 · · · an−1 · an
k=m
Hinweis: Wir haben insgesamt n − m + 1 Faktoren.
Definition 1.2.3 Für alle n ∈ N wird definiert
 n
 Q k = 1 · 2 · 3 · · · n falls
n! :=
 k=1
1
falls
n>0
n=0
(lies n Fakultät“)
”
Hinweise:
(a) Die Definition 0! = 1 mag zwar willkürlich erscheinen, sie vermeidet aber sehr viele
Fallunterscheidungen.
(b) n! wächst mit größer werdendem n sehr stark an, wie die Beispiele
6! = 720,
9! = 362 880,
100! ≈ 0, 9332622 · 10158
zeigen
1.2.3
Vollständige Induktion
Die Beweismethode der vollständigen Induktion beruht darauf, dass man das PeanoAxiom (e) ausnutzt und als Teilmenge M ⊂ N die Menge der natürlichen Zahlen nimmt,
für die eine Aussage A richtig ist. Als Beispiel für eine solche Aussage A wird uns die Glein
P
für n ∈ N dienen. Ein solcher Beweis heißt dann Beweis durch
chung
k = n(n+1)
2
”
k=1
vollständige Induktion“. Nach dem Axiom (e) genügt es also, folgende Beweisschritte
durchzuführen, um die Behauptung A für alle n ∈ N zu beweisen:
7
Induktionsbeginn: Man beweist die Aussage für n = 0 (dies ist meist sehr einfach).
Induktionsannahme: Man nimmt an, die Behauptung A sei für ein festes, aber beliebiges n ∈ N richtig.
Induktionsschluß: Mit Hilfe der Induktionsannahme beweist man, dass die Behauptung
A für n + 1 richtig ist.
Wir beweisen nun als Beispiel die Formel von Gauß, die seine Schulaufgabe löst:
Satz 1.2.1 Für alle n ∈ N gilt
n
X
n(n + 1)
2
k=
k=0
Beweis durch vollständige Induktion:
Induktionsbeginn:
0
P
k=0=
k=0
Induktionsvoraussetzung:
n
P
0·(0+1)
2
k=
k=0
Induktionsbehauptung:
n+1
P
n(n+1)
2
für ein festes n ∈ N
k=
(n+1) (n+1)+1
2
k=0
(überall in der Behauptung A wurde n
durch n + 1 ersetzt.)
Induktionsbeweis: Nach der Definition des Summenzeichens haben wir
n+1
X
k=0
k=
n
X
k+n+1
k=0
Den ersten Summanden auf der rechten Seite können wir mit Hilfe der Induktionsvoraussetzung umformen, also haben wir insgesamt
n+1
X
k=0
k=
n
X
k=0
k+n+1=
n(n + 1)
n(n + 1) + 2(n + 1)
(n + 2)(n + 1)
+n+1=
=
2
2
2
und damit ist die Induktionsbehauptung bewiesen. Und damit ist auch der Satz
bewiesen.
Weitere Beispiele werden in den Übungen besprochen.
1.2.4
Binomischer Lehrsatz
Ziel dieses Abschnitts ist es, eine allgemeine Formel für (a + b)n herzuleiten, die die
binomische Formel (a + b)2 = a2 + 2ab + b2 verallgemeinert. Durch Ausmultiplizieren kann
man für n = 4 erhalten
(a + b)4 = a4 + 4a3 b + 6a2 b2 + 4ab3 + b4
8
Ordnet man die Koeffizienten, die beim Ausmultiplizieren von (a + b)n auftreten, in
einem Dreieck an, dann erhält man das berühmte Pascalsche Dreieck (das nach dem
französischen Philosophen und Mathematiker Blaise Pascal benannt ist):
1
1
1
1
1
1
1
2
3
4
5
6
1
3
6
10
15
1
1
4
10
20
1
5
15
1
6
1
Das Konstruktionsprinzip ist klar erkennbar: die Summe zweier benachbarter Zahlen ergibt die darunterstehende Zahl. Wir geben nun eine Formel an, die es erlaubt, die Zahlen
im Pascalschen Dreieck zu berechnen:
Definition 1.2.4 Für alle n, k ∈ N mit n ≥ k werden die Binomialkoeffizienten durch
n
n!
:=
k!(n − k)!
k
definiert (zu lesen n über k“).
”
4
4
4
4!
4!
= 1, 41 = 1!·3!
= 1·2·3·4
=
4,
=
6,
=
4,
= 1
Zahlenbeispiele: 40 = 0!·4!
1·1·2·3
2
3
4
(Nachrechnen, die Fakultäten nicht ausrechnen, sondern vorher kürzen!) Offensichtlich
erhält man die 4. Zeile des Pascalschen Dreiecks, wenn man beim Zählen mit 0 anfängt.
Eigenschaften der Binomialkoeffizienten:
(a) n0 = 0!n!n! = 1
(b) nn = n!n!0! = 1
n!
(c) n1 = 1!(n−1)!
= 1·2·3···(n−1)·n
=n
1·1·2·3···(n−1)
n
n!
(d) n−1
= (n−1)!
=n
1!
n
n!
n!
= (n−k)!·k!
= nk (Symmetrie!)
(e) n−k
=
(n−k)! n−(n−k) !
(f)
n
k
=
1·2·3···(n−k)·(n−k+1)···n
k!·1·2·3···(n−k)
=
n·(n−1)·(n−2)···(n−k+1)
k!
Diese Identitäten gelten für alle n ∈ N. Sie garantieren bereits, dass die durch Definition 1.2.4 festgelegten Binomialkoeffizienten mit den Zahlen am Rand des Pascalschen
Dreiecks übereinstimmen, wenn man die Zeilen (n) und die waagrechte Position (k) jeweils mit 0 anfängt zu zählen. Die wesentliche Eigenschaft der Zahlen im Pascalschen
Dreieck ist, dass jede Zahl als Summe der beiden darüberstehenden Zahlen entsteht. Das
Dreieck wird mit jeder Zeile nach links (und rechts) größer. Also stehen über der Zahl an
k. waagrechter Position der (n+1). Zeile die Zahlen der n. Zeile an (k −1). (links darüber)
und k. Position (rechts darüber). Die Übereinstimmung der Zahlen im Pascalschen Dreieck mit den Binomialkoeffizienten nach Def. 1.2.4 wird also erst durch den folgenden Satz
geliefert:
9
Satz 1.2.2 Für alle n ∈ N+ und alle k ∈ N+ mit k ≤ n gilt
n+1
n
n
=
+
k
k−1
k
Beweis:
k
n!
(n − k + 1)
n
n
n!
· +
·
+
=
k−1
k
(k − 1)! n − (k − 1) ! k k!(n − k)! (n − k + 1)
n!k + n!(n − k + 1)
n!(k + n − k + 1)
(n + 1)!
=
=
=
k!(n − k + 1)!
k!(n + 1 − k)!
k!(n + 1 − k)!
n+1
=
k
Merke: Die Binomialkoeffizienten nk stehen im Pascalschen Dreieck in der n. Zeile in
der k. Position von links, jeweils von 0 an gezählt.
Satz 1.2.3 (Binomischer Lehrsatz) Für alle n ∈ N0 und für alle a, b ∈ R gilt
n X
n n−k k
n
a b
(a + b) =
k
k=0
Beweis: (durch vollständige Induktion)
Induktionsbeginn: (a + b)0 = 1,
0
P
k=0
0
k
0−k 0
a b = a0 · b 0 = 1
Induktionsvoraussetzung: (a + b)n =
n
P
k=0
Induktionsbehauptung: (a + b)n+1 =
n+1
P
k=0
n
k
an−k bk für ein festes n
n+1
k
n+1−k k
a
b
Induktionsbeweis: Wir multiplizieren beide Seiten der Induktionsvoraussetzung mit
(a + b) und erhalten
n n n X
X
X
n n−k k
n n−k k
n n−k k
n+1
(a + b)
= (a + b)
a b =a·
a b +b·
a b
k
k
k
k=0
k=0
k=0
n n X
X
n n−k k+1
n n−k+1 k
=
a
b +
a b
k
k
k=0
k=0
n n+1
a
+ n1 an b1
+ n2 an−1 b2 + · · · + nn a1 bn
=
0
n n 1
n n−1 2
n
n n+1
1 n
+
a
b
+
a
b
+
·
·
·
+
a
b
+
b
0 1 n−1
n n+1 n+1
n+1 n 1
n+1 n−1 2
n+1 1 n
n+1 n+1
a
+ 1 a b + 2 a b + · · · + n a b + n+1 b
=
0
n+1
P n+1 n+1−k k
=
a
b
k
k=0
n+1
n
Dabei wurde
bei
den
außenstehenden
Summanden
ausgenutzt,
dass
=
=1
0
0
n
n+1
und n = n+1 = 1. Ansonsten wurden die übereinanderstehenden Summanden
(mit denselben Potenzen von a und b) unter Benutzung von Satz 1.2.2 zusammengefaßt.
10
2
2.1
Vektorrechnung
Addition von Vektoren und Multiplikation mit einem Skalar
Vektoren sind gerichtete Größen“, Kraft, Geschwindigkeit, elektrische Feldstärke sind
”
Beispiele aus der Physik. Wir wollen hier Vektoren als geordnete Paare von Punkten
in der Ebene oder im Raum ansehen. Geordnet heißt, dass einer der beiden Punkte der
Anfangspunkt, der andere der Endpunkt ist. Wichtig ist die folgende Vereinbarung:
Zwei Vektoren sind gleich, wenn Sie durch Parallelverschiebung ineinander
übergeführt werden können.
Dies bedeutet, zwei Vektoren sind gleich, wenn sie in Betrag (Länge) und Richtung
übereinstimmen (siehe auch Abb. 1).
Abbildung 1: Zur Gleichheit von Vektoren
Wir werden hier Vektoren durch einen Pfeil über dem Formelbuchstaben wie in ~a, ~b
oder durch Fettdruck a, b gegenüber anderen Größen hervorheben.
Abbildung 2: Zur Addition von Vektoren
Unter dem Antragen eines Vektors in einem Punkt P versteht man an eine Parallelverschiebung des Vektors so, dass sein Anfangspunkt im Punkt P liegt. Ein Vektor ~b
wird zu einem Vektor ~a addiert, indem man ~b im Endpunkt des Vektors ~a anträgt. Der
Vektor ~a + ~b ist dann der Vektor vom Anfangspunkt von ~a zum Endpunkt von ~b. Dies ist
in Abb. 2 veranschaulicht. Geometrisch bedeutet dies:
~a + ~b ist die gerichtete Diagonale des von ~a und ~b aufgespannten Parallelogramms ( Parallelogrammregel“, siehe auch die Abb. 2).
”
11
Der Nullvektor ~0 ist ein Vektor der Länge 0, Anfangs- und Endpukt fallen zusammen.
Der Vektor −~a entsteht aus dem Vektor ~a, indem man Anfangs- und Endpunkt vertauscht,
also seine Richtung umkehrt.
Abbildung 3: Zur Multiplikation von Vektoren mit einem Skalar
Man nennt Größen, die im Unterschied zu Vektoren keine Richtung haben, Skalare.
In der Physik sind beispielsweise Masse, Energie und Zeit Skalare. Hier sind Skalare reelle
Zahlen (wir werden später auch komplexe Zahlen als Skalare zulassen). Die Multiplikation eines Vektors ~a mit einem Skalar t ∈ R ist wie folgt definiert:
• Falls t > 0, dann ist t~a der Vektor derselben Richtung und der t-fachen Länge.
• Falls t < 0, dann ist t~a der Vektor der umgekehrten Richtung (Anfangs- und Endpunkt vertauscht) und der |t|-fachen Länge.
• Falls t = 0, dann ist t~a = ~0, also der Nullvektor.
Dies ist in Abb. 3 veranschaulicht. Es ist plausibel und folgt aus geometrischen Regeln,
dass für die so definierten Rechenoperationen folgende grundlegende Rechenregeln gelten:
Für alle Vektoren ~a, ~b, ~c gilt
~a + ~b = ~b + ~a
(Kommutativgesetz)
(~a + ~b) + ~c = ~a + (~b + ~c)
(Assoziativgesetz)
~
~a + 0 = ~a
(neutrales Element für die Addition)
zu jedem ~a existiert ein −~a mit
~a + (−~a) = ~0
(1)
(2)
(3)
(4)
und für alle Vektoren ~a, ~b und alle Skalare s, t ∈ R gilt
t(~a + ~b)
(s + t)~a
s(t~a)
1 · ~a
=
=
=
=
t~a + t~b
s~a + t~a
(st)~a
~a
(5)
(6)
(7)
(8)
Hinweis: Regel (5) ist der Strahlensatz (siehe Abb. 4).
2.2
Komponentendarstellung von Vektoren
Um mit Vektoren zu rechnen, wählen wir ein Koordinatensystem aus und vereinbaren,
alle Vektoren im Urspung dieses Koordinatensystems anzutragen. Vektoren der Länge 1
heißen Einheitsvektoren. Die Einheitsvektoren in die Richtung der Koordinatenachsen
12
Abbildung 4: Zur Rechenregel (5) (Strahlensatz)
Abbildung 5: Komponentendarstellung von Vektoren
bezeichnen wir mit ~ex , ~ey , ~ez . Betrachten wir einen Vektor ~a in der Ebene (siehe die
Abb. 5). Wir bezeichnen die Koordinanten des Endpunkts mit ax und ay . Wir können
den Vektor ~a also als Summe schreiben
~a = ax · ~ex + ay~ey
Wir bezeichnen dabei ax als Komponente in x-Richtung oder kurz als x-Komponente
und ay als Komponente in y-Richtung. Diese Zerlegung in eine Summe heißt Komponentendarstellung von ~a. Sie gibt Anlaß zu folgender Kurzschreibweise von Vektoren in der
Ebene:
ax
~a =
ay
In dieser Schreibweise wird ~a als Spaltenvektor bezeichnet.
Im Raum geht man analog vor und bezeichnet die Koordinaten des Endpunkts von ~a
mit ax , ay , az . Man erhält die Komponentendarstellung
~a = ax · ~ex + ay~ey + az~ez
und schreibt ~a als Spaltenvektor
 
ax
~a = ay 
az
Der Nullvektor hat die Darstellung
~0 = 0
0
bzw.
13
 
0
~0 = 0
0
Aus der Parallelogrammregel erhält man die folgende Rechenregel für die Addition von
Abbildung 6: Zur Addition von Vektoren in Komponentendarstellung
Vektoren in Komponentendarstellung (siehe hierzu die Abb. 6)
ax + b x
bx
ax
~
=
+
~a + b =
ay + b y
by
ay
Für Vektoren im Raum gilt eine entsprechende Regel:
    

ax
bx
ax + b x
~a + ~b = ay  + by  = ay + by 
az
bz
az + b z
Merke: Vektoren werden komponentenweise addiert.
Für die Multiplikation mit einem Skalar erhalten wir in der Komponentendarstellung in
der Ebene
a
tax
t~a = t x =
ay
tay
und im Raum
   
ax
tax



t~a = t ay = tay 
az
taz
Merke: Ein Vektor wird mit einem Skalar multipliziert, indem man alle Komponenten
mit dem Skalar multipliziert.
Hinweis zur Geometrie:
Der Verbindungsvektor von P nach Q (also der Vektor mit Anfangspunkt P und Endpunkt
−→
Q) wird hier mit P Q bezeichnet. Den Ursprung bezeichnen wir mit O. Der Verbindungs−→
vektor OP vom Ursprung zum Punkt P wird der Ortsvektor des Punktes P genannt.
14
Abbildung 7: Verbindungsvektor von P nach Q
Zwischen den Ortsvektoren zweier Punkte P und Q und deren Verbindungsvektor besteht
der nützliche Zusammenhang
−→
−→ −→ −→ −→
P Q = −OP + OQ = OQ − OP
den man sich am besten anhand einer kleinen Skizze klarmacht (siehe Abb. 7).
Wir gehen im weiteren immer davon aus, dass ein festes Koordinatensystem gewählt
−→
wurde und werden meist den Punkt P mit seinem Ortsvektor OP identifizieren.
Hinweis zur Schreibweise:
Eine Spalte aus zwei oder drei Zahlen nimmt satztechnisch sehr viel Platz weg. Es wäre
viel platzsparender, die zwei oder drei Zahlen als Zeile anzuordnen. Um dies zu erreichen,
ist die Schreibweise
 
a
T

(a, b, c) := b 
c
üblich. Allgemein bedeutet AT die transponierte Matrix (wird später behandelt). Bei
einer Zeile bedeutet dieses Symbol also, dass statt dessen die Spalte gemeint ist.
2.3
Skalarprodukt und Betrag
Die Länge eines Vektors ~a wird hier Betrag des Vektors genannt und |~a| geschrieben. Er
läßt sich aus den Komponenten berechnen:
p 2
a + a2y
falls ~a ein Vektor in der Ebene ist
(9)
|~a| = p x2
ax + a2y + a2z falls ~a ein Vektor im Raum ist
In der Ebene folgt dies unmittelbar aus dem Satz von Pythagoras (siehe Abb. 5). Im
Raum (siehe hierzu Abb. 8) kann man zunächst das Lot vom Endpunkt P des Vektors
auf die xy-Ebene fällen, dies liefert den Hilfspunkt Q, dessen Abstand vom Ursprung man
nach Pythagoras als
q
d = a2x + a2y
berechnet. Wendet man nun den Satz von Pythagoras auf das rechtwinklige Dreieck an,
das die Punkte O, P und Q verbindet, so erhält man
q
p
2
2
|~a| = d + az = a2x + a2y + a2z
15
Abbildung 8: Berechnung des Betrags eines Vektors aus den Komponenten (siehe (9)
Abbildung 9: Winkel zwischen zwei Vektoren
Den Winkel α zwischen zwei Vektoren ~a und ~b wählen stets wir so, dass er zwischen
0 und π liegt (beide Randpunkte eingeschlossen), also 0 ≤ α ≤ π (d.h. wir wählen den
kleineren der beiden möglichen Winkel, siehe Abb. 9). Er ist nur sinnvoll, wenn beide
Vektoren nicht mit dem Nullvektor übereinstimmen.
Definition 2.3.1 Das Skalarprodukt zweier Vektoren ist durch
(
ax b x + ay b y
falls ~a und ~b Vektoren in der Ebene sind
~a · ~b :=
ax bx + ay by + az bz falls ~a und ~b Vektoren im Raum sind
definiert.
Hinweise:
(a) Beachten Sie, dass das Ergebnis des Skalarprodukts stets ein Skalar, also eine reelle
Zahl ist! Daher kommt der Name!
(b) Das Skalarprodukt wird manchmal auch inneres“ Produkt genannt.
”
(c) Für das Skalarprodukt sind auch andere Schreibweisen gebräuchlich. In der Mathematik ist
~a · ~b = (~a, ~b)
sehr verbreitet, in den Ingenieurwissenschaften ist auch
a · b = aT b
üblich. Diese Schreibweise wir erst verständlich, wenn wir das Rechnen mit Matrizen
behandelt haben (die Spaltenvektoren a und b werden als Matrizen mit einer Spalte
und zwei bzw. drei Zeilen aufgefaßt, aT ist dann die transponierte Matrix und mit
aT b ist das Produkt von zwei Matrizen gemeint).
16
Abbildung 10: Zum Beweis von Satz 2.3.1
Satz 2.3.1 Für alle Vektoren ~a gilt
|~a| =
√
~a · ~a
und für alle Vektoren ~a und ~b mit ~a 6= ~0 und ~b 6= ~0 gilt
~a · ~b = |~a| · |~b| · cos(ϕ)
wobei ϕ der Winkel zwischen ~a und ~b ist.
Beweis: Die erste Gleichung folgt unmittelbar aus der Definition. Die zweite wird hier
nur für den Fall bewiesen, dass es sich um Vektoren in der Ebene handelt. Für beliebige
Vektoren ~a 6= ~0, ~b 6= ~0 in der Ebene gilt (siehe Abb. 10)
sin(α) =
ay
,
|~a|
cos(α) =
ax
,
|~a|
sin(β) =
by
,
|~b|
cos(β) =
bx
|~b|
Für ϕ = β − α erhalten wir aus dem Additionstheorem
cos(ϕ) = cos(β − α) = cos(β) cos(α) + sin(β) sin(α) =
b y ay
b x ax
+
·
·
|~b| |~a| |~b| |~a|
Multiplikation beider Seiten mit |~a| · |~b| liefert
|~a| · |~b| · cos(ϕ) = ax bx + ay by
Hinweis: Als Folgerung erhalten wir für alle Vektoren ~a 6= ~0, ~b 6= ~0
~a · ~b = 0
⇐⇒
~a und ~b sind orthogonal (senkrecht)
sowie
|~a · ~b| ≤ |~a| · |~b|
(Cauchy-Schwarz-Ungleichung)
17
Satz 2.3.2 (Rechenregeln für das Skalarprodukt) Für alle Vektoren ~a, ~b, ~c und alle
t ∈ R gilt
~a · ~b = ~b · ~a
(~a + ~b) · ~c = ~a · ~c + ~b · ~c
(t~a) · ~b = t · (~a · ~b)
~a · ~a ≥ 0
und
(10)
(11)
~a · ~a = 0 ⇐⇒ ~a = ~0
(12)
(13)
Diese Rechenregeln ergeben sich unmittelbar aus der Definition.
2.4
2.4.1
Beschreibung von Geraden
Vektorielle Beschreibung
Die Richtung einer Geraden kann durch einen Vektor, ihren Richtungsvektor, vorgegeben
werden. Man kann diesen als Verbindungsvektor zweier beliebiger verschiedener Punkte der Geraden erhalten (siehe auch Abb. 11 links). Der Richtungsvektor ist also nicht
eindeutig bestimmt, wir können ihn länger oder kürzer wählen oder auch die Richtung
umkehren, ohne dass sich dadurch die Richtung der Geraden ändert.
Da sich Vektoren durch Parallelverschiebung nicht ändern, ist eine Gerade durch ihren
Richtungsvektor nicht eindeutig bestimmt. Hierfür müssen wir noch einen Punkt auf der
Gerade auswählen (in der Abb. mit P0 bezeichnet). Auch diese Auswahl ist willkürlich.
Den Ortsvektor jedes Punktes P auf der Gerade erhalten wir also, indem wir zum Orts−−→
vektor des ausgewählten Punktes ~a = OP0 ein Vielfaches des Richtungsvektors ~b addieren.
Dies ist in Abb. 11 links veranschaulicht. Jeder Ortsvektor eines Punktes auf der Geraden
hat also die Darstellung
~x(t) = ~a + t · ~b,
t∈R
(14)
und wir erhalten auf diese Weise alle Punkte der Geraden, wenn wir beliebige t ∈ R
zulassen. Wir nennen (14) die vektorielle Form der Geradengleichung.
Auch Geraden im Raum können analog durch eine Gleichung der Form (14) beschrieben werden, wobei dann die Vektoren ~a und ~b Vektoren im Raum sind.
Abbildung 11: links: zur vektoriellen Form der Geradengleichung (14), rechts: zur Beschreibung einer Geraden durch einen Normalenvektor mit Gleichung (15)
18
2.4.2
Beschreibung einer Geraden durch einen Normalenvektor
Die Richtung einer Geraden in der Ebene können wir auch dadurch festlegen, dass wir
einen Vektor ~v 6= 0 angeben, der senkrecht auf der Geraden steht (siehe auch Abb. 11
rechts). Ein solcher Vektor heißt Normalenvektor. Rechnerisch können wir die Bedingung, dass der Verbindungsvektor
→ −→
~b = −−
OP + OQ = −~a + ~x
zweier beliebiger Punkte der Geraden senkrecht auf ~v steht, mit Hilfe des Skalarprodukts
durch
0 = ~v · ~b = ~v · (−~a + ~x) = −~v · ~a + ~v · ~x
ausdrücken. Die Ortsvektoren ~x beliebiger Punkte erfüllen also die Gleichung
~v · ~x = ~v · ~a
(15)
wobei ~a der Ortsvektor eines vorgegebenen Punktes der Geraden und ~v ein Vektor senkrecht auf der Geraden ist. Beachten Sie, dass die Festlegung des Normalenvektors nur die
Richtung der Geraden festlegt. Geraden durch den Ursprung (also der Ortsvektor eines
Punktes der Geraden ist ~0) sind durch ~v · ~x = 0 gegeben.
Wir merken uns:
Alle Punkte der Ebene, deren Ortsvektoren ~x die Gleichung
~v · ~x = r
(16)
mit gegebenem r ∈ R erfüllen, liegen auf einer Geraden senkrecht zu ~v . Wenn ~v und ein
Punkt der Gerade durch seinen Ortsvektor ~a gegeben ist, dann kann daraus die Konstante
r = ~v · ~a berechnet werden.
1
x
Beispiel: Für ~v =
und r = 5 erhalten wir für den Ortsvektor
2
y
x
~v ·
= x + 2y = 5
y
Wenn wir diese Gleichung nach y auflösen, so erhalten wir eine Geradengleichung in
vertrauter Form
1
5
y =− x+
2
2
Wir wollen nun eine Formel zur Berechnung des Abstands d einer Geraden vom Ursprung
herleiten, die durch eine Geradengleichung der Form (16) gegeben ist. Die Vorgehensweise
ist auch aus Abb. 11 rechts ersichtlich. Wir gehen vom Ursprung aus in Richtung des
Normalenvektors ~v so weit, bis wir die Gerade treffen. Wir fällen also das Lot auf die
Gerade. Wir betrachten dazu Ortsvektoren der Form
~x(t) = t · ~v
mit t ∈ R (für den Fall, dass die Gerade auf der anderen Seite liegt und ~v von der Geraden
weg zeigt, müssen wir auch negative t zulassen). Der gesuchte Fußpunkt des Lots hat also
19
einen Ortsvektor dieser Form. Er muss auf der Geraden liegen, der Ortsvektor muss also
die Geradengleichung erfüllen:
~v · ~x(t) = ~v · (t · ~v ) = t(~v · ~v ) = t · |~v |2 = r
Diese Gleichung können wir nach t auflösen, und wir erhalten dadurch den Ortsvektor
zum Fußpunkt des Lots:
r
r
~x(t) = 2 · ~v
t = 2,
|~v |
|~v |
Die Länge des Ortsvektors zu diesem Fußpunkt ist der gesuchte Abstand d der Geraden
vom Ursprung:
r
|r| · |~v |
|r|
d = |~x(t)| = 2 · ~v =
=
2
|~v |
|~v |
|~v |
Wir erhalten das Ergebnis:
Eine Gerade, die durch eine Gleichung der Form (16) gegeben ist, hat den Abstand d vom
Ursprung mit
|r|
d=
(17)
|~v |
Dieses Ergebnis ermöglicht es, die Geradengleichung (16) etwas anders zu schreiben. Falls
r > 0, teilen wir beide Seiten durch |~v | und erhalten
1
r
~v · ~x =
=d
|~v |
|~v |
und falls r < 0, teilen wir beide Seiten durch (−|~v |) und erhalten
−
1
−r
|r|
~v · ~x =
=
=d
|~v |
|~v |
|~v |
Dies legt nahe, den Vektor
(
~u :=
1
~v
|~v |
1
− |~v| ~v
falls r ≥ 0
falls r < 0
zu definieren. Er hat die Eigenschaft
1 |~v |
|~u| = ± ~v =
=1
|~v |
|~v |
ist also ein Einheitsvektor, der senkrecht auf der Geraden steht. Wir haben damit das
Ergebnis gewonnen:
Die Ortsvektoren ~x der Punkte einer Geraden erfüllen eine Gleichung der Form
~u · ~x = d
(18)
Dabei ist ~u ein Einheitsvektor, der senkrecht auf der Geraden steht, und d der Abstand
der Geraden vom Ursprung. Diese Gleichung heißt Hessesche Normalform der Geradengleichung.
20
Hinweise:
(a) Falls uy 6= 0, können wir die Geradengleichung nach der y-Komponente des Ortsvektors auflösen und damit in die Form y = mx + b bringen. Falls dagegen uy = 0,
liegt eine Gerade senkrecht zur x-Achse vor.
(b) Im Raum führt die Verallgemeinerung des obigen Vorgehens zur Hesseschen Normalform der Gleichung einer Ebene im Raum (siehe Abschnitt 2.6.2).
(c) Wenn eine Geradengleichung in der vektorieller Form (14) vorliegt, dann erhalten
wir aus dem Richtungsvektor ~b mit
by
~v =
−bx
einen Normalenvektor und können damit eine Geradengleichung der Form (16) aufstellen.
2.5
Vektorprodukt
Die Kraft auf ein Elektron in einem Magnetfeld ist senkrecht zu seiner Geschwindigkeit
~ (der das magnetische Feld beschreibt). Zur Beschreibung
~v und senkrecht zum Vektor B
dieser Kraft (und für viele andere Anwendungen) wird das Vektorprodukt benötigt. Wir
geben hier zunächst eine geometrische Definition und später eine dazu äquivalente rechnerische Definition.
Definition 2.5.1 (geometrische Definition des Vektorprodukts) Unter dem Vektorprodukt ~c = ~a × ~b zweier Vektoren ~a, ~b im Raum versteht man den Vektor ~c, der
durch folgende Eigenschaften gegeben ist:
(a) ~c ist orthogonal zu ~a und ~b (also ~a · ~c = ~b · ~c = 0).
(b) |~c| = |~a| · |~b| · sin(α), wobei α der Winkel zwischen ~a und ~b ist (also entspricht |~c|
der Fläche des von ~a und ~b aufgespannten Parallelogramms, siehe auch Abb. 12).
(c) Die Vektoren ~a, ~b und ~c bilden ein Rechtssystem wie Daumen, Zeigefinger und Mittelfinger der rechten Hand ( Rechte-Hand-Regel“, siehe Abb. 13).
”
Abbildung 12: sin(α) = |~hb| =⇒ h = |~b| · sin(α), also ist die Fäche des Parallelogamms
|~a| · |~b| · sin(α) (zu (b) in Def. 2.5.1)
21
Abbildung 13: Zur Rechte-Hand-Regel ((c) in Def. 2.5.1)
Satz 2.5.1 Die folgenden Rechenregeln für das Vektorprodukt gelten für alle Vektoren
~a, ~b, ~c im Raum und alle t ∈ R:
~a × ~b = −~b × ~a
(t~a) × ~b = t(~a × ~b) = ~a × (t~b)
~a × (t~a) = ~0
~a × (~b + t~a) = ~a × ~b,
(~a + t~b) × ~b = ~a × ~b
~a × (~b + ~c) = ~a × ~b + ~a × ~c,
(~a + ~c) × ~b = ~a × ~b + ~c × ~b
~ex × ~ey = ~ez ,
~ey × ~ez = ~ex ,
~ez × ~ex = ~ey
(19)
(20)
(21)
(22)
(23)
(24)
Abbildung 14: Die Flächen des von ~a und ~b und des von ~a und ~b + t~a aufgespannten
Parallelogramms sind gleich (zum Beweis von Satz 2.5.1, (22))
Hinweise zum Beweis:
(19) folgt direkt aus der Rechte-Hand-Regel.
(20) folgt aus der entsprechenden Änderung der Fläche des Parallelogramms.
(21) folgt unmittelbar aus (20) und (19).
(22) folgt aus der Tatsache, dass sich die Fläche des entsprechenden Parallelogramms
nicht ändert (siehe die Abb. 14)
22
(23) aus der geometrischen Definition herzuleiten, ist nicht ganz einfach. Es sei daher hier
nur darauf hingewiesen, dass man mit (22) den allgemeinen Fall auf den Sonderfall
zurückführen kann, dass ~b und ~c senkrecht auf ~a sind (für die erste Gleichung) bzw. ~a
und ~c senkrecht auf ~b sind ( für die zweite Gleichung). Aufgrund von (20) kann man
sich dann darauf beschränken, die Gleichung für den Sonderfall von Einheitsvektoren
zu beweisen. Dies wird hier nicht ausgeführt.
(24) folgt unmittelbar aus der Rechte-Hand-Regel, da die aufgespannten Parallelogramme stets Quadrate der Kantenlänge 1 sind (zur Erinnerung: ~ex , ~ey und ~ez sind die
Einheitsvektoren in Achsrichtung)
Mit Hilfe dieser Rechenregeln können wir das Vektorprodukt beliebiger Vektoren ausrechnen:
~a × ~b = (ax~ex + ay~ey + az~ez ) × (bx~ex + by~ey + bz~ez )
= ay bx (~ey × ~ex ) + az bx (~ez × ~ex ) + ax by (~ex × ~ey )
+az by (~ez × ~ey ) + ax bz (~ex × ~ez ) + ay bz (~ey × ~ez )
= −ay bx~ez + az bx~ey + ax by~ez − az by~ex − ax bz~ey + ay bz~ex
= (ay bz − az by )~ex + (az bx − ax bz )~ey + (ax by − ay bx )~ez
Die folgende rechnerische Definition ist also äquivalent zur geometrischen (Definition
2.5.1):
Definition
2.5.2
 (rechnerische
  Definition des Vektorprodukts) Für beliebige Vekax
bx
toren ~a = ay  und ~b = by  wird das Vektorprodukt ~a × ~b durch
az
bz


ay b z − az b y
~a × ~b := az bx − ax bz 
(25)
ax b y − ay b x
definiert.
Hinweise:
(a) Das Vektorprodukt wird — aufgrund seiner Schreibweise — auch Kreuzprodukt“
”
und zuweilen auch äußeres Produkt“ genannt.
”
(b) Das Assoziativgesetz ist nicht erfüllt, wie das Beispiel
(~ex × ~ey ) × ~ey = ~ez × ~ey = −~ex ,
~ex × (~ey × ~ey ) = ~0
zeigt. Bei Vektorprodukten mit drei (und mehr) Vektoren sind daher Klammern
unbedingt erforderlich!
(c) Vergleicht man die Komponenten auf der rechten Seite von (25), so stellt man fest,
dass die y-Komponente aus der x-Komponente durch folgende Ersetzung vorgeht:
x 7→ y,
y 7→ z,
23
z 7→ x
(26)
Und die z-Komponente erhält man durch dieselbe Substitution aus der y-Komponente.
Diese Substitution nennt man zyklische Vertauschung (es wird im Kreis herum
ersetzt). Entsprechende Beobachtungen kann man bei vielen Formeln machen, bei
denen das Vektorprodukt vorkommt. Auch die Gleichungen (24) gehen durch zyklische Vertauschung ineinander über.
(d) Mit Hilfe von Determinanten (werden später behandelt) kann man die folgende
nützlich Merkregel für das Vektorprodukt formulieren
~ex ax bx ~a × ~b = ~ey ay by ~ez az bz Laplace-Entwicklung nach der 1. Spalte führt gerade auf (25). Es ist anzumerken,
dass es sich dabei nicht um eine richtige“ Determinante handelt, da die Einheits”
vektoren in Achsrichtung (anstelle von Skalaren) als Matrixelemente auftreten.
(e) Das Vektorprodukt ist nur für Vektoren im Raum, also mit drei Komponenten,
definiert!
Satz 2.5.2 Für alle Vektoren ~a, ~b, ~c im Raum gilt
(~a × ~b) × ~c = (~a · ~c) · ~b − (~b · ~c) · ~a
Den Beweis kann man führen, indem man mit etwas Geduld auf der linken und rechten
Seite zunächst die x-Komponente ausrechnet und die Übereinstimmung feststellt (siehe die
entsprechende Übungsaufgabe). Die Übereinstimmung der übrigen beiden Komponenten
erhält man dadurch, dass man sich klarmacht, dass die Ausdrücke für diese Komponenten
durch zyklische Vertauschung aus denen für die x-Komponente hervorgehen.
2.6
2.6.1
Beschreibung von Ebenen im Raum
Vektorielle Beschreibung
Abbildung 15: Der Ortsvektor jedes Punktes der Ebene kann in der Form ~x = t~a + s~b
geschrieben werden.
Der Ortsvektor ~x jedes Punktes in der Ebene kann in der Form
~x = t~a + s~b
24
mit s, t ∈ R geschrieben werden, wenn die beiden Vektoren ~a 6= 0 und ~b 6= 0 erfüllen
und nicht in dieselbe oder in die entgegengesetzte Richtung zeigen. Dies ist in Abb. 15
veranschaulicht. Wenn nun zwei Vektoren im Raum ~a 6= 0 und ~b 6= 0 erfüllen und nicht
in dieselbe oder in die entgegengesetzte Richtung zeigen, dann nennt man die Menge
aller Punkte der Form ~x = t~a + s~b die von ~a und ~b aufgespannten Ebene durch den
Ursprung (denn mit s = 0 und t = 0 erhält man ~x = ~0). Durch Addition eines festen
Vektors ~c verschiebt man diese Ebene. Wir erhalten somit die vektorielle Beschreibung
einer Ebene im Raum durch
E = {~x | ~x = t~a + s~b + ~c, s, t ∈ R}
(27)
Dabei können s, t ∈ R beliebige Werte annehmen. Die Wahl s = t = 0 führt auf ~x = ~c,
also ist ~c Ortsvektor eines Punktes der Ebene. Die Gleichung ~x = t~a + s~b + ~c wird auch
als vektorielle Ebenengleichung bezeichnet. Beachten Sie, dass bei gegebener Ebene (als
Menge von Punkten) die Auswahl der drei Vektoren nicht eindeutig ist. Dies kann man
sich am Spezialfall der xy-Ebene an Abb. 15 leicht klarmachen.
Wenn die Ebene durch die Angabe von drei Punkten P1 , P2 und P3 gegeben ist,
die in der Ebene liegen, dann erhält man die vektorielle Ebenengleichung der Form (27)
beispielsweise durch
−−→
−→
−−→
~b = −
~a = P1 P2 ,
P1 P3 ,
~c = OP1
2.6.2
Beschreibung einer Ebene durch einen Normalenvektor
Die Richtung einer Ebene kann man dadurch festlegen, dass man einen Vektor ~v 6= ~0
angibt, der senkrecht auf der Ebene steht. Dieser Vektor heißt dann Normalenvektor. Alle
Ebenen, die zueinander parallel sind, können durch denselben Normalenvektor beschrieben werden. Beachten Sie, dass der Normalenvektor nicht eindeutig ist, wir können ihn
länger oder kürzer wählen oder seine Richtung umkehren (durch −~v ersetzen), ohne die
Richtung der Ebene zu ändern. Die Ebene wird dann dadurch festgelegt, dass man einen
−→
Punkt P (mit Ortsvektor ~a = OP ) der Ebene angibt. Man kann Abb. 11 rechts als Schnitt
−→
durch eine derartige Ebene auffassen. Der Verbindungsvektor ~b = P Q zu einem beliebigen
−→
Punkt Q mit Ortsvektor ~x = OQ muss dann senkrecht auf dem Normalenvektor stehen,
also muss auch hier gelten
0 = ~v · ~b = ~v · (−~a + ~x) = −~v · ~a + ~v · ~x
Die Ortsvektoren ~x beliebiger Punkte der Ebene erfüllen also die Gleichung
~v · ~x = ~v · ~a
(28)
wobei ~a der Ortsvektor des gegebenen Punktes der Ebene und ~v ein Vektor senkrecht auf
der Ebene ist. Wir haben damit die Gleichung (15) wiedergewonnen mit dem Unterschied,
dass hier eine Ebene im Raum beschrieben wird.
Wir merken uns:
Alle Punkte des Raumes, deren Ortsvektoren ~x die Gleichung
~v · ~x = r
(29)
mit gegebenem r ∈ R erfüllen, liegen auf einer Ebene senkrecht zu ~v . Wenn ~v und ein
Punkt der Ebene durch seinen Ortsvektor ~a gegeben ist, dann kann daraus die Konstante
r = ~v · ~a berechnet werden.
25
Wir fassen weiterhin Abb. 11 rechts als Schnitt durch eine derartige Ebene auf. Dann
können wir die Vorgehensweise von Abschnitt 2.4.2 auf Ebenen übertragen und ganz
analog den Abstand einer Ebene vom Ursprung berechnen, die durch eine Gleichung
der Form (29) gegeben ist. Dabei können wir die Rechnung und die Erklärung von Abschnitt 2.4.2 fast unverändert übernehmen, lediglich das Wort Gerade“ ist durch das
”
Wort Ebene“ zu ersetzen. Wir verlängern oder verkürzen also wieder den Normalen”
vektor ~v , bis wir auf die Ebene treffen, und berechnen so den Fußpunkt des Lotes vom
Ursprung auf die Ebene. Wir erhalten damit ein Ergebnis der selben Form:
Eine Ebene, die durch eine Gleichung der Form (29) gegeben ist, hat den Abstand d vom
Ursprung mit
|r|
(30)
d=
|~v |
Auch hier können wir die Gleichung (29) etwas anders schreiben, indem wir die Vorgehensweise von Abschnitt 2.4.2 unverändert übertragen: Division beider Seiten durch ±|~v |
und Einführung des Vektors
(
1
~v falls r ≥ 0
|~v |
~u :=
1
− |~v| ~v falls r < 0
liefert:
Die Ortsvektoren ~x der Punkte einer Ebene erfüllen eine Gleichung der Form
~u · ~x = d
(31)
Dabei ist ~u ein Einheitsvektor, der senkrecht auf der Ebene steht, und d der Abstand der
Ebene vom Ursprung. Diese Gleichung heißt Hessesche Normalform der Ebenengleichung.
Am Ende von Abschnitt 2.6.1 wurde beschrieben, wie man die vektorielle Beschreibung
einer Ebene erhält, die durch drei Punkte festgelegt ist, deren Ortsvektoren man kennt.
Von der vektoriellen Ebenengleichung (27) erhält man mit Hilfe des Vektorprodukts sofort
einen Normalenvektor durch
~v = ~a × ~b
−−→
Da ein Punkt der Ebene mit Ortsvektor ~c = OP1 bekannt ist, kann man die Konstante
r = ~v ·~c in (29) berechnen. Man kann auf diese Weise die Gleichung einer Ebene aufstellen,
die durch die Angabe dreier Punkte gegeben ist.
3
3.1
3.1.1
Lineare Gleichungssysteme
Gauß-Verfahren
Einfaches Beispiel, Rückwärtsauflösen
Lineare Gleichungssysteme treten in fast allen Anwendungen der Mathematik in der Technik auf. Betrachten wir als Beispiel das in Abb. 16 gezeigte Beispiel eines elektrischen
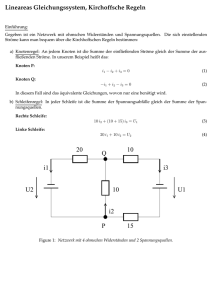
Netzes. Wir bezeichnen die unbekannten Ströme mit x1 = I1 , x2 = I2 , x3 = I3 und wollen hier auf die Angabe der Maßeinheit A für Ampère verzichten. Die Anwendung der
26
Abbildung 16: Einfaches Netz: Ströme gesucht
Kirchhoffschen Regeln liefert
x1
−x2 −x3 = 0
10x2 −6x3 = 0
6x3 = 12
Dies ist ein Beispiel für ein lineares Gleichungssystem: linear deswegen, weil die Unbekannten nur in der ersten Potenz und auch nicht als Argument in Funktionen wie der
Wurzel vorkommen, System, weil es sich um mehrere Gleichungen handelt.
Das hier vorliegende Gleichungssystem hat eine sehr spezielle Form: es liegt in Dreiecksform vor, die Terme in der linken unteren Hälfte fehlen (weil die Koeffizienten null
sind). Derartige Gleichungssysteme sind sehr leicht aufzulösen. Wir multiplizieren beide
Seiten der dritten Gleichung mit 61 und erhalten
x3 = 2
Einsetzen in die 2. Gleichung liefert
10x2 − 6 · 2 = 0
Durch Addition von 12 auf beiden Seiten erhält man
10x2 = 12
und Multiplikation beider Seiten mit
1
10
liefert
x2 =
12
= 1, 2
10
Einsetzen der Ergebnisse für x2 und x3 in die 1. Gleichung ergibt
x1 − 1, 2 − 2 = 0
Durch Addition von 3, 2 auf beiden Seiten erhält man daraus
x1 = 3, 2
Dieses Verfahren heißt Rückwärtseinsetzen oder Rückwärtsauflösen.
27
3.1.2
Umwandlung in Dreiecksform, einfaches Beispiel
Wir gehen von folgendem Gleichungssystem aus:
2x1 +3x2 −5x3 = 10
4x1 +8x2 −3x3 = 19
−6x1 +x2 +4x3 = 11
(Z1)
(Z2)
(Z3)
Das Ziel ist es, dieses Gleichungssystem in Dreiecksform umzuwandeln, es also in die Form
zu bringen
∗x1 + ∗ x2 + ∗ x3 = ∗
0x1 + ∗ x2 + ∗ x3 = ∗
0x1 +0x2 + ∗ x3 = ∗
Dabei steht ∗ für noch zu berechnende Zahlen, die also alle verschieden sein können.
Die Umwandlung des ursprünglichen Gleichungssystems soll so erfolgen, dass sich die
Lösungsmenge nicht ändert.
Wir behalten hierzu die oberste Zeile bei (sie hat ja schon die gewünschte Form) und
addieren in einem ersten Schritt Vielfache der ersten Zeile zu den beiden andern Zeilen,
und zwar so, dass in der linken Spalte Nullen entstehen. Addiert man das (−2)-fache der
1. Zeile
−4x1 −6x2 +10x3 = −20
zur 2. Zeile
4x1 +8x2 −3x3 = 19
(Z2)
so erhält man als neue 2. Zeile
0x1 +2x2 +7x3 = −1
(Z20 )
Entsprechend liefert Addition des 3-fachen der 1. Zeile
6x1 +9x2 −15x3 = 30
zur 3. Zeile
−6x1 +x2 +4x3 = 11
(Z3)
die neue 3. Zeile
0x1 +10x2 −11x3 = 41
Durch diese beiden Operationen haben wir
system
2x1 +3x2 −5x3
0x1 +2x2 +7x3
0x1 +10x2 −11x3
(Z30 )
in einem ersten Schritt das neue Gleichungs= 10
= −1
= 41
(Z1)
(Z20 )
(Z30 )
erhalten. Wir setzen diese Methode in einem zweiten Schritt auf das entstandene kleinere
System (ohne die erste Zeile) fort:
+2x2 +7x3 = −1
+10x2 −11x3 = 41
Addition des (−5)-fachen der Zeile (Z20 )
−10x2 −35x3 = 5
28
(Z20 )
(Z30 )
zur untersten Zeile
(Z30 )
+10x2 −11x3 = 41
liefert die neue unterste Zeile (Z300 )
0x2 −46x3 = 46
(Z300 )
Wir haben also insgesamt das ursprüngliche Gleichungssystem in die gewünschte Dreiecksform gebracht
2x1 +3x2 −5x3 = 10
(Z1)
+2x2 +7x3 = −1
(Z20 )
−46x3 = 46
(Z300 )
Rückwärtsauflösen liefert
x3 = −1
2x2 − 7 = −1,
2x2 = 6,
x2 = 3
2x1 + 9 + 5 = 10,
2x1 = −4,
x1 = −2
Für praktische Rechnungen ist die Probe durch Einsetzen der Lösung in das urprüngliche
Gleichungssystem dringend zu empfehlen. Wenn Sie die Lösung mit einem Rechner berechnen, dann lassen Sie den Rechner die Probe durchführen!
Probe:
2 · (−2) + 3 · 3 − 5 · (−1) = −4 + 9 + 5 = 10
4 · (−2) + 8 · 3 − 3 · (−1) = −8 + 24 + 3 = 19
−6 · (−2) + 3 + 4 · (−1) = 12 + 3 − 4 = 11
Zur Erinnerung: Das Morsezeichen ·−“hat in der Mathematik nichts zu suchen. Daher
”
dürfen die Klammern in dieser Rechnung nicht weggelassen werden!
3.1.3
Weiteres Beispiel zur Umwandlung in Dreiecksform in Kurzschreibweise
2x1 +x2 +x3 =
1
4x1 +x2
= −2
−2x1 +2x2 +x3 =
7
Bei der Rechnung kommt es nur auf die Koeffizienten vor den Unbekannten und die Zahlen
auf der rechten Seite an, daher genügt es, nur diese zu notieren. Hierfür sind verschiedene
Kurzschreibweisen üblich.
Hier wird zunächst eine gemäßigte“ Kurzschreibweise für die Lösung des Gleichungs”
systems angegeben. Sie führt zur Schreibweise des Gleichungssystems mit einer Matrix,
die später behandelt wird. Die Vorgehensweise erfolgt analog zu der des vorangegangenen
Unterabschnitts. Es wird jeweils die oberste Zeile unverändert gelassen und es werden
Vielfache dieser obersten Zeile zu den unteren Zeilen addiert, und zwar so, dass ganz links
29
der Koeffizient 0 entsteht.
2
1
1
1
4
1
0 −2
−2
2
1
7
2
1
1
1
0 −1 −2 −4
0
3
2
8
2
1
1
1
0 −1 −2 −4
0
0 −4 −4
·(−2)
←-
·1
↓
←
·3
←-
Das entstehende Gleichungsystem in Dreiecksform ergibt sich aus dem untersten Abschnitt. Ausführlich aufgeschrieben lautet es
2x1 +x2 +x3 =
1
−x2 −2x3 = −4
−4x3 = −4
Rückwärtsauflösen ergibt:
−4x3 = −4,
x3 = 1
−x2 − 2 = −4,
x2 = 2
2x1 + 2 + 1 = 1,
2x1 = −2,
x1 = −1
Eine noch kompaktere Schreibweise für die Lösung des Gleichungssystems entsteht dadurch, dass die Zeilen, die im weiteren Verlauf des Verfahrens nicht weiter verändert
werden, auch nicht mehr aufgeschrieben werden. Sie werden stattdessen durch eine Einrahmung gekennzeichnet:
2
4
−2
1
1
1
1
0 −2
2
1
7
−1 −2 −4
3
2
8
−4 −4
·(−2)
←-
·1
↓
←
·3
←-
Das entstehende Gleichungsystem in Dreiecksform ergibt sich dann am Schluss aus den
eingerahmten Zeilen. Es wird dann durch Rückwärtsauflösen gelöst. Diese sehr kompakte
Kurzschreibweise ist nur zu empfehlen, wenn man das allgemeine Verfahren verstanden
hat und viel Übung besitzt, ansonsten ist die zuerst beschriebene gemäßigte“ Kurz”
schreibweise vorzuziehen, bei der die nicht veränderten Zeilen bei jedem Schritt erneut
aufgeschrieben werden.
30
3.1.4
Allgemeines Prinzip des Gauß-Verfahrens
Die allgemeine Form eines linearen Gleichungssystems von n Gleichungen mit n Unbekannten ist
a11 x1
a21 x1
a31 x1
a41 x1
..
.
+a12 x2
+a22 x2
+a32 x2
+a42 x2
..
.
+a13 x3
+a23 x3
+a33 x3
+a43 x3
..
.
+a14 x4
+a24 x4
+a34 x4
+a44 x4
..
.
+···
+···
+···
+···
...
an1 x1 +an2 x2 +an3 x3 +an4 x4 + · · ·
+a1n xn
+a2n xn
+a3n xn
+a4n xn
..
.
=
=
=
=
b1
b2
b3
b4
..
.
+ann xn = bn
Dabei ist es üblich, dass der Koeffizient in der i. Zeile und der k. Spalte (also der Koeffizient der k. Unbekannten in der i. Zeile) mit aik bezeichnet wird. Die erste Nummer der
Koeffizienten gibt also stets die Nummer der Zeile an. Die Lösungsmenge eines linearen
Gleichungssystems ist die Menge der {x1 , x2 , x3 , x4 , . . . xn }, die dieses Gleichungssystem
erfüllen. Wir setzen hier zunächst voraus, dass wir genausoviele Gleichungen wie Unbekannte haben; der allgemeine Fall wird später behandelt.
Satz 3.1.1 Folgende Operationen lassen die Lösungsmenge eines linearen Gleichungssystems unverändert:
(a) Vertauschen zweier Zeilen
(b) Multiplikation einer Zeile mit einer beliebigen Zahl c 6= 0, c ∈ R
(c) Addition eines beliebigen Vielfachen einer Zeile zu einer andern Zeile
Hinweis: a) und b) sind unmittelbar klar. Entscheidend dafür, dass sich die Lösungsmenge
bei der Umwandlung des Gleichungssystems nicht ändert, ist dass man den Umwandlungsschritt rückgängig machen kann. Die Addition des c-fachen einer Zeile zu einer andern kann
man durch die Addition des −c-fachen dieser Zeile zu der andern Zeile wieder rückgängig
machen. Die Addition des Nullfachen einer Zeile zu einer anderen ändert gar nichts, also
braucht man hier auch keine Voraussetzung an die Konstante c.
Das Gauß-Verfahren besteht nun darin, dass man durch diese Operationen, die die
Lösungsmenge unverändert lassen, ein beliebiges Gleichungssystem in Dreiecksform bringt.
Durch Addition des c-fachen der 1. Zeile zur 2. Zeile entsteht dort als 1. Summand
(c · a11 + a21 )x1 . Damit dieser wegfällt, muss die Bedingung (c · a11 + a21 ) = 0 erfüllt
. Analog kann
sein. Für den Fall, dass a11 6= 0, erreicht man dies durch die Wahl c = − aa21
11
man für die anderen Zeilen vorgehen. Wir haben also als
1. Schritt des Gauß-Verfahrens:
(a) Wenn a11 6= 0, dann führe folgende Operation für k = 2, 3, 4, . . . n durch:
Addiere das − aak1
-fache der 1. Zeile zur k. Zeile.
11
Dadurch hat man nach Durchlaufen dieser Schleife unterhalb von a11 nur noch
Nullen stehen.
(b) Wenn a11 = 0, dann prüft man für k = 2, 3, 4, . . . n, ob ein ak1 6= 0
31
(a) Wenn ein Koeffizient ak1 6= 0, dann vertauscht man die 1. und die k. Zeile und
führt dann den hier beschriebenen 1. Schritt von vorne durch (dann ist das
neue a11 6= 0).
(b) Wenn für alle Koeffizienten der Spalte a11 = 0, a21 = 0, a31 = 0, . . . an1 = 0 gilt
(die erste Spalte also nur aus Nullen besteht), dann geht man eine Spalte nach
rechts und ersetzt a11 durch den Koeffizienten, der in derselben Zeile weiter
rechts steht, also durch a12 und führt alle hier für den 1. Schritt beschriebenen
Operationen durch, wobei überall in der Beschreibung die Koeffizienten ak1
durch ak2 zu ersetzen ist. Wenn dies nicht zum Erfolg führt, wenn also erneut
a12 = 0, a22 = 0, a32 = 0, . . . an2 = 0, dann geht man nochmal eine Spalte
weiter nach rechts und ersetzt in dieser Beschreibung des 1. Schritts a11 durch
a13 (und alle weiteren Koeffizienten ak1 durch ak3 ). Führt dies wieder nicht
zum Erfolg, wenn also alle Koeffizienten der Spalte, in der man arbeitet, Null
sind, dann geht man nochmal eine Spalte weiter nach rechts. Dies wird so lange
fortgesetzt, bis man auf einen Koeffizienten stößt, der von Null verschieden ist.
Wenn dies nicht der Fall ist, dann stehen nur noch Nullen im Gleichungssystem,
und man hat nichts mehr zu tun.
Als Ergebnis dieses 1. Schrittes erhält man ein Gleichungssystem der Form
a011 x1
0x1
0x1
0x1
..
.
0x1
+a012 x2
+a022 x2
+a032 x2
+a042 x2
..
.
+a013 x3
+a023 x3
+a033 x3
+a043 x3
..
.
+a014 x4
+a024 x4
+a034 x4
+a044 x4
..
.
+···
+···
+···
+···
...
+a0n2 x2 +a0n3 x3 +a0n4 x4 + · · ·
+a01n xn
+a02n xn
+a03n xn
+a04n xn
..
.
=
=
=
=
b01
b02
b03
b04
..
.
+a0nn xn = b0n
Dabei wurden die Koeffizienten hier mit a0ik bezeichnet, da sie sich durch die Rechenoperationen des ersten Schritts geändert haben (die erste Zeile hat sich nur bei einem
Zeilentausch geändert).
Im nächsten Schritt wird die erste Zeile unverändert gelassen und nur noch das kleinere
Gleichungssystem
a022 x2 +a023 x3
a032 x2 +a033 x3
a042 x2 +a043 x3
..
..
.
.
0
0
an2 x2 +an3 x3
+a024 x4 + · · ·
+a034 x4 + · · ·
+a044 x4 + · · ·
..
...
.
+a0n4 x4 + · · ·
+a02n xn = b02
+a03n xn = b03
+a04n xn = b04
..
..
.
.
0
+ann xn = b0n
weiterbearbeitet. Im zweiten Schritt werden dieselben Operationen wie im ersten Schritt
durchgeführt, nur dass jetzt von a022 ausgegangen wird. Im einzelnen heißt dies:
2. Schritt des Gauß-Verfahrens:
(a) Wenn a022 6= 0, dann führe folgende Operation für k = 3, 4, . . . n durch:
a0
Addiere das − ak2
0 -fache der 2. Zeile zur k. Zeile.
22
Dadurch hat man nach Durchlaufen dieser Schleife unterhalb von a022 nur noch
Nullen stehen.
32
(b) Wenn a022 = 0, dann prüft man für k = 3, 4, . . . n, ob ein a0k2 6= 0
(a) Wenn ein Koeffizient a0k2 6= 0, dann vertauscht man die 2. und die k. Zeile und
führt dann den hier beschriebenen 2. Schritt von vorne durch (dann ist das
neue a022 6= 0).
(b) Wenn für alle Koeffizienten der Spalte a022 = 0, a032 = 0, . . . a0n2 = 0 gilt (die
zweite Spalte also nur aus Nullen besteht), dann geht man eine Spalte nach
rechts und ersetzt a022 durch den Koeffizienten, der in derselben Zeile weiter
rechts steht, also durch a023 und führt alle hier für den 2. Schritt beschriebenen
Operationen durch, wobei überall in der Beschreibung die Koeffizienten ak2
durch ak3 zu ersetzen ist. Wenn dies nicht zum Erfolg führt, wenn also erneut
a023 = 0, a033 = 0, . . . a0n3 = 0, dann geht man nochmal eine Spalte weiter nach
rechts und ersetzt in dieser Beschreibung des 2. Schritts a022 durch a024 (und
alle weiteren Koeffizienten a0k2 durch a0k4 ). Führt dies wieder nicht zum Erfolg,
wenn also alle Koeffizienten der Spalte, in der man arbeitet, Null sind, dann
geht man nochmal eine Spalte weiter nach rechts. Dies wird so lange fortgesetzt,
bis man auf einen Koeffizienten stößt, der von Null verschieden ist. Wenn dies
nicht der Fall ist, dann stehen nur noch Nullen im Gleichungssystem, und man
hat nichts mehr zu tun.
Als Ergebnis dieses 2. Schrittes erhält man ein Gleichungssystem der Form
a0022 x2 +a0023 x3
0x2 +a0033 x3
0x2 +a0043 x3
..
..
.
.
0x2 +a00n3 x3
+a0024 x4 + · · ·
+a0034 x4 + · · ·
+a0044 x4 + · · ·
..
...
.
+a00n4 x4 + · · ·
+a002n xn = b002
+a003n xn = b003
+a004n xn = b004
..
..
.
.
+a00nn xn = b00n
Dabei wurden die Koeffizienten hier mit a00ik bezeichnet, da sie sich durch die Rechenoperationen des zweiten Schritts geändert haben. Im nächsten Schritt wird die zweite Zeile
unverändert gelassen und nur noch das kleinere Gleichungssystem
a0033 x3 +a0034 x4 + · · ·
a0043 x3 +a0044 x4 + · · ·
..
..
..
.
.
.
00
00
an3 x3 +an4 x4 + · · ·
+a003n xn = b003
+a004n xn = b004
..
..
.
.
00
+ann xn = b00n
weiterbearbeitet. Im dritten Schritt werden dieselben Operationen wie in den ersten beiden Schritten durchgeführt, nur dass jetzt von a0033 ausgegangen wird. Im einzelnen heißt
dies:
3. Schritt des Gauß-Verfahrens:
(a) Wenn a0033 6= 0, dann führe folgende Operation für k = 4, 5, . . . n durch:
a00
Addiere das − ak3
00 -fache der 3. Zeile zur k. Zeile.
33
Dadurch hat man nach Durchlaufen dieser Schleife unterhalb von a0033 nur noch
Nullen stehen.
33
(b) Wenn a0033 = 0, dann prüft man für k = 4, 5, . . . n, ob ein a0k3 6= 0
(a) Wenn ein Koeffizient a00k3 6= 0, dann vertauscht man die 2. und die k. Zeile und
führt dann den hier beschriebenen 2. Schritt von vorne durch (dann ist das
neue a0033 6= 0).
(b) Wenn für alle Koeffizienten der Spalte a0033 = 0, a0043 = 0, . . . a00n3 = 0 gilt (die
zweite Spalte also nur aus Nullen besteht), dann geht man eine Spalte weiter
nach rechts. Dies wird so lange fortgesetzt, bis man auf einen Koeffizienten
stößt, der von Null verschieden ist. Wenn dies nicht der Fall ist, dann stehen
nur noch Nullen im Gleichungssystem, und man hat nichts mehr zu tun.
Als Ergebnis dieses 3. Schrittes erhält man ein Gleichungssystem der Form
000
a000
33 x3 +a34 x4 + · · ·
0x3 +a000
44 x4 + · · ·
..
..
..
.
.
.
000
0x3 +an4 x4 + · · ·
000
+a000
3n xn = b3
000
+a000
4n xn = b4
..
..
.
.
000
+ann xn = b000
n
Dabei wurden die Koeffizienten hier mit a000
ik bezeichnet, da sie sich durch die Rechenoperationen des dritten Schritts geändert haben. Man setzt das Verfahren nun mit dem
kleineren Gleichungssystem
a000
44 x4 + · · ·
..
..
.
.
000
an4 x4 + · · ·
000
+a000
4n xn = b4
..
..
.
.
000
+ann xn = b000
n
in einem 4. Schritt analog zu den bisherigen fort. Nach insgesamt (n − 1) derartigen
Schritten hat man das ursprüngliche Gleichungsystem umgewandelt in ein System in
Dreiecksform
a11 x1 +a12 x2 +a13 x3 +a14 x4
a22 x2 +a23 x3 +a24 x4
a33 x3 +a34 x4
a44 x4
+···
+···
+···
+···
...
+a1n xn
+a2n xn
+a3n xn
+a4n xn
..
.
ann xn
=
=
=
=
b1
b2
b3
b4
..
.
= bn
Dabei wurde zur Vereinfachung wieder die ursprüngliche Bezeichnungsweise aik der Koeffizienten gewählt — ohne die Striche, die andeuteten, dass sich die Koeffizienten bei der
Durchführung der Umwandlung ändern, also nicht mit denen des ursprünglichen Systems
übereinstimmen.
Zur Berechnung der Unbekannten hat man folgende Fälle zu unterscheiden:
(a) Wenn ann 6= 0, dann können die Unbekannten sofort durch Rückwärtseinsetzen
n
berechnet werden: xnn = abnn
, an−1,n−1 xn−1 + an−1,n xn = bn−1 und damit
xn−1 =
bn−1 − an−1,n ·
bn
ann
an−1,n−1
und entsprechend für die weiteren Unbekannten. Wie man aus der Umwandlung in
die Dreiecksform sieht, ist es nur möglich, dass ann 6= 0, wenn bei der Umwandlung
34
in Dreiecksform nirgends der Sonderfall auftritt, dass eine vollständige Spalte von
Nullen vorliegt und die weitere Bearbeitung eine Spalte weiter rechts fortgesetzt
werden muss. Wenn ann 6= 0, dann gilt in der Dreiecksform für alle übrigen Diagonalelemente a11 6= 0, a22 6= 0, a33 6= 0, . . . an−1,n−1 6= 0. Das Rückwärtsauflösen führt
dann zu einer eindeutigen Lösung x1 , x2 , x3 . . . xn .
(b) Falls ann = 0 und bn 6= 0, dann hat das Gleichungssystem keine Lösung, d.h. die
Lösungsmenge ist dann leer, denn die letzte Zeile in Dreiecksform 0 · xn = bn hat
keine Lösung xn ∈ R.
(c) Falls ann = 0 und bn = 0, dann ist die letzte Zeile in Dreiecksform 0·xn = 0 für beliebige xn ∈ R erfüllt. Man hat dann auf jeden Fall unendlich viele Lösungen, und man
kann mit Hilfe des Gleichungssystems in Dreiecksform versuchen, die Lösungsmenge
zu charakterisieren. Dies soll zunächst an den Beispielen besprochen werden.
Definition 3.1.1 Ein lineares Gleichungssystem mit n Gleichungen und n Unbekannten
heißt singulär, wenn nach der Umwandlung in Dreiecksform mit dem Gauß-Verfahren
der Koeffizient ann = 0 erfüllt. Wenn dagegen ann 6= 0, dann heißt das Gleichungssystem
nichtsingulär.
Hinweis: Ein singuläres Gleichungssystem kann also keine oder unendlich viele Lösungen
haben, ein nichtsinguläres Gleichungssystem hat stets eine eindeutig bestimmte Lösung.
3.2
Geometrische Deutung linearer Gleichungssysteme
Schauen wir uns zunächst ein Beispiel an der Form
a11 x1 +a12 x2 = b1
a21 x1 +a22 x2 = b2
(32)
Wenn wir die in der ersten Zeile stehenden Koeffizienten und die Unbekannten zu einem
Vektor zusammenfassen, also
a11
x1
~u :=
und
~x :=
x2
a12
definieren, dann können wir die erste Zeile schreiben als
~u · ~x = b1
Dies ist die Gleichung einer Geraden senkrecht zu ~u in der Form der Gleichung (16). Wenn
a12 6= 0, dann können wir die erste Zeile des Gleichungssytems mit x1 = x und x2 = y
auch in der gewohnten Form einer Geradengleichung
y=−
a11
b1
x+
a12
a12
schreiben.
Analog können wir mit
a21
~v :=
a22
35
die zweite Gleichung als Gleichung einer Geraden senkrecht zu ~v in der Form
~v · ~x = b2
oder, falls a22 6= 0, in der vertrauten Form
y=−
b2
a21
x+
a22
a22
schreiben.
Das Gleichungssystem zu lösen bedeutet also, den Schnittpunkt zweier Geraden in der
Ebene zu berechnen! Hier können verschiedene Situationen vorliegen:
(a) Im allgemeinen schneiden sich die beiden Geraden in genau einem Punkt. Dann hat
das Gleichungssystem genau eine Lösung.
(b) Es kann aber auch vorkommen, dass die beiden Geraden parallel, aber verschieden
sind. Dann haben sie keinen Schnittpunkt, und die Lösungsmenge des Gleichungssystems ist leer. In diesem Fall haben die beiden Normalenvektoren dieselbe (oder
entgegengesetzte) Richtung, also ein Normalenvektor ist ein Vielfaches des anderen,
~u = s~v
oder
~v = t~u
und durch Addition des (−t)-fachen der ersten Zeile zur zweiten kann man diese in
die Form
0x1 + 0x2 = b2 − tb1
bringen. Wenn die beiden Geraden verschieden sind, dann ist b2 − tb1 6= 0 und diese
Gleichung hat keine Lösung. Das Gleichungssystem ist in diesem Fall aufgrund der
angegebenen neuen Form der zweiten Zeile singulär.
(c) Wenn die beiden Geraden zusammenfallen, dann sind alle Punkte dieser Gerade
Elemente der Lösungsmenge des Gleichungssystems. Rechnerisch heißt dies, dass
die zweite Zeile ein Vielfaches des ersten ist (oder umgekehrt). Dann können wir
mit dem Gauß-Verfahren die zweite Zeile in die Form
0x1 + 0x2 = 0
bringen. Auch in diesem Fall ist das Gleichungssystem singulär. Hier sind alle reellen
Zahlen x1 und x2 Lösung dieser Gleichung. Dann können wir beispielsweise für
x2 eine beliebige reelle Zahl t wählen, also x2 = t schreiben und dann die erste
Gleichung nach x1 auflösen:
a12
b1
−
t
x1 =
a11 a11
Man kann das Ergebnis dann auch vektoriell schreiben
b1 a12 − a11
~x = a11 + t
1
0
Das ist die vektorielle Form einer Geradengleichung.
36
Ob der Normalfall“ (genau eine Lösung) oder einer der beiden Sonderfälle“ (keine oder
”
”
unendlich viele Lösungen, Gleichungssystem singulär) auftreten, sieht man an den beiden
Vektoren ~u und ~v . Wenn ~u = s~v oder ~v = t~u, dann ist das System singulär und es
liegt einer der beiden Sonderfälle“ vor (welcher, das hängt von der rechten Seite ab).
”
Beachten Sie, dass zwei parallele Geraden identisch sind, wenn sie einen gemeinsamen
Punkt haben. Wenn b1 = b2 = 0, dann gehen beide Geraden durch den Ursprung, und
das Gleichungssystem hat genau eine oder unendlich viele Lösungen.
Schauen wir uns ein konkretes Beispiel an:
3x1 +x2 = 4
(33)
2x1 +x2 = 2
3
2
Wir erhalten ~u =
und ~v =
. Die beiden Geradengleichungen lauten in der
1
1
vertrauten Form
y = −3x + 4
und
y = −2x + 2
2
Die beiden Geraden schneiden sich im Punkt ~x =
(siehe auch die Abbildung 17)
−2
Es gibt noch eine zweite geometrische Interpretation unseres Gleichungssystems (32). Wir
Abbildung 17: geometrische Interpretationen des linearen Gleichungssystems (33): links
als Schnittpunkt der Geradengleichungen ~u · ~x = 4 und ~v · ~x = 2, rechts Darstellung
~b = x1 w
~ + x2~z
betrachten die spaltenweise aus den Koeffizienten der linken und rechten Seite gebildeten
Vektoren
a11
a12
~b := b1
w
~=
,
~z :=
und
a21
a22
b2
Wir können damit unser Gleichungssystem schreiben als
a11
a
x1
+ x2 12 = x1 · w
~ + x2 · ~z = ~b
a21
a22
37
Zu drei gegebenen Vektoren w,
~ ~z und ~b suchen wir also Skalare so, dass wir den dritten
~
Vektor b als Summe von Vielfachen der beiden anderen schreiben können. Machen Sie sich
anhand der Abbildung 17 klar, dass dies immer möglich ist, wenn die beiden Vektoren der
linken Seite ein Parallelogramm aufspannen. Dort sind die Zahlenwerte unseres Beispiels
(33) zugrunde gelegt.
Die beiden Skalare sind in diesem Fall eindeutig bestimmt. Der Sonderfall (singuläres
System) kann nur auftreten, wenn ~z ein Vielfaches von w
~ ist (oder umgekehrt). Dann
~
existieren unendlich viele Lösungen, wenn der Vektor b der rechten Seite ebenfalls ein
Vielfaches von w
~ oder ~z ist; sonst existiert keine Lösung des Gleichungssystems.
Abbildung 18: geometrische Interpretationen des linearen Gleichungssystems (34): links
zeilenweise (zwei parallele Geraden), rechts spaltenweise
Durch eine Änderung des Zahlenwerts von a21 und a22 erhalten wir aus unserem Beispiel 33 das System
3x1 +x2 = 4
(34)
6x1 +2x2 = 2
mit ~v = 2~u, die beiden Geraden sind also parallel. Man kann dies auch an den beiden
Geradengleichungen in der vertrauten Form sehen:
y = −3x + 4,
y = −3x + 1
Addition des (−2)-fachen der ersten Zeile zur zweiten liefert die unlösbare Gleichung
0x1 + 0x2 = −6 und zeigt somit auch rechnerisch, dass die Lösungsmenge leer ist. Für die
spaltenweise gebildeten Vektoren erhalten wir w
~ = 3~z, aber ~b ist kein Vielfaches von ~z,
also kann
x1 w
~ + x2~z = (3x1 + x2 )~z = ~b
keine Lösung haben. Die Situation ist in Abb. 18 veranschaulicht.
Eine zusätzliche Änderung von b2 liefert das System
3x1 +x2 = 4
6x1 +2x2 = 8
(35)
bei dem die zweite Zeile das doppelte der ersten ist. Die Lösungsmenge besteht aus
sämtlichen Punkten der zugehörigen Geraden. Für die spaltenweise gebildeten Vektoren
38
erhalten wir dann ~b = 4~z und
x1 w
~ + x2~z = (3x1 + x2 )~z = ~b = 2~z
und damit die erste Zeile unseres Gleichungssystems. Wir können eine der beiden Unbekannten beliebig wählen und dann nach der anderen auflösen, beispielsweise x2 = t und
x1 = − 13 t + 34 oder als vektorielle Geradengleichung geschrieben
1
4
−3
3
+t
~x =
0
1
Halten wir als Ergebnis unserer Überlegungen fest:
Satz 3.2.1 Ein lineares Gleichungssystem
a11 x1 +a12 x2 = b1
a21 x1 +a22 x2 = b2
ist genau dann singulär, wenn für die zeilenweise gebildeten Vektoren
a11
a21
~u :=
und
~v :=
a12
a22
gilt ~u = s~v oder ~v = t~u.
Es ist genau dann singulär, wenn für die spaltenweise gebildeten Vektoren
a11
a12
w
~=
,
und
~z :=
a21
a22
gilt w
~ = s~z oder ~z = tw.
~
Hinweis: Wir können vier beliebige Zahlen stets quadratisch anordnen und daraus zeilenweise und spaltenweise Vektoren bilden. Als Folgerung aus dem Satz erhalten wir, dass die
zeilenweise gebildeten Vektoren genau dann in dieselbe oder entgegengesetzte Richtung
zeigen, wenn dies die spaltenweise gebildeten Vektoren tun.
Wir betrachten nun ein Beispiel mit drei Gleichungen und drei Unbekannten und
verallgemeinern unsere Vorgehensweise entsprechend
3x1 +2x2 −x3 = 2
2x1 −x2 +3x3 = 0
x1 +3x2 −4x3 = 2
Dieses Gleichungssystem hat zwei geometrische Aspekte:
(a) Erster geometrischer Aspekt: Schauen wir uns die erste Zeile an. Definieren wir die
Vektoren
 
 
3
x1



2 ,
~u :=
~x := x2 
−1
x3
dann können wir die Gleichung 3x1 + 2x2 − x3 = 2 auch schreiben als
~u · ~x = 2
39
Sie hat dieselbe Form wie Gleichung (29), ist also die Gleichung einer Ebene senkrecht zu ~u. Mit den Vektoren
 
 
2
1



3
~v := −1 ,
w
~ :=
3
−4
können wir die beiden unteren Zeilen des Gleichungssystems auch als Ebenengleichungen schreiben
~v · ~x = 0,
w
~ · ~x = 2
Diese Überlegung hängt nicht von den hier vorliegenden Zahlenwerten der Koeffizienten ab. Wir können jedes lineare Gleichungssystem von drei Gleichungen mit
drei Unbekannten auffassen als die Aufgabenstellung, den Durchschnitt von drei
Ebenen zu berechnen! Es ist geometrisch plausibel, dass in diesem Durchschnitt im
Normalfall nur ein einziger Punkt liegt (siehe Abb. 19 links). Beachten Sie, dass der
Durchschnitt zweier Ebenen im Normalfall eine Gerade ist (siehe Abb. 19 rechts).
In Sonderfällen kann der Durchschnitt dreier Ebenen leer sein (wie in Abb. 20 links
gezeigt), eine Gerade (wie in Abb. 20 rechts gezeigt) oder auch in Extremfällen eine
ganze Ebene sein.
-2
2
0
4
-4
5
5
0
0
-5
4
-4
-5
2
-2
-4
-2
0
0
0
-2
2
2
4
4-4
Abbildung 19: Im Normalfall ergibt der Schnitt zweier Ebenen eine Gerade (links), der
Schnitt dreier Ebenen einen Punkt (rechts).
4
2
0
2
4
4
3
0
2
2
4
2
0
1
2
0
4
2
4
2
2
0
4
2
0
2
4
Abbildung 20: In Sonderfällen kann der Schnitt dreier Ebenen leer sein (links), oder eine
Gerade ergeben (rechts).
Man kann sich leicht klarmachen, dass der Sonderfall (leerer Durchschnitt von drei
Ebenen oder unendlich viele Punkte im Durchschnitt von drei Ebenen) nur auftreten
kann, wenn die drei Normalenvektoren ~u, ~v , w
~ in einer Ebene liegen.
40
In dem Spezialfall, dass auf der rechten Seite des Gleichungssystems überall Null
steht, gehen alle drei Ebenen durch den Ursprung, und der Nullvektor, d.h. die
triviale Lösung x1 = x2 = x3 = 0 gehört auf jeden Fall zur Lösungsmenge, die also
in diesem Spezialfall nie leer sein kann. Die triviale Lösung kann die einzige Lösung
sein. Sobald ein derartiges System eine Lösung hat, die von der trivialen Lösung
verschieden ist, hat die Lösungsmenge unendlich viele Lösungen (denn sie enthält
eine Gerade).
(b) Zweiter geometrischer Aspekt: Wir können unser Gleichungssystem auch in der
Form schreiben
 
 
   
3
2
−1
2
x1 · 2 + x2 · −1 + x3 ·  3  = 0
1
3
−4
2
Mit den Spaltenvektoren
 
 
3
2
~



~a := 2 ,
b := −1 ,
1
3


−1
~c :=  3  ,
−4
 
2
~

d := 0
2
wird aus dem Gleichungssystem die Aufgabenstellung, Skalare x1 , x2 und x3 zu
suchen, die
x1~a + x2~b + x3~c = d~
erfüllen. Es ist geometrisch plausibel, dass eine derartige Aufgabenstellung im Normalfall genau eine Lösung hat. Wenn jedoch die drei Vektoren ~a, ~b und ~c in einer
Ebene liegen, dann hängt es vom Vektor der rechten Seite d~ ab, ob überhaupt eine
Lösung existiert: Wenn er nicht ebenfalls in dieser Ebene liegt, dann kann keine
Lösung existieren, denn man kommt nie aus der Ebene heraus, in der ~a, ~b und ~c
liegen, egal wie man die Skalare x1 , x2 und x3 wählt. Liegt jedoch d~ auch in der
Ebene von ~a, ~b und ~c, dann gibt es sehr viele Möglichkeiten, d~ in der gewünschten
Weise als Summe darzustellen.
Aus beiden geometrischen Interpretationen wird klar, dass ein lineares Gleichungssystem
genau eine, gar keine oder unendlich viele Lösungen haben kann. Zur Entscheidung, welcher Fall vorliegt, und zur praktischen Berechnung der Lösungsmenge empfiehlt sich das
Gauß-Verfahren. Wenden wir dieses auf unser Beispiel an: Addition des − 32 -fachen der
ersten Zeile zur zweiten sowie des − 13 -fachen der ersten Zeile zur dritten liefert
3x1 +2x2
−x3 = 2
− 73 x2 + 11
x = − 34
3 3
+ 73 x2 − 11
x = 43
3 3
Addition der zweiten zur dritten Zeile liefert schließlich die gewünschte Dreiecksform:
3x1 +2x2
−x3 = 2
7
11
− 3 x2 + 3 x3 = − 34
0x3 = 0
41
Jede reelle Zahl ist Lösung der dritten Gleichung. Es ist sinnvoll x3 = t zu schreiben (mit
t ∈ R beliebig). Einsetzen in die zweite Gleichung liefert
7
11
4
4 11
− x2 + t = − ,
x2 = + t
3
3
3
7
7
und Einsetzen in die erste Gleichung liefert
4 11
14 8 22
7
3x1 + 2
+ t − t = 2,
3x1 =
− − t + t,
7
7
7
7
7
7
x1 =
2 5
− t
7 7
Dieses Ergebnis kann auch mit Hilfe von Vektoren geschrieben werden:
  2
 −5 
x1
7
7
,
~x = x2  =  47  + t ·  11
mit t ∈ R beliebig
7
0
1
x3
Dies ist die Gleichung einer Geraden, was aufgrund der ersten geometrischen Interpretation beim Schnitt von drei Ebenen zu erwarten war.
Halten wir als Ergebnis unserer Überlegungen fest:
Satz 3.2.2 Ein Gleichungssystem
a11 x1 +a12 x2 +a13 x3 = d1
a21 x1 +a22 x2 +a23 x3 = d2
a31 x1 +a32 x2 +a33 x3 = d3
ist genau dann singulär, wenn die drei zeilenweise gebildeten Vektoren
 
 
 
a31
a21
a11





w
~ := a32 
~v := a22 ,
~u := a12 ,
a33
a23
a13
in einer Ebene liegen.
Es ist genau dann singulär, wenn die drei spaltenweise gebildeten Vektoren
 
 
 
a11
a12
a13
~b := a22  ,
~a := a21  ,
~c := a23 
a31
a32
a33
in einer Ebene liegen.
Hinweis: Wir können neun Zahlen stets quadratisch anordnen. Aus dem Satz folgt, dass
die drei zeilenweise gebildeten Vektoren genau dann in einer Ebene liegen, wenn dies die
drei spaltenweise gebildeten tun. Dieses Ergebnis werden wir später verallgemeinern.
3.3
Homogene und inhomogene lineare Gleichungssysteme
Definition 3.3.1 Ein lineares Gleichungssystem heißt homogen, wenn auf der rechten
Seite nur Nullen stehen, wenn es also die Form hat
a11 x1
a21 x1
a31 x1
a41 x1
..
.
+a12 x2
+a22 x2
+a32 x2
+a42 x2
..
.
+a13 x3
+a23 x3
+a33 x3
+a43 x3
..
.
+a14 x4
+a24 x4
+a34 x4
+a44 x4
..
.
+···
+···
+···
+···
...
an1 x1 +an2 x2 +an3 x3 +an4 x4 + · · ·
42
+a1n xn
+a2n xn
+a3n xn
+a4n xn
..
.
=
=
=
=
0
0
0
0
..
.
+ann xn = 0
Die Lösung x1 = x2 = x3 = · · · xn = 0 heißt dann die triviale Lösung des homogenen
Gleichungssystems.
Ein lineares Gleichungssystem heißt inhomogen, wenn es nicht homogen ist, wenn also
in mindestens einer Zeile auf der rechten Seite eine von Null verschiedene Zahl steht.
Bei einem inhomogenen linearen Gleichungssystem ist das zugehörige homogene
Gleichungssystem das Gleichungssystem, das entsteht, wenn man alle Zahlen auf der rechten Seite durch Null ersetzt.
Hinweis: Ob ein lineares Gleichungssystem singulär ist oder nicht, entscheidet sich allein
aufgrund der Koeffizienten, die auf der linken Seite stehen, hängt also überhaupt nicht
von den Zahlen auf der rechten Seite ab. Ein homogenes Gleichungssystem hat stets
mindestens eine Lösung, nämlich die triviale Lösung. Wir haben daher die Aussage
Satz 3.3.1 Ein homogenes lineares Gleichungssystem ist genau dann singulär, wenn es
mindestens eine Lösung hat, die von der trivialen Lösung verschieden ist (bei der mindestens ein xk 6= 0 ist). Es ist genau dann nichtsingulär, wenn es nur die triviale Lösung
hat.
3.4
3.4.1
Unter- und überbestimmte lineare Gleichungssysteme
Unterbestimmte lineare Gleichungssysteme
Lineare Gleichungssysteme, die weniger Gleichungen als Unbekannte haben, nennt man
unterbestimmt. Wir bezeichnen hier die Zahl der Zeilen mit n und die Zahl der Unbekannten mit m. Ein unterbestimmtes Gleichungssystem hat also die Form
a11 x1
a21 x1
a31 x1
a41 x1
..
.
+a12 x2
+a22 x2
+a32 x2
+a42 x2
..
.
+a13 x3
+a23 x3
+a33 x3
+a43 x3
..
.
+a14 x4
+a24 x4
+a34 x4
+a44 x4
..
.
+···
+···
+···
+···
..
.
an1 x1 +an2 x2 +an3 x3 +an4 x4 + · · ·
+a1m xm
+a2m xm
+a3m xm
+a4m xm
..
.
=
=
=
=
b1
b2
b3
b4
..
.
+anm xm = bn
mit m > n. Auch auf derartige Gleichungssysteme ist das Gauß-Verfahren anwendbar, so
wie es in Abschnitt 3.1.4 beschrieben wurde. Man erhält dann allerdings keine Umwandlung in Dreiecksform, sondern in folgende Trapezform“:
”
a11 x1 +a12 x2 +a13 x3 + · · · +a1n xn +a1,n+1 xn+1 + · · · +a1m xm = b1
a22 x2 +a23 x3 + · · · +a2n xn +a2,n+1 xn+1 + · · · +a2m xm = b2
a33 x3 + · · · +a3n xn +a3,n+1 xn+1 + · · · +a3m xm = b3
..
..
..
..
..
...
.
.
.
.
.
ann xn
+an,n+1 xn+1 + · · ·
+anm xm = bn
Wenn ann 6= 0, dann ist zunächst xn+1 = t1 , xn+2 = t2 , . . . xm = tm−n frei wählbar
(t1 , t2 , . . . tm−n ∈ R beliebig), und die letzte Zeile kann nach xn aufgelöst werden. Durch
Einsetzen derartiger Bedingungen in die darüberliegende Zeile erhält man weitere Bedingungen an die Unbekannten. Im allgemeinen hat also ein unterbestimmtes lineares
Gleichungssystem unendlich viele Lösungen. Betrachten wir folgendes Beispiel:
2x1 +3x2 −5x3 = 10
4x1 +8x2 −3x3 = 19
43
Addition des (−2)-fachen der ersten Zeile zur zweiten liefert
2x1 +3x2 −5x3 = 10
2x2 +7x3 = −1
x3 = t ∈ R kann beliebig gewählt werden, damit erhält man aus der unteren Zeile
1 7
x2 = − − t
2 2
2x2 = −1 − 7x3 ,
Einsetzen in die erste Zeile ergibt
1 7
2x1 + 3 − − t − 5t = 10,
2 2
2x1 = 10 +
3 21
10
+ t + t,
2
2
2
x1 =
23 31
+ t
4
4
Die Lösung kann auch vektoriell geschrieben werden
   23 
 31 
x1
4
4
~x = x2  = − 12  + t · − 72 
0
1
x3
Dies ist die vektorielle Gleichung einer Geraden im Raum — in Übereinstimmung mit
der geometrischen Anschauung, dass der Durchschnitt zweier Ebenen im allgemeinen eine
Gerade ergibt.
Es kann auch vorkommen, dass ein unterbestimmtes System unlösbar ist, die Lösungsmenge
also leer ist, wie das folgende Beispiel zeigt:
x1 +x2 +x3 = 1
3x1 +3x2 +3x3 = 2
Interpretiert man diese beiden Gleichungen als Ebenengleichungen, so sieht man, dass der
Normalenvektor der zweiten Gleichung dieselbe Richtung hat wie der der ersten (er ist
das dreifache). Beide Ebenen sind also parallel. Sie fallen aber nicht zusammen, denn die
Multiplikation der ersten Gleichung mit drei liefert nicht dieselbe rechte Seite wie in der
zweiten Gleichung. Die Anwendung des Gauß-Verfahrens führt zum gleichen Ergebnis:
Addition des (−3)-fachen der ersten Gleichung zur zweiten liefert
0x1 + 0x2 + 0x3 = −1
und dies ist für alle reellen Zahlen x1 , x2 , x3 unmöglich. Die Lösungsmenge ist also leer.
3.4.2
Überbestimmte Systeme
Überbestimmte lineare Gleichungssysteme sind Systeme, die mehr Gleichungen als Unbekannte haben. Wir bezeichnen auch hier die Zahl der Zeilen mit n und die Zahl der
Unbekannten mit m. Ein überbestimmtes Gleichungssystem hat also die Form
a11 x1
a21 x1
a31 x1
a41 x1
..
.
+a12 x2
+a22 x2
+a32 x2
+a42 x2
..
.
+a13 x3
+a23 x3
+a33 x3
+a43 x3
..
.
+a14 x4
+a24 x4
+a34 x4
+a44 x4
..
.
+···
+···
+···
+···
..
.
an1 x1 +an2 x2 +an3 x3 +an4 x4 + · · ·
44
+a1m xm
+a2m xm
+a3m xm
+a4m xm
..
.
=
=
=
=
b1
b2
b3
b4
..
.
+anm xm = bn
mit m < n. Dies kommt in der Praxis häufig vor, wenn man beispielsweise mehr Messungen macht als zur Bestimmung der zu berechnenden Größen unbedingt notwendig ist.
Anwendung des Gaußverfahren liefert ein System in der folgenden Form
a11 x1 +a12 x2 +a13 x3 +a14 x4
a22 x2 +a23 x3 +a24 x4
a33 x3 +a34 x4
a44 x4
+···
+···
+···
+···
...
+a1m xm
+a2m xm
+a3m xm
+a4m xm
..
.
=
=
=
=
b1
b2
b3
b4
..
.
amm xm
0 · xm
0 · xm
..
.
= bm
= bm+1
= bm+2
..
.
0 · xm
= bn
Wenn mindestens eine der Zahlen bm+1 , bm+2 , . . . bn von Null verschieden ist, dann hat
ein derartiges System keine Lösung. Bei den Anwendungen, bei denen ein solches System auftritt, ist es allerdings meist nicht sinnvoll, eine exakte Lösung des Systems zu
suchen. Wenn das System, wie als Beispiel schon erwähnt wurde, durch eine größere
Zahl von Messungen, als zur Berechnung der unbekannten Größen unbedingt notwendig
sind, überbestimmt wird, so ist zu erwarten, dass es durch das Auftreten von Meßfehlern
unlösbar wird. In diesem Fall ist eine andere Aufgabenstellung sinnvoll. Addiert man in
jeder Zeile des ursprünglichen Gleichungssystems das Negative der rechten Seite (also −bk
in der k. Zeile), so erhält man ein System in der Form
a11 x1
a21 x1
a31 x1
a41 x1
..
.
+a12 x2
+a22 x2
+a32 x2
+a42 x2
..
.
+a13 x3
+a23 x3
+a33 x3
+a43 x3
..
.
+a14 x4
+a24 x4
+a34 x4
+a44 x4
..
.
+···
+···
+···
+···
an1 x1 +an2 x2 +an3 x3 +an4 x4 + · · ·
+a1m xm
+a2m xm
+a3m xm
+a4m xm
..
.
−b1
−b2
−b3
−b4
..
.
=
=
=
=
0
0
0
0
..
.
+anm xm −bn = 0
Wenn die Koeffizienten aus fehlerbehafteten Messungen stammen, dann ist nicht zu erwarten, dass diese Gleichungen exakt erfüllt sind. Man hat eher davon auszugehen, dass
auf der rechten Seite Zahlen nahe Null stehen, mit wechselndem Vorzeichen, wenn die
Meßfehler zufälliger Natur sind. Es ist daher sinnvoll, statt einer exakten Lösung das
Minimum von
(a11 x1
+(a21 x1
+(a31 x1
+(a41 x1
+a12 x2
+a22 x2
+a32 x2
+a42 x2
+a13 x3
+a23 x3
+a33 x3
+a43 x3
+a14 x4
+a24 x4
+a34 x4
+a44 x4
..
.
+···
+···
+···
+···
+(an1 x1 +an2 x2 +an3 x3 +an4 x4 + · · ·
+a1m xm
+a2m xm
+a3m xm
+a4m xm
−b1 )2
−b2 )2
−b3 )2
−b4 )2
+anm xm −bn )2
zu suchen. Wenn eine exakte Lösung existiert, dann wird diese Summe Null. Man wird in
den Fällen, in denen keine exakte Lösung existiert, die Werte von x1 , x2 . . . xm , für die diese Summe minimal wird, als eine gute Näherung an das ursprüngliche praktische Problem
ansehen, das auf das Gleichungssystem führte. Die Bedingung, dass diese Summe minimal
45
ist, führt auf ein neues Gleichungssystem für die Unbekannten, das m Gleichungen enthält,
also genausoviele wie Unbekannte vorhanden sind. Derartige Überlegungen sind Gegenstand der Ausgleichsrechnung. Wir werden darauf im Abschnitt 10.1 zurückkommen.
Es ist noch anzumerken, dass überbestimmte Systeme nicht immer unlösbar sind. Ein
Beispiel ist
2x1 +3x2 =
8
5x1 −4x2 = −3
7x1 −x2 =
5
Sture Anwendung des Gauß-Verfahrens führt auf das System
2x1
+3x2 =
8
x
=
−23
− 23
2 2
− 23
x = −23
2 2
und man erhält die Lösung x2 = 2, x1 = 1. Man sieht auch beim ursprünglichen System,
dass die dritte Zeile die Summe der beiden ersten Zeilen ist, also keine neue Bedingung
an die Unbekannten enthält.
4
Vektorräume
Vorbemerkungen:
Die bisher behandelten Vektoren haben eine anschauliche geometrische Bedeutung, wir
können sie uns als Pfeile“ in der Ebene oder im Raum vorstellen. In den folgenden
”
Abschnitten werden die hierfür behandelten Konzepte verallgemeinert. Wir werden dabei Objekte als Vektoren ansehen, die sich einer derartigen elementaren geometrischen
Anschauung entziehen. Diese Verallgemeinerung ist jedoch für die moderne Nachrichtentechnik unentbehrlich. Hier sollen zunächst zur Motivation einige nachrichtentechnische
Anwendungen vorgestellt werden.
Als Modelle für Tonsignale betrachten wir Funktionen der Zeit f (t). Die Funktionswerte stehen für die Luftdruckschwangungen oder für die Spannung als Funktion der Zeit,
in die das Mikrophon die Luftdruckschwankungen umsetzt. Eine Verstärkung kann modellmäßig dadurch beschrieben werden, dass die Funktion f mit einer reellen Konstante
c > 1 multipliziert wird, d.h man hat dann die Funktionswerte c · f (t). Treten zwei Schallquellen auf, beispielsweise die Stimme eines Sängers (beschrieben durch die Funktion f )
und seine Gitarre (beschrieben durch die Funktion g), so lässt sich dies modellmäßig als
Addition der beiden Signale f + g beschreiben. Als Ergebnis erhalten wir die Summe
h = f + g. Die Funktionswerte von h sind dabei einfach die Summe der Funktionswerte
von f und g, also h(t) = f (t) + g(t).
Die Idee, eine Funktion als ein einzelnes Objekt“ anzusehen, hat sich als außeror”
dentlich nützlich erwiesen. Man kann solche Objekte addieren und mit einer reellen Zahl
(einer Konstanten) multiplizieren. Überzeugen Sie sich, dass hierfür dieselben Rechenregeln gelten wie für Vektoren ((1) bis (8)). Dem Nullvektor entspricht hier die Nullfunktion
f (t) = 0 für alle t. Wir können also mit Funktionen genauso rechnen wie mit den anschaulichen Vektoren. Alle Rechenregeln, die sich aus den Regeln (1) bis (8) herleiten lassen,
gelten somit auch für Funktionen. Dies ist für die Behandlung der Fourier-Reihen und der
Fourier- und Laplace-Transformation (im 3. Semester) wichtig.
46
In der Nachrichtentechnik werden Tonsignale nicht in der Form von Funktionen eines
kontinuierlichen Parameters behandelt, sondern als Abtastwerte:
yk = f (k∆t),
k∈Z
In der Praxis haben Tonsignale eine endliche Dauer, und wir können die Zeit auf ein
endliches Intervall beschränken. Durch Verschieben des Zeitnullpunkts können wir stets
erreichen, dass dieses Intervall die Form [0, T ] mit T > 0 hat. Dann erhalten wir
yn = f (n∆t),
n = 0, 1, 2, . . . N − 1
wenn ∆t = NT−1 gewählt wurde. Eine derartige Nummerierung lässt sich beispielsweise
in der Programmiersprache C direkt umsetzen. In der Mathematik (und im Programm
Scilab) ist allerdings die Nummerierung
yn = f (n − 1)∆t ,
n = 1, 2, 3, . . . N
üblich. Für Tonsignale ist es sinnvoll, mit ∆t < 10−4 s zu arbeiten. Für ein ganzes Musikstück wird N also recht groß. Die Abtastwerte eines kleinen Ausschnitts eines Tonsignals sind in Abb. 21 gezeigt.
Abbildung 21: Abtastwerte eines Tonsignals (kleiner Ausschnitt)
Eine Verstärkung bedeutet für die Abtastwerte, dass sie alle mit einer Zahl c > 1
multipliziert werden. Bei einer Addition der Tonsignale werden jeweils die Abtastwerte mit
derselben Nummer, also mit demselben Index, addiert. Wir haben also dieselbe Situation
wie bei den anschaulichen“ Vektoren, nur dass die Zahl der Komponenten sehr gross
”
sein kann. Wir können also die Abtastwerte von Tonsignalen als Komponenten eines
Vektors auffassen und dann genauso rechnen wie mit den anschaulichen“ Vektoren. Es
”
gelten hierfür ebenso dieselben Rechenregeln (1) bis (8). Das Ziel dieses Abschnitts ist,
die mathematischen Fachausdrücke hierfür zur Verfügung zu stellen.
4.1
Definition des Begriffs Vektorraum“
”
Definition 4.1.1 Ein Vektorraum ist eine Menge V mit zwei Rechenoperationen, die
die unten angegebenen Grundregeln erfüllen: einer Addition, die jedem Paar ~a, ~b ∈ V
47
eindeutig die Summe ~a + ~b ∈ V zuordnet sowie einer Multiplikation von reellen Zahlen
mit Elementen in V , die jedem Paar t, ~a mit t ∈ R und ~a ∈ V das Element t~a ∈ V
zuordnet. Es werden die folgenden Grundregeln für alle ~a, ~b, ~c ∈ V und alle s, t ∈ R
gefordert:
~a + ~b
(~a + ~b) + ~c
es existiert ein ~0 ∈ V mit
~a + ~0
zu jedem ~a ∈ V existiert ein −~a ∈ V mit
~a + (−~a)
t(~a + ~b)
~b + ~a
~a + (~b + ~c)
~a
~0
= t~a + t~b
(s + t)~a = s~a + t~a
s(t~a) = (st)~a
1 · ~a = ~a
=
=
=
=
Die Elemente eines Vektorraums werden Vektoren genannt.
Hinweise:
(a) Zur Verdeutlichung wird für die Multiplikation von reellen Zahlen mit Vektoren
zuweilen auch ein Punkt geschrieben: t · ~a = t~a.
(b) Statt mit dem umständlichen Pfeil werden Vektoren häufig auch durch Fettdruck
gekennzeichnet: also a ∈ V statt ~a ∈ V .
(c) Das neutrale Element bzgl. der Addition ~0 wird auch hier Nullvektor genannt.
(d) In die Definition wurden die grundlegenden Rechenregeln von Abschnitt 2.1 übernommen, die für die dort behandelten anschaulichen“ Vektoren der Ebene und
”
des Raumes gelten. Die Vorgehensweise ist typisch für die Mathematik. Regeln, die
bei bestimmten Beispielen festgestellt werden, werden in eine allgemeine Definition
übernommen. Sind diese Regeln für eine Menge und die dort definierten Rechenoperationen erfüllt, dann bekommt die Menge einen bestimmten Namen“ oder Titel“:
”
”
Vektorraum, Körper, Ring, Gruppe, Algebra.
Beispiele:
(a) Die Menge der in Abschnittt 2.1 behandelten anschaulichen“ Vektoren der Ebene
”
oder des Raumes ist ein Vektorraum.
(b) Wenn wir vereinbaren, dass wir Paare und Tripel von reellen Zahlen hier spaltenweise
aufschreiben, dann können wir Vektoren der Ebene in der in Abschnitt 2.2 behandelten Komponentenschreibweise als Elemente von R2 und Vektoren des Raumes
als Elemente von R3 ansehen. Mit den in Abschnittt 2.1 behandelten Regeln sind
also R2 und R3 Vektorräume.
(c) Eine Menge mit nur einem einzigen Element kann zum Vektorraum gemacht werden,
wenn man dieses Element als den Nullvektor ansieht. V = {~0} ist ein triviales
Beispiel für einen Vektorraum.
48
(d) Die Menge V = R der reellen Zahlen erfüllt alle Bedingungen der Definition (prüfen
Sie das zur Übung nach!). Auch dieses Beispiel wird von den Mathematikern als
trivial eingestuft.
(e) Wir nehmen als Menge V die Menge der Polynome höchstens 17. Grades, also
(
)
17
X
V := f (x) =
ak x k
k=0
Die Addition von zwei Vektoren f (x) =
17
P
ak xk und g(x) =
k=0
bk xk kann durch
k=0
17
X
f (x) + g(x) :=
17
P
(ak + bk )xk
k=0
definiert werden, entsprechend für t ∈ R
t · f (x) :=
17
X
t · ak xk
k=0
Überzeugen Sie sich, dass diese Menge mit den so definierten Rechenoperationen
tatsächlich allen Bedingungen der Definition eines Vektorraums erfüllt! Als Nullvektor dient das Nullpolynom (bei dem alle Koeffizienten Null sind).
(f) Die Vorgehensweise beim vorangehenden Beispiel kann man verallgemeinern und
als Menge V die Menge aller Polynome höchstens n. Grades nehmen, wobei n ∈ N
beliebig ist.
(g) Auch wenn man als Menge V die Menge aller Polynome nimmt (ohne Einschränkung
hinsichtlich des Grades) ist die entstehende Menge bezüglich der oben erklärten
Addition und Multiplikation mit reellen Zahlen ein Vektorraum.
(h) Wir nehmen ein beliebiges abgeschlossenes nichtleeres Intervall [a, b] ⊂ R und als
Menge V die Menge aller Funktionen mit Zielmenge R, deren Definitionsbereich das
Intervall [a, b] ist, also
V := {f | f : [a, b] → R, x 7→ f (x)}
Die Summe zweier Funktionen f und g wurde in Definition 2.3.3 des AnalysisSkriptes definiert (zur Erinnerung: f + g : [a, b] → R, x 7→ f (x) + g(x)). Analog
kann man die Multiplikation einer Funktion f ∈ V mit einer reellen Zahl t durch
tf : [a, b] → R,
x 7→ t · f (x)
definieren. Als Nullvektor dient die Funktion
0 : [a, b] → R,
x 7→ 0
Überzeugen Sie sich (als Übungsaufgabe), dass alle Bedingungen der Definition
erfüllt sind!
49
(i) Statt eines abgeschlossenen Intervalls kann man auch R als Definitionsbereich wählen,
also
V := {f | f : R → R, x 7→ f (x)}
Auch diese Menge ist mit der oben definierten Addition und Multiplikation ein
Vektorraum.
Dem wichtigsten Beispiel wird der ganze nächste Unterabschnitt gewidmet:
4.2
Der Rn
Definition 4.2.1 Rn für n ∈ N+ ist das n-fache kartesische Produkt von R mit sich
selbst, wobei wir hier die Zahlen spaltenweise anordnen. Die Elemente eines n-fachen
kartesischen Produkts werden zuweilen auch n-tupel“genannt. Rn ist also die Menge aller
”
n-tupel reeller Zahlen:
   


a
1






 a2  

   


n
a
R :=
 3  ak ∈ R, k = 1, 2, 3 . . . n

. 


  ..  






an
Satz 4.2.1 Mit der Addition und Multiplikation mit t ∈ R
 

 

b1
a1 + b 1
a1
 b2 
 a2 + b 2 
 a2 
 

 


 


~b = 
~a + ~b :=  a3 + b3  ,
~a =  a3  ,
 b3  ,
 .. 
 .. 
 .. 
.
 . 
.
an
bn
an + b n


ta1
 ta2 
 
 
t~a =  ta3 
 .. 
 . 
tan
ist Rn ein Vektorraum.
Hinweis: In Analogie zur Situation bei n = 2 und n = 3 nennen wir ak die k. Komponente
von ~a.
In der Einleitung dieses Abschnitts wurden die abgetasteten Werte eines Tonsignals als
wichtiges Anwendungsbeispiel erwähnt. Hierfür ist lediglich die Schreibweise ungewöhnlich,
dass wir uns die Abtastwerte als untereinandergeschriebene Komponenten eines Vektors
vorstellen.
Definition 4.2.2 Sei V ein Vektorraum. Eine Abbildung
(~a, ~b) 7→ ~a · ~b
V × V → R,
heißt Skalarprodukt, wenn sie für alle ~a, ~b, ~c ∈ V und alle t ∈ R die folgenden
Grundregeln erfüllt:
~a · ~b = ~b · ~a
(~a + ~b) · ~c = ~a · ~c + ~b · ~c
(t~a) · ~b = t · (~a · ~b)
~a · ~a ≥ 0,
~a · ~a = 0 ⇐⇒ ~a = ~0
50
(36)
(37)
(38)
(39)
Wenn in V ein Skalarprodukt existiert, dann wird der Betrag oder die Länge eines
Vektors ~a ∈ V durch
√
|~a| := ~a · ~a
definiert. Die Länge eines Vektors ~a wird auch Norm von ~a genannt.
Zwei Vektoren ~a, ~b ∈ V heißen orthogonal, wenn ~a · ~b = 0.
Satz 4.2.2 Durch
 
 
a1
b1
 a2 
 b2 
 
 
 a3 
 
~
~a =   ,
b =  b3  ,
 .. 
 .. 
.
.
an
bn
~a · ~b := a1 b1 + a2 b2 + a3 b3 + · · · + an bn =
n
X
ak b k
k=1
ist in Rn ein Skalarprodukt definiert. Für n = 2 und n = 3 stimmt die dadurch definierte
Länge eines Vektors
v
u n
uX
|~a| = t
a2k
k=1
mit der elementaren geometrischen Länge überein.
Für unser Beispiel von Tonsignalen heißt dies, dass wir den Abstand zweier Tonsignale ~a
und ~b durch
v
u n
uX
~
|~a − b| = t (ak − bk )2
k=1
beschreiben. Wenn dieser Abstand klein ist, dann sehen wir ~a als eine gute Näherung für
~b an.
4.3
Lineare Abhängigkeit, lineare Unabhängigkeit
Zur Vorbereitung betrachten wir, was es geometrisch bedeutet, wenn ein lineares Gleichungssystem mit n Gleichungen und n Unbekannten singulär ist. Aufgrund von Satz 3.3.1
genügt es, zu untersuchen, ob das zugehörige homogene Gleichungssystem eine nichttriviale Lösung hat.
n = 1 Das System“ a11 x1 = 0 ist genau dann singulär, wenn a11 = 0.
”
n = 2 Schreiben wir das System vektoriell (nach dem zweiten geometrischen Aspekt“,
”
siehe Abschnitt 3.2), dann haben wir
a11
a
x1
+ x2 12 = ~0
a21
a22
Mit
a11
~u :=
,
a21
a12
~v :=
a22
erhält das System die Form
x1~u + x2~v = ~0
51
Es ist genau dann singulär, wenn ~u und ~v dieselbe Richtung haben, wenn also
~u = t~v oder ~v = s~u mit einem t ∈ R oder s ∈ R (dies folgt aus der Existenz einer
nichttrivialen Lösung mit x1 6= 0 oder x2 6= 0, dann kann man nach einem der beiden
Vektoren auflösen).
n = 3 Auch hier wählen wir die vektorielle Darstellung. Mit
 
 
 
a11
a12
a13
~u1 = a21  ,
~u2 = a22  ,
~u3 = a23 
a31
a32
a33
lautet das zugehörige homogene Gleichungssystem
x1~u1 + x2~u2 + x3~u3 = ~0
Die Existenz einer nichttrivialen Lösung bedeutet, es gibt eine Lösung mit x1 6= 0
oder x2 6= 0 oder x3 6= 0 (oder im mathematischen Sinn!). Wenn nun x1 6= 0, dann
kann man diese Vektorgleichung nach ~u1 auflösen
x1~u1 = −x2~u2 − x3~u3 ,
~u1 = −
x3
x2
~u2 − ~u3
x1
x1
also liegt dann ~u1 in der von ~u2 und ~u3 aufgespannten Ebene. Eine analoge Überlegung
kann man in den beiden andern Fällen (x2 6= 0, x3 6= 0) anstellen. Wir haben als
Ergebnis, dass das System genau dann singulär ist, wenn (mindestens) ein Spaltenvektor in der von den beiden andern Spaltenvektoren aufgespannten Ebene liegt.
Definition 4.3.1 Sei V ein Vektorraum und n ∈ N+ .
(a) Eine Linearkombination ist eine Summe der Form
t1~u1 + t2~u2 + t3~u3 + · · · + tn~un
wobei n ∈ N+ , t1 t2 t3 . . . tn ∈ R und ~u1 , ~u2 , ~u3 . . . ~un ∈ V .
(b) Die Vektoren ~u1 , ~u2 , ~u3 . . . ~un ∈ V heißen linear unabhängig, wenn aus
t1~u1 + t2~u2 + t3~u3 + · · · + tn~un = ~0
folgt, dass
t1 = t2 = t3 = · · · = tn = 0
(c) Die Vektoren ~u1 , ~u2 , ~u3 . . . ~un ∈ V heißen linear abhängig, wenn sie nicht linear
unabhängig sind, also wenn eine Linearkombination
t1~u1 + t2~u2 + t3~u3 + · · · + tn~un = ~0
existiert, bei der mindestens ein Skalar tk 6= 0 erfüllt (1 ≤ k ≤ n).
52
Hinweise:
(a) Wenn die Vektoren ~u1 , ~u2 , ~u3 . . . ~un linear abhängig sind, dann kann die laut Definition existierende Linearkombination mit tk 6= 0 nach dem Vektor ~uk aufgelöst
werden, also
n
n
X
X
tl
~ul
tk ~uk = −
tl ~ul ,
~uk = −
tk
l=1
l=1
l6=k
l6=k
also ist dann stets ein Vektor ~uk als Linearkombination der übrigen Vektoren darstellbar.
(b) Beachten Sie, dass im Fall V = Rm in der Definition nicht verlangt ist, dass die Zahl
der Komponenten m und die Zahl der Vektoren n übereinstimmt. Der Fall V = Rm
ist in Satz 4.3.1 behandelt.
Sonderfälle und Beispiele:
(a) Ein einzelner Vektor ~u ist genau dann linear unabhängig, wenn ~u 6= ~0. Ein einzelner
Vektor ~u ist genau dann linear abhängig, wenn ~u = ~0, denn ~u = ~0 =⇒ 1 · ~u = ~0,
t~u = ~0 mit t 6= 0 =⇒ 1t · t~u = ~u = ~0
(b) Wenn zwei Vektoren ~u, ~v linear abhängig sind, dann existiert eine Linearkombination
t1~u + t2~v = ~0 mit t1 6= 0 oder t2 6= 0, also
t2
~u = − ~v
t1
oder
t1
~v = − ~u
t2
(c) Wenn drei Vektoren ~u, ~v , w
~ linear abhängig sind, dann existiert eine Linearkombination
t1~u + t2~v + t3 w
~ = ~0
mit t1 6= 0 oder t2 6= 0 oder t3 6= 0.
t3
t2
t1 6= 0 =⇒ ~u = − ~v − w
~
t1
t1
In den anderen Fällen läßt sich ebenfalls einer der Vektoren als Linearkombination
der beiden andern schreiben.
(d) Wenn einer der beteiligten Vektoren der Nullvektor ist, wenn also ~uk = ~0 für ein k
mit 1 ≤ k ≤ n, dann sind die Vektoren ~u1 , ~u2 , ~u3 . . . ~un linear abhängig, denn mit
tk = 1 hat man die Linearkombination
0~u1 + 0~u2 + · · · + 1 · ~uk + · · · + 0~un = ~0
Der für die Praxis ganz besonders wichtige Fall V = Rn wird im folgenden Satz behandelt:
Satz 4.3.1 Sei V = Rn und gegeben seien m Vektoren ~u1 , ~u2 , ~u3 . . . ~um ∈ Rn .
53
(a) Wenn m ≤ n (die Zahl der Vektoren also nicht größer ist als die der Komponenten),
dann sind die Vektoren ~u1 , ~u2 , ~u3 . . . ~um genau dann linear unabhängig, wenn das
homogene lineare Gleichungssystem
x1~u1 + x2~u2 + x3~u3 + · · · + xm~um = ~0
nur die triviale Lösung hat.
(b) Wenn m > n (die Zahl der Vektoren also größer ist als die der Komponenten), dann
sind die Vektoren ~u1 , ~u2 , ~u3 . . . ~um stets linear abhängig.
Hinweise:
(a) Im Fall a) ist die Aussage des Satzes eine reine Wiederholung der Definition (mit
dem Unterschied, dass die Skalare hier xk genannt werden — im Gegensatz zu tk in
der Definition. Er ermöglicht aber eine einfache praktische Entscheidung, ob m gegebene Vektoren linear unabhängig sind. Man hat nur aus den gegebenen Vektoren ein
lineares Gleichungssystem aufzubauen“, sie also spaltenweise zu einem Gleichungs”
system zusammenzusetzen. Die Koeffizienten (in der Notation des Abschnitts 3.1.4)
erhält man durch


 
 
 
a1m
a1k
a12
a11
 a2m 
 a2k 
 a22 
 a21 


 
 
 
 a3m 
 a3k 
 a32 
 a31 
=
~
u
,
·
·
·
=
~
u
,
·
·
·
=
~
u
,

 = ~um
 
 
 
k
2
1
 .. 
 .. 
 .. 
 .. 
 . 
 . 
 . 
 . 
anm
ank
an2
an1
Das Gauß-Verfahren liefert dann die Lösungsmenge (wobei hier nur von Interesse
ist, ob sie ein Element enthält, das nicht der Nullvektor ist). Das Gleichungssystem
ist überbestimmt, falls m < n (also mehr Komponenten als Vektoren vorhanden
sind).
(b) Konkrete Beispiele: Es soll geprüft werden, ob die folgenden Vektoren linear unabhängig sind:
1. Beispiel:


2
4

~u1 = 
−2 ,
8


1
 −6 

~u2 = 
 7 ,
−12
 
1
0

~u3 = 
2
1
Das homogene lineare Gleichungssystem
x1~u1 + x2~u2 + x3~u3 = ~0
lautet hier
2x1
+x2 +x3
4x1 −6x2
−2x1 +7x2 +2x3
8x1 −12x2 +x3
54
=
=
=
=
0
0
0
0
Umwandlung in Dreiecksform mit Hilfe des Gauß-Verfahrens liefert
2x1
+x2 +x3
−8x2 −2x3
x3
0x3
=
=
=
=
0
0
0
0
Die einzige Lösung ist x1 = x2 = x3 = 0, also sind die drei Vektoren ~u1 , ~u2 , ~u3
linear unabhängig.
2. Beispiel:


2
4

~u1 = 
−2 ,
8


1
 −6 

~u2 = 
 7 ,
−12


3
−2

~u3 = 
5
−4
Das homogene lineare Gleichungssystem
x1~u1 + x2~u2 + x3~u3 = ~0
lautet hier
2x1
+x2
4x1 −6x2
−2x1 +7x2
8x1 −12x2
+3x3
−2x3
+5x3
−4x3
=
=
=
=
0
0
0
0
Umwandlung in Dreiecksform mit Hilfe des Gauß-Verfahrens liefert
2x1
+x2 +3x3
−8x2 −8x3
0x3
0x3
=
=
=
=
0
0
0
0
mit den Lösungen x3 = t, x2 = −t, x1 = −t mit beliebigem t ∈ R. Die Wahl
t = −1 liefert ~u1 + ~u2 − ~u3 = ~0, was man auch direkt hätte sehen können. Also
sind die drei Vektoren ~u1 , ~u2 , ~u3 linear abhängig.
(c) Im Sonderfall n = m erhalten wir aus Satz 4.3.1 die Regel:
Merke: Ein lineares Gleichungssystem mit n Gleichungen und n Unbekannten
ist genau dann singulär, wenn die aus den Koeffizienten spaltenweise gebildeten
Vektoren in Rn linear abhängig sind; es ist genau dann nichtsingulär, wenn diese
Vektoren linear unabhängig sind.
(d) Beweis von Fall b) des Satzes 4.3.1: Gesucht ist eine Linearkombination
x1~u1 + x2~u2 + x3~u3 + · · · + xn~un + xn+1~un+1 + · · · + xm~um = ~0
mit mindestens einem xk 6= 0. Schreibt man diese Gleichung komponentenweise, so
erhält man ein lineares Gleichungssystem, das laut Voraussetzung (m > n) unterbestimmt ist. Das Gauß-Verfahren liefert hierfür ein Gleichungssystem in Trapezform
55
(siehe Abschnitt 3.4.1)
a11 x1 +a12 x2 +a13 x3 + · · ·
a22 x2 +a23 x3 + · · ·
a33 x3 + · · ·
...
+a1n xn +a1,n+1 xn+1 + · · ·
+a2n xn +a2,n+1 xn+1 + · · ·
+a3n xn +a3,n+1 xn+1 + · · ·
..
..
..
.
.
.
ann xn +an,n+1 xn+1 + · · ·
+a1m xm = 0
+a2m xm = 0
+a3m xm = 0
..
..
.
.
+anm xm = 0
Wenn ann 6= 0, dann ist xn+1 = t1 , xn+2 = t2 , . . . xm = tm−n frei wählbar, und die
übrigen Unbekannten x1 , x2 , x3 , . . . xn können durch Rückwärtsauflösen durch die
Parameter t1 , t2 , . . . tm−n ∈ R ausgedrückt werden. Mit beispielsweise t1 = 1 erhält
man dann die für die lineare Abhängigkeit geforderte nichttriviale Linearkombination. Wenn ann = 0, dann kann mindestens xn = t ∈ R beliebig gewählt werden, und
man erhält durch die Wahl t = 1 eine gewünschte nichttriviale Linearkombination.
Die übrigen Unbekannten können durch Rückwärtsauflösen durch t und eventuell
weitere frei wählbare Zahlen ausgedrückt werden. Sollte eine der Gleichungen die
Form bxn = 0 mit b 6= 0 haben, dann kann mindestens eine andere Unbekannte einen beliebigen Wert t, also beispielsweise t = 1 annehmen. Denn jede weiter
oben stehende Zeile des Gleichungssystems enthält eine Unbekannte mehr als die
darunterliegende.
(e) In Rn existieren n linear unabhängige Vektoren, nämlich
 
 
 
1
0
0
0
1
0
 
 
 
0
1
0
 
 
 
~e1 := 0 ,
~e2 := 0 ,
~e3 := 0 , · · ·
 
 
 
 .. 
 .. 
 .. 
.
.
.
0
0
0
 
0
0
 
0
 
~en := 0
 
 .. 
.
1
(40)
Diese Vektoren ~ek sind überaus nützlich, nur die k. Komponente ist 1, alle übrigen
Komponenten sind 0. (Überzeugen Sie sich zur Übung mit Hilfe von Satz 4.3.1, dass
diese Vektoren tatsächlich linear unabhängig sind, schreiben Sie das entsprechende
Gleichungssystem explizit auf!)
(f) Im Spezialfall m = n + 1 > n erhält man aus Satz 4.3.1 die Regel
Merke: n + 1 Vektoren ~u1 , ~u2 , ~u3 . . . ~un , ~un+1 ∈ Rn sind stets linear abhängig.
4.4
Basis, Dimension
Definition 4.4.1 Sei V ein Vektorraum. Die Vektoren
{~u1 , ~u2 , ~u3 , . . . ~un }
mit ~uk ∈ V
für k = 1, 2, 3 . . . n
heißen Basis von V , wenn sie linear unabhängig sind und wenn jeder Vektor ~x ∈ V
darstellbar ist als Linearkombination
~x = t1~u1 + t2~u2 + t3~u3 + · · · + tn~un =
n
X
k=1
mit tk ∈ R für k = 1, 2, . . . n.
56
tk ~uk
Hinweis: Wenn {~u1 , ~u2 , ~u3 , . . . ~un } eine Basis in V ist und wenn ~x =
n
P
tk ~uk , dann sind
k=1
die Koeffizienten t1 , t2 , t3 , . . . tn eindeutig bestimmt, denn
~x =
n
X
tk ~uk =
k=1
n
X
k=1
sk ~uk =⇒
n
X
(tk − sk )~uk = ~0 =⇒ tk − sk = 0 für alle k = 1, 2 . . . n
k=1
Beispiele:
(a) In V = Rn haben wir die Basis {~e1 , ~e2 , ~e3 , . . . ~en }, wobei wir die Vektoren ~ek in
(40) definiert haben. Dass diese Vektoren linear unabhängig sind, wurde schon im
vorigen Unterabschnitt festgestellt. Jeder Vektor ~x ∈ Rn hat die Darstellung
 
x1
 x2 
n
  X
 x3 
~x =   =
xk~ek
 .. 
k=1
.
xn
Dies ist eine unmittelbare Folge der Definition der Addition in Rn . Im Spezialfall
n = 2 haben wir
1
0
x1
1
0
~e1 =
,
~e2 =
,
~x =
= x1
+ x2
= x1~e1 + x2~e2
0
1
x2
0
1
(b) In R2 haben wir auch die Basis {~u1 , ~u2 } mit
1
−1
~u1 =
,
~u2 =
1
1
Diese beiden Vektoren sind tatsächlich linear unabhängig (Übungsaufgabe!), und
der Versuch
x1
1
−1
t1 − t2
~x =
= t1
+ t2
=
x2
1
1
t1 + t2
führt auf das Gleichungssystem
t1 − t2 = x1 ,
t1 + t2 = x2
mit der Lösung t1 = 21 (x1 +x2 ), t2 = 12 (x2 −x1 ). Man kann sich dies auch anschaulich
an Abb. 22 klarmachen.
(c) Im vorigen Unterabschnitt wurde als Beispiel für einen Vektorraum die Menge aller
Polynome höchstens n. Grades behandelt:
V = {f : R → R | f (x) = a0 + a1 x + a2 x2 + a3 x3 + · · · + an xn }
Hier ist die Menge der speziellen Polynome
{1, x, x2 , x3 , . . . xn }
57
Abbildung 22: Auch ~u1 und ~u2 bilden eine Basis in R2 .
eine Basis. Diese speziellen Polynome fk (x) = xk sind tatsächlich linear unabhängig,
denn aus
f (x) = t0 + t1 x + t2 x2 + t3 x3 + · · · tn xn = 0 für alle x ∈ R
folgt t0 = t1 = t2 = t3 = · · · = tn = 0 aufgrund von Satz 2.3.5 des Analysis-Skripts.
Und die Menge der Polynome höchstens n. Grades ist gerade als die Menge der
Linearkombinationen der Funktionen fk (x) = xk definiert.
Abbildung 23: Abtastwerte eines Tonsignal, Vokal u“ (Ausschnitt)
”
Anwendungsbeispiel:
Betrachten wir als Anwendung den in Abb. 23 gezeigten Ausschnitt eines Tonsignals.
Er ist durch 152 Abtastwerte gegeben, also durch einen Vektor y ∈ Rn mit n = 152.
Bezüglich der Standardbasis in Rn hat er also die Darstellung
y = y1 e1 + y2 e2 + y3 e3 + · · · + yn en
mit n = 152 Summanden. Für die Darstellung derartiger Tonsignale gibt es jedoch eine
weitaus geschicktere Basis, nämlich die Vektoren c, uk (für k = 1, 2, . . . n2 ) und vk ∈ Rn
58
(für k = 1, 2, . . . n2 − 1), wobei die l. Komponente dieser Vektoren (l = 1, 2, . . . n) jeweils
gegeben ist durch c(l) = 1,
n
2π
n
2π
, k = 1, 2, . . . ,
vk (l) = sin k · l ·
, k = 1, 2, . . . − 1
uk (l) = cos k · l ·
n
2
n
2
Beachten Sie, dass wir damit wieder n Basisvektoren haben (die Konstruktion ist für
ungerades n leicht abzuändern). Man müsste (und kann) beweisen, dass es sich dabei
tatsächlich um eine neue Basis im Rn handelt. Die Komponenten der neuen Basisvektoren
sind gerade die Abtastwerte der Funktionen
2π
2π
fk (t) = cos k · t ·
und
gk (t) = sin k · t ·
n
n
für ganzzahlige Argumente. Für n = 6 erhalten wir damit die folgenden neuen Basisvektoren in R6 :
 √3 
 √3 
 
 1 
 1 
 
1
−1
2
2
2
2
 √3 
 √3 
1
− 1 
− 1 
1
−




 
 2
 2
 
 2
 2 
1
 −1 
 1 
−1
 0 
 0√ 

 
 
 
c=
, v2 =  √3 
1 , u1 = − 1  , u2 = − 1  , u3 =  1  , v1 = 
3

 2 

 
 12 
 12 
 
 √ 
− √2 
1
 
 
−1
− 3 
− 3 
2
2
2
2
1
1
1
1
0
0
Für n = 152 erhalten wir auf diese Weise 152 neue Basisvektoren. Unser Tonsignal lässt
sich mit diesen neuen Basisvektoren als Linearkombination
y = c0 c + a1 u1 + a2 u2 + a3 u3 + · · · + a76 u76 + b1 v1 + b2 v2 + b3 v3 + · · · + b75 v75
(41)
darstellen. Es wird Gegenstand der Lehrveranstaltungen des 3. Semesters sein, wie man
die zugehörigen Koeffizienten c0 , a1 , a2 . . . a76 und b1 , b2 . . . b75 berechnet. In der Praxis
wird man hierzu einen Computer benutzen. Die Koeffizienten ak und bk für das hier
benutzte Tonsignal sind in Abb. 24 grafisch dargestellt.
Wie man dieser Darstellung entnehmen kann, sind die Koeffizienten ak und bk für
k > 8 sehr klein. Wir erhalten als gute Näherung für unser Tonsignal
y ≈ ya = 3c + 18u1 − 12u2 − 12u3 + u4 + 2u5 − u6 − u8
+58v1 + 23v2 − 7v3 + 6v4 − 2v5 + v6
(42)
Dabei wurden die Koeffizienten auf ganze Zahlen gerundet. Die Näherung ya ist in Abb. 25
schwarz, die ursprünglichen Abtastwerte sind zum Vergleich grau dargestellt.
Beachten Sie, dass wir in der Näherung (42) für die neuen Basisvektoren nur 14 Koeffizienten benötigen. Mit den ursprünglichen Basisvektoren ek brauchen wir dagegen 152
Koeffizienten. Durch die Wahl einer neuen, geschickten Basis erreichen wir also eine erhebliche Datenkompression, wenn wir akzeptieren, dass sich die Werte gegenüber den
ursprünglichen ein wenig ändern.
Definition 4.4.2 Sei V ein Vektorraum. Die maximale Anzahl linear unabhängiger Vektoren in V heißt die Dimension von V , abgekürzt dim V . Wenn es Teilmengen beliebig
großer Anzahl von linear unabhängigen Vektoren ~u1 , ~u2 , ~u3 , . . . in V gibt, dann schreibt
man dim V = ∞ und nennt V unendlichdimensional.
59
Abbildung 24: Koeffizienten des Tonsignals in der Summe (41)
Abbildung 25: Näherung (schwarz) der Abtastwerte des Tonsignals durch (42), zum Vergleich die ursprünglichen Werte (grau)
Beispiele:
(a) V = Rn . Nach Satz 4.3.1 und dem Hinweis zu den Vektoren ~ek (siehe (40)) gilt
dim Rn = n.
(b) Sei V die Menge aller Polynome. Auch Sie ist ein Vektorraum (siehe Beispiel g)
nach Definition 4.1.1). Die Vektoren 1, x, x2 , x3 , . . . xn sind für alle n ∈ N linear unabhängig (aufgrund von Satz 2.3.5 des Analysis-Skripts), also gibt es keine
maximale Anzahl linear unabhängiger Vektoren.
Satz 4.4.1 Wenn dim V = n und die Vektoren ~u1 , ~u2 , ~u3 , . . . ~un in V linear unabhängig
sind, dann ist ~u1 , ~u2 , ~u3 , . . . ~un eine Basis.
Beweis: Sei ~x ∈ V beliebig. Wenn dim V = n, dann sind n + 1 Vektoren stets linear
abhängig, also sind die Vektoren ~u1 , ~u2 , ~u3 , . . . ~un , ~x linear abhängig. Also existiert eine
60
Linearkombination
t1~u1 + t2~u2 + t3~u3 + · · · tn~un + tn+1~x = ~0
bei der mindestens ein tk 6= 0. Nun ist tn+1 = 0 nicht möglich, denn wenn tn+1 = 0, dann
kann man den letzten Summanden weglassen und man hat
t1~u1 + t2~u2 + t3~u3 + · · · tn~un = ~0
woraus wegen der linearen Unabhängigkeit der Vektoren ~u1 , ~u2 , ~u3 , . . . ~un sofort folgt,
dass t1 = t2 = t3 = · · · tn = 0, und dann wären alle tk = 0. Also muß tn+1 6= 0 gelten, und
man hat
t2
t3
tn
t1
~u1 −
~u2 −
~u3 − · · · −
~un
~x = −
tn+1
tn+1
tn+1
tn+1
Also ist ~x als Linearkombination der Vektoren ~uk darstellbar, und damit ist ~u1 , ~u2 , . . . ~un
eine Basis.
Satz 4.4.2 Seien ~u1 , ~u2 , ~u3 , . . . ~un und ~v1 , ~v2 , ~v3 , . . . ~vm Basen (Mehrzahl von Basis) in
einem Vektorraum V . Dann stimmt die Zahl der Basisvektoren überein und diese stimmt
auch mit der Dimension von V überein, also
n = m = dim V
(ohne Beweis)
Definition 4.4.3 Sei V ein Vektorraum. Eine Teilmenge U ⊂ V heißt Unterraum von
V , wenn U ein Vektorraum bezüglich der Addition und Multiplikation mit Skalaren ist.
Hierzu ist nur nachzuprüfen, ob
~u, ~v ∈ U, t ∈ R
~u + ~v ∈ U
=⇒
und
t~u ∈ U
denn die Rechenregeln gelten für Vektoren in U , weil U ⊂ V und V ein Vektorraum ist.
Hinweis: Wenn U ein Unterraum ist, dann muß insbesondere auch ~0 ∈ U erfüllt sein.
Außerdem gilt dim U ≤ dim V .
Beispiele:
(a) V = R3 , U = {~u ∈ R3 | u3 = 0} (Übungsaufgabe!) Welche geometrische Interpretation hat U ?
(b) V = R3 , ~v ∈ R3 sei gegeben, ~v 6= 0.
U = {~u ∈ R3 | ~v · ~u = 0}
Prüfen Sie nach, dass U ein Unterraum von R3 ist! Welche geometrische Interpretation hat U ?
(c) V sei der Vektorraum aller Polynome, U der Vektorraum aller Polynome höchstens
17. Grades. Es wurde schon früher überprüft, dass U ein Vektorraum ist. Also ist
U als Teilmenge von V tatsächlich ein Unterraum.
(d) V sei der Vektorraum aller Funktionen f : R → R, x 7→ f (x). Nun sei U der Vektorraum aller Polynome. U ⊂ V und U ist ein Vektorraum, also ist U ein Unterraum
von V .
61
5
Matrizen
5.1
Matrix als Koeffizientenschema
Definition 5.1.1 Eine (m × n)-Matrix
komplexen) Zahlen nach dem Schema

a11 a12
 a21 a22

 a31 a32

A = a
 41 a42
 ..
..
 .
.
ist eine rechteckige Anordnung von reellen (oder
a13
a23
a33
a43
..
.
a14
a24
a34
a44
..
.
···
···
···
···
...
am1 am2 am3 am4 · · ·

a1n
a2n 

a3n 

a4n 

.. 
. 
amn
mit m Zeilen und n Spalten. Die einzelnen Zahlen aik heißen Matrixelemente. Dabei
bezeichnet der erste Index, also hier i, die Zeilennummer, der zweite Index, also hier k,
die Spaltennummer. Die Mehrzahl von Matrix“ ist Matrizen“. Der k. Spaltenvektor von
”
”
A (1 ≤ k ≤ n) ist der Vektor


a1k
 a2k 


 a3k 


 a4k 


 .. 
 . 
amk
Dies ist ein Vektor in Rm .
Wo kommen Matrizen vor, wo werden sie benötigt?
• Beschreibung linearer Gleichungssysteme
• lineare Abbildungen (z.B. Drehungen)
• Beschreibung von Systemen von Differentialgleichungen (beispielsweise bei Mehrfachregelungen)
• Beschreibung von Netzwerken
• Beschreibung digitaler Bilder
• Atomphysik
• numerische Näherungsverfahren (z.B. FEM)
Zahlenbeispiel: (eine (3 × 4)-Matrix)


3
1 −4 5
2
3 
A =  −1 0
5 −2 4 −1
Weiteres Beispiel: Das digitale Bild mit 16 × 16 Pixeln
62
wird durch die Matrix




























































160
130
117
108
114
104
104
133
177
197
204
197
190
198
213
205
167
118
110
114
114
104
112
163
190
217
243
246
230
223
242
234
194
138
118
112
110
104
112
134
160
177
217
251
255
238
238
247
177
142
114
114
117
117
100
91
104
104
142
201
238
255
246
251
137
121
110
122
118
102
98
110
140
140
126
134
177
231
254
255
142
122
112
106
110
110
117
137
177
208
198
126
122
181
239
255
142
125
112
102
110
102
106
118
148
189
204
187
133
133
204
255
133
112
106
110
96
98
100
91
92
142
179
198
167
118
171
234
133
117
106
106
94
98
91
88
88
94
151
181
181
117
147
231
133
117
106
102
96
102
98
88
88
88
140
190
173
125
160
246
126
108
106
102
102
96
137
140
98
117
167
185
160
129
187
255
112
112
102
102
100
100
147
197
167
209
217
156
133
159
250
255
98
110
104
96
94
112
134
151
167
201
185
125
125
215
255
255
102
110
125
104
147
137
173
156
110
129
117
126
209
255
255
255
118
114
108
112
138
164
242
223
118
114
148
231
255
255
255
255
142
110
114
121
177
254
255
255
255
255
255
255
255
255
255
255




























































beschrieben. Die Zahlenwerte entsprechen den Grautönen der einzelnen Pixel (0 schwarz,
255 weiß).
5.2
Lineare Gleichungssysteme und Matrizen
Bisher haben wir ein lineares Gleichungssystem mit m Gleichungen (Zeilen) und n Unbekannten umständlich geschrieben als
a11 x1
a21 x1
a31 x1
a41 x1
..
.
+a12 x2
+a22 x2
+a32 x2
+a42 x2
..
.
+a13 x3
+a23 x3
+a33 x3
+a43 x3
..
.
+a14 x4
+a24 x4
+a34 x4
+a44 x4
..
.
+···
+···
+···
+···
...
am1 x1 +am2 x2 +am3 x3 +am4 x4 + · · ·
+a1n xn
+a2n xn
+a3n xn
+a4n xn
..
.
=
=
=
=
b1
b2
b3
b4
..
.
+amn xn = bm
Wir wollen die auftretenden Koeffizienten aik zu einer Matrix A zusammenfasssen. Die
Unbekannten x1 , x2 , . . . xn schreiben wir als Vektor ~x und analog die Zahlen auf der
rechten Seite b1 , b2 , . . . bn als Vektor ~b. Das Produkt A~x wird nun gerade so definiert, dass
wir das Gleichungssystem in der Kurzschreibweise
A~x = ~b
schreiben können.
63
Definition 5.2.1 Für Vektoren ~x ∈ Rn (also mit n Komponenten) und (m×n)-Matrizen
A (also mit n Spalten) wird der Vektor A~x ∈ Rm definiert durch


  n
P
 a11 x1 + a12 x2 + a13 x3 + a14 x4 + · · · + a1n xn
  k=1 a1k xk 


  P


  n
 a21 x1 + a22 x2 + a23 x3 + a24 x4 + · · · + a2n xn
 
a x 

  k=1 2k k 


  P


  n
a3k xk 
 a31 x1 + a32 x2 + a33 x3 + a34 x4 + · · · + a3n xn
 

 =  k=1
A~x := 


  P
 a x + a x + a x + a x + ··· + a x
  n a x 

 
4k k 
41 1
42 2
43 3
44 4
4n n


  k=1


 
..
..




.


  n .


  P
amk xk
am1 x1 + am2 x2 + am3 x3 + am4 x4 + · · · + amn xn
k=1
Hinweis: Beachten Sie, dass das Schema zur Berechnung der k. Komponente von A~x
gedanklich dadurch zustande kommt, dass man den Spaltenvektor ~x um π2 gegen den
Uhrzeigersinn dreht und über die k. Zeile der Matrix A schiebt. Dies ist in Abb. 26
verdeutlicht.
Abbildung 26: Zur Berechnung der k. Komponente von A~x
Zahlenbeispiel:


 
 

2 3 −5
−2
2 · (−2) + 3 · 3 + (−5) · 1
0
 4 8 3   3  =  4 · (−2) + 8 · 3 + 3 · 1  =  19 
−6 1 4
1
−6 · (−2) + 1 · 3 + 4 · 1
19
Für dieses Produkt gelten folgende Rechenregeln:
Satz 5.2.1 Sei A eine (m × n)-Matrix. Dann gilt für alle Vektoren ~x, ~y ∈ Rn und alle
t∈R
A(~x + ~y ) = A~x + A~y
A(t~x) = t · (A~x)
(43)
(44)
Der Beweis kann durch Nachrechnen unter Benutzung der Definition 5.2.1 erfolgen.
Satz 5.2.2 Sei A eine (m × n)-Matrix. Dann ist die Lösungsmenge des homogenen linearen Gleichungssystems
A~x = ~0
ein Unterraum von Rn .
64
Beweis: Wir haben nur nachzuweisen, dass die Summe zweier Lösungsvektoren wieder
ein Lösungsvektor ist und das skalare Vielfache eines Lösungsvektors ebenfalls wieder ein
Lösungsvektor ist (siehe Def. 4.4.3). Aufgrund der Rechenregeln von Satz 5.2.1 haben wir
A~x = ~0 und A~y = ~0 =⇒ A(~x + ~y ) = A~x + A~y = ~0 + ~0 = ~0
sowie für beliebiges t ∈ R
A~x = ~0 =⇒ A(t~x) = t · (A~x) = t · ~0 = ~0
Satz 5.2.3 Sei A eine (m×n)-Matrix und ~b ∈ Rn und sei ~x eine Lösung des inhomogenen
linearen Gleichungssystems A~x = ~b und sei ~y eine Lösung des zugehörigen homogenen
~ y = ~0.
Systems A~
Dann ist auch ~x + ~y eine Lösung des inhomogenen linearen Gleichungssystems, d.h.
A(~x + ~y ) = ~b
Beweis: Nachrechnen mit Hilfe der Rechenregeln von Satz 5.2.1 ergibt
A(~x + ~y ) = A~x + A~y = ~b + ~0 = ~b
Spezielles Zahlenbeispiel:


 

1 0 0
x1
x1
 0 1 0   x2  =  x2 
0 0 1
x3
x3
für alle ~x ∈ R3 . Dies gibt Anlaß zur Definition
Definition 5.2.2 Die (n × n)-Matrix




E=


deren Matrixelemente
1
0
0
..
.
0
1
0
..
.
0
0
1
..
.
···
···
···
..
.
0 0 0 ···
0
0
0






0 
1
(
1 falls i = k
aik =
0 falls i 6= k
erfüllen, heißt (n × n)-Einheitsmatrix. Sie wird hier mit E bezeichnet.
Hinweise:
(a) Wenn E die (n × n)-Einheitsmatrix ist, dann gilt
E~x = ~x
für alle ~x ∈ Rn
Dies folgt durch Nachrechnen unmittelbar aus den Definitionen.
(b) Für k = 1, 2, 3 . . . n ist der k. Spaltenvektor von E der k. Basisvektor ~ek in Rn , der
in (40) definiert wurde
(c) In Scilab, MATLAB und Octave können Sie eine (n × n)-Einheitsmatrix durch
die Anweisung E=eye(n,n) erzeugen (der Variablen n muß vorher ein Zahlenwert
zugewiesen worden sein).
65
Wichtige allgemeine Eigenschaften des Produkts A~x:
A sei eine (m × n)-Matrix und ~x ∈ Rn
(a) Darstellung von A~x mit Hilfe der Spaltenvektoren von A:


a11 x1 + a12 x2 + a13 x3 + · · · + a1n xn
 a21 x1 + a22 x2 + a23 x3 + · · · + a2n xn 




A~x =  a31 x1 + a32 x2 + a33 x3 + · · · + a3n xn 


..


.
am1 x1 + am2 x2 + am3 x3 + · · · + amn xn








a11
a12
a13
a1n
 a21 
 a22 
 a23 
 a2n 








 a31 
 a32 
 a33 


= x1 
 +x2 
 +x3 
 + · · · + xn  a3n  (45)
 .. 
 .. 
 .. 
 .. 
 . 
 . 
 . 
 . 
am1
am2
am3
amn
| {z }
| {z }
| {z }
| {z }
1. Spalten2. Spalten3. Spaltenn. Spaltenvektor von A vektor von A vektor von A
vektor von A
(b) Mit den in (40) definierten Basisvektoren ~ek in Rn (k = 1, 2 . . . n) erhält man








a11
a12
a1k
a1n
 a21 
 a22 
 a2k 
 a2n 








 a31 
 a32 
 a3k 
 a3n 
A~e1 = 
 A~e2 = 
 A~ek = 
 A~en = 

 .. 
 .. 
 .. 
 .. 
 . 
 . 
 . 
 . 
am1
am2
amk
amn
| {z }
| {z }
| {z }
| {z }
1. Spalten2. Spaltenk. Spaltenn. Spaltenvektor von A
vektor von A
vektor von A
vektor von A
5.3
Lineare Abbildungen und Matrizen
Abbildungen und Funktionen liegt dieselbe mathematische Idee zugrunde. In der Analysis
ist es üblich, den Namen Funktion“ zu benutzen. In der linearen Algebra wird der Name
”
Abbildung“ bevorzugt.
”
Definition 5.3.1 Seien A und B Mengen. Unter einer Abbildung T mit der Definitionsmenge A und der Zielmenge B versteht man eine eindeutige Zuordnungsvorschrift,
die jedem Argument“ a ∈ A das Bild T (a) ∈ B zuordnet. Man schreibt hierfür symbo”
lisch:
T : A → B, a 7→ T (a)
(46)
Hinweis: Zu einer Abbildung gehört also dreierlei: eine Definitionsmenge, eine Zielmenge
und eine eindeutig bestimmte Zuordnungsvorschrift. Man sieht also Abbildungen, die
sich nur in der Definitionsmenge oder in der Zielmenge, aber nicht in der Zuordnungsvorschrift unterscheiden, als verschieden an. Dies mag übertrieben pingelig erscheinen,
und mancher Anfänger wird sich wundern, warum man so eine merkwürdige Sicht- oder
Sprechweise vereinbart. Es wird sich aber später zeigen, dass bestimmte Eigenschaften
einer Abbildung, z.B. injektiv“ oder surjektiv“ zu sein, entscheidend von Definitions”
”
oder Zielmenge abhängen.
66
Beispiele:
x1
cos(ϕ) · x1 − sin(ϕ) · x2
(a) T : R → R ,
7→
x2
sin(ϕ) · x1 + cos(ϕ) · x2
Diese Abbildung ordnet jedem Vektor der Ebene den um den Winkel ϕ um den Ursprung gedrehten Vektor zu (siehe das Ergebnis der entsprechenden Übungsaufgabe
der Analysis-Übungen; dieses Ergebnis war dort mit Hilfe der Additionstheoreme
sowie der geometrischen Eigenschaften von sin und cos gewonnen worden). Diese
Abbildung kann mit Hilfe einer Matrix beschrieben werden: T (~x) = D~x für alle
~x ∈ R2 mit
cos ϕ − sin ϕ
D=
sin ϕ cos ϕ
2
2
(b) T : R3 → R3 , ~x 7→ T (~x) = −~x. Dies ist geometrisch eine Spiegelung am Ursprung.
 
x1
x1
3
2  
(c) P : R → R , x2 7→
x2
x3
Dies ist geometrisch eine Projektion des dreidimensionalen Raumes auf die Ebene.
Sie kann mit einer Matrix beschrieben werden, P (~x) = A~x für alle ~x ∈ R3 mit
1 0 0
A=
0 1 0
In der Tat gilt
 
x1
1 0 0  
x1
x2 =
0 1 0
x2
x3
für alle ~x ∈ R3
 
x1
x1
2
3

(d) T : R → R ,
7→ x2 
x2
0
Eine derartige Abbildung wird in der Mathematik eine Einbettung“ genannt. Die
”
hier vorliegende Zuordnungsvorschrift kann durch eine Matrix beschrieben werden,
wir haben T (~x) = A~x für alle ~x ∈ R2 mit




 
1 0
1 0 x1
0 1 x1 = x2 
A = 0 1 ,
denn
x2
0 0
0 0
0
2
x1
x1
(e) T : R → R ,
7→
x2
x22
2
2
(f) Rn → Rn , ~x 7→ ~x. Diese Abbildung wird identische Abbildung genannt.
(g) Die Abbildung Rn → Rn , ~x 7→ ~0 wird als uninteressant oder trivial“ angesehen.
”
(h) Sei V der Vektorraum aller Polynome. Dann ist T : V → R, f 7→ f (1) eine Abbildung (jedem Polynom wird der Funktionswert an der Stelle 1 zugeordnet).
67
Wir werden uns hier fast ausschließlich mit Abbildungen beschäftigen, deren Definitionsmenge Rn und deren Zielmenge Rm ist (mit m, n ∈ N+ ). Die folgende Definition ist
grundlegend für die weiteren Abschnitte:
Definition 5.3.2 Seien V, W Vektorräume. Eine Abbildung T : V → W , ~x 7→ T (~x) heißt
linear, wenn
T (~u + ~v ) = T (~u) + T (~v )
für alle ~u, ~v ∈ V
(47)
und
T (s~u) = sT (~u)
für alle ~u ∈ V
und alle
s∈R
(48)
Beachten Sie die Ähnlichkeit der in dieser Definition geforderten Regeln mit denen in
Satz 5.2.1. Als unmittelbare Folge erhalten wir
Satz 5.3.1 Sei A eine (m × n)-Matrix. Die Abbildung T : Rn → Rm , ~x 7→ T (~x) sei durch
T (~x) := A~x
für alle ~x ∈ Rn
definiert. Dann ist T eine lineare Abbildung.
Eine Abbildung, deren Zuordnungsvorschrift aus der Multiplikation mit einer Matrix besteht, ist also stets linear. Alle vorangegangenen Beispiele bis auf Beispiel (e) sind linear.
Bei den meisten ist die zugehörige Matrix, die die Zuordnungsvorschrift erzeugt, angegeben, bei den übrigen sind die Rechenregeln aus Def. 5.3.2 unmittelbar klar. Um zu zeigen,
dass die Abbildung von Beispiel (e) nicht linear ist, genügt es beispielsweise einen Vektor
~x ∈ R2 und eine Zahl s ∈ R anzugeben, die die Regel T (s~x) = sT (~x) nicht erfüllen:
4
2
1
2
~x =
, s = 2, s~x =
, T (~x) = ~x, T (s~x) =
= 4~x 6= sT (~x) =
0
0
0
0
Weitere Eigenschaften linearer Abbildungen:
Wir setzen generell voraus, dass T : V → W , ~x 7→ T (~x) linear ist.
(a) Aus (47) mit ~v = −~u und (48) mit s = −1 erhalten wir
T (~u − ~u) = T (~0) = T (~u) + T (−1)~u = T (~u) − T (~u) = ~0
und damit T (~0) = ~0 für alle linearen Abbildungen.
(b) T (s1~a1 + s2~a2 + s3~a3 + · · · + sk~ak ) = s1 T (~a1 ) + s2 T (~a2 ) + s3 T (~a3 ) + · · · + sk T (~ak ) für
alle s1 , s2 , . . . sk ∈ R und alle ~a1 ~a2 . . . ~ak ∈ V und alle k ∈ N+ (durch vollständige
Induktion über k aus (47) und (48) zu beweisen).
(c) Betrachten wir den Spezialfall V = W = R2 oder V = W = R3 . Wir hatten Geraden
in der Ebene und im Raum durch
~x(t) = ~a + t · ~b,
t∈R
beschrieben (siehe (14)). Wir erhalten hier
T ~x(t) = T (~a) + t · T (~b)
68
Alle Bildpunkte T x(t) liegen wieder auf einer Geraden, das Bild einer Geraden
unter einer linearen Abbildung ist also wieder eine Gerade! Wenn die Gerade durch
−→
−→
zwei Punkte P und Q mit den Ortsvektoren OP und OQ gegeben ist (so wie das
beispielsweise in Abb. 11 rechts gezeigt ist) , dann erhalten wir die Geradengleichung
in der angegebenen Form, indem wir
−→
~a = OP
und
→
~b = −~a + −
OQ
setzen. Den Punkt P bekommen wir mit t = 0, den Punkt Q mit t = 1, und die
dazwischenliegenden Punkte, indem wir t auf den Bereich 0 < t < 1 einschränken.
Entsprechendes gilt für die Punkte, die auf der Geraden zwischen den Bildpunkten
−→
−→
mit den Ortsvektoren T (OP ) und T (OQ) liegen. Um das Bild von Geradenstücken
zu berechnen, genügt es also, das Bild der Anfangs- und Endpunkte zu berechnen
und diese wieder mit einer Geraden zu verbinden. Dies ermöglicht eine nette Veranschaulichung von linearen Abbildungen der Ebene in sich der Form T (~x) = A~x
mit verschiedenen Matrizen A, wie sie in Abb. 27 gezeigt ist.
1 0
0 1
cos(2)
− sin(2)
sin(2)
cos(2)
0, 7 0, 3
0, 3 0, 7
0 1
1 0
0, 6 0, 6
−0, 5 0, 9
0 1, 1
0, 3 0, 3
Abbildung 27: Veranschaulichung linearer Abbildungen der Form
T : R2 → R2 , ~x 7→ T (~x) = A~x mit verschiedenen Matrizen A.
69
(d) Die Frage stellt sich, welche Funktionen f : R → R, x 7→ f (x) lineare Abbildungen
sind. Wenn ein solches f linear ist, dann gilt
f (s) = f (s · 1) = s · f (1) = a · s
für alle s ∈ R mit a = f (1)
Die einzigen linearen Abbildungen von R in R sind also Polynome ersten Grades
der Form f (x) = ax, deren Graphen Geraden durch den Ursprung sind, sowie das
Nullpolynom!
Der Satz 5.3.1 legt die Frage nahe, ob alle linearen Abbildungen T : Rn → Rm , ~x 7→ T (~x)
durch eine Matrix mit
T (~x) = A~x
für alle ~x ∈ Rn
gegeben sind und wie man gegebenenfalls die zugehörige Matrix A aus der Zuordnungsvorschrift T (~x) erhält, wenn diese auf andere Weise gegeben ist. Wir schreiben zur Untersuchung dieser Frage ~x ∈ Rn mit Hilfe der Basisvektoren ~ek (die in (40) definiert sind):
~x = x1~e1 + x2~e2 + x3~e3 + · · · + xn~en
Aufgrund der Regeln für lineare Abbildungen haben wir
T (~x) = T (x1~e1 + x2~e2 + · · · + xn~en ) = x1 T (~e1 ) + x2 T (~e2 ) + · · · + xn T (~en )
Vergleich mit Gleichung (45) liefert
Satz 5.3.2 Seien n, m ∈ N+ . Zu jeder linearen Abbildung T : Rn → Rm , ~x 7→ T (~x)
existiert eine eindeutige (m × n)-Matrix A, die
T (~x) = A~x
für alle ~x ∈ Rn
erfüllt. Für k = 1, 2, . . . n ist T (~ek ) der k. Spaltenvektor von A, wobei die Vektoren ~ek
durch (40) gegeben sind.
Hinweis: Bei gegebener Zuordnungsvorschrift T (~x) können wir also die zugehörige Matrix
A dadurch berechnen, dass wir die Bilder der Einheitsvektoren T (~e1 ), T (~e2 ), . . . T (~en )
spaltenweise zu einer Matrix zusammenbauen“. Man kann dies knapp zu einer Merkregel
”
zusammenfassen:
Die Spalten der Matrix sind die Bilder der Einheitsvektoren ~ek .
Beispiele:
(a) Gegeben sei ein (zahlenmäßig bekannter) Vektor ~a ∈ R3 (beispielsweise a1 = 1,
a2 = 5, a3 = 2). Mit dem Vektorprodukt wird durch die Zuordnungsvorschrift
T (~x) = ~a × ~x
eine Abbildung T : R3 → R3 definiert, die aufgrund der Rechenregeln des Vektorprodukts linear ist. Überprüfen Sie dies bitte durch Nachrechnen! Die zugehörige
Matrix erhalten wir, indem wir






0
−a3
a2
T (~e1 ) = ~a ×~e1 =  a3  , T (~e2 ) = ~a ×~e2 =  0  , T (~e3 ) = ~a ×~e3 = −a1 
−a2
a1
0
70
spaltenweise zur Matrix


0 −a3 a2
0 −a1 
A =  a3
−a2 a1
0
(49)
zusammenbauen, die ~a × ~x = A~x für alle ~x ∈ R3 erfüllt.
(b) Gegeben seien zwei Vektoren ~a, ~b ∈ R3 (sie seien also zahlenmäßig bekannt, beispielsweise ~a wie im vorangehenden Beispiel und b1 = 3, b2 = −3, b3 = −1. Dann
kann man durch die Zuordnungsvorschrift
T (~x) = (~a · ~x) · ~b
eine Abbildung R3 → R3 definieren, die aufgrund der Rechenregeln des Skalarprodukts linear ist. Überprüfen Sie dies bitte ebenfalls durch Nachrechnen! Die
zugehörige Matrix erhalten wir, indem wir
T (~e1 ) = a1~b,
T (e2 ) = a2~b,
T (~e3 ) = a3~b
spaltenweise zur Matrix

a1 b 1 a2 b 1 a3 b 1
A =  a1 b 2 a2 b 2 a3 b 2 
a1 b 3 a2 b 3 a3 b 3

zusammensetzen. Diese erfüllt (~a · ~x) · ~b = A~x für alle ~x ∈ R3 .
5.4
Matrixmultiplikation und -addition
Im letzten Unterabschnitt war der enge Zusammenhang von Matrizen und linearen Abbildungen deutlich geworden. Die rechnerisch komplizierte Multiplikation von Matrizen
wird nur dann verständlich, wenn man sich anschaut, was mit den zugehörigen linearen
Abbildungen geschieht.
Definition 5.4.1 Seien
T : U → V,
u 7→ T (u)
und
S : V → W,
v 7→ S(v)
Abbildungen. Wir gehen also davon aus, dass die Zielmenge der Abbildung T die Definitionsmenge der Abbildung S ist. Dann wird die Hintereinanderausführung oder Komposition von S und T durch
S ◦ T : U → W, u 7→ S(T (u))
definiert.
Hinweis: Die Hintereinanderausführung von Funktionen ist in der Analysis in genau
derselben Weise definiert worden. Wir müssen also auch hier damit rechnen, dass die
Hintereinanderausführung in umgekehrter Reihenfolge, wenn sie möglich ist, eine andere
Abbildung liefern kann.
71
Beispiele:
(a) Sei ~a ∈ R3 ein vorgegebener Vektor, T : R3 → R3 , ~x 7→ ~a × ~x und
 
 
x1
x1
x1
3
2






x2 7→ S
x2
S:R →R ,
=
x2
x3
x3
Dann ist (siehe (49), rechnen Sie zur Übung nach!)
 
x1
−a3 x2 + a2 x3
3
2


x2 7→
S◦T :R →R ,
a3 x 1 − a1 x 3
x3
(b) Sei P die schon als Beispiel angegebene Projektion
 
x1
x1
3
2
P : R → R , x2  7→
x2
x3
und sei
T : R2 → R3 ,
 
x1
x1

7→ x2 
x2
0
die schon angegebene Einbettung“. Dann ist
”
 
 
x1
x1
T ◦ P : R3 → R3 , x2  7→ x2 
x3
0
und P ◦ T : R2 → R2 , ~x 7→ ~x, also P ◦ T = idR2 . Somit ist hier offensichtlich
P ◦ T 6= T ◦ P .
Eine wichtige Regel ist, dass die Hintereinanderausführung linearer Abbildungen wieder
zu einer linearen Abbildung führt, ausführlicher:
Satz 5.4.1 Seien
T : U → V,
~u 7→ T (~u)
und
S : V → W,
~v 7→ S(~v )
lineare Abbildungen. Wir setzen also voraus, dass die Zielmenge der Abbildung T die
Definitionsmenge der Abbildung S ist. Dann ist die Hintereinanderausführung von S und
T
S ◦ T : U → W, ~u 7→ S(T (~u))
eine lineare Abbildung.
Beweis: (~x + ~y ) 7→ S T (~x + ~y ) = S T (~x) + T (~y ) = S T (~x) + S T (~y ) für alle ~x, ~y ∈ U
S T (t~x) = S tT (~x) = tS T (~x) für alle ~x ∈ U und alle t ∈ R.
Wir definieren nun die Multiplikation von Matrizen durch die Hintereinanderausführung
der zugehörigen linearen Abbildungen:
72
Definition 5.4.2 Gegeben seien die (k × m)-Matrix A und die (m × n)-Matrix B (mit
k, m, n ∈ N+ ). Seien S und T die linearen Abbildungen
S : Rm → Rk , ~y 7→ S(~y ) = A~y ,
T : Rn → Rm , ~x 7→ T (~x) = B~x
Dann ist C := AB die (k × n)-Matrix, die
S T (~x) = A B~x = C~x
für alle ~x ∈ Rn
und damit
S ◦ T : Rn → Rk ,
~x 7→ C~x
erfüllt.
Hinweis: Zur Definition der Hintereinanderausführung von Abbildungen haben wir vorausgesetzt, dass die Zielmenge der zuerst auszuführenden Abbildung mit der Definitionsmenge der danach auszuführenden Abbildung übereinstimmt. Dem entspricht hier, dass
das Matrixprodukt AB nur definiert ist, wenn die Zahl der Spalten von A mit der Zahl
der Zeilen von B übereinstimmt.
Beispiel:
0 −1
1 1
A=
,
B=
1 0
1 2
S : R2 → R2 ,
T : R2 → R2 , ~x 7→ T (~x) = B~x
S ◦ T : R2 → R2 , ~x 7→ A B~x = C~x
1 1
x1
x1 + x2
B~x =
=
1 2
x2
x1 + 2x2
0 −1
x1 + x2
−x1 − 2x2
A B~x =
=
= C~x
1 0
x1 + 2x2
x1 + x2
~y 7→ S(~y ) = A~y ,
Nach Satz 5.3.2 erhalten wir mit ~x = ~e1 und ~x = ~e2
−1
−2
A B~e1 =
,
A B~e2 =
1
1
die beiden Spalten von C = AB und damit
−1 −2
C = AB =
1
1
Herleitung einer allgemeinen Formel zur Berechnung des Matrixprodukts:
Ausgangspunkt ist eine (k × m)-Matrix A und eine (m × n)-Matrix B, also




a11 a12 a13 · · · a1m
b11 b12 b13 · · · b1n
a21 a22 a23 · · · a2m 
 b21 b22 b23 · · · b2n 




a31 a32 a33 · · · a3m 


A=
B =  b31 b32 b33 · · · b3n 

 ..
 ..
..
.. . .
.. 
..
..
.. 
..
 .
 .
.
.
.
.
. 
.
.
. 
ak1 ak2 ak3 · · · akm
bm1 bm2 bm3 · · · bmn
Nach Satz 5.3.2 ist der Vektor A B~el die l-te Spalte der gesuchten Matrix C = AB, die
laut Definition eine (k ×n)-Matrix ist, also ist dieser Vektor für l = 1, 2 . . . n zu berechnen.
73
Nun ist B~el der l-te Spaltenvektor der Matrix B (siehe das Ende von Abschnitt 5.2), und
B hat insgesamt n Spalten, also
 
b1l
 b2l 
 
 
B~el =  b3l  ,
l = 1, 2, 3 . . . n
 .. 
 . 
bml
Nach Def. 5.2.1 ist

a11
a21


A B~el = a31
 ..
 .
ak1
P
m
a12 a13
a22 a23
a32 a33
..
..
.
.
ak2 ak3

a b
i=1 1i il 

P

m
 a2i bil 

= 

i=1 .


..


m

P
aki bil
  

· · · a1m
b1l
a11 b1l + a12 b2l + · · · + a1m bml
  

· · · a2m 
  b2l   a21 b1l + a22 b2l + · · · + a2m bml 




· · · a3m   b3l  =  a31 b1l + a32 b2l + · · · + a3m bml 


..   ..  
..
..

.
.  .  
.
· · · akm
bml
ak1 b1l + ak2 b2l + · · · + akm bml
i=1
Wir haben damit als Ergebnis gewonnen:
Satz 5.4.2 Seien A eine (k × m)-Matrix und B eine (m × n)-Matrix (mit k, m, n ∈ N+ )
und sei C = AB.
Dann ist das Matrixelement cij der i. Zeile und j. Spalte der Produktmatrix C
cij =
m
X
ail blj ,
i = 1, 2, . . . k,
j = 1, 2, . . . n
l=1
Hinweise:
(a) Man kann die in einer Zeile einer Matrix stehenden Zahlen zu einem Vektor zusammenfassen, so wie wir das mit einer Spalte bereits in Def. 5.1.1 getan haben.
Dann können wir nach dem obigen Satz das Matrixelement cij auffassen als das
Skalarprodukt des i. Zeilenvektors von A mit dem j. Spaltenvektor von B.
(b) Einen Vektor ~x ∈ Rm kann man als (m × 1)-Matrix auffassen, also als Matrix mit
m Zeilen und einer Spalte, indem man die Komponenten des Vektors spaltenweise untereinanderschreibt. Dann folgt aus dem Satz, dass das Matrixprodukt nach
Def. 5.4.2 und das Produkt Matrix mal Vektor“ nach Def. 5.2.1 übereinstimmen.
”
(c) Beachten Sie, dass in der zur Berechnung von cij auszurechnenden Summe die Summation über den innen stehenden Index l beim Produkt ail blj läuft und die innere“
”
Zahl bei der Größe übereinstimmen muß (nur das Produkt einer (k × m)-Matrix mit
einer (m × n)-Matrix ist definiert).
74
Falk-Schema:
Dieses Schema zur Matrixmultiplikation soll hier am Beispiel der beiden Matrizen


3 −2
2 −1 5
A=
und
B= 0 1 
−2 1 0
1 −1
erläutert werden. Zur Berechnung des Produkts AB schreibt man die Matrizen zunächst
in der folgenden Art auf
..
.
3 −2
B
..
.
0
1
..
.
A
1 −1
2 −1 5
−2
1 0
In jedes freie Feld trägt man nun das entsprechende Matrixelement der Produktmatrix ein,
indem man das Skalarprodukt des außen links in derselben Zeile stehenden Zeilenvektors
von A mit dem ganz oben darüber stehenden Spaltenvektor von B bildet:
...
B
...
A
2 −1
−2
1
3
−2
0
1
..
.
1 −1
5 11 −10
0 −6
5
Das Ergebnis lautet in der üblichen mathematischen Schreibweise
11 −10
AB =
−6 5
Für das Produkt in umgekehrter Reihenfolge BA erhalten wir das Falk-Schema
..
.
B
3
0
1
A
2 −1
..
. −2
1
−2 10 −5
1 −2
1
−1
4 −2
5
0
15
0
5
und damit das Ergebnis


10 −5 15
BA = −2 1 0 
4 −2 5
Ein Vorteil beim Falk-Schema ist, dass beim Produkt von mehr als zwei Faktoren das
Zwischenergebnis nicht nochmal neu aufgeschrieben werden muß, sondern der neue Faktor
einfach rechts oben angefügt werden kann.
75
Eigenschaften des Matrixprodukts:
(a) Wie das gerade behandelte Beispiel zeigt, ist das Produkt nicht kommutativ, im
allgemeinen haben wir
AB 6= BA
(b) Das Assoziativgesetz ist erfüllt, wir haben
(AB)C = A(BC)
für alle Matrizen A, B, C, für die das auftretende Produkt definiert ist. Es ist
etwas aufwändig, dies anhand der Berechnungsformel von Satz 5.4.2 zu beweisen.
Es ist dagegen unmittelbar plausibel, dass es beim Hintereinanderausführen von drei
Abbildungen
R : W → Z, w 7→ R(w),
S : V → W, v 7→ S(v),
T : U → V, u 7→ T (u)
nicht auf die Klammerung ankommt, dass also gilt
(R ◦ S) ◦ T = R ◦ (S ◦ T )
Das Assoziativgesetz für die Matrixmultiplikation folgt dann unmittelbar aus der
Definition 5.4.2.
(c) Wenn E die (n × n)-Einheitsmatrix ist, dann gilt (weil E zur identischen Abbildung
~x 7→ ~x gehört)
EA = A
AE = A
für alle (n × m)-Matrizen A
für alle (m × n)-Matrizen A
Analog zur Definition der Summe von reellwertigen Funktionen können wir die Summe
von linearen Abbildungen definieren:
Definition 5.4.3 Seien S : V → W , ~v 7→ S(~v ) und T : V → W , ~v 7→ T (~v ) lineare
Abbildungen und sei c ∈ R. Dann ist die Summe von S und T durch
S + T : V → W,
~v 7→ S(~v ) + T (~v )
und cT durch
cT : V → V,
~v 7→ cT (~v )
definiert. Wenn S und T lineare Abbildungen S, T : Rn → Rm mit den zugehörigen
(m × n)-Matrizen A und B sind mit S(~v ) = A~v und T (~v ) = B~v mit




a11 a12 a13 · · · a1n
b11 b12 b13 · · · b1n
 b21 b22 b23 · · · b2n 
 a21 a22 a23 · · · a2n 




 a31 a32 a33 · · · a3n 
 b31 b32 b33 · · · b3n 
A=
B=


 ..
 ..
..
..
.. 
..
..
.. 
..
...
 .


.
.
.
.
.
.
.
. 
am1 am2 am3 · · · amn
bm1 bm2 bm3 · · · bmn
76
dann entspricht der Summe der linearen Abbildungen die folgende Summe der Matrizen


a11 + b11 a12 + b12 a13 + b13 · · · a1n + b1n
 a21 + b21 a22 + b22 a23 + b23 · · · a2n + b2n 




A + B :=  a31 + b31 a32 + b32 a33 + b33 · · · a3n + b3n 


..
..
..
..
...


.
.
.
.
am1 + bm1 am2 + bm2 am3 + bm3 · · · amn + bmn
und analog für skalare Vielfache

cb11 cb12 cb13
 cb21 cb22 cb23


cB :=  cb31 cb32 cb33
 ..
..
..
 .
.
.
cbm1 cbm2 cbm3
···
···
···
..
.
···

cb1n
cb2n 

cb3n 

.. 
. 
cbmn
Hinweise:
(a) Es wurde schon erwähnt, dass man Vektoren aus Rn als (n × 1)-Matrizen auffassen
kann. Dann stimmt die bisher vereinbarte Addition und Multiplikation mit einem
Skalar mit der durch diese Definition definierten Addition und Multiplikation mit
einem Skalar überein.
(b) Beachten Sie, dass die Addition nur für Matrizen definiert ist, deren Zeilen- und
Spaltenzahl übereinstimmen.
Satz 5.4.3 Wenn A, B und C Matrizen sind, deren Größe so ist, dass die jeweiligen
Rechenoperationen definiert sind, dann gilt
A(B + C) = AB + AC
und
(A + B)C = AC + BC
Eine (n × n)-Matrix A kann mit sich selbst multipliziert werden, das Ergebnis AA ist
wieder eine (n × n)-Matrix und kann erneut mit A multipliziert werden. Wir können also
für (n × n)-Matrizen Potenzen definieren:
Definition 5.4.4 Sei A eine (n × n) mit n ∈ N+ und sei k ∈ N+ . Dann wird definiert
Ak := |A · A · A
{z · . . . · A}
k Faktoren
Anwendungsbeispiel:
Wie wir bereits im Abschnitt 4.4 besprochen haben, kann man die Abtastwerte eines Tonsignals als Vektor in Rn auffassen (siehe auch Abb. 23). In Abb. 28 ist eine verrauschte
Version dieses Tonsignals zusammen mit dem ursprünglichen Tonsignal gezeigt. Die beiden Tonsignale sind durch Vektoren aus Rn mit n = 152 gegeben. Das Rauschen kann
beispielsweise durch Übertragung über eine schlechte Telefonleitung entstehen, es wurde
hier allerdings rechnerisch erzeugt (mit Hilfe von Zufallszahlen).
Beim Vergleich der beiden Signale kann man auf die Idee kommen, den Einfluss des
Rauschens durch eine Mittelwertbildung zu vermindern. Bezeichnen wir das verrauschte
77
120
ursprünglich
verrauscht
100
80
60
40
20
0
- 20
0
20
40
60
80
100
120
140
160
- 40
- 60
- 80
Abbildung 28: Abtastwerte eines verrauschten Tonsignal, Vokal u“ (Ausschnitt) zusam”
men mit dem ursprünglichen Tonsignal
Tonsignal mit u ∈ Rn , so liegt es nahe, die Komponenten uk zu ersetzen durch vk =
1
(uk−1 + uk ). Wir müssen dann lediglich noch festlegen, was wir mit u1 machen, und
2
eine Möglichkeit besteht darin, diese Komponente unverändert zu lassen, also v1 = u1 zu
setzen. Wir definieren also eine Abbildung
(
uk
falls k = 1
T : Rn → Rn , u 7→ v = T (u) mit T (u) k = vk = 1
(uk−1 + uk ) falls k > 1
2
Dabei wurde die k. Komponente von T (u) mit T (u) k bezeichnet. Diese Abbildung ist
linear (zur Übung nachrechnen!) und man kann sich fragen, wie die (152 × 152)-Matrix A
aussieht, die T (u) = Au erfüllt. Nach der Regel Die Spalten der Matrix sind die Bilder
”
der Einheitsvektoren ek“ erhalten wir folgende Matrix


1 0 0 ··· ··· ··· ··· ···
 1 1 0 · · · · · · · · · · · · · · ·
2 2

 1 1 ..

. · · · · · · · · · · · ·
0 2 2

.
 .. 0 1 . . . . . . · · · · · · · · ·


2

.
.
A=
(50)
.
.
.
.
..
. . · · · · · ·
 .. .. . . . .


 .. .. .. . .

..
.
. 12
. . .
0
0
. . .

..
... 1
 .. .. ..

1
.
0


2
2
.. .. ..
..
..
1
1
. . .
.
.
0
2
2
In Abb. 29 ist das Ergebnis v = Au grafisch dargestellt, und tatsächlich unterscheidet
sich das durch Mittelwertbildung geglättete“ Signal weniger vom ursprünglichen Signal
”
als das verrauschte Signal, es ist also eine Verringerung des Rauschens erfolgt.
Es liegt nun nahe, die Glättung“ zu wiederholen, die Abbildung einfach nochmal
”
anzuwenden, also das Signal
w = T T (u) = A2 u
auszurechnen. Die Anwendung für unser verrauschtes Tonsignal ist in Abb.30 gezeigt.
78
120
ursprünglich
1 mal geglättet
100
80
60
40
20
0
- 20
0
20
40
60
80
100
120
140
160
- 40
- 60
- 80
Abbildung 29: durch Mittelwertbildung geglättete“ Abtastwerte des verrauschten Ton”
signal zusammen mit dem ursprünglichen Signal
120
ursprünglich
2 mal geglättet
100
80
60
40
20
0
- 20
0
20
40
60
80
100
120
140
160
- 40
- 60
Abbildung 30: Verminderung des Rauschens durch zweifache Anwendung der Glättungs”
abbildung“ (zusammen mit dem ursprünglichen Signal)
Rechnerisch erhalten für k > 2
1
1
wk = T T (u)
= T (u) k−1 + T (u) k
2 2
k
1
1 1
1
1 1
=
uk−2 + uk−1 +
uk−1 + uk
2 2
2
2 2
2
1
1
1
1
=
uk−2 + uk−1 + uk = (uk−2 + 2uk−1 + uk )
4
2
4
4
sowie für k = 2
1
1
1
1 1
1
3
1
w2 = T T (u)
= T (u) 1 + T (u) 2 = u1 +
u1 + u2 = u1 + u2
2
2
2
2 2
2
4
4
2
und für k = 1
w1 = T T (u)
= T (u) 1 = u1
1
79
Die zweifache Anwendung der Glättungsabbildung“ wird also beschrieben durch die Ma”
trix


4 0 ··· ··· ··· ··· ··· ··· ··· ···
3 1
0 · · · · · · · · · · · · · · · · · · · · ·


1 2
1
0 · · · · · · · · · · · · · · · · · ·


0 1

2
1
0
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·


.
. .. ..

..
..
..
.
.
.
.
. · · · · · · · · · · · ·
.


1 . . .
.. ..
. . . . . . . . . . . . . . · · · · · · · · ·
A2 = 

4
. .

..
 .. ..
.
0
1
2
1
0 · · · · · ·


 .. ..

..
..
. .
.
.
0
1
2
1
0 · · ·
. .

..
..
..
. .

.
.
.
0
1
2
1
0
. .
.. ..
..
..
..
..
. .
.
.
.
.
0
1
2
1
Beachten Sie, dass hier die Binomialkoeffizienten auftreten!
120
ursprünglich
3 mal geglättet
100
80
60
40
20
0
- 20
0
20
40
60
80
100
120
140
160
- 40
- 60
Abbildung 31: Verminderung des Rauschens durch dreifache Anwendung der Glättungs”
abbildung“ (zusammen mit dem ursprünglichen Signal)
120
120
ursprünglich
5 mal geglättet
100
80
80
60
60
40
40
20
20
0
- 20
- 40
- 60
verrauscht
5 m al geglättet
100
0
0
20
40
60
80
100
120
140
160
- 20
0
20
40
60
80
100
120
140
160
- 40
- 60
- 80
Abbildung 32: Verminderung des Rauschens durch fünffache Anwendung der Glättungs”
abbildung“ (links zusammen mit dem ursprünglichen Signal, rechts zusammen mit dem
verrauschten Signal)
Man kann das Spiel“ fortsetzen und prüfen, ob die mehrfache Anwendung der Glät”
”
tungsabbildung“ zu einer weiteren Verringerung der Rauschanteile führt. Wir schauen uns
hierzu die Signale
w = An u
80
an, für n = 3 und n = 5 sind diese in Abb. 31 sowie Abb. 32 dargestellt. Es ist tatsächlich
eine weitere Verringerung der Rauschanteile aufgetreten, allerdings wird das Signal selbst
etwas verfälscht und ein Stück nach rechts verschoben. Die Matrizen haben eine charakteristische Struktur, beispielsweise


32 0 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·
31 1
0 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · ·


26 5

1
0
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·


16 10 5
1
0 · · · · · · · · · · · · · · · · · · · · · · · ·


 6 10 10 5

1
0
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·


 1 5 10 10 5
1 · · · · · · · · · · · · · · · · · · · · ·


 0 1 5 10 10 5

1
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·

1 
5
 ..

A =
. 0 1
5 10 10 5
1
0 · · · · · · · · · · · ·
32 
.

..
 ..
.
0
1
5 10 10 5
1
0 · · · · · · · · ·


.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. · · · · · ·
.
.


 ..

..
..
..
.
.
.
.
0
1
5 10 10 5
1
0 · · ·
.

..
..
..
..
.

.
.
.
.
0
1
5 10 10 5
1
0
.
..
..
..
..
..
..
.
.
.
.
.
.
0
1
5 10 10 5
1
In einem Band entlang der Hauptdiagonale treten die Binomialkoeffizienten auf, außerhalb
dieses Bandes stehen nur Nullen, lediglich in der linken oberen Ecke treten Sonderfälle
auf. Die Beschreibung der zugehörigen linearen Abbildung durch eine derartige Matrix ist
umständlich. Eine einfachere Beschreibung von w = A5 u wäre für k > 5
wk =
1
(uk + 5uk−1 + 10uk−2 + 10uk−3 + 5uk−4 + uk−5 )
32
und entsprechende Sonderfälle für k = 1, 2, . . . 5. Derartige lineare Abbildungen spielen
in der Signalverarbeitung eine große Rolle, man spricht dort von Filtern“. Das Beispiel
”
macht vielleicht ein wenig klar, dass es nützlich ist, für solche einfach konstruierte lineare
Abbildungen weniger umständliche Beschreibungen zur Verfügung zu haben, die auch den
Zusammenhang zwischen A und A5 leicht erkennen lassen.
5.5
Die Umkehrabbildung und die inverse Matrix
Die inverse Matrix gehört zur inversen Abbildung oder Umkehrabbildung. Wir haben
zunächst einige vorbereitende Definitionen vorzunehmen.
Definition 5.5.1 Seien V, W Mengen und sei T : V → W , v 7→ T (v) eine Abbildung.
Dann ist die Bildmenge T (V ) die Menge aller Bilder T (v), also
T (V ) := {w ∈ W | Es existiert ein v ∈ V mit w = T (v)}
Es ist für die Bildmenge auch die Bezeichnungsweise Bild(T ) := T (V ) üblich.
T heißt surjektiv, wenn die Bildmenge T (V ) mit der Zielmenge W übereinstimmt, also
wenn T (V ) = W .
T heißt injektiv, wenn die Bilder zweier verschiedener Elemente aus V stets verschieden
sind, wenn also
v1 6= v2 , v1 , v2 ∈ V =⇒ T (v1 ) 6= T (v2 )
81
T heißt bijektiv, wenn T injektiv und surjektiv ist.
Wenn V und W Vektorräume sind und T eine lineare Abbildung ist, dann ist der Kern
von T definiert als die Menge der Vektoren, die auf den Nullvektor abgebildet werden:
Kern(T ) := {v ∈ V | T (v) = ~0}
Hinweise:
(a) In der Analysis nennen wir die Bildmenge einer Funktion Wertebereich und schreiben Wf statt f (Df ), der mathematische Begriff ist aber derselbe.
(b) Hier äquivalente Formulierungen der Bedingung dafür, dass T injektiv ist:
• T (v1 ) = T (v2 ) =⇒ v1 = v2
• Die Gleichung T (v) = w hat für jedes w ∈ W höchstens eine Lösung v ∈ V .
(c) Eine zur angegebenen Definition äquivalente Bedingung dafür, dass T surjektiv ist,
lautet:
Die Gleichung T (v) = w hat für jedes w ∈ W mindestens eine Lösung v ∈ V .
(d) In dem hier fast ausschließlich betrachteten Fall, dass V und W Vektorräume sind
und T eine lineare Abbildung ist, haben wir
• T (V ) ist ein Unterraum von W .
Beweis: Wenn w1 ∈ T (V ) und w2 ∈ T (V ), dann existieren v1 , v2 ∈ V mit
T (v1 ) = w1 und T (v2 ) = w2 und damit
T (v1 + v2 ) = T (v1 ) + T (v2 ) = w1 + w2
also w1 + w2 ∈ T (V ). Analog gilt T (sv1 ) = sT (v1 ) = sw1 für alle s ∈ R, also
folgt aus w1 ∈ T (V ), dass auch sw1 ∈ T (V ).
• Kern(T ) ist ein Unterraum von V (Beweis als Übungsaufgabe!)
• T ist injektiv ⇐⇒ Kern(T ) = {~0} (Beweis als Übungsaufgabe, {~0} ist der
triviale Unterraum, der als einzigen Vektor den Nullvektor enthält.)
Beispiele:
(a) Sei V die Menge der zu übermittelnden Zeichen (z.B. V = {a, b, c, . . . A, B, C, . . .}).
Wir setzen voraus, dass V mindestens zwei Elemente enthält. Zur Entdeckung von
Übertragungsfehlern ist folgende Abbildung vor der Übermittlung denkbar: Jedes
Zeichen wird verdoppelt. Man kann dies durch die Abbildung
T : V → V × V = W,
v 7→ (v, v)
beschreiben. Diese Abbildung ist injektiv. Dies ist wichtig dafür, dass das ursprüngliche Zeichen rekonstruierbar ist. Sie ist nicht surjektiv, denn die Zielmenge enthält
laut Voraussetzung mindestens ein Element der Form (v1 , v2 ) mit v1 6= v2 . Also ist
T (V ) eine echte Teilmenge von W :
T (V ) = {(v1 , v2 ) ∈ V × V | v1 = v2 }
82
Man kann nun einen erheblichen Teil der Übermittlungsfehler daran erkennen, dass
das übertragene Zeichen Element von W , aber nicht von T (V ) ist, denn die Wahrscheinlichkeit, dass bei zwei aufeinanderfolgenden Zeichen derselbe Übermittlungsfehler auftritt, ist gering. Mit etwas mehr mathematischem Aufwand kann man
Abbildungen konstruieren, die Ähnliches leisten, ohne die Anforderungen an die
Übertragungskapazität so stark zu erhöhen.
 
x1
x1
2
3

(b) T : R → R ,
7→ x2 
x2
0
ist injektiv, aber nicht surjektiv.
 
x1
x1
3
2  
(c) P : R → R , x2 7→
x2
x3
ist surjektiv, aber nicht injektiv. Geben Sie zur Begründung Vektoren ~v1 ∈ R3 und
~v2 ∈ R3 an, die P (~v1 ) = P (~v2 ) erfüllen.
(d) Die Drehung um den Winkel ϕ (die in Abschnitt 5.3 bereits besprochen wurde)
x1
cos(ϕ) · x1 − sin(ϕ) · x2
2
2
T :R →R ,
7→
x2
sin(ϕ) · x1 + cos(ϕ) · x2
ist bijektiv (Begründen Sie dies ausführlich!).
Definition 5.5.2 Sei T : V → W v 7→ T (v) bijektiv. Dann ist die Umkehrabbildung oder
inverse Abbildung T −1 : W → V , w 7→ T −1 (w) durch
v = T −1 (w) ⇐⇒ T (v) = w
definiert.
Hinweise:
(a) Die Umkehrfunktion ist derselbe mathematische Begriff und die Definition erfolgte
hier völlig analog zu der entsprechenden Definition in der Analysis.
(b) Man kann die Abbildungsvorschrift der Umkehrabbildung auch formulieren als
T −1 : W → V,
T (v) 7→ v
(c) Beachten Sie, dass die Gleichung T (v) = w für jedes w ∈ W mindestens eine Lösung
v ∈ V hat, weil wir T als surjektiv vorausgesetzt haben, und höchstens eine Lösung
hat, weil wir T als injektiv vorausgesetzt haben.
(d) Die Umkehrabbildung ist gerade so definiert, dass
T −1 ◦ T = idV
und
T ◦ T −1 = idW
oder ausführlich geschrieben
T −1 T (v) = v
T T −1 (w) = w
83
für alle v ∈ V
für alle w ∈ W
(e) Die unmittelbar vor der Definition als Beispiel angegebene Drehung in R2 um den
Winkel ϕ hat eine anschaulich leicht anzugebende Umkehrabbildung: Man dreht um
den Winkel −ϕ:
x1
cos(ϕ) · x1 + sin(ϕ) · x2
−1
2
2
T :R →R ,
7→
x2
− sin(ϕ) · x1 + cos(ϕ) · x2
Rechnen Sie nach, dass dies tatsächlich die Umkehrabbildung
ist, indem Sie bei
−1
spielsweise die Zuordnungsvorschrift T
T (~x) für beliebiges ~x ∈ R2 aufschreiben
und vereinfachen. Einfacher ist es, wenn Sie mit der in Abschnitt 5.3 für dieses
Beispiel angegebenen Matrix arbeiten.
(f) Die Verschlüsselung von Nachrichten erfolgt mit bijektiven Abbildungen und deren
Umkehrabbildungen. Wenn V die Menge der Nachrichten im Klartext ist, dann wird
eine Nachricht v ∈ V zunächst verschlüsselt, also in T (v) ∈ W umgewandelt. Dabei ist W die Menge der veschlüsselten Nachrichten. T (v) wird an den Empfänger
versandt. Dieser bildet dann T −1 T (v) = v. Die Abbildungssvorschrift für die Umkehrabbildung T −1 ist geheim zu halten! Bei modernen Verschlüsselungsmethoden
werden sehr anspruchsvolle mathematische Verfahren verwandt!
Im Rest dieses Unterabschnitts beschränken wir uns auf lineare Abbildungen T : Rn →
Rn . Nach Satz 5.3.2 werden diese durch (n × n)-Matrizen, also quadratische Matrizen
A beschrieben mit T (~x) = A~x für alle ~x ∈ Rn . Die Bedingung, dass T injektiv ist, also
T (~x1 ) = A~x1 = T (~x2 ) = A~x2 nur möglich ist, wenn ~x1 = ~x2 , führt hier auf die Bedingung,
dass A~x1 − A~x2 = A(~x1 − ~x2 ) = ~0 nur möglich ist, wenn ~x1 − ~x2 = ~0. Wir haben also
Satz 5.5.1 Sei T : Rn → Rn , ~x 7→ T (~x) = A~x eine lineare Abbildung mit der dazugehörigen (n × n)-Matrix A. Dann ist T injektiv genau dann, wenn die Matrix A nicht
singulär ist, das homogene lineare Gleichungssystem A~x also nur die triviale Lösung ~x = ~0
hat.
Zu Beginn dieses Unterabschnitts wurde angekündigt, dass die inverse Matrix zur Umkehrabbildung gehört. Es liegt also nahe, zu definieren
Definition 5.5.3 Eine (n × n)-Matrix A heißt invertierbar, wenn eine (n × n)-Matrix B
existiert mit
BA = AB = E
wobei E die (n × n)-Einheitsmatrix ist. Man schreibt dann B = A−1 und nennt A−1 die
inverse Matrix zu A. Wir haben also mit dieser Schreibweise, wenn A invertierbar ist
A−1 A = AA−1 = E
Die Matrixmultiplikation ist so definiert, dass sie der Hintereinanderausführung der entsprechenden linearen Abbildungen entspricht. Wir haben insgesamt das Ergebnis:
Satz 5.5.2 Sei A eine (n × n)-Matrix und T die lineare Abbildung
T : Rn → Rn
~x 7→ T (~x) = A~x
Dann sind die folgenden Bedingungen äquivalent:
84
(a) A ist invertierbar.
(b) Das homogene lineare Gleichungssystem A~x = ~0 hat nur die triviale Lösung ~x = ~0.
(c) Für jedes ~b ∈ Rn ist das lineare Gleichungssystem A~x = ~b nicht singulär.
(d) Die lineare Abbildung T ist bijektiv.
(e) Alle Spaltenvektoren von A sind linear unabhängig.
Wenn A invertierbar ist, dann gehört die inverse Matrix A−1 zur Umkehrabbildung T −1 ,
d.h.
T −1 (~x) = A−1~x
für alle ~x ∈ Rn
Beispiel: Mehrfach war als Beispiel für eine Abbildung die Drehung der Ebene um den
Winkel ϕ angegegeben worden. Die Umkehrabbildung ist die Drehung der Ebene um den
Winkel −ϕ. Die zugehörigen Matrizen sind
cos ϕ − sin ϕ
cos ϕ sin ϕ
−1
D=
und
D =
sin ϕ cos ϕ
− sin ϕ cos ϕ
Rechnen Sie als Übungsaufgabe nach, dass tatsächlich DD−1 = D−1 D = E erfüllt ist.
Wie am Ende von Abschnitt 5.3 erläutert wurde, liefert B~ek den k. Spaltenvektor
einer (m × n)-Matrix B, wenn ~ek der durch (40) definierte Einheitsvektor ist. Wir gehen
davon aus, dass die (n × n)-Matrix A invertierbar ist und bezeichnen den unbekannten
k. Spaltenvektor von A−1 mit ~xk . Dann gilt
~xk = A−1~ek
Multiplikation beider Seiten (von links) mit A liefert
A~xk = AA−1~ek = E~ek = ~ek
Dabei haben wir die (n × n)-Einheitsmatrix mit E bezeichnet. Wir haben damit eine
Berechnungsmöglichkeit für die inverse Matrix:
Satz 5.5.3 Sei A eine invertierbare (n × n)-Matrix und sei ~xk der k. Spaltenvektor von
A−1 , k = 1, 2, . . . n und sei ~ek durch (40) definiert. Dann kann man die Spaltenvektoren
von A−1 durch Lösung der linearen Gleichungssysteme
A~xk = ~ek
für k = 1, 2, . . . n
berechnen.
Hinweis: Wenn man A−1 kennt, dann erhält man die Lösung eines linearen Gleichungssystems A~x = ~b durch Multiplikation beider Seiten mit A−1 (von links):
A−1 A~x = E~x = ~x = A−1~b
Wenn es aber nur um die Lösung eines linearen Gleichungssystems A~x = ~b geht, dann
ist in der Praxis stets dringend zu empfehlen, es direkt — beispielsweise mit dem GaußVerfahren — zu lösen und nicht den Umweg über die erheblich aufwändigere Berechnung
der inversen Matrix zu gehen. Wie aus dem Satz ersichtlich ist, müßte man eigentlich
n lineare Gleichungssysteme lösen, um alle n Spalten der inversen Matrix zu erhalten.
Diese Gleichungssysteme unterscheiden sich nur auf der rechten Seite, so dass man sie
gleichzeitig für verschiedene rechte Seiten lösen kann:
85
Berechnung der inversen Matrix A−1 nach dem Verfahren von Gauß-Jordan:
Beim Gauß-Verfahren für lineare Gleichungssysteme der Form A~x = ~b werden die Koeffizienten zu einer erweiterten Matrix (A|~b) zusammengestellt. Auf diese erweiterte Koeffizientenmatrix werden dann die einzelnen Operationen des Gauß-Verfahrens (Addition
des Vielfachen einer Zeile zu einer anderen, eventuell Zeilentausch) angewandt. Da wir
hier gleichzeitig n verschiedene rechte Seiten (~ek für k = 1, 2, . . . n) behandeln wollen,
stellen wir alle rechten Seiten ~ek zur Einheitsmatrix zusammen. Wir gehen also von der
erweiterten Matrix (A|E) aus und wenden auf diese das Gauß-Verfahren an. Ziel ist es,
zunächst die linke Hälfte dieser Matrix in Dreiecksform zu bringen. Ausgangspunkt ist
also die Matrix


a11 a12 a13 · · · a1n 1 0 0 · · · 0
 a21 a22 a23 · · · a2n 0 1 0 · · · 0 


 a31 a32 a33 · · · a3n 0 0 1 · · · 0 


 ..
.. .. .. . . .. 
..
..
..
.
.
 .
. . 
.
. . .
.
.
.
an1 an2 an3 · · · ann 0 0 0 · · · 1
Hierauf wird nun das Gauß-Verfahren angewandt, so wie es in Abschnitt 3.1.4 beschrieben
ist. Durch einen eventuellen Zeilentausch stellt man also sicher, dass a11 6= 0 und addiert
-fache der ersten Zeile zur zweiten usw. Der einzige Unterschied zum Abdann das − aa21
11
schnitt 3.1.4 ist, dass wir hier gleichzeitig n rechte Seiten bearbeiten. Als Ergebnis erhalten
wir eine Matrix, deren linke Hälfte in Dreiecksform vorliegt, also die folgende Gestalt hat
(die Koeffizienten haben sich geändert, sie sind hier zur besseren Übersichtlichkeit auf der
linken Hälfte erneut mit aik bezeichnet):


a11 a12 a13 · · · a1n c11 c12 c13 · · · c1n
 0 a22 a23 · · · a2n c21 c22 c23 · · · c2n 


 0
0 a33 · · · a3n c31 c32 c33 · · · c3n 


 ..
..
.. . .
..
..
..
.. . .
.. 
 .
.
.
.
.
.
.
.
.
. 
0
0
0 · · · ann cn1 cn2 cn3 · · · cnn
Hier ist zu prüfen, ob ann 6= 0, denn nur dann ist die Matrix A invertierbar. Beim Lösen
eines linearen Gleichungssystems mit nur einem Vektor auf der rechten Seite erhielten wir
nun die Lösung durch Rückwärtsauflösen.
Hier setzen wir zur Berechnung von A−1 das Gauß-Verfahren rechts unten beginnend
nach oben und dann von rechts nach links fort. In einem ersten Schritt werden in der
letzten Spalte der rechten Hälfte oberhalb von ann Nullen erzeugt: Das − an−1,n
-fache der
ann
an−2,n
n. Zeile wird zur n − 1. Zeile addiert, das − ann -fache der n. Zeile wird zur n − 2. Zeile
2n
1n
addiert, . . . , das − aann
-fache der n. Zeile wird zur 2. Zeile addiert, das − aann
-fache der
n. Zeile wird zur 1. Zeile addiert. Schließlich wird die n. Zeile durch ann dividiert. Als
Ergebnis dieses Schritts erhält man eine Matrix der Form (zur besseren Übersichtlichkeit
sind die Koeffizienten wieder mit aik und cik bezeichnet, obwohl sie sich geändert haben):


a11 a12 a13 · · · 0 c11 c12 c13 · · · c1n
 0 a22 a23 · · · 0 c21 c22 c23 · · · c2n 


 0

c
c
c
·
·
·
c
0
a
·
·
·
0
33
31
32
33
3n


 ..
..
.. . . .. ..
..
.. . .
.. 
 .
.
.
.
.
. .
.
.
. 
0
0
0 · · · 1 cn1 cn2 cn3 · · · cnn
86
Dies wird dann von an−1,n−1 ausgehend in der (n − 1). Spalte fortgesetzt, so dass als Ergebnis des zweiten Schritts an der Stelle von an−1,n−1 eine 1 steht und darüber nur noch
Nullen. In einem letzten Schritt dividiert man dann die erste Zeile durch (das geänderte)
a11 . Als Ergebnis erhält man ein Koeffizientenschema der Form (zur Verdeutlichung, dass
sich die Koeffizienten geändert haben, sind sie jetzt auf der rechten Hälfte mit bik bezeichnet):


1 0 0 · · · 0 b11 b12 b13 · · · b1n
 0 1 0 · · · 0 b21 b22 b23 · · · b2n 


 0 0 1 · · · 0 b31 b32 b33 · · · b3n 


 .. .. .. . . .. ..
..
.. . .
.. 
 . . .
. . .
.
.
.
. 
0 0 0 · · · 1 bn1 bn2 bn3 · · · bnn
Das ursprüngliche Koeffizientenschema (A|E) ist also in die Form (E|B) gebracht worden.
Die Lösungsmenge hat sich dabei nicht geändert. Wir haben also die Gleichungssysteme
A~xk = ~ek für k = 1, 2, . . . n umgewandelt in die Gleichungssysteme E~xk = ~xk = ~bk umgewandelt, wenn wir den k. Spaltenvektor der in der rechten Hälfte entstandenen Matrix B
mit ~bk bezeichnen. Das heißt, wir können die Lösungen unserer Gleichungssysteme spaltenweise in der rechten Hälfte des entstandenen Koeffizientenschemas ablesen. Da wir mit
~xk den unbekannten k. Spaltenbektor von A−1 bezeichnet haben, steht im Koeffizientenschema rechts das gesuchte Ergebnis A−1 = B.
Zahlenbeispiel: (Zum Nachrechnen und Vergleichen, bitte beachten Sie, dass das bloße
Lesen keinen Sinn macht!)


2
1 1
A =  4 −6 0
−2 7 2
Ausgangspunkt:
2
1 1 1 0 0
4 −6 0 0 1 0
−2
7 2 0 0 1
1. Schritt:
2
1
1
1 0 0
0 −8 −2 −2 1 0
1 0 1
0
8
3
3. Schritt:
2
1 0
2 −1 −1
0 −8 0 −4
3
2
0
0 1 −1
1
1
4. Schritt:
3
2 0 0
− 58 − 43
2
1
0 1 0
− 38 − 41
2
0 0 1 −1
1
1
2. Schritt:
2
1
1
1 0 0
0 −8 −2 −2 1 0
0
0
1 −1 1 1
5. Schritt:
3
5
1 0 0
− 16
− 38
4
1
3
0 1 0
− 8 − 14
2
0 0 1 −1
1
1
Als Ergebnis haben wir erhalten:

5
− 16
− 38
− 38 − 41 
=
−1 1
1

A−1
3
4
1
2
Allgemeine Eigenschaften der inversen Matrizen:
Satz 5.5.4 Seien A und B invertierbare (n×n)-Matrizen. Dann ist auch AB invertierbar
und es gilt
−1
AB
Beweis:
AB
= B−1 A−1
B−1 A−1 = A BB−1 A−1 = AEA−1 = AA−1 = E
87
−1
B A
−1
−1
AB = B
A A B = B−1 EB = B−1 B = E
−1
Hinweise:
(a) Beachten Sie die Änderung der Reihenfolge bei der Berechnung von AB
−1
= A für alle invertierbaren (n × n)-Matrizen.
(b) A−1
−1
(c) Wenn A, B und C invertierbare (n × n)-Matrizen sind, dann gilt
−1
−1
−1
ABC
= (AB)C
= C−1 AB
= C−1 B−1 A−1
5.6
.
(51)
Die transponierte Matrix
Definition 5.6.1 Sei A eine (m × n)-Matrix. Die an der Hauptdiagonale gespiegelte
Matrix (also eine (n × m)-Matrix) heißt die zu A transponierte Matrix und wird mit
AT bezeichnet, also
AT = B ⇐⇒ aik = bki
Eine (n × n)-Matrix A heißt symmetrisch, wenn AT = A, also aik = aki für alle
Matrixelemente gilt.
Beispiel:
A=
2 1 4
0 −2 5


2 0
AT =  1 −2 
4 5
,
Satz 5.6.1 Seien A eine (k × m)-Matrix und B eine (m × n)-Matrix. Dann gilt
T
AB = BT AT
Beweis: Für die Matrixelemente gilt
AB
ik
=
m
X
m
T X
AB ik =
akl bli
ail blk ,
l=1
BT AT
ik
=
m
X
BT
l=1
il
AT
l=1
lk
=
m
X
l=1
bli akl =
m
X
akl bli
l=1
Hinweise:
(a) Beachten Sie die Änderung der Reihenfolge bei der Berechnung von AB
T
(b) AT = A für alle Matrizen A.
T
.
(c) Durch eine zu (51) analoge Rechnung erhalten wir als Folgerung aus dem Satz
T
ABC = CT BT AT
(52)
für alle Matrizen A, B, C, für die das Produkt ABC definiert ist.
88
(d) Faßt man Vektoren ~x, ~y ∈ Rn als (n × 1)-Matrizen auf und schreibt sie dann
zweckmäßigerweise auch in der Form ~x = x, ~y = y, dann kann das Skalarprodukt
auch als Matrixprodukt aufgefaßt und geschrieben werden in der Form
~x · ~y = xT y
(machen Sie sich dies anhand des Falk-Schemas klar!)
(e) Als Folgerung aus dem Satz erhalten wir für alle Vektoren ~x, ~y ∈ Rn und alle
(n × n)-Matrizen A mit dieser Schreibweise
(AT~x) · ~y = (AT x)T y = xT (AT )T y = xT Ay = ~x · (A~y )
(53)
Dies bedeutet, dass in Skalarprodukten der Form ~x ·(A~y ) die Matrix durch Übergang
zur transponierten Matrix dem anderen Faktor zugeschlagen“ werden kann.
”
T
(f) Für alle (m × n)-Matrizen A ist A eine (n × m)-Matrix, also kann das Produkt
AT A gebildet werden. AT A ist dann eine symmetrische (n × n)-Matrix, denn es
gilt (AT A)T = AT (AT )T = AT A.
(g) Die (n × n)-Einheitsmatrix E erfüllt ET = E für alle n ∈ N+ .
(h) Wenn A eine invertierbare (n × n)-Matrix ist, dann kann man auf beiden Seiten der
Gleichung AA−1 = E die transponierte Matrix bilden und erhält
T
T
AA−1 = A−1 AT = E
und analog für die Gleichung A−1 A = E
T
T
A−1 A = AT A−1 = E
Damit haben wir für alle invertierbare (n × n)-Matrizen A
A−1
T
= AT
−1
(i) Als Folgerung von (b) und (h) erhalten wir folgende Aussage, die Satz 5.5.2 um
weitere Bedingungen ergänzt:
Die folgenden Bedingungen sind für alle (n × n)-Matrizen A äquivalent:
• A ist invertierbar.
• AT ist invertierbar.
• Alle Spaltenvektoren von A sind linear unabhängig.
• Alle Zeilenvektoren von A sind linear unabhängig.
Definition 5.6.2 Eine invertierbare (n × n)-Matrix A heißt orthogonal, wenn
AT = A−1
erfüllt ist.
89
Hinweise:
(a) A ist also orthogonal, wenn AT A = AAT = E.
(b) Das Matrixelement cij der Produktmatrix C = AB entsteht als Skalarprodukt des
i. Zeilenvektors von A mit dem j. Zeilenvektor von B (siehe Satz 5.4.2 und den
ersten Hinweis danach). Der i. Zeilenvektor von A ist der i. Spaltenvektor von
AT und umgekehrt. Also ist A genau dann orthogonal, wenn alle verschiedenen
Spaltenvektoren zueinander orthogonal sind und alle Spaltenvektoren die Länge
eins haben. Analog ist auch A genau dann orthogonal, wenn alle verschiedenen
Zeilenvektoren zueinander orthogonal sind und alle Zeilenvektoren die Länge eins
haben. Dies erklärt den Namen orthogonal“ für eine Matrix.
”
(c) Matrizen, die Drehungen (in der Ebene oder im Raum) beschreiben, sind orthogonal.
So beschreibt die Matrix


cos ϕ − sin ϕ 0
D =  sin ϕ cos ϕ 0
0
0
1
eine Drehung um die z-Achse im dreidimensionalen Raum. Überzeugen Sie sich,
dass D tatsächlich eine orthogonale Matrix ist.
(d) Orthogonale Matrizen lassen das Skalarprodukt unverändert, d.h. wenn die (n × n)Matrix A orthogonal ist, dann gilt aufgrund von (53) für alle Vektoren x, y ∈ Rn :
(A~x) · (A~y ) = (AT A~x) · ~y = (E~x) · ~y = ~x · ~y
und damit bleiben alle Längen und Winkel unter der Abbildung ~x 7→ A~x unverändert.
5.7
Der Rang einer Matrix
Definition 5.7.1 Sei A eine (m × n)-Matrix. Dann ist der Zeilenrang von A die maximale Anzahl linear unabhängiger Zeilenvektoren und der Spaltenrang von A die maximale Anzahl linear unabhängiger Spaltenvektoren. Der Rang der linearen Abbildung
T : Rn → Rm , ~x 7→ T (~x) = A~x ist die Dimension des Vektorraums T (Rn ), d.h. die
maximale Anzahl linear unabhängiger Vektoren in der Bildmenge T (Rn ).
Satz 5.7.1 Der Zeilenrang und der Spaltenrang einer (m × n)-Matrix A bleiben bei den
(in Satz 3.1.1 beschriebenen) Operationen des Gauß-Verfahrens unverändert.
Satz 5.7.2 Sei A eine (m × n)-Matrix, T : Rn → Rm , ~x 7→ T (~x) = A~x die zugehörige
lineare Abbildung.
Dann gilt: Der Zeilenrang und der Spaltenrang von A sowie der Rang von T stimmen
überein
Hinweis: (kein Beweis!) Man kann zunächst das Gauß-Verfahren anwenden und die Matrix damit beispielsweise in die Form




∗ ∗ ∗ ∗ ∗ ∗
∗ ∗ ∗
 0 ∗ ∗
 0 0 ∗ ∗ ∗ ∗ 




oder
 0 0 ∗
 0 0 0 0 ∗ ∗ 
0 0 0 0 0 0
0 0 0
90
bringen. Dabei steht ∗ symbolisch für Matrixelemente, die von Null verschieden sind. Alle Zeilen, die vom Nullvektor verschieden sind, sind linear unabhängig. Zu jedem vom
Nullvektor verschiedenen Zeilenvektor kann ein Spaltenvektor so ausgewählt werden, dass
die ausgewählten Spaltenvektoren linear unabhängig sind. Bei der links gezeigten Matrix kann man beispielsweise den 1., den 3. und den 5. Spaltenvektor auswählen, diese
drei Spaltenvektoren sind dann linear unabhängig. Die Linearkombinationen der linear
unabhängigen Spaltenvektoren von A ergeben den Vektorraum T (Rn ) (siehe (45)).
Definition 5.7.2 Sei A eine (m × n)-Matrix. Der Zeilenrang oder der Spaltenrang (die
übereinstimmen!) wird kurz Rang der Matrix genannt, abgekürzt Rang(A).
Praktische Berechnung des Rangs einer Matrix:
Man führt die Matrix mit dem Gauß-Verfahren in Dreiecks- oder Trapezform über. Die
Zahl der vom Nullvektor verschiedenen Zeilenvektoren ergibt dann den Rang der Matrix.
Beispiele: (nach Umwandlung in Dreiecksform)




1 3 2
1
3
5
7
9
 0 2 1 

A=
B =  0 0 3 2 1  Rang(B) = 2
 0 0 −5  , Rang(A) = 3,
0 0 0 0 0
0 0 0
6
6.1
Endliche Körper und ihre Anwendungen bei der
Kodierung
Restklassen
Beobachtung: Das folgende C-Programm
#include<stdio.h>
main()
{unsigned char a,b,s,p;
a=2; b=255;
s=a+b;
p=a*b;
printf("a= %hd, b=%hd, a+b= %hd, a*b= %hd \n",a,b,s,p);}
liefert die Ausgabe
a= 2, b=255, a+b= 1, a*b= 254
und eine entsprechende Abänderung liefert
a= 128, b=128, a+b= 0, a*b= 0
Erklärung: Variablen vom Typ unsigned char“ erhalten auf den meisten Rechnern einen
”
Speicherplatz mit 8 Bits, also sind nur die Zahlen 0, 1, 2, 3, . . . 255 darstellbar. Von den
Rechenergebnissen werden daher nur die letzten 8 Bits abgespeichert, weitere Bits gehen
verloren. So hat beispielsweise 257 die Binärdarstellung 1 0000 00012 , und wenn man die
letzten 8 Bits 0000 00012 übrigbehält, so entspricht das einer dezimalen 1.
91
Man könnte beim Dezimalsystem denselben Effekt erzielen, wenn man vereinbart, nur
die letzte Ziffer aufzuschreiben. Man würde dann für die Menge der Zahlen {0, 1, 2, 3, . . . 9}
merkwürdige Rechenergebnisse, beispielsweise 4 + 7 = 1, 2 · 5 = 0, 9 · 9 = 1 erhalten. Es ist
nun sinnvoll, den beobachteten Effekt mathematisch zu beschreiben, und zwar unabhängig
von den hier gewählten Zahlen wie 256 und 10. Grundlegend ist der folgende
Satz 6.1.1 Seien m, n ∈ Z und sei n > 0. Dann existieren eindeutige Zahlen q, r ∈ Z
mit 0 ≤ r < n und
m=n·q+r
(54)
Hinweise:
(a) Mit Brüchen kann man die (54) auch intuitiver schreiben
r
m
=q+
n
n
mit 0 ≤
r
<1
n
und wir haben die Zerlegung eines Bruch als Summe aus einer ganzen Zahl und
einem echten Bruch.
(b) r ist der ganzzahlige Rest bei Division von m durch n
(c) Für den nicht negativen Rest in (54) ist die Schreibabkürzung
r = m mod n
(55)
üblich; sie ist zu lesen m modulo n“. Für m < 0 wird sie allerdings auch oft anders
”
definiert (siehe Hinweis (e)).
(d) Für m ≥ 0 kann m mod n mit C durch r=m%n; berechnet werden, mit Scilab durch
r=modulo(m,n).
(e) Für m < 0 führt die Festlegung im Satz n > 0 und 0 ≤ r < n (positiver Rest) zum
Beispiel auf die Zerlegung
−7 = 3 · (−3) + 2
dagegen führt die Zerlegung
−7 = 2 · (−3) − 1
auf einen negativen Rest. Manchen erscheint die Zerlegung mit dem negativen Rest
natürlicher, daher sind für m < 0 sind unterschiedliche Konventionen für die Schreibweise (55) üblich (hier ist die Übereinkunft so, dass stets m mod n ≥ 0). Beachten
Sie, dass in C für m < 0 der Wert von m%n möglicherweise ist. Bei Scilab sind
unterschiedliche Funktionen vorhanden (modulo und pmodulo), deren Werte sich
unterscheiden, wenn das erste Argument negativ ist.
Beispiele:
257 mod 256 = 1,
7 mod 3 = 1, 4711 mod 100 = 11,
(2 · 255) mod 256 = 2 · (256 − 1) mod 256 = (256 + 254) mod 256 = 254
92
Definition 6.1.1 Seien p, q ∈ Z und n ∈ N+ .
Wir sagen, p ist kongruent zu q modulo n, geschrieben
p≡q
(mod n)
wenn p−q ein ganzzahliges Vielfaches von n ist, also ein m ∈ Z existiert mit p−q = m·n,
d.h. wenn p und q bei Division durch n denselben Rest r mit 0 ≤ r < n haben.
Für p ∈ Z heißt die Menge
p̄ := {q ∈ Z | p ≡ q
(mod n)}
Restklasse von p modulo n.
Hinweise zur Schreibweise:
(a) Wir haben hier
p≡q
(mod n)
⇐⇒
p mod n = q mod n
Beachten Sie, dass p ≡ q (mod n) eine Aussage ist und p mod n eine Zahl.
(b) Zur Bezeichnung der Restklasse von p modulo n wird statt p̄ auch gelegentlich [p]
oder p̂ verwendet. Wenn kein Missverständnis möglich ist, wird auch einfach p statt
p̄ geschrieben.
Beispiele:
(a) 7 ≡ 11 (mod 2), 83 ≡ 243 (mod 10), 259 ≡ 3 (mod 256), −1 ≡ 127 (mod 128)
(b) Die Restklasse von 0 modulo 2 ist die Menge der geraden ganzen Zahlen, die Restklasse von 1 modulo 2 die Menge der ungeraden ganzen Zahlen.
(c) Für n = 3 haben wir die Restklassen modulo 3
0̄ := {. . . − 6, −3, 0, 3, 6, . . .},
1̄ := {. . . − 5, −2, 1, 4, 7, . . .},
2̄ := {. . . − 4, −1, 2, 5, 8, . . .}
Die Restklasse von p modulo n hat die Form
p̄ = {q ∈ Z | p ≡ q (mod n)}
= {. . . p − 3n, p − 2n, p − n, p, p + n, p + 2n, p + 3n, . . .}
beispielsweise für n = 3 und p = 2:
{. . . − 8, −5, −2, 1, 4, 7, 10, 13, . . .}
Es gibt verschiedene sinnvolle Möglichkeiten, eine Restklasse p̄ durch Auswahl eines besonders einfachen Elements r ∈ p̄ mit p̄ = r̄ zu charakterisieren:
• r = p mod n mit der Eigenschaft 0 ≤ r ≤ n − 1
• für gerades n: − n2 ≤ r ≤
n
2
−1
93
• für ungerades n: − n−1
≤r≤
2
n−1
2
Es gibt n verschiedene Restklassen modulo n.
Definition 6.1.2 Die Menge aller Restklassen modulo n wird hier mit Zn bezeichnet:
Zn := {0̄, 1̄, 2̄, 3̄, . . . n − 1}
Hinweis: Mit Zn wird in der Mathematik auch eine andere Menge bezeichnet (die hier
nicht behandelt wird). Um Missverständnisse zu vermeiden, ist daher für die Menge der
Restklassen modulo n anderswo auch die Abkürzung Z/nZ gebräuchlich.
Beispiele:
Z2 = {0̄, 1̄}, Z3 = {0̄, 1̄, 2̄} = {−1, 0̄, 1̄},
Z5 = {0̄, 1̄, 2̄, 3̄, 4̄} = {−2, −1, 0̄, 1̄, 1̄},
Z256 = {0̄, 1̄, 2̄, 3̄, . . . 255} = {−128, −127, −126, . . . 126, 127}
Definition 6.1.3 Sei n ∈ N+ , Zn die Menge der Restklassen modulo n, für beliebige
p ∈ Z sei p̄ = {q ∈ Z | p ≡ q (mod n)}.
Für beliebige ā, b̄ ∈ Zn wird durch
ā ⊕ b̄ := (a + b),
ā b̄ := (a · b)
eine Addition und eine Multiplikation in Zn definiert.
Beispiele für Z256 :
2̄ ⊕ 255 = 2 + 255 = 257 = 257 mod 256 = 1̄
und
2̄ 255 = 2 · 255 = 510 = 510 mod 256 = 254
Hinweis: Die Definition 6.1.3 ist gefährlich“; denn die Summe der beiden Mengen ā
”
und b̄ ist durch die Summe der beiden Elemente a ∈ ā und b ∈ b̄ definiert! Der Wert
der Summe könnte von der Auswahl dieser Vertreter“ a und b abhängen! Wir haben zu
”
beweisen, dass dies nicht der Fall ist (in der Fachsprache der Mathematik, dass die Summe
und das Produkt wohldefiniert“ sind).
”
Beweis, dass die Definition 6.1.3 nicht von der Auswahl der Elemente in den Restklassen
abhängt:
Für beliebige c ∈ ā und d ∈ b̄ gilt:
c ≡ a (mod n) und d ≡ b (mod n) =⇒ c = a + k · n und d = b + l · n mit k, l ∈ Z
=⇒ c + d = a + k · n + b + l · n = a + b + (k + l)n =⇒ (c + d) ≡ (a + b) (mod n)
=⇒ c + d = a + b
Analog beweist man c · d = (a · b).
Satz 6.1.2 Für die in Definition 6.1.3 definierte Addition und Multiplikation in Zn gelten
das Kommutativgesetz und das Assoziativgesetz und
k⊕0=k
und
k1=k
für alle k ∈ Zn
Hinweis zur Schreibweise: Die hier verwandte Schreibweise ist in der Literatur unüblich
ist. Es wird meist darauf verzichtet, der Addition und Multiplikation in Zn ein besonderes
Symbol zuzuweisen. Man schreibt meist direkt + statt ⊕ und · statt .
94
Man kann sich Zn gut veranschaulichen, wenn man die Restklassen in C abbildet:
f : Zn → C,
2π
k̄ 7→ f (k̄) = ejk n
Die Abbildungsvorschrift hängt nicht davon ab, welchen Vertreter k wir aus der Restklasse
k̄ auswählen, denn
l ∈ k̄ ⇐⇒ k ≡ l
2π
2π
(mod n) ⇐⇒ k − l = m · n mit m ∈ Z ⇐⇒ ejk n = ejl n
Die entsprechenden Bildpunkte sind für Z5 in Abb. 33 grafisch dargestellt, sie liegen alle
auf dem Einheitskreis. Die Addition in Z5 entspricht der Addition der entsprechenden
Phasen. Durch fortgesetzte Addition derselben Phase (beispielsweise der Phase, die 1
entspricht, also 2π
) läuft man im Kreis herum.
n
Abbildung 33: Veranschaulichung der Restklassen Z5 durch Abbildung in C, die Bilder
liegen auf dem Einheitskreis.
Es mag vielleicht hier etwas ungewöhnlich erscheinen, dass mit Restklassen, also mit
Mengen, gerechnet wird, als wenn es sich um Zahlen handeln würde. Man muß dabei nur
sorgsam darauf achten, dass das Rechenergebnis nicht davon abhängt, welchen Vertreter
man aus der Menge auswählt. Es ist daher hier nützlich darauf hinzuweisen, dass die
Elemente von Q, der Menge der rationalen Zahlen, auch Mengen sind. So ist beispielsweise
n
o
m
1 2 3 4 5 6
, , , ,
,
,... =
| m ∈ Z, m 6= 0
2 4 6 8 10 12
2m
eine rationale Zahl, und wir haben uns daran gewöhnt, den Vertreter 12 auszuwählen, als
16
auftreten.
Rechenergebnis kann aber auch 32
Eine der ältesten bekannten Verschlüsselungsmethoden, die von Julius Caesar benutzt
wurde, kann mit der Addition in Z26 beschrieben werden. Man kann den Buchstaben des
Alphabets eindeutig die Zahlen {0, 1, 2, 3, . . . 25} zuordnen (mathematisch gesprochen, die
Menge {A, B, C, D, . . . Z} mit einer bijektiven Abbildung in Z26 abbilden), indem man
sie mit 0 beginnend nummeriert. Die Verschlüsselung besteht nun darin, dass man ein
p ∈ Z26 mit p 6= 0 auswählt (das dem Empfänger und möglichst nur ihm bekannt ist) und
auf jeden Buchstaben die Abbildung
f : Z26 → Z26 ,
x 7→ f (x) = x ⊕ p = (x + p) mod 26
anwendet. So wird beispielsweise das Wort ALGEBRA zunächst in die Elemente in Z26 ,
also in (0, 11, 6, 4, 1, 17, 0) umgewandelt. Nach der Verschlüsselung wird daraus für das
Zahlenbeispiel p = 3
(f (0), f (11), f (6), f (4), f (1), f (17), f (0)) = (3, 14, 9, 7, 4, 20, 3)
95
In Buchstaben umgewandelt lautet die verschlüsselte Nachricht DOJHEUD. Damit eine Entschlüsselung überhaupt möglich ist, muß die Abbildung f bijektiv sein. Zur Entschlüsselung muß die Umkehrabbildung bestimmt werden. Nach der Merkregel
y = f −1 (x) ⇐⇒ x = f (y)
müssen wir hier die Gleichung
x = f (y) = y ⊕ p = (y + p) mod 26
auflösen nach y. Dies ist einfach:
f −1 : Z26 → Z26 ,
x 7→ f −1 (x) = (x − p) mod 26 = (x + 26 − p) mod 26 = x ⊕ (26 − p)
Derartige Verschlüsselungen sind nicht besonders effektiv. In der deutschen oder englischen Sprache ist der Buchstabe E bei weitem am häufigsten. Man braucht zum Knacken“
”
eines derartigen Codes nur das am häufigsten vorkommende Zeichen bzw. das entsprechende Element q ∈ Z26 zu bestimmen. Da E in Z26 der Zahl 4 enspricht, hat man dann
die Gleichung f (4) = 4 ⊕ p = (4 + p) mod 26 = q nach p aufzulösen, also
p = (q − 4) mod 26 = (q + 26 − 4) mod 26 = q ⊕ 22
und kann dann damit die Entschlüsselung vornehmen. Effektivere Verschlüsselungen werden in der Lehrveranstaltung IT-Sicherheit“ behandelt. Restklassen spielen bei vielen
”
eine wichtige Rolle.
Am Beispiel von Caesars Verschlüsselung haben wir gesehen, wie man in Zn Gleichungen nach einem unbekannten Summanden auflösen kann. Die Gleichung
p ⊕ x = (p + x) mod n = 0
kann nach x aufgelöst werden, die Lösung ist −p mod n = (n − p) mod n = n − p. Wir
haben also für jedes p ∈ Zn ein inverses Element bzgl. der Addition (n − p) mit der
Eigenschaft p ⊕ (n − p) = 0 und können damit Gleichungen mit Summen umformen oder
auflösen.
Für diese Überlegungen wäre es zweckmäßiger, als Vertreter unserer Restklassen nicht
0, 1, 2, . . . n − 1 auszuwählen, sondern symmetrisch vorzugehen, also beispielsweise für Z5
die Zahlen {−2, −1, 0, 1, 2} auszuwählen. Bei geradem n kann diese Auswahl allerdings
nicht symmetrisch erfolgen. So wird bei der ganzzahligen Rechnung im Computer meist
der Bereich {− n2 , − n2 + 1, . . . n2 − 1} ausgewählt, für 8 Bit also von -128 bis 127. Ersetzt
man im Beispielprogramm die Deklaration unsigned char durch char und ändert die
entsprechende Zuweisung in a=4; b=127;, so erhält man (bei den meisten Rechnern) als
Ausgabe a= 4, b=127, a+b= -125, a*b= -4.
6.2
Endliche Körper
Untersuchen wir, wie es mit der Auflösung entsprechender Gleichungen für die Multiplikation steht. Es ist klar, dass die 1 das neutrale Element der Multiplikation in Zn ist,
d.h. wir haben 1 k = k für alle k ∈ Zn . Wir haben jedoch beispielsweise in Z256 das
Unglück“, dass das Produkt von Null verschiedener Restklassen Null ergeben kann. So
”
hatten wir 128 128 = 0, weil 128 · 128 mod 256 = 0. Es kann also kein q ∈ Z256 geben
96
mit 128 q = 1, denn eine Multiplikation dieser Gleichung mit 128 würde sofort den
Widerspruch 128 = 0 liefern. Dieses Unglück“ haben wir immer, wenn n sich schreiben
”
lässt als n = k ·l mit k 6= n, also wenn n keine Primzahl ist, denn dann haben wir k l = 0
und die Gleichung k x = 1 hat keine Lösung x ∈ Zn . Dieses Problem tritt nicht auf,
wenn n eine Primzahl ist. Schauen wir uns als Beispiel einmal die Rechenoperationen in
Z5 in den folgenden Tabellen an.
+
0
1
2
3
4
0
0
1
2
3
4
1
1
2
3
4
0
2
2
3
4
0
1
3
3
4
0
1
2
·
0
1
2
3
4
4
4
0
1
2
3
0
0
0
0
0
0
1
0
1
2
3
4
2
0
2
4
1
3
3
0
3
1
4
2
4
0
4
3
2
1
Wir haben dabei die Addition wieder als + statt ⊕ und die Multiplikation als · statt geschrieben. Man kann durch Nachschauen in der Multiplikationstabelle zu jedem k ∈ Z5
mit k 6= 0 das entsprechende inverse Element x = k −1 finden, das die Gleichung k · x = 1
löst. Hier das Ergebnis:
k
1 2 3 4
k −1 1 3 2 4
Es gelten also mit dieser Addition und Multiplikation in Z5 dieselben Rechenregeln wie
in R. Entsprechendes gilt immer für Zn , wenn n eine Primzahl ist. Wir formulieren das
Ergebnis ein wenig allgemeiner.
Definition 6.2.1 Eine Menge K heißt Körper, wenn in der Menge zwei Rechenoperationen definiert sind, nämlich eine Addition, die jedem Paar a, b ∈ K eindeutig das Element
a+b ∈ K zuordnet, und eine Multiplikation, die jedem Paar a, b ∈ K das Element a·b ∈ K
zuordnet und folgende Regeln gelten für alle a, b, c ∈ K:
a+b
a·b
(a + b) + c
(a · b) · c
a · (b + c)
=
=
=
=
=
b+a
b·a
a + (b + c)
a · (b · c)
a·b+a·c
(Kommutativgesetz für die Addition)
(Kommutativgesetz für die Multiplikation)
(Assoziativgesetz für die Addition)
(Assoziativgesetz für die Multiplikation)
(Distributivgesetz)
Es existiert eine eindeutige Zahl 0 ∈ K mit der Eigenschaft
a+0=a
für alle
a∈K
0 ist das neutrale Element der Addition.
Es existiert eine eindeutige Zahl 1 ∈ K, 1 6= 0, mit der Eigenschaft
a·1=a
für alle
a∈K
1 ist das neutrale Element der Multiplikation.
Für alle a ∈ K hat die Gleichung a + x = 0 genau eine Lösung x ∈ K. Man schreibt diese
Lösung als x = −a und hat damit die Regel
für alle a ∈ K
a + (−a) = 0
97
−a ist das zu a inverse Element der Addition.
Für alle a ∈ K mit a 6= 0 hat die Gleichung a · x = 1 genau eine Lösung x ∈ K. Man
schreibt diese Lösung als x = a−1 und hat damit die Regel
a · a−1 = 1
für alle
a∈K
mit
a 6= 0
a−1 ist das zu a inverse Element der Multiplikation.
Man vereinbart für beliebige a, b ∈ K die Schreibweise ab := a·b. K heißt endlicher Körper,
wenn K nur endlich viele Elemente enthält.
Satz 6.2.1 Zn , die Menge der Restklassen modulo n, ist genau dann ein Körper, wenn
n eine Primzahl ist.
Ein für die Nachrichtentechnik (denken Sie an die Bedeutung des binären Zahlensystems
bei der Übertragung von Daten!) besonders wichtiger Körper ist Z2 , der zwei Elemente 0
und 1 hat. Zur Verdeutlichung die Rechenoperationen in Tabellenform
· 0 1
0 0 0
1 0 1
+ 0 1
0 0 1
1 1 0
Die Rechenregeln sind alle erfüllt (prüfen Sie dies nach!). Dieser Körper wird auch mit
GF (2) bezeichnet (Galois field, Galois französischer Mathematiker, field englisch Körper,
2 Elemente). Allgemein wird ein Körper mit q Elementen mit GF (q) bezeichnet. Beliebige
Körper werden hier mit K bezeichnet. Wir haben bisher die Beispiele R, Q, C, GF (2),
GF (3) und GF (5) behandelt.
Definition 6.2.2 Ein Vektorraum über einem Körper K ist eine Menge V mit zwei
Rechenoperationen, die die in Definition 4.1.1 angegebenen Grundregeln erfüllen: einer
Addition, die jedem Paar a, b ∈ V eindeutig die Summe a + b ∈ V zuordnet sowie einer
Multiplikation von Elementen des Körpers K mit Elementen in V , die jedem Paar t, a
mit t ∈ K und a ∈ V das Element ta ∈ V zuordnet. Es werden dieselben Grundregeln für
alle a, b, c ∈ V und alle s, t ∈ K wie in Definition 4.1.1 gefordert (wobei wir hier a statt
~a geschrieben haben).
Beispiel: Für jedes n ∈ N+ ist Kn , die Menge der n-tupel von Elementen in K ein
Vektorraum über K mit der Addition und Multiplikation mit Elementen t ∈ K:
    

   
b1
a1 + b 1
a1
ta1
a1
 a2   b 2   a2 + b 2 
 a2   ta2 

   
    
a + b =  ..  +  ..  =  ..  ,
ta = t  ..  =  .. 
. .  . 
.  . 
an
bn
an + b n
an
tan
Matrizen können ganz entsprechend auch für Elemente beliebiger Körper definiert werden.
Analog können auch lineare Abbildungen zwischen Vektorräumen über demselben Körper
definiert werden.
Beispiel:
T : GF (2)5 → GF (2)4 , x 7→ T (x) = Ax
98
mit

1
1
A=
1
1
0
1
0
1
1
1
0
0
0
1
1
0

0
1

0
1
Kern(T) ist die Lösungsmenge des linearen Gleichungssystems
Ax = 0
Das systematische Gauß-Verfahren liefert das Gleichungssystem:
1
0
0
0
0
1
0
0
1
0
1
0
0
1
1
0
0
1
0
0
0
0
0
0
x5 = t, x4 = s, s, t ∈ GF (2) beliebig
x3 + s = 0 =⇒ x3 = s
x2 + s + t = 0 =⇒ x2 = s + t
x1 + s = 0 =⇒ x1 = s
Beachten Sie, dass b+b = 0 für alle b ∈ GF (2) gilt. Außerdem erhalten wir aus der Matrix
in Dreiecksform das Ergebnis Rang(A) = 3. Für die allgemeine Lösung des Gleichungssystems Ax = 0 erhalten wir

 
 

s
1
0
s + t
1
1

 
 

 
 

x=
s, t ∈ GF (2) beliebig
 s  = s 1 + t 0
 s 
1
0
t
0
1
Beachten Sie, dass die Lösungsmenge (und damit Kern(T)) aus 4 Elementen besteht.
6.3
Kanalcodierung: Beispiele
Bei der Übertragung von Signalen über einen gestörten Nachrichtenkanal versucht man
durch eine entsprechende Codierung, die Kanalcodierung, Übertragungsfehler möglichst
erkennbar zu machen. Noch besser ist es, sie in möglichst vielen Fällen auch gleich korrigieren zu können. Ein einfaches Beispiel wäre, bei der Übertragung jedes Bit zu wiederholen, also beispielsweise die Nachricht 01001101 als 0011000011110011 zu verschicken.
Der Empfänger kann dann am Auftauchen von zwei nicht in dieses Paarschema passenden
Bits in der empfangenen Nachricht erkennen, dass ein Übertragungsfehler aufgetreten ist,
und eine erneute Übertragung anfordern. Im Beispiel wird der Empfänger das empfangene Signal 0011001011110011 zurückweisen. Zwei Übertragungsfehler in zwei unmittelbar
hintereinanderfolgenden Bits können dennoch unentdeckt bleiben. Sie sind aber weniger
wahrscheinlich. Dreifache Wiederholung ermöglicht sogar eine Korrektur eines Teils der
Fehler. Wir schauen uns dieses Beispiel genauer an und zeigen, dass die mathematische
Beschreibung mit Z2 nützlich ist:
Wiederholungscode:
Die Codierung durch dreifache Wiederholung kann durch folgende Abbildung beschrieben
werden:
 
 
b
1
3



T : Z2 → Z2 , b 7→ T (b) = b = b · 1
b
1
99
Dabei wird (ganz analog zur Menge R3 ) die Menge aller Tripel von Bits (dargestellt als
Vektor mit Komponenten in Z2 ) mit Z32 bezeichnet. Die Multiplikation mit einem Skalar
wird analog wie in R3 definiert (es gibt hier nur zwei verschiedene Skalare). Diese Abbildung ist injektiv, das ist auch notwendig, sonst hätte man keine Chance, die übersandte
Nachricht wieder zu rekonstruieren. Die Bildmenge dieser Abbildung T (Z2 ) (entspricht
dem Wertebereich einer Funktion) wird hier als die Menge der Codeworte bezeichnet.
Die Wiederherstellung der abgesandten Nachricht, die Decodierung D, muß mindestens
in dieser Menge definiert sein und D ◦ T = idZ2 , also D(T (b)) = b erfüllen. Hier können
wir sogar jedes Element aus Z32 decodieren. Wenn in einem Tripel von Bits nicht alle
drei übereinstimmen, dann muß mindestens ein Übertragungsfehler vorliegen. Die Wahrscheinlichkeit, dass nur einer vorliegt, sollte größer sein als die, dass zwei vorliegen, und
somit kann man bei der Decodierung eine Mehrheitsentscheidung“ treffen. Damit kann
”
die Abbildung zur Decodierung auf ganz Z32 durch die folgende Tabelle definiert werden:
x 000 001 010 011 100 101 110 111
D(x) 0
0
0
1
0
1
1
1
x ∈ T (Z2 ) ja nein nein nein nein nein nein ja
In den Fällen, in denen x 6∈ T (Z2 ), liegt ein Übertragungsfehler vor. Der einfacheren
Darstellung wegen wurden die Elemente x ∈ Z32 in der Tabelle als Zeilenvektor (ohne
Klammern) und nicht als Spaltenvektor dargestellt. Wir bezeichnen die Komponenten
von x ∈ Z32 mit x1 , x2 , x3 . Es liegt kein Übertragungsfehler vor, wenn die empfangene
Nachricht x den Gleichungen
x1 = x 2
und
x2 = x 3
genügt. Zur Vorbereitungen auf heute tatsächlich verwandte Codes formulieren wie diese
Gleichungen etwas um. Sie können in der üblichen Weise als lineares Gleichungssystem
geschrieben werden:
x1 + x2 = 0,
x2 + x3 = 0
Dabei haben wir ausgenutzt, dass in Z2 gilt 1 + 1 = 0, also −1 = +1. Dieses Gleichungssystem kann mit einer Matrix beschrieben werden, und wir haben als Ergebnis, dass genau
dann kein Übertragungsfehler vorliegt, wenn die empfangene Nachricht x
0
1 1 0
Hx =
mit
H=
0
0 1 1
erfüllt. Die Vorteile dieses Codes werden durch eine Verdreifachung der Zahl der zu
übertragenden Bits erkauft. Professionelle Kanalcodes können entsprechende Vorteile mit
erheblich weniger Aufwand, aber einer mathematisch anspruchsvolleren Codierung erreichen.
Gerade Parität:
Wenn Texte mit dem 7-Bit-ASCII-Code codiert sind, dann liegt die zu übermittelnde
Nachricht in Blöcken zu je 7 Bit vor. Zur Codierung wird nun ein 8. Bit, das Paritätsbit,
zugefügt. Es ist 0, wenn die übrigen 7 Bits eine gerade Zahl von Einsen enthalten, und 1,
wenn sie eine ungerade Anzahl von Einsen enthalten. Dies ermöglicht zwar keine Korrektur, aber eine Erkennung eines einzelnen Übertragungsfehlers innerhalb des übertragenen
100
Blocks. Wird in den ersten 7 Bits ein Bit durch einen Fehler umgekehrt, dann ändert
sich gerade die Parität, also die Eigenschaft, ob die Gesamtzahl der Einsen gerade oder
ungerade ist. Ein Übertragungsfehler im 8. Bit ist ebenfalls erkennbar. Allerdings lässt
sich eine gerade Anzahl von Übertragungsfehlern, also bereits zwei Fehler, innerhalb eines
8-Bit-Blocks so nicht erkennen.
Es ist sinnvoll, diese Codierung etwas mathematischer zu beschreiben. Ausgangspunkt
sind 7 Bits, also ein Element x ∈ Z72 mit den Komponenten x1 , x2 , x3 , . . . x7 . Die Definitionsmenge der Codierungsabbildung T ist demnach Z72 , die Zielmenge Z82 , also
T : Z72 → Z82 ,
x 7→ y = T (x)
Die ersten 7 Bits werden unverändert übernommen, also yk = xk für k = 1, 2, 3, . . . 7. Das
8. Bit lässt sich mit der Addition in Z2 ausrechnen: y8 = x1 + x2 + x3 + · · · x7 . Beachten
Sie, dass wir in Z2 1+1 = 0 haben und so die Summe tatsächlich das gewünschte Ergebnis
hat. Es mag zwar für diesen einfachen Code etwas umständlich erscheinen, es ist aber im
Hinblick auf andere Codes sehr lehrreich, diese Codierung mit einer Matrix zu beschreiben:


1 0 0 0 0 0 0
0 1 0 0 0 0 0


0 0 1 0 0 0 0


0 0 0 1 0 0 0


y = T (x) = Ax
mit
A=
(56)

0
0
0
0
1
0
0


0 0 0 0 0 1 0


0 0 0 0 0 0 1
1 1 1 1 1 1 1
Das 8. Bit, das Paritätsbit, wird also gerade so gesetzt, dass die Gesamtzahl der Einsen
im übertragenen Block gerade ist. Wenn kein Fehler aufgetreten ist, dann ist also die
Gesamtzahl der Einsen in einem empfangenen Block stets gerade. Dies kann kontrolliert
werden, indem man die Summe in Z2 ausrechnet. Diese Kontrolle kann auch mit einer
Matrix beschreiben werden, allerdings mit einer (1 × 8)-Matrix:
y = Ax ⇐⇒ y1 +y2 +y3 +· · · y7 +y8 = 0 ⇐⇒ Hy = 0 mit H = 1 1 1 1 1 1 1 1
Die Matrix H wird Prüfmatrix (check matrix) genannt. Fehler können hier nicht korrigiert werden, die Decodierung wird also nur auf der Menge der Codeworte definiert. Sie
besteht darin, einfach das letzte Bit, das Paritätsbit, wegzulassen. Formulieren Sie dies
zur Übung mit Hilfe einer Matrix!
Linearer Code mit Fehlerkorrektur:
Dieses Beispiel soll zeigen, dass mit etwas mehr mathematischem Aufwand einfache Fehler innerhalb eines Blocks korrigiert werden können, wobei die übermittelten Daten nur
verdoppelt sind. Wir gehen davon aus, dass die zu übermittelnden Nachrichten zu Blöcken
von drei Bits zusammengefaßt sind und fügen drei Kontrollbits dazu. Die Codierung wird
durch folgende Abbildung beschrieben:


1 0 0
 0 1 0 


 0 0 1 
3
6

T : Z2 → Z2 , x 7→ y = T (x) = Ax
mit
A=
(57)
 0 1 1 


 1 1 0 
1 0 1
101
Die Prüfmatrix H ist hier


0 1 1 1 0 0
H= 1 1 0 0 1 0 
1 0 1 0 0 1
Sie prüft, ob wir eine codierte Nachricht korrekt empfangen haben, also
y = Ax ⇐⇒ Hy = 0
(58)
Diese Aussage kann man allgemein für Matrizen, die auf diese Weise blockweise aufgebaut
sind, beweisen oder in unserem Beispiel konkret überprüfen. y = Ax heißt zunächst
x1 = y1 , x2 = y2 , x3 = y3 , der obere Block von A ist die (3 × 3)-Einheitsmatrix. Die drei
letzten Komponenten von y = Ax lauten damit
y4 = x2 + x3 = y2 + y3 ,
y5 = x1 + x2 = y1 + y2 ,
y6 = x1 + x3 = y1 + y3
Bringt man in diesen Gleichungen alle Summanden auf eine Seite (zur Erinnerung: b+b = 0
für alle b ∈ Z2 ), so erhält man die äquivalenten Gleichungen
y2 + y3 + y4 = 0,
y1 + y2 + y5 = 0,
y1 + y3 + y6 = 0
Dies sind gerade die Komponenten der Gleichung Hy = 0.
Die Decodierung korrekt übertragener Blöcke y ist einfach: man lässt die drei letzten
Bits, die Prüfbits, weg (nach Überprüfung, ob Hy = 0). Das Auftreten eines einzelnen
Fehlers im k. Bit eines übertragenen Blocks kann man dadurch beschreiben, dass zum
korrekt codierten Block y = Ax der Einheitsvektor ek addiert wird (der im k. Bit eine
1 und sonst überall eine 0 hat). Beachten Sie, dass die Addition einer 1 ein Bit stets
umkehrt. Bei einem Übertragungsfehler im k. Bit empfangen wir also statt y tatsächlich
z = y + ek . Beim Prüfen berechnen wir
Hz = H(y + ek ) = Hy + Hek = 0 + Hek = Hek
Nach der alten Merkregel die Bilder der Einheitsvektoren sind die Spalten der Matrix“
”
können wir einen Übertragungsfehler im k. Bit des empfangenen Blocks z daran erkennen,
dass wir beim Prüfen mit Hz den k. Spaltenvektor von H berechnen. Diesen Fehler können
wir dann korrigieren, indem wir das k. Bit in z umkehren, also z durch z + ek ersetzen.
Hieran sieht man, dass derartige Codes eine Fehlererkennung erlauben, wenn keine
Spalte von H der Nullvektor ist, und eine Fehlerkorrektur, wenn nicht zwei Spalten von
H übereinstimmen.
Wenn zwei Übertragungsfehler auftreten, dann kann man dies dadurch beschreiben,
dass man statt y den Vektor z = y + ek + el mit k 6= l empfängt. Beim Prüfen erhält man
dann
Hz = H(y + ek + el ) = Hy + Hek + Hel = Hek + Hel
also die Summe zweier Spaltenvektoren von H. Nun gilt
Hek + Hel = 0 ⇐⇒ Hek = Hel
Wenn nicht 2 Spaltenvektoren von H übereinstimmen, dann können derartige Fehler
erkannt werden. Sie werden aber falsch korrigiert, wenn die Summe zweier Spaltenvektoren
mit einem dritten übereinstimmt. In unserem Beispiel liefert ein Übertragungsfehler im
1. und 2. Bit
z = y + e1 + e2 ,
Hz = He1 + He2 = He3
102
und es wird fälschlicherweise das 3. Bit korrigiert. Wenn dagegen im 1. und 4. Bit ein
Fehler auftritt, dann hat man
z = y + e1 + e4 ,
Hz = He1 + He4 = (111)T
und z stimmt mit keinem Spaltenvektor von H überein. Hier würde man erkennen, dass
mehr als ein Übertragungsfehler vorliegt.
Spezielle Notation der Kanalcodierung
Leider wird in der Kanalcodierung eine Notation benutzt, die abweicht von der, die in
der Mathematik und anderen Bereichen der Technik gebräuchlich ist. Vektoren werden
als Zeilenvektoren notiert, Vektoren aus Zk2 werden also als (1 × k)-Matrizen aufgefasst.
Die Codierung eines Datenwortes a = (a0 , a1 , a2 , . . . ak−1 ) ∈ Zk2 mit einem linearen Code
erfolgt dann durch die lineare Abbildung
T : Zk2 → Zn2 ,
a 7→ c = aG
mit der (k × n)-Matrix G, die Generatormatrix genannt wird. Der Zeilenvektor c heißt
dann Codewort. Vergleich mit (56) und (57) liefert G = AT . Die übliche Notation
erhalten wir also durch Transponieren der bisher benutzten Matrizen A. Für die gerade
Parität beim 7-Bit-ASCII-Code (56) erhalten wir somit die Generatormatrix


1 0 0 0 0 0 0 1
 0 1 0 0 0 0 0 1 


 0 0 1 0 0 0 0 1 



0
0
0
1
0
0
0
1
G=


 0 0 0 0 1 0 0 1 


 0 0 0 0 0 1 0 1 
0 0 0 0 0 0 1 1
und für das Beispiel des linearen Codes mit

1 0
G= 0 1
0 0
Fehlerkorrektor (57) ist die Generatormatrix

0 0 1 1
0 1 1 0 
1 1 0 1
Die Bezeichnung H für die Prüfmatrix entspricht der Notation der Kanalcodierung. Wir
können die Prüfmatrizen der angegebenen Beispiele daher unverändert übernehmen. Die
Prüfbedingung (58) muss jedoch umformuliert werden, da wir hier Zeilenvektoren benutzen. Sie lautet in der neuen Notation
c = aG ⇐⇒ cHT = 0
(59)
Beachten Sie, dass cHT = (HcT )T und machen Sie sich klar, dass H eine (m × n)-Matrix
sein muss. Manchmal wird die Prüfbedingung auch in der Form c = aG ⇐⇒ HcT = 0
geschrieben.
Unter dem Code C versteht man den Unterraum
C := Bild(T ) = T (Zk2 ) = {c ∈ Zn2 | c = aG, a ∈ Zk2 }
103
und mit Hilfe der linearen Abbildung
P : Zn2 → Zm
2 ,
c 7→ cHT
kann man den Code C als Kern von P charakterisieren:
C = Kern(P ) = {c ∈ Zn2 | cHT = 0}
Damit haben wir Kern(P ) = Bild(T ), also gilt für die Hintereinanderausführung der
beiden linearen Abbildungen P ◦ T = 0. Für die Matrizen bedeutet dies GHT = 0.
Überzeugen Sie sich durch explizite Rechnung, dass dies bei den beiden in diesem Unterabschnitt als Beispiel angegebenen angegebenen Codes tatsächlich der Fall ist!
Aus allgemeinen
Ergebnissen der linearen Algebra folgt, dass die Prüfmatrix H eine
(n − k) × n -Matrix sein muss, wenn die Generatormatrix eine (k × n)-Matrix ist. Außerdem muss der Rang der Generatormatrix stets k sein, die Zeilen von G sind also linear
unabhängig.
7
Determinanten
7.1
Determinanten für n = 2 und n = 3, Cramersche Regel
Wozu braucht man Determinanten?
• Lösung von Gleichungssystemen für 2 und 3 Unbekannte
• Flächen- und Volumenberechnung
• Korrekturfaktor bei Substitutionen in Flächen- und Volumenintegralen
• Berechnung von Eigenwerten für kleine Matrizen
Der Name Determinante“ kommt von ihrer Rolle als entscheidende (determinierende)
”
Größe, ob ein lineares Gleichungssystem singulär ist. Betrachten wir die Lösung eines
linearen Gleichungssystems A~x = ~b mit dem Gauß-Verfahren im Sonderfall, dass A eine
21
(2 × 2)-Matrix ist. Durch Addition des − aa11
-fachen der ersten Zeile zur zweiten erhalten
wir aus der ursprünglichen erweiterten Koeffizientenmatrix
a11 a12 b1
a21 a22 b2
die Matrix in Dreiecksform
a11
a12
b1
0 a22 − a21a11a12 b2 − aa21
b1
11
falls kein Zeilentausch notwendig ist, also wenn a11 6= 0. In diesem Fall ist das System
genau dann singulär, wenn
a22 −
a21 a12
a11 a22 − a21 a12
=
=0
a11
a11
Hierfür ist entscheidend, ob der Zähler verschwindet. Dies motiviert die
104
Definition 7.1.1 Sei A eine (2 × 2)-Matrix. Dann ist die Determinante von A durch
a11 a12 := a11 a22 − a21 a12
det(A) = a21 a22 definiert.
Falls a11 = 0 ist ein Zeilentausch bei der Lösung des Gleichungssystems notwendig. Ein
Zeilentausch (der auch erlaubt ist, wenn a11 6= 0) führt auf die Determinante
a21 a22 = a21 a12 − a11 a22 = − a11 a12 a11 a12 a21 a22 Ein Zeilentausch führt also zu einem Vorzeichenwechsel bei der Determinante.
Satz 7.1.1 Sei A eine (2 × 2)-Matrix.
Dann ist A genau dann invertierbar, wenn det(A) 6= 0. Wenn det(A) 6= 0, dann gilt
1
a22 −a12
−1
A =
det(A) −a21 a11
Die erste Aussage ergibt sich aus den einleitenden Bemerkungen vor der Definition, die
nützliche Formel kann man durch Nachrechnen überprüfen (tun Sie dies, indem Sie AA−1
und A−1 A ausrechnen!).
Satz 7.1.2 (Cramersche Regel) Sei A eine (2 × 2)-Matrix mit det(A) 6= 0 und sei
~b ∈ R2 . Dann hat das lineare Gleichungssystem A~x = ~b die Lösungen
b1 a12 a11 b1 1
1
,
x1 =
x2 =
det(A) b2 a22 det(A) a21 b2 Der Beweis kann durch Einsetzen in das Gleichungssystem erfolgen.
Definition 7.1.2 Sei
det(A) = A eine (3 × 3)-Matrix. Dann ist die Determinante von A durch
a11 a12 a13 a21 a22 a23 := a11 a22 a33 + a12 a23 a31 + a13 a21 a32
−a31 a22 a13 − a32 a23 a11 − a33 a21 a12
a31 a32 a33 definiert.
Die Berechnung der Determinante erfolgt nach dem folgenden Schema, das Regel von
”
Sarrus“ genannt wird:
Ein derartiges Schema liefert nur für (3 × 3)-Matrizen die Determinante, eine Definition
für größere Matrizen erfolgt im nächsten Kapitel.
Satz 7.1.3 Sei A eine (3 × 3)-Matrix. Dann gilt:
105
(a) A ist invertierbar ⇐⇒ det A 6= 0
(b) Wenn det A 6= 0 und ~b ∈ R3 , dann hat das Gleichungssystem A~x = ~b die Lösung
(Cramersche Regel)
b1 a12 a13 a11 b1 a13 1 1 ,
b
a
a
a
b
a
x
=
x1 =
2
22
23
21
2
23
2
det A det
A
a31 b3 a33 b3 a32 a33 a11 a12 b1 1 a21 a22 b2 x3 =
det A a31 a32 b3 Hinweise:
(a) Schon für den hier vorliegenden Fall einer (3 × 3)-Matrix erfordert die Lösung eines
Gleichungssystems nach der Cramerschen Regel mehr Rechenoperationen als die
nach dem Gauß-Verfahren. Man kann die Cramersche Regel zwar für größere Gleichungssysteme entsprechend verallgemeinern, der Rechenaufwand ist jedoch dann
drastisch größer als bei der Anwendung des Gauß-Verfahrens. Für zwei und drei
Gleichungen hat sie jedoch den Vorteil, dass man Gleichungssysteme formelmäßig
auflösen kann, wenn die Koeffizienten nicht zahlenmäßig bekannt sind.
(b)
ax b x ~
ay by = ±|~a| · |b| sin ϕ
für alle Vektoren ~a, ~b ∈ R2 , wobei ϕ der von den beiden Vektoren eingeschlossene
Winkel ist. |det(A)| ist also die Fläche des von den Spaltenvektoren von A aufgespannten Parallelogramms. Dies kann man sich klarmachen, indem man die beiden
Vektoren ~a und ~b durch az = 0 und bz = 0 zu Vektoren in R3 macht und |~a × ~b|
ausrechnet.
(c) Für (3 × 3)-Matrizen A ist |det(A)| das Volumen des von den Spaltenvektoren von
A aufgespannten Parallelepipeds (Spats).
7.2
Laplacesche Entwicklung
Betrachten wir als Beispiele zwei andere Berechnungsmöglichkeiten für Determinanten
von (3 × 3)-Matrizen:
• Entwicklung
a11
a21
a31
nach der 1. Zeile:
a12 a13 a
a
a22 a23 = a11 22 23
a
a
32
33
a32 a33 • Entwicklung
a11
a21
a31
nach der 1. Spalte:
a12 a13 a
a
a22 a23 = a11 22 23
a32 a33
a32 a33 − a12 a21 a23
a31 a33
+ a13 a21 a22
a31 a32
− a21 a12 a13
a32 a33
+ a31 a12 a13
a22 a23
106
• Analog kann eine Entwicklung nach einer anderen Zeile oder Spalte erfolgen. Die Determinante, die als Faktor hinter dem jeweiligen Matrixelement aik kommt, entsteht
durch Streichen der i. Zeile und k. Spalte, das Vorzeichenschema ist schachbrettartig:
+ − + − + − + − + Definition 7.2.1 (Laplacesche Entwicklung) Sei A eine (n × n)-Matrix, sei 1 ≤ i ≤
n und 1 ≤ k ≤ n. Wir bezeichnen hier mit Aik die (n − 1) × (n − 1)-Matrix, die aus A
durch Streichen der i. Zeile und der k. Spalte entsteht. Damit wird rekursiv definiert:
Entwicklung nach der i. Zeile:
n
X
det A :=
(−1)i+k aik det(Aik )
k=1
Entwicklung nach der i. Spalte:
n
X
(−1)i+k aki det(Aki )
det A :=
k=1
Für (1 × 1)-Matrizen a ist det(a) := a definiert.
Hinweise:
(a) Die Entwicklung nach der i. Zeile und die Entwicklung nach der i. Spalte ergeben
denselben Wert für det(A) für alle i = 1, 2, 3, . . . n.
(b) Für n = 2 und n = 3 ist diese Definition äquivalent zu den bisher gegebenen.
(c) Für große n ist die praktische Berechnung von Determinanten nach dieser Definition
extrem rechenaufwändig. Es wird später eine Methode angegeben, die es ermöglicht,
mit dem Gauß-Verfahren Determinanten großer Matrizen (wenn dies denn aus irgendeinem Grund notwendig und sinnvoll ist), zu berechnen.
Berechnungsbeispiel: (Entwicklung nach der 1. Spalte)
2 −1 0
0 2 −1 0 −1 0
0 −1 2 −1 0 = 2 −1 2 −1 + 1 −1 2 −1 0 −1 2 −1 0 −1 2 0 −1 2 0
0 −1 2 2 −1 −1 0 2 −1 + 1
= 2 2 −1 2 + 1 −1 −1 2 −1 2 = 2(2 · 3 − 2) − 3 = 5
107
Merkregel für die Berechnung des Vektorprodukts:
~
~a × b = = ~e1 a1 b1 ~e2 a2 b2 ~e3 a3 b3 a1 b 1 a1 b 1 a2 b2 ~e + ~e
~e − a3 b 3 1 a3 b 3 2 a2 b 2 3
Beachten Sie, dass dies nur als Merkregel aufzufassen ist, die erste Determinante ist keine
richtige“ Determinante. Die Determinante einer Matrix ist stets ein Skalalar!
”
7.3
Eigenschaften der Determinante
Wir führen hier für die Menge aller (n × n)-Matrizen die Schreibabkürzung
Mn := {A | A ist (n × n)-Matrix}
ein. Die Determinante ist also eine Abbildung
Mn → R,
A 7→ det(A)
mit den Eigenschaften (für alle A ∈ Mn )
(a) det(A) = det(AT ) (dies ist für n = 2 trivial, auf einen Beweis für n > 2 wird hier
verzichtet).
(b) Beim Vertauschen zweier Zeilen ändert det(A) das Vorzeichen.
(c) Beim Vertauschen zweier Spalten ändert det(A) das Vorzeichen.
(d) Addition des Vielfachen einer Zeile zu einer anderen ändert den Wert von det(A)
nicht.
(e) Addition des Vielfachen einer Spalte zu einer anderen ändert den Wert von det(A)
nicht. Geometrisch ist dies für n = 2 die Scherungsinvarianz“ der Fläche eines Pa”
rallelogramms, vergleichen Sie hierzu Hinweis (b) nach Satz 7.1.3 sowie die Abb. 14.
(f) Die Determinante einer oberen Dreiecksmatrix ist leicht zu berechnen:
a11 a12 a13 · · · a1n 0 a22 a23 · · · a2n 0
0
a
·
·
·
a
33
3n
= a11 · a22 · a33 · · · ann
..
..
.. . .
.. .
.
.
.
. 0
0
0 · · · ann (60)
Damit kann — wenn unbedingt nötig — die Determinante einer großen Matrix
berechnet werden, indem man sie durch die Operationen des Gauß-Verfahrens (Addition des Vielfachen einer Zeile zu einer anderen sowie gegebenenfalls Zeilentausch)
in eine obere Dreiecksmatrix überführt und dabei festhält, wie oft ein Zeilentausch
erfolgte.
108
(g) Die Abbildung A 7→ det(A) ist
a11 a12 · · ·
a21 a22 · · ·
.
..
..
.
.
.
.
ak1 ak2 · · ·
.
..
..
..
.
.
a
a
···
n1
n2
linear in jeder
a1n a11
a2n a21
.. ..
. .
+
akn bk1
.. ..
. .
a a
nn
Zeile, also
a12 · · ·
a22 · · ·
..
..
.
.
bk2 · · ·
..
..
.
.
an2
n1
a11
a12
a21
a22
..
..
.
.
=
ak1 + bk1 ak2 + bk2
..
..
.
.
an1
an2
···
···
..
.
···
..
.
···
bkn .. . · · · ann a1n
a2n
..
.
akn + bkn ..
.
a
a1n
a2n
..
.
nn
wobei vorausgesetzt ist, dass sich die beiden Matrizen (links vom Gleichheitszeichen)
nur in der k. Zeile unterscheiden, sowie
a11 a12 · · · a1n a11 a12 · · · a1n a21 a22 · · · a2n a21 a22 · · · a2n .
..
..
.. ..
..
.. .
..
.
.
. .
.
. .
.
für alle t ∈ R
=t·
tak1 tak2 · · · takn ak1 ak2 · · · akn .
.
..
..
.. ..
..
.. ..
..
.
.
.
.
.
. a
a
··· a
a
a
··· a n1
n2
nn
n1
n2
nn
(h) Analog ist die Abbildung A 7→ det(A) linear in jeder Spalte.
(i) det(E) = 1 (E ist die Einheitsmatrix)
(j) det(AB) = det(A) · det(B) für alle A, B ∈ Mn
(k) det(A) = 0 ⇐⇒ Rang(A) < n
(l) det(A) 6= 0 ⇐⇒ A ist invertierbar
(m) det(A) 6= 0 =⇒ det(A−1 ) =
7.4
1
det(A)
Determinanten und Permutationen
Definition 7.4.1 Eine Umordnung der Zahlen (1, 2, 3, 4, . . . n) (alle Zahlen verschieden!)
in eine andere Reihenfolge heißt Permutation. Mathematisch ist eine Umordnung“ eine
”
bijektive Abbildung von
{1, 2, 3, 4, . . . n} → {1, 2, 3, 4, . . . n}
Die Menge aller Permutationen der Zahlen (1, 2, 3, 4, . . . n) wird hier mit Sn bezeichnet.
109
Beispiel: Die Menge aller Permutationen der Zahlen (1, 2, 3) ist
S3 = {(1, 2, 3), (1, 3, 2), (3, 1, 2), (2, 1, 3)(2, 3, 1)(3, 2, 1)}
Dieses Beispiel legt die Frage nahe, wieviel Permutationen es gibt (in Abhängigkeit von
n). Für n = 3 sind es gerade 6 = 3 · 2 Permutationen. Aus einer beliebigen Permutation
(i, k, l) für n = 3 erhält man für n = 4 die Permutationen
(4, i, k, l), (i, 4, k, l), (i, k, 4, l), (i, k, l, 4)
und man kann sich überzeugen, dass man aus allen Permutationen für n = 3 auf diese
Weise alle 4 · 6 = 24 Permutationen für n = 4 erhält. Entsprechend erhält man aus einer
beliebigen Permutation (i, k, l, m) für n = 4 die Permutationen für n = 5
(5, i, k, l, m), (i, 5, k, l, m), (i, k, 5, l, m), (i, k, l, 5, m), (i, k, l, m, 5)
und man erhält auf diese Weise alle 5 · 4 · 3 · 2 = 5! = 120 Permutationen für n = 5. Wir
erhalten so das Ergebnis (genauer Beweis durch vollständige Induktion):
Satz 7.4.1 Für alle n ∈ N+ existieren genau n! verschiedene Permutationen der Zahlen
(1, 2, 3, 4. . . . n).
Vertauschungen nächster Nachbarn sind spezielle Permutationen. Permutationen als bijektive Abbildungen der Zahlen {1, 2, 3, . . . n} in sich können hintereinanderausgeführt
werden. Für n = 3 kann man feststellen, dass jede Permutation durch Hintereinanderausführung von Vertauschungen nächster Nachbarn entsteht:
(1, 2, 3) 7→ (1, 3, 2) 7→ (3, 1, 2) 7→ (3, 2, 1) 7→ (2, 3, 1) 7→ (2, 1, 3)
(61)
Dies gilt für alle Permutationen, also für beliebige n ∈ N+ (ohne Beweis):
Satz 7.4.2 Für alle n ∈ N+ erhält man jede Permutation p ∈ Sn durch Hintereinanderausführung von Vertauschungen nächster Nachbarn. Für jedes p ∈ Sn hängt es nur von p
ab, ob die Anzahl dieser Vertauschungen gerade ist (dann heißt p gerade) oder ungerade
ist (dann heißt p ungerade).
Dies erlaubt für alle n ∈ N+ die Definition der folgenden Funktion σ : Sn → {−1, +1},
p 7→ σ(p):
(
+1 falls p gerade
σ(p) :=
(62)
−1 falls p ungerade
Aus (61) erhalten wir für den Fall n = 3 folgende Wertetabelle für diese Funktion σ:
(1, 2, 3) (1, 3, 2) (3, 1, 2) (3, 2, 1) (2, 3, 1) (2, 1, 3)
p
σ(p)
+1
−1
+1
−1
+1
−1
Eine Permutation p ∈ Sn kann einfach durch die Aufzählung der Bilder der Zahlen
1, 2, 3, . . . n, also in der Form p(1), p(2), p(3), . . . p(n) angegeben werden.
Schauen wir uns die Determinante det(A) für beliebiges A ∈ M3 (mit der Regel von
Sarrus oder durch Laplace-Entwicklung berechnet) nochmal an:
a11 a12 a13 a21 a22 a23 = a11 a22 a33 + a12 a23 a31 + a13 a21 a32 − a13 a22 a31 − a11 a23 a32 − a12 a21 a33
a31 a32 a33 110
Dabei wurden bei den Summanden mit dem −“-Zeichen die Faktoren in der umgekehrten
”
Reihenfolge gegenüber Definition 7.1.2 aufgeschrieben. Es fällt zunächst auf, dass auf der
rechten Seite genau soviel Summanden stehen, wie es Permutationen für n = 3 gibt. In
der Tat kann man alle Summanden in der Form ±a1p(1) a2p(2) a3p(3) schreiben mit p ∈ S3 ,
und das Vorzeichen ist gerade durch σ(p) gegeben. Wir haben also
a11 a12 a13 X
a21 a22 a23 =
σ(p)a1p(1) a2p(2) a3p(3)
a31 a32 a33 p∈S3
Eine entsprechende Aussage ist auch für beliebiges n gültig: (ohne Beweis)
Satz 7.4.3 Sei n ∈ N+ , A eine (n × n)-Matrix und sei σ(p) für p ∈ Sn durch (62)
definiert. Dann gilt
X
det(A) =
σ(p)a1p(1) · a2p(2) · a3p(3) · · · anp(n)
p∈Sn
Hinweis: Auch die Berechnung der Determinante durch Laplace-Entwicklung liefert eine
derartige Summe. Die Berechnung einer Determinante einer (n × n)-Matrix nach der
Definition (ohne die Matrix mit dem Gauß-Verfahren in Dreiecksform zu bringen) führt
also auf eine Summe mit n! Summanden mit jeweils n Faktoren. Aus diesem Grund sind
Verfahren, die die Determinante benutzen, für größere Matrizen ungeeignet.
8
8.1
Eigenwerte
Eigenwerte und Eigenvektoren
Beispiel zur Motivation:
Wir betrachten die lineare Abbildung:
2
2
T :R →R ,
~x 7→ T (~x) = A~x
mit A =
0 1
1 0
Geometrisch ist dies eine Spiegelung (siehe die Abbildung 34). Hier wird die Frage gestellt,
welche Vektoren ihre Richtung beibehalten (oder umkehren). Offensichtlich sind das
(a) die Vektoren in Richtung der Winkelhalbierenden, also Vektoren der Form
u
1
−1
~x =
,
beispielsweise ~x =
oder ~x =
u
1
−1
1
−1
A~x = ~x
für ~x =
und ~x =
1
−1
(b) die Vektoren senkrecht zur Winkelhalbierenden, also Vektoren der Form
u
1
−1
~y =
,
beispielsweise ~y =
oder ~y =
−u
−1
1
1
−1
A~y = −~y = (−1)~y
für ~y =
und ~y =
−1
1
111
Abbildung 34: Spiegelung an der Winkelhalbierenden x1 = x2
Definition 8.1.1 Sei A eine (n × n)-Matrix. Ein Vektor ~x ∈ Rn mit ~x 6= ~0 heißt Eigenvektor (englisch eigenvector) und λ ∈ R (oder λ ∈ C) heißt Eigenwert (englisch
eigenvalue), wenn
A~x = λ~x
λ heißt Eigenwert von A, wenn ein zugehöriger Eigenvektor existiert.
Hinweise:
(a) Wenn ~x Eigenvektor von A ist, dann ist auch t~x Eigenvektor von A für alle t ∈ R
mit t 6= 0, denn
A~x = λ~x =⇒ A(t~x) = tA~x = tλ~x = λ(t~x)
(b) Damit ~x Eigenvektor von A ist, wird verlangt, dass ~x 6= 0, denn es gilt A~0 = 0 · ~0
für alle Matrizen A.
(c) 0 kann jedoch ein Eigenwert von A sein. Nach der Definition ist dies der Fall, wenn
ein Vektor ~x 6= ~0 existiert mit A~x = 0 · ~x = ~0. Also ist 0 genau dann Eigenwert von
A, wenn das homogene lineare Gleichungssystem A~x = ~0 eine nichttriviale Lösung
~x 6= ~0 besitzt, wenn das Gleichungssystem also singulär ist.
(d) Es ist Tradition, dass für Eigenwerte der griechische Buchstabe λ benutzt wird.
Sie können jedoch auch einen anderen lateinischen oder griechischen Buchstaben
benutzen (beispielsweise in der Definition überall λ durch s oder α ersetzen).
Wir können die Bedingung, dass ~x Eigenvektor von A zum Eigenwert λ ist, auch etwas
umformen. Dabei ist E die Einheitsmatrix derselben Größe wie A und ~x 6= ~0.
A~x = λ~x ⇐⇒ A~x = λE~x ⇐⇒ A~x − λE~x = ~0 ⇐⇒ (A − λE)~x = ~0
Also ist λ genau dann Eigenwert von A, wenn die Matrix A − λE nicht invertierbar ist.
Wir haben also
112
Satz 8.1.1 Sei A eine (n × n)-Matrix und E die (n × n)-Einheitsmatrix. Dann ist λ
genau dann Eigenwert von A, wenn
det(A − λE) = 0
Hinweis: Die Gleichung det(A − λE) = 0 heißt charakteristische Gleichung“ von A.
”
Beispiele:
1 1
(a) A =
,
1 2
1 1
1 0
1−λ
1
A − λE =
−λ
=
1 2
0 1
1
2−λ
det(A − λE)q= (1 − λ)(2 − λ) − 1 = 2 − 2λ − λ + λ2 − 1 = λ2 − 3λ + 1 = 0,
√
√
√
also λ = 23 ± 94 − 44 = 23 ± 12 5, λ1 = 32 + 12 5 ≈ 2, 618, λ2 = 23 − 12 5 ≈ 0, 382. Zur
Bestimmung der Eigenvektoren muß für jeden der beiden Werte von λ das homogene
Gleichungssystem (A − λE)x = ~0 gelöst werden, also
1−λ
1
x1
0
=
1
2−λ
x2
0
λ ist so bestimmt worden, dass dieses System singulär ist, daher liefert das GaußVerfahren das äquivalente System (rechnen Sie dies nach!)
1−λ 1
x1
0
=
0
0
x2
0
Die erste Zeile lautet
(1 − λ)x1 + x2 = 0
Die Festlegung x1 = 1 liefert einen Eigenvektor zu λ1 = 32 +
1√
1
~x = 1 1
≈
1, 61
+2 5
2
√
Zu λ2 = 23 − 21 5 erhalten wir einen Eigenvektor
1√
1
~y = 1 1
≈
−0, 618
−2 5
2
1
2
√
5
Beobachtung: Beide Eigenvektoren sind orthogonal:
1 1√ 1 1√
1 5
5)( −
5) = 1 + − = 0
~x · ~y = 1 + ( +
2 2
2 2
4 4
cos ϕ − sin ϕ
cos ϕ − λ − sin ϕ
(b) A =
, A − λE =
sin ϕ cos ϕ
sin ϕ
cos ϕ − λ
det(A − λE)p
= cos2 ϕ − 2λ cos ϕ + λ2 + sin2 ϕ = λ2 − 2 cos(ϕ) · λ + 1 = 0, also
λ = cos ϕ ± cos2 ϕ − 1. Die Matrix beschreibt eine Drehung um den Winkel ϕ
(siehe das Beispiel (a) zu Beginn von Abschnitt 5.3). Es ist daher auch geometrisch
plausibel, dass für ϕ 6= 0 und ϕ 6= π keine reellen Eigenwerte existieren können,
denn bei einer Drehung in der Ebene behält kein Vektor seine Richtung oder kehrt
seine Richtung um (außer für ϕ = 0 oder ϕ = π). Komplexe Eigenwerte hätten
auch komplexe Komponenten für die Eigenvektoren zur Folge. Dies soll hier nicht
behandelt werden.
113
Satz 8.1.2 Sei A eine (n × n)-Matrix und E die (n × n)-Einheitsmatrix. Dann ist
P (x) := det(A − x · E)
(63)
ein Polynom n. Grades. Der Koeffizient von xn ist (−1)n , also hat P (x) die Form
P (x) = b0 + b1 x + b2 x2 + b3 x3 + · · · + (−1)n xn
Hinweis: Das durch (63) definierte Polynom heißt charakteristisches Polynom“.
”
Folgerungen aus Satz 8.1.2:
(a) Die charakteristische Gleichung einer (n × n)-Matrix hat also i.a. n komplexe Lösungen, ihrer Vielfachheit nach gezählt.
(b) Eine (n × n)-Matrix hat höchstens n verschiedene Eigenwerte.
(c) Eine (n × n)-Matrix mit ungeradem n hat mindestens einen reellen Eigenwert, denn
lim P (x) = lim (−1)n xn = −∞ und lim P (x) = lim (−1)n xn = +∞ und
x→∞
x→∞
x→−∞
x→−∞
dazwischen liegt aufgrund des Zwischenwertsatzes mindestens eine reelle Nullstelle.
Weitere Hinweise:
(a) Für gerades n kann es vorkommen, dass eine (n×n)-Matrix keine reellen Eigenwerte
hat. Dies wurde für n = 2 am Beispiel der Matrix deutlich, die eine Drehung um
den Winkel ϕ beschreibt.
(b) Für n ≥ 3 ist es im allgemeinen Fall sehr schwierig, die Eigenwerte durch die Berechnung der Nullstellen des charakteristischen Polynoms zu bestimmen. Für numerische
Verfahren ist es bei großen Matrizen ungünstig, die Eigenwerte durch Berechnung
der Nullstellen des charakteristischen Polynoms zu bestimmen, da der Einfluß von
Rundungsfehlern dann sehr groß ist. Es existieren jedoch numerische Verfahren, die
es erlauben, Eigenwerte auch größerer Matrizen näherungsweise zu berechnen. In
Scilab erhält man durch den Befehl spec(A) alle Eigenwerte der Matrix A zu einem Spaltenvektor zusammengefaßt (siehe auch Abschnitt 6 der Kurzeinführung
”
in Scilab“). Erläuterungen zur Berechnung der Eigenvektoren werden hier später
gegeben.
(c) Da also für n ≥ 3 die Eigenwerte im allgemeinen nur numerisch zu bestimmen sind,
ist es sinnvoll einige allgemeine Aussagen in den folgenden Sätzen zur Verfügung zu
haben.
Satz 8.1.3 Seien λ1 , λ2 , λ3 , . . . λn die n Eigenwerte einer (n × n)-Matrix A, ihrer Vielfachheit als Nullstelle von P (x) = det(A − xE) nach aufgeführt. SpurA sei die Summe
der Diagonalelemente von A, also
n
X
SpurA :=
akk
k=1
Dann gilt
n
X
λk = SpurA
und
λ1 · λ2 · λ3 · · · λn = det(A)
k=1
114
Zum Beweis: Der Beweis der Aussage über SpurA ist etwas schwieriger, der für die
Determinante jedoch einfach: Aufgrund von Satz 8.1.2 gilt für alle x ∈ R
det(A − x · E) = (−1)n · (x − λ1 )(x − λ2 )(x − λ3 ) · · · (x − λn )
Setzt man x = 0, dann erhält man
det(A) = (−1)n (−λ1 )(−λ2 )(−λ3 ) · · · (−λn ) = (−1)2n · λ1 · λ2 · λ3 · · · λn = λ1 · λ2 · λ3 · · · λn
Satz 8.1.4 Sei A eine (2 × 2)-Matrix. Dann lautet ihre charakteristische Gleichung
det(A − xE) = x2 − (SpurA) · x + det(A) = 0
Beweis:
a11 − x
a12
a21
a22 − x
= (a11 − x)(a22 − x) − a21 a12
= x2 − (a11 + a22 )x + a11 a22 − a21 a12
= x2 − (SpurA) · x + det(A)
Satz 8.1.5 Sei A eine symmetrische (n × n)-Matrix mit reellen Matrixelementen, also
AT = A. Dann gilt
(a) Alle Eigenwerte von A sind reell.
(b) Wenn λ1 und λ2 Eigenwerte von A mit den Eigenvektoren ~x und ~y sind und wenn
λ1 6= λ2 , dann gilt ~x ·~y = 0. Die Eigenvektoren zu verschiedenen Eigenwerten sind
also orthogonal.
Beweis:
Aus Gleichung (53) und AT = A folgt die für alle ~x, ~y ∈ Rn gültige Aussage
(A~x) · ~y = ~x · (A~y )
(64)
Dies wird für den Beweis beider Teilaussagen benötigt.
(a) Sei λ = α +jβ ∈ C ein Eigenwert von A mit α, β ∈ R. Den zugehörigen Eigenvektor
bezeichnen wir mit
  

z1
x1 + jy1
 z2   x2 + jy2 
  

~z =  ..  = 
 = ~x + j~y
..
. 

.
zn
xn + jyn
wobei wir davon ausgehen, dass die Komponenten von ~x und ~y reell sind. Um Teilaussage (a) zu beweisen, haben wir nun zu zeigen, dass β = 0. Wir haben
A~z = λ~z = A(~x + j~y ) = (α + jβ)(~x + j~y ) = α~x − β~y + j(β~x + α~y )
= A~x + jA~y
115
Weil die Matrixelemente von A reell sind, folgt daraus
A~x = α~x − β~y
A~y = β~x + α~y
=⇒
=⇒
~y · (A~x) = α~y · ~x − β|~y |2
~x · (A~y ) = β|~x|2 + α~x · ~y
Subtraktion der beiden rechts stehenden Gleichungen und Benutzung von (64) liefert
~x · (A~y ) − ~y · (A~x) = 0 = β(|~x|2 + |~y |2 ) =⇒ β = Im (λ) = 0
denn für einen Eigenvektor gilt stets ~z 6= ~0 und damit |~x|2 + |~y |2 6= 0.
(b)
A~x = λ1~x
A~y = λ2 ~y
=⇒
=⇒
~y · (A~x) = λ1 ~y · ~x
~x · (A~y ) = λ2~x · ~y
Subtraktion der beiden rechts stehenden Gleichungen und Benutzung von (64) liefert
0 = ~x · (A~y ) − ~y · (A~x) = (λ2 − λ1 )~x · ~y =⇒ ~x · ~y = 0
weil laut Voraussetzung λ2 − λ1 6= 0.
Hinweis: Die in Beispiel (a) nach Satz 8.1.1 behandelte Matrix ist symmetrisch. Beide
Eigenwerte sind reell, und es wurde durch explizite Rechnung gezeigt, dass die zugehörigen
Eigenvektoren orthogonal sind.
Satz 8.1.6 Sei A eine (n × n)-Matrix

a11
 0


A= 0
 ..
 .
0
in oberer Dreiecksform, also

a12 a13 · · · a1n
a22 a23 · · · a2n 

0 a33 · · · a3n 

..
.. . .
.. 
. . 
.
.
0
0 · · · ann
Dann sind die Zahlen a11 , a22 , a33 . . . ann die Eigenwerte der Matrix A.
Beweis: Nach (60) lautet die charakteristische Gleichung
det(A − λE) = (a11 − λ)(a22 − λ)(a33 − λ) · · · (ann − λ) = 0
Warnung: Man könnte aufgrund des Satzes auf die Idee kommen, zur Bestimmung der
Eigenwerte eine Matrix mit dem Gauß-Verfahren in obere Dreiecksform zu bringen. Dies
macht keinen Sinn, denn die Operationen des Gauß-Verfahren (Zeilentausch, Addition
des Vielfachen einer Zeile zu einer andern Zeile) ändern die Eigenwerte einer Matrix!
Der folgende Satz stellt eine Zusammenstellung allgemeiner Eigenschaften von Matrizen, Eigenwerten und Eigenvektoren dar:
Satz 8.1.7 Sei A eine (n × n)-Matrix. Dann gilt
(a) A ist genau dann invertierbar, wenn 0 nicht Eigenwert von A ist.
(b) A und AT haben dieselben Eigenwerte.
116
(c) Wenn A invertierbar ist und λ Eigenwert von A mit Eigenvektor ~x ist (wegen (a)
ist λ 6= 0), dann ist λ−1 Eigenwert von A−1 mit demselben Eigenvektor ~x.
(d) Wenn λ Eigenwert von A mit Eigenvektor ~x ist, dann ist für jedes m ∈ N+ λm
Eigenwert der Matrix Am := A · A · · · A (m Faktoren) mit demselben Eigenvektor
~x.
(e) Wenn λ Eigenwert von A mit Eigenvektor ~x ist, dann ist λ + α Eigenwert von
A + αE mit demselben Eigenvektor ~x (E ist die (n × n)-Einheitsmatrix).
Beweis:
(a) A ist nicht invertierbar ⇐⇒ det(A) = 0 ⇐⇒ det(A − 0 · E) = 0 ⇐⇒ 0 ist
Eigenwert von A
(b) det (A − λE)T = det(AT − λET ) = det(AT − λE) = det(A − λE) (siehe (a) in
Abschnitt 7.3), also det(A − λE) = 0 ⇐⇒ det(AT − λE) = 0.
(c) A~x = λ~x =⇒ A−1 A~x = A−1 (λ~x) = λA−1~x = E~x = ~x Multiplikation mit λ−1
liefert A−1~x = λ−1~x.
(d) A~x = λ~x =⇒ AA = A(λ~x) = λ(A~x) = λ · λ~x = λ2~x analog für höhere Potenzen
(ein korrekter Beweis müßte mit vollständiger Induktion erfolgen!)
(e) A~x = λ~x =⇒ (A + αE)~x = A~x + αE~x = λ~x + α~x = (λ + α)~x
Hinweis: Teilaussage (d) ist von entscheidender Bedeutung für die Untersuchung der
Stabilität digitaler Regelungen!
Satz 8.1.8 Seien A und B (n×n)-Matrizen, B sei invertierbar. Dann haben die Matrizen
A und C := B−1 AB dieselben Eigenwerte.
Beweis: Sei A~x = λ~x mit ~x 6= ~0 und sei ~y := B−1~x. Dann gilt
C~y = B−1 AB~y = B−1 ABB−1~x = B−1 AE~x = B−1 A~x = B−1 (λ~x) = λB−1~x = λ~y
Sei umgekehrt C~y = λ~y mit ~y 6= 0 und sei ~x := B~y . Aus C = B−1 AB folgt durch
Multiplikation mit B von links
BC = BB−1 AB = EAB = AB
Multiplikation beider Seiten mit B−1 von rechts liefert A = BCB−1 . Damit erhalten wir
A~x = BCB−1~x = BCB−1 B~y = BCE~y = BC~y = B(λ~y ) = λB~y = λ~x
Hinweis: Der Beweis zeigt darüber hinaus, wie man aus den Eigenvektoren von A die
Eigenvektoren von C bekommt und umgekehrt. Wir werden dies bei späteren Rechnungen
benötigen.
Satz 8.1.9 Sei A eine (n × n)-Matrix und sei B := AT A. Dann hat B nur reelle und
nicht negative Eigenwerte (die Eigenwerte λ von B erfüllen also λ ≥ 0).
117
Beweis: BT = (AT A)T = AT (AT )T = AT A = B (siehe Satz 5.6.1), also ist B symmetrisch und hat nach Satz 8.1.5 nur reelle Eigenwerte. Sei λ ein Eigenwert von B mit
Eigenvektor x. Mit (53) und (AT )T = A erhalten wir
~x · (B~x) = ~x · (AT A~x) = ~x · AT (A~x) = (AT )T~x) · A~x = (A~x) · (A~x) = |A~x|2
= ~x · (λ~x) = λ(~x · ~x) = λ|~x|2 ≥ 0
Dies ist nur möglich, wenn λ ≥ 0, denn ~x 6= ~0 (als Eigenvektor und damit |~x|2 > 0) und
|A~x|2 ≥ 0.
8.2
Vielfachheit von Eigenwerten
Beispiele:
2 0
(a) A =
, die Eigenwerte erhält man aus det(A − λE) = (2 − λ)2 = 0, also
0 2
ist λ = 2 eine zweifache Nullstelle des charakteristischen Polynoms. Jeder Vektor
~x ∈ R2 ist Eigenvektor, und wir haben eine Basis von Eigenvektoren, beispielsweise
{~e1 , ~e2 }.
2 1
(b) B =
, det(B − λE) = (2 − λ)2 = 0 liefert erneut λ = 2 als zweifache
0 2
Nullstelle des charakteristischen Polynoms. Eigenvektoren sind die nichttrivialen
Lösungen ~x 6= ~0 des Gleichungssystems (B − 2 · E)~x = ~0, ausgeschrieben
0x1 + 1x2 = 0;
0x1 + 0x2 = 0
Die Lösungsmenge des Gleichungssystems
ist {~x ∈ R2 | x2 = 0}, und alle Ei t
genvektoren haben die Form ~x =
mit t 6= 0, sind also skalare Vielfache des
0
1
Eigenvektors ~e1 =
.
0
Definition 8.2.1 Sei λ ein Eigenwert der (n × n)-Matrix A. Der Eigenraum zum Eigenwert λ ist
Uλ := {~x ∈ Rn | A~x = λ~x}
Die geometrische Vielfachheit von λ ist die Dimension des Unterraums Uλ (d.h. die
maximale Anzahl linear unabhängiger Vektoren in Uλ ). Die algebraische Vielfachheit
von λ ist die Vielfachheit von x = λ als Nullstelle des charakteristischen Polynoms P (x) =
det(A − x · E).
Hinweise:
(a) Uλ ist tatsächlich ein Unterraum von Rn , seine Elemente sind die Eigenvektoren und
der Nullvektor. Er ist die Lösungsmenge des homogenen linearen Gleichungssystems
(A − λE)~x = ~0.
(b) Beim Beispiel (a) ist für λ = 2 die geometrische und die algebraische Vielfachheit
2, beim Beispiel (b) dagegegen ist für λ = 2 die geometrische Vielfachheit 1 und die
algebraische Vielfachheit 2. Im allgemeinen ist stets die geometrische Vielfachheit
eines Eigenwerts kleiner oder gleich seine algebraische Vielfachheit.
118
8.3
Diagonalisierung von Matrizen
In vielen Situationen möchte man eine Beziehung der Art
y = Ax
durch eine Matrix beschreiben, die einfacher ist als A. Hierzu kann man statt x einen
neuen“ Vektor u benutzen mit der Umrechnung x = Bu, also u = B−1 x. Entsprechend
”
nimmt man v statt y mit y = Bv. Man hat also
y = Ax = ABu = Bv
und damit
v = B−1 ABu
Die neue“ Matrix C entsteht also aus der alten“ durch
”
”
C = B−1 AB
sie hat also nach Satz 8.1.8 dieselben Eigenwerte. Das Ziel in der Praxis ist, durch eine geschickte Wahl von B die Matrix A durch eine einfachere Matrix C zu ersetzen. Besonders
einfach sind Matrizen,
der Hauptdiagonale nur Nullen haben.
die außerhalb
1 2
Beispiel: A =
, mit dem Eigenwert λ1 = 3 und dem zugehörigen Eigenvek2 1
1
1
tor ~u =
sowie dem Eigenwert λ2 = −1 mit dem zugehörigen Eigenvektor ~v =
.
1
−1
Wir stellen uns nun als Aufgabe, eine Matrix B zu konstruieren mit der Eigenschaft
3 0
−1
C = B AB =
(65)
0 −1
Die Matrix C ist einfacher, sie muß dieselben Eigenwerte wie A haben, die Eigenvektoren sind ~e1 und ~e2 . Wenn wir auf diese Weise eine Matrix in Diagonalform bekommen,
dann stehen auf der Hauptdiagonalen die Eigenwerte von A. Der Beweis von Satz 8.1.8
gibt uns einen Hinweis, wie wir die Matrix B konstruieren können: Diese bildet nämlich
die Eigenvektoren von C auf die Eigenvektoren von A ab. Wir wählen also die lineare
Abbildung
T : R2 → R2 ,
~e1 7→ T (~e1 ) = ~u, ~e2 7→ T (~e2 ) = ~v
Damit ist die lineare Abbildung eindeutig festgelegt, denn jeder Vektor ~x ∈ R2 erfüllt
~x = x1~e1 + x2~e2 und damit gilt
T (~x) = T (x1~e1 + x2~e2 ) = x1 T (~e1 ) + x2 T (~e2 ) = x1~u + x2~v
Wir definieren versuchsweise die Matrix B als die Matrix, die T (~x) = B~x für alle ~x ∈ R2
erfüllt. Nach Satz 5.3.2 ( Die Spalten der Matrix sind die Bilder der Einheitsvektoren“)
”
erhalten wir
u1 v1
1 1
B=
=
u2 v2
1 −1
mit det(B) = −2. Mit Satz 7.1.1 können wir die inverse Matrix sofort aufschreiben:
1 1 1
−1
B =
2 1 −1
119
Durch explizites Multiplizieren der Matrizen können wir nun überprüfen, dass wir unser
Ziel tatsächlich erreicht haben und mit dieser Matrix B tatsächlich Gleichung (65) erfüllt
ist. Statt der umständlichen Multiplikation
1 1 1
1 2
1 1
2 1
1 −1
2 1 −1
ist die folgende Rechnung einfacher:
(B−1 AB)~x = (B−1 AB)(x1~e1 + x2~e2 ) = B−1 A(x1 B~e1 + x2 B~e2 ) = B−1 A(x1~u + x2~v )
= B−1 (x1 A~u + x2 A~v ) = B−1 (x1 λ1~u + x2 λ2~v ) = λ1 x1 B−1~u + λ2 x2 B−1~v
= λ1 x1~e1 + λ2 x2~e2
Speziell für ~x = ~e1 und ~x = ~e2 erhalten wir damit
λ1
3
0
0
−1
−1
(B AB)~e1 = λ1~e1 =
=
und
(B AB)~e2 = λ2~e2 =
=
0
0
λ2
−1
Nach der Merkregel Die Spalten der Matrix sind die Bilder der Einheitsvektoren“ erhalten
”
wir das gewünschte Ergebnis
λ1 0
3 0
−1
B AB =
=
0 λ2
0 −1
Für diese Vorgehensweise ist entscheidend, dass ~u und ~v , die beiden Eigenvektoren von
A, linear unabhängig sind (sonst wäre die so konstruierte Matrix B nicht invertierbar).
Für den allgemeinen Fall ist daher der folgende Satz nützlich:
Satz 8.3.1 Sei A eine (n × n)-Matrix. Dann sind die Eigenvektoren zu verschiedenen
Eigenwerten linear unabhängig.
Hinweis zum Beweis: Wir führen den Beweis nur für den Fall von zwei Eigenvektoren,
also für A~u = λ1~u und A~v = λ2~v mit λ1 6= λ2 . Wir haben also zu zeigen, dass die
Gleichung s~u + t~v = ~0 nur für s = t = 0 möglich ist. Multiplikation beider Seiten der
Gleichung mit A, λ1 und λ2 ergibt die drei Gleichungen
λ1 s~u + λ2 t~v = ~0,
λ1 s~u + λ1 t~v = ~0,
λ2 s~u + λ2 t~v = ~0
Zieht man die zweite von der ersten ab, dann erhält man (λ2 − λ1 )t~v = ~0 und damit t = 0.
Subtraktion der dritten von der ersten Gleichung liefert analog s = 0. Auf entsprechende
Weise kann man durch vollständige Induktion beweisen, dass Eigenvektoren ~u1 , ~u2 . . . ~um
mit Eigenwerten λ1 , λ2 , . . . λm stets linear unabhängig sind, wenn die Eigenwerte alle
verschieden sind. Beachten Sie, dass m ≤ n, denn es kann höchstens n verschiedene
Eigenwerte geben.
Definition 8.3.1 Die (n×n)-Matrix A heißt diagonalisierbar, wenn eine invertierbare
Matrix B existiert mit


λ1 0 0 · · · 0
 0 λ2 0 · · · 0 




B−1 AB =  0 0 λ3 · · · 0 
(66)
 ..
..
.. . .
.. 
 .
. . 
.
.
0 0 0 · · · λn
Dabei sind λ1 , λ2 , λ3 . . . λn die Eigenwerte von A (nicht notwendigerweise verschieden)
und in der rechten Matrix stehen außerhalb der Hauptdiagonalen nur Nullen.
120
Satz 8.3.2 Die (n × n)-Matrix A ist genau dann diagonalisierbar, wenn die geometrische
und die algebraische Vielfachheit aller n Eigenwerte übereinstimmen. Jede der folgenden
Bedingungen ist hinreichend dafür, dass die Matrix A diagonalisierbar ist:
(a) Alle n Eigenwerte von A sind algebraisch einfach (also verschieden).
(b) A ist symmetrisch, also AT = A.
Hinweis zum Beweis: Wir beweisen hier nur, dass A diagonalisierbar ist, wenn alle
Eigenwerte verschieden sind. Wir wählen Eigenvektoren ~u1 , ~u2 . . . ~un zu den Eigenwerten
λ1 , λ2 . . . λn und setzen diese Vektoren spaltenweise zur Matrix B zusammen. Die Matrix
B erfüllt also
B~ek = ~uk
für k = 1, 2, . . . n
Nach Satz 8.3.1 sind die Spaltenvektoren linear unabhängig, also ist B invertierbar. Die
inverse Matrix gehört zur Umkehrabbildung, wir haben also
B−1~uk = ~ek
für k = 1, 2, . . . n
Wir haben damit für k = 1, 2, . . . n
(B−1 AB)~ek = B−1 A~uk = B−1 (λk ~uk ) = λk B−1~uk = λk~ek
Nach der Merkregel Die Spalten der Matrix sind die Bilder der Einheitsvektoren“ haben
”
wir damit Gleichung (66) erhalten.
Hinweis: Beachten Sie, dass im Satz ausdrücklich von n Eigenwerten gesprochen wird.
Wenn man sich auf reelle Eigenwerte und reelle Matrixelemente beschränkt, dann ist eine
(n × n)-Matrix A, die weniger als n reelle Eigenwerte besitzt, nicht diagonalisierbar.
Beispiel:


7 1 0
A= 0 7 1 
det(A − λE) = (7 − λ)3
0 0 7
also ist λ = 7 algebraisch dreifacher Eigenwert. Der Eigenraum Uλ ist die Lösungsmenge
des Gleichungssystems (A − 7E)~x = ~0, ausgeschrieben

   
0 1 0
x1
0
 0 0 1  x2  = 0
0
0 0 0
x3
also
x2 = 0, x3 = 0 und
Uλ = {~x ∈ R3 | x2 = x3 = 0} = {t~e1 | t ∈ R},
dim(Uλ ) = 1
und λ = 7 ist geometrisch nur einfacher Eigenwert. Also ist A nicht diagonalisierbar. Dies
kann man hier auch direkt einsehen: Wir nehmen an, es würde eine Matrix existieren mit


7 0 0
B−1 AB =  0 7 0  = 7 · E
0 0 7
Daraus folgt B−1 AB~ek = 7E~ek = 7~ek für k = 1, 2, 3 und daraus erhält man durch
Multiplikation mit B
AB~ek = B(7~ek ) = 7B~ek
121
Dies hieße, dass für die drei Spaltenvektoren ~uk := B~ek gilt A~uk = 7~uk , sie wären also
Eigenvektoren von A. Als Spaltenvektoren einer invertierbaren Matrix sind sie linear
unabhängig. Dies ist im Widerspruch zu den obigen Ergebnissen, dass alle Eigenvektoren
von A skalare Vielfache von ~e1 sind.
Eine entsprechende Überlegung kann man auch im allgemeinen Fall anstellen:
Satz 8.3.3 Wenn die (n × n)-Matrix A diagonalisierbar ist, wenn also eine Matrix B
existiert mit
B−1 AB = D
wobei D eine Matrix ist, bei der auf der Hauptdiagonale die Eigenwerte λk = dkk von A
und außerhalb überall Nullen stehen, dann ist für k = 1, 2 . . . n der k. Spaltenvektor von
B ein Eigenvektor zum Eigenwert λk = dkk .
Hinweis: Aus der Konstruktion der Matrix B im Beweis von Satz 8.3.2 ist klar, dass
die Matrix B nicht eindeutig ist. Man kann beispielsweise in der Konstruktion jeden
Eigenvektor mit einer reellen Zahl tk 6= 0 multiplizieren und erhält dann eine andere
Matrix B, die A diagonalisiert.
In Scilab ist eine solche Matrix B und die Diagonalmatrix D durch das Kommando [D,B]=bdiag(A)] erhältlich. Falls A nicht diagonalisierbar ist, dann ist das an der
Matrix D ersichtlich: diese ist dann nicht diagonal. Wenn in einer Spalte in D außerhalb
der Hauptdiagonale nichtverschwindende Matrixelemente stehen, ist die entsprechende
Spalte von B kein Eigenvektor. Dies ist dann der Fall, wenn die geometrische Vielfachheit eines Eigenwerts kleiner als seine algebraische Vielfachheit ist oder wenn nicht n
reelle Eigenwerte existieren (ihrer Vielfachheit nach gezählt). Nähere Erläuterungen zur
numerischen Berechnung von Eigenwerten und Eigenvektoren stehen in Abschnitt 6 der
Kurzeinführung in Scilab“.
”
9
9.1
Weitere Methoden der Algebra in der Nachrichtentechnik: ein Ausblick
Polynome und Körpererweiterungen
In diesem Unterabschnitt werden einige Vorbereitungen getroffen, die zum Verständnis der
in der modernen Nachrichtentechnik gebräuchlichen Codes notwendig sind. Wir hatten
in der Analysis Polynome als Funktionen der Form f (x) = a0 + a1 x + a2 x2 + · · · + an xn
definiert. Das ist hier nicht allgemein genug, denn wir haben insgesamt nur 4 verschiedene
Funktionen Z22 → Z22 . Wir verstehen unter Polynomen mit Koeffizienten aus einem Körper
K formale Summen der Form
f (X) = a0 + a1 X + a2 X 2 + a3 X 3 + · · · + an X n
mit ak ∈ K
wobei nicht festgelegt ist, aus welcher Menge X sein soll, X steht einfach als Platzhalter.
f heißt Polynom n. Grades, wenn an 6= 0. Wir schreiben dies als grad(f ) = n. Polynome
0. Grades sind die Konstanten a0 6= 0, a0 ∈ K. Dem Nullpolynom f (X) = 0 wird kein
Grad (oder der Grad −1 oder −∞) zugewiesen.
Es werden für die Addition und die Multiplikation von zwei Polynomen die Rechenregeln
aX n + bX n = (a + b)X n , X n X m = X n+m
122
für alle a, b ∈ K und alle m, n ∈ N vereinbart. Mit diesen Rechenregeln ist gewährleistet,
dass die Summe und das Produkt von zwei Polynomen wieder ein Polynom ist (beim
Produkt einfach ausmultiplizieren und nach Potenzen von X sortieren). Ebenso kann
ein Polynom mit einem Element des Körpers K multipliziert werden. Die Menge aller
Polynome mit Koeffizienten in K wird mit K[X] bezeichnet. So sind beispielsweise
f (X) = 1 + X
und
g(X) = 1 + X + X 2
Polynome in Z2 [X], die
f (X)g(X) = (1 + X)(1 + X + X 2 ) = 1 + X + X 2 + X + X 2 + X 3 = 1 + X 3
erfüllen, denn X + X = 1X + 1X = (1 + 1)X = 0X = 0 (beachten Sie 1 + 1 = 0), analog
X 2 + X 2 = 0. Aufgrund der für X n vereinbarten Potenzrechenregel haben wir für das
Produkt von zwei Polynomen
grad(f g) = grad(f ) + grad(g)
Ein Polynom ist gegeben durch den Vektor der Koeffizienten. Zwei Polynome sind also
genau dann gleich, wenn alle Koeffizienten übereinstimmen. Die Summe ist so definiert,
dass die Koeffizientenvektoren komponentenweise zu addieren sind. Wenn sie ungleich
lang sind, dann ist der kürzere Vektor (der zum Polynom mit niedererem Grad gehört)
mit Nullen zu verlängern.
Ein Element t ∈ K heißt Nullstelle des Polynoms f (X) = a0 +a1 X +a2 X 2 +· · ·+an X n ,
wenn f (t) = a0 +a1 t+a2 t2 +· · ·+an tn = 0. In diesem Fall kann (wie in R[X]) ein Polynom
ersten Grades X − t ausgeklammert werden und wir haben
f (X) = (X − t)(b0 + b1 X + b2 X 2 + · · · + bn−1 X n−1 )
und die Koeffizienten bk können mit dem Horner-Schema oder durch Polynomdivision
berechnet werden.
Wenn ein Polynom f (X) ∈ K[X] keine Nullstelle hat, dann kann man sich fragen, ob
man den Körper K geeignet erweitern kann, also einen größeren Körper findet, in dem K
eine Teilmenge ist und in dem f (X) eine Nullstelle hat. Wir sind in R so vorgegangen. Das
Polynom f (X) = 1 + X 2 hat in R keine Nullstelle. Wir haben dann einfach angenommen,
dass in einem größeren Körper eine Nullstelle j existiert, also 1 + j 2 = 0 erfüllt ist.
Aus den Rechenregeln für Körper und dieser Annahme haben wir dann den Körper der
komplexen Zahlen konstruiert als die Menge der Zahlen a + b · j mit a, b ∈ R. Mit der
Gleichung j 2 = −1 kann man dann die bei Produkten auftretenden höheren Potenzen von
j ausrechnen, so dass man in der Tat immer wieder Zahlen der Form x + jy als Ergebnis
der elementaren Rechenoperationen bekommt.
Wir haben bei den Restklassen Zn gesehen, welche Rechenregel problematisch ist,
wenn man in einer Menge eine Addition und Multiplikation definiert hat und sich fragt,
ob ein Körper entstanden ist: es ist die Auflösbarkeit von Gleichungen der Form ax = 1
nach x. Ein unüberwindbares Hindernis sind hierfür Elemente mit ab = 0 und a 6= 0 und
b 6= 0. Bei der Konstruktion von C ging alles gut, denn wir haben (durch Erweitern mit
dem konjugiert Komplexen des Nenners) explizit eine Lösung z = x + jy von wz = 1 bei
gegebenem w 6= 0 konstruiert.
Im allgemeinen Fall ist ein wichtiges Ergebnis, dass eine derartige Konstruktion zur
Erweiterung eines Körpers erfolgreich ist, wenn das Polynom f (X) nicht auf nichttriviale
123
Weise in ein Produkt zerlegbar ist. Jedes Polynom kann in trivialer Weise
als Produkt
−1
geschrieben werden durch f (X) = 1 · f (X) oder f (X) = a · a f (X) mit a ∈ K. Eine
Zerlegung als Produkt ist also nichttrivial, wenn jeder der Faktoren einen Grad hat, der
echt kleiner als der von f (X) ist. Eine ähnliche Situation hat man auch bei Zahlen. Zahlen,
die nicht in nichttrivialer Weise als Produkt zerlegbar sind, sind Primzahlen. Entscheidend
für den Erfolg der Konstruktion von C ist also, dass f (X) = 1 + X 2 in R[X] nicht als
nichttriviales Produkt von zwei Polynomen schreibbar ist.
Nach diesen Vorbereitungen können wir uns Erweiterungen des Körpers Z2 zuwenden,
die bei der Kanalkodierung eine wichtige Rolle spielen.
Beispiele für Erweiterungen von Z2 :
(a) Das Polynom f (X) = X 2 + X + 1 hat in Z2 keine Nullstelle. Dies ist einfach
nachzuprüfen, denn Z2 hat nur 2 Elemente: f (0) = 1, f (1) = 1 + 1 + 1 = 1. Es
hat den Grad 2. Wenn man es als Produkt von zwei Polynomen niedereren Grades
f (X) = f1 (X)f2 (X) schreiben könnte, dann hätten die Faktoren zwangsläufig beide
den Grad 1. Die einzigen Polynome vom Grad 1 in Z2 [X] sind X und 1 + X und
beide haben eine Nullstelle. Also kann f (X) tatsächlich nicht als nichttriviales Produkt zweier Polynome in Z2 [X] geschrieben werden. Wir können unser erfolgreiches
Konzept zur Konstruktion von C hier anwenden. Wir führen als Element α eines zu
konstruierenden größeren Körpers eine Nullstelle von f (X) ein (analog zu j). Wir
haben dann für dieses α die Rechenregel
f (α) = α2 + α + 1 = 0
oder
α2 = 1 + α
Dabei haben wir nach α2 aufgelöst, indem wir α + 1 auf beiden Seiten addiert
haben. Damit können wir in Produkten höhere Potenzen von α ersetzen. Unser
neuer, größerer Körper ist damit explizit
K = GF(4) := {0, 1, α, 1 + α}
Die Bezeichnungsweise gibt an, dass er 4 Elemente hat. Mit den Rechenregeln für
Körper und α2 = 1 + α bekommen wir als Vorbereitung für die Additions- und
Multiplikationstabelle:
α + α = (1 + 1)α = 0
(1 + α)(1 + α) = 1 + α + α + α2 = 1 + α2 = 1 + 1 + α = α
α3 = α2 · α = (1 + α) · α = α + α2 = α + 1 + α = 1
Als Ergebnis erhalten wir die Tabellen
0
1
α
1+α
+
0
0
1
α
1+α
1
1
0
1+α
α
α
1+α
0
1
α
1+α 1+α
α
1
0
·
0
1
α
1+α
0
1
α
1+α
0
0
0
0
0
1
α
1+α
0
α
1+α
1
0 1+α
1
α
Aufgrund der Rechenregel α2 = 1 + α können wir auch schreiben
K = GF(4) = {0, 1, α, α2 }
124
und wir haben bereits α3 = 1 ausgerechnet. Als weitere Nullstelle unseres Ausgangspolynoms f (X) = X 2 + X + 1 kommt nur α2 = 1 + α infrage. Durch Nachrechnen
erhält man in der Tat
f (α2 ) = α4 + α2 + 1 = α3 · α + 1 + α + 1 = α + α = 0
Wenn wir es als Polynom in GF(4)[X] auffassen, dann können wir es als Produkt
schreiben
f (X) = (X − α)(X − α2 )
Aus der Multiplikationstabelle ist direkt sichtbar, dass für jedes a ∈ GF(4) mit
a 6= 0 die Gleichung ax = 1 eine eindeutige Lösung x ∈ GF(4) besitzt.
(b) Dasselbe Spiel nochmal mit g(X) = X 3 + X + 1. Wir haben in Z2 keine Nullstelle,
denn g(0) = 1, g(1) = 1+1+1 = 1. Wir haben grad(g) = 3, bei einem nichttrivialen
Produkt g(X) = g1 (X)g2 (X) müsste mindestens einer der beiden Faktoren Grad 1
und damit eine Nullstelle haben. Also existiert keine nichttriviale Zerlegung in ein
Produkt. Wir erweitern den Körper Z2 um eine Nullstelle β dieses Polynoms und
haben damit zusätzlich zu den Körperaxiomen die Rechenregel
β3 + β + 1 = 0
oder
β3 = 1 + β
Wir können also alle Potenzen β n mit n ≥ 3 ausdrücken durch Polynome höchstens
zweiten Grades in β. Unser neuer Körper besteht also aus Elementen der Form
a0 + a1 β + a2 β 2
mit ak ∈ Z2
Jedes Element aus diesem Körper ist durch die drei Zahlen a0 , a1 , a2 mit ak = 0 oder
ak = 1 charakterisiert, und wir haben insgesamt 23 = 8 verschiedene Elemente. Der
Körper heißt daher GF(8). Es ist vorteilhafter, die Elemente durch Potenzen von β
zu charakterisieren. Mit Hilfe der definierenden Rechenregel β 3 = 1 + β erhalten wir
β4
β5
β6
β7
=
=
=
=
β · β3
β · β4
β · β5
β · β6
= β(β + 1) = β 2 + β
= β(β 2 + β) = β 3 + β 2 = β 2 + β + 1
= β(β 2 + β + 1) = β 3 + β 2 + β = β 2 + β + β + 1 = β 2 + 1
= β(β 2 + 1) = β 3 + β = 1 + β + β = 1
Wir können daher schreiben
GF(8) = {0, 1, β, β 2 , β 3 β 4 , β 5 , β 6 }
und haben die Additions- und Multiplikationstabelle
+
0
1
β
β2
β3
β4
β5
β6
0
0
1
β
β2
β3
β4
β5
β6
1
1
0
β3
β6
β
β5
β4
β2
β
β
β3
0
β4
1
β2
β6
β5
β2
β2
β6
β4
0
β5
β
β3
1
β3
β3
β
1
β5
0
β6
β2
β4
β4
β4
β5
β2
β
β6
0
1
β3
β5
β5
β4
β6
β3
β2
1
0
β
β6
β6
β2
β5
1
β4
β3
β
0
125
·
0
1
β
β2
β3
β4
β5
β6
0
0
0
0
0
0
0
0
0
1
0
1
β
β2
β3
β4
β5
β6
β
0
β
β2
β3
β4
β5
β6
1
β2
0
β2
β3
β4
β5
β6
1
β
β3
0
β3
β4
β5
β6
1
β
β2
β4
0
β4
β5
β6
1
β
β2
β3
β5
0
β5
β6
1
β
β2
β3
β4
β6
0
β6
1
β
β2
β3
β4
β5
Durch Nachschauen in den Tabellen kann man sich überzeugen, dass die Gleichung
a + x = 0 für alle a ∈ GF(8) eine eindeutige Lösung x = −a = a hat, und entsprechend für alle a 6= 0 die Gleichung ax = 1 eine eindeutige Lösung x = a−1 hat. Wir
haben β als Nullstelle des Polynoms g(X) = X 3 + X + 1 unserem Körper hinzugefügt. Für die Beurteilung von Codes, die mit diesem Polynom erzeugt werden, ist
es von Interesse, zu überprüfen, welche höheren Potenzen von β ebenfalls Nullstellen
sind. Nachrechnen ergibt
g(β 2 ) = β 6 + β 2 + 1 = 1 + 1 = 0
g(β 3 ) = β 18 + β 3 + 1 = β 4 + β = β 2 6= 0
Durch Polynomdivision oder mit dem Horner-Schema kann man die vollständige
Zerlegung in Linearfaktoren
g(X) = (X + β)(X + β 2 )(X + β 4 )
und damit die dritte Nullstelle β 4 erhalten.
Bei Codes, die durch Polynome in Z2 [X] erzeugt werden, erhält man über derartige Erweiterungskörper eine bessere Einsicht, so wie es oft vorteilhaft ist, in C statt in R zu
arbeiten.
9.2
Zyklische Codes
Sehr viele in der Praxis nützliche Codes sind zyklische Codes.
Definition 9.2.1 Ein Code C heißt zyklisch, wenn
c = (c0 , c1 , c2 , . . . cn−1 ) ∈ C =⇒ (cn−1 , c0 , c1 , . . . cn−2 ) ∈ C
wenn also die zyklische Vertauschung eines Codewortes stets wieder ein Codewort liefert.
Zyklische Vertauschungen kann man sehr leicht mit Hilfe von Polynomen beschreiben.
Jedem Vektor c = (c0 , c1 , c2 , . . . cn−1 ) ∈ Zn2 kann man eindeutig das Polynom höchstens
(n − 1). Grades c0 + c1 X + c2 X 2 + · · · + cn−1 X n−1 zuordnen, umgekehrt kann man jedem
Polynom höchstens (n − 1). Grades den Vektor c ∈ Zn2 der Koeffizienten zuordnen. Bei
Polynomen erreicht man eine Verschiebung der Koeffizienten durch eine Multiplikation
mit X, denn
X · (c0 + c1 X + c2 X 2 + · · · + cn−1 X n−1 ) = c0 X + c1 X 2 + c2 X 3 + · · · + cn−1 X n
Dabei wird jedoch der Grad des Polynoms um 1 erhöht, und man fügt eine 0 als Koeffizienten von X 0 ein. Eine zyklische Vertauschung erhält man, wenn man die Regel“
”
X n = 1 vereinbart. Dann erhält man durch Multiplikation mit X das neue Polynom
cn−1 + c0 X + c1 X 2 + c2 X 3 + · · · cn−2 X n−1 , man bekommt also tatsächlich die gewünschte
zyklische Vertauschung.
Schauen wir uns einmal an, was die Anwendung dieser Regel bei beliebigen Polynomen
bewirkt. Diese Regel bedeutet, dass wir das Polynom X n −1 als das Nullpolynom ansehen.
Wenn wir also von einem gegebenen Polynom X n − 1 abziehen, dann sehen wir das
neue Polynom als dasselbe wie das ursprüngliche an, und wir können dies auch mehrfach
durchführen. Wenn f (X) ein beliebiges Polynom ist, dann haben wir auch das Produkt
126
f (X)·(X n −1) als das Nullpolynom anzusehen. Mit Hilfe des Divisionsalgorithmus können
wir jedes beliebige Polynom schreiben als
p(X) = q(X) · (X n − 1) + r(X)
Dabei ist r(X) der Rest bei der Division, sein Grad ist kleiner als n, also höchstens
n − 1. Mit Hilfe dieser Regel können wir also aus der Menge aller Polynome die Menge
der Polynome höchstens n. Grades erzeugen, und die Anwendung dieser Regel bedeutet
nichts anderes als die Bildung des Rests bei Division durch X n − 1. Mathematisch wird
die auf diese Weise erzeugte Menge aller Polynome höchstens (n − 1). Grades mit der
Polynommultiplikation und anschließender Bildung des Restes mit dem Symbol
K[X]/hX n − 1i
bezeichnet.
Diese Vorgehensweise sollte Ihnen eigentlich bekannt vorkommen. Im Unterabschnitt 6.1
erhielten wir die Menge Zn aus der Menge der ganzen Zahlen mit Hilfe der Regel“
”
n≡0
(mod n)
Addition und Multiplikation sind so definiert, dass stets der Rest bei Division durch
n zu bilden ist. Wir sehen also in Zn die Zahlen n, −n, 2n, −2n als 0 an, so wie wir
hier alle Vielfache von X n − 1 als Nullpolynom ansehen. Bezeichnet man die Menge der
ganzzahligen Vielfachen von n mit nZ, dann kann man
Zn = Z/nZ
schreiben.
Schauen wir uns nun an, wie diese Überlegungen nutzbringend bei der Codierung
einzusetzen sind. Wir betrachten als Beispiel den Code, der durch die Prüfmatrix


1 0 0 1 0 1 1
H = 0 1 0 1 1 1 0
0 0 1 0 1 1 1
beschrieben wird. Aus den Überlegungen von Unterabschnitt 6.3 folgt, dass wir Codeworte von 7 Bits und Datenworte von 4 Bits haben. Aus dieser Form der Prüfmatrix
ist überhaupt nicht klar, wie sie konstruiert wurde. Hierzu haben wir Methoden des
Unterabschnitts 9.1 anzuwenden. Jedem Vektor a = (a0 , a1 , a2 ) können wir das Element a0 + a1 β + a2 β 2 ∈ GF (8) zuordnen, wobei wir mit β die Nullstelle des Polynoms g(X) = 1 + X + X 3 bezeichnet haben. Beachten Sie, dass wir dabei die Regel“
”
1 + β + β 3 = 0 benutzt haben. In der hier eingeführten Schreibweise bedeutet dies, dass
wir die Konstruktion
GF (8) = Z2 [X]/h1 + X + X 3 i
benutzt haben. Wenn wir nun jeden Spaltenvektor a von H als Polynom a0 + a1 β + a2 β 2
ansehen und die in Unterabschnitt 9.1 aufgestellten Regeln für die höheren Potenzen von
β benutzen, dann können wir die Prüfmatrix schreiben als
H = 1 β β2 β3 β4 β5 β6
127
Die Prüfbedingung cHT = 0 kann dann ebenfalls ganz einfach geschrieben werden, wenn
man dem Codewort c = (c0 , c1 , c2 , . . . c6 ) das Codewort-Polynom
c(X) = c0 + c1 X + c2 X 2 + · · · + c6 X 6
zuordnet. Dann lautet die Prüfbedingung c(β) = 0. Ein beliebiges Polynom höchstens 6.
Grades ist also genau dann ein Codewort-Polynom, wenn es eine Nullstelle in β hat. An
dieser Bedingung sieht man sofort, dass es sich hier um einen zyklischen Code handelt.
Hierzu sehen wir die Menge der beliebigen Polynome höchstens 6. Grades an als beliebige
Polynome mit der Regel X 7 = 1. Beachten Sie, dass das Element β ∈ GF (8) ebenfalls
dieser Regel genügt, also β 7 = 1 erfüllt.
Für die Praxis sollte man allerdings noch wissen, wie man die Codeworte aus den
Datenworten erzeugt. Hierzu hat man zu beachten, dass
X 7 − 1 = g(X) · h(X) mit g(X) = (1 + X + X 3 ) und h(X) = (1 + X + X 2 + X 4 )
(rechnen Sie dies durch Ausmultiplizieren nach). Im allgemeinen hat man eine Zerlegung
der Art
X n − 1 = g(X) · h(X)
wobei Grad g(X) = n − k und Grad h(X) = k. Unser Beispielcode geht von Datenworten der Länge 4 Bit, also a = (a0 , a1 , a2 , a3 ) ∈ Z42 aus. Jedem solchen Datenwort kann
man das Polynom a0 + a1 X + a2 X 2 + a3 X 3 zuordnen. Der Körper GF (8) wurde so konstruiert, dass wir β als Nullstelle von g(X) dazugenommen haben, also g(β) = 0. Jedes
Codewort-Polynom c(X) muss c(β) = 0 erfüllen. Dies könnte man erreichen, indem man
zur Codierung das Datenpolynom mit g(X) multiplizieren:
a(X) · g(X) = (a0 + a1 X + a2 X 2 + a3 X 3 ) · (1 + X + X 3 )
Ausmultiplizieren ergibt
a(X)·g(X) = a0 +(a0 +a1 )X +(a1 +a2 )X 2 +(a0 +a2 +a3 )X 3 +(a1 +a3 )X 4 +a2 X 5 +a3 X 6
Dem Datenwort (1, 0, 0, 0) würde das Polynom g(X) = (1 + X + X 3 ) und damit das
Datenwort (1, 1, 0, 1, 0, 0, 0) zugeordnet. Die Decodierung müsste mit Hilfe einer Division
durch g(X) erfolgen. Dies ist jedoch unpraktisch. Erwünscht ist stattdessen, dass den 4
Bits des Datenworts 4 unveränderte Datenbits und 3 zusätzliche Prüfbits entsprechen.
Wenn die Prüfbedingung erfüllt ist, möchte man das Codewort einfach durch Weglassen
der drei Prüfbits decodieren.
Dies kann man hier erreichen, indem man die k Datenbits um die Zahl (n − k) der
Prüfbits verschiebt und dann die Prüfbits geeignet setzt. Bei den Polynomen erreicht
man eine Verschiebung der Koeffizienten durch Multiplikation mit X n−k . Als CodewortPolynom wird also
c(X) = X n−k a(X) + t(X)
gewählt. Dabei legt das Polynom t(X) die Prüfbits, also die ersten (n − k) Bits, fest. Es
ist also ein Polynom höchstens (n − k − 1). Grades. Man hat es so zu wählen, dass c(X)
ein Vielfaches von g(X) ist. In Analogie zur Definition 6.1.1 schreiben wir bei Polynomen
f1 , f2 , q, p
f1 (X) = f2 (X) mod q(X) ⇐⇒ f1 (X) − f2 (X) = p(X) · q(X)
128
also f1 (X) = f2 (X) mod q(X) genau dann, wenn f1 (X) und f2 (X) bei Division durch q
denselben Rest ergeben. Der Divisionsalgorithmus von Polynomen liefert bei Division von
f (X) durch q(X) den Rest als das eindeutige Polynom r(X), dessen Grad kleiner als der
des Quotienten q(X) ist und das
f (X) = r(X) mod q(X)
erfüllt. Mit dieser Schreibweise können wir die Forderung, dass das Polynom c(X) ein
Vielfaches von g(X) ist, formulieren als
c(X) mod g(X) = (X n−k a(X) + t(X) mod g(X) = 0
Daraus erhalten wir die Bedingung
t(X) mod g(X) = − X n−k a(X) mod g(X)
Da Grad t(X) < (n − k) gefordert wird, können wir t(X) aus der Berechnung des
Restes bei der Polynomdivision von X n−k a(X) durch g(X) bekommen. Für unser Beispiel
mit n = 7 und k = 4 erhalten wir für ein beliebiges Datenwort a0 , a1 , a2 , a3 mit dem
zugehörigen Polynom a(X) = a0 + a1 X + a2 X 2 + a3 X 3 mit Hilfe des Divisionsalgorithmus
X 3 a(X) = a0 + a2 + a3 + (a1 + a3 )X + a2 X 2 + a3 X 3 · 1 + X + X 3 ) + t(X)
mit
t(X) = a0 + a2 + a3 + (a0 + a1 + a2 )X + (a1 + a2 + a3 )X 2
Die Codierung
c(X) = X 3 a(X) + t(X)
kann dann in der Schreibweise der Kanalcodierung
worte c durch c = aG mit der Generatormatrix

1 1 0 1 0
0 1 1 0 1
G=
1 1 1 0 0
1 0 1 0 0
für die Datenworte a und die Code0
0
1
0

0
0

0
1
beschrieben werden. Überprüfen Sie durch explizite Rechnung, ob die Bedingung GHT =
0 erfüllt ist! Die Tatsache, dass es sich hier um einen zyklischen Code handelt, ist aus
der Generatormatrix nicht sofort ersichtlich. Das Codewort zu a = (0, 1, 0, 0) steht in
der zweiten Zeile von G und entsteht durch zyklische Vertauschung des Codewortes zu
a = (1, 0, 0, 0). Das Codewort, das durch zyklische Vertauschung aus der zweiten Zeile
entsteht, steht jedoch in keiner Zeile von G. Man erhlält es als Summe der ersten und der
dritten Zeile von G
(0, 0, 1, 1, 0, 1, 0) = (1, 1, 0, 1, 0, 0, 0) + (1, 1, 1, 0, 0, 1, 0)
Es ist daher Codewort von a = (1, 0, 1, 0). Durch einen Übermittlungsfehler beim k. Bit
entstehen Worte der Form
v = c + ek = aG + ek
wobei hier ek den Zeilenvektor bezeichnet, der als k. Komponente 1 und sonst überall
Nullen hat. Für jedes empfangene Wort v wird das Syndrom s von v gebildet:
s = vHT
129
Bei einem Übermittlungsfehler im k. Bit erhalten wir als Syndrom
s = (aG + ek )HT = ek HT
T
erhalten wir in diesem Fall also als Syndrom den k.
Aufgrund von ek HT = (HeT
k)
Spaltenvektor von H als Zeilenvektor geschrieben. Es wurde schon früher festgestellt, dass
ein solcher Fehler erkannt werden kann, wenn kein Spaltenvektor von H der Nullvektor
ist. Er kann korrigiert werden, wenn alle Spaltenvektoren von H verschieden sind.
Wie an diesem Beispiel sichtbar wird, kann der Code selbst zwar mit Hilfe der Matrizen
H und G mit Elementen aus den Vektorräumen Z42 und Z72 beschrieben werden. Verstehen
kann man ihn jedoch erst, wenn man Daten- und Codeworte durch die entsprechenden
Polynome beschreibt und die Körpererweiterung GF (8) benutzt. Die Nützlichkeit dieser
Körpererweiterungen wird noch deutlicher sichtbar, wenn man zyklische Codes konstruiert, bei denen mehr als ein Fehler korrigiert werden kann. Hierzu wird auf die Literatur
verwiesen.
130
10
10.1
Näherungen
Näherungslösungen für überbestimmte Gleichungssysteme
Abbildung 35: Infolge von Messfehlern liegen die Messpunkte nicht auf der Geraden, auf
der sie nach den physikalischen Gesetzen liegen sollten, z.B. x = I, y = U in der rechts
abgebildeten Schaltung.
Schauen wir uns das in der Analysis ebenfalls behandelte praktische Beispiel an. Die
physikalische Größe y hängt — in vielen Anwendungen — linear von der Größe x ab
(Beispiel x = I, y = U in der in Abb, 35 rechts abgebildeten Schaltung). Es gilt also
ein Gesetz der Form y = ax + b. Die beiden Unbekannten a und b können aus zwei
Paaren von Messwerten berechnet werden. Dann hat man zwei Gleichungen der Form
xk · a + b = yk . Mehr als zwei Paare von Messwerten liegen aufgrund von Messfehlern
nicht exakt auf der durch das lineare Gesetz beschriebenen Geraden. Dann hat man mehr
als zwei Gleichungen für die beiden Unbekannten und damit im allgemeinen ein unlösbares
überbestimmtes lineares Gleichungssystem. Wir wollen dieses Gleichungssystem hier mit
den Methoden der Linearen Algebra behandeln. Wir haben also für die Unbekannten a
und b ein Gleichungssystem der Form
x1 · a + b
x2 · a + b
x3 · a + b
..
.
= y1
= y2
= y3
.
= ..
xn · a + b = y n
mit n > 2. Mit Hilfe der Matrix A und den Vektoren c und z mit


 
x1 1
y1
 x2 1
 y2 


 
a
 x3 1
 y3 
A=
c= 
und
z=
,
b
 .. .. 
 .. 
 . .
.
xn 1
yn
können wir es in der gewohnten Form schreiben
Az = c
oder
131
Az − c = 0
Um zur gewohnten Schreibweise zurückzukehren, schreiben wir x statt z und b statt c:
Ax − b = 0
Wir wollen allgemein eine (n×m)-Matrix mit n > m zulassen (im Beispiel ist also m = 2).
Dann ist x ein Spaltenvektor mit m Komponenten und Ax und b sind Spaltenvektoren mit
n Komponenten; die Matrix A hat mehr Zeilen als Spalten, also die Form eines Rechtecks
im Hochformat“. Entsprechende Gleichungssysteme wurden bereits in Abschnitt 3.4.2
”
behandelt. Da wir das Gleichungssystem z.B. aufgrund von Messfehlern nicht exakt lösen
können, wollen wir stattdessen einen Vektor x so suchen, dass
|Ax − b|
minimal ist. Da die Wurzelfunktion [0, ∞[→ R, x 7→
ist dies äquivalent dazu, dass die Funktion
g : Rm → R,
√
x streng monoton wachsend ist,
x 7→ g(x) = |Ax − b|2 = (Ax − b) · (Ax − b)
minimal ist. Dabei ist mit · das Skalarprodukt gemeint. Da
(Ax − b) · (Ax − b) = (Ax) · (Ax) − 2b · (Ax) + b · b
und b · b konstant ist, ist dies wiederum äquivalent dazu, dass
f : Rm → R,
x 7→ f (x) = (Ax) · (Ax) − 2b · (Ax)
minimal ist. Man kann sich davon überzeugen, dass unsere früher behandelte Rechenregel
für transponierte Matrizen (53) auch für rechteckige“ (n×m)-Matrizen gilt (man benötigt
”
bei der Herleitung nicht, dass A eine quadratische Matrix ist). Also haben wir hier
u · (Av) = (AT u) · v
für alle Vektoren u ∈ Rn und v ∈ Rm . Wir können damit unsere Funktion f (x) etwas
anders schreiben. Wir suchen also das Minimum der Funktion
f (x) = (Ax) · (Ax) − 2b · (Ax) = (AT Ax) · x − 2(AT b) · x = x · (AT Ax) − 2x · (AT b)
Die Lösung liefert der folgende
Satz 10.1.1 Sei A eine (n × m)-Matrix, b ∈ Rn , sei f : Rm → R durch
f (y) = y · (AT Ay) − 2y · (AT b)
definiert und sei x ∈ Rm eine Lösung des linearen Gleichungssystems
AT Ax = AT b
Dann gilt für alle y ∈ Rm
f (y) ≥ f (x)
132
Beweis: Wir haben
(y − x) · AT A(y − x) = A(y − x) · A(y − x) = |A(y − x)|2 ≥ 0
(67)
und für die Lösung x von AT Ax = AT b
f (y) − f (x) = y · (AT Ay) − 2y · (AT b) − x · (AT Ax) + 2x · (AT b)
= y · (AT Ay) − 2y · (AT b) − x · (AT b) + 2x · (AT b)
= y · (AT Ay) − 2y · (AT b) + x · (AT b)
(68)
Weil (AT A)T = AT A, gilt außerdem für die Lösung x von AT Ax = AT b
(y − x) · AT A(y − x) = y · (AT Ay) + x · (AT Ax) − x · (AT Ay) − y · (AT Ax)
= y · (AT Ay) − 2y · (AT Ax) + x · (AT Ax)
= y · (AT Ay) − 2y · (AT b) + x · (AT b)
(69)
Vergleich von (67), (68) und (69) liefert
f (y) − f (x) = (y − x) · AT A(y − x) ≥ 0
Folgerung:
Für ein überbestimmtes Gleichungssystem Ax − b ist |Ax − b|2 minimal, wenn
AT Ax = AT b.
Der Vorteil ist, dass AT A eine m × m-Matrix, also eine quadratische Matrix ist. Wir
können also versuchen, das Gleichungssystem AT Ax = AT b nach dem Gauß-Verfahren
zu lösen.
Kehren wir zurück zu unserem Anwendungsbeispiel. Dort ist m = 2, und wir haben
 n

n
P 2 P
xk 
 xk
k=1
k=1

AT A = 
n
P

xk
n
k=1
und

n
P

 xk yk 
k=1

A b=
n
 P

yk
T
k=1
und wir erhalten für die beste Näherung für die Parameter a und b in der Geradengleichung
y = ax + b die Lösung des Gleichungssystems
 n

 n

n
P 2 P
P
k=1 xk k=1 xk  a
k=1 xk yk 
 n

 n

P
 b = P

xk
n
yk
k=1
k=1
Die Lösung ist im Analysis-Skript ausführlich diskutiert.
Die Vorteile der hier angewandten Methode sind, dass wir keine Ableitungen benötigen,
dass wir automatisch mitgeliefert bekommen, dass wir ein Minimum erhalten und dass sich
diese Methoden leicht auf andere Probleme übertragen lassen, die beispielsweise größere
überbestimmte Gleichungssysteme liefern.
133
10.2
Beste Näherung durch Vektoren aus einem Unterraum
In der Analysis hatten wir das Problem untersucht, eine beliebige stückweise stetige mit
der Periode T periodische Funktion f (t) möglichst gut anzunähern durch trigonometrische
Polynome. Wir haben dort Koeffizienten c0 , ak und bk so bestimmt, dass die Näherung
f (t) ≈ Pm (t) = c0 +
+
+
+
+
a1 cos(ωt) + b1 sin(ωt)
a2 cos(2ωt) + b2 sin(2ωt)
a3 cos(3ωt) + b3 sin(3ωt)
···
am cos(mωt) + bm sin(mωt)
möglichst gut ist. Möglichst gut“ heißt dabei, dass das Quadrat des Abstands
”
ZT
2
f (t) − Pn (t) dt
kf − Pm k2 =
0
ein Minimum annimmt. Wir haben hierzu die partiellen Ableitungen dieses Quadrats
des Abstands berechnet und diese Null gesetzt. Dies ist sehr aufwändig, und es ist verblüffend, wie man mit Mitteln der Linearen Algebra sehr viel einfacher und schneller zu
den gewünschten Gleichungen kommt. Und das ist interessant, weil eine derartige Vorgehensweise in vielen andern Zusammenhängen angewandt wird. Sie kann nämlich leicht
auf andere Beispiele angewandt werden.
Wir gehen davon aus, dass die Menge der Funktionen, die approximiert werden sollen,
einen Vektorraum V bilden. In unserem Beispiel sind dies periodische Funktionen, die
stückweise (d.h. bis auf einzelne Ausnahmestellen in einer Periode) stetig sind. Addition
und Multiplikation derartiger Funktionen mit einem Skalar ergibt wieder eine stückweise
stetige Funktion. Der Nachteil dieses Vektorraums ist, dass er zu groß“ ist, und wir
”
würden lieber mit einfacheren Funktionen arbeiten, die man als Linearkombination endlich vieler besonders einfacher Funktionen darstellen kann, in unserem Beispiel sind dies
trigonometrische Polynome, also Linearkombinationen von
fk (t) = cos(kωt); k = 0, 1, 2, 3, . . . m sowie gk (t) = sin(kωt); k = 1, 2, 3, . . . m
(70)
In der Sprache der Linearen Algebra heißt dies, wir wollen in einem Unterraum U ⊂ V
bleiben, der aus Linearkombinationen vorgegebener besonders einfacher Vektoren besteht.
Dies bedeutet, wir kennen die Basis. Wir wollen hier von den unwichtigen eher störenden
Einzelheiten des konkreten Beispiels absehen (abstrahieren) und uns auf die wesentlichen
Dinge beschränken. Der Unterraum U hat also eine Basis, und wir nehmen an, dass diese
Basis aus endlich vielen Vektoren besteht, die wir nun mit u1 , u2 , u3 , . . . un bezeichnen.
Für unser Beispiel der trigonometrischen Polynome müssen wir eine Umnumerierung vornehmen in der Form n = 2m + 1 sowie
u1 = f0 , u2 = f1 , . . . um+1 = fm ,
um+2 = g1 , um+3 = g2 , . . . u2m+1 = gm
(71)
Für Approximationen ist es wesentlich, ihre Güte“ bewerten zu können, und hierfür
”
reicht es, wenn wir für Vektoren v ∈ V eine Länge zur Verfügung haben, die wir hier
(wie in der modernen Mathematik üblich) mit kvk bezeichnen und auch Norm“ nennen.
”
Die beste Näherung u ∈ U an den Vektor v ∈ V ist also der Vektor u ∈ U , der
ku − vk
134
minimal macht. Da die Funktion f (x) = x2 für x ≥ 0 monoton wachsend ist, ist dies der
Vektor, der
ku − vk2
minimal macht. Für unser Beispiel stückweise stetiger Funktionen f ist die Länge oder
Norm durch
v
u T
uZ
u
kf k = t f (t)2 dt
0
gegeben. Besonders vorteilhaft ist es, wenn die Länge aus√einem Skalarprodukt gebildet
werden kann, wie wir das im R3 haben, dort ist |~x| = ~x · ~x. Für stückweise stetige
periodische Funktionen schreiben wir das Skalarprodukt als (f, g), es ist durch
ZT
(f, g) :=
f (t)g(t)dt
(72)
0
definiert und wir haben ebenfalls
kf k =
p
(f, f )
Für die Berechnung der Fourierkoeffizienten ist der Satz 9.9.2 ( Ortogonalitätsrelationen“)
”
aus dem Analysis-Skript wichtig. Seine wesentliche Aussage ist, dass für die Integrale
ZT
ZT
cos(mωt) cos(nωt)dt = 0
und
0
sin(mωt) sin(nωt)dt = 0
0
gilt, wenn m 6= n sowie
ZT
cos(mωt) sin(nωt)dt = 0
0
für alle m, n ∈ N. Mit der durch (70) und (71) festgelegten Notation und Numerierung
ist die Aussage des Satzes 9.9.2 aus der Analysis knapp
(uk , ul ) = 0
falls
k 6= l
die Basisvektoren uk sind also orthogonal. Eine solche Basis heißt Orthogonalbasis. Sieht man von den unwichtigen Einzelheiten ab, dann ist die Aufgabe, die Fourier-
135
Koeffizienten ak , bk zu berechnen, das folgende Approximationsproblem:
Gegeben
ist ein Vektorraum V mit einem Skalarprodukt (., .) und einer durch
p
(v, v) definierten Norm sowie ein Unterraum U ⊂ V mit einer Basis
kvk =
{u1 , u2 , . . . un }, die orthogonal ist, also
(uk , ul ) = 0
k 6= l, k, l = 1, 2, . . . n
wenn
erfüllt. Weiterhin ist ein beliebiger Vektor v ∈ V gegeben. Gesucht ist der Vektor
n
P
w=
ck uk ∈ U , der v am besten approximiert, also
k=1
2
n
X
kv − wk = v −
ck uk 2
k=1
zum Minimum macht.
Konkret suchen wir eine Berechnungsformel, die es uns ermöglicht, die Koeffizienten ck
aus dem gegebenen Vektor v zu berechnen. Mit Hilfe einer Funktion formuliert heißt dies,
wir versuchen, zu gegebenem v ∈ V den Vektor w ∈ U zu berechnen, an dem die im
Unterraum U definierte Funktion fv (x) := kv − xk2 ihr Minimum annimmt.
v
U
w-v
w
x-v
x
Abbildung 36: Die beste Näherung durch einen Vektor w der Ebene U an einen beliebigen
Vektor v erhalten wir genau dann, wenn der Differenzvektor w − v senkrecht steht auf
der Ebene U .
Hierzu ist es sinnvoll, sich ein geometrisches Beispiel vorzustellen: V = R3 , U eine
Ebene durch den Ursprung, die von zwei orthogonalen Vektoren aufgespannt ist. Der
Vektor v ist im allgemeinen nicht in der Ebene U . Aber den Vektor w der Ebene, der
ihn am besten approximiert (ihm am nächsten ist), erhalten wir, indem wir von v das
Lot auf die Ebene U fällen. Das bedeutet, der Verbindungsvektor w − v steht senkrecht
oder orthogonal auf der Ebene U . Dies ist in Abb. 36 veranschaulicht. In der im obigen
Rahmen beschriebenen allgemeineren Situation gilt eine entsprechende Aussage:
Satz 10.2.1
Sei V ein Vektorraum V mit einem Skalarprodukt (., .) und einer durch
p
kvk = (v, v) definierten Norm. Weiterhin sei U ⊂ V ein Unterraum. Außerdem sei
v ∈ V beliebig und sei fv die Abbildung
fv : U → R,
x 7→ fv (x) = kv − xk2
136
Dann gilt
fv (x) = kx − vk2 ≥ fv (w) = kw − vk2
für alle x ∈ U
(73)
genau dann, wenn
(w − v, y) = 0
für alle
y∈U
(74)
D.h. die Funktion fv (x) nimmt in x = w genau dann ihr Minimum an, wenn der Differenzvektor w − v orthogonal zu U ist.
Beweis: Mit h := x − w ∈ U und damit x = w + h können wir die Bedingung, dass die
Funktion fv (x) in x = w ihr Minimum annimmt, auch schreiben als
fv (x) = fv (w + h) = kw + h − vk2 = k(w − v) + hk2 = (w − v) + h, (w − v) + h
= (w − v, w − v) + (h, h) + 2(w − v, h) = kw − vk2 + khk2 + 2(w − v, h)
≥ fv (w) = kw − vk2
für alle h ∈ U
(75)
Zusammenfassend stellen wir fest, dass das Minimum von fv (x) genau dann in w liegt,
wenn
fv (x) = kw − vk2 + khk2 + 2(w − v, h) ≥ fv (w) = kw − vk2
(76)
für alle h ∈ U . Statt für alle y“ in der Aussage des Satzes steht in dieser Umformung
”
für alle h“ und wir können unmittelbar ablesen, dass
”
fv (x) = kw − vk2 + khk2 ≥ kw − vk2 = fv (w)
für alle h ∈ U , wenn (w − v, h) = 0 für alle h ∈ U erfüllt ist. Aus der Orthogonalitätsbedingung (74) folgt also, dass das Minimum in w liegt.
Nehmen wir nun umgekehrt an, dass das Minimum von fv (x) in w liegt, also (73)
erfüllt ist. Daraus haben wir die Orthogonalitätsbedingung (74) zu beweisen. Wir wählen
einen indirekten Beweis und nehmen an, es gäbe ein h ∈ U mit a := (w − v, h) 6= 0.
Dann ist notwendigerweise h 6= 0 und wir führen als Schreibabkürzung b := khk2 > 0 ein.
Weiterhin definieren für alle t ∈ R die Funktion
g(t) := fv (w + t · h)
Sie erfüllt aufgrund der Rechnung in (75)
g(t) = kw − vk2 + t2 khk2 + 2t(w − v, h) = bt2 + 2at
und nimmt laut Voraussetzung ihr Minimum in t = 0 an. Quadratische Ergänzung oder
Ableiten liefert sofort, dass dies ist nur möglich ist, wenn a = 0 im Widerspruch zur
Annahme a = (w − v, h) 6= 0. Damit ist die Äquivalenz von (73) und (74) bewiesen.
Hinweis: Beachten Sie, dass wir in diesem Satz nicht vorausgesetzt haben, dass wir in U
eine Basis zur Verfügung haben!
Jetzt können wir den Vektor w ausrechnen. Hierzu nutzen wir aus, dass wir eine Basis
n
P
in U kennen und w ∈ U schreiben können als w =
ck uk . Wir setzen diesen Ansatz“
”
k=1
in die Orthogonalitätsbedingung (74) ein und erhalten
n
n
X
X
ck uk − v, y) =
ck (uk , y) − (v, y) = 0
(
k=1
k=1
137
für alle y ∈ U
(77)
wobei wir die Rechenregeln für das Skalarprodukt angewandt haben. Wir setzen nun
y = ul mit beliebigem l = 1, 2, . . . n und nutzen aus, dass die Basisvektoren uk orthogonal
sind, also (uk , ul ) = 0, falls k 6= l. Wir erhalten so
n
X
ck (uk , ul ) − (v, ul ) = cl (ul , ul ) − (v, ul ) = cl kul k2 − (v, ul ) = 0
k=1
Diese Gleichung können wir nach cl auflösen und erhalten als Ergebnis:
Satz 10.2.2
Sei V ein Vektorraum V mit einem Skalarprodukt (., .) und einer durch
p
kvk = (v, v) definierten Norm. Weiterhin sei U ⊂ V ein Unterraum mit einer Basis
{u1 , u2 , . . . un }, die orthogonal ist. Außerdem sei v ∈ V beliebig und sei fv die Abbildung
x 7→ fv (x) = kv − xk2
fv : U → R,
Dann nimmt fv (x) ihr Minimum in x = w an mit
w=
n
X
ck uk
wobei
ck =
k=1
(v, uk )
kuk k2
Hinweise:
(a) Die erhaltene Formel wird noch einfacher, wenn die Basis zusätzlich zur Orthogonalität die Normierungsbedingung kuk k = 1 für alle k = 1, 2, . . . n erfüllt. Eine solche
Basis nennt man dann Orthonormalbasis. Hierfür ist der Vektor w, der v am
besten approximiert, gegeben durch
n
X
w=
(v, uk )uk
k=1
(b) Für die durch (70) und (71) gegebene Basis des Unterraums U der trigonometrischen
Polynome erhält man aus unserem Satz 10.2.2 sofort Satz 9.2.3 aus dem AnalysisSkript mit den dort angegebenen Formeln für die reellen Fourier-Koeffizienten.
(c) Man kann die Funktionen hk (t)
hk (t) = ejkωt
k = −m, −m + 1, . . . m − 1, m
(78)
als neue Basis uk des Unterraums U der trigonometrischen Polynome höchstens m.
Grades ansehen. Man hat dann zu beachten, dass die Numerierung von −m bis
+m läuft. Integrale, in denen komplexwertige Funktionen vorkommen, können mit
Definition 9.2.5 (Analysis-Skript) definiert und mit Hilfe von Satz 9.2.4 ausgerechnet
werden. Beim Skalarprodukt komplexwertiger Funktionen müssen wir allerdings eine
Änderung anbringen und es durch
ZT
(f, g) :=
f (t)g(t)∗ dt =
0
ZT
f (t)g(t)dt
0
138
(79)
definieren. Dies ist notwendig, damit durch
v
v
u T
u T
uZ
uZ
p
u
u
∗
t
f (t)f (t) dt = t |f (t)|2 dt
kf k = (f, f ) =
0
0
wieder eine Länge oder Norm definiert wird. Ohne den Übergang zum konjugiertkomplexen Wert im 2. Faktor stünde sonst für viele komplexwertige Funktionen eine
komplexe oder eine negative reelle Zahl unter der Wurzel! Satz 9.2.5 sagt dann aus,
dass wir auch hiermit eine Orthogonalbasis vorliegen haben. Wenn wir für stückweise
stetige T -periodische Funktionen f (t) Näherungen der Form
f (t) ≈
m
X
ck ejkωt
k=−m
betrachten, so sagt unser Satz 10.2.2, dass wir die beste Approximation mit
1
(v, uk )
ck =
2 =
T
kuk k
ZT
f (t)e−jkωt dt
0
erhalten. Dies entspricht der Gleichung (167) im Analysis-Skript für die komplexen
Fourier-Koeffizienten.
(d) Es gibt zahlreiche weitere Anwendungsbeispiele von Satz 10.2.2. Hier sei noch eines
angeführt. Wir definieren den Vektorraum V als die Menge aller auf dem Intervall
[−1, 1] stückweise stetigen beschränkten reellwertigen Funktionen (stückweise stetig
soll hier heißen, es gibt höchstens endlich viele Stellen, an denen die Funktion nicht
stetig ist). Das Skalarprodukt wird definiert durch
Z+1
(f, g) := f (x)g(x)dx
−1
Als Unterraum U nehmen wir die Menge der Polynome höchstens n. Grades. Die
naheliegende Basis {1, x, x2 , . . . xn } hat den Nachteil, dass sie keine Orthogonalbasis
ist. Eine Orthogonalbasis für diesen Unterraum bilden die Legendre-Polynome,
die rekursiv durch
1
(2n−1)xPn−1 (x)−(n−1)Pn−2 (x)
für n ≥ 2
P0 (x) := 1, P1 (x) := x, Pn (x) :=
n
definiert werden können. Sie sind orthogonal, d.h.
+1
R
−1
und erfüllen
Z+1
Pk (x)Pk (x)dx =
−1
139
2
2k + 1
Pk (x)Pl (x)dx = 0 für k 6= l
und die ersten Pk (x) sind durch
1
1
P2 (x) = (3x2 − 1), P3 (x) = (5x3 − 3x),
2
2
1
1
P4 (x) =
(35x4 − 30x2 + 3), P5 (x) = (63x5 − 70x3 + 15x),
8
8
1
P6 (x) =
(231x6 − 315x4 + 105x2 − 5)
16
P0 (x) = 1,
P1 (x) = x,
gegeben. Sie sind in Abb. 37 grafisch dargestellt. Für die Funktion f (x) = sin(πx)
erhält man für die Approximation
sin(πx) ≈
n
X
ck Pk (x)
k=0
die Koeffizienten ck = 0 für k gerade und
c1 =
3
,
π
c3 =
7(−15 + π 2 )
,
π3
c5 =
11(945 − 105π 2 + π 4 )
π5
Die Approximationen c1 P1 (x) + c3 P3 (x) und c1 P1 (x) + c3 P3 (x) + c5 P5 (x) sind in
Abb. 38 gezeigt. Beachten Sie den Unterschied zu den Taylor-Polynomen! Hier ist
der Abstand“
”
Z+1
2
f (x) − Pn (x) dx
−1
minimiert, was zu einer guten Approximation über die gesamte Länge des Intervalls führt. Die Approximation mit dem Polynom 5. Grades ist kaum mehr von
der ursprünglichen Funktion zu unterscheiden. Im Fall n = 1 erhalten wir eine
Gerade mit einer deutlich geringeren Steigung π3 < 1 als die Tangente, da in den
Abstand auch die Punkte weit weg vom Ursprung eingehen. Eine wesentliche Anwendung der Legendre-Polynome ist die Konstruktion orthogonaler Funktionen auf
der Kugeloberfläche.
(e) Wenn wir im Unterraum U nur eine Basis {u1 , u2 , . . . un } zur Verfügung haben, die
nicht orthogonal ist, dann können wir immer noch die Orthogonalitätsbedingung
(74) ausnutzen und in (77) y = ul einsetzen. Wir erhalten so
n
X
ck (uk , ul ) = (v, ul )
für l = 1, 2, . . . n
k=1
Dies ist ein lineares Gleichungssystem für die unbekannten Koeffizeinten c1 , c2 . . . cn ,
das wir beispielsweise numerisch lösen können. Als Matrix tritt eine symmetrische
Matrix A mit den Matrixelementen Aik = (ui , uk ) auf. Es kann gezeigt werden, dass
diese Matrix nicht singulär ist, wenn {u1 , u2 , . . . un } linear unabhängig sind. Dies
ist aber bei einer Basis vorausgesetzt.
(f) Wir haben bei unseren ursprünglichen Beispielen der trigonometrischen Polynome zwar darauf hingewiesen, dass die Basisfunktionen orthogonal sind, aber nicht
140
Abbildung 37: grafische Darstellung der ersten Legendre-Polynome (aus Wikipedia)
Abbildung 38: Approximation der Funktion f (x) = sin(πx) auf [−1, 1] durch ein Polynom
3. und 5. Grades (Konstruktion mit Legendre-Polynomen)
überprüft, dass diese linear unabhängig sind. Dies folgt jedoch aus der Orthogonalität (frühere Übungsaufgabe): Skalare Multiplikation von
n
X
tk uk = 0
k=1
auf beiden Seiten mit ul liefert aufgrund der Orthogonalität sofort tl (ul , ul ) =
141
tl kul k2 = 0 und damit tl = 0 für alle l = 1, 2, . . . n.
142
A
Anhang: Ergänzungen
Hier folgen einige Erklärungen, die eigentlich in den Abschnitt 1 oder in den Abschnitt
Grundlagen“ des Analysis-Skripte gehören. Aus Zeitgründen konnten die hier erläuterten
”
Begriffe dort nicht eingeführt werden. Sie werden aber in vielen andern Lehrbüchern und
Skripten am Anfang eingeführt und später benutzt. Dieser Anhang dient also dazu, die
Benutzung anderer Skripte und Lehrbüchern zu erleichtern.
A.1
Gruppen
Abbildung 39: Symmetrieoperationen für ein Quadrat (aus der englischen Version von
Wikipedia)
Schauen wir uns erstmal ein Beispiel an. Gruppen tauchen unter anderem dort auf, wo
es um Symmetrien geht. Ein Quadrat hat viele Symmetrien. Man kann es um π4 und vielfache von π4 drehen, ohne es zu verändern. Außerdem kann man es horizontal, vertikal sowie
an den beiden Diagonalen spiegeln. Abb. 39 zeigt diese Symmetrieoperationen. Dabei ist
der Winkel im Gradmaß angegeben, und die Drehungen sind in mathematisch negativer
Richtung vorgenommen. Es ist plausibel, dass dies alle Symmetrieoperationen sind. Die
Symmetrieoperation, gar nichts zu tun, ist explizit aufgeführt und mit id bezeichnet. Sie
werden sich daran erinnern, dass die Addition von 0 oder die Multiplikation mit 1 bei
rellen Zahlen auch gar nichts tut“. Beachten Sie bei der Benennung der Spiegelungen in
”
Abb. 39, dass nicht die Achse, an der gespiegelt wird, in den Index eingeht, sondern die
Richtung, in der die Ecken bewegt werden. fv ist also eine Spiegelung an der horizontalen
Achse, die Ecken 1 und 2 bewegen sich vertikal nach unten, die Ecken 3 und 4 vertikal
nach oben.
Man kann zwei Symmetrieoperationen hintereinanderausführen. Dies ergibt wieder eine Symmetrieoperation. Das Ergebnis einer solchen Hintereinanderausführung muss also
wieder in der Abbildung 39 aufgeführt sein. Wir wählen hier als Symbol für das Hintereinanderausführen das Zeichen ∗. Mathematisch gesehen handelt es sich bei den Symmetrieoperationen um Abbildungen der Ebene in sich, die das Quadrat unverändert lassen. Dies
143
erklärt auch die Bezeichnungsweise id für die identische Abbildung. Wir haben in Definition 5.4.1 für die Hintereinanderausführung von Abbildungen das Symbol ◦ gewählt. Da
geplant ist, einen ganz allgemeinen Begriff, die Gruppe“, einzuführen, benutzen wir hier
”
das allgemeinere Symbol ∗. Wir halten an der wichtigen Konvention von Definition 5.4.1
fest, dass die rechts stehende Abbildung zuerst ausgeführt wird. Wir können also in diesem
Beispiel das Symbol ∗ als nach“ lesen.
”
Überzeugen Sie sich selbst, dass eine Spiegelung in horizontaler Richtung (also an der
vertikalen Achse) nach einer Drehung um 3 mal 90 Grad insgesamt einer Spiegelung an
der Hauptdiagonale entspricht, also
fh ∗ r3 = fd
Dass Hintereinanderausführungen von Abbildungen von der Reihenfolge abhängen können,
sollte Ihnen bekannt sein. Wir erhalten tatsächlich für die umgekehrte Reihenfolge (Drehung nach Spiegelung) das Ergebnis
r3 ∗ f h = f c
Das Ergebnis aller derartiger Hintereinanderausführungen von Symmetrieoperationen
Abbildung 40: Tabelle für die Hintereinanderausführung der Symmetrieoperationen von
Abb. 39; fh ∗ r3 heißt fh nach r3 ausgeführt, das Ergebnis ist blau hinterlegt (Abb. aus
der englischen Version von Wikipedia)
steht in Abb. 40, das erste Beispiel (fh ∗ r3 = fd ) ist blau hinterlegt.
In der Mathematik stehen die Rechenregeln für derartige Operationen im Vordergrund.
Es war bei der Behandlung der Hintereinanderausführung von Abbildungen plausibel gemacht worden, dass dabei das Assoziativgesetz gilt. Wir haben also für alle Symmetrieoperationen a, b, c des Quadrats
(a ∗ b) ∗ c = a ∗ (b ∗ c)
Die identische Abbildung (gar nichts tun) ist das neutrale Element bezüglich der Hintereinanderausführung, wir haben für alle Symmetrieoperationen a
a ∗ id = id ∗ a = a
144
Wenn es ein neutrales Element gibt, interessiert man sich für die Auflösbarkeit von Gleichungen der Form
a ∗ x = id
oder
x ∗ b = id
Durch Nachschauen in der Tabelle finden wir, dass es zu jeder Symmetrieoperationen
a genau eine Lösung für beide Gleichungen gibt, also für alle Symmetrieoperationen a
des Quadrats existiert genau eine Symmetrieoperation x als gleichzeitige Lösung beider
Gleichungen
a ∗ x = id
und
x ∗ a = id
Wir nennen diese Lösung das inverse Element von a. Es wird häufig a−1 geschrieben.
Wenn diese Rechenregeln erfüllt sind für eine Rechenoperation ∗, dann nennen wir die
entsprechende Menge eine Gruppe. Bevor wir uns die allgemeine Definition anschauen,
sollten wir noch eine allgemeine Sprachregelung treffen.
Definition A.1.1 Eine Verknüpfung ist eine Abbildung
f : A × B → C,
(a, b) 7→ c = f (a, b)
und wird häufig mit Hilfe eines speziellen Symbols in der Form
(a, b) 7→ a ∗ b, (a, b) 7→ a ◦ b, (a, b) 7→ a × b, (a, b) 7→ a · b, (a, b) 7→ a + b
geschrieben. Es sind auch andere Symbole gebräuchlich. Wenn kein Symbol auftaucht in
der Form (a, b) 7→ ab dann wird dies als a · b interpretiert.
Wir sind bisher schon zahlreichen Verknüfungen begegnet. In vielen Fällen sind die drei
beteiligten Mengen gleich, also A = B = C; hierfür nur einige Beispiele:
(a) + : Z × Z → Z, (m, n) 7→ m + n
(b) · : Z × Z → Z, (m, n) 7→ m · n
(c) × : R3 × R3 → R3 , (~x, ~y ) 7→ ~x × ~y (das Vektorprodukt)
(d) Betrachten wir die Menge aller Abbildungen mit derselben Definitions- und Zielmenge A. Dann ist die Hintereinanderausführung stets definiert und die Hintereinanderausführung oder Komposition ist eine Verknüpfung (f, g) 7→ f ◦ g für alle
Abbildungen f, g : A → A.
Die hier ∗ geschriebene Hintereinanderausführung der Symmetrieoperationen des Quadrats ist somit eine Verknüpfung.
Definition A.1.2 Eine Menge G mit der Verknüpfung ∗ : G × G → G heißt Gruppe,
wenn die folgenden Rechenregeln (Axiome) erfüllt sind:
(a) a ∗ (b ∗ c) = (a ∗ b) ∗ c für alle a, b, c ∈ G (Assoziativegesetz)
(b) Es existiert ein e ∈ G mit a ∗ e = e ∗ a = a für alle a ∈ G.
(e heißt neutrales Element)
(c) Für alle a ∈ G existiert ein x ∈ G mit a ∗ x = x ∗ a = e.
(x heißt inverses Element zu a)
145
Beispiele:
(a) Die Menge R der reellen Zahlen mit der Addition + als Verknüpfung (statt ∗). Das
neutrale Element ist e = 0 und das zu a inverse Element x ist x = −a.
(b) Die Menge R \ {0} mit der Multiplikation als Verknüpfung. Das neutrale Element
ist e = 1 und das zu a 6= 0 inverse Element ist a1 .
(c) Die triviale Gruppe G = {e}, die nur aus dem neutralen Element besteht.
(d) Die Gruppe der Symmetrieoperationen des Quadrats von Abb. 39 mit der Hintereinanderausführung als Verknüpfung ∗. Diese Gruppe wird mit D4 bezeichnet.
(e) Allgemein wird die Gruppe der Symmetrieoperationen eines regelmäßigen n-Ecks
mit Dn bezeichnet. Diese Gruppen heißen Diedergruppen (englisch dihedral groups)
und bestehen aus n Drehungen und n Spiegelungen (das neutrale Element zu den
Drehungen gerechnet).
(f) Die Menge der reellen nichtsingulären (2×2)-Matrizen mit der Matrixmultiplikation
als Verknüpfung, der Einheitsmatrix E = e als neutralem Element und der inversen
Matrix als inverses Element. Sie wird mit GL(2, R) bezeichnet.
(g) Auch das Beispiel (f) kann man verallgemeinern. Die nichtsingulären (n×n)-Matrizen
sind ebenfalls eine Gruppe, die mit GL(n, R) bezeichnet wird.
Hinweise:
(a) Z mit der Multiplikation ist keine Gruppe, nur +1 und −1 haben ein inverses Element.
(b) N mit der Addition ist ebenfalls keine Gruppe, nur 0 hat ein inverses Element
(c) Das Kommutativgesetz ist nicht verlangt, damit eine Menge mit Verknüpfung Gruppe heißt. In der Tat ist in den Beispielen (d), (e) für n ≥ 3, (f), (g) für n ≥ 2 das
Kommutativgesetz nicht erfüllt. Dagegen gilt das Kommatativgesetz in den Beispielen (a), (b) und trivialerweise im Beispiel (c).
Definition A.1.3 Eine Gruppe G mit der Verknüpfung ∗ heißt kommutativ oder abelsch,
wenn das Kommutativgesetz
a∗b=b∗a
für alle
a, b ∈ G
erfüllt ist.
Hinweise:
(a) Das Adjektiv abelsch nimmt Bezug auf den Mathematiker Niels Henrik Abel. Da es
so häufig vorkommt, wird es im allgemeinen mit kleinem a“ geschrieben.
”
(b) Der Begriff abelsche Gruppe“ erlaubt es, einige frühere sehr umfangreiche Defini”
tionen erheblich kürzer und prägnanter zu fassen:
146
Körper: Äquivalent zu Definition 6.2.1 kann definiert werden:
Eine Menge K heißt Körper, wenn zwei Verknüpfungen + : K × K → K und
· : K × K → K definiert sind mit den Eigenschaften
• Es existiert ein 0 ∈ K, so dass K mit der Verknüpfung + und dem neutralen
Element 0 eine abelsche Gruppe ist.
• Es existiert ein 1 ∈ K mit 1 6= 0, so dass K \ {0} mit der Verknüpfung ·
und dem neutralen Element 1 eine abelsche Gruppe ist.
• Für alle a, b, c ∈ K gilt das Distributivgesetz
a · (b + c) = a · b + a · c
Vektorraum: Äquivalent zu Definition 6.2.2 kann definiert werden:
Ein Vektorraum über einem Körper K ist eine Menge V mit zwei Verknüpfungen + : V × V → V und · : K × V → V mit den Eigenschaften
• Es existiert ein Nullvektor 0 ∈ V , so dass V mit der Verknüpfung + und
dem neutralen Element 0 eine abelsche Gruppe ist.
• Die Verknüpfung · erfüllt für alle s, t ∈ K und alle a, b ∈ V die folgenden
Rechenregeln (Axiome)
t · (a + b)
(s + t) · a
s · (t · a)
1·a
A.2
=
=
=
=
t·a+t·b
s·a+t·a
(s · t) · a
a
Relationen
Auch hier beginnen wir mit einem Beispiel. Das Wort hat etwas mit dem Begriff rela”
tionale Datenbank“ zu tun (das ist einer der Gründe, warum es hier behandelt wird).
Betrachten wir die Mengen von Vornamen
V = {Thomas, Michael, Manuela, Maria, Alexander, Nicolas, Katharina, Elke}
und die Menge von Familiennamen
F = {Maier, Müller, Lehmann, Schmidt, Schmitz, Bourbaki, Fischer, Weber}
Ein vollständiger Name einer Person stellt dann eine Beziehung zwischen einem Vornamen aus V und einem Familiennamen aus F her. Mathematisch gesehen ist dann eine
Namensliste eine Teilmenge des kartesischen Produkts V × F beispielsweise in der Form
N = {(Nicolas, Bourbaki), (Katharina, Weber), (Manuela, Schmitz), (Thomas, Maier)}
Hinzu könnte noch eine Menge M von Matrikelnummern kommen, und Teilnehmerlisten
eines Praktikums sind dann Teilmengen des dreifachen kartesischen Produkts V × F × M
mit beispielsweise dem Element (Manuela, Schmitz, 47114711). Dies motiviert die
Definition A.2.1 Eine Teilmenge R ⊂ M × N heißt eine (binäre oder zweistellige)
Relation zwischen M und N . Falls M = N , heißt R Relation auf M . Wenn (x, y) ∈ R,
dann erfüllen x und y die Relation R. Dies wird dann auch in der Form xRy geschrieben.
Entsprechend heißt eine Teilmenge R ⊂ M × N × Q eine dreistellige Relation, n-stellige
Relationen sind Teilmengen eines n-fachen kartesischen Produkts.
147
Beispiele:
(a) M = N = R und R = (x, y) ∈ R2 | x < y ist eine wichtige Relation (daher kommt
der Name Ordnungsrelation“)
”
(b) M = N = Z und R = (m, n) ∈ Z2 | m ist ganzzahliger Teiler von n
(c) M = N = N und R = (m, n) ∈ N2 | m = n + 1 , m ist Nachfolger von n beim
Zählen in N.
(d) Der Graph einer Funktion oder Abbildung f : A → B, a 7→ f (a) (siehe Def. 5.3.1 in
diesem Skript sowie Def. 2.1.1 und Def. 2.1.5 im Analysis-Skript) ist als Teilmenge
von A × B und damit als Relation durch
G(f ) = (a, b) ∈ A × B | b = f (a)
definiert.
Zahlreiche Beispiele im Analysis-Skript zeigen, dass nicht jede Teilmenge von A×B Graph
einer Funktion oder Abbildung f : A → B, a 7→ f (a) ist. Unmittelbar aus Def. 5.3.1 in
diesem Skript sowie Def. 2.1.1 und Def. 2.1.5 im Analysis-Skript ergibt sich der
Satz A.2.1 Eine Relation R ⊂ A × B ist genau dann der Graph einer Abbildung
f : A → B, a 7→ f (a)
mit
R = (a, b) ∈ A × B | b = f (a)
wenn die Relation die folgende Eigenschaft erfüllt:
Für alle a ∈ A existiert genau ein b ∈ B mit (a, b) ∈ R.
(80)
Hinweis:
Wir haben hier ein wenig gemogelt“. Mathematisch korrekt wäre es, durch eine Rela”
tion, die die Bedingung (80) erfüllt, den Begriff der Funktion oder Abbildung zu definieren.
Denn der in Def. 5.3.1 und Def. 2.1.5 im Analysis-Skript angegebene Begriff der Zuord”
nungsvorschrift“ ist letztlich ein Appell an außermathematische Alltagserfahrung. Eine
Zuordnungsvorschrift sollte man eigentlich korrekt mit Hilfe einer Relation definieren, die
die Eigenschaft (80) erfüllt. Unsere Vorgehensweise, den Begriff der Zuordnungsvorschrift
ohne saubere Definition durch eine Relation zu benutzen, war ein Eingeständnis zugunsten
einer besseren Verständlichkeit, aber zulasten der mathematischen Korrektheit.
Definition A.2.2 Für eine Relation R auf M (also R ⊂ M × M ) werden folgende Eigenschaften definiert:
(a) R heißt reflexiv, wenn (x, x) ∈ R für alle x ∈ M
(b) R heißt symmetrisch, wenn (x, y) ∈ R =⇒ (y, x) ∈ R
(c) R heißt transitiv, wenn (x, y) ∈ R und (y, z) ∈ R =⇒ (x, z) ∈ R
148
Beispiele
(a) Die Relation ≤ (d.h. R = (x, y) ∈ R2 | x ≤ y ist reflexiv und transitiv, aber nicht
symmetrisch.
(b) Die Relation < (d.h. R = (x, y) ∈ R2 | x < y ist transitiv, aber weder reflexiv
noch symmetrisch.
(c) Die Relation R = (m, n) ∈ Z2 | m − n ist gerade ist reflexiv, symmetrisch und
transitiv.
Definition A.2.3 Eine Relation R auf M (also R ⊂ M ×M ) heißt Äquivalenzrelation,
wenn sie reflexiv, symmetrisch und transitiv ist. Teilmengen von M der Form
ȳ = {x ∈ M | (x, y) ∈ R}
heißen dann Äquivalenzklassen. Bei Äquivalenzrelationen wird häufig x ∼ y geschrieben, wenn (x, y) ∈ R. Die Äquivalenzklassen werden statt ȳ auch ŷ oder [y] geschrieben.
Hinweise:
(a) Aufgrund der Definition gilt für die von x bzw. y erzeugten Äquivalenzklassen
x̄ = ȳ ⇐⇒ (x, y) ∈ R
(b) Zur Erinnerung: Wir haben in Definition 6.1.1 die Schreibweise (n ∈ N+ ) eingeführt
p≡q
(mod n)
⇐⇒
p mod n = q mod n
(zu lesen: p ist kongruent zu q modulo n). Dabei ist
p≡q
In Z wird durch
(mod n) ⇐⇒ p − q = m · n für ein m ∈ Z
R = (p, q) ∈ Z2 | p ≡ q
(mod n)
eine Äquivalenzrelation eingeführt. Die zugehörigen Restklassen laut Def. 6.1.1 sind
die Äquivalenzklassen laut Def. A.2.3. Die Bezeichnungsweise für Restklassen und
allgemeine Äquivalenzklassen ist auch übereinstimmend gewählt.
(c) Die Elemente der Menge der rationalen Zahlen Q sind Äquivalenzklassen! Zur Konstruktion von Q schreibt man zunächst die Elemente von Z2 = Z × Z statt in der
. Dann definiert man in Z2 ×Z2 unter Benutzung
üblichen Form (m, n) in der Form m
n
dieser Schreibweise die Relation
m1 m2
k · m2
m2
k · m1
2
2 m1
R=
,
∈Z ×Z =
oder
=
mit k ∈ Z
n1 n2
n1
k · n2
n2
k · n1
Man kann sich überzeugen, dass diese Relation reflexiv, symmetrisch und transitiv ist (kleine Übungsaufgabe!). Die Elemente von Q sind dann die zugehörigen
Äquivalenzklassen, die man eigentlich m
schreiben sollte. In der Praxis wird jedoch
n
fast immer die schlampige Schreibweise m
benutzt.
n
149
(d) Eine Äquivalenzrelation führt man ein, wenn man in einem bestimmten mathematischen Kontext eigentlich verschiedene Objekte als im wesentlichen gleich, gleichwertig oder äquivalent ansehen möchte, wie beispielsweise Brüche, die man durch
Erweitern oder Kürzen ineinander überführen kann. Die neuen mathematischen Objekte sind dann die Äquivalenzklassen. Meist wird dann in vielen praktischen Fällen
schlampig darüber hinweggesehen, dass man mit einer Äquivalenzklasse zu tun hat
und nicht zwischen dem Vertreter“ x und der Äquivalenzklasse x̄ unterschieden, da
”
ja in der betrachteten Situation alle Elemente aus x̄ gleich gut“ sind. Dabei muss
”
man natürlich aufpassen. Wenn man beispielsweise eine Funktion von Q nach Q
durch einen arithmetischen Ausdruck definiert, dann muss man sicherstellen, dass
der Funktionswert für einen gekürzten Bruch derselbe ist wie für den ungekürzten
Bruch. Die mathematische Sprechweise ist dann, dass die Funktion wohldefiniert“
”
ist. So ist
2
m
m
7→ 2
f : Q → Q,
n
n
statt m
geschrieben) wohldefitrotz der schlampigen Schreibweise (wir haben m
n
n
2
2
2
k·m
k ·m
m
niert, denn k·n 7→ k2 ·n2 ∼ n2 . Dagegen definiert die Zuordnungsforschrift m
7→
n
m keine Abbildung Q → Q. Man müsste sie abändern und vereinbaren, dass
m
vor Anwendung der Zuordnungsvorschrift so weit wie möglich zu kürzen ist.
n
Auch für die Verknüpfungen Addition und Multiplikation hat man bei der Definition sorgfältig darauf zu achten, dass diese nicht von der Auswahl des Vertreters aus der Äquivalenzklasse abhängt. Für die Addition ist das etwas verwickelt
(Übungsaufgabe!)
m1 · n2 + m2 · n1
m1 m2
+
:=
n1
n2
n1 · n2
für die Multiplikation schon etwas einfacher
m1 · m2
m1 m2
·
:=
n1 n2
n1 · n2
Auch bei der Definition der Verknüpfungen ⊕ und in Def. 6.1.3 hatten wir darauf hingewiesen, dass die Definition nicht von der Auswahl des Vertreters aus der
Restklasse abhängen darf (unter dem Hinweis steht dort der ausführliche Beweis).
(e) Man kann sich fragen, warum nicht der Name Äquivalenzmengen“ und Restmen”
”
gen“ verwendet wird, denn es handelt sich im hier behandelten Rahmen einwandfrei
um Teilmengen einer Menge M bzw. der Menge Z. Die Bezeichnung Klassen“ wird
”
bevorzugt, weil man dann die Bezeichnungsweise nicht ändern muss, wenn man
den Begriff der Äquivalenzrelation verallgemeinert auf Situationen, wo man keine
Mengen mehr hat. Das Problem ist, dass die Menge aller Mengen“ nicht existiert,
”
auch die Menge aller Vektorräume“ existiert nicht. Der Versuch, damit zu arbei”
ten, führt zu einer mathematischen Katastrophe, nämlich zu einem Widerspruch,
der Russelschen Antinomie (näheres z.B. bei Wikipedia). Bei Vorhandensein eines
Widerspruchs kann man mit Hilfe eines indirekten Beweises beweisen, dass jede
Aussage wahr ist, und man kann auch beweisen, dass die Verneinung jeder Aussage wahr ist. Also werden alle Aussagen wahr und falsch, und das ist in der Tat
katastrophal! Der Ausweg ist, von Klassen“ zu reden, beispielsweise von der Klas”
se der reellen Vektorräume. Dann kann man zum Beispiel eine Äquivalenzrelation
einführen, indem man zwei Vektorräume V und W als äquivalent ansieht, wenn eine
150
bijektive lineare Abbildung T : V → W existiert (reflexiv, symmetrisch, transitiv).
Die Äquivalenzklasse von Rn besteht dann aus allen Vektorräumen V , für die eine
bijektive Abbildung T : Rn → V existiert. Und hier könnte man wirklich nicht von
einer Äquivalenzmenge sprechen. Deswegen wird dies generell vermieden.
A.3
Potenzmenge
Definition A.3.1 Für eine beliebige Menge M ist die Potenzmenge von M die Menge
aller Teilmengen von M . Sie wird hier mit P(M ) bezeichnet.
Beispiel:
M = {0, 1, 2},
P(M ) = ∅, {0}, {1}, {2}, {0, 1}, {0, 2}, {1, 2}, {0, 1, 2}
Beachten Sie die Schreibweise! Es gilt 1 6∈ P(M ), aber {1} ∈ P(M ). Alle Elemente von
P(M ) sind selbst Mengen!
Abschließend ein Beispiel zur mathematischen Allgemeinbildung mit Querverbindung
zur Informatik. Wir gehen von der Potenzmenge der natürlichen Zahlen ohne die 0 aus,
also von P(N+ ). Wir definieren eine Abbildung f : P(N+ ) → R, indem wir zunächst für
jede Teilmenge B ∈ P(N+ ) (also B ⊂ N+ ) eine Folge
(
1 falls k ∈ B
(B)
(81)
ak :=
0 falls k 6∈ B
definieren. Mit Hilfe dieser Folge definieren wir die Abbildung
f : P(N+ ) → R,
B 7→ f (B) =
∞
X
(B)
ak 2−k
(82)
k=1
(B) (B) (B) (B) (B) (B)
Wir können den Funktionswert als Dualbruch 0, a1 a1 a3 a4 a5 a6 . . .2 interpretieren. Damit ist f (B) ∈ [0, 1] und f (∅) = 0. Noch ein Beispiel zur Berechnung des Funktionswertes von f :
f {1, 3, 6, 10} = 2−1 + 2−3 + 2−6 + 2−10 = 0, 10100100012
Beim Dezimalsystem haben wir
0, 99999999999 . . .10 =
∞
X
9 · 10−k = 1
k=1
(siehe die entsprechende Übungsaufgabe in Analysis, es handelt sich um eine geometrische
Reihe). Entsprechend haben wir 0, 09999910 = 0, 1. Die Darstellung durch Dezimalbrüche
ist also nicht eindeutig. Für Dualbrüche haben wir
0, 1111111 . . .2 =
∞
X
1 · 2−k = 1
(83)
k=1
und analog
1
0, 0111111 . . .2 = 0, 12 = ,
2
und
151
0, 0011111 . . .2 = 0, 012 =
1
4
Damit haben wir die Funktionswerte
f (N+ ) = 1,
1
f {1} = f {2, 3, 4, 5, . . .} = ,
2
1
f {2} = f {n ∈ N+ | n ≥ 3} =
4
Unsere Funktion ist also nicht injektiv. Die Dezimalbruchdarstellung kann man eindeutig
machen, indem man unendliche Folgen von aufeinanderfolgenden Ziffern 9 ausschließt.
Entsprechend können wir hier unsere Funktion injektiv machen, indem wir die Definitionsmenge kleiner machen, also Teilmengen aus P(N+ ) herausnehmen“, die unendliche
”
Folgen von aufeinanderfolgenden Ziffern 1 im Dualbruch verursachen. Dabei lassen wir
N+ selbst im Definitionsbereich, denn 0, 1111111 . . .2 ist die einzige Möglichkeit, 1 als Dualbruch in der Form 0, . . .2 darzustellen. Wir nehmen also Ausnahmemengen“ A mit der
”
Eigenschaft
{n ∈ N+ | n > n0 mit n0 ∈ N+ } ⊂ A
aus der Definitionsmenge der Abbildung f heraus. Wir definieren somit als Menge der
Ausnahmemengen“
”
n
o
+ A := A ∈ P(N ) {n ∈ N | n > n0 mit n0 ∈ N+ } ⊂ A
(84)
Neben einer Verkleinerung des Definitionsbereichs verkleinern wir auch die Zielmenge und
ersetzen sie durch den Wertebereich (oder die Bildmenge) der Abbildung. Da wir mit der
Änderung von Definitions- und Zielmenge die Abbildung geändert haben, ändern wir auch
die Bezeichnungsweise f in g. Wir erhalten damit eine bijektive Abbildung
+
g : P(N ) \ A → [0, 1],
B 7→ g(B) =
∞
X
(B)
ak 2−k
(85)
k=1
(B)
Dabei ist die Folge ak nach wie vor durch (81) gegeben.
Diese Funktion spielt eine wichtige Rolle in der Mengenlehre beim Vergleich der
Größe“ der betrachteten Mengen, die beide unendlich viele Elemente haben. Zwei Men”
gen, die durch eine bijektive Abbildung ineinander abgebildet werden können, sieht man
als gleich groß“ an. Wir können also hier anschaulich festhalten, dass es aufgrund der
”
bijektiven Abbildung (85) ein wenig mehr“ Teilmengen von N+ als reelle Zahlen in [0, 1]
”
gibt. Wir können dies hier nicht vertiefen. Interessierte sind auf den richtigen Fachbegriff
Mächtigkeit von Mengen (anstatt Größe“) verwiesen (siehe beispielsweise bei Wikipe”
dia).
A.4
Ergänzungen zur Logik
Um den einleitenden Abschnitt 1.1 im Analysis-Skript nicht durch eine Vielzahl von
Abkürzungen zu überfrachten, wurde dort auf die Benutzung vieler üblicher Abkürzungen
verzichtet. Insbesondere bei den Themen Logische Verknüpfungen“ und Anmerkungen
”
”
zur Logik und Beweistechnik“ sind folgende Abkürzungen sehr gebräuchlich:
∨
∧
∃
∀
¬
oder
und
es existiert
für alle
nicht (logische Verneinung)
152
Damit kann die Aussage
Es gilt nicht, dass für alle n ∈ Z gilt
ein n ∈ Z existiert mit n1 6∈ Z.
1
n
∈ Z, ist gleichbedeutend damit, dass
sehr viel prägnanter (aber für den Anfänger auch schwerer lesbar) als
1
1
∈ Z ⇐⇒ ∃n ∈ Z :
6∈ Z
¬ ∀n ∈ Z :
n
n
aufgeschrieben werden. Die Methode des indirekten Beweises kann durch
(A =⇒ B) ⇐⇒ (¬B =⇒ ¬A)
begründet werden. Derartige Aussagen, die stets wahr sind (für alle Teilaussagen, die
durch A und B gekennzeichnet sind, heißen Tautologien. Noch ein Beispiel für eine
Tautologie:
(A = B) ∧ (B = C) =⇒ A = C
Aussagen sind Ausdrücke, bei denen man im Prinzip entscheiden können sollte, ob sie
wahr oder falsch sind. So ist der Ausdruck In drei Wochen wird wahrscheinlich besseres
”
Wetter sein“ keine Aussage, aber auch a3 + 3a2 b + 3ab2 + b3 ist keine Aussage. Dagegen
ist 17 ist eine Primzahl“ und Es gibt stetige auf ganz R definierte Funktionen, die
”
”
nirgends differenzierbar sind“ eine Aussage. Die Formulierung bei denen man im Prinzip
”
entscheiden können sollte“ wurde so vorsichtig gewählt, da es mathematische Aussagen
gibt, bei denen Kurt Gödel bewiesen hat, dass es unmöglich ist, zu entscheiden, ob sie
wahr oder falsch sind (Unvollständigkeitssatz).
Betrachten wir Ausdrücke wie beispielsweise
x2 > 0,
y ≤ z,
A =⇒ B,
ab = ba oder A ∩ B ⊂ C
Ob sie wahr oder falsch sind, hängt davon ab, welche Bedeutung man a, b, A, B, C, x, y, z
zuweist. So wird durch A = [−2, 1], B = [1, 2], C = [− 23 , − 32 ] der Ausdruck A ∩ B ⊂ C zu
einer wahren Aussage.
Man nennt bei derartigen Ausdrücken a, b, A, B, C, x, y, z Variable, und ein derartiger Ausdruck selbst heißt Aussagefunktion, Aussageform oder Prädikat. Durch
Einsetzen von Werten“ wie A = [−2, 1] wird also aus einem Prädikat eine Aussage.
”
Prädikate können durch ∧, ∨, =⇒ oder ⇐⇒ verknüpft werden. Außerdem können
sie durch ¬ verneint werden. So erhält man aus den Prädikaten A ⊂ B, B ⊂ C ein
neues Prädikat (A ⊂ B) ∧ (B ⊂ C). Da Prädikate als Funktionen aufgefasst werden,
die von Variablen abhängen, werden sie häufig auch in einer entsprechenden Schreibweise
symbolisch aufgeschrieben.
Man kann also das Prädikat x2 > 0 symbolisch als A(x), das Prädikat x 6= 0 als B(x)
und das Prädikat (x2 = y) ∧ (x ≥ 0) als C(x, y) schreiben. Durch Setzen von x = 1 ∈ R
wird A(x) wahr, durch x = j ∈ C wird A(x) falsch (denn j 2 = −1). Dies rechtfertigt den
Sprachgebrauch Aussagefunktion. Die Menge der Funktionswerte ist {wahr, falsch}.
Statt einer konkreten Belegung in der Form x = 1 oder A = [−2, 1] können auch die
Quantoren ∀ und ∃ benutzt werden, um aus einem Prädikat eine Aussage zu machen.
Betrachten wir hierzu ein Prädikat der Form A(x).
• ∀x A(x)
Diese Aussage ist wahr, wenn sie für alle Einsetzungen x wahr ist.
zu lesen: für alle x gilt A(x)
153
• ∃x A(x)
Diese Aussage ist wahr, wenn sie für mindestens eine Einsetzung x wahr ist.
zu lesen: es existiert ein x, so dass A(x) gilt
Man sagt dann, dass die Variable x durch den Quantor gebunden wird. Nur wenn alle
Variable durch Quantoren gebunden werden, wird aus einem Prädikat eine Aussage.
Beispiele:
√
(a) ∃x ∈ R x2 = 2 ist wahr, beispielsweise für x = − 2.
(b) ∃x ∈ R x2 = y ist keine Aussage, sondern ein Prädikat, die Variable y wird nicht
gebunden.
(c) ∀x ∈ R x 6= 0 ⇐⇒ x2 > 0 ist wahr.
154