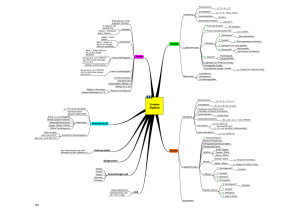
Analytische Geometrie Punkte im Raum: Basisvektoren: Addition

Analytische Geometrie
Punkte im Raum:

Darstellung: A ax ay az

Entfernung vom Ursprung:
d  0; A  
 ax    ay    az 
2
2
2
Entfernung Punkt ↔ Punkt:
d  A; B  
 bx  ax    by  ay    bz  az 
2
2
2
Basisvektoren:
1 
0
0
 
 
 
ex   0  ; ey   1  ; ez   0 
0
0
1 
 
 
 
Ortsvektor zu A:
Vektor von A nach B:
Betrag des Vektors
Addition und Subtraktion von Vektoren:
http://mathematik-sek1.bodautor.de
You Tube
1
Dr. Andreas Rueff
:
Skalar-Multiplikation:
Wenn gilt:
 ax   s  ax 
  

s  a  s   ay    s  ay 
 a   sa 
z
 z 
heißen die Vektoren
linear abhängig.
und
Skalarprodukt:
(Koordinatenform)
 ax   bx 
   
a  b   ay    by   ax  bx  ay  by  az  bz
a  b 
 z  z
Für orthogonale Vektoren gilt:
ab  0
a  b  a  b  cos 
 : Winkel zwischen a und b

ab
Vektorprodukt (Kreuzprodukt):
 ax   bx   aybz  azby 

    
a  b   ay    by    azbx  ax bz 
a  b  a b  a b 
y x
 z  z  x y
Für c  a  b gilt:
1) c ist orthogonal zu a und b :
ac ; bc
2) Der Betrag vom Vektor c ist gleich den Flächenihnalt
des von a und b aufgespannten Parallelogramms:
c  a  b  a  b  sin 
http://mathematik-sek1.bodautor.de
You Tube
2
Dr. Andreas Rueff