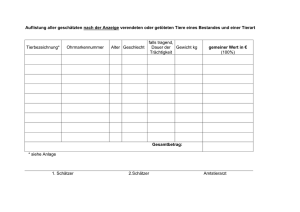
Statistik III - Waldemar Miller
Werbung

Statistik III WiSe 2013/2014 Statistik III Schätzen und Testen nach der Vorlesung von Dr. Thorsten Ziebach zuletzt bearbeitet am 15. Januar 2014 In LATEXgesetzt von Waldemar Miller Korrekturgelesen von Carmen van Meegen Hi, Hier die geTEXte Mitschrift der Veranstaltung Statistik III. Leider habe ich es erst bis Kapitel 3 geschafft, Kapitel 4 + 5 folgen in den nächsten Tagen/Wochen. Zwar wurde das Skript korrektur-überflogen, die meisten Fehler sind aber noch drin. Deswegen: Keine Garantie auf Richtigkeit. Verbesserungen, Fehler melden, etc. per E-Mail an: [email protected] Viel Spaß bei der Lektüre und viel Erfolg beim Arbeiten damit. Waldemar Inhaltsverzeichnis 1 Motivation 4 2 Summe von unabhängigen Zufallsvariablen, bedingte Verteilung 7 3 Punktschätzung 21 3.1 Grundbegriffe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 3.2 Methoden zur Gewinnung brauchbarer Punktschätzer . . . . . . . . . . 24 3.2.1 Momentmethode . . . . . . . . . . . . . . . . . . . . . . . . . . 24 3.2.2 Maximum-Likelihood-Methode . . . . . . . . . . . . . . . . . . . 27 3.2.3 Bayes-Schätzer . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 Kriterien zur Beurteilung der Güte einer Schätzfunktion . . . . . . . . 36 3.3.1 Mean Square Error (MSE) . . . . . . . . . . . . . . . . . . . . . 39 3.3.2 Erwartungstreue und Verzerrung . . . . . . . . . . . . . . . . . 43 3.3.3 Konsistenz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46 3.3.4 Effizienz und Cramer-Rao-Ungleichung . . . . . . . . . . . . . . 48 3.3.5 Suffizienz und Satz von Rao-Blackwell . . . . . . . . . . . . . . 59 3.3.6 Vollständige Statistiken und Satz von Lehmann Scheffé . . . . . 67 3.3 3 1 Motivation Beispiel 1.1 (Galtons Erbinnen). Ist die Wahrscheinlichkeit, dass ein Kind eine Tochter wird, von Familie zu Familie unterschiedlich? Grund der Frage: Francis Galton (1822–1911) beobachtete ein Aussterben von Namen reicher englischer Familien. Vermutung: Reiche Söhne heirateten reiche Erbinnen. Diese stammen aus Familien, bei denen die Wahrscheinlichkeit einer Mädchengeburt höher ist als bei anderen Familien (ansonsten wären Brüder die Erbfolger). Daten: Geschlecht der Kinder von 7745 Familien mit 4 Kindern. Betrachte zunächst eine Familie: Mögliche Ergebnisse sind (T =Tochter, S =Sohn): ω1 = SSSS ω5 = T SSS ω9 = ST T S ω13 = T ST T ω2 = SSST ω6 = SST T ω10 = T ST S ω14 = T T ST ω3 = SST S ω7 = ST ST ω11 = T T SS ω15 = T T T S ω4 = ST SS ω8 = T SST ω12 = ST T T ω16 = T T T T Ereignisraum Ω = {ω1 , . . . , ω16 } mit σ-Algebra A mit Ereignissen A ⊂ Ω, und es gibt ein Wahrscheinlichkeitsmaß P auf (Ω, A) mit diskreter Dichte pi := P ({ωi }), wobei 0 ≤ pi ≤ 1 und P16 i=1 1 ≤ i ≤ 16, pi = 1 gilt. Also: Es gibt nicht nur ein Wahrscheinlichkeitsmaß P , sondern eine Menge P von Wahrscheinlichkeitsmaßen P. Welches P ∈ P das wahre ist, ist für uns immer unbekannt. Beispiel 1.2. Seien x1 , . . . , xn Beobachtungen unabhängiger Zufallsvariablen Xi , i = 1, . . . , n, alle mit der selben Verteilung Xi ∼ Bin(1, p), i = 1, . . . , n, mit p ∈ [0, 1] unbekannt. Zum Beispiel: Klinischer Versuch mit n unabhängigen Patienten. Erprobe ein neues Medikament mit p = b Erfolgswahrscheinlichkeit, Heilungschance und interpretiere xi = 1 = b Medikament ist erfolgreich, xi = 0 = b Medikament erfolglos. 4 Mögliche Fragestellungen: (a) Punktschätzproblem Wir geben eine Schäzung für das wahre p ∈ [0, 1] Aufgrund von x = (x1 , . . . , xn ), xi ∈ {0, 1}, i = 1, . . . , n (b) Testproblem Frage: Ist p ≤ p0 oder p ≥ p0 sinnvoll für z. B.p = bekannte Heilungswahrscheinlichkeit eines bereits vorhandenen Medikaments., z. B. p0 = 21 , d.h. hat das Medikament überhaupt einen positiven Effekt. (c) Intervallschï¿ 12 tzung Finde zu x = (x1 , . . . , xn ) Zahlen pbu (x), pbo (x) mit pbu (x) ≤ pbo (x), sodass [pbu (x), pbo (x)] das wahre (aber unbekannte) p ∈ [0, 1] enthält mit einer vorgegebenen (möglichst großen) Wahrscheinlichkeit. Beispiel 1.3 (Qualitätskontrolle). Betrachte Warensendung aus N Stücken, N bekannt, davon eine unbekannte Anzahl s sind defekt. Ziehe ohne Zurücklegen eine Stichprobe zufällig vom Umfang n N Beobachtungen, sind dann x = (x1 , . . . , xn ) ∈ {0, 1}n . xi = 1 = b das i-te Stück ist defekt. xi = 0 = b das i-te Stück ist o.k. Situation ist eine andere als in Beispiel 1.1 bei der Schätzung der unbekannten Anzahl s, denn für jedes s besitzt x die Zähldichte fs (x) = fs (x1 , . . . , xn ) = s N −s · n−Σx Σxi i N n · n Σxi Die Einzelbeobachtungen sind hier nicht stochastisch unabhängig. Die Randverteilungen (d.h. Verteilungen, die zum einmaligen Ziehen gehört) sind alle Bin(1, Ns )-verteilt und ⊗Bin(1, Ns ) hat die Dichte n Y s 1−xi s Σxi s n−Σxi s xi gs (x) = · 1− = · 1− N N N N i=1 und offensichtlich gilt fs (x) 6= gs (x) für alle s ∈ {0, 1, . . . , n}. 5 Alternativ: Betrachte statt der Einzelbeobachtungen nur die Gesamtzahl der defekten Stücke in der Stichprobe: T (x) = n X xi i=1 Jetzt: Das Bildmaß von P s unter der Abbildung T ist die hypergeometrische Verteilung HypN,s,n mit der Zähldichte hN,s,n (t) = s t · N −s n−t N n , t ∈ {0, 1, . . . , n} d. h. die Anzahl der möglichen Ergebnisse reduziert sich um die Permutationsmöglichkeiten. Sind die unterstellten Modelle äquivalent, obwohl wir im letzten Fall Datenreduktion P (x1 , . . . , xn ) → ni=1 xi erfolgte? Beispiel 1.4 (Hochrechnung zur Wahl). Es stehen k Parteien zur Wahl, 0 ≤ p1 ≤ · · · ≤ pk ≤ 1 seien die wahren, aber unbekannten Prozentanteile der Parteien mit Pk j=1 pj = 1. Es liege eine Auswertung von n Stimmabgaben vor: x = (x1 , . . . , n), xi ∈ {0, 1, . . . , n}, k X xi = n. i=1 Falls die Stichprobe repräsentativ ist, d. h. aufzufassen als zufällige Ziehung aus der Gesamtheit aller Wähler (Anzahl N , N n) ergibt sich als Zähldichte von x: fn,p1 ,...,pn (x) = fn,p1 ,...,pn (x1 , . . . , xn ) k Y n! X = P j x1 ! · · · · · xk ! j=1 j Der Term ist offensichtlich nicht zusammengesetzt aus unabhängigen EinzelexperiPk menten, denn i=1 = n. Weiterhin ist f die Zähldichte einer M ulti(n, p1 , . . . , pk )Verteilung. Wie kann man in diesem Fall die entsprechenden Wähleranteile auf Basis der Stichproben schätzen? 6 Ziel der Vorlesung: In Beispiel 1.1 bis Beispiel 1.4 sind Stichproben gegeben. Versuche anhand des Stichprobenergebnisses, unbekannte Parameter (z. B. Anteile, Lebensdauern, Durchschnittsgrößen, . . . ) zu schätzen. • Wie findet man solche Schätzer ? • Wie gut sind diese Schätzer ? • Wie können wir unterschiedliche Arten von Schätzungen (Punkt- oder Bereichsschätzung) angeben? • Wie können wir Entscheidungen finden bei Vorliegen einer Behauptung wie in Beispiel 1.2 2 Summe von unabhängigen Zufallsvariablen, bedingte Verteilung Wiederholung aus Statistik II: Beispiel (in Anlehnung an Beispiel 1.1). Xn = b Anzahl der Jungengeburten unter n Geburten Xn ∼ Bin(n, p) mit p = Wahrscheinlichkeit, dass ein Junge geboren wird. Schlage in statistischen Jahrbüchern nach: Für großes n liegt der Anteil der Jungengeburten bei 0.51. → Es greift das schwache Gesetz der großen Zahlen, d. h. ∀ε > gilt: X n n→∞ P − p −→ 0 n Vielmehr kann man bei festem p die Grenzverteilung der Binomialverteilung angeben, √ denn n · Xnn − p verhält sich für große n wie eine normalverteilte Zufallsvariable, konkret: Die Verteilungsfunktion Fn der Zufallsvariable Zn := 7 √ n Xn n −p · √ 1 p·(1−p) konvergiert gegen Φ, der Verteilungsfunktion der N (0, 1)-Verteilung. Mit anderen Worten: ∀x ∈ R gilt: lim Fn (x) = Φ(x) n→∞ Wichtig z. B. zur Berechnung von P (a < Zn ≤ b) n→∞ −→ Φ(b) − Φ(a). Herleitung der Resultate Bestimme zunächst die Momente von X̄: Satz 2.1. Seien X1 , . . . , Xn unabhängig identisch verteilt (u.i.v.) mit E(Xi ) = µ und P V ar(Xi ) = σ 2 für i = 1, . . . , n. Für X̄ := n1 ni=1 Xi gilt: σ2 E(¯(X)) = µ und V ar(X̄) = −→ n Beweis. Bekannt aus Statistik II. Satz 2.2 (Schwaches Gesetzt der Groï¿ 12 en Zahlen). Seien (Xn )n∈N eine Folge von unabhängig identisch verteilten Zufallsvariablen (d. h. fï¿ 12 r jedes n ∈ N sind X1 , . . . , Xn u. i. v.) mit E(Xi2 ) < ∞, i = 1, . . . , n. P Sei ferner für jedes n : X̂n := n1 ni=1 Xi . Dann gilt ∀ε > 0 : lim P |X̂n − µ| > ε = 0, n→∞ Beweis. Mit Satz 2.1 gilt: ∀n ∈ N : E(X̂n ) = µ, ⇒ 0 ≤ P |X̂n − µ| > ε Cherb. ≤ mit µ = E(Xi ) V ar(X̂n ) = σ 2 /n. σ2 1 −→ 0 fï¿ r n → ∞ n 2 Aus Satz 2.2 folgt nicht, dass P |X̂n − µ| = 0 −→ 1 gilt. n→∞ Hï¿ 12 ufig ist vielmehr P |X̂n − µ| = 0 −→ 0, z. B. beachte im diskreten Fall: Beachte: 1 u.i.v. X1 , . . . , Xn ∼ Bin(1, √ ) 2 1 ⇒ µ = E(Xi ) = √ 6∈ Q, 2 aber fï¿ 12 r jedes ω ∈ Ω ist X1 (ω)+···+Xn (ω) n ∈ Q, folglich ist P |X̂n − µ| = 0 = 0 ∀n ∈ N. 8 Dieses schwache Gesetzt der groï¿ 12 en Zahlen lï¿ 12 sst uns fï¿ 21 r die Summen von u. i. v. Zufallsvariablen interessieren: Oftmals ist es jedoch schwierig, die Verteilung von Summen von u. i. v. Zufallsvariablen zu berechnen. Zunï¿ 12 chst fï¿ 12 r diskrete Zufallsvariablen: Satz 2.3 (Faltungssatz). Seien X1 , X2 stochastisch unabhï¿ 12 ngige Zufallsvariablen, P Xi (die Verteilung von Xi ) diskret mit Zï¿ 12 hldichte fi und Trï¿ 21 ger Ti , i = 1, 2. Dann ist auch P X1 +X2 diskret mit der Dichte f1,2 (z) = X f1 (x) · f2 (z − x) x∈T1 und dem Trï¿ 12 ger T1,2 = {z ∈ R : ∃x ∈ T1 und ∃y ∈ T2 mit z = x + y} Beweis. T1,2 ist hï¿ 12 chstens abzï¿ 21 hlbar, und es gilt P X1 +X2 (T1,2 ) = P (X1 + X2 ∈ T1,2 ) = P (X1 ∈ T1 und X2 ∈ T2 ) = P {ω ∈ Ω : X1 (ω) ∈ T1 } ∩ {ω ∈ Ω : X2 = (ω) ∈ T2 } unabh. = P (X1 ∈ T1 ) · P (X2 ∈ T2 ) = 1 · 1 = 1 ⇒ P X1 +X2 ist diskret und fï¿ 12 r die Dichte gilt: f1,2 (z) = P (X1 + X2 = z) = P X1 ,X2 {(x y)t ∈ R2 : x + y = z} {z } | =:B XX = g(x, y) x y mit der Dichte g von P X1 ,X2 und T ist T = T1 × T2 . Damit ist f1,2 = XX g(x, y) = x∈T1 y∈T2 y=z−x g(x, z − x) falls z − x ∈ T2 , 0 sonst, also z − x 6∈ T2 Aber auch g(x, z − x) = f1 (x) · f2 (z − x) = 0, falls z − x 6∈ T2 . ⇒ f1,2 = X g(x, z − x) = x∈T1 X x∈T1 9 f1 (x) · f2 (z − x). Beispiel 2.4. Seien X1 ∼ Bin(n, p) und X2 ∼ Bin(m, p), und X1 , X2 stochastisch unabhï¿ 12 ngig. ⇒ P X1 +X2 ist diskrete Verteilung mit Trï¿ 21 ger T1,2 = {0, 1, . . . , n + m} Berechnung der Dichte von X1 + X2 : fX1 +X2 n X m n x n−x pz−x (1 − p)m−z+x = p (1 − p) z − m x x=1 n X n m 2 n+m−z = p · (1 − p) x z−x x=0 m X n n x z−x 2 n+m−z n + m = p · (1 − p) · n+m z z x=0 | {z } hypergeom. {z } | =1 n+m = · pz · (1 − p)n+m−z z Dichte der Bin(n + m, p) -Verteilung! Mittels vollstï¿ 12 ndiger Induktion gilt daher: Seien X1 , . . . , Xn u. i. v. mit P Xi = Bin(1, p), i = 1, . . . , n. Dann gilt: P X1 +···+Xn = Bin(n, p). Bemerkung. Sei X eine Zufallsvariable mit P X = Bin(n, p). Dann besitzt die Zufallsvariable n1 X die gleiche Verteilung wie der Mittelwert von n u. i. v. Zufallsvariablen mit Verteilung Bin(1, p) (2.2) ==⇒ P | 1 − p| > ε −−−→ 0. n→∞ n Betrachte nun stetige Zufallsvariablen Satz 2.5 (Transformationssatz fï¿ 21 r Dichten). Seien X1 , . . . , Xn Zufallsvariablen, deren gemeinsame Verteilung P X1 ,...,Xn stetig ist mit einer Dichte f : Rn → [0, ∞). Sei A eine konvexe Teilmenge des Rn mit P X1 ,...,Xn (A) = 1. Sei ferner t : A → B eine bijektive Abbildung, mit weiterer konvexer Menge B ⊂ Rn und der entsprechenden Umkehrabbildung t−1 : B → A, sodass t und t−1 stetig differenzierbar sind. 10 Die Zufallsvariablen Z1 , . . . , Zn mit Z1 := t1 (X1 , . . . , Xn ), ... , Zn := tn (X1 , . . . , Xn ) haben die gemeinsame stetige Verteilung P Z1 ,...,Zn mit stetiger Dichte g : Rn → [0, ∞) , wobei −1 · 1B (z1 , . . . , zn ) (z , . . . , z ) · J(z , . . . , z ) g z1 , . . . , zn = f t−1 (z , . . . , z ), . . . , t 1 n 1 n 1 n n 1 und J(z1 , . . . , zn ) = det | {z } Jacobideterminante ∂t−1 1 (z1 ,...,zn ) ∂z1 ... ... .. . ∂t−1 n (z1 ,...,zn ) ∂z1 ... ∂t−1 1 (z1 ,...,zn ) ∂zn .. . ∂t−1 n (z1 ,...,zn ) ∂zn Beweis. Folgt direkt aus der Substitutionsformel in der Integralrechnung. Beispiel 2.6. Sei X1 ∼ Erlang(n, λ), d. h. P X1 hat die Dichte fX1 mit fX1 (x) = λ · e−λx · (λx)n−1 · 1[0,∞) (x) (n − 1)! und sei X2 ∼ Exp(λ), d. h. P X2 hat die Dichte fX2 mit fX2 (x) = λ · e−λx · 1[0,∞) (x). Seien weiterhin X1 und X2 stochastisch unabhï¿ 12 ngig, dann hat die gemeinsame Verteilung von X1 und X2 die Dichte fX1 ,X2 mit fX1 ,X2 (x, y) = fX1 (x) · fX2 (y) = λ2 · (λx)n−1 −λ(x+y) ·e · 1[0,∞) (x) · 1[0,∞) (y) (n − 1)! Bestimme nun die Verteilung von X1 + X2 : Wï¿ 21 hle t : R2 → R2 mit: z1 = t1 (x, y) = x z2 = t2 (x, y) = x + y Dann ist t bijektive Abbildung mit differenzierbarer Umkehrfunktion t−1 : R2 → R2 mit t−1 1 (z1 , z2 ) = z1 , t−1 2 (z1 , z2 ) = z2 − z1 . Die Jacobi-Determinante ist J(z1 , z2 ) = det 11 1 0 −1 1 ! =1 Mit Satz 2.5 haben Z1 = X1 und Z2 = X1 + X2 die gemeinsame stetige Dichte gZ1 ,Z2 mit gZ1 ,Z2 (z1 , z2 ) = fX1 ,X2 (z1 , z2 − z1 ) · J(z1 , z2 ) · 1[0,∞) (z1 ) · 1[0,∞) (z2 − z1 ) = λ2 · Stat II ⇒ (λ z)n−1 −λ (z1 +z2 −z1 ) ·e · 1[0,∞) (z1 ) · 1[0,∞) (z2 − z1 ) (n − 1)! P X1 +X2 = P Z2 hat die Dichte Z gz1 ,z2 (x, z) dx gz2 = R Z λ2 · = R 2 =λ ·e (λ x)n−1 −λx ·e 1[0,∞) (x) · 1[0,∞) (z − x) dx (n − 1)! | {z } =1[0,∞) (z)·1[0,z] (x) −λz n−1 λ · · 1[0,∞) (z) · (n − 1)! Z z xn−1 dx | 0 {z } 1 n z n λn n · z · 1[0,∞) (z) n! Dichte der Erlang(1, λ)-Verteilung! = λ · e−λz · Also ist die Verteilung P X1 +X2 = Erlang(n + 1, λ). Da die Dichte der Erlang(1, λ)Verteilung gleich der Dichte der Exp(λ)-Verteilung, folgt direkt fï¿ 21 r u. i. v. X1 , . . . , Xn mit P Xi = Exp(λ), dass P X1 +···+Xn = Erlang(n, λ) Ein Spezialfall von Satz 2.5 Satz 2.7. Seien X1 , . . . , Xn stochastisch unabhï¿ 12 ngig, P X, stetig mit Dichte f1 und P X2 stetig mit Dichte f2 . Dann ist auch P X1 +X2 stetig verteilt mit Dichte g, wobei Z ∞ f1 (x) · f2 (z − x) dx. g(z) = −∞ Beweis. wie in Beispiel 2.6. Wir werden nun die asymptotische Verteilung der Zufallsvariable Pn i=1 Xi betrachten, da die Verteilung schwer zu bestimmen bzw. analytisch nicht zu ermitteln ist. Was verstehen wir unter einer Grenzverteilung bzw. asymptotischen Verteilung, dazu nun: 12 Definition 2.8. Sei (Xn )n∈N eine Folge von Zufallsvariablen. Sei Fn die Verteilungsfunktion von P Xn , n ∈ N und G die Verteilungsfunktion einer Verteilung Q. W Die Folge der Verteilungen P Xn , n ∈ N konvergiert schwach gegen Q (kurz P Xn −→ Q), falls fï¿ 12 r jedes x ∈ R, fï¿ 12 r das G stetig ist in x, gilt: lim Fn (x) = G(x) n→∞ W Bemerkung. Falls P Xn −→ Q, dann gilt ∀a < b: T a < Xn ≤ b = Fn (b) − Fn (a) W −→ G(b) − G(a) = Q (a, b] Beispiel 2.9. Huhu (a) Seien P Xn diskret gleichverteilt auf { n1 , n2 , . . . , nn } ⇒ Fn (x) = 0 , x< k , n 1 k n 1 n ≤x< k+1 n ∀ k = 1, . . . , n , x≥1 Offensichtlich: Fn (x) ≥ x fï¿ 12 r x < 1 ⇒ lim Fn (x) = n→∞ 0 k n 1 , x<0 , 0≤x<1 , x≥1 ⇒ G ist Verteilungsfunktion einer stetigen Rechteckverteilung R[0, 1], d. h. Q = R[0, 1]. Also konvergiert die Folge der diskreten Gleichverteilungen auf { n1 , n2 , . . . , nn } schwach gegen die R[0, 1]-Verteilung. In Formeln: W P Xn −→ Q ⇒ lim Fn (x) = G(x) n→∞ (Grenzverteilung) (VF der Grenzverteilung) schwache Konvergenz 13 (b) Sei (Xn )n∈N eine Folge u. i. v. Zufallsvariablen mit E (Xi2 ) < ∞ , i = 1, . . . , n. P Bezeichne mit (X̄n )n∈N die Folge der Mittelwerte, d. h. X̄n = n1 ni=1 Xi . Mit µ := E(Xi ) gilt nach dem schwachen Gesetz der groï¿ 12 en Zahlen: ∀ε > 0 : P X̄n − µ n→∞ −→ 0. Fï¿ 12 r Fn als Verteilungsfunktion von X̄n gilt: ∀x<µ Fn (x) = P X̄n ≤ x = P X̄n − µ ≤ x − µ | {z } <0 ≤ P |X̄n − µ| ≥ µ − x | {z } =: 2ε ≤ P |X̄n − µ| > ε 1 SwGGZ −→ 0 fï¿ r n → ∞. 2 ∀x>µ Fn (x) = P X̄n − µ ≤ x − µ = 1 − P X̄n − µ > ε | {z } ≤P (|X̄n −µ|>ε) x=µ keine Aussage ï¿ 12 ber Fn mï¿ 12 glich. Also: n→∞ ∀x<µ n→∞ ∀y>µ Fn (x) −→ 0 Fn (x) −→ 1 Sei Q die Einpunktverteilung in µ, d. h. Q hat die Verteilungsfunktion G mit 1 f alls x ≥ µ G(x) = 0 f alls x < µ Also konvergiert P X̄n schwach gegen die Einpunktverteilung in µ. Diese Aussage ist zu grob fï¿ 12 r die Statistische Anwendung, versuche stattdessen die 14 Grenzverteilung fï¿ 21 r standardisiertes X̄n bzw. Pn i=1 Xi zu finden. ACHTUNG HIER FEHLT EINE ZEICHNUNG Beispiel 2.10. Sei (Xn )n∈N u. i. v. mit P Xi = Exp(λ). Dann ist nach Beispiel 2.6 fï¿ 12 r P ein beliebiges n ∈ N die Zufallsvariable Yn := ni=1 Xi Erlang(n, λ)-verteilt (sprich: Erlang–n–verteilt mit Parameter λ). E(Yn ) = nλ , Weiter gilt: V ar(Yn ) = n . λ2 Betrachte nun die standardisierte Zufallsvariable √ Ȳn − λ1 n · X̄n − λ1 Yn − nλ q = = n· q , Zn = p √ 1 1 n/λ2 n · λ2 λ2 r 1 mit = b Standardabweichung. λ2 Sei t : 12 R → R definiert durch t(g) = √g−n 2 , dann ist Zn = t(Yn ) und t ist bijektiv n/λ √ mit Umkehrabbildung t−1 : R → R mit t−1 (z) = λ1 ( n · z + n). √ Es gilt J(z) = n . λ Aus dem Transformationssatz fï¿ 12 r Dichten (Satz 2.5) folgt, dass P Zn die stetige Dichte √ 1 √ n ( n · z + n) · (fYn Dichte der Erlang-Verteilung) gn (z) = fYn n λ n−1 √ √ √ λ · λ1 ( n · z + n) 1 √ 1 n n·z+n −λ·( λ ( n·z+n)) Also gn (z) = λ · ·e · · 1[0,∞) 2 (n + 1)! λ λ √ n−1 √ √ ( n · z + n) = · n · e−( n·z+n) · 1[−√n,∞) (z) (n − 1)! | {z } | {z } n→∞ −→ 1 2 √1 ·exp − z 2 2π mit Stirlingformel n→∞ −→ Fï¿ 12 r alle z ∈ R gilt gn (z) −→ = ϕ(z) , n→∞ (Dichte der N (0, 1)-Verteilung) d. h. fï¿ 21 r die Verteilungsfunktion Fn von Zn gilt limn→∞ Fn (z) = Φ(z). √ X̄n −E(X1 ) X̄n −E(X̄n ) Damit konvergiert die Verteilungsfunktion von Zn = n √ =√ schwach V ar(X1 ) V ar(Xn ) gegen Φ. Dies gilt unter schwachen Forderungen fï¿ 12 r beliebige Verteilungen, nicht nur fï¿ 12 r die Exp-Verteilung. Satz 2.11 (Zentraler Grenzwertsatz nach Lindeberg-Levy). Sei (Xn )n∈N eine Folge von u. i. v. Zufallsvariablen mit µ = E(Xi ), i ∈ N, σ 2 = V ar(X) ∈ [0, ∞) 15 Dann gilt fï¿ 12 r die Folge der standardisierten Mittelwerte Zn := √ n Xnσ−µ : W P Zn −→ N (0, 1) Beweis. Statistik IV! Folgender ZGWS (Zentraler Grenzwertsatz) fordert eine schï¿ 12 rfere Bedingung an die Momente, jedoch ist nur die Unabhï¿ 12 ngigkeit der Zufallsvariablen (Xn )n∈N gefordert: Satz 2.12 (Zentraler Grenzwertsatz nach Ljapunov). Seien (Xn )n∈N stochastisch unabhï¿ 12 ngige 2 Zufallsvariablen mit V ar(Xj ) = σj > 0, σj2 < ∞, j = 1, . . . , n. Gibt es ein δ > 0, sodass 2+δ |X − E(X − j)| E j i=1 n→∞ −→ 0 2+δ qP n 2 j=1 σj Pn gilt, dann gilt: Pn (Xj − E(Xj )) W qP −→ N (0, 1). 2 n σ j=1 j j=1 Beispiel 2.13. Sei Xn = Anzahl der Jungen bei n Geburten. Xn ∼ Bin(n, p), p unbekannt, p ∈ (0, 1). Wir kï¿ 21 nnen P ∈ P mit Parameter p charakterisieren. Bezeichne daher die Verteilungen bei gegebenen p mit PpXn . Vermutung: p = p0 = 0.5 ist das wahre p. In 2008 gab es in Deutschland 682 514 Geburten, davon 349 862 mï¿ 12 nnlich. Ist ein so hoher Anteil mï¿ 21 nnlicher Kinder mit der Hypothese p = Unter p = p0 = 1 2 1 2 vertrï¿ 12 glich? gilt: P0.5 (Xn ≥ x) = = 1 − P0.5 (Xn < x) 1 − P0.5 Xn n − p0 √ x − p0 √ ! p n < p n p0 (1 − p0 ) p0 (1 − p0 ) Xn /n ist der Mittelwert von n stochastisch unabhï¿ 12 ngigen Bin(1, p0 )-verteilten Zup0 (1−p0 ) fallsvariablen mit Ep0 (Xn /n) = p0 und V arp0 (X! n /n) = n Xn − p √ 0 einsetzen =⇒ P0.5 (Xn ≥) ≈ 1 − Φ np n = 1 − Φ(22.83) < 0.001 p0 (1 − p0 ) 16 Bedingte Verteilung und bedingter Erwartungswert Betrachte zweidimensionale Zufallsvariable (X, Y ) im allgemeinen nicht unabhï¿ 12 ngig voneinander. Sei z. B. fï¿ 12 r eine Population gegeben: 1 1 1 X = Kï¿ rpergrï¿ ï¿ e eines Mannes in cm 2 2 2 1 Y = Kï¿ rpergewicht eines Mannes in kg 2 Offensichtlich sind X und Y abhï¿ 12 ngig, denn z.B. P (Y > 100) hï¿ 21 ngt stark davon ab, wie groï¿ 12 eine Person ist, d. h. die Frage „Wie groï¿ 12 ist die Wahrscheinlichkeit, dass ein kleinwï¿ 12 chsiger Mann ( < 170 cm) mehr als 100 kg wiegt“, ist eine bedingte Wahrscheinlichkeit. Weiter: Kï¿ 21 rpergewichtsverteilung fï¿ 21 hrt zu bedingtem Verteilungsbegriff. Definition 2.14. Sei (X, Y ) eine zweidimensionaler stetiger oder diskreter Zufallsvektor mit gemeinsamer Wahrscheinlichkeitsfunktion / –Dichte fX,Y gegeben. Fï¿ 12 r jedes y ∈ R mit fy (y) > 0 heiï¿ 12 t fX|Y (x|y) := fX,Y (x, y) fy (y) die bedingte Wahrscheinlichkeitsfunktion bzw. -Dichte von X gegeben Y = y. Ebenso kï¿ 12 nnen wir fï¿ 12 r jedes x ∈ R mit fX (x) > 0 auch definieren: fY |X (y|x) = fX,Y (x, y) fX (x) Beispiel 2.15 (bedingte diskrete Verteilung). Gegeben: zweidimensionale Verteilung von (X, Y ) mit folgender gegebener gemeinsamer Dichte fX,Y : fX,Y (0, 10) = fX,Y (0, 20) = 2/18 fX,Y (1, 10) = fX,Y (1, 30) = 3/18 fX,Y (1, 20) = fX,Y (2, 30) = 4/18 17 Randverteilung von X: fX (0) =P (X = 0) = P (X = 0, Y = 10) + P (X = 0, Y = 20) = 4/18 fX (1) = . . . = 10/18 fX (2) = . . . = 4/18 Somit sind die bedingten Verteilungen: fY |X=0 (10|0) = fY |X=0 (20|0) = fY |X=1 (10|1) = fY |X=1 (20|1) = fY |X=1 (30|1) = fY |X=2 (10|2) = fX,Y (0, 10) = fx (0) 1 ... = 2 3 ... = 10 4 ... = 10 3 ... = 10 ... = 1 2 18 4 18 = 1 2 In Analogie zur bedingten Verteilung lassen sich auch fï¿ 12 r beding Verteilungen die Momente bestimmen. So berechnet sich der bedingte Erwartungswert von g(Y ): Im diskreten Fall: E(g(Y )|X = x) = X g(y) · fY |X (y|x) y Im stetigen Falle: Z ∞ g(x) · fY |X (y|x) dy E(g(Y )|X = x) = −∞ Weiter mit Beispiel 2.15: 1 1 + 20 · + 30 · 0 = 15 (hier g(y) = y) 2 2 3 3 3 E(Y |X = 1) = 10 · + 20 · + 30 · = 20 10 10 10 E(Y |X = 2) = 30 · 1 = 30 E(Y |X = 0) = 10 · Fasse somit E(Y |X = x) als Funktion der Werte x der Zufallsvariablen X auf. Fï¿ 12 r jedes x ergibt E(Y |X = x) eine bestimmte Zahl. Andererseits ist diese Funktion selbst wiederum eine Zufallsvariable, wï¿ 12 hle als Transformation g(Y ) = E(Y |X) und erhal- 18 te: E (E(Y |X)) = 15 · P (E(Y |X) = 15) +20 · P (E(Y |X) = 20) +30 · P (E(Y |X) = 30) 10 4 380 1 4 + 20 · + 30 · = = 21 + = 15 · 18 18 18 18 9 Betrachte: E(Y ) = . . . = 21 + 91 . Ist das Zufall oder nicht? Antwort: Nein, nicht zufï¿ 12 llig. Herleitung folgt nun: Satz 2.16 (wichtige Rechenregeln fï¿ 12 r bedingte E-Werte). Gegeben sei ein zweidimensionaler Zufallsvektor (X, Y ), dann gilt: E(X) = E (E(X|Y )) Beweis. (fï¿ 12 r den stetigen Fall). Z ∞ Es gilt: Z ∞ x · fX,Y (x, y) dx dy E(X) = Z−∞ ∞ Z−∞ ∞ x · fX|Y (x, y) · fY (y) dx dy = x · fX|Y (x|y) dx ·fY (y) dy −∞ −∞ | {z } = Z−∞ ∞ −∞ Z ∞ =E(X|Y =y) Beispiel 2.17. Ein Insekt lege eine Anzahl von Eiern, von denen jedes mit Wahrscheinlichkeit p ï¿ 12 berlebt. Unterstelle fï¿ 21 r Y = Anzahl der gelegten Eier, dass Y ∼ P oi(λ), sowie fï¿ 12 r X = Anzahl ï¿ 12 berlebender Eier, dass (X|Y = y) ∼ Bin(y, p). Wieviele Eier ï¿ 12 berleben im Durchschnitt? Suche E(X)! Mit E(X|Y = y) = y · p ist E(X|Y ) = Y · p und nach Satz 2.16 gilt: E(X) = E (E(X|Y )) = E(Y · p) = p · E(Y ) = Y ∼P oi(λ) p · λ. Abschlieï¿ 21 end zwei wichtige Rechenregeln fï¿ 12 r bedingte E-Werte: Satz 2.18. Gegeben sei ein zweidimensionaler Zufallsvektor (X, Y ) und h1 , h2 zwei messbare Funktionen, dann gilt: 19 (a) E (h1 (X) + h2 (X)|Y = y) = E (h1 (X)|Y = y) + E (h2 (X)|Y = y) (b) E (h1 (X) · h2 (Y )|Y = y) = h2 (y) · E (h1 (X)|Y = y) 20 3 Punktschätzung Anteil männlicher Geburten in 2008 X n = Anzahl männlicher Geburten Anzahl aller Geburten = 349 862 682 514 = 0.513 Daher vernünftige Vermutung: der wahre Anteil liegt bei p = 0.513 Benutze also die Beobachtung x zu einer Schätzung p̂(x). Offensichtlich: p̂(X) = X n ist eine Realisation einer Zufallsvariable. 3.1 Grundbegriffe Definition 3.1. (a) Seien (Ω, A) messbarer Raum, P eine Familie von Wahrscheinlichkeitsmaßen auf A. Dann heißt (Ω, A, P) statistischer Raum. (b) Sei (X , C) ein messbarer Raum, X : Ω → X sei A − C-messbar und P := {P X : P X (C) = P (X −1 (C)) ∀C ∈ C und ∀P ∈ P} und wird eine Realisation von X beobachtet. Dann heißen (X , C, P X ) ein Stichprobenraum, X eine Stichprobe und x eine Realisation der Stichprobe. (c) Gilt (X , C, P X ) = (Rm , B, P)n mit Zufallsvariablen Xj := (Ω, A) → (Rm , B n ) und sei Xj ∼ P0 ∈ P ∀j ∈ {1, . . . , n}. Dann heißt (X1 , . . . , Xn ) eine einfache Stichprobe vom Umfang n. | {z } =X Beispiel 3.2. Eine Münze wird zweimal geworfen, notiere Adler (A) oder Zahl (Z). Ω = {(A, A); (A, Z); (Z, A); (Z, Z)} A = P(Ω) = b Potenzmenge von Ω Betrachte zwei Wahrscheinlichkeitsmaße P1 : P1 {ω} P2 : P2 {(A, A)} = 1 4 ∀ω ∈ Ω = 1 , 81 8 P2 {(A, Z)} = P2 {(Z, A)} = 81 64 P2 {(Z, Z)} = 81 21 Sei P = {P1 , P2 }, und (Ω, A, P) ein statistischer Raum. Definiere die Zufallsvariablen 1 falls A oben liegt Xi = ∀ i ∈ {1, 2} 0 falls Z oben liegt ! X1 X= , X = R, C = B 2 , P = P X,P1 , P X,P2 X2 mit 1 = P X,P1 4 = P X,P1 = P X,P1 = P X,P1 X= X= X= X= 1 !! 1 1 !! 0 0 !! 1 0 !! 0 und analog P X,P2 . . . und R2 , B 2 , P X als Stichprobenraum. Definition 3.3. Sei Θ eine beliebige Teilmenge des Rk und g : Θ → P X eine bijektive Abbildung. Dann heißen Θ eine Parametermenge für P X , θ ∈ Θ ein Parameter(vektor) von P X , und g eine parametrische Funktion bzw. Parametrisierung von P X . Notation: g(θ) = P X|θ∈Θ P X = P X|θ : θ ∈ Θ = PθX : θ ∈ Θ Beispiel 3.4. Betrachte die sog. Cobb-Douglas-Produktionsfunktion Yj = c · Kjα · Lβj · Uj , Dabei ist Yj Produktionsmenge (in Periode j) c Kj Kapitaleinsatz (in Periode j) Uj Lj Arbeitsansatz (in Periode j) α, β 22 j = 1, . . . , n nichtkonstanter Faktor, techn. Fortschritt Störfaktor (in Periode j) Parameter (unbekannt, zu schätzen) Durch Logarithmieren erhalten wir ln Yj = ln c + α · ln Kj + β · ln Lj + ln Uj Die Interpretation von ist dann: d ln Yj = β, d ln Lj d ln Yj = α, d ln Kj α, β als Produktionselastizitäten Aber auch α + β von Interesse, da Yj (λKj , λLj ) = λα+β Yj (Kj , Lj ) α + β heißen Skalenelastizitäten, gibt die prozentuale Erhöhung des Outputs Nun: an, wenn die Einsatzmengen (Kapital, Arbeit) jeweils um 1% erhöht werden. Falls α+β =1 ⇒ Yj (λKj , λLj ) = λ Yj (Kj , Lj ) α+β >1 ⇒ positive Skaleneffekte (increasing returns) α+β <1 ⇒ negative Skaleneffekte (decreasing returns Mit θ = α (linear homogen) ! β ∈ R2 ist g(θ) = α + β parametrische Funktion. Definition 3.5. Sei X , C, P X ein Stichprobenraum, so heißt die C − B l -messbare Abbildung t: X −→ Rl eine Stichprobenfunktion. Bemerkung. (a) t(X) = T (ω) ist ein Rl -Zufallsvektor. (b) t ist völlig bekannt, insbesondere unabhängig von θ. (c) Falls die Verteilung von T nicht von θ abhängt, so enthält T keine Information über θ Beispiel 3.6. (a) X1 , . . . , Xn u. i. v. Zufallsvariablen mit P Xi = N (µ, σ 2 ) , i = 1, . . . , n , µ ∈ R, σ 2 > 0 unbekannt. X := (X1 , . . . , Xn )0 ist die Stichprobe, x := (x1 , . . . , xn )0 die Realisation. ! Pn j=1 Xj T = t (X1 , . . . , Xn ) = ist eine höchst sinnvolle StichprobenfunktiPn 2 X j j=1 on. 23 Denn mit!Θ = R × R+ ⊂ R2 hängt die Verteilung von T offensichtlich von a θ := ab! b (b) Situation wie in (a), aber jetzt mit σ 2 = 1 bekannt. Dann gilt: T := t(X1 , . . . , Xn ) = n X Xj − X̄ 2 j=1 Aus Statistik II bekannt: 2 P T = Xn−1 ist unabhängig von θ := µ. Spezielle Bezeichnungen von t und T bei der Parameterschätzung: Definition 3.7. (a) Soll mit T = t(X) auf (X , C, P X ) der wahre Parameter θ der tatsächlichen Verteilung von X geschätzt werden, so heißt T ein Schätzer für θ, dabei ist t die Schätzfunktion. Eine Realisation t(x) = t(x1 , . . . , xn ) = T (ω) = θ̂ heißt eine Schätzung oder Schätzwert für θ. (b) Soll mit T = t(X) die Funktion g(θ) geschätzt werden, so heißt T ein Schätzer für g(θ) d und t(x) = g(θ). Bemerkung (Eine wirklich kleine Bemerkung). Meistens ist X = Rn oder X = Rn·m , wobei n der Stichprobenumfang ist. Daher verwenden wir die Borel’sche σ-Algebra, d.h. C = B n bzw. B n·m , schreibe also Rn , B n , P X . 3.2 Methoden zur Gewinnung brauchbarer Punktschätzer Älteste Methoder zur Findung von Punktschätzern: 3.2.1 Momentmethode Beispiel 3.8. Seien X1 , . . . , Xn u. i v. Zufallsvariablen mit P Xi = Exp(λ), i = 1, . . . , n und λ > 0. Suche einen geeigneten Schätzer für λ: 1. Variante (nicht gut für uns) Betrachte die Dichte und Verteilungsfunktion f (x) = λ · e− λ x · 1[0,∞) (x) Z ∞ F (x) = P (X ≤ x) = λ · e−λ x = 1 − e−λ x · 1(0,∞) (x). −∞ 24 Nutze Eigenschaft der Verteilungsfunktion F (x̃0.5 ) = 0.5 und löse die Gleichung nach λ auf: F (x̃0.5 ) = 0.5 1 − e−λ x̃0.5 = 0.5 ⇔ ⇔ − ln(0.5) λ ln(2) − ln(0.5) = λ= x̃0.5 x̃0.5 x̃0.5 = ⇔ Ersetze nun das 50-Quantil x̃0.5 durch xmed = med {x1 , . . . , xn }, d.h. erhalte als Schätzer für λ. λ̂1 = 2. Variante ln(2) med {x1 , . . . , xn } über den Erwartungswert: Mit E (Xi ) = 1 1 ⇔ λ= λ E (Xi ) ersetzte theoretisches Moment E(Xi ) durch empirisches Moment X̄ und erhalte offensichtliche Schätzung für λ: λ̂2 = 1 X̄ . Eigenschaften von λ̂1 äußerst schwierig herzuleiten, hinter der 2. Variante steht ein altbewährtes Konzept, denn: Definition und Satz 3.9. Sei (Xn )n∈N eine Folge von Zufallsvariablen. Falls a ∈ R existiert, sodass ∀ ε > gilt: lim = P (|Xn − a| > 0) = 0, n→∞ dann konvergiert die Folge (Xn )n∈N stochastisch gegen a. Im Falle u. i v. Zufallsvariablen und existierendem l-ten Moment, d.h. sei l ∈ R und P ∈ P, sodass µ(l) := Ep Xil existiert, dann konvergiert die Folge der empirischen l-ten Momente n Zn = 1X l X n i=1 i stochastisch gegen µ(l) . 25 Beweis. Betrachte die Folge (Yn )n∈N mit Yi = Xil , dann ist n 1X Yi = Ȳi , wobei E(Yi ) = E(Xil ) = µ(l) Zn = n i=1 ∀ i = 1, . . . , n Die Behauptung folgt direkt aus dem schwachen Gesetz der großen Zahlen (Siehe 2.2) Bemerkung. Die zusätzlichie Voraussetzung E(X 2l ) < ∞ wird nicht benötigt! Mehr dazu in Stat V. Definition 3.10 (Moment-Methode). Sei (Ω, A, P) statistischer Raum mit parametrischer Verteilungsfamilie P = {Pθ : θ ∈ Θ}, mit Θ ∈ Rk , θ unbekannt, Θ bekannt. Sei g parametrische Funktion und l ∈ N, sowie (Xn )n∈N eine Folge von u. i. v. Zufallsvariablen. Eine Realisation (x1 , . . . , xn ) von (X1 , . . . , Xn ) sei beobachtbar, g(θ) soll geschätzt werden. Dann heißt das folgende Verfahren die Moment-Methode: Beginne mit i = 1, wobei der i-te Schritt: • Existiert Eθ (X1i ) HIER FEHLT WAS! HIIIILFE!!! ∀ θ ∈ Θ (mit X1 als Re- präsentant wegen u. i. v.) Wenn nein =⇒ Momenten-Methode versagt. Falls ja =⇒ berechne Eθ (X1i ) =: µi (θ) • Ist dann g(θ) durch die g(θ) = h µ1 (θ), . . . , µi (θ) ∀θ ∈ Θ bestimmt. Mit h ist stetige Funktion, dann wähle als Schätzer für g(θ): n n n 1X 1X 2 1 X i g(θ) = h Xj , X , ... , X . n j=i n j=i j n j=i j Falls g(θ) nicht in Abhängigkeit von µ1 (θ), . . . , µi (θ) bestimmt ist, erhöhe i um 1, d. h. nehme (i + 1)-ten Schritt. Ist die Lösung im i-ten Schritt nicht eindeutig, so wähle denjenigen Schätzer für g(θ) mit besseren Schätzeigenschaften. Der so gewonnene Schätzer für g(θ) heißt Momentenschätzer für g(θ). Beispiel 3.11. 26 (a) Pθ = N (0, θ2 ), suche Schätzer für g(θ) = θ, θ > 0. 1. Schritt Eθ (X1 ) = 0 ⇒ g(θ) ist nicht bestimmt. 2. Schritt Eθ (X12 ) = σ 2 ⇒ g(θ) ist bekannt. ˆ = θˆ2 = 1 Pn X 2 = X̄ 2 (also h(a, b) = b) g(θ) j n√ j=1 ⇒ θ̂1,2 = ± X̄. √ Da − X̄ 6∈ Θ, folgt: 1 θ̂ = X̄ 2 2 (b) Pθ = N (µ, σ 2 ), 0 θ = (µ, σ 2 ) , Θ = R × (0, ∞) Suche Schätzer für g(θ) = θ: 1. Schritt: ⇒ g(θ) ist nicht bestimmt. 2. Schritt: ⇒ Eθ (X1 ) = µ =: µ1 (µ, σ 2 ) Eθ (X12 = σ 2 + µ2 =: µ2 (µ, σ 2 ) löse beide Gleichungen nach µ und σ 2 auf. µ = µ1 (µ, σ 2 ) und σ 2 = µ2 (µ, σ 2 ), d. h. wähle h(a, b) = a , b − a2 mit h : R2 → R2 , somit folgt dann d = ..U N LESERLICHERM IST.. ⇒ g(θ) Weitere Bemerkungen (inkl. Eigenschaften) zum Momentenschätzer unter Abschnitt 3.3. 3.2.2 Maximum-Likelihood-Methode Bekannte Methode, brauchbare Schätzer für unbekannte Parameter zu gewinnen, ist das Maximum-Likelihood-Prinzip (Prinzip der maximalen Wahrscheinlichkeit). Beispiel 3.12. Ein sechsseitiger Würfel besteht aus roten bzw. schwarzen Punkten (auf jeder Seite). Werfe n = 5 mal, bei 3 Würfen zeigt der Würfel “Rot” an. Gesucht ist eine Schätzung von θ, θ = Anzahl roter Seiten. Offensichtlich ist Θ = {0, 1, . . . , 6}. ML-Prinzip: Berechne für jedes θ ∈ Θ die Wahrscheinlichkeit dafür, dass bei n = 5 Würfen genau drei mal “Rot” zu beobachten ist, und wähle als ML-Schätzung dasjenige θ, für welches diese Wahrscheinlichkeit am größten ist. 27 Formel: X1 , . . . , X5 sind u. i. v. Zufallsvariablen mit P P X1 = Bin(1, p) mit p = Wahr- θ . 6 scheinlichkeit “Rot” = P Pn Xi ⇒ = Bin 5, 6θ . i=1 Xi = Anzahl “rote Würfe” unter 5 mit P 3 2 P5 Somit ist P = 53 · 6θ · 1 − 6θ . i=1 Xi = 3 Erhalte als Ergebnis: θ P( Pn i=1 0 1 2 3 4 5 6 Xi = 3) 0.000 0.032 0.165 0.313 0.329 0.161 0.000 Achtung! Dies ist keine Wahrscheinlichkeitsfunktion, d.h. im Allgemeinen gilt X ⇒ pi 6= 1. für θ = 4 ist die Wahrscheinlichkeit für “3 Mal Rot unter 5 Würfen” am größten, ⇒ θ̂M L 5 X ! Xi = 3 = 4. i=1 Definition 3.13. Sei (Ω, A, P statistischer Raum mit P = {Pθ : θ ∈ Θ} und seien X1 , . . . , Xn Zufallsvariablen. Es gelte: Für alle θ ∈ Θ hat P X1 ,...,Xn die Dichte (diskret oder stetig) fθ : Rn → [0, 1] bzw. [0, ∞) . Sei x = (x1 , . . . , xn )0 , dann heißt LX : Θ → [0, ∞) mit Lx (θ) := fθ (x) die Likelihood-Funktion. Die Funktion lX : Θ → R mit lx (θ) := ln Lx (θ) heißt Log-Likelihood-Funktion. Ein Wert θ̂M L = θ̂M L (x1 , . . . , xn ) ∈ Θ, für den gilt: LX X̂M L = max Lx (θ) θ∈Θ ( bzw. θ̂M L = arg max LX (θ) ) θ∈Θ heißt Schätzwert nach der Maximum-Likelihood-Methode für θ. Sei g : Θ → R eine parametrische Funktion, dann heißt ξˆM L := g θ̂M L die ML-Schätzung für g(θ). 28 zu Definition 3.13 Die Schätzfunktion (Statistik) T mit T (ω) = θ̂M L (X1 (ω), . . . , Xn (ω)) heißt ML-Schätzer für θ. Die Statistik T̃ mit T̃ (ω) = g (T (ω)) = g θ̂M L (X1 (ω), . . . , Xn (ω)) heißt ML-Schätzer für g(θ). Beispiel 3.14. (a) Sei X1 , . . . , Xn u. i. v. mit P Xi = N (µ, σ 2 ), µ ∈ R, σ 2 > 0, d.h. θ = µ ! σ2 mit Xi Θ = R × (0, ∞). Dann besitzt P(µ,σ 2 ) die stetige Dichte (x − µ)2 f(µ,σ2 ) (x) = √ exp − 2σ 2 2πσ 2 1 ! Somit ergibt sich für die gemeinsame Dichte von X1 , . . . , Xn n Y (xi − µ)2 √ exp − f(µ,σ2 ) (x1 , . . . , xn ) = 2 2σ 2 2πσ i=1 ! n n X (xi − µ)2 1 exp − = √ 2σ 2 2πσ 2 i=1 1 = fµ,σ2 (x1 ) · . . . · fµ,σ2 (xn ) ⇒ Likelihood-Funktion: LX µ, σ 2 = √ n 1 2πσ 2 exp − n X (xi − µ)2 i=1 ! 2σ 2 Zur Bestimmung eines möglichen Maximums verwende die Log-Likelihood-Funktion: n n n 1 X 2 lX (µ, σ ) = ln LX (µ, σ ) = − ln(2π) − ln σ − 2 xi − µ 2 2 2 2σ i=1 2 2 29 mit den Ableitungen: n 1 X 1 d ln (LX (µ, σ 2 )) =− 2 2 (xi − µ) (−1) = 2 dµ 2σ i=1 σ n X ! xi − nµ i=1 n d ln (LX (µ, σ 2 )) n 1 1 X (xi − µ)2 = + 4 2 2 dσ 2 σ 2σ i=1 Durch Nullsetzen der Ableitungen erhält man die Lösung n n 1X µ= xi = x̄ , n i=1 1X σ = (xi − x̄)2 , n i=1 2 Pn (xi − x̄) 6= 0 gilt. P Beachte: Falls ni=1 (xi − x̄) = 0, und alle Beobachtungen sind identisch, dann falls i=1 existiert keine simultane Nullstelle mit σ 2 > 0. Überprüfe die hinreichende Bedingung für ein Maximum, bestimme dazu die zweiten Ableitungen: dLX (µ, σ 2 ) n =− 2 2 dµ σ ! n dLX (µ, σ 2 ) n X =− 4 xi − nµ dµ dσ 2 σ i=1 n = − 4 (x̄ − µ) σ n 2 dLX (µ, σ ) n 1X =− 4 − (xi − µ)2 2 dµ 2σ σ i=1 Für die Hesse-Matrix an der Stelle µ̂ = x̄ und σ 2 = H= = 1 n Pn i=1 (xi − x̄)2 hat die Form ! − σn2 (x̄ − µ) P − σn2 (x̄ − µ) 2σn4 − σ16 ni=1 (xi − µ)2 ! ! n − σ̂n2 0 0 σ̂ 2 = −1 · 1 2 0 − σ̂6 n σ̂ 0 σ̂n4 | {z } − σn2 positiv definit Die Hesse-Matrix ist negativ definit (neg. def), und n θ̂M L = arg max lX (µ, σ 2 ) = arg max lX | {z } θ∈Θ θ∈Θ =θ 30 1X x̄, (xi − x̄)2 n i=1 ! Beachte: Falls Pn i=1 (xi − x̄)2 = 0 gilt, so existiert der ML-Schätzer nicht. (b) HIER NICHT SICHER OB θ ODER ANDERER BUCHSTABE!!! Seien X1 , . . . , Xn u. i. v. mit P Xi = Cauchy(θ), einer Verteilung mit viel Wahrscheinlichkeitsmasse an den Rändern. P Xi besitzt die stetige Dichte fθ (x) = 1 1 · π 1 + (x − θ)2 mit θ= ˆ Zentrum der Verteilung. Momentmethode versagt bei der Cauchy-Verteilung, da keine endlichen Erwartungswerte. Aber: θ = med (x). Bestimme ML-Schätzer mit der Likelihoot-Funktion 2 Y n n Y 1 1 1 1 LX (θ) = · . 2 = π 1 + xi − θ π 1 + (xi − θ)2 i=1 i=1 Betrachte die Log-Likelihood-Funktion lX (θ) = ln (LX (θ)). n dlx (θ) X 2(xi − θ) = ⇒ dθ 1 + (xi − θ)2 i=1 und erhalte globales Maximum durch numerische Methoden, denn dlX (θ) dθ = 0 bedeutet aufsuchen der Nullstellen eines Polynoms vom Grad 2n − 1. Für n = 3 erhalte eindeutiges globales Maximum: Mit x1 < x2 < x3 ist θ̂M L = x1 (x3 − x2 )2 + x2 (x3 − x1 )2 ) + x3 (x2 − x1 )2 (x3 − x2 )2 + (x3 − x1 )2 + (x2 − x1 )2 (s. Fergason (1978), JASA 73, 211-213, für n = 3, 4) Interessantes Phänomen, führt zu Irritationen: x1 = −1, x2 = 0 und x3 > 0 beliebig. Dann folgt θ̂(−1,0,x3 )M L = x3 (1 − x3 ) 2(x23 + x3 + 1) HIER FEHLT EINE GRAFIK Falls x3 = 1, so ist θ̂(−1,0,1)M L = 0, für x3 > 1 folgt θ̂(−1,0,1)M L < 0, und limx3 →∞ θ̂(−1,0,x3 )M L = − 12 31 Aber: ML-Schätzung fasst die Beobachtung x3 als Extremwert auf, sofern x3 nur groß genug ist. ⇒ Zentrum der Verteilung wandert gegen das arithmetische Mittel von x1 und x2 , also x1 +x2 2 . (c) Sei X1 , . . . , Xn u. i. v. mit P Xi = Bin(1, p), mit p ∈ [0, 1] und der Zähldichte fp (x) px · (1 − p)1−x x ∈ {0, 1} 0 sonst Schreibe x = (x1 , . . . , xn ). Es folgt die Likelihood-Funktion: Q n px · (1 − p)1−x i=1 i LX (p) = 0 x ∈ {0, 1}n sonst Falls x1 = x2 = · · · = xn = 0: θ̂M L = p̂M L n Y = arg max (1 − p) = arg max (1 − p)n = 0 p∈[0,1] p∈[0,1] i=1 Falls x1 = x2 = · · · = xn = 1: θ̂M L = p̂M L = arg max p∈[0,1] Sei nun x ∈ {0, 1}n mit 0 < lX (p) = Pn n X i=1 n Y p = arg max pn = 1 p∈[0,1] i=1 xi < n, dann ist ! xi ln(p) + n+ n X ! xi ln(1 − p) i=1 i=1 stetig in p ∈ (0, 1) mit lim lX (p) = −∞ p→0 lim lx (p) = −∞ , und p→1 somit hat lX (p) ein Maximum in (0, 1). Differenzieren und Nullsetzten ergibt: dlX (p) ! = 0 ⇐⇒ dp Pn i=1 xi p Erhalte eine eindeutige Lösung: p̂M L = Momentenmethode). 32 1 n P n − ni=1 xi − =0 1−p Pn i=1 xi = x̄ (ist auch Schätzer der 3.2.3 Bayes-Schätzer Bisher: X1 , . . . , Xn Zufallsvariablen mit P Xi ∈ P = {Pθ : θ ∈ Θ} und θ ist unbekannt aber fest, d. h. schätze die Verteilung aus den Realisationen x1 , . . . , xn durch θ̂. Jetzt: Sehe den Parameter selbst als Zufallsvariable mit Verteilung Q (sogenannte a-priori-Verteilung). Definition 3.15. Sei Rm , B m , P X ein Stichprobenraum mit P X = PθX : θ ∈ Θ und eindeutiger Parametrisierung. Auf Θ sei eine σ-Algebra ς gegeben. Dann heißt ein Wahrscheinlichkeitsmaß Q auf (Θ, ς) eine a-priori-Verteilung auf Θ. Die Menge aller a-priori-Verteilungen auf Θ sei mit Q bezeichnet. Sei θ nun selber eine Zufallsvariable mit der sogenannten a-priori-Verteilung Q. Beispiel 3.16. (a) Ist etwa P X = {N (µ, 1) , µ ∈ R}, dann wäre eine sinnvolle a-priori-Verteilung (oder auch Vorbewertung), für die etwa Q ( {µ||µ| > 50} ) “sehr klein” ist, z. B. falls Xi : Wirtschaftswachstum in % im i-ten Jahr. (b) Seien X1 , . . . , Xn u. i..̌ Zufallsvariablen mit P Xi = Bin(1, p), p ∈ [0, 1), z. B. p = Heilungswahrscheinlichkeit eines Medikamentes (vergleiche Beispiel 1.2). Eher unwahrscheinlich als a-priori-Verteilung: Q1 := R [0, 1] (sozusagen: Ohne Vorbewertung) Vorstellbar wären a-priori-Verteilungen der Form: Q2 := Dreieck-Verteilung. A-Priori-Verteilungen werden völlig subjekiv gewählt, auf alle Fälle vor Einsichtnahme in die Datenlage. Mit der Stichprobeninformation über θ wird diese a-priori-Verteilung aktualisiert (korrigiert), und erhalte damit die sog. a-posteriori-Verteilung. Genauer: Sei x = (x1 , . . . , xn )0 ∈ R2 beobachtet, so heißt die bedingte Verteilung von θ bei gegebenem x, d. h. P θ|X=x die a-posteriori-Verteilung über dem Parameterraum Θ bei Beobachtung x zur a-priori-Verteilung Q. Nach dem Satz von Bayes gilt: f (θ|X = x) = R hθ (x) · f (θ) , dabei ist h (x) · f (θ) dθ Θ θ f (θ|X = x) Dichte der a-posteriori-Verteilung f (θ) Dichte der a-priori-Verteilung hθ (x) Dichte von X 33 Verwende nun a-posteriori-Verteilung zur Schätzung von θ (bzw. g(θ)), in dem Z θ · f (θ|X = x) dθ | {z } θ̂Bayes = Θ Erwartungswert der a-posteriori-Verteilung Hier nun eine Definition des Bayes-Schätzers. In der Entscheidungstheorie (Stat VI) wird gezeigt, dass er unter gewissen Voraussetzungen diese Gestalt annimmt. Definition 3.17. Sei (Ω, A, P) statistischer Raum mit P = {Pθ : θ ∈ Θ} und sei Q eine Verteilung auf (Θ, |{z} S ) mit Q ∈ Q, Q Menge aller a-priori-Verteilungen auf σ-Algebra Θ. Q besitzt die Dichte f . Weiterhin seien X1 , . . . , Xn Zufallsvariablen und es gelte: ∀ θ ∈ Θ hat P X1 ,··· ,Xn die Dichte hθ : Rn → [0, ∞)oder[0, 1]. Sei g : : Θ → R parametrische Funktion, dann heißt R Θ b = g (θ) g(θ) · hθ (x) · f (θ) dθ R h (x) · f (θ) dθ Θ θ der Bayes-Schätzer für g(θ) bezüglich der a-priori-Verteilung Q. Beispiel 3.18. Suche Bayes-Schätzer für den Parameter p einer Binomialverteilung mit a-priori-Verteilung Beta(α, β). Seien X1 , . . . , Xn u. i. v. mit P X1 = Bin(1, p), p ∈ [0, 1]. Als a-priori-Verteilung Q des Parameters p sei die Beta-Verteilung mit Parametern α, β > 0 vorgegeben, d. h. Q = Beta(α, β) besitzt die Dichte 1 pα−1 (1 − p)β−1 , p ∈ [0, 1] B(α, β) Z 1 = pα−1 (1 − p)β−1 dp für die gilt: fα,β (p) = wobei B(α, β) | {z } 0 Beta−F unktion B(α, β) = Γ(α) Γ(β) mit Γ = Gammafunktion . Γ(α + β) Γ(α) = (α − 1) · Γ(α − 1). P Betrachte nun Y = ni=1 Xi , d. h. Y ist die Anzahl der Erfolge n Versuchen mit P Y = Beachte: Bin(n, p) Mit g(p) = p ergibt sich als Bayes-Schätzer für p bezüglich Q = Beta(α, β) durch: R g(p)Bayes = pBayes = Θ 34 g(θ) · hp (y) · f (p) dp R , h (y) · f (p) dp Θ p wobei hp (y) = n y · py · (1 − p)n−y · 1 Beta(α,β) ∀ y ∈ {0, 1, . . . , n}. Berechne also: R1 pBeta(α,β) = n 1 py (1 − p)n−y B(α,β) pα−1 (1 − p)β−1 dp y 0 R 1 n 1 py (1 − p)n−y B(α,β) pα−1 (1 − p)β−1 dp 0 y Z 1 n Γ(α + β) α+y n−y+β−1 p · · p (1 − p) dp y Γ(α) Γ(β) 0 Z 1 n Γ(α + β) Nenner = · · pα+y−1 (1 − p)n−y+β−1 dp y Γ(α) Γ(β) 0 R 1 α+y p (1 − p)n−y+β−1 dp ⇒ pBayes (y) = R 10 pα+y−1 (1 − p)n−y+β−1 dp 0 B(α + y + 1, n − y + β) = B(α + y, n − y + β) Γ(α) Γ(β) Γ(α + y + 1) Γ(n − y + β) Γ(n + α + β) B(α, β) = →= · Γ(α + β) Γ(n + α + β + 1) Γ(α + y) · Γ(n − y + β) α+y Γ(α + 1) = α · Γ(α) → = α+β+n Zähler = Also speziell für Beta(1, 1) = R[0, 1] ergibt sich p̂Bayes = Der ML-Schätzer p̂M L = y n y+1 n+2 ergibt sich offenbar keine der a-priori-Verteilungen Beta(α, β). Beispiel 3.19. Suche Bayes-Schätzer für den parameter µ einer Normalverteilung mit a-priori-Normalverteilung. Seien X1 , . . . , Xn u. i. v. mit P Xi = N (µ, σ02 ), µ ∈ R, σ02 > 0 gegeben. Als a-priori-Verteilung Q des Parameters µ wähle eine Normalverteilung Q = N (0, κ2 ), mit κ2 > 0, d.h. Q besitzt die Dichte µ2 fκ (µ) = √ exp − 2 . 2κ 2πκ2 1 Die gemeinsame Dichte von P X1 ,...,Xn lautet: hµ (x) = 1 p !n 2πσ02 exp Bestimme Bayes-Schätzer für g(µ) = µ: 35 n 1 X − 2 (xi − µ)2 2σ0 i=1 ! . Betrachte zunächst !n ! n µ 1 X p exp − 2 − 2 (xi − µ)2 fκ (µ) · hµ (x) = √ 2 2 2κ 2σ 2πκ 2πσ0 0 0 i=1 n 1 X 2 1 1 n 2 µ + nx x̄ · µ − =− + 2 2 2 κ2 σ0 σ0 2σ02 i=1 i −1 1 n 2 mit τ = folgt + κ2 σ 2 ! !n n 1 2nτ 2 1 1 1 X 2 2 p x · exp − 2 µ − 2 x̄µ =√ exp − 2 2σ0 i=1 i 2σ0 σ0 2πκ2 2πσ02 ! √ 2 2τ 2 1 nτ 2 µ − 2 x̄ = c(κ, x) · √ · exp − p σ0 2πκ2 2πσ02 ! ! √ n n nτ x2 2τ 2 1 X 2 1 p x + exp − 2 mit c(κ, x) = √ 2σ0 i=1 i 2τ 2 σ06 2πκ2 2πσ02 1 1 Also ist fκ (µ) · hµ (x) = c(κ, x) | {z } die Dichte von N unabh. von µ nτ 2 2 x̄, τ . σ02 Somit erhalten wir nun den Bayes-Schätzer für µ: R µ̂Bayes (x) = Θ R µ · fκ (µ) · hµ (x) dµ f (µ) · hµ (x) dµ Θ κ c(κ, x) · 1. Moment einer N = c(κ, x) nτ nx̂ = = 2 x̄ = σ0 σ02 κ12 + σ12 2 0 nτ 2 x̄, τ 2 σ02 nκ2 σ02 + nκ2 | {z } x̄. <1,d.h. x̄ wird geschrumpft Für κ → ∞ erhalte µ̂Bayes (x) = x̄ = µ̂M L . Mehr zu Bayes-Schätzer in Statik VI - Entscheidungstheorie. Weitere Konzepte zur Findung von Schätzern: Punktschätzer, Lineare Modelle. 3.3 Kriterien zur Beurteilung der Güte einer Schätzfunktion Ein Motivationsbeispiel zur Einführung Beispiel 3.20. Sei Xi die Lebenszeit des i-ten Bauteils einer Charge mit P Xi = Exp(λ), λ > 0, λ ist dabei die Ausfallrate. 36 Hier von Interesse: Halbwertszeit, d. h. die Zeit, die von der Hälfte überdauert wird. Lieferant stellt zwei identisch aussehende Versionen her: Kosten: prog. HWZ: Version A billig 69.3 Tage Version B teuer 55.4 Tage Der Kunde erhält Lieferung von Teilen (bezahlt als Version A), von denen sehr schnell die ersten verwendeten Teile ausfallen. Ziehe eine Stichprobe vom Umfang n = 99 und beobachte die Lebenszeiten Xi mit 1 ≤ i ≤ 99 in Tagen. Ziel: Untersuche die Halbwertszeit (HWZ) der gelieferten Teile. Mit P Xi = Exp(λ), nehme also an, dass es zwei Möglichkeiten für λ gibt, d. h. λ ∈ {λ1 , λ2 } = Θ. Zusammenhang zwischen Ausfallrate λ und Halbwertszeit h(λ): 1 ! = Pλ (X ≥ h(λ)) = 1 − Pλ (x ≤ h(λ)) 2 = 1 − Fλ (h(x)) 1 ⇔ exp (−λ · h(λ)) = 2 ⇔ −λ · h(λ) = − ln(2) ⇔ h(λ) = ln(2) ln(2) bzw. λ = λ h(λ) Also: Version A Version B HWZ h(λ) 69.3 35.4 Ausfallrate λ1 = ln(2) ≈ 0.01 69.3 ln(2) λ2 = 35.4 ≈ 0.0125 Das Modell lautet daher: X1 , . . . , Xn u. i. v. mit P Xi = {Exp(λ) : λ ∈ {0.01, 0.0125}}. Die Stichprobe liefert den Beobachtungsvektor x ∈ R99 mit dem arithmetischen Mittel x̄ = 92.66 und dem Median xmed = 63.2. Zum Schätzen der Halbwertszeit betrachte 5 Möglichkeiten: 1. Momentschätzer Es gilt Eλ (Xi ) = 1 . λ Mit h(λ) = ĥM om (x) = ln(2) · X̄ (im Bsp. XXXXX.XXXX) 37 ln(2) λ = ln(2) · E(Xi ) ist also 2. ML-Schätzer Die Dichte von PλXi ist fλXi = λ · exp(−λ x) · 1[0,∞) (x). Die gemeinsame Dichte fλX1 ,...,X99 von PλX1 ,...,X99 ist fλX1 ,...,X99 (x1 , . . . , x99 ) = λ99 · exp −λ · 99 X ! xi i=1 =: Lx (λ) (falls xi > 0 für i = 1, . . . , 99). Der ML-Schätzer wählt dasjenige λ ∈ Θ aus, für das Lx (λ) maximal ist, also entweder λ1 oder λ2 : Somit ist λ̂irgendwas (x) = λ1 ⇔ Lx (λ1 ) > Lx (λ2 ) ! ! n n X X ⇔ λ99 xi > λ99 xi 1 · exp −λ1 2 · exp −λ2 i=1 99 X ⇔ 99 · ln(λ1 ) − λ1 · ⇔ (λ1 − λ2 ) · | {z } >0 i=1 99 X i=1 xi > 99 · ln(λ2 ) − λ2 · 99 X xi i=1 xi > 99 · (ln(λ2 ) − ln(λ1 )) i=1 99 1 X ln(λ2 ) − ln(λ1 ) ⇔ xi > 99 i=1 λ2 − λ1 ⇒ x̄ > IrGeN | {zdW as} =89.26 Falls x̄ < 89.26, entscheide man sich für λ2 als ML-Schätzer. Falls x̄ = 89.26, also Lx (λ1 ) = Lx (λ2 ), ist der ML-Schätzer nicht eindeutig, somit willkürliche Wahl von λ. ML-Schätzer der Halbwertszeit: ĥM L = ln(2) · 1 λ̂M L (x) (Im Beispiel: Aus λ̂M L (x) = λ1 = 0.01 folgt ĥM L (x) = 69.3). 3. Empirische Halbwertszeit Die Hälfte der Bauteile bis zur Zeit xmed = 63.2 ausgefallen. Wähle daher als Schätzer ĥmed (x) = xmed 38 (Im Beispiel: 63.2 = ĥmed (x)) 4. Pessimistischer Schätzer Gehe immer – unabhängig von den Beobachtungen – von einer Lieferung der Version B, d. h. der schlechteren, aus. (Im Beispiel: ĥpess (x) = 55.4 ∀x ∈ R99 ) 5. Optimistischer Schätzer Gehe immer von einer Lieferung der Version A, also der besseren, aus. (Im Beispiel: ĥopt (x) = 55.4 ∀x ∈ R99 ) Darstellung der Schätzfunktionen ĥM om , ĥM L , ĥpess und ĥopt : ... ... . . . Hier fehlt . . . eine Grafik ... ... Der Schätzer ĥmed ist in diesem Bild nicht darstellbar, da der Median alle Einzelbeobachtungen benötigt und nicht x̄. Es stellt sich die Frage: Welchen Schätzer soll man wählen? 3.3.1 Mean Square Error (MSE) Wann ist ein Schätzer gut? Beispiel 3.21 (Fortsetzung von Bsp. 3.20). Ein Schätzer ist immer dann gut, falls 2 A(x, λ1 ) = ĥ(x) − h(λ) möglichst klein wird. Dieser Term hängt vom wahren Parameter λ und den Beobachtungen x ab. 1. Fall: Sei λ = λ1 = 0.01 und h(λ1 ) =: h1 = 69.3, d. h. der Kunde erhält tatsächlich Version A. Dann ist 2 Aopt (x, λ1 ) = ĥopt (x) − h(λ) = 0 ∀ x ∈ R99 . Vergleich von ĥopt , ĥM L und ĥpess : 39 Falls x̄ < 79.9: AM om (x, λ1 ) > AM L (x, λ1 ) = Apess (x, λ1 ) x̄ ∈ (79.9, 89.26): AM om (x, λ1 ) < AM L (x, λ1 ) = Apess (x, λ1 ) x̄ ∈ (89.26, 120.0): AM L (x, λ1 ) < AM om (x, λ1 ) < Apess (x, λ1 ) | {z } =0 x̄ > 120.0: AM L (x, λ1 ) < Apess (x, λ) < AM om (x, λ) 2. Fall: λ = λ2 = 0.0125 und h2 (λ) = 55.4, d. h. der Kunde erhält Version B. Hier ist Apess (x, λ2 ) = 0. Vergleich von ĥopt , ĥM L und ĥopt : Analog zu Fall 1. Fazit: Unter den vier Schätzern ist keiner für alle x ∈ R99 und jedes λ ∈ Θ der Beste. A wird auch als Verlust bezeichnet, den wir bei der Wahl des Schätzers ĥ erleiden. Aus Beispiel 3.21 ist sinnvoll: Betrachte den durchschnittlichen oder erwarteten Verlust 2 Eλ ĥ(x) − h(λ) . (∗) Wähle die Schätzfunktion ĥ so, dass (∗) minimal wird. Dazu die folgende Definition: Definition 3.22. Sei (Ω, A, P) ein statistischer Raum mit P := {Pθ : θ ∈ Θ} und sei g : Θ → R eine parametrische Funktion und X1 , . . . , Xn Zufallsvariablen. Sei ĝ(θ) := T := t(X1 , . . . , Xn ) ein Schätzer für g(θ). Dann heißt M SEθ (ĝ(θ)) := Eθ (ĝ(θ) − g(θ))2 der erwartete Verlust oder Mean Squared Error (MSE) von ĝ(θ) bei Vorliegen von θ. Bemerkung 3.23. (a) Im Allgemeinen hängt die Verteilung von ĝ(θ) − g(θ) von θ ab. (b) Abgesehen von Ausnahmefällen gibt es keinen Schätzer, der verglichen mit jedem anderen Schätzer für jedes θ ∈ Θ einen kleineren MSE hätte als z. B. X1 , . . . , Xn u. i. v. mit P Xi besitzt fθ (x), θ ∈ R. θ sei zu schätzen, d. h. g(θ) = θ. Suche θ̂∗ für θ, sodass ∗ Eθ θ̂ − θ 2 ≤ Eθ θ̂ − θ für jedes θ ∈ Θ und jeden Schätzer θ̂ gilt. Betrachte den Schätzer θ̂(X1 , . . . , Xn ) = θ0 , θ0 fest, 40 2 2 ⇒ Eθ0 θ̂(X1 , . . . , Xn ) − θ0 = Eθ0 (θ0 − θ0 )2 = 0. Konstruiere solchen Schätzer für beliebiges, aber festes θ0 , dann folgt für θ̂∗ mit obigen Eigenschaften: ∗ Eθ θ̂ − θ 2 = 0 ∀θ ∈ Θ. Einen solche Schätzer gibt es im Allgemeinen aber nicht! Beispiel 3.24 (Fortführung von Beispiel 3.21). 1. Fall Falls λ = λ1 = 0.01 bzw. h(λ1 ) =: h1 =: 69.3: Momentenschätzer: 2 M SEλ1 (ĥM om ) = Eλ1 ĥM om (X1 , . . . , Xn ) − h(λ1 ) 2 ln(2) = Eλ1 X̄ · ln(2) − λ1 2 = (ln(2))2 · Eλ1 X̄ − Eλ1 (X̄) 1 = (ln(2))2 · V arλ1 (X1 ) n 2 1 1 = ln(2) = 48.53 99 0.01 (erw. Verlust des Momentenschätzers für λ = λ1 = 0.01) ML-Schätzer: 2 M SEλ1 (ĥM L ) = Eλ1 ĥM L (X1 , . . . , Xn ) − h(λ1 ) = (55.4 − 69.3)2 · Pλ1 (X̄ < 89.26) + (69.3 − 69.3)2 · Pλ1 (X̄ ≥ 89.26) ! n n X X = 193.21 · Pλ1 Xi < 89.26 · n ( Xi ist Erl(n, λ)-verteilt) Z i=1 89.26·n = 193.21 · λ1 0 i=1 n−1 (λ1 · x) e−λ·x dx (n − 1)! = 193.21 · 0.1410 = 27.25. Alternative Berechnung: Sei X̄ − Z= q 1 λ1 1 λ1 41 · √ n, dann ist mit Satz 2.10 W PλZ1 −→ Pλ1 X̄ − 1 λ1 1 λ1 89.26 − √ · n< 1 1 λ1 · √ ! n λ1 89.26 − 100 √ = Pλ1 Z < · 99 100 {z } | ≈−1.07 ≈ 1 − Φ(1.07) ≈ 0.1423 Empirische Halbwertszeit: Exakte Verteilung von ĥmed = med(x1 , . . . , xn ) ist schwierig zu bestimmen. Aber für große n und unabhängig identisch verteilte X1 , . . . , Xn mit P Xi = Exp(λ) gilt (vgl. Theorem 8.51 aus Arnold, Balakrishnan, Nagaraja: A first course in order statistics): P med(X1 ,...,Xn ) approx ∼ N 1 1 ln(2) , 2 λ nλ . Somit ergibt sich 2 M SEλ1 (ĥmed ) = Eλ1 ĥmed (X1 , . . . , Xn ) − h(λ1 ) = V arλ1 ((med(X1 , . . . , Xn )) 1 1 = = 101.11 ≈ 2 nλ1 99 · 0.012 Pessimistischer Schätzer: 2 M SEλ1 (ĥpess ) = Eλ1 ĥopt (X1 , . . . , Xn ) − h(λ) = (55.4 − 69.3)2 = 193.21 Optimistischer Schärtzer: M SEλ1 (ĥopt ) = Eλ1 ((X1 , . . . , Xn ) − h(λ1 ))2 = (69.3 − 69.3)2 = 0 42 2. Fall λ = λ2 = 0.0125 bzw. h(λ2 ) = 55.4. Analog zum ersten Fall erhalten wir: M SEλ2 (ĥM om ) = 31.00 M SEλ2 (ĥM L ) = 23.19 M SEλ2 (ĥmed ) = 64.65 M SEλ2 (ĥpess ) = 0 M SEλ2 (ĥopt ) = 193.21 Keiner der fünf vorgestellten Schätzer minimiert für alle λ ∈ {λ1 , λ2 } den M SEλ ! Satz 3.25 (zur Berechnung des M SE). Unter der Definition 3.22 gilt: M SEθ (ĝ(θ)) = V arθ (ĝ(θ)) + (Eθ (ĝ(θ)) − g(θ))2 Beweis. 2 M SEθ (ĝ(θ)) = Eθ ĝ(θ) |{z} abh. von ZV. − g(θ) |{z} fest 2 = Eθ ĝ(θ) − Eθ ĝ(θ) + Eθ ĝθ − g(θ) {z } | {z } | a b 2 2 = Eθ ĝ(θ) − Eθ ĝ(θ) + Eθ ĝθ − g(θ) · Eθ ĝ(θ) − g(θ) − 2 · Eθ ĝ(θ) − Eθ ĝ(θ) {z } | =0 2 2 = Eθ ĝ(θ) − Eθ g(θ) + Eθ ĝ(θ) − g(θ) 2 = V ar ĝ(θ) + Eθ ĝ(θ) − g(θ) Die Zerlegung des MSE motiviert weitere Gütekriterien: 3.3.2 Erwartungstreue und Verzerrung Definition 3.26. Situation wie in (3.22) 43 (a) Eine Schätzfunktion T = t(X) heißt erwartungstreu oder unverzerrt, (unbiased) für g(θ), falls Eθ (T ) = g(θ) gilt für alle θ ∈ Θ. (b) T heißt verzerrt (unbiased), falls Eθ (T ) = g(θ) + b(θ), mit b(θ) = 0 für mindestens ein θ ∈ Θ, und (c) Gilt Eθ (Tn ) = Eθ (t(X1, . . . , Xn )) = g(θ)+bn (θ) und limn→∞ bn (θ) = 0, dann heißt Tn asymptotisch erwartungstreu. Bemerkung. (a) Die Einschränkungen auf unverzerrte Schätzer befreit uns in (3.20) von den lokalen Schätzern ĥpess und ĥopt , aber auch ML-Schätzer ĥM L (X1 , . . . , Xn ) fällt weg. (b) Falls T erwartungstreu für g(θ), so folgt im Allgemeinen nicht, dass g(T ) erwartungstreu für g(θ) ist! (c) Satz 3.25 besagt: M SE = V ar + Bias2 (d) Wünschenswert: T ist erwartungstreu und T besitzt kleine Varianz, jedoch oftmals nicht beides vereinbar. Illustration ... ... ... ... ... ... Satz 3.27. Seien X1 , . . . , Xn Zufallsvariablen mit E(Xi ) = µ (für alle i ∈ 1, . . . , n), P µ ∈ R, σ 2 > 0. Dann ist T := µ̂ := X̄ = n1 ni=1 Xi erwartungstreu. Beweis. Eµ (X̄) = Eµ 1 n Pn i=1 Xi = 1 n Pn i=1 Eµ (Xi ) = 1 n Pn i=1 µ = µ. Nun zu Eigenschaften von Varianzschätzern: Satz 3.28. Seien X1 , . . . , Xn stochastisch unabhängige Zufallsvariablen mit E(Xi ) = µ und V ar(Xi ) = σ 2 , i ∈ {1, . . . , n}, µ ∈ R,σ 2 > 0. Dann folgt: P ˆ 21 := s2 = 1 n (Xi − X̄)2 ist asymptotisch erwartungstreu für σ 2 . (a) T1 := sigma i=1 n 44 (b) T2 := σ̂22 := σ̂ 2 = 1 n−1 Pn i=1 (Xi − X̄)2 ist erwartungstreu, falls n > 1. Beweis. Sei θ = (µ, σ 2 )T ∈ R. (a) 1 2 (Xi − µ + X̄ − µ) Eθ (s ) = Eθ n ! n 1X = Eθ (Xi − µ)2 + Eθ (Xi − µ)2 n i=1 X n 1 − 2 · Eθ (Xi − µ) ·(Xi − µ) n i=1 | {z } 2 =X̄−µ X n 1 2 = Eθ (Xi − µ) − Eθ (X̄ − µ)2 n i=1 n 1X Eθ (Xi − µ)2 −V ar(X̄) = {z } n i=1 | =V ar(Xi ) 1 n−1 1 2 σ2 2 2 2 Daraus folgt Eθ (s ) = · n · σ − σ = σ − =σ · . n n n 2 n σ Für bn (s2 ) = − als Verzerrung gilt: limn→∞ bn (s2 ) = 0, d. h. s2 ist asymn ptotisch erwartungstreu für σ 2 . 2 (b) folgt direkt aus (a), denn n n−1 2 n n 2 2 ·σ = · σ = σ2. E(s2 ) = Eθ (σ̂ ) = Eθ n−1 n−1 n−1 n Durchaus nützlich zur Findung erwartungstreuer Schätzer ist: Satz 3.29. Sei T := t(X1 , . . . , Xn ) ein Schätzer und g(θ) parametrische Funktion mit θ ∈ Θ und es gilt: Eθ (t(X)) = Eθ (T ) = a + c · g(θ), a, c ∈ R, c 6= 0 konstant. T −a erwartungstreu für g(θ). c 1 T −a 1 Beweis. Es gilt: Eθ = Eθ (T ) − a = a + c · g(θ) − a = g(θ). b c c Dann ist 45 Dieser Satz findet z. B. Anwendung bei: X1 , . . . , Xn u. i. v. Zufallsvariablen mit P Xi = R[0, θ] (Rechteckverteilung), d. h. die 1 Verteilung der Xi besitzt die Dichte fθ (x) = 1[0,θ] (x). θ Mit Eθ (Xi ) = 21 θ ist Eθ (2X̄i ) = θ ein erwartungstreuer Schätzer für θ. (2X̄ ist Schätzer nach der Momentenmethode) 3.3.3 Konsistenz Fordere: Die Schätzfunktion θ̂ soll möglichst nahe bei dem zu schätzenden Parameter θ liegen. Die Quantitative Präzision ist auf verschiedene Weisen möglich. 1. Parameter θ soll im Durchschnitt von der Schätzung θ̂ getroffen werden, → Erwartungstreue 2. Die Schätzung θ̂ wird mit steigendem Stichprobenumfang immer genauer und im Grenzfall (n → ∞) verschwindet der Schätzfehler (θ̂ − θ), → Konsistenzbegriff Definition 3.30. Sei (Ω, A, P) ein statistischer Raum, und X1 , . . . , Xn Zufallsvariablen mit gemeinsamer VerteilungPθX1 ,...,Xn , θ ∈ Θ. Sei weiterhin g : Θ → R parametrische Funktion. Eine Stichprobenfunktion Tn = tn (X1 , . . . , Xn ) für g(θ) heißt: (a) schwach konsistent für g(θ), falls lim Pθ (|Tn − g(θ)| > ε) = 0 ∀ ε > 0, θ ∈ Θ. n→∞ (b) stark konsistent für g(θ), falls Pθ lim Tn = g(θ) = 1 ∀ θ ∈ Θ. n→∞ (c) konsistent im quadratischen Mittel für g(θ), wenn 2 n→∞ Eθ Tn − g(θ) −−−→ 0 (MSE gegen 0) 46 ∀θ∈Θ Bemerkung 3.31. (a) Konsistenzbegriffe stehen in direktem Zusammenhang zu den Konvergenzbegriffen (Vergleiche (2.8): schwache Konvergenz). Beim schwächeren Konsistenzbegriff werden nicht spezielle Realisationen der Schätzfunktion betrachtet, sondern Wahrscheinlichkeiten für bestimmte Ereignisse. (b) Es gilt: Schwache Konvergenz ) Konsistenz i. q. M. =⇒ schwache Konsistenz im Allg. starke Konsistenz ⇐⇒ Konsistenz i. q. M. (c) Ist θ̂ stark oder schwach konsistent und g stetige parametrische Funktion, dann ist ĝ(θ) konsistent für g(θ) in dem entsprechenden Sinne. n→∞ (d) Konsistenz i. q. M. ⇔ M SEθ (Tn ) −→ 0 und mit (3.25) ist M SEθ (Tn ) = V arθ (Tn ) + b2n (Tn ), sodass n→∞ V arθ (Tn ) −→ 0 n→∞ M SEθ (Tn ) −→ 0 ⇐⇒ Bias (T ) = b (T ) n→∞ −→ 0 θ n θ n (e) Überprüfe schwache Konsistenz mittels Tscherbyschev-Ungleichung, denn aus Eθ (Tn ) = g(θ) ∀ θ ∈ Θ folgt Pθ (|Tn − g(θ)| > ε) ≤ V arθ (Tn ) . ε2 Für die starke Konvsistenz verwende die Kolmogoriv’sche Ungleichung, Nachweis gestaltet sich häufig schwierig. (∗) Satz 3.32. Der in (3.10) definierte Momentschätzer für g(θ) ist n Tn = ĝ(θ) = h n n 1X 1X 2 1X i Xj , Xj , . . . , X n j=1 n j=1 n j=1 j ! , ist schwach konsistent, wobei h eine stetige Funktion und g(θ) in Abhängigkeit von µ1 (θ), . . . , µn (θ) bestimmt ist. 47 Beweis. Wegen (3.9) gilt für jedes r ∈ N, 1 ≤ r ≤ i: µ̂r := Pn i=1 Xir konvergiert stochastisch gegen das theoretische Moment µr (θ). (∗) Mit der Stetigkeit von h gilt: ∀ θ > 0 ∃ ε > 0, sodass, falls |µ̂1 − µ1 | ≤ ε , . . . , |µ̂i − µi | ≤ ε, dann gilt: |h (µ̂1 , . . . , µ̂i ) − h (µ1 (θ), . . . , µi (θ))| ≤ δ. Also ist |h (µ̂1 , . . . , µ̂i ) − h (µ1 (θ), . . . , µi (θ))| > δ, falls mind. ein |µ̂i − µi (θ)| > δ. Schließlich gilt: 0 ≤ Pθ (|h(µ̂1 , . . . .µ̂i ) − h (µ1 (θ), . . . , µi (θ))| > θ) ≤ Pθ ( min. ein |µ̂r − µr (θ)| > ε) ≤ Pθ (|µ̂1 − µ1 (θ)| > ε)) + · · · + Pθ (|µ̂i − µi (θ)| > ε)) | {z } {z } | →0 wegen (∗) →0 wegen (∗) → 0, da nur endlich viele Summanden i vorliegen. 3.3.4 Effizienz und Cramer-Rao-Ungleichung In (3.25) hatten wir: M SEθ ĝ (θ) = V arθ ĝ(θ) + Bias2 , Wobei Bias2 = 0 für alle erwartungstreuen Schätzer ĝ(θ), d.h. gemessen am MSE wäre unter den erwartungstreuen Schätzern derjenige besser, der die kleinere Varianz besitzt. Definition 3.33. (a) Seien T1 = t1 (X1 , . . . , Xn ) und T2 = t2 (X1 , . . . , Xn ) erwartungstreu für die parametrische Funktion g(θ). Dann heißt T1 effizienter als T2 zur Schätzung von g(θ), falls V arθ (T1 ) ≤ V arθ (T2 ) ∀ θ ∈ Θ und V arθ (T1 ) ≤ V arθ (T2 ) für wenigstens ein θ ∈ Θ. (b) Sei M die Menge aller erwartungstreuen Schätzer t(X1 , . . . , Xn ) für g(θ), so heißt 48 ein Schätzer t∗ (X1 , . . . , Xn ) effizient für g(θ), falls t∗ (X1 , . . . , Xn ) ∈ M und V arθ (t∗ (X1 , . . . , Xn )) ≤ V arθ (T2 ) ∀ θ ∈ Θ und ∀ t ∈ M (c) Ist M∗ die Menge aller asymptotisch erwartungstreuen Schätzer für g(θ), so heißt t∗n (X1 , . . . , Xn ) asymptotisch effizient, wenn t∗n (X1 , . . . ,Xn ) ∈ M∗ und lim V arθ (t∗ (X1 , . . . , Xn )) ≤ lim V arθ (t∗ (X1 , . . . , Xn )) n→∞ n→∞ ∀ θ ∈ Θ und tn ∈ M∗ . Wie finden wir effiziente Schätzer? Beispiel 3.34. Seien X1 , . . . , Xn u. i. v. Zufallsvariablen mit P Xi = {Bin(1, p) : p ∈ (0, 1)}. Der Schätzer X̄ := t∗ (X1 , . . . , Xn ) ist erwartungstreu für p mit V arp (X̄) = n 1 1 X · p · (1 − p). V ar (X ) = p i n2 i=1 n Betrachte einen beliebigen anderen erwartungstreuen Schätzer t(X1 , . . . , Xn ) für p. Ist es möglich, dass t(X1 , . . . , Xn ) für irgendein p ∈ (0, 1) eine kleinere Varianz hat als X̄? Da t(X1 , . . . , Xn ) erwartungstreu ist für p, gilt: gem. Zähldichte p = Ep (t(X1 , . . . , Xn )) = X x1 ··· X z }| { X1 ,...,Xn t(x1 , . . . , xn ) · fp (x1 , . . . , xn ) xn P P p xi · (1 − p)n− x1 , falls xi ∈ {0, 1} mit fpX1 ,...,Xn (x1 , . . . , xn ) = 0, sonst. 49 Also gilt für p ∈ (0, 1): p= 1 X 1 X ··· x1 =0 t(X1 , . . . , Xn ) · p P xi · (1 − p)n− P xi xn =0 {z } | d 1= ( ∗ ) dp X X X P P 1 1 xi −1 n− xi xi ) · = xi · p · (1 − p) · xi · − (n − p 1−p X X P P 1 1 xi −1 n− xi = xi · p · (1 − p) · xi · − (1 − xi ) · p 1−p | {z } | {z } X ,...,X ableiten ⇒ fθ d. h. 1 = 1 X 1 X ··· x1 =0 = Ep n 1 =lp∗ (xi ) (x1 ,...,xn ) A(x1 , . . . , xn ) · n X xn =0 lp∗ (xi ) · fpX1 ,...,Xn (x1 , . . . , xn ) i=1 t(X1 , . . . , Xn ) · n X ! lp∗ (Xi ) i=1 Nun ist Ep Pn ∗ i=1 lp (Xi ) Pn = i=1 X u.i.v. Ep lp∗ (Xi ) i = n · Ep lp∗ (X1 ) mit X1 als Reprä- sentant, und mit Ep lp∗ (X1 ) = 1 X i=0 lp∗ (x) · f X1 (xi ) | {z } Bernulli-Vert. = lp∗ (0) · fpX1 (0) + lp∗ (1) · fpX1 (1) 1 1 = (0 − 1 · ) · (1 − p) + (1 · − 0) 1−p p = −1 + 1 = 0 Erhalte daher: 1= t(X1 , . . . , Xn ) · n X ! lp∗ (Xi ) i=1 = Covp t(X1 , . . . , Xn ) , n X − Ep | t(X1 , . . . , Xn ) · Ep {z } | =p n. Vor. ! lp∗ (Xi ) i=1 v u q u ≤ V arp (t(X1 , . . . , Xn )) · tV arp n X i=1 50 ! lp∗ (Xi ) (+) n X ! lp∗ (Xi ) i=1 {z =0 } Da X1 , . . . , Xn u. i. v. sind, gilt: V arp n X ! lp∗ (Xi ) = i=1 n X V arp lp∗ (Xi ) = n · V arp lp∗ (X1 ) i=1 = n · Ep d. h. V arp n X 2 lp∗ (Xi ) ! lp∗ (Xi ) = n · lp∗ (0)2 · fpXi (0) + lp∗ (1)2 · fpXi (1) i=1 " 1 − 1−p =n· =n· 2 1 1 + 1−p p 2 # 1 · (1 − p) + ·p p =n· 1 p · (1 − p) Durch einsetzen in (+) folgt: ⇒ V arp (t(X1 , . . . , Xn )) ≥ 1 n· 1 p·(1−p) = p · (1 − p) = V arp (X̂), n d. h. es gibt unter den erwartungstreuen Schätzern für p keinen effizienteren Schätzer als X̄. Das Ergebnis aus (3.34) lässt sich verallgemeinern, nämlich in der Klasse der regulärten Verteilungsfamilien. Definition 3.35. Sei (Ω, A, P) statistischer Raum mit P = {Pθ : θ ∈ Θ} und sei X eine Zufallsvariable. Für jedes x ∈ R definiere die Likelihood LX (θ) : Θ → [0, ∞) mit LX (θ) = fθ (x).Es gilt:(R1) Θ ist ein offenes Intervall in R. (R2) Entweder gibt es ein abzählbares T ⊂ R, sodass für alle θ ∈ Θ PθX diskret ist mit Zähldichte fθ und Träger T . (R3) L0X (θ) existiert und ist stetig für alle θ ∈ Θ. R 0 Pn 0 X X (R4) i=1 LX (θ) = 0 falls Pθ diskret, und T LX (θ) dx = 0 falls Pθ stetig. Unter den Regularitätsbedingungen (R1) – (R4) heißt P X reguläre Verteilungsfamilie. Beispiel 3.36 (Fortführung von (3.34)). P X {Bin(1, p) : p ∈ (0, 1)} ist reguläre Familie, denn: (R1) Θ = (0, 1) ist Teilmenge des R und offenes Intervall. 51 (R2) PpX hat die diskrete Dichte fp (x) = px · (1 − p)1−x falls x ∈ {0, 1}, 0 sonst. (R3) Für x = 0 ist Lx (p) = fp (0) = (1 − p). Das ist differenzierbar und die Ableitung L0x (p) = 1 für alle p ∈ (0, 1) ist stetig. Für x = 1 ist Lx (p) = fp (1) = p für alle p ∈ (0, 1) differenzierbar und auch die Ableitung L0x (p) ist stetig. Für x 6∈ {0, 1} ist Lx (p) = 0. Somit ist Lx differenzierbar und L0x (p) = 0∀p ∈ Θ, und L0x ist stetig. (R4) Der Träger von PpX ist aber T = {0, 1} für alle p ∈ Θ. Damit gilt 1 X L0x (p) = −1 + 1 = 0 i=0 Somit ist P X eine reguläre Familie. Bemerkung 3.37. Bei diskretem PθX gilt ∀θ ∈ Θ: X 1= fθ (x) = X Lx (θ) x∈T x∈T d X ⇒ 0= Lx (θ) dθ x∈T Da L0x (θ) = d L(θ), ist (R4) äquivalent zu: dθ X d d X ! ! Lx (θ) = 0 = Lx (θ). dθ x∈T dθ x∈T Bei endlichem Träger gilt also (R4) immer dann, wenn L0x (θ) für jedes x ∈ T existiert, dies wird durch (R3) garantiert. Zeige genauso bei stetigem PθX : Z ∞ (R4) erfüllt ⇔ ! L0x (θ) dx = −∞ d dθ Z ∞ Lx (θ) dx −∞ Beispiel 3.38. P X = N (µ, σ 2 ), µ ∈ R, σ > 0 ist keine reguläre Familie, da Θ = R × (0, ∞) kein Intervall im R1 ist. 52 Aber: P X = {N (µ, σ02 ) : µ ∈ R}, mit σ02 > 0 fest, ist eine reguläre Familie, denn (R1) θ = R ist ein offenes Intervall. (R2) Für alle µ ∈ R hat PµX die stetige Dichte fµ mit 1 1 1 2 · exp − 2 (x − µ) Lx (µ) := fµ (x) = √ · 2σ0 2π σ0 (R3) L0x (µ) 1 1 1 1 2 =√ · · exp − 2 (x − µ) · 2 · 2 · (x − µ) 2σ0 2σ 2π σ0 } | } | 0 {z {z x−µ σ2 | {z0 } fµ (x) · Rest =:lµ∗ (x) und L0x ist stetig. (R4) Z ∞ L0x (µ) ∞ x−µ · fµ (x) dx 2 −∞ σ0 X −µ = Eµ σ02 1 = 2 (Eµ (X) − µ) = 0 σ0 Z dx = −∞ Sind X1 , . . . , Xn unabhängige Zufallsvariablen, dann ist die Gesamtlikelihood unabh. Lx1 ,...,xn (θ) = Lx1 (θ) · · · · · Lxn (θ). Für die Gesamt-Log-Likelihood gilt (falls Lx1 ,...,xn (θ) > 0), dass lx1 ,...,xn (θ) = lx1 , dabei ist lx (θ) := ln Lx (θ), wenn Lx (θ) > 0. In (3.34) ist übrigens für festes x ∈ R und falls Lx (θ) > 0: lθ∗ (x) = lx0 (θ) = d L0 (θ) (ln Lx (θ)) = x dx Lx (θ) ( ⇒ lθ x) · Lx (θ) = L0x (θ). Das gilt auch, falls für ein θ0 ∈ Θ : Lx (θ0 ) = 0, da Lx an der Stelle θ0 ein Minimum hat (Lx : Θ → [0, ∞)). Andererseits ist Lx nach Voraussetzung stetig differenzierbar 53 und Θ offen, sodass L0x (θ0 ) = 0. Definition 3.39. Unter den Voraussetzungen und Bezeichnungen von (3.35) definiere für festes θ ∈ Θ die messbare Abbildung lθ∗ : R → R durch l0 (θ) falls Lx (θ) > 0, x lθ∗ (x) = 0 sonst. Die Abbildung Inf : Θ → ∞ mit V arθ (l∗ (x)) falls Eθ (l∗ (Xi )2 ) < ∞, θ θ Inf(θ) := ∞ sonst die Fisher-Information von PθX . Beispiel 3.40. (a) Sei P X = {Bin(1, p) : p ∈ (0, 1)}. (Wie in (3.34)), dann ist wie dort gezeigt lp∗ (xi ) = xi · 1 1 − (1 − xi ) · , p 1−p und weiter ist die Fisher-Information Inf(p) = Var L∗p (X) = 1 p · (1 − p) (b) Für P X = {N (µ, σ02 ) : µ ∈ R} aus (3.38) ist 1 1 1 2 Lx (µ) = √ · · exp − 2 (x − µ) . 2σ0 2π σ0 Für alle µ ∈ R und x ∈ R ist lp∗ (x) = lx0 (µ) = x−µ . σo2 Die Fisher-Information ist ⇒ Inf(µ) = V arµ lµ∗ (X) 2 = Eµ lµ∗ (X)2 − Eµ lµ∗ (X) 2 2 ! X −µ X −µ = Eµ − σ02 σ2 | {z0 } =0 1 = 4 E(X − µ)2 σ0 1 1 = 4 V arµ (X) = 2 σ0 σ0 54 NUN FEHLEN NOCH EINIGE ZEICHNUNGEN. Bemerkung. Falls P X eine reguläre Verteilung ist, gilt (R4): (diskret) 0 = ! X = X L0x (θ) = lθ∗ (x) · Lx (θ) x∈T x∈T ! X lθ∗ (x) · fθ (x) = Eθ (lθ (X)) x∈T Z ∞ (stetig) 0 = L0x (θ) dθ Z = −∞ = lθ∗ (x) · fθ (x) dx R Eθ (lθ∗ (x)) Nun ein zentraler Satz zur Bestimmung einer unteren Schranke für die Varianz eines Schätzers: Satz 3.41 (Cramer-Rao-Ungleichung, 1945; Frichet, 1943). Sei (Ω, A, P) ein Statistischer Raum mit P = {Pθ : θ ∈ Θ} sowie X1 , . . . , Xn u. i. v. Zufallsvariablen, sodass P Xi eine reguläre Familie ist. Ferner sei g : Θ → R eine differenzierbare parametrische Funktion mit existierender Ableitung g 0 . Sei T = t(X1 , . . . , Xn ) ein beliebiger erwartungstreuer Schätzer für g(θ) und für ein festes θ0 ∈ Θ gelte Inf(θ0 ) > 0 und der Schätzer T erfülle folgende Regularitätsbedingung: (R5) Eθ0 T · Pn ∗ l (X ) = g 0 (θ0 ). i i=1 θ0 Dann gilt: (g 0 (θ0 ))2 V arθ0 (T ) ≥ n · Inf(θ0 ) Beweis. Zunächst ist Eθ0 n X i=1 ! lθ∗0 (Xi ) = n X Eθ0 lθ∗0 (Xi ) i=1 (R4), Bem. vor 3.41 = n · Eθ0 lθ∗0 (X1 ) = 0 (∗) 55 Es gilt mit (R4): |g 0 (θ0 )| = Eθ0 T = Eθ0 T = Covθ0 · n X i=1 ! lθ∗0 (Xi ) n X X · lθ∗0 (Xi ) − Eθ0 (T ) · Eθ0 lθ∗0 (Xi ) | {z } | {z } i=1 =g(θ0 )<∞ =0 wegen (∗) ! n X ∗ T, lθ0 (Xi ) i=1 v ! u n X u p (Cauchy,Schwarz) ≤ V arθ0 (T ) · tV arθ0 lθ∗0 (Xi ) ! i=1 (unabh., X1 Repräsentant) = n · V arθ0 lθ∗0 (X1 ) p p = V arθ0 (T ) · n · Inf(θ0 ) Durch Quadrieren und Umstellen erhält man die Behauptung V arθ0 (T ) ≥ (g 0 (θ0 ))2 . n · Inf(θ) Was besagt die Regularitätsbedingung (R5)? Für diskretes PθXi hat die gemeinsame Dichte fθ von PθX1 ,...,Xn die Form ⇒ Mit fθ (x1 , . . . , xn ) = fθX1 (x1 ) · · · · · fθXn (xn ) n Y X d X fθXi (xi ) · fθ j (xj ). f (x1 , . . . , xn ) = dθ i=1 i6=j d Xi fθ (xi ) = L0Xi (θ) = fθXi (xi ) · lθ∗ (xi ) gilt: dθ n XY X d fθ j (xj ) · fθXi (xi ) · lθ∗ (xi ) fθ (x1 , . . . , xn ) = dθ i=1 i6=j = n X lθ∗ (xi ) · fθ (x1 , . . . , xn ) i=1 56 Also gilt für die linke Seite von (R5): Eθ T· n X ! lθ∗ (Xi ) = X ··· X x1 xn = X ··· X = X i=1 x1 x1 T· n X lθ∗ (xi ) · fθ (x1 , . . . , xn ) i=1 T· xn d fθ (x1 , . . . , xn ) dθ X d ··· T · fθ (x1 , . . . , xn ) dθ x n und für die rechte Seite gilt: d Eθ (T ) dθ X X = ··· T · fθ (x1 , . . . , xn ) g 0 (θ) = x1 xn Die Summe wird über alle (x1 , . . . , xn )0 ∈ Rn gebildet. (R5) bedeutet daher: für den Erwartungswert von T dürfen die Ableitung und die Summenbildung vertauscht werden. Falls der Träger endlich ist, dann ist dies wegen (R3) immer erfüllt. Analoges gilt für stetiges PθXi . Allgemein: Jeder unverzerrte Schätzer T = t(x1 , . . . , xn ) für g(θ), der überall (R5) erfüllt, heißt regulärer erwartungstreuer Schätzer für g(θ). Bemerke: Die meisten erwartungstreuen Schätzer sind regulär, gehe daher – wenn nicht explizit erwähnt – nicht weiter auf (R5) ein. Beispiel 3.42 (Fortsetzung von (3.40)). Für P X = {N (µ, σ02 ) , σ02 bekannt, µ ∈ R} ist der Schätzer X̄ erwartungstreu für µ. Weiter ist V arµ (X̄) = σ02 ∀ µ ∈ R, n falls X1 , . . . , Xn u. i. v. sind. 1 Schließlich ist Inf(µ) = 2 > 0 und Cramer-Rao besagt, dass für beliebige µ ∈ R jeder σ0 reguläre erwartungstreue Schätzer T für µ V arµ (T ) ≥ σ02 1 1 = = = V arµ (X̄) n · Inf(µ) n n · σ12 0 erfüllen muss. Also besitzt der optimale Schätzer T ∗ = X̄ für jedes µ ∈ R unter allen regulären erwartungstreuen Schätzern für µ minimale Varianz. 57 Definition 3.43. Sei (Ω, A, P) ein statistischer Raum mit P = {Pθ : θ ∈ Θ} mit parametrischer Funktion g : Θ → R. Seien X1 , . . . , Xn Zufallsvariablen und T ∗ = t∗ (x1 , . . . , xn ) ein erwartungstreuer Schätzer für g(θ). Gilt für jeden beliebigen erwartungstreuen Schätzer T = t(x1 , . . . , xn ) für g(θ) V arθ (T ) ≥ V arθ (T ∗ ) ∀ θ ∈ Θ, dann heißt T gleichzeitig bester erwartungstreuer Schätzer für g(θ). (UMVUE = uniformly minimum variance unbiased estimator) In (3.34) haben wir gezeigt, dass X̄ UMVUE ist für p. In (3.42) haben wir nur gezeigt, dass X̄ unter allen regulären erwartungstreuen Schätzern der gleichzeitig Beste für µ ist. Die Verletzung der Regularitätsbedingung für die Varianzschranke: Beispiel 3.44. Betrachte die Situation aus Aufgabe 21, d. h. X1 , . . . , Xn u. i. v. mit P Xi = {R(0, θ) , θ ∈ (0, ∞)}. Tn = θ̂ML = max(X1 , . . . , Xn ) ist nicht erwartungstreu, aber der Schätzer Tn∗ = n+1 max(X1 , . . . , Xn ) n ist erwartungstreu. Weiter besitzt mit Aufgabe (21)(a) die stetige Dichte fθ mit xn−1 fθ (x) = n · n · 1[0,θ] (x) θ ⇒ V arθ (Tn ) = Eθ (Tn2 ) − [Eθ (Tn )]2 2 Z θ n xn−1 2 θ = x · n n dx − θ n−1 0 n 2 n2 = θ − θ2 n+2 (n + 1)2 n = · θ2 2 (n + 2) · (n + 1) Und daher ist V arθ (Tn∗ ) = (n + 1)2 n 1 · θ2 − θ2 2 2 n (n + 2) · (n + 1) n · (n + 2) | {z } beunruhigend klein! Wäre P X1 eine reguläre Familie und Inf(θ) > 0, dann müsste mit (3.41) (Cramer-Rao) 58 gelten: 1 1 ≤ V arθ (Tn∗ ) = θ2 n · Inf(θ) n · (n + 2) ⇒ ∀n ∈ N : θ 1 ≥ und das gilt für Inf(θ) ∈ R im Allgemeinen nicht! n+2 Inf(θ) Aber: P X1 ist keine reguläre Familie, d. h. die Supereffizienz von Tn∗ ist kein Widerspruch zur Cramer-Rao-Ungleichung. 3.3.5 Suffizienz und Satz von Rao-Blackwell Suche Abbildungen, die einen hochdimensionalen Datenvektor in eine einfachere Form transformieren, ohne dabei wesentliche Informationen über die Wahrscheinlichkeitsverteilung zu verlieren. Beispiel 3.45. Seien X1 , . . . , Xn u. i. v. Zufallsvariablen mit P Xi = {Poi(µ) , µ ∈ (0, 1)} P und T = t(X1 , . . . , Xn ) = ni=1 Xi . Die Verteilung von T ist (siehe Übungsaufgabe) gleich der Poi(n · µ)-Verteilung. Also hat die gemeinsame Verteilung von X1 und T die diskrete Dichte fX1 ,T . Es gilt für z ≥ x: Pµ (X1 = x , T = z) = Pµ (X1 = x , X2 + · · · + Xn = z − xn ) Dabei gilt (a) X1 und X2 + · · · + Xn sind stochastisch unabhängig. (b) X2 + · · · + Xn ist poissonverteilt , d. h. PµX2 +···+Xn = Poi ((n − 1) · µ). Also ist fX1 ,T (x, z) = Pµ (x1 = x) · Pµ (x2 + · · · + xn = z − x) x 2 µ · e−µ · [(n − 1) · µ] · e−(n−1)·µ falls x, z ∈ N0 (z − x)! = x! 0 sonst. z z−x µ · z · (n − 1) falls x, z ∈ N0 enµ = z! x 0 sonst. 59 Die bedingte Dichte fX1 |T ( · |z) von P X1 |T =z ist dann z−x −nµ µz z n · n−1 ·e fX1 ,T (x, z) z! x fX1 |T (x|z) = = 1/2 (n·µ) fT (z) · e−nµ z! z−x x 1 z n−1 · = · n n x (falls fT (z) ≥ 0) Dies ist die Dichte der Bin(z, n1 )-Verteilung (und diese Dichte hängt nicht mehr von µ ab). Die bedingte Erwartung Eµ (X1 |T ) = n1 T hängt ebenfalls nicht nicht von µ ab. Durch die Tatsache, dass Eµ (X1 |T ) nicht von µ abhängt ist er auch ohne Kenntnis von µ und n 1 1X Eµ (X1 |T ) = T = Xi = X̄ n n i=1 Definition 3.46. Sei (Ω, A, P) ein statistischer Raum mit P = {Pθ : θ ∈ Θ} und X1 , . . . , Xn Zufallsvariablen. Sei T = t(X1 , . . . , Xn ) ein Schätzer, sodass ∀ θ ∈ Θ die Verteilung PθT (stetige oder diskrete) Dichte fθT hat. Falls ein weiterer beliebiger Schätzer S mit T gemeinsame (stetige oder diskrete) Dichte S|T fθS,T besitzt, sodass die bedingte Dichte fθ ( · |z) ∀ θ ∈ Θ jeweils o d. h. n gleich ist, S|T ∀ x, z ∈ R ist fθ nicht von θ abhängig, dann heißt T suffizient für PθX1 ,...,Xn . Häufige Aussage: T suffizient für θ ∈ Θ. Nachweis der Suffizienz gestaltet sich oftmals schwierig. Hilfreich: Satz 3.47 (Faktorisierungssatz nach Neyman). Sei (Ω, A, P) ein statistischer Raum mit P = {Pθ : θ ∈ Θ} und X1 , . . . , Xn Zufallsvariablen mit gemeinsamer Dichte fθX1 ,...,Xn : R → [0, ∞). Sei T = t(X1 , . . . , Xn ) ein Schätzer.Wenn sich die gemeinsame Dichte fθX1 ,...,Xn faktorisieren lässt zu fθX1 ,...,Xn (x1 , . . . , xn ) = hθ (t(x1 , . . . , xn )) · g(x1 , . . . , xn ), wobei g nicht von θ abhängt, dann ist T suffizient für θ. 60 Also: fθX1 ,...,Xn (x1 , . . . , xn ) = hθ (t(x1 , . . . , xn )) · g(x1 , . . . , xn ) ⇒ T = t(X1 , . . . , Xn ) ist suffizient für θ ∈ Θ. Beweis. Sei fθX1 ,...,Xn diskret. Sei S = s(X1 , . . . , Xn ) ein beliebiger Schätzer. Dann gilt für die gemeinsame Dichte gθS,T von PθS,T , dass gθS,T (a, b) = P (S = a, T = b) = Pθ ({(x1 , . . . , xn ) ∈ Rn : s(x1 , . . . , xn ) = a, t(x1 , . . . , xn ) = b}) X X X ,...,x = ··· fθ 1 n (x1 , . . . , xn ) x1 ,...,xn ∈ Träger Mit s(x1 , . . . , xn ) = a und t(x1 , . . . , xn ) = b = hθ (b) · g(x1 , . . . , xn ) nach Voraussetzung gilt: hθ (b) · X ··· X | g(x1 , . . . , xn ) {z } =: r(a,b) fest, und unabh. von θ Für die Randdichte qθT von PθT gilt: qθT (b) = X qθS,T (a, b) = hθ (b) · X a r(a, b) a Somit ist für alle b mit qθT (b) > 0 die bedingte Dichte: S|T qθ (a|b) = qθS,T (a, b) hθ (b) · r(a, b) P = T hθ (b) · b r(a, b) qθ (b) Dies hängt nicht von θ ab, und damit ist T suffizient für θ. Beispiel 3.48. (a) Fortführung von (3.45): Seien X1 , . . . , Xn u. i. v. Zufallsvariablen mit P Xi = Poi(λ). Die gemeinsame Dichte ist fµX1 ,...,Xn (x1 , . . . , xn ) = µx1 −µ µxn −µ e · ··· · e x1 xn = µx1 +···+xn · e−nµ · ⇒ T = Pn i=1 1 x1 ! · · · · · x n ! xi ist suffizient für µ. (b) Seien X1 , . . . , Xn u. i. v. mit P Xi = {N (µ, σ 2 ), µ ∈ R, σ 2 > 0}, d. h. θ = und Θ = R × (0, ∞). Finde nun eine suffiziente Statistik! 61 µ σ2 ! Die gemeinsame Dichte ist −n 2 fµX1 ,...,Xn (x1 , . . . , xn ) = (2π) n 1 X −n (xi − µ)2 · σ · exp − 2 2σ i=1 n ! 1 X n = (2π) · σ −n · exp − 2 (xi − x̄)2 − 2 (x̄ − µ)2 2σ i=1 2σ n−1 2 n −n 2 −n σ̂ − 2 (x̄ − µ) = (2π) 2 · σ · exp − | {z } 2σ 2 2σ {z } g(x1 ,...,xn ) | ! −n 2 hθ (x̄,σ̂ 2 ) ⇒ (x̄, σ̂ 2 )0 ist suffizient für (µ, σ 2 ). Bemerkung: Aus (x̄, σ̂ 2 ) suffizient für (µ, σ 2 ) folgt nicht im Allgemeinen, dass X̄ suffizient für µ und σ̂ 2 suffizient für σ 2 ist. Weiter mit der Verbesserung für erwartungstreue Schätzer Satz 3.49 (Satz von Rao-Blackwell). Sei (Ω, A, P) ein statistischer Raum mit P = {Pθ : θ ∈ Θ} und X1 , . . . , Xn Zufallsvariablen. Sei T = t(x1 , . . . , xn ), und sei U = u(x1 , . . . , xn ) ein erwartungstreuer Schätzer für g(θ) mit g parametrische Funktion. Sei V = v(T ) definiert durch v(b) := Eθ (U |T = b) ∀ b ∈ R, dann gilt: (i) V hängt nicht von θ ab, d.h. V = v(T ) = Eθ (U |T ) ∀ θ ∈ Θ, d. h. V kann aus den Beobachtungen x1 , . . . , xn berechnet werden und V ist ein erwartungstreuer Schätzer für g(θ). (ii) V arθ (V ) ≤ V arθ (U ) für alle θ ∈ Θ mit Eθ (U 2 ) < ∞. Beweis. (i) T ist suffizient für Θ, somit ist P U |T unabhängig von θ. Da Eθ (U |T = t) = E(U |T = t) für alle θ ∈ Θ gilt, so ist V = E(U |T ) ein Schätzer und g(θ) = Eθ (U ) = Eθ (E(U |T )) = Eθ (V ). 62 (ii) mit Übung 29c ist V arθ (U ) = V arθ (Eθ (U |T )) + Eθ V arθ (U |T ) | {z } | {z } =V >0 wegen A<q(n) Die Konstruktion eines verbesserten Schätzers V aus U gemäß (3.49) heißt auch Rao-Blackwellisieren. Falls es unter den Voraussetzungen von (3.49) einen gleichmäßig besten erwartungstreuen Schätzer U gibt, dann muss auch V = E(U |T ) UMVUE sein. Mit anderen Worten gibt es einen gleichmäßig besten erwartungstreuen Schätzer, so gibt es einen solchen Schätzer, der von den Beobachtungen (der suffizienten Statistik) nur über T = t(X1 , . . . , Xn ) abhängt. Beispiel 3.50. Betrache Würfel mit k Seiten, k unbekannt, die Seiten sind durchnummeriert. Erhalte aus vier Würfen folgendes Ergebnis: 9, 2, 9, 12. Seien daher X1 , . . . , X4 u. i. v. Zufallsvariablen mit P Xi = GV ({1, . . . , k}), k unbekannt. Die gemeinsame Dichte bei gegebenen k ist 4 1 fk (x1 , . . . , xn ) = · 1{1,...,k} ( max xi ) · 1{1,...,k} ( min xi ) 1≤i≤4 1≤i≤4 k Weiter ist k 1X k+1 k · (k + 1) 1 · = i= Ek (Xi ) = k i=1 2 k 2 Hieraus folgt direkt k̂Mom = 2X̄ − 1. (Im Beispiel: k̂Mom = 15) ML-Schätzer: k̂ML = max(X1 , X2 , X3 , X4 ). (Im Beispiel: k̂ML = 12) Suche ”guten” erwartungstreuen Schätzer (verallgemeinere dafür auf n Würfe). Mit n 1 fk (x1 , . . . , xn ) = 1{1,...,k} ( max xi ) · 1{1,...,k} ( min xi ) 1≤i≤n 1≤i≤n k {z } | {z } | =g(x1 ,...,xn ) hk (max1≤i≤k xi ) n o ist T = t(X1 , . . . , Xn ) suffizient für PkX1 ,...,Xn : k ∈ N 63 (zu Aufg. 28c) Wähle einfachen erwartungstreuen Schätzer U mit U = 2X1 − 1, da Ek (X1 ) = k+1 2 (ACHTUNG: Hier nicht sicher ob X1 oder Xi !!!) Berechne nun die bedingte Erwartung Ek (U |T ): Ek (U |T = t) = Ek (2X̄ − 1|T = b) = k X Xi |T (2x − 1)fk (x|b) i=1 Bestimme nun die bedingte Dichte von X1 unter T = b: (1) Randdichte fkT von PkT fkT (b) = Pk (T = b) = Pk (T ≤ b) − Pk (T ≤ b − 1), und mit Pk (T ≤ b) = Pk max Xi ≤ b 1≤i≤n = Pk (X1 ≤ b, . . . , Xn ≤ b) = Pk (X1 ≤ b) · · · · · Pk (Xn ≤ b) = (Pk (X1 ) ≤ n)n n b = k Somit ist fkT (b) (Xi unabh.) (Xi id. vert.) n n b b−1 = − k k (2) gemeinsame Dichte fkX1 ,T von PkX1 ,T fkX,T (x, b) = Pk X1 = x, max xi = b 1≤i≤n P (X = x, max2≤i≤n = b) x < b k 1 = Pk (X1 = x, max2≤i≤n ≤ b) x = b 0 x>0 64 P (X = x) · Pk (max1≤i≤n Xi = b) x < b k 1 = Pk (X1 = b) · Pk (max1≤i≤n Xi = b) x = b 0 x>b bn−1 1 · n−1 x, b ∈ {1, . . . , k} und x < b k kn−1 n−1 − (b − 1) = 1·b x, b ∈ {1, . . . , k} und x = b k k n−1 0 sonst X1 |T (3) bedingte Dichte fk Für b ∈ {1, . . . , n} und für x ≤ b ist: bn−1 − (b − 1)n−1 n X |T b − (b − 1)n fk 1 (x|b) = bn−1 n b − bn−1 x<b x=b Erhalte also: b−1 X bn−1 − (b − 1)n−1 bn−1 (2x − 1) Ek (U |T = b) = + (2b − 1) bn − (b − 1)n bn − (b − 1)n x=1 = ... = bn+1 − (b − 1)n+1 bn − (b − 1)n Somit ist V := Ek (U |T ) = T n+1 − (T − 1)n+1 T n − (T − 1)n ein erwartungstreuer Schätzer für k ∈ N. 125 − 115 Im Beispiel: max1≤i≤4 xi = 12, n = 4, also k̂ = 4 ≈ 14 12 − 114 Zusammenhang zwischen Suffizient und ML-Schätzer: Satz 3.51. Sei T = t(X1 , . . . , Xn ) suffizient für θ. Dann gilt: Entweder: Gibt es nur einen ML-Schätzer θ̂ML für θ, so hängt θ̂ML echt von T ab. (θ̂ML nicht konstante Funktion von T ). Oder: Gibt es mehrere ML-Schätzer, so hängt wenigstens einer echt von T ab. 65 Beweis. (3.47) T suffizient ⇐⇒ fθX1 ,...,Xn (x1 , . . . , xn ) = hθ (t(x1 , . . . , xn )) · g(x1 , . . . , xn ), (wobei g(x1 , . . . , xn ) nicht von θ abhängt, also bei festen x1 , . . . , xn eine bestimmte reelle Zahl ist) =⇒ θ̂ML = arg max fθX1 ,...,Xn (x1 , . . . , xn ) θ∈Θ = arg max hθ (t(x1 , . . . , xn )) θ∈Θ Abschließend betrachte nun Asymptotik von ML-Schätzern unter Regularitätsbedingungen (Suffizienz ist nicht erforderlich!): Satz 3.52. Sei (Ω, A, P) ein statistischer Raum mit P = {Pθ : θ ∈ Θ}. Sei (Xn )n∈N eine Folge von u. i. v. Zufallsvariablen, sodass P X1 eine reguläre Familie ist und sei Inf(θ) die Fisher-Information mit Inf(θ0 ) > 0 für θ0 ∈ Θ. Sei θ̂ML,n = tn X1 , . . . , Xn ein ML-Schätzer für θ, n ∈ N. Unter zusätzlichen Regularitätsbedingungen (siehe z. B. Wasan, M. T. (1970): Parametric Estimation, McGrawHill, S. 158 ff.), dann gilt: (a) θ̂ML,n ist konsistent für θ, (b) θ̂ML,n ist asymptotisch normalverteilt mit √ n→∞ n θ̂ML,n − θ0 ∼ N 1 0, Inf(θ0 ) , (c) θ̂ML,n ist asymptotisch effizient. Beweis. siehe Wasan (1970). Teil (c) ist offensichtlich, denn die Cramer-Rao-Schranke besagt: Für jeden regulären erwartungstreuen Schätzer T für θ gilt, dass V arθ (T ) ≥ 1 . Inf(θ0 ) Mit (b) ist θ̂ML,n asymptotisch erwartungstreu, so dass für n → ∞ eine Annäherung an die untere Varianzschranke, d. h. asymptotisch effizient, gilt. 66 Zurück zur Findung von UMVUE: Konkret: Ist V (verbesserter Schätzer nach Rao-Blackwellisieren) UMVUE? Beantwortung fordert technisches Kriterium: 3.3.6 Vollständige Statistiken und Satz von Lehmann Scheffé Wäre V = E(U |T ) (mit U erwartungstreu und T suffizient für θ) UMVUE für g(θ) und E(θ̂|T ) = g(θ), d. h. weiterer erwartungstreue Schätzer für g(θ). ˆ = g(θ) − g(θ) = 0 für alle θ ∈ Θ. Würde daraus nun auch folgen, =⇒ Eθ (V − g(θ)) ˆ = 0 fast überall gilt, dass V − g(θ) ˆ . =⇒ V arθ (V ) = V arθ (g(θ) Das wäre erfüllt, wenn für jede Funktion h : R → R für die Eθ (h(T )) = 0 für alle θ ∈ Θ folgt, dass h(t) = 0 für fast alle t. Definition 3.53. Sei (Ω, A, P) ein statistischer Raum und X1 , . . . , Xn Zufallsvariablen. Sei T = t(x1 , . . . , xn ) eine Statistik. (a) Eine messbare Funktion h : R → R heißt P T -fast sicher, falls es eine Menge N gibt, sodass (i) für alle P ∈ P T ist P T (N ) = P (T ∈ N ) = 0 (also auf dem Träger immer 0, und sonst ist es egal, wie die Funktion gewählt ist) (ii) für alle x 6∈ N ist die Funktion h(x) = 0. (b) Eine Familie P T = {P T : P ∈ P} heißt vollständig, wenn ∀ P ∈ P für eine integrierbare Funktion h : R → R, für die EP (h(t)) = 0 folgen muss, dass h = 0 P T -fast sicher ist. Sage auch: T ist vollständig. Beispiel 3.54 (vgl. 3.50). (a) Sei (Ω, A, P) ein statistischer Raum mit P = {Pk : k ∈ N} und X1 , . . . , Xn u. i. v. mit PkX1 = GV({1, . . . , k}). Sei h : R → R mit h(x) = 0 ∀ x ∈ N, beliebig ∀ x 6∈ N. Setzte N = {x ∈ R : x 6∈ N}, dann gilt: 67 (i) für jedes k ∈ N: Pk (N ) = 0 (ii) für jedes x 6∈ N gilt: x ∈ N ⇒ h(x) = 0, d. h. h ist P X1 -fast sicher Null (0). Sei T = t(X1 , . . . , Xn ) = max Xi . Dann ist PkT nach (3.50) die diskrete 1≤i≤n bn − (b − 1)n Dichte fkT (b) = mit Träger {1, . . . , k} und h ist auch P T -fast kn sicher Null. (b) Zeige nun: P T = {PkT : k ∈ N} ist vollständig. Sei h : R → R eine beliebige, messbare Funktion, so dass ∀k ∈ N Ek (h(T )) = 0 Zeige (mit vollständiger Induktion): h(b) = 0 ∀ b ∈ N. (aus (a) folgt auch: h ist P T -f. s. Null). Induktionsvoraussetzung: 0 = Ek (h(T )) = k X h(b) · b=1 bn − (b − 1)n ∀k ∈ N kn Zeige nun: h(1) = 0: Sei k = 1 ⇒ 0 = h(1) · 1n − (1 − 1)n = h(1) 1n Induktionsschluss: Sei K ∈ N und h(1) = h(2) = · · · = h(K) = 0, dann ist h(K + 1) = 0. Sei K = k + 1, dann ist 0= K X h(b) · b=1 = h(K) · bn − (b − 1)n , Kn mit h(b) = 0 ∀ b ≤ k = K − 1 K n − (K − 1)n n K | {z } >0 ⇒ 0 = h(K) = h(k + 1) (c) Ebenso kann gezeigt werden, dass P X1 = {GV ({1, . . . , K})} vollständig ist. (d) Dagegen ist P̃ T = {PKT : K ≥ 2} nicht mehr vollständig, denn: Wähle h : R → R mit h(1) = 2n − 1, h(2) = −1, und h(x) = 0 sonst. 68 Es gilt: EK (h(T )) = K X h(b) · bn − (b − 1)n Kn h(b) · bn − (b − 1)n Kn i=1 = 2 X b=1 1 1 · 1n + (−1) · 2 · (2n − 1) 2 K K ∀ K ≥ 2. = (2n − 1) · =0 Aber: h ist nicht P̃ T -f. s. Null. Konsequenz der Vollständigkeit von T = max Xi . 1≤i≤n n+1 n+1 T (T − 1) ein erwartungstreuer Schätzer für K, der von n T − (T − 1)n den Beobachtungen nur noch über T = X abhängt. Sei V = v(T ) = 1≤i≤ni Sei h : R → R durch h(b) = v(b) − w(b) definiert, dann gilt für alle K ∈ N: EK (h(T )) = EK (v(b) − w(b)) = EK (V ) − EK (W ) T vollst. ⇒ Rao−Bl. = 0 h ist P T -f. s. Null ⇒ ∀ b ∈ N gilt: 0 = h(b) = v(b) − w(b) ⇔ v(b) = w(b). Also ist für jede Beobachtung von max Xi = T , die möglich ist, V = W . 1≤i≤n Somit: 1) Da T suffizient ist, lässt sich nach Rao-Blackwell zu jedem beliebigen erwartungstreuen Schätzer U ein mindestens genauso guter Schätzer V = EK (U |T ) herleiten; dieser hängt nur von T ab. 2) Da T vollständig ist, gibt es nur einen einzigen erwartungstreuen Schätzer, der nur von T abhängt, d. h. V − W ist bei allen möglichen Beobachtungen gleich Null. Insgesamt: V ist UMVUE für K. Satz 3.55 (Lehmann-Scheffé). Sei (Ω, A, P) ein statistischer Raum mit P = {Pθ : θ ∈ Θ} und g : Θ → R eine parametrische Funktion. Seien X1 , . . . , Xn Zufallsvariablen und T = t(X1 , . . . , Xn ) eine suffiziente und vollständige Statistik. Ferner sei U = u(X1 , . . . , Xn ) ein beliebiger (möglichst einfach gewählter) erwartungstreuer Schätzer für g(θ), ∀ θ ∈ Θ. 69 Dann ist V := Eθ (U |T )) = E(U |T ) PθT -f. s. eindeutig für alle θ ∈ Θ, und V ist effizient, d. h. V ist UMVUE. Beweis. nur noch zu zeigen: V ist PθT -f. s. eindeutig ∀ θ ∈ Θ. Seien V und W erwartungstreue Schätzer für g(θ), die beide nur noch über die suffiziente und vollständige Statistik T von θ abhähngen, dann ⇒ ∀ θ ∈ Θ gilt 0 = Eθ (V ) − Eθ (W ) = Eθ (v(T )) − Eθ (w(T )) ⇒ v − w ist P T -f. s. Null. (folgt aus der Vollständigkeit von T ) ⇒ v(T ) und w(T ) haben fast sicher die gleiche Verteilung, d. h. insbesondere für alle θ ∈ Θ, bei denen V arθ (V ) oder V arθ (W ) existieren, gilt: V arθ (V ) = V arθ (W ). Klausurtipp: Suche eines UMVUE-Schätzers für g(θ) 1. Suche erwartungstreuen Schätzer U = u(X1 , . . . , Xn ) für g(θ). 2. Suche suffiziente Statistik T (z. B.: mit Faktorisierungssatz) für θ. 3. Bestimme V := E(U |T ) mittels Rao-Blackwellisieren (V ist nicht schlechter als U ). 4. Überprüfe, ob T vollständig ist (V ist UMVUE, falls T vollständig). In Beispiel 3.54 (b) ist P̃ T = {PKT : K ≥ 2} nicht vollständig, z. B. n = 3, K = 4, T = max{X1 , X2 , X3 } P (T P (T P (T P (T 2 1 1 = 1) = = 4 64 3 2 7 2 −1 = 2) = = 3 4 64 33 − 23 19 = 3) = = 45 64 27 37 = 4) = 1 − = 64 64 70 Somit ist für U = 2X1 − 1 x1 (1) = E(U |T = 1) = 1 · P (U = 1|T = 1) =1·1=1 x2 (2) = E(U |T = 2) = 1 · P (U = 1|T = 2) + 3 · P (U = 3|T = 2) 4 15 3 =1· +3· = 7 7 7 Wähle nun Zufallsvariable U − 7, T = 1 W = U + 1, T = 2 U, T ∈ {3, 4} ⇒ E(U |T = b) 6= E(W |T = b) für b ∈ {1, 2}, aber | {z } | {z } =V1 =V2 E(V1 ) = E (E(U |T = b)) = E(E(W |T = b)) = E(V2 ) E(E(W |T = b)) = E(V1 ) − 7 · P (T = 1) + 1 · P (T = 2) 7 1 +1· = E(V1 ) = E(V1 ) − 7 · 64 64 Nachweis der Vollständigkeit gestaltet sich häufig als schwierig, dazu gleich mehr, vorab noch Satz 3.56 (Satz von Basu). Sei T eine suffiziente und vollständige Statistik für P = {Pθ : θ ∈ Θ} und V eine nutzlose Statistik für θ, d. h. die Verteilung von V hängt nicht von θ ab, d. h. PθV = P V , ∀ θ ∈ Θ. Dann gilt: V ist unabhängig von T . Beweis. Ohne. Beispiel 3.57. Seien X1 , . . . , Xn u. i. v. mit P X1 = N (µ, σ02 ), µ ∈ R, σ02 > 0 bekannt. 71 Dann ist X̄ = 1 n Pn i=1 Xi = T suffizient für µ, denn: 1 fµX1 ,...,Xn (x1 , . . . , xn ) = 2πσ0 {z | − n2 ! n n 1 X (xi − x̄)2 − 2 (x̄ − µ)2 · exp − 2 2σ0 i=1 2σ0 } | {z } =g(x1 ,...,xn ) Ferner ist (n − 1) · =hµ (x̄) σ̂ 2 2 ∼ Xn−1 2 σ d. h. σ̂ 2 ist nutzlos für µ. Mit dem Satz von Basu und der Vollständigkeit von T folgt: n n 1X 1 X ⇒ X̄ = Xi , σ̂ 2 = (Xi − X̄)2 n i=1 n − 1 i=1 sind stochastisch unabhängig! Vollständige Statistiken lassen sich in speziellen Verteilungsklassen leicht finden. Definition 3.58. Sei (Ω, A, P) ein statistischer Raum mit P = {Pθ : θ ∈ Θ} und X1 , . . . , Xn , n ≥ 1, Zufallsvariablen. Die n-dimensionale Verteilungsfamile P X1 ,...,Xn = {PθX1 ,...,Xn : θ ∈ Θ} heißt einparametrige Exponentialfamile, falls folgendes gilt: (i) Θ ⊂ R (ii) Für alle θ ∈ Θ existiert die Dichte fθX1 ,...,Xn von PθX1 ,...,Xn . Falls f diskret ist, so hat sie für alle θ ∈ Θ den gleichen Träger. (iii) ∃ C : Θ → R, ∃ A : Θ → R, wobei A nicht konstant, ∃ g : Rn → R messbar, und ∃ t : Rn → R messbar, wobei t nicht konstant ist, sodass ∀ θ ∈ Θ und ∀ (x1 , . . . , xn )0 ∈ Rn gilt: fθX1 ,...,Xn (x1 , . . . , xn ) = C(θ) · eA(θ)·t(x1 ,...,xn ) · g(x1 , . . . , xn ). Beispiel 3.59. Folgende eindimensionale Verteilungsfamilien sind Exponentialfamilien: (a) {Bin(n, p) : p ∈ (0, 1)} 72 n fp (x) = · px · (1 − p)n−1 · 1{0,...,n} (x) p x n p n = · 1{0,...,n} (x) · (1 − p) · p 1−p p n n = (1 − p) ·exp ln ·x · · 1{0,...,n} (x) | {z } 1−p p | {z } | {z } =C(x) =A(x)·f (x) =g(x) (b) {Poi(µ) : µ > 0} 1 −µ · e · 1N0 (x) x! 1 −µ = |{z} e ·exp ln(µ) · x · · 1N0 (x) | {z } |x! {z } =C(µ) =A(µ)·t(x) fµ (x) = µx · g(x) (c) {Exp(λ) : λ > 0} fλ (x) = |{z} λ ·exp =C(λ) −λ · x | {z } =A(λ)·t(x) · 1[0,∞) (x) | {z } (Weitere Beispiele siehe Blatt 10.) Bezeichnung: Ist x ∈ R und t(x) = x, dann liegt die Exponentialfamilie in kanonischer Form vor und A(θ) wird natürlicher Parameter der Verteilung genannt. Falls X1 , . . . , Xn u. i. v. mit P Xi einparametrige Exponentialfamile, dann ist fθX1 ,...,Xn (x1 , . . . , xn ) = n Y fθXi (xi ) i=1 = n Y c̃(θ) · exp Ã(θ) · t̃(xi ) · g̃(xi ) i=1 n = (c̃(θ)) · exp Ã(θ) · n X i=1 73 ! t̃(xi ) · n Y i=1 g̃(xi ) d. h. also auch P X1 ,...,Xn ist einparametrige Exponentialfamilie mit C(θ) = (c̃(θ))n A(θ) = Ã(θ) n Y g(x1 , . . . , xn ) = g̃(xi ) und i=1 t(x1 , . . . , xn ) = n X t̃(xi ) i=1 Nachweis der Suffizienz und Vollständigkeit nun leicht durchzuführen. Satz 3.60. Sei P X1 ,...,Xn eine einparametrige Exponentialfamile, dann ist unter den obigen Bezeichnungen T = t(X1 , . . . , Xn ) = n X t̃(Xi ) i=1 suffizient für {PθX1 ,...,Xn : θ ∈ Θ}. Falls {A(θ) : θ ∈ Θ} einen inneren Punkt hat, so ist T vollständig. Beweis. Suffizient folgt direkt mit dem Faktorisierungssatz (3.47). Vollständigkeit siehe z. B. Withing, H. (1985), Math Statistics 1, Satz 3.39 Bemerkung. Ein Punkt x ∈ M heißt innerer Punkt von M , wenn es eine offene Menge U gibt mit U ⊂ M und x ∈ M . Jede offene nichtleere Menge M besitzt daher mindestens einen inneren Punkt. Beispiel 3.61. (a) Aus Beispiel 3.59 (c) ist bekannt: {Exp(λ) : λ ∈ (0, ∞)} ist einparametrige Exponentialfamile mit A(λ) = −λ und t(x) = x. Die Menge {A(λ) : λ ∈ (0, ∞)} hat inneren Punkt, da sie offen und nichtleer ist. . T = Pn t(Xi ) = Pn Xi (3.60) i=1 i=1 ⇐⇒ T = Pn X i=1 Außerdem: X̄ = Pn i=1 Xi = i 1 T n ist suffizient ist vollständig ist erwartungstreu für Beobachtungen nur über T ab. Lehm.-Scheffé =⇒ X̄ ist UMVUE für 74 1 . λ 1 , λ und hängt von den (b) Aus (3.59)(a) bekannt: {Bin(1, p) : p ∈ (0, 1)} ist einparametrige Exponentialfamilie mit A(p) = ln p 1−p und t(x) = x. (3.60) =⇒ T = n X t(Xi ) ist suffizient für p ∈ (0, 1) i=1 Weiter ist {A(p) : p ∈ (0, 1)} = p = R, ln 1−p | {z } ∈(0,1) d. h. A hat inneren Punkt. =⇒ T = n X Xi ist vollständig i=1 und X̄ = 1 T ist erwarungstreu für p. n Mit Lehmann-Scheffé folgt: X̄ = n1 T ist UMVUE für p ∈ (0, 1). (Bereits in 3.34 umständlich gezeigt.) (c) Sei X1 , . . . , Xn u. i. v. mit P Xi = {N (µ, σ 2 ) : µ ∈ R, σ 2 > 0}. Suche gleichmäßig besten Schätzer für g(θ) = g(µ, σ 2 ). Achtung! Hier liegt keine einparametrige Exponentialfamile vor. (i) Sei σ 2 = σ02 > 0 beliebig, aber fest, d. . betrachte P̃ Xi = {N (µ, σ02 ) : µ ∈ R}. µ Mit Aufgabe 30(b) ist P̃ Xi einparametrige Exponentialfamilie mit A(µ) = 2 σ0 und t(x1 ) = x1 . P Mit (3.60) ist T = Xi suffizient für P̃ X1 ,...,Xn und da {A(µ) : µ ∈ R} = µ :µ∈R =R σ02 einen inneren Punkt hat, ist T auch vollständig. Der Schätzer X̄ = n1 T ist erwartungstreu für µ und hängt von den Beobachtungen nur über T ab. Lehm.-Scheffé =⇒ X̄ ist UMVUE für µ ∈ R, sofern σ02 fest ist. (ii) Nun sei σ 2 beliebig, in (i) gezeigt: Sei Ũ ein beliebiger erwartungstreuer 75 Schätzer für µ bei festem σ02 , d. h. mit Eµ,σ02 (Ũ ) = µ folgt ⇒ Varµ,σ02 (Ũ ) ≥ Varµ,σ02 (X̄). (∗) Weiter sei für jedes µ, σ 2 : Eµ,σ2 (X̄) = µ. Sei nun U beliebiger Schätzer für µ: ∀ µ ∈ R, ∀ σ 2 ∈ (0, 1) : Eµ,σ2 (X̄) = µ insb. =⇒ ∀ µ ∈ R : Eµ,σ2 (U ) = µ (*) =⇒ ∀ µ ∈ R : Varµ,σ2 (U ) ≥ Varµ,σ2 (X̄). Da σ02 > 0 beliebig, gilt somit für alle σ 2 > 0 und ∀ µ ∈ R: Varµ,σ2 (U ) ≥ Varµ,σ2 (X̄), d. h. X̄ ist auch UMVUE für µ, falls σ 2 unbekannt. 76