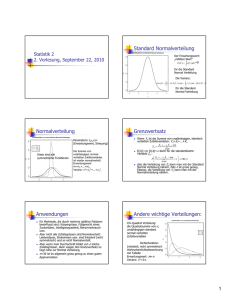
Die Streuung der Stichprobenmittelwerte

Die Streuung der Stichprobenmittelwerte
S TREUUNG
VON
PARAMETERSCHÄTZERN
Neben Erwartungstreue und Konsistenz wünscht man sich von einer
guten Schätzfunktion auch, dass ihre Streuung möglichst gering ist. Im
folgenden Beispiel soll der Parameter α geschätzt werden (der wahre
Wert von α sei hier 200). Es stehen zwei Schätzfunktionen zur Verfügung: λ̂ und ϕ̂. λ̂ sei erwartungstreu und konsistent, ϕ̂ sei ebenfalls konsistent, aber nicht erwartungstreu (leichter negativer Bias). Betrachtet
man nun die Schätzwerte...
Beispiel
i
λ̂i
1
112
2
223
3
166
4
198
5
308
6
211
7
244
8
148
9
127
10
265
∑i 2002
ϕ̂i
178
202
197
189
192
199
183
200
191
189
1920
... so sieht man Folgendes: Obwohl λ̂ durchschnittlich deutlich besser
¯
schätzt (λ̂ = 200.2; ϕ̂¯ = 192.0), sind die meisten λ̂i sehr weit vom wahren
Wert entfernt, wogegen ϕ̂i großteils passable Schätzungen ergibt. Der
Grund dafür ist, dass die λ̂-Werte zu stark streuen.
Falls man α also aufgrund einer einzelnen Stichprobe schätzen müsste, so wäre man wohl mit dem Schätzer ϕ̂ besser beraten, obwohl dieser
nicht erwartungstreu ist. (Alternative: Da λ̂ konsistent ist, könnte man
auch versuchen, die Genauigkeit zu erhöhen, indem man den Stichprobenumfang vergrößert, was in der Praxis aber oft schwierig oder gar
nicht durchführbar ist.)
1
VARIANZ
DER
S TICHPROBENMITTELWERTE
Wie stark streuen die Stichprobenmittelwerte x̄ um den wahren Mittelwert µx ?
σ2X̄ = E[(X̄ − µX )2 ] =
= E(X̄ 2 ) − 2 · µX · E(X̄) + E(µ2X ) =
Wegen E(X̄) = µX und E(µ2X ) = µ2X gilt:
= E(X̄ 2 ) − 2 · µ2X + µ2X
σ2X̄ = E(X̄ 2 ) − µ2X
Wir wissen (siehe Punkt 1.3. Bias und Biaskorrektur: Bias der Stichprobenvarianz, Einschub 2):
E(X̄ 2 ) =
1
n−1 2
· E(X 2 ) +
· µX
n
n
Eingesetzt in obige Gleichung erhalten wir:
σ2X̄ =
=
=
=
=
σ2X̄ =
1
n−1 2
· E(X 2 ) +
· µX − µ2X =
n
n
1
n−1 2 n 2
· E(X 2 ) +
· µX − · µX =
n
n
n
1 2
1
2
· E(X ) − · µX =
n
n
1
2
· [E(X ) − µ2X ] =
n
1 2
·σ
n X
σ2X
n
In Worten: Die Varianz der Stichprobenmittelwerte erhält man, indem
man die Populationsvarianz durch die Stichprobengröße dividiert.
Man erkennt hier auch, dass x̄ ein konsistenter Schätzer ist: Je größer
die Stichproben sind, umso genauer ist der Schätzer und umgekehrt.
2