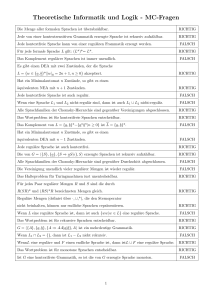
T h eoretisch e In form atik 1 T h eoretisch e In form atik fu r L eh ram

Theoretische Informatik 1
www.logic.at/lvas/thinf1
Theoretische Informatik für Lehramt I
www.logic.at/lvas/tila1
Christian Fermüller, [email protected]
1
Gernot Salzer, [email protected]
Beurteilung
Übung
N . . . Anzahl aller Übungsbeispiele (≥ 50)
k
ti
)
n . . . Anzahl der angekreuzten Übungsbeispiele
k . . . Anzahl der Tafelergebnisse (≥ 2)
= min(1,
n
·
N −5
t . . . Ergebnis an der Tafel (t ∈ {0.0, 0.5, 1.0, 1.2})
i
i
P
u
3
Do, 13:15–14:45, AudiMax
Vorlesungtermine: Di, 16:15–17:45, AudiMax
Übungsteil:
• in Kleingruppen, betreut von TutorInnen
• Anmeldung ab Mittwoch, 8.3.2006, 10:00 unter
https://ugm.logic.at (Ja zum Zertifikat! https!)
• Erste Übungseinheit: 20.3.-24.3.
2
• Übungsbeispiele in der Vorwoche auf Homepage
Vorlesungprüfung
• Haupttermin: Freitag, 30.6.2006, 18:00-20:00, Anmeldung!
• 3 Ersatztermine im Herbst
• Voraussetzung: u ≥ 0.3
60 ≥ g ≥ 51
70 ≥ g ≥ 61
85 ≥ g ≥ 71
100 ≥ g ≥ 86
g := round(30u + 70v)
5
4
3
2
1
Note
• v = Pp
(p . . . erreichte Punkte, P . . . erreichbare Punkte)
Gesamtnote
50 ≥ g ≥ 0
4
Unterlagen
• Skriptum: Donnerstag, 16.3.2006, 12:45 vor AudiMax
• Vorlesungsfolien
• Bücher für ersten Teil:
– P.Linz: An Introduction to Formal Languages and
Automata. Jones and Bartlett Publishers Inc., 2001.
– J.Hopcroft, R.Motwani, J.Ullman: Einführung in die
Automatentheorie, Formale Sprachen und
Komplexitätstheorie. Pearson Studium, 2002.
Weitere Literatur: siehe Homepage der Lehrveranstaltung.
5
Handbook of Theoretical Computer Science
Formale Sprachen und Automaten
Algebraische Spezifikation
Modelle verteilter Berechnungen
Theorie relationaler Datenbanken
Handbook of Theoretical Computer Science
7 Kapitel Komplexität:
Maschinenunabhängige Komplexität
Komplexität von Problemen, Algorithmen
Komplexität von Schaltkreisen und VLSI-Schaltungen
Algorithmen:
Suchen von Mustern in Zeichenketten
Computergraphik
Planen von Roboterbewegungen
Algorithmen auf Graphen
Algorithmen der Zahlentheorie
Kryptographie
Parallele Algorithmen
6
Typische Aussagen der theoretischen
Informatik
• Ein optimaler Sortieralgorithmus benötigt zum Sortieren von
n Datensätzen etwa n log(n) Rechenschritte.
• Java ist berechnungsuniversell: jeder vorstellbare Algorithmus
kann als Java-Programm formuliert werden.
• Das Halteproblem für Visual Basic Programme ist
unentscheidbar.
Syntax und Semantik
von imperativen, funktionalen, logikorientierten Sprachen
von Rewrite-Systemen
• Reguläre Sprachen sind abgeschlossen unter Durchschnitt und
Komplementbildung.
8
• Die Prädikatenlogik erster Stufe ist vollständig axiomatisierbar,
die Arithmetik hingegen nicht.
Aussagen über Programme (z.B. Verifikation):
Hoare Logik
Dynamische Logik
Temporal- und Modallogik
7
Lehrziel und Inhalt
Ziel: Vermittlung der Grundbegriffe der theoretischen Informatik,
Einführung in ihre mathematisch-formale Methodik.
Inhalt:
• Formale Sprachen und Automaten
• Grundbegriffe der Komplexitätstheorie
• Aussagenlogik
• Prädikatenlogik
• Grundbegriffe der formalen Verifikation
9
Formale Sprachen und Automaten
Inhalt
• Grundlagen
• Reguläre Sprachen: reguläre Mengen, reguläre Ausdrücke
(Algebra, EBNF, grep), Syntaxdiagramme
• Endliche Automaten (EA):
reguläre Menge → NEA → DEA → reguläre Menge
• Grammatiken: regulär, kontextfrei, monoton/kontextsensitiv
• Kellerautomaten, beschränkte Maschinen, Turing-Maschinen
• Chomsky-Hierarchie
11
Za wos brauch’ i des?
• Weil es im Studienplan steht.
• Weil Sie es in der Praxis brauchen:
reguläre Ausdrücke, EBNF, Aussagenlogik, . . .
• Weil es Basiswissen einer akademischen InformatikerIn ist:
Halteproblem, P vs. NP, Church-Turing-These, . . .
10
• Weil es Ihr Abstraktionsvermögen und Ihr formales
Verständnis schult.
Was sind formale Sprachen?
Formale Sprache: (un)endliche Menge von endlichen Zeichenketten
Beispiele:
Programmiersprachen (C, Java, . . . )
Markup-Sprachen (Html, . . . )
Kommunikationsprotokolle
natürliche Sprachen
Warum formale Spezifikation?
Referenz für Anwender, Implementierer, Auftragnehmer/geber
Automatische Programmgenerierung: Compilergeneratoren
Formale Verifikation (Korrektheit, Deadlockfreiheit, . . . )
Kriterium für Spezifikationsmethode: Endlichkeit
Jede Methode induziert eine Sprachklasse.
12
Beispiele für Spezifikationsmethoden
Reguläre Ausdrücke:
DOS: dir a*.exe
Unix: ^[0-9]+\.[0-9]*(E[+-]?[0-9]+)?$
Syntaxdiagramme:
digit - .
- ScaleFactor
- digit
Automaten:
digit
?
q0j digit- q1j
Grammatik:
q4j
@
digit@ digit
@ R?
@
h
q5j
Hw
Art
ZwP
HwP
Satz
⇒
⇒
⇒
⇒
⇒
⇒
fressen
wird
Katze | Dosenfutter
die | das
Hzw HwP Zw
Art Hw
HwP ZwP
digit
Hzw
⇒
+, −
digit
. - q?
h E - q3j
j
2
Zw
14
Grundlagen: Sprachen
13
Grundlagen: Wörter
Formale Sprache über Σ: beliebige Teilmenge von Σ∗
= {s1 · · · sn | si ∈ Σ, 1 ≤ i ≤ n}
Potenzbildung:
L0 = {ε}
Stern-Operator: L∗ =
Ln
Ln
n≥0
[
n≥1
hP(Σ∗ ), ·, {ε}i bildet Monoid.
Plus-Operator: L+ =
16
Kleene-Stern“
”
und Ln+1 = L · Ln für n ≥ 0.
[
L1 · L2 = {w1 · w2 | w1 ∈ L1 , w2 ∈ L2 }
Verkettung: Sei L1 , L2 ∈ P(Σ∗ ).
P(Σ∗ ): Menge aller Sprachen
Alphabet: endliche, nicht-leere Menge atomarer Symbole (Σ, T ).
Wort über Σ: endliche Folge von Symbolen aus Σ.
Leerwort: ε
Σ+
= Σ+ ∪ {ε}
Σ+ : Menge aller nicht-leeren Wörter über Σ.
Σ∗
Verkettung: Sei w, w1 , w2 ∈ Σ∗ .
w1 · w2 = w1 w2
w·ε=ε·w =w
w0 = ε, wn+1 = w · wn
hΣ∗ , ·, εi bildet Monoid.
15
Rechenregeln
A · (B ∪ C)
A · (B · C)
A ∪ (B ∪ C)
= B·A∪C ·A
= A·B∪A·C
= (A · B) · C
= (A ∪ B) ∪ C
= B∪A
A · A∗
(A∗ )∗
(A ∪ {ε})∗
= A+
= A∗
= A∗
A · {ε} = A
{ε} · A = A
A∪B
(B ∪ C) · A
A∗ · A = A+
=
{E, E+, E−} · digit +
{0, . . . , 9}
A+ ∪ {ε} = A∗
digit
=
digit + · {.} · digit ∗ · ({ε} ∪ scale)
Beispiel. Real-Zahlen
scale
=
Bildungsregel f : B n → B
real
17
Grundmenge A0 ⊆ B,
Induktive Definition
Gegeben:
[
i≥0
für i nach unendlich:
=
Ai
Ai+1 = Ai ∪ {f (e1 , . . . , em ) | e1 , . . . , em ∈ Ai }
Stufenweise Konstruktion von Mengen:
Limes von
Ai
A
f (x1 , . . . , xn ) ∈ A
Definition. A heißt abgeschlossen unter f , wenn gilt:
x1 , . . . , xn ∈ A ⇒
19
Reguläre Sprachen
• Gebildet durch Vereinigung, Verkettung und Kleene-Stern
• Äquivalent: endliche Automaten, reguläre Grammatiken
Anwendungen in der Informatik:
• Compilerbau: Tokens bilden reguläre Sprache, verarbeitet
durch Scanner (Lexer).
Reguläre Ausdrücke dienen als Eingabe für Scannergeneratoren
(lex, flex).
• Texteditoren: erweiterte Suche
18
• DOS, Unix-Shells, grep, awk, Perl, Xml, . . .
Satz.
(a) A ist abgegeschlossen unter f .
(b) Ist A0 abgeschlossen unter f und gilt A0 ⊆ A0 ⊆ B,
dann gilt A ⊆ A0 .
D.h.: A ist die kleinste Menge, die A0 enthält und abgeschlossen ist
unter f .
Schema der induktiven Definition
A ist die kleinste Menge, für die gilt:
(a) A0 ⊆ A
(b) x1 , . . . , xn ∈ A ⇒ f (x1 , . . . , xn ) ∈ A
(A ist abgeschlossen unter f )
20
Definition. Die Menge der regulären Sprachen über Σ, Lreg (Σ), ist
die kleinste Menge, sodass
(a) {}, {ε}, {s} ∈ Lreg (Σ) für alle s ∈ Σ
(b) A, B ∈ Lreg (Σ) ⇒ A ∪ B, A · B, A∗ ∈ Lreg (Σ)
Satz. Lreg (Σ) ist abgeschlossen gegenüber Vereinigung,
Durchschnitt, Verkettung, Komplement, Differenz, Stern- und
Plus-Operator, Homomorphismen und Quotientenbildung.
Satz. Seien L1 und L2 reguläre Sprachen spezifiziert durch
Verkettung, Vereinigung und Stern-Operator. Die Probleme
(a) Gehört ein Wort w der Sprache L1 an?
(b) Ist L1 leer, endlich, unendlich?
(c) Gilt L1 = L2 ?
sind entscheidbar.
21
{ A}
[ A]
A| B
AB
EBNF
(A)
A∗
{ε} ∪ A
A∪B
A·B
reg. Menge
s∈Σ
Gruppierung
Wiederholung
Option
Alternativen
Aufeinanderfolge
EBNF-Notation
( A)
{s}
Kommentar
"s "
Beispiel. Real-Zahlen (EBNF)
real = digit {digit} "." {digit} [scale]
scale = "E" ["+"|"-"] digit {digit}
digit = "0"|"1"|"2"| · · · |"9"
23
s
statt
statt
{}
{ε}
{s} für s ∈ Σ
L∗
L1 L2
L1 + L2
bleibt
statt
statt
L∗
L1 · L2
L1 ∪ L2
Algebraische Notation
ε
statt
hat die höchste Priorität, + die niedrigste.
∅
∗
digit
= E (ε + + + −) digit digit ∗
= 0+ ···+ 9
Beispiel. Real-Zahlen (algebraisch)
scale
= digit digit ∗ . digit ∗ (ε + scale)
A∪B
A·B
A∗
A+
{s}
A
reg. Menge
[ A]
A| B
AB
{ A}
A{ A}
"s"
A
EBNF
22
real
Syntaxdiagramm
A
s A ∪ {ε}
Syntaxdiagramme
-A
A
-A -B -A
-B
-A
24
Beispiel. Real-Zahlen (Syntaxdiagramm)
real
- digit
digit
- .
s
Zeichen s
Zeichen s (kein Spezialsymbol)
\s
alle Zeichen außer Zeilenende
25
scale
- +
- E
- digit
- egrep unter Unix
.
Zeilenanfang
selektiert
^
Zeilenende
Ausdruck
$
alle Zeichen in {s1 , . . ., sn }
null Mal oder öfter r
[s1 · · · sn ]
r*
ein Mal oder öfter r
alle Zeichen außer {s1 , . . ., sn }
r+
null oder ein Mal r
[^s1 · · · sn ]
r?
27
scale
digit
- 0
- 1
.
.
.
..
..
..
- 9
Reguläre Definitionen
Verwendung von Abkürzungen für reguläre Teilausdrücke.
Erhöht nicht die Ausdruckskraft.
Bessere Strukturierung, bessere Lesbarkeit.
selektiert
26
ist nicht zulässig!
Keine direkte oder indirekte Rekursivität:
Ausdruck
i Mal r
digits = digit · digits ∪ {ε}
r{i}
i Mal oder öfter r
r1 gefolgt von r2
r{i,}
r1 r2
r1 oder r2
i bis j Mal r
r1 |r2
r
r{i,j}
(r)
Beispiel. Real-Zahlen (egrep)
^[0-9]+\.[0-9]*(E[+-]?[0-9]+)?$
28
Endliche Automaten
%
NEA
Modell für Systeme mit Ein/Ausgaben aus endlichem Wertebereich
und mit endlichem Speicher.
Reguläre
$
'Menge
?
6
minimaler
DEA
6
&
DEA
DEA . . . deterministischer endlicher Automat
NEA . . . nichtdeterministischer endlicher Automat
29
Deterministischer endlicher Automat
A = hQ, Σ, δ, q0 , F i, wobei
Q . . . endliche Menge von Zuständen
Σ . . . Eingabealphabet
∈ Q . . . Anfangszustand
δ: Q × Σ → Q . . . Übergangsfunktion (total)
q0
F ⊆ Q . . . Menge von Endzuständen
δ ∗ (q, aw) = δ ∗ (δ(q, a), w)
Erweiterte Übergangsfunktion: δ ∗ : Q × Σ∗ → Q
δ ∗ (q, ε) = q,
für alle q ∈ Q, w ∈ Σ∗ , a ∈ Σ.
Akzeptierte Sprache: L(A) = {w ∈ Σ∗ | δ ∗ (q0 , w) ∈ F }
31
Beispiel.
.
h
j
- q?
2
E
- q3j
Deterministischer endlicher Automat (DEA)
+,digit
digit
?
q0j digit- q1j
.
- q?
h
j
2
E
ε
-
5
digit- q?
h
j
digit
q4j
@
digit@
digit
@ Rq?
@
h
j
5
digit
?
- q4j
6
Nichtdeterministischer endlicher Automat (NEA)
digit
digit
+
?
q0j digit- q1j
- q3j
30
Nichtdeterministischer endlicher Automat
Übergangsfunktion: δ: Q × (Σ ∪ {ε}) → P(Q)
δ ∗ (q, w) = {q 0 ∈ Q | q ; q 0 }
w
Erweiterte Übergangsfunktion: δ ∗ : Q × Σ∗ → P(Q)
w
q ; q 0 . . . es gibt einen mit w beschrifteten Pfad von q nach q 0
Akzeptierte Sprache:
L(A) = {w ∈ Σ∗ | δ ∗ (q0 , w) ∩ F 6= {}}
Definition. Automaten A und A0 sind äquivalent, falls
L(A) = L(A0 ).
32
s ∈ (Σ ∪ {ε})
Reguläre Menge → NEA
j s - h
j
Satz. Zu jeder regulären Sprache L gibt es einen endlichen
Automaten A, sodass L = L(A).
j
h
j
L = {}:
L = {s}:
L = L1 ∪ L2 :
j
j
q0,1A1qf,1 H
*
H
ε
ε
H
j
H
j
j
h
HH *
ε
ε
H
j j
H
j
A
2
q
q
0,2 f,2
33
Determinisierung (NEA → DEA)
Satz. Zu jedem NEA gibt es einen äquivalenten DEA.
NEA: A = hQ, Σ, δ, q0 , F i
für alle q̂ ∈ Q̂, a ∈ Σ
DEA: Â = hQ̂, Σ, δ̂, q̂0 , F̂ i, wobei
δ ∗ (q, a)
Q̂ = P(Q)
[
q∈q̂
{q̂ ∈ Q̂ | q̂ ∩ F =
6 {}} ∪ {q̂ } falls ε ∈ L(A)
0
{q̂ ∈ Q̂ | q̂ ∩ F =
6 {}}
sonst
= {q0 }
=
δ̂(q̂, a) =
q̂0
F̂
Tipp: Berechne die Übergangsfunktion ausgehend von q̂0 nur für
tatsächlich erreichbare Zustände.
35
L = L1 · L2 :
L = (L1 )∗ :
j A1
j ε - j A2
j
h
q
q
q
q
0,1 f,1
0,2 f,2
34
ε
?
j ε - j
j ε - j A1
h
q
q
0,1 f,1
6
ε
Minimierung
Satz. Zu jeder regulären Sprache gibt es einen bis auf
Umbenennung der Zustände eindeutigen, minimalen DEA.
oder
δ ∗ (q, w) ∈ F
δ ∗ (p, w) ∈
/F
Definition. Zwei Zustände p, q heißen unterscheidbar durch ein
Wort w ∈ Σ∗ , wenn man von p aus mit w in einen Endzustand
gelangen kann, aber nicht von q aus, bzw. umgekehrt:
δ ∗ (p, w) ∈ F
δ ∗ (q, w) ∈
/F
p und q sind ununterscheidbar, wenn sie durch kein Wort
unterschieden werden können.
Minimierung: Entfernen aller nicht-erreichbaren Zustände,
Zusammenfassen aller ununterscheidbaren Zustände.
36
Algorithmus zur Minimierung
1. Entferne alle Zustände, die nicht vom Anfangszustand aus
erreichbar sind.
2. Markiere alle Zustandspaare (p, q) als unterscheidbar, für die
p ∈ F und q ∈
/ F gilt oder umgekehrt.
3. Wiederhole den folgenden Schritt, bis keine Zustandspaare
mehr als unterscheidbar markiert werden können.
Berechne für alle Zustandspaare (p, q) und alle a ∈ Σ das
Nachfolgerpaar (δ(p, a), δ(q, a)); ist letzteres bereits als
unterscheidbar markiert, markiere auch (p, q) als
unterscheidbar.
4. Fasse alle voneinander ununterscheidbaren Zustände zu einem
einzigen zusammen.
37
DEA → reguläre Menge
Satz. Jede von einem DEA akzeptierte Sprache ist regulär.
A = h{q1 , . . ., qn }, Σ, δ, q1 , F i
=
=
qj }
{s ∈ Σ | δ(qi , s) = qj }
{s ∈ Σ |
=
∪ {ε}
[
n
R1j
k−1
k−1
k−1 ∗
k−1
= Rij
∪ Rik
· (Rkk
) · Rkj
δ(qi , s)
k>0
i 6= j
i=j
k
Rij
. . . Menge aller Wörter, mit denen man von qi nach qj gelangt,
ohne einen Zustand mit einem Index größer als k zu berühren.
0
Rij
k
Rij
L(A)
qj ∈F
39
Beispiel.
i
j
6
0
0
0
0
38
1
h
- j
q2 @
I
@
@
@
1
0, 1
?
j
- h
q3
?
0
1
0
- bj
- cj
h
aj
dj
@
@
6@
I
1 @
1
@1
@0
@
@
@
@
@
@
@
@
@
@ 1
@
@
0
0
@
@
@ Rj
@
R?
@
@j
1
1
0
gj
ej
f
h
YH
H
6
H
H
H
H
HH
1
Beispiel.
q1
40
k
R31
k
R23
k
R22
k
R21
k
R13
k
R12
k
R11
{0, 1}
{}
{1}
{ε}
{0}
{1}
{0}
{ε}
k=0
{ε}
{0, 1}
{}
{1, 01}
{ε, 0 0}
{0}
{1}
{0}
{ε}
k=1
{ε} ∪ {0, 1} · {0} · {1}
{0, 1} · {0 0}
{0, 1} · {00} · {0}
{0}∗ · {1}
{0 0}∗
{0} · {00}∗
{0}∗ · {1}
{0} · {00}∗
{0 0}∗
k=2
∗
k
R32
{ε}
∗
∗
k
R33
41
Folgende Probleme sind für reguläre Sprachen L, L0 entscheidbar.
• Gehört ein Wort w der Sprache L an?
Konstruiere einen DEA für L und prüfe δ ∗ (q0 , w) ∈ F .
• Ist L leer?
Konstruiere einen DEA für L und prüfe, ob von q0 aus ein
Endzustand erreichbar ist.
• Ist L endlich oder unendlich?
L ist unendlich gdw. der minimale DEA für L einen Zyklus
enthält.
• Gilt L = L0 ?
Überprüfe, ob L − L0 und L0 − L leer sind.
43
Eigenschaften regulärer Sprachen
Lreg (Σ) ist abgeschlossen gegenüber
• Vereinigung, Verkettung, Stern-Operator: per Definition.
• Plus-Operator: A+ = A∗ · A.
• Komplement bzgl. Σ∗ : konstruiere DEA und vertausche Endund Nichtendzustände.
• Durchschnitt: A ∩ B = A ∪ B.
• Differenz: A − B = A ∩ B.
• Homomorphismen: Sei h: Σ → Σ0∗ eine Abbildung von
Symbolen aus Σ auf Worte über Σ0 .
Ist L eine reguläre Sprache, dann auch h(L) = {h(w) | w ∈ L}.
Beweis: repräsentiere L durch regulären Ausdruck und ersetze
alle Vorkommnisse von a durch Ausdruck für h(a).
42
Grenzen regulärer Sprachen
Beispiel. Modulo-Arithmetik
L . . . Menge aller binären Numerale ohne führende Nullen, die
kongruent 0 modulo 5 sind
wert(11 01)
= 1 · 23 + 1 · 22 + 0 · 21 + 1 · 20
= (((0 · 2 + 1) · 2 + 1) · 2 + 0) · 2 + 1
wert(11 01) mod 5
= (((0 · 2 + 1) · 2 + 1) · 2 + 0) · 2 + 1 mod 5
(((0 · 2 + 1) mod 5 · 2 + 1) mod 5 · 2 + 0) mod 5 · 2 + 1 mod 5
=
44
1
Zustand i . . . bisherige Zahl ist kongruent i mod 5“
”
δ(i, 0) = (i · 2 + 0) mod 5
δ(i, 1) = (i · 2 + 1) mod 5
i
j
0
3j
I
@
@
1
1
@0
@
@j
4
6
1
?
?
- 1j 0 - 2j 0
I
@
@
1
@1
@
?
@ j
0h 0
45
Pumping Lemma für reguläre Sprachen
Sei L eine unendliche reguläre Sprache.
Beispiel. Geschachtelte Strukturen
L = {an bn | n ≥ 0} regulär?
Angenommen, es gibt DEA A = hQ, Σ, δ, q0 , F i für L.
Wir betrachten δ ∗ (q0 , ai ) für i = 1, 2, 3, . . . .
Schubfachprinzip: es gibt m, n sodass
m 6= n aber δ ∗ (q0 , am ) = q = δ ∗ (q0 , an ) .
= δ ∗ (δ ∗ (q0 , am ), bn )
an bn ∈ L(A), daher gilt δ ∗ (q, bn ) = qf ∈ F .
Wir erhalten:
δ ∗ (q0 , am bn )
= δ ∗ (q, bn )
= qf
46
d.h., am bn ∈ L(A) obwohl m 6= n!
Folgerung: L ist nicht regulär.
Beispiel. L = {an bn | n ≥ 0}
• Lemma gilt für alle w mit |w| ≥ m, m unbekannt.
Wäre L regulär, müsste Pumping Lemma gelten.
Für alle hinreichend großen Worte w ∈ L existiert eine Zerlegung
w = xyz mit y 6= ε, sodass xy i z ∈ L für alle i = 0, 1, 2, . . .
• Wähle w = am bm .
48
• Betrachte w0 = am−k bm .
Da w0 ∈
/ L, ist L nicht regulär.
Formal: Es gibt m > 0, sodass für alle w ∈ L mit |w| ≥ m gilt:
für alle i ≥ 0.
mit |xy| ≤ m und y 6= ε
• y besteht aus lauter a’s, also y = ak für k > 0.
w = xyz
w kann geschrieben werden als
sodass
wi = xy i z ∈ L
47
Pumping Spiel
Gegeben: unendliche Sprache L
Proponent: versucht Widerspruch zum Pumping Lemma zu finden
Opponent: versucht dies zu verhindern
1. Opponent wählt Schranke m.
2. Proponent wählt w ∈ L mit |w| ≥ m.
3. Opponent zerlegt w als xyz, sodass |xy| ≤ m und y 6= ε.
4. Proponent sucht ein i, sodass wi ∈
/ L.
Gelingt ihm das, gewinnt er, anderfalls der Opponent.
49
L ist nicht regulär, wenn Proponent eine Gewinnstrategie besitzt.
Formale Definitionen
. . . Variable (Nonterminale)
. . . Terminalsymbole (V ∩ T = {})
⊆ (V ∪ T )+ × (V ∪ T )∗ . . . Produktionen
∈ V . . . Startsymbol
Grammatik G = hV, T, P, Si, wobei
V
T
P
S
α ⇒ β statt (α, β) ∈ P
α ⇒ β1 | · · · | βn statt α ⇒ β1 , . . . , α ⇒ βn
51
Grammatiken
Satz ⇒ HwP ZwP
Hw ⇒ Katze | Dosenfutter
Art ⇒ die | das
Beispiel.
HwP ⇒ Art Hw
Hzw ⇒ wird
HwP ZwP
Art Hw
fressen
fressen
ZwP ⇒ Hzw HwP Zw
Art Hw
wird
das
Zw ⇒ fressen
`
Katze
wird
Satz
`P
die
Katze
Hzw HwP Zw
`P
die
50
Dosenfutter
`P
Direkte Ableitbarkeit:
xαy ` xβy falls α ⇒ β ∈ P und x, y ∈ (V ∪ T )∗
Ableitbarkeit von w aus v in n Schritten:
Es gibt Wörter w0 , w1 , . . . , wn , sodass v = w0 , w = wn und
wi−1 ` wi für 1 ≤ i ≤ n.
Schreibweise: v ` w1 ` · · · ` wn−1 ` w
Ableitbarkeit in mehreren Schritten:
∗
v`
w . . . reflexiver und transitiver Abschluss von `
Durch G erzeugte Sprache L(G):
∗
L(G) = {w ∈ T ∗ | S `
w}
Grammatiken G1 und G2 heißen äquivalent, wenn L(G1 ) = L(G2 )
gilt.
52
Reguläre Grammatiken
oder
A⇒ε
Definition. Eine Grammatik heißt regulär, wenn alle Produktionen
von der Form
A ⇒ aB
sind (A, B ∈ V , a ∈ T ).
Satz. Eine Sprache ist genau dann regulär, wenn sie von einer
regulären Grammatik generiert wird.
53
Kontextfreie Grammatiken
Definition. Eine Grammatik heißt kontextfrei, wenn alle
Produktionen von der Form A ⇒ β sind, wobei A ∈ V und
β ∈ (V ∪ T )∗ .
Eine Sprache L heißt kontextfrei, wenn es eine kontextfreie
Grammatik G gibt, sodass L = L(G).
Linksableitbarkeit:
xAy `L xβy falls A ⇒ β ∈ P und x ∈ T ∗
Rechtsableitbarkeit:
xAy `R xβy falls A ⇒ β ∈ P und y ∈ T ∗
Parallelableitbarkeit:
x0 A1 x1 · · · An xn `P x0 β1 x1 · · · βn xn falls
A1 ⇒ β1 , . . . , An ⇒ βn ∈ P und x0 , . . . , xn ∈ T ∗
55
T
V
= Real
= {0, . . ., 9, ., E, +, −}
= {Real , A, B , C , D, E }
Beispiel. Real-Zahlen; G = hV, T, P, Si
S
⇒ 0 A | ··· | 9 A
= {
E
D
C
B
⇒ ε | 0 E | ··· | 9 E
⇒ 0 E | ··· | 9 E
⇒ 0 E | ··· | 9 E | + D | − D
⇒ ε | 0 B | ··· | 9B | EC
A ⇒ 0 A | ··· | 9 A | . B
Real
P
}
54
∗
= {w ∈ T ∗ | S `
w}
Satz. Ist G eine kontextfreie Grammatik, dann gilt:
L(G)
∗
= {w ∈ T ∗ | S `
L w}
∗
= {w ∈ T ∗ | S `
R w}
∗
= {w ∈ T ∗ | S `
P w}
Eine Grammatik heißt mehrdeutig, wenn es ein Wort mit mehreren
Linksableitungen gibt.
Eine Sprache heißt (inhärent) mehrdeutig, wenn alle kontextfreien
Grammatiken für sie mehrdeutig sind.
56
V
= {0, . . ., 9, ., E, +, −}
= {Real , ScaleFactor , Sign, Digits, Digit}
Beispiel. Wohlgeformte Klammerausdrücke
Beispiel. Real-Zahlen; G = hV, T, P, Si
T
WKA ist die kleinste Menge, sodass
WKA i
Beispiel. If-then-else Anweisung
⇒ if expr then Anw
| if expr then Anw else Anw
| others
zwei Linksableitungen besitzt.
60
if expr then if expr then others else others
G1 ist mehrdeutig, da das Wort
Anw
wobei P1 folgende Produktionen sind:
P1 , Anw i
G1 = h {Anw }, {if, then, else, expr, others},
58
{WKA ⇒ ε | ( WKA ) | WKA WKA},
G = h {WKA}, {(, )},
• w1 , w2 ∈ WKA ⇒ w1 w2 ∈ WKA
• w ∈ WKA ⇒ (w) ∈ WKA
• ε ∈ WKA
= Real
⇒ Digit Digits . Digits ScaleFactor
S
Real
⇒ ε | E Sign Digit Digits
⇒ ε | Digit Digits
⇒ ε|+|−
Digits
⇒ 0 | ··· | 9
57
Digit
Sign
ScaleFactor
Produktionen:
Beispiel.
G = h {S }, {a, b}, {S ⇒ ε | a S b}, S i
L(G) = {an bn | n ≥ 0} = {ε, a b, aa bb, . . .}
Beispiel. Palindrome über {a, b}
G = h {S }, {a, b},
{S ⇒ ε | a | b | a S a | b S b}, S i
L(G) = {ε, a, b, aa, b b, aa a, ab a, ba b, b bb, . . .}
59
Eindeutige Grammatik:
G2 = h {Anw , AnwT , AnwTE },
{if, then, else, expr, others}, P2 , Anw i
⇒ if expr then Anw
| AnwTE
⇒ AnwT
wobei P2 folgende Produktionen sind:
Anw
AnwT
| if expr then AnwTE else AnwT
AnwTE ⇒ if expr then AnwTE else AnwTE
| others
61
Backus-Naur-Form (BNF)
Synonym für kontextfreie Produktionen.
Notation: Nonterminale in spitzen Klammern
hReali ⇒ hDigiti hDigitsi . hDigitsi hSFi
Erweiterte Backus-Naur-Form (EBNF)
Auch: Regular Right Part Grammar (RRPG)
Reguläre Ausdrücke auf rechter Seite der Produktionen
Zweck: Abkürzung häufiger Situationen
A ⇒ w1 {w2 }w3 ermöglicht A ` w1 w2n w3 für beliebiges n.
63
Beispiel. Inhärent mehrdeutige Sprachen
L1 = {am bm cn | m, n ≥ 0}
L2 = {am bn cn | m, n ≥ 0}
L = L1 ∪ L2
S1
S
⇒ aAb|ε
⇒ S1 c | A
⇒ S1 | S2
B
S2
⇒ bBc|ε
⇒ a S2 | B
L ist kontextfrei:
A
Grammatik ist mehrdeutig, da an bn cn zwei verschiedene
Ableitungen besitzt.
Man kann zeigen, dass alle Grammatiken für L mehrdeutig sind,
d.h., L ist inhärent mehrdeutig.
62
entspricht A ⇒ w1 B w3
B ⇒ ε | w2 B
entspricht A ⇒ w1 B w3
B ⇒ w2
entspricht A ⇒ w1 B w3
Elimination der EBNF-Notationen:
A ⇒ w1 (w2 ) w3
A ⇒ w1 {w2 } w3
A ⇒ w1 [w2 ] w3
B ⇒ ε | w2
64
identlist ⇒ ident { , ident }
Beispiel. Listen von Bezeichnern
EBNF:
⇒ ε | , ident B
Ohne EBNF: identlist ⇒ ident B
B
SF ⇒ E [+ | −] Digit {Digit}
Beispiel. Skalierungsfaktor Real-Zahlen
EBNF:
65
Ohne EBNF: SF ⇒ E B1 Digit B2
B1 ⇒ ε | + | −
B2 ⇒ ε | Digit B2
Beispiel. Identifier (Bezeichner)
L = (GB ∪ KB ) · (GB ∪ KB ∪ Ziff )∗
A
⇒ a B | ··· | zB | A B | ··· | Z B | 0 B | ··· | 9 B | ε
⇒ a B | ··· | zB | A B | ··· | Z B
Reguläre Grammatik:
G = h{A, B}, {a, . . ., z, A, . . ., Z, 0, . . ., 9}, P, Ai, wobei P :
B
Kontextfreie Grammatik in EBNF:
G0 = h{A, B, Z}, {a, . . ., z, A, . . ., Z, 0, . . ., 9}, P 0 , Ai, wobei P 0 :
B
⇒ 0 | ··· | 9
⇒ A | ··· | Z | a | ··· | z
A ⇒ B {B | Z }
Z
67
Syntaxdiagramme
Erlaubt man rekursive Diagramme, können beliebige kontextfreie
Grammatiken in EBNF dargestellt werden.
Beispiel. Wohlgeklammerte Ausdrücke
66
- WKA
WKA
- ( - WKA - )
- WKA
⇒
E + E | E ∗ E | ( E ) | id
Beispiel. G = h{E}, {+, ∗, (, ), id}, P, Ei wobei P :
E
E + E `L




E
+
E
E
+
` id + E + E `L id + id + E
 id + E  L
`L
id + id + id
G ist mehrdeutig:
E
`L
T ⇒T ∗F |F
F ⇒ ( E ) | id
L(G) ist aber nicht mehrdeutig, da es eindeutige Grammatik gibt:
G0 = h{E, T, F }, {+, ∗, (, ), id}, P 0 , Ei wobei P 0 :
E ⇒E+T |T
Ohne Klammern wäre L(G) regulär: id { ( + | ∗ ) id } (EBNF)
68
Beispiel. L = {am +bn =cm+n | m, n ≥ 0}
aSc
`
T
S
aa +b b T c c cc
aa S c c
⇒ bT c|=
⇒ aSc|+T
` a a+ bb =c cc c
` a a+ T c c
Kontextfreie Grammatik G = h{S, T }, {a, b, c, +, =}, P, Si
wobei P :
`
aa +b T cc c `
a a+b b =cc c c ∈ L(G):
S
`
∗
Beispiel. L = {w ∈ {a, b} | anza (w) = 2 · anzb (w)}
⇒ aSaSbS |aSbSaS |bSaSaS |ε
G = h{S}, Σ, P, Si, wobei P :
S
69
Normalformen kontextfreier Grammatiken
A, B, C . . . Nonterminale (A, B, C ∈ V )
a . . . Terminalsymbol (a ∈ T )
α . . . Folge von Nonterminalen (α ∈ V ∗ )
Chomsky Normalform: Alle Produktionen besitzen die Form
A⇒BC
oder
A⇒a
(a ∈ T , A, B, C ∈ V ) .
Greibach Normalform: Alle Produktionen besitzen die Form
A ⇒ ax
(a ∈ T , A ∈ V , x ∈ V ∗ ) .
Satz. Zu jeder kontextfreien Sprache ohne Leerwort gibt es eine
Grammatik in Chomsky NF und eine in Greibach NF.
71
Transformation von Produktionen
Substitution (Ersetzung) Eine Produktion A ⇒ uBw darf durch
A ⇒ uv1 w | · · · | uvn w
ersetzt werden, falls B ⇒ v1 | · · · | vn alle B-Produktion sind.
Nutzlose Produktionen Entfernen aller Produktionen, die von der
Startvariablen aus nicht erreichbar sind oder aus denen kein
w ∈ T ∗ ableitbar ist.
ε-Produktionen Entfernen aller Produktionen A ⇒ ε
Einheitsproduktionen Entfernen aller Produktionen A ⇒ B
70
Satz. Zu jeder kontextfreien Sprache ohne Leerwort gibt es eine
kontextfreie Grammatik ohne nutzlose, ohne ε- und ohne
Einheitsproduktionen.
Kellerautomaten
Kellerautomat = endlicher Automat + Stack
K = hQ, Σ, Γ, δ, q0 , z, F i, wobei
Q . . . endliche Menge von Zuständen
Σ . . . Eingabealphabet
Γ . . . Kelleralphabet
δ: Q × (Σ ∪ {ε}) × Γ → P(Q × Γ∗ ) . . . Übergangsfunktion
q0 ∈ Q . . . Anfangszustand
z ∈ Γ . . . Anfangskellersymbol
F ⊆ Q . . . Menge von Endzuständen
72
(q, w, u) . . . Konfiguration, beschreibt den momentanen Zustand
des Kellerautomaten, wobei
q . . . momentaner Zustand des endlichen Automaten
w . . . noch nicht verarbeiteter Teil der Eingabe
u . . . momentaner Inhalt des Stacks
Rechenschrittrelation `:
(q1 , aw, bx) ` (q2 , w, yx) genau dann, wenn (q2 , y) ∈ δ(q1 , a, b)
∗
`
. . . reflexiver und transitiver Abschluss von `
Akzeptierte Sprache:
∗
L(K) = {w ∈ Σ∗ | (q0 , w, z) `
(qf , ε, u), qf ∈ F, u ∈ Γ∗ }
Satz. Eine Sprache ist kontextfrei genau dann, wenn sie von einem
Kellerautomaten akzeptiert wird.
73
und Schnitt mit regulären Sprachen;
Eigenschaften kontextfreier Sprachen
∗
Kontextfreie Sprachen sind . . .
• abgeschlossen bzgl. ∪, ·,
• nicht abgeschlossen bzgl. Durchschnitt und Komplement.
b/a/ε
Beispiel. Kellerautomat für L = {an bn | n ≥ 0}.
a/a/a
a
?
?
a/z/a
b/a/ε
ε/z/z
z
0
3
1
2
x/y/z: Eingabe x gelesen, y weg vom Stack, z auf den Stack
Formale Beschreibung: L = L(K), wobei
δ(2, b, a) = {(2, ε)}
und
δ(1, a, a) = {(1, aa)}
δ(2, ε, z) = {(3, z)}
K = h{0, 1, 2, 3}, {a, b}, {a, z}, δ, 0, z, {0, 3}i
δ(0, a, z) = {(1, a z)}
δ(1, b, a) = {(2, ε)}
Es gilt: a a bb ∈ L(K), da
(0, a a b b, z) ` (1, a b b, a z) ` (1, b b, a a z) ` (2, b, a z) ` (2, ε, z) ` (3, ε, z)
74
Pumping Lemma für kontextfreie Sprachen
Sei L eine unendliche kontextfreie Sprache.
Für alle hinreichend großen Worte w ∈ L existiert eine Zerlegung
w = uvxyz mit |vxy| ≤ m und vy 6= ε, sodass uv i xy i z ∈ L für alle
i = 0, 1, 2, . . .
Formal: Es gibt m > 0, sodass für alle w ∈ L mit |w| ≥ m gilt:
Entscheidbare Probleme:
• Ist die k.f. Sprache L leer/endlich/unendlich?
für alle i ≥ 0.
mit |vxy| ≤ m und |vy| ≥ 1
76
wi = uv i xy i z ∈ L
w = uvxyz
w kann geschrieben werden als
sodass
• Liegt Wort w in der k.f. Sprache L? (Parsing-Problem)
Unentscheidbare Probleme:
• Gilt L = Σ∗ , L1 = L2 (Äquivalenzproblem), L1 ⊆ L2 ,
L1 ∩ L2 = {}?
• Ist L regulär? Ist L1 ∩ L2 bzw. Σ∗ − L kontextfrei?
75
Pumping Spiel Nr. 2
Gegeben: unendliche Sprache L
Proponent: versucht Widerspruch zum Pumping Lemma zu finden
Opponent: versucht dies zu verhindern
1. Opponent wählt Schranke m.
2. Proponent wählt w ∈ L mit |w| ≥ m.
3. Opponent zerlegt w als uvxyz, sodass |vxy| ≤ m und |vy| ≥ 1.
4. Proponent sucht ein i, sodass wi = uv i xy i z ∈
/ L.
Gelingt ihm das, gewinnt er, anderfalls der Opponent.
L ist nicht kontextfrei, wenn Proponent eine Gewinnstrategie
besitzt.
77
Jenseits der Kontextfreiheit
Beispiel. Formale Sprachen
{an bn cn | n ≥ 0} ist nicht kontextfrei.
Beispiel. Programmiersprachen
Typen- und Deklarationsbedinungen nicht oder nur schwer
kontextfrei darstellbar.
Beispiel. Natürliche Sprachen
Schweizer Dialekt:
Mer d’chind em Hans es huus
haend wele laa hälfe aastriiche.
Hochdeutsch:
Wir wollten die Kinder dem Hans
helfen lassen, das Haus anzustreichen.
79
Beispiel. Zu zeigen: L = {an bn cn | n ≥ 0} ist nicht kontextfrei.
1. Gegner wählt m.
2. Wir wählen w = am bm cm .
Da |vxy| ≤ m, kann vxy nicht gleichzeitig a’s und c’s enthalten.
3a. vxy enthält keine c’s.
Wegen |vy| ≥ 1 enthält vy mindestens ein a oder b.
4a. Wir wählen i = 0.
w0 = uxz enthält mindestens ein a oder b weniger als c’s.
Also w0 ∈
/ L.
3b. vxy enthält keine a’s.
Wegen |vy| ≥ 1 enthält vy mindestens ein b oder c.
4b. Wir wählen i = 0.
w0 = uxz enthält mindestens ein b oder c weniger als a’s.
Also w0 ∈
/ L.
78
Monotone Grammatiken
Definition. Grammatik heißt monoton, wenn für alle Produktionen
α ⇒ β die Länge von α kleiner gleich der Länge von β ist (α 6= ε).
Kommt Startvariable S auf keiner rechten Seite vor, ist auch S ⇒ ε
zugelassen.
Beispiel. L = {an bn cn | n ≥ 0}
G = h {S , T , C }, {a, b, c}, P, S i
S
⇒ a T b C | ab C
⇒ ε | ab c | a T b c
Cc ⇒
Cb ⇒
cc
bC
wobei P folgende Produktionen sind:
T
Es gilt: L(G) = L.
80
Kontextsensitive Grammatiken
Definition. Eine Grammatik heißt kontextsensitiv, wenn alle
Produktionen die Form uAv ⇒ uβv besitzen, wobei
u, v ∈ (V ∪ T )∗ , A ∈ V und β ∈ (V ∪ T )+ .
Kommt Startvariable S auf keiner rechten Seite vor, ist auch S ⇒ ε
zugelassen.
Satz. Für jede Sprache, die von einer monotonen Grammatik
erzeugt wird, gibt es auch eine kontextsensitive Grammatik, und
umgekehrt.
Typ 0
(rekursiv aufzählb.)
Sprachfamilie
kontextsensitiv
monoton
uneingeschränkt
Grammatiktyp
Kellerautomat
(= EA + Stack)
Linear beschränkter Aut.
(= EA + beschr.RAM)
Turing-Maschine
(= EA + RAM)
Maschinenmodell
81
Typ 1
(kontextsensitiv)
kontextfrei
endlicher Automat (EA)
Chomsky-Hierarchie
Typ 2
(kontextfrei)
regulär
Typ 3 (regulär)
Satz. Typ 3 & Typ 2 & Typ 1 & Typ 0
83
Beispiel. L = {an bn cn | n ≥ 0}
G = h {S , T , B , C , X , Y }, {a, b, c}, P, S i
T
S
⇒
⇒
⇒
b
a T B C | ab C
ε | ab c | a T B c
XY
CY
CB
⇒
⇒
⇒
XC
XY
CY
wobei P folgende Produktionen sind:
B
cc
XC
⇒
BC
Es gilt: L(G) = L.
Cc ⇒
82
Deterministische Turing-Maschine
Turing-Maschine = endlicher Automat + unendliches Band (RAM)
T = hQ, Σ, Γ, δ, q0 , 2, F i, wobei
Q . . . endliche Menge von Zuständen
Σ . . . Eingabealphabet (Σ ⊆ Γ − {2})
Γ . . . Bandalphabet
δ: Q × Γ → Q × Γ × {L, R} . . . Übergangsfunktion
q0 ∈ Q . . . Anfangszustand
2 ∈ Γ . . . Leersymbol
F ⊆ Q . . . Menge von Endzuständen
L = links“, R = rechts“
”
”
84
uqav . . . Konfiguration (u, v ∈ Γ∗ , a ∈ Γ, q ∈ Q)
beschreibt den momentanen Zustand der Turing-Maschine, wobei
2−∞ uav2∞ . . . Inhalt des Bandes
q . . . momentaner Zustand
a . . . Symbol unter dem Schreib-/Lesekopf
Rechenschrittrelation `:
uqav ` ubq 0 v genau dann, wenn δ(q, a) = (q 0 , b, R)
ucqav ` uq 0 cbv genau dann, wenn δ(q, a) = (q 0 , b, L)
(u, v ∈ Γ∗ , a, b, c ∈ Γ, q, q 0 ∈ Q)
∗
`
. . . reflexiver und transitiver Abschluss von `
Akzeptierte Sprache:
85
∗
L(T ) = {w ∈ Σ∗ | q0 w `
uqf v, qf ∈ F , u, v ∈ Γ∗ }
Formale Beschreibung von T :
y
(2, z, R)
z
(5, 2, R)
2
h{0, 1, 2, 3, 4, 5}, {a, b, c}, {a, b, c, x, y, z, 2}, δ, 0, 2, {5}i
wobei δ definiert ist durch:
x
a
(4, y, R)
c
δ
(1, x, R)
(1, y, R)
b
0
(1, a, R) (2, y, R)
(2, b, R) (3, z, L)
(3, a, L) (3, b, L)
(4, y, R) (4, z, R) (5, 2, R)
(0, x, R) (3, y, L) (3, z, L)
1
2
3
4
5
87
a/x
?
Rj
y,z
4
y
?
i
Rj
0
a,y
- Rj
61
b/y
b,z
- Rj
62
c/z
a,b,y,z
- Lj
63
Beispiel. Turing-Maschine T , sodass L(T ) = {an bn cn | n ≥ 0}.
x
2
2
?
h
- Rj
5
s
s/s0
- m
∆
q0
- m
∆
q0
wenn δ(q, s) = (q 0 , s0 , ∆)
wenn δ(q, s) = (q 0 , s, ∆)
Graphische Notation für richtungsgebundene Turing-Maschinen:
m
q
m
q
86
∗
q0 d `
qf f (d)
(qf ∈ F )
Turing-berechenbare Funktionen
Eine Funktion f : D → R heißt Turing-berechenbar oder einfach nur
berechenbar, wenn es eine Turing-Maschine hQ, Σ, Γ, δ, q0 , 2, F i
gibt, sodass
gilt für alle d ∈ D.
Mehrstellige Funktionen: Trennsymbol zwischen Argumenten
Beispiel. f (x, y) = x + y für x, y ∈ ω ist Turing-berechenbar.
1
?
j
-R
+/1
2
- Lj
1/2 -
1
?
Lj
2
h
- Rj
Unärkodierung für x, y und f (x, y), Trennsymbol +.
1
?
i
Rj
88
(Church-)Turing-These
Jede mechanische Berechnung kann auch von einer
”
Turing-Maschine ausgeführt werden.“
Problem versus Algorithmus
Problem: parametrisierte Frage spezifiziert durch die Beschreibung
• aller Parameter
• der zulässigen Lösungen (Antworten) und ihrer Eigenschaften.
Instanz eines Problems: Satz konkreter Werte für die Parameter
Argumente für diese These:
• Alle Computerberechnungen auch von Turing-Maschinen
ausführbar.
Algorithmus: Verfahren zur Lösung eines Problems
n−1
X
i=1
d(sπ(i) , sπ(i+1) ) + d(sπ(n) , sπ(1) )
92
semientscheidbar: unentscheidbar, aber es gibt Algorithmus, der
ersten Punkt erfüllt, aber im zweiten Fall manchmal nicht
terminiert.
Andernfalls heißt Π unentscheidbar.
2. A liefert auf Eingabe x1 , . . . , xn das Ergebnis 0 wenn die
Anwort auf Π für die Werte x1 , . . . , xn “Nein” lautet.
1. A liefert auf Eingabe x1 , . . . , xn das Ergebnis 1 wenn die
Anwort auf Π für die Werte x1 , . . . , xn “Ja” lautet.
Ein Entscheidungsproblem Π mit Parametern x1 , . . . , xn heißt
entscheidbar, wenn ein Algorithmus A existiert, sodass gilt:
Unentscheidbare Probleme
90
Instanzen des Problems Primzahl: 5, 18, . . .
• Lösung: “Ja”, falls n Primzahl; “Nein” sonst.
• Parameter: natürliche Zahl n
Beispiel. Entscheidungsproblem Primzahl:
Entscheidungsproblem: Ja/Nein-Problem
• Kein Problem mit Lösungsalgorithmus bekannt, für das keine
Turing-Maschine konstruierbar wäre.
89
• Kein Alternativvorschlag zur Formalisierung des Begriffs
mechanische Berechnung“ ist mächtiger.
”
Definition. Algorithmus zur Berechnung einer Funktion f : D → R:
Turing-Maschine T , die für jeden Input d ∈ D mit der Antwort
∗
f (d) ∈ R auf dem Band hält, d.h., q0 d `
qf f (d) für alle d ∈ D.
L =
Beispiel. Traveling Salesman
Parameter: Städte {s1 , . . ., sn }, Entfernungen d(si , sj )
Lösung: Permutation π, sodass die Länge der Rundreise
minimal ist.
Beispiel einer Instanz:
s1
JJ
5 J
Lösung: π = h1, 2, 4, 3i
9
10 J
Länge der Rundreise: L = 27
J
s
3
6 HH 3 J
H
J
H
s2
s4
9
91
Primzahl:
entscheidbar
entscheidbar
Beispiele
Traveling Salesman:
Halteproblem: Hält das Programm P bei Eingabe von x?“
”
semientscheidbar
unentscheidbar
nicht semientscheidbar
Äquivalenzproblem:
Berechnen die Programme P1 und P2 dieselbe Funktion?“
”
93
Lösungsaufwand ist i.A. proportional zur Größe der Eingabe.
Kodierungsschema: bildet Eingabe auf Zeichenkette ab.
Länge der Zeichenkette = Größe der Instanz
Beispiel. s[1]s[2]s[3]s[4]//10/5/9//6/9//3
Größe der Instanz: 32
Zeitkomplexitätsfunktion: ordnet jeder Größe den maximalen
Zeitaufwand zu, den der Algorithmus für eine Instanz dieser Größe
benötigt.
Ordnung einer Funktion: f (n) ist O(g(n)) – f (n) ist von der
Ordnung g(n) – wenn gilt:
es gibt Konstante c, sodass |f (n)| ≤ c · |g(n)| für fast alle n ≥ 0.
Ein Algorithmus ist polynomiell, wenn seine Zeitkomplexitätsfunktion O(p(n)) ist, wobei p ein Polynom in n ist. Anderfalls heißt
der Algorithmus exponentiell.
95
Komplexitätstheorie
Analyse von Algorithmen und Problemen hinsichtlich Rechenzeit,
Speicherplatz, . . .
Komplexität eines Problems: Komplexität des effizientesten
Algorithmus
Zeit-/Speicherkomplexität: Funktion der Eingabegröße
Worst-case Komplexität: Maximum über alle Eingaben gleicher
Größe
Erwartete Komplexität: gewichtetes Mittel über alle Eingaben
gleicher Größe
94
3n
2n
n5
n3
n2
n
9.8 s
.059 s
.001 s
.1 s
.001 s
.0001 s
.00001 s
10
3a
58 m
1.0 s
3.2 s
.008 s
.0004 s
.00002 s
20
2.6×107 a
6.5 a
17.9 m
24.3 s
.027 s
.0009 s
.00003 s
30
3.0×1014 a
3.9×105 a
12.7 d
1.7 m
.064 s
.0016 s
.00004 s
40
2.8×1021 a
2.3×1010 a
35.7 a
5.2 m
.125 s
.0025 s
.00005 s
50
Instanzengröße n
5n
96
Problem polynomiell unlösbar: es gibt keinen polynomiellen Alg.
n3
n2
n
N4
N3
N2
N1
heute.
N5 + 6.6
2.5 · N4
4.6 · N3
10 · N2
100 · N1
der 100mal
schneller ist.
N6 + 6.3
N5 + 10
4 · N4
10 · N3
31.6 · N2
1000 · N1
der 1000mal
schneller ist.
(deterministisch) polynomiell lösbar
indeterministisch polynomiell lösbar
indeterministisch polynomiell unlösbar
unentscheidbar
Polynomielle Lösbarkeit unabhängig von Kodierungsschema und
Maschinenmodell.
n5
N5
N6 + 4.2
N7 + 4.3
Größe der größten, in einer bestimmten
Zeit lösbaren Instanz mit einem Computer
2n
N6
N7 + 2.9
• Lösung ist von exponentieller Länge
Grobe Problemklassifizierung:
100
leichte Probleme
Beispiel. SAT ist polynomiell auf das Entscheidungsproblem zu
Traveling Salesman (TS) reduzierbar ⇒ TS ist NP-hart.
TS liegt außerdem in NP ⇒ TS ist NP-vollständig.
Stephen Cook, 1971: Das Erfüllbarkeitsproblem für propositionale
Formeln (SAT) ist NP-vollständig.
Π ist NP-vollständig, wenn Π in NP liegt und NP-hart ist.
Folgerung: Ist Π polynomiell lösbar, dann alle Probleme in NP.
Ist irgendein Problem in NP polynomiell unlösbar, dann auch Π.
Problem Π ist NP-hart, wenn jedes Problem in NP polynomiell
auf Π reduzierbar ist.
NP (Nichtdeterministisch Polynomiell): Klasse aller
Entscheidungsprobleme, die von einem indeterministischen
Computer (=beliebige Parallelität ohne Kooperation) in
polynomieller Zeit gelöst werden können.
98
schwere Probleme
• Finden der Lösung erfordert exponentiellen Aufwand
Ursachen für polynomielle Unlösbarkeit:
3n
N7
Zeitkomplexitätsfunktion
5n
97
NP-vollständige Probleme
Untersuchung der relativen Komplexität von Problemen zueinander
mittels Problemreduktion.
Π1 .
Problem Π1 auf Problem Π2 reduzierbar: jede Instanz von Π1
kann in eine Instanz von Π2 transformiert werden.
Ein Algorithmus für
löst damit auch
Π2
Polynomielle Reduktion: Transformation in polynomieller Zeit.
Polynomieller Alg. für Π2 liefert auch polynomiellen Alg. für Π1 .
P: Klasse aller Entscheidungsprobleme, die von einem
deterministischen (realen) Computer in polynomieller Zeit gelöst
werden können.
99
Entscheidungsprobleme
d(si , sj ),
Schranke D
Gegeben durch: Beschreibung der Parameter + Ja/Nein Frage
Entfernungen
Beispiel. Traveling Salesman
Parameter: Städte
s 1 , . . . , sn ,
Frage: Gibt es Rundreise mit Länge ≤ D, d.h., gibt es Permutation
Pn−1
π, sodass i=1 d(sπ(i) , sπ(i+1) ) + d(sπ(n) , sπ(1) ) ≤ D?
Entscheidungsproblem – formal:
Menge aller Instanzen (INSTΠ ) + Menge der Ja-Instanzen (JAΠ )
Sprache zu Problem Π unter Kodierungsschema K:
L(Π, K) = {x ∈ Σ∗ | x kodiert Ja“-Instanz}
”
101
Von Kodierungsschema unabhängige Eingabelänge:
length: INSTΠ → ω+
Muss polynomiell verwandt sein mit allen vernünftigen
Kodierungsschemata.
length heisst polynomiell verwandt mit Kodierungsschema K, wenn
Polynome p, p0 existieren, sodass für alle Instanzen I gilt:
length(I) ≤ p(|K(I)|) und |K(I)| ≤ p0 (length(I))
Beispiel. Primzahl
Parameter: natürliche Zahl n
Ja/Nein Frage: Ist n eine Primzahl?
Kodierungsschema K: Binärdarstellung
L(Primzahl, K) = {10, 11, 10 1, 11 1, 1 01 1, . . .}
Eigenschaften wie polynomiell/exponentiell sind unabhängig vom
Kodierungsschema, soferne dieses vernünftig gewählt wird:
1. kein exponentielles Aufblähen durch Füllsymbole;
2. keine unäre Darstellung von Zahlen.
102
Turing-Maschinen und Entscheidungsprob.
Turing-Maschine T löst Problem Π unter Schema K, wenn T auf
allen Eingaben hält und L(T ) = L(Π, K).
Zeitkomplexität:
timeT (n) = max{m | es gibt x mit |x| = n und
T heisst polynomiell, wenn timeT (n) von der Ordnung O(p(n)) für
ein Polynom p ist.
T macht m Schritte auf x}
length(I) = n + dlog(max {D, d(s1 , s2 ), d(s1 , s3 ), . . .})e
104
Beispiel. Traveling Salesman
103
= {L | L = L(T ) für polynomielle deterministische TM T }
Klasse der polynomiell erkennbaren Sprachen:
P
Alle vernünftigen Kodierungsschemata sind in polynomiellen
Grenzen zueinander äquivalent.
Alle realistischen Berechnungsmodelle sind in polynomiellen
Grenzen zu deterministischen TMs äquivalent.
Daher ist P die Klasse der in polynomieller Zeit lösbaren
Entscheidungsprobleme.
105
Indeterministische Turing-Maschine (IDTM)
Indeterminismus
Modelliert Verifizierbarkeit in polynomieller Zeit
Indeterministischer Algorithmus = Rateteil + Prüfteil
106
Löst Problem Π, wenn für alle I ∈ INSTΠ gilt:
I ∈ JAΠ genau dann, wenn es eine (geratene) Struktur S gibt,
sodass der Prüfteil auf S und I die Antwort Ja“ liefert.
”
Ist polynomiell, wenn ein Polynom p und für jedes I ∈ JAΠ eine
Struktur S existiert, sodass der Prüfteil innerhalb der Zeit
p(length(I)) die Antwort Ja“ liefert.
”
P versus N P
= Ratemodul + deterministische Turing-Maschine (DTM)
Ratemodul: schreibt willkürliche Zeichenkette S neben Eingabe x
auf Band, dann startet erst die DTM.
Trivial: P ⊆ N P
108
Satz. Für jedes Π ∈ N P gibt es ein Polynom p, sodass Π von einem
deterministischen Algorithmus in der Zeit O(2p(n) ) gelöst werden
kann.
Offene Vermutung P 6= N P .
Eine IDTM T akzeptiert x, wenn es ein S gibt, sodass die DTM die
Eingabe x + S akzeptiert.
Rechenzeit: minimale Zahl der Rechenschritte der DTM (über alle
akzeptierenden Berechnungen)
= {L | L = LM für polynomielle IDTM M }
Klasse der indeterministisch-polynomiell erkennbaren Sprachen:
NP
Auch N P kann als Klasse von Entscheidungsproblemen aufgefasst
werden.
107
Polynomielle Reduktion
Eine Sprache L heißt NP-vollständig, wenn
NP-Vollständigkeit
Die Begriffe Problemreduktionen“ und NP-Vollständigkeit“
”
”
können auf Entscheidungsprobleme erweitert werden.
L gehört zu den härtesten“ Sprachen in N P .
”
Satz. Seien L1 , L2 ∈ N P und L1 ≥ L2 .
Ist L1 NP-vollständig, dann ist auch L2 NP-vollständig.
(b) L0 ≥ L für alle Sprachen L0 ∈ N P .
(a) L ∈ N P ,
f : Σ1∗ → Σ2∗ ist polynomielle Reduktion von L1 ⊆ Σ1∗ auf L2 ⊆ Σ2∗ ,
wenn gilt:
(a) f ist durch polynomielle DTM berechenbar;
(b) x ∈ L1 genau dann, wenn f (x) ∈ L2 .
Schreibweise: L1 ≥ L2 , wenn eine polynomielle Reduktion von L1
auf L2 existiert.
Satz. Sei L1 ≥ L2 .
Verfahren zum Beweis der NP-Vollständigkeit eines Problems Π:
≥ ist transitiv: L1 ≥ L2 , L2 ≥ L3 ⇒ L1 ≥ L3
(a) Aus L2 ∈ P folgt L1 ∈ P .
(a) Zeige Π ∈ N P .
112
M(I, ( t1 + t2 )) = M(I, t1 ) + M(I, t2 ) für t1 , t2 ∈ T
M(I, v) = I(v) für v ∈ {x, y, z, . . .}
M(I, 0) = 0, . . . , M(I, 9) = 9
ENV . . . Menge aller Speicherbelegungen ( Environments“)
”
Erweiterung der Semantikfunktion: M: ENV × T → ω
Speicherbelegung I: {x, y, z, . . .} → ω
Semantik: M(x) = 1 oder M(x) = 2 ?
Syntax: T ⇒ x | y | z | · · ·
Behandlung von Variablen
110
(b) Zeige Π0 ≥ Π für ein bekanntes NP-vollständiges Problem Π0 .
(b) Aus L1 ∈
/ P folgt L2 ∈
/ P.
109
L1 , L2 polynomiell äquivalent, wenn L1 ≥ L2 und L2 ≥ L1 .
Syntax vs. Semantik
Ein einfaches Beispiel: additive Terme
= {T ⇒ 0 | ··· | 9 | ( T + T )}
Sei T = L(G) mit G = h{T }, {(, ), +, 0, . . . , 9}, P, T i mit
P
M: T → ω . . . Meaning“, interpretiert T als additive Ausdrücke
”
M(0) = 0, . . . , M(9) = 9
M(( t1 + t2 )) = M(t1 ) + M(t2 ) für t1 , t2 ∈ T
= M((1+2 )) + M(3)
Beispiel. Auswertung von ((1 +2 )+3):
M(((1 +2) +3))
= M(1) + M(2) + M(3)
= 1+2+3=6
111
Beispiel. Auswertung von ((x +2 )+y)
. . . für I(x) = 1, I(v) = 3 für alle v 6= x:
= M(I, x) + M(I, 2) + M(I, y)
T ⇒ 0 | ··· | 9
T = L(G)
Grammatik
{x, y, z} ⊆ T
{0, . . . 9} ⊆ T
T ist kl. Menge mit:
Induktive Definition
M(I, x) = I(x), . . .
M(I, 0) = 0, . . .
M: ENV × T → ω
Rekursion
Grammatik vs. Induktive Definition
= I(x) + 2 + I(y)
T ⇒x|y|z
M(I, ( t1 + t2 ))
M(I, ((x +2 )+y )) = M(I, (x+2 )) + M(I, y)
= 1+2+3=6
t1 , t2 ∈ T
Grammatik
∃ ist kl. Menge mit:
Induktive Definition
M(0) = 0, . . .
M: ∃ → ω
Rekursion
t1 , t2 ∈ T → ( t1 + t2 ) ∈ T :
114
F ⇒+E |∗E |
Problem:
Ableitungen entsprechen nicht der intendierten Semantik.
Die übliche Prioritätsregel ‘∗ vor +’ soll berücksichtigt werden.
E ⇒ 0F | ··· | 9F
Im Gegensatz zur Grammatik ist die Sprache ∃ eindeutig;
es gibt eine eindeutige (reguläre) Grammatik für ∃:
Auflösung der Mehrdeutigkeit
statt
t∈T →(t+t)∈T
T ist nicht mehr kontextfrei!
→ ( t1 + t2 ) ∈ T
= M(I, t1 ) + M(I, t2 )
Beachte:
Die verschiedenen Vorkommen von T in ( T + T ) entsprechen
den verschiedenen (metasprachlichen) Variablen t1 und t2 !
T ⇒(T +T )
. . . für J(x) = 5, J(y) = 2, J(v) = 0 sonst:
M(J, (( x+2 )+y )) = M(J, ( x+2 )) + M(J, y)
= M(J, x) + M(J, 2) + M(J, y)
= J(x) + 2 + J(y)
= 5+2+2=9
∃ = L(G)
{0, . . . 9} ⊆ ∃
113
E ⇒ 0 | ··· | 9
M(e1 + e2 )
= M(e1 ) · M(e2 )
M(e1 ∗ e2 )
= M(e1 ) + M(e2 )
e1 , e2 ∈ ∃
e1 , e2 ∈ ∃
→ e1 + e2 ∈ ∃
E ⇒E+E
E ⇒E∗E
→ e1 ∗ e2 ∈ ∃
1. Prioritätsregel (nur) in die Definition von M einbauen
Zwei Möglichkeiten:
M(3+3 ∗3) = M(3) + M(3∗ 3) = M(3) + M(3) · M(3) = 12
Problem: M ist keine Funktion mehr!
M(3+3 ∗3) = M(3 +3) · M(3) = (M(3) + M(3)) · M(3) = 18
116
2. Prioritätsregel gleich in die Definition von ∃ einbauen:
Definition von ∃ hierarchisch gestalten
Grund: Grammatik für ∃ ist mehrdeutig; verschiedene Ableitungen
führen zu verschiedenen Werten.
115
H⊆∃
∃ ist kleinste Menge mit:
e1 , e2 ∈ H → e1 ∗ e2 ∈ H
{0, 1, . . ., 9} ⊆ H
H ist kleinste Menge mit:
Hierarchische Definition von ∃
e1 , e2 ∈ ∃ → e1 + e2 ∈ ∃
Modellstrukturen
F ...
D ...
endliche Menge totaler Prädikate
endliche Menge totaler Funktionen
D k → {t, f }
Dk → D
nicht-leere Menge (Gegenstandsbereich/Domäne)
Quadruppel hD, F, P, Ki, wobei:
MH (0) = 0, . . . , MH (9) = 9
P ...
Davon lassen sich Definitionen M∃ und MH ableiten:
M∃ (e) = MH (e)
MH (e1 ∗ e2 ) = MH (e1 ) · MH (e2 )
falls e ∈ H
M∃ (e1 + e2 ) = M∃ (e1 ) + M∃ (e2 )
K⊆D
=
0s
Binäre Stacks:
S = hS, {push0, push1, pop}, {ist0?, ist1?, istleer?}, {ε}i
∗
wobei die Stacks durch Worte aus S = {0, 1} dargestellt werden.
118
Modellstrukturen können als abstrakte Datentypen
aufgefasst werden
Menge von Konstanten
+
M∃ (4)
K ...
=
M∃ (2∗ 3)
Als einzigen Wert von 2∗3 +4 erhält man:
M∃ (2 ∗3 +4)
= MH (2∗ 3) + MH (4)
= 2 · 3 + 4 = 10
117
Ganze Zahlen:
Z = hZ, {+, −, ∗}, {<, =}, Zi
wobei Z = {. . ., −2, −1, 0, 1, 2, . . .}
push0(s)
=
1s
ε
s0
+, −, ∗ . . . übliche artihmetische Funtktionen
push1(s)
=
es gibt ein s0 sodass s = 0s0
. . . kleiner“-, bzw. ist-gleich“-Relation
”
”
pop(s)
⇐⇒
es gibt ein s0 sodass s = 1s0
<, =
ist0?(s)
⇐⇒
120
für s = ε
für s = 0s0 oder s = 1s0
Natürliche Zahlen:
[ACHTUNG: kleine Abweichung von Skriptum!]
. ∗}, {<, =}, {0, 1}i
N = hω, {+, −,
wobei ω = {0, 1, 2, . . .} und
ist1?(s)
s=ε
⇐⇒
x−y
0
istleer?(s)
. y=
x−
für x ≥ y
für x < y
(Ansonst wie für Z)
119
Familie X:
FamX = hDX , FX , PX , KX i
wobei
CX = PersonenX (Menge der Mitglieder der Familie X)
FX = {Vater, Mutter }
PX = {Geschwister, Onkel, weiblich, männlich, = }
KX = {Abdul, Berta, Chris, Dorlan, Ege, . . .}
Funktionen Vater und Mutter müssen total sein.
=⇒
PersonenX unendlich; oder mit Element ‘Unbekannt’, wobei
Vater(Unbekannt) = Mutter(Unbekannt) = Unbekannt
121
Natürliche Zahlen:
. ∗}, FS (N) = {} für n 6= 2
FS 2 (N) = {+, −,
n
PS 2 (N) = {<, =}, PS n (N) = {} für n 6= 2
KS (N) = {0, 1}
Binäre Stacks:
FS 1 (S) = {push0, push1, pop}, FS n (S) = {} für n > 1
PS 1 (S) = {ist0?, ist1?, istleer?}, PS n (S) = {} für n > 1
KS (S) = {leer}
123
Signaturen
Die Signatur zur Modellstruktur D legt das Alphabet einer Sprache
fest, die sich entsprechend auf die Gegenstände in D bezieht.
FS (D), PS (D), KS (D) . . . Funktions-, Prädikaten-, Konst.symbole
FS n (D), PS n (D) . . . n-stellige Symbole
122
Ganze Zahlen:
FS 2 (Z) = {+, −, ∗}, FS n (Z) = {} für n 6= 2
PS 2 (Z) = {<, =}, PS n (Z) = {} für n 6= 2
KS (Z) = {. . . , −2, −1, 0, 1, 2, . . .}
Signatur zur Familie X:
FS 1 (FamX) = {Vater, Mutter},
FS n (FamX) = {} für n > 1,
PS 1 (FamX) = {weiblich, männlich},
PS 2 (FamX) = {Geschwister, Onkel, =},
PS n (FamX) = {} für n > 2.
KS (FamX) = {Abdul, Berta, Chris, Dorlan, Ege, . . .}
124
Terme über Modellstrukturen
Syntax:
Alphabet: neben FS (D) und KS (D) auch
Individuenvariablensymbole IVS : {x, y, z, x1 , . . .}
Hilfssymbole: ( und ) und ,
T (D) ist die kleinste Menge, für die gilt:
(T1) IVS ⊆ T (D)
(T2) KS (D) ⊆ T (D)
(T3) f 0 ( t1 , . . . , tn ) ∈ T (D)
wenn f 0 ∈ FS n (D) und t1 , . . . , tn ∈ T (D)
125
Boolesche Ausdrücke über Modellstrukturen
Syntax:
BA(D) ist die kleinste Menge, für die gilt:
...
,tn )
(BA1) p0 (t1 , . . . ,tn ) ∈ BA(D), wenn p0 ∈ PS n (D) und
t1 , . . . , tn ∈ T (D);
heißt Atomformel;
p0
(t1 ,
(BA2) ¬ F ∈ BA(D), wenn F ∈ BA(D);
(BA3) ( F ∧ G ) ∈ BA(D), wenn F, G ∈ BA(D);
(BA4) ( F ∨ G ) ∈ BA(D), wenn F, G ∈ BA(D).
127
Semantik
ENV (D) . . . Menge aller Abbildungen IVS → D
(Variablenbelegungen, Environments, auch: Interpretationen)
MT : ENV (D) × T (D) → D ist rekursiv definiert durch
(M1) MT (I, v) = I(v) für v ∈ IVS ;
(M2) MT (I, c0 ) = c für c0 ∈ KS (D)
(c . . . Konstante zu Konstantensymbol c0 )
(M3) MT (I, f 0 ( t1 , . . . , tn )) = f (MT (I, t1 ), . . . , MT (I, tn ))
(f . . . Funktion zum Funktionssymbol f 0 )
126
Boolesche Ausdrücke über Modellstrukturen
Semantik:
Definition. Die Semantik von BA(D) wird durch die Funktion
MBA : ENV × BA(D) → {t, f } festgelegt:
(MBA1)
(MBA2)
(MBA3)
(MBA4)
MBA (I, p0 (t1 , . . . ,tn )) = p(MT (I, t1 ), . . . , MT (I, tn )),
wobei p das Prädikat zum Symbol p0 ∈ PS n (D) ist.
t falls MBA (I, F ) = f
MBA (I, ¬ F ) =
f falls MBA (I, F ) = t
M (I, ( F ∧ G )) =
BA
t falls MBA (I, F ) = t und MBA (I, G) = t
f sonst
M (I, ( F ∨ G )) =
BA
t falls MBA (I, F ) = t oder MBA (I, G) = t
f sonst
128
Notationsvereinbarungen
/
¬ (t1 <t2 )
• Infixnotation für Terme über Z und N:
( 1 +x) steht für + ( 1 ,x) etc.
steht für
¬ (t1 =t2 )
• Infixnotation auch für Atomformeln:
(t1 =t2 ) steht für = (t1 ,t2 ) etc.
/
t1 ≥t2
• t1 >t2 steht für t2 <t1
•
t1 6= t2
• Klammereinsparungen, sofern keine Gefahr der
Mehrdeutigkeit besteht
129
Eine einfache Programmiersprache
ALI . . . Assignment Language für Integers
(Statements/Programme über Z)
Syntax: ALI ist die kleinste Menge, für die gilt:
etc.
(AL1) Ist v ∈ IVS und t ∈ T (Z), dann ist v ← t ∈ ALI.
(AL2) Sind α, β ∈ ALI, dann ist begin α; β end ∈ ALI.
(AL3) Ist B ∈ BA(Z) und sind α, β ∈ ALI, dann ist
if B then α else β ∈ ALI.
(AL4) Ist B ∈ BA(Z) und α ∈ ALI, dann ist
while B do α ∈ ALI.
131
Beispiel Wert von B = y+x6= 0 ∨ x<y über Z in einer
Variablenbelegung I mit I(x) = 4 und I(y) = −2.
=
M BA4
t falls MBA (I, y+x6= 0) = t oder MBA (I, x<y) = t
Erinnerung: B ist ‘offiziell’ ( ¬ = ( + (y,x) , 0 ) ∨ < (x,y) )
MBA (I, B)
=
=
M T 3,M T 2
M BA1
=
M BA2
(−2 + 4 = 0) = (2 = 0) = f

(M (I, y+x) = M (I, 0))
T
T


(MT (I, y) + MT (I, x) = 0)
t falls MBA (I, y+x= 0) = f
Wir bestimmen zunächst MBA (I, y+x6= 0):
MBA (I, y+x6= 0)

MBA (I, y+x= 0)



=
MT 1
Daher erhalten wir MBA (I, B) = t.
130
Beispiel:
Ein ALI-Programm zur Multiplikation zweier positiver Zahlen:
begin
z ← 0;
while (0<y) do begin
z ← (z + x) ;
y ← (y − 1)
end
end
Beachte: Die intendierte Semantik muss erst gerechtfertigt werden!
132
Syntaktische Analyse
AL1
• z ∈ IVS , 0 ∈ T (Z) =⇒ α1 = z ← 0 ∈ ALI
AL1
• z ∈ IVS , (z + x) ∈ T (Z) =⇒ α2 = z ← (z + x) ∈ ALI
AL1
AL4
∈ AL =⇒ β = begin α2 ; α3 end ∈ ALI
AL2
• y ∈ IVS , (y − 1) ∈ T (Z) =⇒ α3 = y ← (y − 1) ∈ ALI
•
α2 , α3
• (0<y) ∈ BA(Z), β ∈ ALI =⇒ γ = while (0<y) do β ∈ ALI
AL2
133
• α1 , γ ∈ ALI =⇒ begin α1 ; γ end ∈ ALI
Semantik von ALI
Die Funktion MAL : ENV × ALI → ENV ist definiert durch:
(MAL1) MAL (I, v ← t) = I 0 , wobei I 0 (v) = MT (I, t) und
v
I 0 (w) = I(w) für alle w ∈ IVS mit w 6= v, d.h. I 0 ∼ I.
(MAL2) MAL (I, begin α; β end) = MAL (MAL (I, α), β)
(MAL3) MAL (I, if B then α else β) =
MAL (I, α) falls MBA (I, B) = t
MAL (I, β) falls MBA (I, B) = f
(MAL4) MAL (I, while B do α) =
M (M (I, α), while B do α) für MBA (I, B) = t
AL
AL
I
für MBA (I, B) = f
135
Notationsvereinbarung:
α ; α2 ; . . . ; αn
1
steht für
α1 ; begin α2 ; begin . . . ; αn end end
Beachte: Die offizielle Syntax von ALI bleibt unverändert.
(Das erleichtert die syntaktische und semantische Analyse)
Eine Hilfsdefinition:
v
Für I, I 0 ∈ ENV und v ∈ IVS schreibt man I ∼ I 0
wenn I(w) = I 0 (w) für alle w ∈ IVS für die w 6= v.
134
Beispiel: Multiplikationsprogramm
Abkürzungen:
β = begin z ← (z + x); y ← (y − 1) end
γ = while (0<y) do β
Auswertung für I(x) = 3, I(y) = 1, (I(z) beliebig)
M AL2
M AL1
wobei I 0 (z) = MT (I, 0) = 0 und I 0 (v) = I(v) für v 6= z
= (0<I(y)) = (0<1) = t
MBA (I 0 , (0<y) = (MT (I 0 , 0)<MT (I 0 , y)) = (0<I 0 (y))
M (I 0 , while (0<y) do β)
 AL

MAL (MAL (I 0 , β), while (0<y) do β)


MAL (I, begin z ← 0; γ end) = MAL (MAL (I, z ← 0), γ) = MAL (I 0 , γ)
=
=
M AL4
136
0
, β), while (0<y) do β)
MAL (MAL (MAL (I 0 , z ← z+x), y ← y−1), while (0<y) do β)
MAL (MAL (I
=
M AL2
M AL1
I 00 (v) = I 0 (v) für v 6= z
= I 0 (z) + I 0 (x) = 0 + I(x) = 0 + 3 = 3
I 00 (z) = MT (I 0 , z+x) = MT (I 0 , z) + MT (I 0 , x)
MAL (MAL (I 00 , y ← y−1), while (0<y) do β)

I 000 (y) = MT (I 00 , y−1) = MT (I 00 , y) − MT (I 00 , 1)


= I 00 (y) − 1 = I 0 (y) − 1 = I(y) − 1 = 1 − 1 = 0
I 000 (v) = I 00 (v) für v 6= y
= (0<I 000 (y)) = (0<0) = f
MBA (I 000 , (0<y)) = (MT (I 000 , 0)<MT (I 000 , y))
I 000

wobei
MAL (I 000 , while (0<y) do β)
wobei
=
M AL1
=
=
M AL4
Was ist mathematische Logik?
• Logik untersucht allgemeine Prinzipien korrekten Schließens
• Mathematische Logik stellt zu diesem Zweck formale
Kalküle bereit und analysiert die Beziehung zwischen Syntax
und Semantik von Aussagen.
• Die Logik hat viele Anwendungen in der Informatik.
• Vor allem aber bietet die (formale) Logik den geeigneten
methodischen Rahmen zur Lösung zahlreicher Probleme der
Informatik.
Motto:
The applied math of computer science is formal logic.“
”
138
Anwendungen der Logik in der Informatik 2
137
Anwendungen der Logik in der Informatik 1
C. Korrektheit von Programmen
– Kalküle für Korrektheitsbeweise (z.B. Hoare-Kalkül)
A. Programmierung
– Logik-nahe Programmiersprachen (PROLOG etc.)
– Lösbarkeits- und Komplexitätsfragen
– Design von (Logik-nahen) Datenformaten
D. Datenbanken
– (partielle) Automatisierung von Korrektheitsbeweisen
– boolean expressions“
”
– Zusicherungen
– Extraktion von Programmen aus Spezifikationen
– Automatische Programmierung
– Datenconstraints
– Aspekte wie: Inkonsistenz, Unvollständigkeit, etc.
– Extraktion von Information aus Datenmengen (WWW)
– Design und Analyse von Abfragesprachen
– dynamisches Verhalten (Temporallogiken, . . . )
B. Spezifikation: Sprachen, Schließen über Spezifikationen
– Soll/Muss-Verhalten (deontische Logik)
140
– Update-Problem“
”
– Datenbanktheorie
– Konsistenz von Spezifikationen
139
Anwendungen der Logik in der Informatik 3
G. Computermathematik:
Anwendungen der Logik in der Informatik 4
– logische Aspekte von Geometrie-Systemen
– Repräsentation matematischer Beweise und Theoreme
– Symbolic Computation, Computeralgebra
– automatisches Beweisen
E. Wissensrepräsentation:
– Design von geeignete Repräsentationssprachen
– Web-Ontologien, Description-Logics
– Schließen mit unsicherer/vager/unvollständiger Information
I. (Deskriptive) Komplexitätstheorie
– Formale Modellierung natürlicher Sprache
– Repräsentation von Modalitäten“ (z.B. Wissen/Glauben)
”
– “revisable reasoning“ (nicht-montone Logiken, . . . )
J. Berechenbarkeitstheorie (Rekursionstheorie)
H. Semantik von Programmiersprachen
– räumliches Schließen
K. Unifikationstheorie
L. Konstruktive Mathematik
F. Hardware
– Spezifkation von Schaltkreisen, Chips etc.
M. Komplexität logischer Probleme und Algorithmen
usw. usw. . . .
144
(b < c) ∨ (d < a) ⇒ Negation äquivalent zu: (b ≥ c) ∧ (d ≥ a)
Viel Redundanz!
Kompakte Formulierung der negierten Bedingung:
• Ende des ersten Intervalls liegt im zweiten: c ≤ b und b ≤ d
• Ende des zweiten Intervalls liegt im ersten: a ≤ d und d ≤ b
• Anfang des ersten Intervalls liegt im zweiten: c ≤ a und a ≤ d
• Anfang des zweiten Intervalls liegt im ersten: a ≤ c und c ≤ b
• Zweites Intervall enthält das erste: c ≤ a und b ≤ d
• Erstes Intervall enthält das zweite: a ≤ c und d ≤ b
if hBedingungi then write Kollision!“
”
Auflistung aller Überlappungsmöglichkeiten:
[a, b], [c, d] . . . Zeitintervalle: von a bis b“, von c bis d“
”
”
Aufgabe: Warnung ausgegeben wenn eine Terminkollision vorliegt:
142
– (Automatische) Verfikation von Hardware
– Schaltkreistheorie
141
if-, case-, while-Bedingungen:
if (x = 0) ∧ (y > 1) then P1 else P2
Vertauschen von then- und else-Zweig
de-Morgan-Regel: ¬(A ∧ B) = ¬A ∨ ¬B
if (x 6= 0) ∨ (y ≤ 1) then P2 else P1
⇐ Zusicherung
⇐ Nachbedingung
⇐ Vorbedingung
Spezifikation von Programmeigenschaften
Assertions: Diagnoseanweisungen in Programmen
Pre- und Postconditions in der Programmverifikation
hx = a ∧ y = b ∧ y ≥ 0i
while y > 0 do [
x ← x − 1;
y ← y − 1;
assert(y ≥ 0);]
hx = a − bi
143
natürliche Sprache“

”

Sokrates ist ein Mensch.
⇒ Sokrates ist sterblich.
Alle Menschen sind sterblich. 
(∀x)M (x) ⊃ S(x)
sp
M (s) ⊃ S(s)
mp
S(s)
Formalisierung: Festlegung der Syntax und Semantik der Logik
M (s) (∀x)M (x) ⊃ S(x)
S(s)
(Modus ponens)
M (s)
Beweistheorie: Untersuchung der Schlussregeln und Beweisformen
(∀x)F[x]
A
A
⊃ B mp
sp
F[t]
B
(Spezialisierung)
Semantische Fragestellungen: Ist eine Aussage unter jeder /
mancher / keiner Interpretation der nicht-logischen Symbole wahr?
Welche Form haben Beispiele (Modelle) bzw. Gegenbeispiele?
Folgt eine Aussage aus anderen?
(2)
(1)
∀x i(x) ◦ x = e
∀x e ◦ x = x
∀x∀y∀z x ◦ (y ◦ z) = (x ◦ y) ◦ z
Gruppentheorie:
(3)
(5) ∀x x ◦ i(x) = e
(6) ∀x i(i(x)) = x
Immer wenn (1), (2) und (3) erfüllt sind, dann gelten auch auch
(4) ∀x x ◦ e = x
Diese logische Konsequenz -Behauptung ist äquivalent zu:
[(1) ∧ (2) ∧ (3)] ⊃ [(4) ∧ (5) ∧ (6)] ist gültig.
Analysis:
f : R → R konvergiert gegen a: Für jedes positive bleibt für alle
”
hinreichend großen n die Distanz zwischen f (n) und a unter .“
Formalisiert: ∀∃x0 ∀x ( > 0 ∧ x ≥ x0 ) ⊃ |f (x) − a| < B0
0
S0
0
0
C0
0
1
0
Ai
1
1
0
0
Bi
0
0
0
0
Ci−1
0
1
1
0
Si
1
0
0
0
Ci
Ci
Si
C0
S0
= (Ai ∧ Bi ) ∨ (Ai ∧ Ci−1 ) ∨ (Bi ∧ Ci−1 )
(¬Ai ∧ Bi ∧ Ci−1 ) ∨ (Ai ∧ Bi ∧ Ci−1 )
= (Ai ∧ Bi ∧ ¬Ci−1 ) ∨ (Ai ∧ ¬Bi ∧ Ci−1 )∨
= (Ai 6≡ Bi ) 6≡ Ci−1
= A0 ∧ B0
= (¬A0 ∧ B0 ) ∨ (A0 ∧ ¬B0 ) = A0 6≡ B0
146
A0
0
1
0
1
145
0
0
1
1
Halb-/Volladdierer: S = A + B
1
1
0
0
0
0
1
1
1
1
0
0
1
1
1
1
0
• Verifikation von Eigenschaften
• Umformung, Vereinfachung, Optimierung
A = An · · · A0 , B = Bn · · · B0 , S = Sn · · · S0
Ci . . . Überträge
0
1
1
1
1
Problemstellungen:
1
0
1
148
• Spezifikation von Schaltkreisen, von boole-schen Funktionen
1
147
Formen und Typen der Logik
• Neben der klassischen Logik sind auch verschiedenste Typen
nicht-klassischer Logiken von Bedeutung:
– intuitionistische Logik (konstruktive Logik)
– mehrwertige Logiken, Fuzzy-Logik
– Modallogiken: Temporallogiken, dynamische Logik, . . .
– ...
t
t
f
t
t
t
OR, Disjunktion
f
t
t
f
t
t
f
t
t
t
t
f
NAND
t
f
f
f
f
f
t
f
f
t
f
f
NOR
t
t
f
f
t
f
t
t
f
6⊂ ≡ 6≡
XOR, exkl. Oder
• Logik wird auf unterschiedlichen Stufen ( Ordnungen“)
”
analysiert:
t
f
f
f
Implikation
151
NEXOR, gdw.
– Aussagenlogik (Logik 0-ter Stufe)
– (Prädikaten)logik 1-ter Stufe
149
– Logiken höherer Ordnung
Aussagenlogik
f
t
∧ ∨ ⊃ ⊂ ↑ ↓ 6⊃
t
t
¬
Logische Konnektive (Junktoren, Operatoren)
sind Funktionen über den Wahrheitwerten:
t
f
f
f
AND, Konjunktion
f
Negation
Logische Kalküle, Beweisprozeduren
Werkzeug zum Beweis (bzw. zur Widerlegung) logischer Aussagen
Keine Bezugnahme auf Bedeutung (Semantik)
Nur syntaktische Manipulation von Formeln (Zeichenketten)
Eigenschaften logischer Kalküle:
Korrektheit: Kalkül beweist nur wahre Aussagen
(widerlegt nur falsche Aussagen).
Vollständigkeit: Jede wahre Aussage ist im Kalkül beweisbar
(jede falsche Aussage ist widerlegbar).
In dieser Vorlesung:
Sequentialkalkül, Tableaux und Resolution für Aussagenlogik
Tableaux und Resolution für Prädikatenlogik
150
Syntax:
AV = {A, B, C, . . .} . . . aussagenlogische Variable
t, f . . . aussagenlogische Konstanten
Definition. Die Menge der aussagenlogischen Formeln AF ist
die kleinste Menge, für die gilt
(AF1) AV ⊆ AF
(AF2) {t, f } ⊆ AF
(AF3) ¬F ∈ AF , wenn F ∈ AF
(AF4) (F ◦0 G) ∈ AF , wenn F, G ∈ AF und
◦0 ∈ {∧, ∨, ⊃, ⊂, ↑, ↓, 6⊃ , 6⊂ , 6≡ , 6≡ }.
AV ∪ {t, f } . . . Atomare Formeln (Atome)
152
Semantik:
INT . . . Variablenbelegungen/Interpretationen: AV → {t, f }
Definition.
Die Semantik aussagenlogischer Formeln ist durch die Funktion
MAF : INT × AF → {t, f } festgelegt:
t) = t und
MAF (I,
f) = f
(MAF1) MAF (I, A) = I(A), wenn A ∈ AV
(MAF2)
MAF (I,
(MAF3) MAF (I, ¬F ) = ¬MAF (I, F )
153
(MAF4) MBA (I, (F ◦0 G)) = MBA (I, F ) ◦ MBA (I, G),
wobei ◦ die zum Symbol ◦0 gehörende Funktion ist.
Notationsvereinbarungen:
• keine Unterstreichungen mehr
F1 ∧ . . . ∧ Fn
steht für
steht für
(F1 ∨ (. . . ∨ Fn ))
(F1 ∧ (. . . ∧ Fn ))
• überflüssige Klammern können weggelassen werden:
F1 ∨ . . . ∨ Fn
Beachte:
Klammereinsparungen sind durch die Semantik gerechtfertigt:
Die Funktionen ∧ und ∨ sind assoziativ.
155
Alternative Sichtweise von aussagenlogischen Formeln:
[Siehe Vorlesungsskriptum]
Syntax:
Terme über Datentyp B = h{t, f }, {¬, ∧, ∨, ⊃, . . .}, {}, {t, f }i
Dazu die Notationsvereinbarung:
• Infix- statt Prefix-Notation
=⇒
Semantik:
MAL entspricht MT über B
154
Definition. Eine Formel F ∈ AF heißt
gültig oder Tautologie, wenn MAF (I, F ) = t für alle I ∈ INT.
erfüllbar, wenn MAF (I, F ) = t für ein I ∈ INT.
(I heißt Modell von F .)
widerlegbar, wenn MAF (I, F ) = f für ein I ∈ INT.
(I heißt Gegenbeispiel für F .)
unerfüllbar, wenn MAF (I, F ) = f für alle I ∈ INT.
Definition. Zwei Formel F, G ∈ AF heißen äquivalent, wenn
MAF (I, F ) = MAF (I, G) für alle I ∈ INT.
Wir schreiben dafür auch: F = G.
Satz. F und G sind äquivalent genau dann, wenn F ≡ G gültig ist.
156
Beispiel. A ⊃ (B ⊃ A) ist gültig und daher auch erfüllbar:
A
f
B
t
t
t
t
t
f
f
f
f
A B
t
f
C
f
f
(B ∧ C)
f
f
t
f
f
f
F
f
f
G
A B
t
¬B
t
f
t
t
f
t
t
t
t
f
f
t
t
f
f
t
t
t
f
t
f
t
f
t
f
f
f
t
f
t
t
t
t
t
t
t
t
t
t
t
f
t
t
t
t
t
f
t
t
t
t
t
f
(A ∨ B) (A ∨ C)
f
t
f
t
G
f
f
f
t
F
t
t
t
Beispiel. (Distributivgesetz ) A ∨ (B ∧ C) = (A ∨ B) ∧ (A ∨ C).
|
{z
} |
{z
}
f
t
(B ⊃ A) A ⊃ (B ⊃ A)
t
f
f
f
f
(A ∧ ¬B) ∨ B ist erfüllbar, aber nicht gültig, also auch widerlegbar:
t
t
f
(A ∧ ¬B) (A ∧ ¬B) ∨ B
f
t
A∧B
= (A ↑ A) ↑ (B ↑ B)
= (A ↑ B) ↑ (A ↑ B)
= ¬(¬A ∨ ¬B)
A↓B
A↑B
= ¬(A ∨ B)
= ¬A ∨ ¬B
h
F · · · Fn
1
A1 · · · An
h
i
. . . Substitution, die alle Ai durch Fi ersetzt.
F
h
X∨¬Y ¬X∧Y
A
B
i
160
Beispiel. F = (A ∧ (A ⊃ B)) ⊃ B ist gültig, daher auch
= (X∨¬Y ) ∧ (X∨¬Y ) ⊃ (¬X∧Y ) ⊃ (¬X∧Y )
Das heißt: Formeln können als Schemata aufgefasst werden, wobei
Variablen als Platzhalter für Formeln dienen.
Satz. Gilt F ≡ G, dann auch F σ ≡ Gσ.
Satz. Ist F eine Tautologie, dann auch F σ.
i
F1 · · · Fn . . . Formel, die aus F entsteht, indem alle A
Fσ = F A
i
1 · · · An
durch Fi ersetzt werden.
σ=
Formeln und Formelschemata
158
t
157
Eine Menge von Operatoren heißt funktional vollständig, wenn alle
Funktionen durch sie ausgedrückt werden können.
A∨B
Beispiel. {↑} ist funktional vollständig. Etwa:
= A ↑ (B ↑ B)
¬A = A ↑ A
A⊃B
A∧B
= ¬A ∨ B
Beispiel. {¬, ∨} ist funktional vollständig. Etwa:
A⊃B
159
h
A⊃B B
B C
Bσ2
i
und σ2 =
F σ2
h
¬A∨B B
B C
Satz. Seien σ1 , σ2 Substitutionen, sodass Aσ1 ≡ Aσ2 für alle
Variablen A gilt. Dann gilt F σ1 ≡ F σ2 für alle Formeln F .
Bσ1
(A ⊃ B) ≡ (¬A ∨ B)
| {z } | {z }
Beispiel. Sei F = (A ∧ B) ⊃ C, σ1 =
Da
gilt, erhalten wir
F σ1
(A ∧ (A⊃B)) ⊃ B ≡ (A ∧ (¬A∨B)) ⊃ B
{z
} |
{z
}
|
161
i
.
Logische Konsequenz und Implikation
Definition. Formel G ist eine logische Konsequenz der Formeln
F1 , . . . , Fn , geschrieben F1 , . . . , Fn |= G, wenn für alle I gilt:
Wenn MAF (I, Fi ) = t für 1 ≤ i ≤ n, dann gilt MAF (I, G) = t.
Für n = 0 ist |= G gleichbedeutend mit G ist gültig“.
”
Satz. (Deduktionstheorem)
F1 , . . . , Fn |= G gdw. F1 , . . . , Fn−1 |= (Fn ⊃ G).
Folgerung. F1 , . . . , Fn |= G gilt
gdw. F1 ⊃ (F2 ⊃ · · · (Fn ⊃ G) · · ·) gültig ist
gdw. (F1 ∧ · · · ∧ Fn ) ⊃ G gültig ist.
Beispiel. B ist eine logische Konsequenz aus A und A ⊃ B, d.h., es
gilt A, A ⊃ B |= B.
Die Formel A ∧ (A⊃B) ⊃ B ist daher eine Tautologie.
162
A 6⊃ B = A ∧ ¬B
Satz. Zu jeder aussagenlogischen Formel gibt es eine äquivalente in
DNF bzw. in KNF.
A ⊃ B = ¬A ∨ B
A 6⊂ B = ¬A ∧ B
Normalformen
A ⊂ B = A ∨ ¬B
¬(A ∨ B) = ¬A ∧ ¬B
Schritt 2: Schiebe Negationen vor die Variablen.
¬(A ∧ B) = ¬A ∨ ¬B
A∨t=t
A ∨ f = A ¬t = f
Schritt 3: Eliminiere die Konstanten t und f .
A∧f =f
164
¬f = t
Schritt 4: Forme um in DNF/KNF mittels Distributivgesetz.
A∧t=A
¬¬A = A
(A ≡ B) = (A ∧ B) ∨ (¬A ∧ ¬B) (A 6≡ B) = (¬A ∧ B) ∨ (A ∧ ¬B)
A ↓ B = ¬A ∧ ¬B
Syntaktische (algebraische) Methode:
Schritt 1: Ersetze alle Operatoren durch ∧, ∨ und ¬.
∨ ··· ∨
A ↑ B = ¬A ∨ ¬B
A, ¬A . . . Literal“ falls A ∈ IVS
”
Seien Li,j Literale.
Disjunktive Normalform (DNF):
∧ ··· ∧
(Lm,1
Lm,nm )
(L1,1 ∧ · · · ∧ L1,n1 ) ∨ · · · ∨ (Lm,1 ∧ · · · ∧ Lm,nm )
∨ ···∨
L1,n1 )
Konjunktive Normalform (KNF, CNF):
(L1,1
implizite Berücksichtigung von Assoz., Kommut., Idempotenz ⇒
Mengenschreibweise:
{{L1,1 , . . ., L1,n1 }, . . ., {Lm,1 , . . ., Lm,nm }}
(Li,1 ∨ · · · ∨ Li,ni ) heißt auch Klausel (engl. clause), eine KNF heißt
auch Klauselnormalform (clause normal form).
163
Beispiel. (A ↑ (B ∨ C)) ⊃ ¬D
Schritt 1: ¬(¬A ∨ ¬(B ∨ C)) ∨ ¬D
Schritt 2: (A ∧ (B ∨ C)) ∨ ¬D
Schritt 3: (A ∧ (B ∨ C)) ∨ ¬D
(A ∧ B) ∨ (A ∧ C) ∨ ¬D
Schritt 4: Ausdistribuieren
DNF:
(A ∨ ¬D) ∧ (B ∨ C ∨ ¬D)
{{A, ¬D}, {B, C, ¬D}}
I∈INT,MAF (I,F )=f
165
KNF:
KNF(F ) =
_
A in F
LA
LA =
A
falls I(A) = f
¬A falls I(A) = t
enthält ein Literal LA für jede Variable A in Formel F :
KNF: enthält Disjunktion DI für jedes I mit MAF (I, F ) = f :
^
DI
DI
DI =
Es gilt: DI ist falsch nur in I, und wahr sonst, d.h.:
MAF (I, DI ) = f und MAF (I 0 , DI ) = t für I 0 6= I .
KNF(F ) ist falsch in I gdw. KI in KNF(F ) vorkommt. Daher:
MAF (I, KNF(F )) = f gdw. MAF (I, F ) = f .
KNF(F ) ist die eindeutig bestimmte vollständige KNF von F :
jede Disjunktion DI enthält alle Variablen.
167
Semantische Methode F ∈ AF . . . aussagenlogische Formel
DNF(F ) =
^
A in F
LA
LA =
A
falls I(A) = t
¬A falls I(A) = f
enthält ein Literal LA für jede Variable A in Formel F :
I∈INT,MAF (I,F )=t
DNF: enthält Konjunktion KI für jedes I mit MAF (I, F ) = t:
_
KI
KI
KI =
Es gilt: KI ist wahr nur in I, und falsch sonst, d.h.:
MAF (I, KI ) = t und MAF (I 0 , KI ) = f für I 0 6= I .
DNF(F ) ist wahr in I gdw. KI in DNF(F ) vorkommt. Daher:
MAF (I, DNF(F )) = t gdw. MAF (I, F ) = t .
f
f
t
t
t
A↑(B∨C)
t
t
t
t
t
f
f
f
f
f
f
t
t
t
¬D
t
t
t
t
t
t
f
f
t
f
t
t
t
t
F
A ∨ ¬B ∨ ¬C ∨ ¬D
¬A ∧ B ∧ ¬C ∧ ¬D
KI bzw. DI
DNF(F ) ist die eindeutig bestimmte vollständige DNF von F :
jede Konjunktion KI enthält alle Variablen.
166
f f f f
t f f f
t
f
t
f
t
f
t
t
t
f
t
f
t
f
Beispiel. F = (A ↑ (B ∨ C)) ⊃ ¬D
f tf f
t
t
t
t
t
f
f
t
t
t
t
f
f
A B C D B∨C
f
f
f
f
f
t
t
t
t
t
t
f
t
(12 Konjunktionen)
f
t
t
t
t
f
f
f
f
t
t
t
f
t
f
t
f
t
f
t
f
t
t
t
DNF(F ) = · · · ∨ (¬A ∧ B ∧ ¬C ∧ ¬D) ∨ · · ·
(4 Disjunktionen)
t
f
f
t
t
f
f
t
t
f
f
t t t t
f t t t
KNF(F ) = · · · ∧ (A ∨ ¬B ∨ ¬C ∨ ¬D) ∧ · · ·
168
Eigenschaften von DNFs und KNFs
Der Sequentialkalkül
Vater“ aller modernen Logik-Kalküle
”
G. Gentzen, 1935: Untersuchungen über das logische Schließen
korrekt und vollständig für Aussagen- und Prädikatenlogik
F, G . . . endliche Teilmengen von AF
• Eine DNF ist unerfüllbar wenn jede Konjunktion eine
Variable A enthält, die sowohl als A als auch als ¬A vorkommt.
• Eine KNF ist gültig wenn jede Disjunktion eine Variable A
enthält, die sowohl als A als auch als ¬A vorkommt.
Definition. (Verallgemeinerte Konsequenzrelation)
Wir schreiben F |= G, wenn für alle Interpretationen I gilt:
Fi =
V
W
{F1 , . . . , Fn }
{F1 , . . . , Fn }
X
` G1 F2 ` G2
F3 ` G3
F `G
F 0 ` G0
Schreibweise:
F1
X
172
dann (F3 , G3 ) ∈ `.
(X) Wenn (F1 , G1 ) ∈ ` und (F2 , G2 ) ∈ `,
dann (F 0 , G 0 ) ∈ `.
(X) Wenn (F, G) ∈ `,
F ` G . . . Sequent“
”
Motivation: syntaktische Ableitung von F ` G statt semantischem
Beweis von F |= G
Basisfälle der induktiven Definition: Axiome“
”
2 Abschlussbedingungen pro Operator
Sequentialkalkül: induktive Definition einer binären Relation ` mit
der Eigenschaft ` = |=
170
MAF (I, F ) = f für mindestens ein F ∈ F
oder MAF (I, G) = t für mindestens ein G ∈ G.
Gleichbedeutend mit:
Wenn MAF (I, F ) = t für alle F ∈ F,
dann gilt MAF (I, G) = t für mindestens ein G ∈ G.
• Die Länge einer DNF/KNF kann exponentiell größer sein als
die ursprüngliche Formel.
Ursache bei algebraischer Methode: Elimination von ≡ und 6≡,
Anwenden der Distributivität
Ursache bei semantischer Methode: Anzahl der möglichen
Interpretationen (vgl. Wahrheitstafel)
169
{F } |= {} . . . F ist unerfüllbar.
{} |= {G} . . . G ist gültig (Tautologie).
V
W
Satz. F |= G gilt gdw. ( F) ⊃ ( G) gültig ist.
{} = f ,
V
.
V
V
V
{} = t,
({F } ∪ F) = F ∧ F
.
W
W
({F } ∪ F) = F ∨ F
W
F1 ∧ . . . ∧ Fn =
W
i∈{1,...,n}
Fi =
i∈{1,...,n}
F1 ∨ . . . ∨ Fn =
171
⊃-l
∨-l
F ` G, A, B
∨-r
⊃-r
F ` G, B
F ` G, A ∨ B
F ` G, A
F ` G, A ∧ B
F, A ` G, B
∧-r
[d.h.: F 0 ` G 0 ist Axiom, falls F 0 ∩ G 0 6= {}]
Sequentialkalkül für die Aussagenlogik
∧-l
F, B ` G
Axiome: F, A ` G, A
F, A ` G
F, A ∨ B ` G
F, A, B ` G
F, B ` G
F, A ∧ B ` G
F ` G, A
F ` G, A ⊃ B
¬-r
F, A ⊃ B ` G
¬-l
F ` G, ¬A
F, A ` G
F, ¬A ` G
F ` G, A
173
Beobachtung:
Jede Ableitung ist ein Baum von Sequenten, dessen Blätter
Axiome sind.
Die anderen Knoten (d.h. Sequente) des Baums
erfüllen folgende Bedingung:
Die (ein oder zwei) Kindknoten zu jedem Elternknoten sind
die Prämissen einer Regelanwendung,
die zum Elternknoten als Konklusion führt.
175
Axiom
A, B ` B
Axiom
Axiom
⊃-l
Axiom
B ` A, B
Axiom
∨-l
∧-l
¬-l
(A ∨ B) ∧ ¬A ` B
A ∨ B, ¬A ` B
A ∨ B ` A, B
A ` A, B
⊃-r
∧-l
` ((A ⊃ B) ∧ A) ⊃ B
(A ⊃ B) ∧ A ` B
A ⊃ B, A ` B
A ` A, B
Beispiel. Ableitung von ` ((A ⊃ B) ∧ A) ⊃ B
¬-l
B, ¬A ` B
∧-l
∨-l
Beispiel. Ableitung von (A ∨ B) ∧ ¬A ` B
Axiom
A ` A, B
A, ¬A ` B
A ∨ B, ¬A ` B
(A ∨ B) ∧ ¬A ` B
174
∨-r
¬-r
Beispiel. Ableitung von ` (A ⊃ (B ⊃ C)) ∨ ¬(A ⊃ (B ⊃ C))
Axiom
A ⊃ (B ⊃ C) ` A ⊃ (B ⊃ C)
` (A ⊃ (B ⊃ C)), ¬(A ⊃ (B ⊃ C))
` (A ⊃ (B ⊃ C)) ∨ ¬(A ⊃ (B ⊃ C))
Axiom
kein Axiom!
∧-r
¬-r
A, C, B ` A A, C, B `
A ⊃ B, A, C, B `
A ⊃ B, A, C ` ¬B
⊃-l
Beispiel. Ableitungsversuch für A ⊃ B, A, C ` C ∧ ¬B
Axiom
A ⊃ B, A, C ` C
A ⊃ B, A, C ` C ∧ ¬B
176
Satz. Der Sequentialkalkül ist korrekt: aus F ` G folgt F |= G.
Beweis. Wir zeigen:
1. Basisfall: Aus F ∩ G =
6 {} folgt F |= G.
F 0 `G 0
F `G
: aus F 0 |=G 0 folgt F |=G.
Sei H ∈ F ∩ G. Wenn MAF (I, F ) = t für alle F ∈ F, dann
MAF (I, H) = t. Da H ∈ G, gilt MAF (I, G) = t für mindestens
ein G ∈ G. D.h.: es gilt F |= G.
2. Für jede Regel
F `G, A, B
∨-r :
F `G, A∨B
MAF (I, F ) = t für alle F ∈ F
⇒ MAF (I, G) = t für ein G ∈ G ∪ {A, B} (da F |=G, A, B)
⇒ MAF (I, G) = t für ein G ∈ G ∪ {A∨B} (Def. von ∨)
D.h.: aus F |= G, A, B folgt F |= G, A∨B.
Die Korrektheit der Regeln ∧-l, ⊃-r, ¬-l und ¬-r folgt analog.
177
Beobachtung:
F ` G ist sicher nicht ableitbar, wenn F und G nur atomare
Formeln enthalten und F ∩ G = {} ( Anti-Axiom“).
”
Definition:
Ein Ableitungsversuch von F ` G ist ein Baum von Sequenten
mit Wurzel F ` G.
Die Blätter sind Axiome oder Anti-Axiome.
Die anderen Sequente des Baums sind jeweils Prämissen zu einer
Regelanwendung, deren Konklusion der entsprechende
Elternknoten ist.
M.a.W.: Ein Ableitungsversuch ist wie eine Ableitung
Definition:
Endet ein Zweig eines Ableitungsversuchs von F ` G mit einem
Anti-Axiom, dann sagen wir: Der Ableitungsversuch scheitert.
179
3. Für jede Regel
F 0 `G 0 F 00 `G 00
F `G
: aus F 0 |=G 0 , F 00 |=G 00 folgt F |=G.
F, A|=G und F, B|=G legt folgende Fallunterscheidung nahe:
F , A`G F , B`G
∨-l :
F , A∨B`G
Fall 1: MAF (I, F ) = f für ein F ∈ F
F, A∨B |= G folgt unmittelbar.
Fall 2: MAF (I, G) = t für ein G ∈ G
F, A∨B |= G folgt unmittelbar.
Fall 3: MAF (I, A) = f und MAF (I, B) = f .
Aus der Definition von ∨ folgt MAF (I, A ∨ B) = f .
Daher auch in diesem Fall: F, A∨B |= G.
Die Korrektheit der Regeln ∧-r und ⊃-l folgt analog.
Aus dem Fundamentalsatz der Induktion folgt damit ` ⊆ |=.
178
Satz. Scheitert ein Ableitungsversuch von F ` G, dann gilt F 6|= G.
Beweis. F 6|= G bedeutet: Es gibt eine Interpretation I, sodass
MAF (I, F ) = t für alle F ∈ F und MAF (I, G) = f für alle G ∈ G.
F 0 `G 0
F `G
: Aus F 0 6|=G 0 folgt F 6|=G.
1. Basisfall: Sei F ` G Anti-Axiom. Wir können I definieren als:
I(F ) = t für alle F ∈ F und I(G) = f für alle G ∈ G.
2. Für jede Regel
F `G, A, B
∨-r :
F `G, A∨B
F 6|= G, A, B
⇒ es gibt I, sodass MAF (I, F ) = t für alle F ∈ F
und MAF (I, G) = f für alle G ∈ G ∪ {A, B}
⇒ es gibt I, sodass MAF (I, F ) = t für alle F ∈ F
und MAF (I, G) = f für alle G ∈ G ∪ {A∨B}
⇒ F 6|= G, A∨B
Analoges gilt für die Regeln ∧-l, ⊃-r, ¬-l und ¬-r.
180
3. Für jede Regel
F 0 `G 0 F 00 `G 00
F `G
:
Wenn F 0 6|=G 0 oder F 00 6|=G 00 dann auch F 6|=G.
F , A`G F , B`G
∨-l :
F , A∨B`G
O.B.d.A.: F, A6|=G (Fall F, B6|=G analog).
⇒ es gibt I, sodass MAF (I, F ) = t für alle F ∈ F ∪ {A}
und MAF (I, G) = f für alle G ∈ G
⇒ es gibt I, sodass MAF (I, F ) = t für alle F ∈ F ∪ {A∨B}
und MAF (I, G) = f für alle G ∈ G
⇒ F, A∨B 6|= G
Analoges gilt für die Regeln ∧-r und ⊃-l.
181
Eigenschaften des Sequentialkalküls:
• ‘Schlussweisenkalkül’: Konsequenzbehauptungen als Objekte.
Folgerung. Der (aussagenlogische) Sequentialkalkül ist vollständig:
Aus F |= G folgt F ` G.
Beweis. Aus dem Satz folgt, dass es mindestens einen
Ableitungsversuch von F ` G gibt, der nicht scheitert, falls F |= G.
Da jeder Ableitungsversuch, der nicht scheitert, zu einer Ableitung
führt, folgt F ` G.
Folgerung. Endet ein Ableitungszweig eines Ableitungsversuches
von F ` G mit einem Anti-Axiom, dann gilt F 6` G.
Beweis. Endet ein Ableitungszweig von F ` G mit einem
Anti-Axiom, gilt F 6|= G. Wegen der Korrektheit des
Sequentialkalküls folgt daraus F 6` G.
Folgerung. ` = |=
Beweis. Aus Korrektheit (` ⊆ |=) und Vollständigkeit (` ⊇ |=)
folgt ` = |=.
182
Folgerung. {} ` F gilt genau dann, wenn F Tautologie ist.
Hilbert-Typ Kalkül
Axiome: 1. (A ⊃ (B ⊃ A))
2. ((A ⊃ (B ⊃ C)) ⊃ ((A ⊃ B) ⊃ (A ⊃ C)))
• Einfache Axiome, viele Regeln (den Wahrheitstafeln folgend).
• Korrektheit: Aus F ` G folgt F |= G.
B
A A⊃B
184
(Modus ponens)
9. ((¬A ⊃ ¬B) ⊃ ((¬A ⊃ B) ⊃ A))
8. ((A ∧ B) ⊃ B)
7. ((A ∧ B) ⊃ A)
6. (A ⊃ (B ⊃ (A ∧ B)))
5. ((A ⊃ C) ⊃ ((B ⊃ C) ⊃ ((A ∨ B) ⊃ C)))
4. (B ⊃ (A ∨ B))
3. (A ⊃ (A ∨ B))
Regel:
• Vollständigkeit: Aus F |= G folgt F ` G.
• Don’t-care-Indeterminismus: Wenn F ` G gilt, führt jede
Zerlegung zu Axiomen.
• Analytizität:
Die Prämissen bestehen aus Bestandteilen der Konklusion.
analytisch:
nicht analytisch (wegen X):
F, A, B ` G
F ` G, X X, F ` G
Schnitt
F, A ∧ B ` G
F `G
Analytizität ist wichtig für automatische Beweissuche.
• Einfache Formeln besitzen einfache Beweise.
183
A⊃((A⊃A)⊃A)
Ax. 1: B7→(A⊃A)
(A⊃((A⊃A)⊃A))⊃((A⊃(A⊃A))⊃(A⊃A))
(A⊃(A⊃A))⊃(A⊃A)
Axiom 2: B7→(A⊃A), C7→A
Beispiel. Ableitung von A ⊃ A
A⊃(A⊃A)
Ax. 1: B7→A
A⊃A
Eigenschaften des Hilbert-Typ Kalküls:
• viele Axiome, eine einzige Regel
• Korrektheit: jede ableitbare Formel ist gültig.
• Vollständigkeit: jede gültige Formel ist ableitbar.
• Nicht analytisch wegen Formel A in Modus ponens, schwer
automatisierbar.
• Komplizierte Beweise auch von einfachen Formeln.
185
Tableau: Baum mit Wahrheitswert-Formel-Paaren als Knoten
@
@
@
@ =⇒
@
@
@
@ =⇒
@
@
w:F σ
@
@
w:F σ
w:F σ
@
@
@
@
@
@
@
@
w1 :F1 σ
w2 :F2 σ
@
@
w:F σ
Tableau-Expansionsregel: legt fest, wie ein Baum erweitert werden
kann. Zwei Typen: Und-Regeln, Oder-Regeln.
Und-Regeln:
w:F
w1 : F1
w2 : F2
Oder-Regeln:
w2 : F2
w:F
w1 : F1
@
@
@
@
w1 :F1 σ w2 :F2 σ
w, w1 , w2 . . . Wahrheitswerte, F, F1 , F2 . . . Formeln, σ. . . Substitution
187
Semantische Tableaux
Indirekter Beweis von F : die Annahme, dass F widerlegbar ist
(MAF (I, F ) = f für ein I), wird auf einen Widerspruch geführt.
Annahme
Zerlegung
Zerlegung
Zerlegung
Zerlegung
(1)
(1)
(2)
(2)
t:A∧B
t:A
t : ¬A
f :B
f : ¬A
f :A
t:B
t:A
f :A
f :A∧B
Zerlegung von (4)
Widerspruch zu (5) bzw. (3)
von
von
von
von
Untereinander: Direkte Folgefälle (semantisches Und).
Nebeneinander: Fallunterscheidung (semantisches Oder).
(7) t : B
×
t:B
t:B
186
f : ((A ⊃ B) ∧ A) ⊃ B
t : (A ⊃ B) ∧ A
f :B
t:A⊃B
t:A
Beispiel. Tableau für ((A ⊃ B) ∧ A) ⊃ B
(1)
(2)
(3)
(4)
(5)
(6) f : A
×
f :A
t:A⊃B
t:A
t:A∨B
Tableau-Expansionsregeln
f :A∨B
f :A
f :B
f :A⊃B
t:A
f :B
Für jeden binären Operator eine Und-Regel und eine Oder-Regel
(plus zwei simple Regeln für den unären Negations-Operator)
Die Regeln entsprechen den Regeln des Sequentialkalküls
bzw. den Wahrheitstafeln
188
(2)
(1)
f :B
t : (A ∨ B) ∧ ¬A
f : ((A ∨ B) ∧ ¬A) ⊃ B
Zerlegung von 2
Zerlegung von 1
Zerlegung von 1
Beispiel. Geschlossenes Tableau für ((A ∨ B) ∧ ¬A) ⊃ B
Ein Tableau-Ast heißt geschlossen, wenn auf ihm sowohl t:G als
auch f :G für irgendeine Formel G vorkommt.
(3)
t:A∨B
f : ((A ∨ B) ∧ A) ⊃ B
Zerlegung von 1
t:A
Zerl. v. 5
Zerl. v. 4
× (Widerspruch: 7/3)
Zerlegung von 4
Zerlegung von 2
(6)
f :A
t : ¬A
(8)
× (Widerspruch: 6/8)
192
• Einfache Formeln besitzen einfache Beweise.
• Analytizität: die Expansionsregeln fügen nur Bestandteile der
ursprünglichen Formel hinzu.
• Don’t-care-Indeterminismus: Ist eine Formel gültig, liefert jede
Folge von Expansionsschritten irgendwann ein geschlossenes
Tableaux, wobei keine Formel mehr als einmal pro Ast
expandiert werden muss.
• Vollständigkeit: Ist eine Formel gültig, so besitzt sie ein
geschlossenes Tableau.
• Korrektheit: Besitzt eine Formel ein geschlossenes Tableau, ist
sie gültig.
Eigenschaften des Tableau-Kalküls:
190
(5)
Annahme
Ein Tableau heißt geschlossen, wenn alle Äste geschlossen sind.
(4)
(1)
t : (A ∨ B) ∧ A
Zerlegung von 1
(7) t : B
Ein Tableau-Beweis einer Formel F ist ein geschlossenes Tableau
mit f :F an der Wurzel.
Satz. Eine Formel F ist gültig genau dann, wenn es einen
Tableau-Beweis für sie gibt.
Ein Tableau-Ast der nicht geschlossen werden kann spezifiziert ein
Gegenbeispiel für die Formel an der Wurzel.
189
Beispiel. Tableau für ((A ∨ B) ∧ A) ⊃ B
(2)
f :B
Zerlegung von 2
Annahme
(3)
t:A∨B
Zerlegung von 4
(4)
(7) t : B
Zerlegung von 2
Zerl. v. 4
t:A
t:A
×
(5)
(6)
Ast bleibt offen!
⇒ I mit I(A) = t und I(B) = f ist ein Gegenbeispiel zu
((A ∨ B) ∧ A) ⊃ B
Bzw.: für die angegebene Interpretation I gilt:
MAF (I, ((A ∨ B) ∧ A) ⊃ B) = f
191
Resolution
Indirekter Beweis der Gültigkeit einer Formel (wie bei Tableaux):
Gültigkeit von F wird gezeigt durch Widerlegung von ¬F ,
d.h. dem Nachweis der Unerfüllbarkeit von ¬F .
Resolutionsableitungen beziehen sich auf Klauselmengen (KNF).
Daher: 2 Stufen
1. Transformiere ¬F in eine äquivalente Klauselmenge cl(F ), d.h.
berechne eine konjunktive Normalform (Klauselform) von ¬F .
2. Wende die Resolutionsregel an um schrittweise neue Klauseln
abzuleiten. Wenn die leere Klausel ableitbar ist, so haben wir
einen Widerspruch gefunden.
Hinweis zur Klauselformberechnung
Meist interessiert man sich für den Nachweis von Behauptungen
der Form
F1 , . . . , Fn |= G
cl(Fi )
Wegen des Deduktionstheorems ist dies gleichbedeutend mit der
Gültigkeit der Formel
(F1 ∧ . . . ∧ Fn ) ⊃ G
bzw. der Unerfüllbarkeit der Formel
¬((F1 ∧ . . . ∧ Fn ) ⊃ G)
= ¬(¬(F1 ∧ . . . ∧ Fn ) ∨ G)
S
i∈{1,...,n}
= ¬¬(F1 ∧ . . . ∧ Fn ) ∧ ¬G
= F1 ∧ . . . ∧ Fn ∧ ¬G
Daher ist die relevante Klauselmenge cl(¬G) ∪
Resolutionsableitung
194
Die Resolutionsregel
193
Es seien C und D Klauseln, die duale Literale enthalten;
.
.
d.h. C = C 0 ∪ {A} und D = {¬A} ∪ D 0
K1 , . . . , Km
196
• K` ist eine Resolvent von Ki und Kj mit i, j < `.
• entweder K` ∈ Π,
sodass für alle 1 ≤ ` ≤ m:
Sei Π eine Klauselmenge.
Eine (Resolutions-)Ableitung von Km aus Π ist eine Folge von
Klauseln
.
Die Resolutionsregel zur Ableitung von neuen Klauseln lautet:
.
C 0 ∪ {A}
{¬A} ∪ D 0
C 0 ∪ D0
C 0 ∪ D 0 heißt Resolvente der (Eltern-)Klauseln C und D.
A nennt man auch das resolvierte Atom.
195
Beispiel
Die Folge
1
2
3
4
5
6
7
}|
{ z }| { z }| { z }| { z }| { z }| { z}|{
z
{A, B, ¬C}, {¬B, ¬C}, {A, ¬C}, {¬A}, {¬C}, {C, A}, {C}
ist eine Ableitung von {C} aus
Π = {A, B, ¬C}, {¬B, ¬C}, {¬A}, {A, C}, {A, D}
Begründung:
• 1, 2, 4, 6 ∈ Π
197
• 3 ist Resolvente von 1 und 2
5 ist Resolvente von 3 und 4
7 ist Resolvente von 4 und 6
Beweis von (a):
.
.
Es genügt zu zeigen, dass die Resolutionsregel korrekt ist:
D.h., jedes Modell der Klauseln C und D ist auch
ein Modell ihrer Resolventen.
Es seien C = C 0 ∪ {A} und D = D 0 ∪ {¬A} in I wahr.
Zu zeigen ist: C 0 ∪ D 0 ist ebenfalls in I wahr.
.
1. I(A) = t: Laut Voraussetzung MAF (I, D) = MAF (I, D 0 ∪
{¬A}) = MAF (I, D 0 ) ∨ MAF (I, ¬A) = t. Somit wegen
MAF (I, ¬A) = f : MAF (I, D 0 ) = t. Daher: MAF (I, C 0 ∪ D 0 ) =
MAF (I, C 0 ) ∨ MAF (I, D 0 ) = MAF (I, C 0 ) ∨ t = t, d.h., die
Resolvente ist wahr in I.
.
2. I(A) = f : Laut Voraussetzung MAF (I, C) = MAF (I, C 0 ∪
{A}) = (MAF (I, C 0 ) ∨ MAF (I, A)) = t. Somit wegen
MAF (I, A) = f : MAF (I, C 0 ) = t. Daher: MAF (I, C 0 ∪ D 0 ) =
MAF (I, C 0 ) ∨ MAF (I, D 0 ) = t ∨ MAF (I, D 0 ) = t.
199
Satz
(a) Resolution ist korrekt:
Ist eine Klausel D aus Π ableitbar, dann Π |= D.
(b) Resolution ist vollständig:
Wenn Π |= D, dann ist D entweder eine Tautologie oder es ist
ein D 0 aus Π ableitbar, mit D 0 ⊆ D.
198
(c) Es ist in endlich vielen Schritten entscheidbar, ob eine Klausel
D aus Π ableitbar ist oder nicht.
Beweis von (c):
Es gibt nur endliche viele verschiedene Variablensymbole in Π.
Es gibt nur endlich viele verschiedene Klauseln, die man aus diesen
Variablensymbolen bilden kann.
Resolution führt keine neuen Variablensymbole ein.
Daher sind aus Π nur endlich viele verschiedene Klauseln ableitbar.
Diese endliche Menge R∗ (Π) ableitbarer Klauseln ist effektiv
herstellbar, da es auch nur endlich viele Ableitungen ohne
Wiederholung von Klauseln geben kann.
Es bleibt nur nachzuprüfen, ob D Element von R∗ (Π) ist.
200
Widerlegungsvollständigkeit
Eine Ableitung der leeren Klausel {} aus Π heißt
Resolutionswiderlegung von Π.
Folgerung aus dem Satz:
Π ist unerfüllbar genau dann, wenn es eine Resolutionswiderlegung
von Π gibt.
Beweis:
1. Die leere Klausel ist unerfüllbar.
Daher folgt aus der Korrektheit: Π hat ebenfalls kein Modell.
2. Wenn Π unerfüllbar ist, so ist jede Klausel eine Konsequenz
von Π, insbesonders auch {}.
Da {} keine Tautologie ist und auch keine Teilmengen besitzt,
folgt aus der Vollständigkeit, dass {} aus Π ableitbar ist.
201
Wir bezeichnen die Klauseln in Π:
{1.{A, B, D}, 2.{¬B, C}, 3.{¬A, B}, 4.{¬C}, 5.{¬D}}
und erhalten folgende Resolutionswiderlegung:
3. {¬A, B} ∈ Π
2. {¬B, C} ∈ Π
1. {A, B, D} ∈ Π
9. {} aus 8, 5
8. {D} aus 6, 7
7. {¬B} aus 2, 4
6. {B, D} aus 1, 3
5. {¬D} ∈ Π
4. {¬C} ∈ Π
203
Einfaches Beispiel zum Resolutionskalkül
Zeigen Sie, dass A ∨ B ∨ D, B ⊃ C, A ⊃ B |= C ∨ D.
= cl(A ∨ B ∨ D) ∪ cl(B ⊃ C) ∪ cl(A ⊃ B) ∪ cl(¬(C ∨ D))
Es ist die Unerfüllbarkeit folgender Klauselmenge zu zeigen:
K
{¬D}
= {{A, B, D}, {¬B, C}, {¬A, B}, {¬C}, {¬D}}
{}
{¬B, C}
{¬C}
{¬B}
Resolutionswiderlegung in Baumform:
{A, B, D}
{¬A, B}
{B, D}
{D}
202
The Winds and the Windows Puzzle
1. There is always sunshine when the wind is in the East.
2. When it is cold and foggy, my neighbor practices the flute.
3. When my fire smokes, I set the door open.
4. When it is cold and I feel rheumatic, I light my fire.
5. When the wind is in the East and comes in gusts, my fire smokes.
6. When I keep the door open, I am free from headache.
7. Even when the sun is shining and it is not cold, I keep my window
shut if it is foggy.
8. When the wind does not come in gusts, and when I have a fire and
keep the door shut, I do not feel rheumatic.
9. Sunshine always brings on fog.
10. When my neighbor practices the flute, I shut the door, even if I have
no headache.
11. When there is a fog and the wind is in the East, I feel rheumatic.
Show that when the wind is in the East, I keep my windows shut.
204
Wir formalisieren die Aussagen unter Verwendung folgender
Abkürzungen:
R . . . Rauch
. . . Feuer
F
Rh . . . Rheuma
. . . Sonnenschein
Fl . . . Flötenspiel
S
. . . Kälte
W . . . Windstöße
K
. . . Nebel
Z . . . Fenster zu
. . . Tür offen
N
. . . Ostwind
T
O
Kw . . . Kopfweh
205
19. {¬K, ¬T }
18. {¬K, ¬R}
17. {¬K, Fl }
16. {¬Fl , ¬R}
15. {N }
14. {S}
5, 12
10, 17
16, 17
2, 15
3, 10
9, 14
1, 12
33. {W }
32. {T, W }
31. {¬F, T, W }
30. {¬T }
29. {¬W }
28. {F }
27. {K}
26. {K, Z}
29, 33
30, 32
28, 31
8, 23
19, 27
21, 27
24, 27
13, 26
15, 25
25. {¬N, K, Z} 7, 14
aus Klauseln
21. {¬K, ¬W } 18, 20
20. {¬W, R}
11, 12
34. {}
Resolvente
22. {¬N, Rh}
15, 22
aus Klauseln
23. {Rh}
4, 23
Resolvente
24. {¬K, F }
207
Aussage
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
Behauptung
Behauptung negiert
12.
13.
206
Klausel
{¬O, S}
{¬K, ¬N, Fl}
{¬R, T }
{¬K, ¬Rh, F }
{¬O, ¬W, R}
{¬T, ¬Kw }
{¬S, K, ¬N, Z}
{W, ¬F, T, ¬Rh}
{¬S, N }
{¬Fl, ¬T }
{¬N, ¬O, Rh}
{O}
{¬Z}
Redundanzelimination
aus Formel
O⊃S
(K ∧ N ) ⊃ Fl
R⊃T
(K ∧ Rh) ⊃ F
(O ∧ W ) ⊃ R
T ⊃ ¬Kw
(S ∧ ¬K ∧ N ⊃ Z
(¬W ∧ F ∧ ¬T ) ⊃ ¬Rh
S⊃N
Fl ⊃ ¬T
(N ∧ O) ⊃ Rh
O⊃Z
¬(O ⊃ Z)
Subsumtion:
Wenn C ⊆ D sagt man: C subsumiert D.
Es gilt dann offensichtlich C |= D.
Jede Klausel einer vollständigen Generation von Resolventen
die von einer Klausel dieser Generation subsumiert wird, kann
eliminiert werden.
.
.
.
C 0 ∪ {A} {¬A, B, ¬B} ∪ D 0
C 0 ∪ {B, ¬B} ∪D 0
.
Tautologieelimination:
C ist eine Tautologie gdw. {A, ¬A} ⊆ C für irgendein A.
Tautologien können immer eliminiert werden, da aus
Tautologien nur wieder Tautologien bzw. von Elternklauseln
subsumierte Klauseln ableitbar sind:
C 0 ∪ {A} {¬A, A} ∪ D 0
C 0 ∪ {A} ∪ D 0
208
Heuristiken und Strategien
{A}
{¬A} ∪ D 0
D0
.
Klauseln mit nur einem Literal nennt man Einerklauseln oder
Unit-Klauseln.
.
C 0 ∪ {A} {¬A}
C0
Resolution mit einer Einerklausel (Unit-Resolution) garantiert also
eine kleinere Klausel als Resolvente.
Ausserdem subsumiert jede Unit-Resolvente eine Elternklausel:
Diese Elternklausel wird redundant.
Generell ist ‘Bevorzugung von kürzeren Klauseln’
eine gute Heuristik.
209
(prädikatenlogische Formeln)
Prädikatenlogik (klassische Logik erster Stufe)
Syntax
Gegeben: Signatur Σ = hFS , PS , KS i
PF Σ ist die kleinste Menge, für die gilt:
(PF1) p0 (t1 , . . . , tn ) ∈ PF Σ (Atomformel)
wenn p0 ∈ PS n und t1 , . . . , tn ∈ TΣ
(PF2) ¬F ∈ PF Σ wenn F ∈ PF Σ
(PF3) (F ∧ G) ∈ PF Σ wenn F, G ∈ PF Σ
(PF4) (F ∨ G) ∈ PF Σ wenn F, G ∈ PF Σ
(PF5) (F ⊃ G) ∈ PF Σ wenn F, G ∈ PF Σ
(PF6) (∀v)F ∈ PF Σ wenn v ∈ IVS und F ∈ PF Σ
(PF7) (∃v)F ∈ PF Σ wenn v ∈ IVS und F ∈ PF Σ
211
Eigenschaften des Resolutions-Kalküls:
• Basisobjekte: Klauseln
• Zweistufiges Verfahren: KNF-Transformation + Resolution
• Indirektes Verfahren: Suche nach Widerlegung
• Korrektheit: Jede aus Π abgeleite Klausel ist Konsequenz von Π
• Vollständigkeit: Relevant ist nur
Widerlegungsvollständigkeit: Aus unerfüllbaren Klauselmengen
ist die leere Klausel ableitbar
• Keine Axiome, eine einfache Regel; daher gut automatisierbar
210
• In der Praxis sind diverse (Beweis-)Strategien und
Redundanzeliminationen von großer Bedeutung
Anmerkungen:
• Die Definition bezieht sich nur auf Signaturen und nicht
direkt auf entsprechende Modellstrukturen.
(=⇒ Saubere Trennung von Syntax und Semantik!)
• TΣ = T (D) für jede Modellstruktur D mit Signatur Σ.
• Bis auf (PF5)–(PF7) ist PF Σ genau wie BA(D) definiert.
• ∀ heißt All-Quantor, ∃ heißt Existenz-Quantor.
• Die Zeichensequenz (∀x) stellt ein Quantoren-Vorkommen da.
• Wir machen von den selben Klammereinsparungen wie für
aussagenlogische Formeln Gebrauch. Z.B.: F1 ∧ F2 ∧ F3 .
• Erweiterung auf andere Konnektive, wie für AF , möglich.
212
Variablenvorkommen
V (t), V (F ) . . . Variablen, die in Term t bzw. Formel F vorkommen
Die Menge FV (F ) der Variablen, die frei (ungebunden) in F
vorkommen, ist wie folgt definiert:
• für Atomformeln: FV (p(t1 , . . . , tn )) = V (p(t1 , . . . , tn ))
• FV (¬F ) = FV (F )
• FV (F ◦ G) = FV (F ) ∪ FV (G) für ◦ ∈ {∧, ∨, ⊃}
• FV ((Qx)F ) = FV (F ) − {x} für Q ∈ {∀, ∃}
‘(Qx) bindet die freien Vorkommen von x in F ’
‘F ist der Bindungsbereich von (Qx) in (Qx)F ’
Achtung: x kann gleichzeitig frei und gebunden vorkommen!
213
F bzw. t ist geschlossen bedeutet: F V (F ) = {},
bzw. F V (t) = V (t) = {}.
Variablensubstitution
Notation:
F (x/t) bezeichnet die Formel die aus F entsteht, indem alle freien
Vorkommen von x in F durch den Term t ersetzt werden.
Beispiele:
Sei F = (∀x)[P (x, y) ⊃ Q(x, y)] ∧ R(x) und t = f (a)
• F (x/t) = (∀x)[P (x, y) ⊃ Q(x, y)] ∧ R(f (a))
• F (y/t) = (∀x)[P (x, f (a)) ⊃ Q(x, f (a))] ∧ R(x)
215
...
...
...
...
Konstantensymbole
Funktionssymbole
Prädikatensymbole
Variable (Variablensymbole)
Schreibkonventionen: (Neben den Signaturen zu N, Z, etc.)
a, b, c, d, e
f, g, h
P, Q, R
x, y, z, u, v, w
Um die Lesbarkeit zu erhöhen: auch ‘[’, ‘]’ für ‘(’ und ‘)’
214
Beispiele
Folgende Formeln sind wohlgeformt:
• F = [¬P (f (x), a) ∧ P (g(a, y), b)] FV (F ) = {x, y}
• F = (∀x)[¬P (f (x), a) ∧ P (g(a, x), b)] FV (F ) = {}
• F = [(∀x)¬P (f (x), a) ∧ P (g(a, x), b)] FV (F ) = {x}
• F = (∀x)(∃y)[¬P (f (y), a) ∧ P (g(a, x), b)] FV (F ) = {}
• F = (∀x)P (y, z) FV (F ) = {y, z}
• F = (∀x)(∃x)P (x, x) FV (F ) = {}
Semantik
Prädikatenlogik ist sehr ausdrucksstark!
Beispiele:
‘R ist eine Äquivalenzrelation’ kann man — in der Signatur
h{}, {R}, {}i — als F1 ∧ F2 ∧ F3 ausdrücken, wobei:
F1 = (∀x)R(x, x)
F2 = (∀x)(∀y)[R(x, y) ⊃ R(y, x)]
F3 = (∀x)(∀y)(∀z)[(R(x, y) ∧ R(y, z)) ⊃ R(x, z)]
Spezifikation von Eigenschaften der Modellstruktur Z:
• (∀x)x + 0 = x
• (∀x)(∃y)x + y = 0
• (∀x)(∀y)(x < y ⊃ 0 − y < 0 − x)
‘x ist Primzahl’ als Formel über der Signatur von N:
• (∀y)(∀z)[x = y ∗ z ⊃ (y = 1 ∨ z = 1)] ∧ 1 < x
216
PL-Interpretation
Eine (prädikatenlogische) Interpretation J über der
Signatur Σ = hFS Σ , PS Σ , KS Σ i ist ein Tupel hD, Φ, Ii, wobei
• D = hD, FD , PD , KD i ist eine Modellstruktur
Zur Erinnerung: D ist eine nicht-leere Menge
• Φ ist eine Signaturinterpretation, die jedem f 0 ∈ FS Σ ,
jedem p0 ∈ PS Σ , jedem c0 ∈ KS Σ eindeutig ein (der Stelligkeit
entsprechendes) f ∈ FD , p ∈ PD , bzw. c ∈ KD zuweist
• I : IVS → D ist eine Variablenbelegung
PINT Σ . . . Menge aller (PL-)Interpretation über der Signatur Σ
217
Anmerkung:
Im Kapitel 2 haben wir Standard-Signaturinterpretationen Φ durch
die ‘Unterstreichungskonvention’ festgelegt.
Wir machen uns von dieser (oft zu engen) Konvention nun frei!
Semantik (Beispiel)
x
Modellstruktur: D = h{3, 4}, {id}, {=}, {}i,
id . . . Identitätsfunktion (id(n) = n)
Signatur: Σ = h{f }, {P }, {}i, f unär, P binär
Interpretation über Σ: J = hD, Φ, Ii, wobei Φ(f ) = id, Φ(P ) ==
und I(x) = 3, I(y) = 3
Auswertung von F = (∀x)(∃y)¬P (x, f (y)):
MPF6
MPF7
y
MPF (J , F ) = t ⇐⇒ MPF (J 0 , (∃y)¬P (x, f (y)) = t für alle J 0 ∼ J
⇐⇒ MPF (J 00 , ¬P (x, f (y)) = t für ein J 00 ∼ J 0
MPF2
MPF1
⇐⇒ MPF (J 00 , P (x, f (y)) = f
y
(I 00 , y)) ⇐⇒ I 00 (x) 6= I 00 (y)
⇐⇒ MT (I 00 , x) 6= MT (I 00 , f (y)) für J 00 = hD, Φ, I 00 i
⇐⇒ I 00 (x) 6=
MT1,MT3
id(MT
x
MPF (J , F ) = t, da zu jedem J 0 ∼ J ein J 00 ∼ J 0
mit J 00 (x) 6= J 00 (y) existiert
219
Semantik (Auswertungsfunktion)
MPF : PINT Σ × PF Σ → {t, f } ist rekursiv definiert durch
(MPF1) MPF (J , p0 (t1 , . . . , tn )) = p(MT (I, t1 ), . . . , MT (I, tn ))
wobei p = Φ(p0 ) (Prädikat zum Prädikatensymbol p0 )
I ist die Variablenbelegung in J = hD, Φ, Ii
(MPF2) MPF (J , ¬F ) = ¬MPF (J , F )
(MPF3) MPF (J , (F ∧ G)) = MPF (J , F ) ∧ MPF (J , G)
(MPF4) MPF (J , (F ∨ G)) = MPF (J , F ) ∨ MPF (J , G)
(MPF5) MPF (J , (F ⊃ G)) = MPF (J , F ) ⊃ MPF (J , G)
v
v
(MPF6) MPF (J , (∀v)F ) = t gdw MPF (J 0 , F ) = t für alle J 0 ∼ J
v
(MPF7) MPF (J , (∃v)F ) = t gdw MPF (J 0 , F ) = t für ein J 0 ∼ J
v
J ∼ J 0 . . . J = hD, Φ, Ii und J 0 = hD, Φ, I 0 i, wobei I ∼ I 0
v
Erinnerung: I ∼ I 0 . . . I(w) = I 0 (w) für alle w ∈ IVS mit w 6= v
218
Semantische Grundbegriffe (PL)
Eine Formel F ∈ PF Σ heißt
• erfüllbar, wenn MPF (J , F ) = t für ein J ∈ PINT Σ
J heißt Modell von F
• widerlegbar, wenn MPF (J , F ) = f für ein J ∈ PINT Σ
J heißt Gegenbeispiel oder Gegenmodell zu F
• unerfüllbar, wenn MPF (J , F ) = f für alle J ∈ PINT Σ
(also: alle Interpretationen sind Gegenbeispiele)
• (allgemein) gültig, wenn MPF (J , F ) = t für alle J ∈ PINT Σ
(also: alle Interpretationen sind Modelle)
220
Bezogen auf eine gegebene Modellstruktur D und
eine entsprechende Signaturinterpretation Φ heißt F ∈ PF Σ :
• erfüllbar in D (bzgl. Φ), wenn MPF (J , F ) = t
für ein J ∈ PINT Σ der Form J = hD, Φ, Ii
• widerlegbar in D (bzgl. Φ), wenn MPF (J , F ) = f
für ein J ∈ PINT Σ der Form J = hD, Φ, Ii
• unerfüllbar in D (bzgl. Φ), wenn MPF (J , F ) = f
für alle J ∈ PINT Σ der Form J = hD, Φ, Ii
221
• gültig in D (bzgl. Φ), wenn MPF (J , F ) = t
für alle J ∈ PINT Σ der Form J = hD, Φ, Ii
Beispiel
Wir können in Z (über der Standardsignatur) folgende Prädikate
bzw. Sätze ausdrücken.
[Prädikate . . . freie Variable / Sätze . . . geschlossene Formeln]
• x ist ein echter Teiler von y: [binäres Prädikat]
(∃z)(x ∗ z = y ∧ z 6= 1 ∧ z 6= y)
• y ist die (ganzzahlige) Lösung einer quadratischen Gleichung
(mit ganzzahligen Koeffizienten): [unäres Prädikat]
(∃u)(∃v)(∃w) u ∗ (y ∗ y) + v ∗ y = w
• Nicht alle Kubikzahlen sind positiv: [Satz]
¬(∀x)((∃y) x = y ∗ y ∗ y ⊃ 0 < x)
223
Beispiel
Sei F =
F1
∧
F1
= (∀x)(∀y)[P (x, y) ⊃ P (x, f (y, a))]
= (∀x)¬P (x, x)
∧ F3 wobei
F2
= (∀x)P (x, f (x, a))
F2
F3
F ist erfüllbar in N bzgl. Φ: Φ(P ) =<, Φ(f ) = +, Φ(a) = 1.
M.a.W.: J = hN, Φ, Ii ist ein Modell von F , für alle I.
Ein anderes Modell von F : J 0 = hD, Φ, Ii, wobei
D = h{0, 1}∗ , {concat}, {≺}, {0}i mit concat(s, r) = sr
und s ≺ r = ‘s ist ein echter Teilstring von r’.
Φ(P ) =≺, Φ(f ) = concat, Φ(a) = 0, I beliebig.
222
Satz: F hat keine endlichen Modelle.
Für alle Interpretationen J = hhD, F, P, Ki, Φ, Ii folgt aus
MPF (J , F ) = t dass der Gegenstandsbereich D unendlich ist.
Folgende Formeln sind gültig:
• (∀x)[P (x) ∨ ¬P (x)] bzw. auch P (x) ∨ ¬P (x)
• [(∀x)P (x) ∨ ¬(∀y)P (y)] und [(∀x)P (x) ⊃ (∃y)P (y)]
• ¬(∀x)P (x) ⊃ (∃x)¬P (x) und ¬(∃x)P (x) ⊃ (∀x)¬P (x)
• (∀x)(∀y)Q(x, y) ⊃ (∀y)(∀x)Q(x, y)
Folgende Formeln sind unerfüllbar:
• (∀x)[P (x) ∧ ¬P (x)] bzw. auch P (x) ∧ ¬P (x)
• ¬[(∀x)P (x) ∨ ¬(∀y)P (y)] und (∃x)P (x) ∧ (∀x)¬P (x)
Folgende Formeln sind erfüllbar und widerlegbar:
• (∃x)P (x) ⊃ (∀x)P (x) und P (x) ⊃ P (y)
• (∀x)P (x) ∨ (∀x)¬P (x) und (∃x)P (x) ⊃ (∀x)¬P (x)
• (∀x)(∀y)[Q(x, y) ⊃ Q(y, x)], (∀x)[(∀y)Q(x, y) ⊃ (∀y)Q(y, x)]
224
Logische Konsequenz und Implikation (PL)
Definition. Formel G ist eine logische Konsequenz der Formeln
F1 , . . . , Fn , geschrieben F1 , . . . , Fn |= G, wenn für alle J gilt:
Wenn MPF (J , Fi ) = t für 1 ≤ i ≤ n, dann gilt MPF (J , G) = t.
Für n = 0 ist |= G gleichbedeutend mit G ist gültig“.
”
Satz. (Deduktionstheorem)
F1 , . . . , Fn |= G gdw. F1 , . . . , Fn−1 |= (Fn ⊃ G)
gdw. |= (F1 ∧ . . . ∧ Fn ) ⊃ G
Beobachtung:
Keine Änderung gegenüber der Aussagenlogik!
225
Logische Äquivalenz und
Erfüllungsäquivalenz
Definition. Zwei Formel F, G ∈ PF Σ heißen (logisch) äquivalent,
wenn MPF (J , F ) = MPF (J , G) für alle I ∈ PINT Σ .
Wir schreiben dafür auch: F =PL G.
Es gilt: F =PL G gdw. F |= G und G |= F .
Definition. Zwei Formel F, G ∈ PF Σ heißen erfüllungsäquivalent,
wenn F und G beide erfüllbar oder beide unerfüllbar sind.
Wir schreiben dafür auch: F ∼e G.
Beobachtung:
Keine Änderung gegenüber der Aussagenlogik!
(Wir hätten auch Erfüllungsäquivalenz schon für Formeln ∈ AF
definieren können).
227
Beispiele zur logischen Konsequenz:
• (∀x)P (x) |= (∃y)P (y), aber (∃x)P (x) 6|= (∀y)P (y)
• P (x) |= [P (x) ∨ Q(y, y)], aber P (x) 6|= [P (y) ∨ Q(y, y)]
• (∃y)(∀x)Q(x, y) |= (∀x)(∃y)Q(x, y), aber
(∀x)(∃y)Q(x, y) 6|= (∃y)(∀x)Q(x, y)
Gegenbeispiel: J = hN, Φ, Ii, Φ(Q) =<
• (∃x)(∀y)Q(x, y) 6|= (∃y)(∀x)Q(x, y)
Gegenbeispiel: ähnlich wie J 0 , aber Φ(Q) =≤
• (∀x)F (x) |= F (x/t), für beliebige Terme t
aber im Allgemeinen: F (x) 6|= F (x/t)
226
Beispiele zu den Äquivalenzbegriffen:
• (∀x)P (x) =PL (∀y)P (y), daher auch (∀x)P (x) ∼e (∀y)P (y),
aber P (x) 6=PL P (y) und trotzdem: P (x) ∼e P (y)!
• (∀x)(∀y)Q(x, y) =PL (∀y)(∀x)Q(x, y) und
(∀x)(∀y)Q(x, y) =PL (∀x)(∀y)Q(y, x), aber Q(x, y) 6=PL Q(y, x)
• (∀x)(∃y)Q(x, y) 6=PL (∃y)(∀x)Q(x, y), aber
(∀x)(∃y)Q(x, y) ∼e (∃y)(∀x)Q(x, y)
• P (x) ∼e ¬P (x) ∼e Q(x, y) ∼e Q(y, x) ∼e (∃x)P (x) ∼e
(∀x)P (x) ∼e (∀y)P (x) ∼e P (x) ∨ Q(x, y) ∼e P (x) ∧ Q(x, y) etc.
aber natürlich sind diese Formeln nicht logisch äquivalent!
Beobachtung: Die Relation ∼e hat nur zwei Äquivalenzklassen
228
Wichtige Eigenschaften der Prädikatenlogik
• Es gibt keinen Algorithmus mit dem man die Gültigkeit (oder
die Erfüllbarkeit) von Formeln in PF entscheiden kann.
(‘Unentscheidbarkeit der PL’ — Turing, Church, 1936.)
• Es gibt (nicht terminierende) Algorithmen, die genau alle
gültigen Formeln aufzählen.
(‘Vollständigkeit der PL’ — Gödel, 1929)
• Es gibt keinen Algorithmus, der genau die in N gültigen
Formeln aufzählt.
(folgt aus ‘Unvollständigkeitssatz’ — Gödel, 1931)
229
• Jede erfüllbare Formel hat ein Modell mit
Gegenstandsbereich ω.
(‘Satz von Löwenheim-Skolem’, 1915, 1919)
Tableaux für PL
Aufgabe: Erweiterung von Tableaux von AL auf PL.
Wir benötigen geeignete Regeln zur Analyse von Quantoren:
Zur Erinnerung: t : (∀x)F , also MPF (J , (∀x)F ) = t, bedeutet:
x
F ist wahr in allen Interpretation J 0 ∼ J , daher auch
MPF (J , F (x/t)) = t für alle Terme t.
Ähnlich: f : (∃x)F =⇒ F (x/t) ist für alle t falsch.
t : (∀x)F
f : F (x/t)
f : (∃x)F
Entsprechend können wir folgende Regeln formulieren:
t : F (x/t)
für beliebige geschlossene Terme t
Problem: Wir können nicht garantieren, dass alle Elemente des
Gegenstandsbereichs durch einen Term repräsentiert werden.
231
Hilbert-Typ-Kalkül für PL
(Z.B.) Erweiterung des Hilbert-Typ-Kalkül für AL um die Axiome
11. (∀x)A(x) ⊃ A(x/t) für alle Terme t
12. (∀x)A ⊃ ¬(∃x)¬A
13. ¬(∃x)¬A ⊃ (∀x)A
A⊃B
gen
A ⊃ (∀x)B
und die Generalisierungs-Regel
wobei x 6∈ FV (A).
Wie für AL: Dieser Kalkül ist korrekt und vollständig, aber
äußerst ungünstig für automatische Beweissuche.
230
Analyse der existentiellen Quantifizierung:
MPF (J , (∃x)F ) = t bedeutet, dass F in mindestens einer
x
Interpretationen J 0 ∼ J wahr wird. (Ähnlich für f : (∀x)F )
Problem:
Wir wissen nicht, welchen Term t wir für x substituieren können.
Noch schlimmer: wir können nicht garantieren, dass es überhaupt
einen geschlossenen Term (in der Sprache zu F ) gibt, der einen
entsprechenden ‘Zeugen’ für (∃x)F repräsentiert.
Lösung: (vgl. Satz von Löwenheim-Skolem)
1. Erweiterung der Sprache um (abzählbar) unendlich viele
zusätzliche Konstanten, genannt: Parameter.
2. Bei der Zerlegung von t : (∃x)F und f : (∀x)F verlangt man,
dass der jeweilige ‘Zeuge’ für F neu ist (d.h., im Tableau noch
nicht vorkommt).
232
Beispiel
f : (∀x)P (x) ⊃ [P (a) ∧ P (f (a))]
von 1
Zeige die Gültigkeit von (∀x)P (x) ⊃ [P (a) ∧ P (f (a))].
(1)
t : (∀x)P (x)
von 1
f : (∃x)F
(2)
f : P (a) ∧ P (f (a))
t : (∀x)F
ΣP ar . . . Signatur Σ erweitert um Parameter c, d, e, . . .
t : (∀x)F und f : (∃x)F heißen γ-Formeln
f : (∀x)F und t : (∃x)F heißen δ-Formeln
γ-Regeln:
δ-Regeln:
(1)
t : (∀x)[P (x) ∨ Q(x)]
f : (∀x)[P (x) ∨ Q(x)] ⊃ [(∃x)P (x) ∨ (∀x)Q(x)]
von 1
von 1
t : P (a)
f : P (a)
von 2
von 3
(7)
(5)
t : P (f (a))
f : P (f (a))
von 2
von 3
f : (∃x)(∀y)R(x, y) ⊃ (∀y)(∃x)R(x, y)
von 1
Wid.: 5/7
(1)
t : (∃x)(∀y)R(x, y)
von 1
×
(2)
f : (∀y)(∃x)R(x, y)
von 2
Wid.: 4/6
(3)
t : (∀y)R(c, y)
von 3
×
(4)
f : (∃x)R(x, d)
von 4
234
(5)
t : R(c, d)
von 5
Wid.: 6/7
Annahme
(6)
f : R(c, d)
236
Beachte: In Zeile 5 musste ein neuer Parameter gewählt werden!
×
(7)
Beispiel
(5)
Annahme
(3)
f : F (x/t)
t : (∃x)F
(4)
t : F (x/t)
f : (∀x)F
t : F (x/c)
für beliebige geschlossene Terme t über ΣP ar
f : F (x/c)
für einen neuen Parameter c in ΣP ar
Alle anderen Regeln (auch Abschluss) sind wie für AL!
Achtung: γ-Regeln müssen i.A. auf die selbe γ-Formel öfters, mit
verschiedenen t angewendet werden. (Im Gegensatz zur δ-Regel.)
=⇒ Größe eines Tableau ist nicht beschränkbar!
(2)
f : (∃x)P (x) ∨ (∀x)Q(x)
von 3
233
(3)
f : (∃x)P (x)
von 3
Beispiel
(4)
f : (∀x)Q(x)
Annahme
(5)
von 5
Wid.: 6/9
von 7
f : Q(c)
×
t : Q(c)
(6)
(9)
von 2
von 7
t : P (c) ∨ Q(c)
t : P (c)
von 4
(7)
(8)
f : P (c)
Wid.: 8/10
(10)
×
Gute Heuristik: ‘δ vor γ’ (damit die Wahl geeigneter
‘Zeugen-Terme’ für γ-Formeln leichter fällt!)
235
Beispiel
Die Formel (∀x)(∃y)R(x, y) ⊃ (∃y)(∀x)R(x, y) ist widerlegbar.
Entsprechend kann folgendes Tableau auch nicht geschlossen
werden:
(6)
(5)
(4)
(3)
(2)
(1)
t : R(a, b)
f : (∀x)R(a, x)
t : (∃y)R(a, y)
f : (∃y)(∀x)R(x, y)
t : (∀x)(∃y)R(x, y)
f : (∀x)(∃y)R(x, y) ⊃ (∃y)(∀x)R(x, y)
von 5
von 4
von 3
von 2
von 1
von 1
Annahme
(7)
f : R(a, c)
.
..
Beachte: In Zeile 6 und 7 musste jeweils ein neuer Parameter
gewählt werden!
237
Nachweis von Konsequenzbehauptungen
(vgl. Beweise mittels Resolution)
(n)
(1)
.
..
f :G
t : Fn
t : F1
.
..
Annahme
Annahme
Annahme
.
..
Eine Konsequenzbehauptungen F1 , . . . , Fn |= G gilt
— wegen Vollständigkeit und Korrektheit — genau dann,
wenn es ein geschlossenes Tableau gibt, das wie folgt beginnt:
(n + 1)
239
Eigenschaften des Tableau-Kalküls (PL):
• Korrektheit: Besitzt eine geschlossene Formel ein
geschlossenes Tableau, so ist sie gültig.
• Vollständigkeit: Ist eine geschlossene Formel gültig, so besitzt
sie ein geschlossenes Tableau.
• Analytizität: die Expansionsregeln fügen nur Instanzen von
bereits vorhandenen Teilformeln hinzu.
• Eingeschränkter Indeterminismus: Ist eine geschlossene
Formel gültig, liefert jede Folge von Expansionsschritten ein
geschlossenes Tableaux unter folgender Bedingung:
– γ-Formeln werden so oft wie nötig expandiert,
alle Terme über ΣP ar werden dabei berücksichtigt
• Beweissuche kann optimiert werden durch Übergang zu
Free Variable Tableaux (mit ‘Skolemisierung’)
238
(2)
(1)
f : (∃x)Q(x)
t : ¬(∃x)P (x)
t : (∀x)[P (x) ∨ Q(f (x))]
Ann.
Ann.
Ann.
Beispiel. Geschlossenes Tableau für
(∀x)[P (x) ∨ Q(f (x))], ¬(∃x)P (x) |= (∃x)Q(x)
(3)
von 2
von 5
f : (∃x)P (x)
t : Q(f (c))
(4)
(7)
von 1
von 5
von 3
t : P (c) ∨ Q(f (c))
t : P (c)
f : Q(f (c))
(5)
(6)
(9)
Wid.: 7/9
von 4
×
f : P (c)
Wid.: 6/8
(8)
×
Beobachtungen:
Es gibt keine δ-Formel im Tableau.
Für die γ-Formel (1) muss in (5) ein geschlossener Term
gewählt werden =⇒ Parameter c
240
Beispiel
(2)
(1)
t : (∀x)(∀y)[R(x, y) ⊃ R(y, x)]
t : (∀x)(∀y)(∀z)[(R(x, y) ∧ R(y, z)) ⊃ R(x, z)]
Ann.
Ann.
von 4
Ann.
von 3
Ann.
f : R(c, c)
von 6
f : (∀x)R(x, x)
(5)
t : R(c, d)
t : (∃y)R(c, y)
t : (∀x)(∃y)R(x, y)
(6)
(3)
(7)
von 8
von 2
(4)
trans, sym, nontriv |= refl ,
t : R(c, d) ⊃ R(d, c)
von 1
t : (∀y)[R(c, y) ⊃ R(y, c)]
t : (∀y)(∀z)[(R(c, y) ∧ R(y, z)) ⊃ R(c, z)]
von 11
von 10
(8)
(10)
t : (R(c, d) ∧ R(d, c)) ⊃ R(c, c)
(18) f : R(d, c)
× (5/16)
(16) t : R(c, c) v. 12
von 9
t : (∀z)[(R(c, d) ∧ R(d, z)) ⊃ R(c, z)]
t : R(d, c)
(17) f : R(c, d)
× (14/18)
242
× (7/17)
(15) f : R(c, d) ∧ R(d, c) v. 12
(14)
(11)
1 : {P (c)}
244
20 : {¬P (c), Q(f (c))}
{Q(f (c)}
{}
30 : {¬Q(f (c))}
AL-Resolution auf 1 und 2 anwendbar, wenn wir 2 durch die
Instanz 20 = {¬P (c), P (f (c))} ersetzen. (Ähnlich für Klausel 3):
• cl(¬(∃x)Q(x)) = cl((∀x)¬Q(x)) = {¬Q(x)}
=⇒ Resolution auf {P (c)}, {¬P (y), Q(f (y)}, {¬Q(x)}
{z
} | {z }
| {z } |
anwenden:
1
2
3
• cl((∀y)(∃z)[P (y) ⊃ Q(z)]) = cl((∀y)(∃z)[¬P (y) ∨ Q(z)]) =
{¬P (y), Q(f (y)}, für ein neues Funktionssymbol f
• cl((∃x)P (x)) = {P (c)}, für eine neue Konstante c
Quantorenelimination ähnlich wie in Tableaux:
Beispiel: Zeige (∃x)P (x), (∀y)(∃z)[P (y) ⊃ Q(z)] |= (∃x)Q(x)
× (7/13)
(13) f : R(c, d) v. 9
(12)
(9)
Zeigen Sie mit dem Tableau-Kalkül, dass jede nicht-triviale,
symmetrische und transitive Relation auch reflexiv ist.
Also:
wobei
trans = (∀x)(∀y)(∀z)[(R(x, y) ∧ R(y, z)) ⊃ R(x, z)]
sym = (∀x)(∀y)[R(x, y) ⊃ R(y, x)]
241
nontriv = (∀x)(∃y)R(x, y)
refl = (∀x)R(x, x)
Resolution für PL
Zur Erinnerung:
Resolution ist eine zweistufige, indirekte Beweismethode:
1. Transformation von ¬F in Klauselform (KNF) cl(¬F )
2. Wiederholte Anwendung der Resolutionsregel
Wenn {} (leere Klausel) aus cl(¬F ) ableitbar ist, dann ist F gültig
(= Korrektheit der Methode).
Verallgemeinerung von AL auf PL:
• Wie sehen Klauselformen von Formeln in PF Σ aus?
• Wie erzeugt man diese?
• Wie muss die Resolutionsregel erweitert werden?
243
Transformation in Klauselform
Schritt A: Eliminiere ‘⊃’ und ziehe alle ‘¬’ nach innen
(d.h., vor die Atome) [≈ Schritt 1-2 bei AL]
Schritt B: Eliminiere ‘∃’ durch Einführung neuer Konstantenund Funktionssymbole
(‘Skolemisierung’ – nach Thoralf Skolem)
Schritt C: Eliminiere ‘∀’ (einfach weglassen)
245
Schritt D: Transformiere in KNF durch wiederholte Anwendung
der Distributivgesetze [≈ Schritt 4 bei AL]
Schritt A — Beispiel
Bringe die Formel A = ¬(∀x)(∃y)[(P (x, y) ∧ Q(y)) ⊃ R(y)] in NNF.
⇒
⇒
A ⇒
(∃x)(∀y)[¬¬(P (x, y) ∧ Q(y)) ∧ ¬R(y)]
(∃x)(∀y)¬[¬((P (x, y) ∧ Q(y)) ∨ R(y)]
(∃x)(∀y)¬[(P (x, y) ∧ Q(y)) ⊃ R(y)]
(∃x)¬(∃y)[(P (x, y) ∧ Q(y)) ⊃ R(y)]
T5
⇒
(∃x)(∀y)[(P (x, y) ∧ Q(y)) ∧ ¬R(y)]
T4
T3
T1
T6
⇒
247
Schritt A:
(T1)
(A ⊃ B) ⇒ (¬A ∨ B)
(T2) ¬(A ∧ B) ⇒ (¬A ∨ ¬B),
(T3) ¬(A ∨ B) ⇒ (¬A ∧ ¬B),
¬(∀u)A ⇒ (∃u)¬A,
¬¬A ⇒ A,
(T5)
¬(∃u)A ⇒ (∀u)¬A.
(T4)
(T6)
Wenn keine der Ersetzungsregeln (T1)–(T6) mehr anwendbar ist,
ist die Formel in Negationsnormalform (NNF).
Die NNF einer Formel ist eindeutig.
246
Regeln (T1)–(T6) erhalten logische Äquivalenz.
Genauer: Wenn F 0 die NNF von F ist so gilt F 0 =PL F .
Schritt B — Vorbereitung
Es ist günstig zunächst folgende ‘Syntax-Bereinigung’
vorzunehmen:
(Q1) verschiedene Vorkommen von Quantoren sollen verschiedene
Variablen binden
(Q2) keine Variable soll gleichzeitig gebunden und frei vorkommen
⇒
⇒
(∃y)(∀x)P (x, x)
A(x) ∧ (∀y)A(y)
(∀x)A(x) ∧ (∃y)B(y)
Q1
Q2
⇒
Q1
=⇒ entsprechende Umbenennung von Variablen: Z.B.
(∀x)A(x) ∧ (∃x)B(x)
A(x) ∧ (∀x)A(x)
(∃x)(∀x)P (x, x)
248
Schritt B — Notation
Notation:
Wir schreiben (Q1 v) @ (Q2 w) wenn (Q2 w) im Bindungsbereich
von (Q1 v) vorkommt.
D.h., es gibt Teilformeln G und H, sodass G = (Q1 v)H
und in H kommt (Q2 w) vor.
Beispiel:
A = (∀y)[(∃x)P (x, y) ∧ (∀u)(∃v)(¬R(u, y) ∨ Q(v))]
• (∀y) @ (∃x), (∀y) @ (∀u), (∀y) @ (∃v), (∀u) @ (∃v)
249
• (∃x) 6@ (∀u), (∃x) 6@ (∃v), etc.
Schritt B — Beispiel
Vollständige Skolemisierung von A =
(∃x)Q(x) ∧ (∀y)[(∃x)R(x, x) ∧ (∀u)(∃v)(¬P (u, y, v) ∨ (∃x)R(x, v))]
Syntax-Bereinigung:
(∃z)Q(z) ∧ (∀y)[(∃x)R(x, x) ∧ (∀u)(∃v)(¬P (u, y, v) ∨ (∃w)R(w, v))]
⇒ Q(a) ∧ (∀y)[(∃x)R(x, x) ∧ (∀u)(∃v)(¬P (u, y, v) ∨ (∃w)R(w, v))]
Sko
⇒ Q(a) ∧ (∀y)[R(f (y), f (y)) ∧ (∀u)(∃v)(¬P (u, y, v) ∨ (∃w)R(w, v))]
Sko
⇒ Q(a) ∧ (∀y)[R(f (y), f (y)) ∧ (∀u)(¬P (u, y, g(y, u)) ∨ (∃w)R(w, g(y, u)))]
Sko
⇒ Q(a) ∧ (∀y)[R(f (y), f (y)) ∧ (∀u)(¬P (u, y, g(y, u)) ∨ R(h(y, u), g(y, u))]
Sko
251
Schritt B:
Zu jedem Vorkommen (∃u) eines Existenzquantors in A definieren
wir einen Skolemterm tu wie folgt:
• tu = c, neue Konstante, falls (∀x) 6@ (∃u) für alle (∀x) in A.
• tu = f (x1 , . . . , xn ), für ein neues n-stelliges Funktionssymbol f
falls (∀x1 ), . . . , (∀xn ) alle Vorkommen von All-Quantoren in A
sind, für die (∀xi ) @ (∃u) gilt.
⇒
Sko
A−(∃u) (u/tu )
Transformationsregel (‘Skolemisierung’):
A
250
wobei A−(∃u) = A nach Entfernung von (∃u) aus A
Schritt B — Eigenschaften:
Terminologie:
Eine Formel A in NNF ist in Skolem-Normalform falls sich die
Regel ‘Sko’ nicht mehr auf A anwenden lässt.
Die Skolem-Normalform ist bis auf die Symbolnamen eindeutig.
Beobachtung:
Da Skolemisierung die Signatur ändert (= neue Symbole einführt)
kann dieser Transformationsschritt die logische Äquivalenz
nicht erhalten!
Aber es gilt: A ∼e B falls B eine Skolem-Normalform von A ist.
Das reicht für unsere Zwecke (indirekter Beweis):
Wir wollen ¬F als unerfüllbar nachweisen. Offensichtlich gilt:
Falls G unerfüllbar ist und ¬F ∼e G, dann ist auch ¬F unerfüllbar.
252
Schritt C:
Beobachtung:
Da nach Schritt A und B alle Variablen (eindeutig) all-quantifiziert
sind tragen diese Quantoren-Vorkommen keine Information mehr.
=⇒ alle Vorkommen der Form (∀v) einfach weglassen!
Rechtfertigung:
Schritt D:
KNF-Bildung durch wiederholte Anwendung der
Distributivgesetze
(‘Verteilung’ von ∨ über ∧).
Genau so wie für AL!
⇒ (A ∨ B) ∧ (B ∨ C)
Zur Erinnerung:
A ∨ (B ∧ C)
⇒
D1
⇒
254
[(¬P (x, f (x)) ∧ Q(x, y)) ∨ R(u)] ∧ [(¬P (x, f (x)) ∧ Q(x, y)) ∨ Q(v, v)]
[¬P (x, f (x)) ∧ Q(x, y)] ∨ R(u)
⇒
⇒
[¬P (x, f (x)) ∨ Q(v, v)] ∧ [Q(x, y) ∨ Q(v, v)]
[¬P (x, f (x)) ∨ R(u)] ∧ [Q(x, y) ∨ R(u)]
256
[¬P (x, f (x)) ∨ Q(v, v)] ∧ [Q(x, y) ∨ Q(v, v)]
KNF(A) = [¬P (x, f (x)) ∨ R(u)] ∧ [Q(x, y) ∨ R(u)] ∧
Die rechten Seiten der letzten beiden Zeilen sind bereits in KNF.
Daher:
D2
[¬P (x, f (x)) ∧ Q(x, y)] ∨ Q(v, v)
D2
Die äußeren Teilformeln können separat transformiert werden:
A
A = [¬P (x, f (x)) ∧ Q(x, y)] ∨ [R(u) ∧ Q(v, v)] ist in
Skolem-Normalform.
Schritt D — Beispiel
Dieser Transformationsschritt erhält logische Äquivalenz.
D2
D1
• (∀v)F ◦ G =PL (∀v)(F ◦ G) und F ◦ (∀v)G =PL (∀v)(F ◦ G),
für ◦ ∈ {∧, ∨}, falls v in G nicht vorkommt
(A ∧ B) ∨ C
_
(A ∨ C) ∧ (B ∨ C)
• D.h.: alle All-Quantoren können nach außen gebracht werden
253
• (∀x1 ) . . . (∀xn )F =PL ∀xπ(1) . . . (∀xπ(n) )F für jede
Permutation π über {1, . . . , n}
Schritt D — Klauselmengen
^
Li,j ,
(L1,1 ∨ · · · ∨ L1,n1 ) ∧ · · · ∧ (Lm,1 ∨ · · · ∨ Lm,nm )
Zur Erinnerung:
Die KNF der Ausgangsformel ist von der Form
bzw.
1≤i≤m 1≤j≤ni
wobei die Li,j Literale, also negierte oder unnegierte Atome sind.
Wir bevorzugen die Mengennotation
{{L1,1 , . . ., L1,n1 }, . . ., {Lm,1 , . . ., Lm,nm }}
In einer solchen Klauselmenge ist die Assoziativität, Kommutativität und Idempotenz von ∨ und ∧ implizit berücksichtigt.
255
Gesamtbeispiel:
G = [(∀x)(∃y)P (x, y) ∧ (∀u)(∀v)(P (u, v) ⊃ R(u))] ⊃ (∀z)R(z)
AF = (∀x)(∃y)P (x, y)∧(∀u)(∀v)[¬P (u, v)∨R(u)]∧(∃z)¬R(z)
G ist gültig. Daher ist F = ¬G unerfüllbar. Wir bilden cl(F ).
Schritt A:
T1−T6
⇒
AF ist die NNF von F , daher AF =PL F .
Schritt B: (Skolemisierung)
⇒ BF = (∀x)P (x, f (x)) ∧ (∀u)(∀v)[¬P (u, v) ∨ R(u)] ∧ ¬R(a)
Sko
Schritt C: ⇒ CF = P (x, f (x)) ∧ [¬P (u, v) ∨ R(u)] ∧ ¬R(a)
257
CF ist bereits in KNF. Daher ist Schritt D leer.
Die Klauselform von F lautet also:
cl(F ) = {P (x, f (x))}, {¬P (u, v), R(u)}, {¬R(a)}
Substitution, Unifikation
Eine Substitution ist eine Abbildung ρ : IVS → TΣ wobei
ρ(v) 6= v nur für endlich viele Variablen v.
Wir schreiben: ρ = {x1 ← t1 , . . . , xn ← tn }, wenn
ρ(x1 ) = t1 , . . . , ρ(xn ) = tn und ρ(v) = v für alle v 6∈ {x1 , . . . xn }.
Anstatt E(x1 /t1 ) · · · (xn /tn ) schreiben wir ρ(E).
Aufgabe zur Anwendung der Resolutionsregel:
Wir suchen Substitutionen, die die Atome A und B zweier dualer
Literale A und ¬B bzw. ¬A und B gleich machen.
Wenn ρ(A1 ) = . . . = ρ(An ) dann nennt man ρ einen Unifikator
von {A1 , . . . , An }.
Zur Erinnerung:
x, y, z, u, v, w . . . Variablensymbole
a, b, c, d . . . Konstantensymbole
259
Die Resolutionsregel für PL-Klauseln
Zur Erinnerung: Der Schluss
1 : {P (c)}
2 : {¬P (y), Q(f (y)}
20 : {¬P (c), Q(f (c))}
{Q(f (c)}
kombiniert AL-Resolution mit Instanzierung (Substitution).
Tatsächlich ist diese Kombination von AL-Resolution und
Substitution nicht nur korrekt sondern auch
(widerlegungs-)vollständig!
258
Problem: Welche Instanzen muss man in Betracht ziehen?
Wenn für jeden Resolutionsschritt der gesamte (unendliche)
Suchraum aller Substitutionen relevant ist, dann ist die Methode
kaum brauchbar!
Unifikatoren – Beispiele
• Q(a) und Q(b) nicht unifizierbar
• P (x, x) und P (y, f (y)) sind ebenfalls nicht unifizierbar
• A = P (z, x, f (y)) und B = P (u, g(u, a), u) haben unendlich
viele Unifikatoren. Z.B.
ρ1 = {z ← f (a), x ← g(f (a), a), y ← a, u ← f (a)},
ρ2 = {z ← f (g(a, a)), x ← g(f (g(a, a)), a), y ← g(a, a),
u ← f (g(a, a))},
ρ3 = {z ← f (y), x ← g(f (y), a), u ← f (y)}, . . .
Aber ρ = {z ← u, x ← g(u, a), u ← f (y)} ist kein Unifikator:
ρ(A) = P (u, g(u, a), f (y)) und ρ(B) = P (f (y), g(f (y), a), f (y))
Beobachtung:
Alle Unifikatoren von A und B kann man aus ρ3 durch weitere
Instanzierung der Terme ρ3 (v) (v ∈ IVS ) gewinnen!
260
Allgemeinster Unifikator
Definition: Es seien E und F Terme, Atome oder Literale.
E heißt allgemeiner als F — geschrieben: E ≤s F — falls F eine
Instanz von E ist, also falls ρ(E) = F für eine Substitution ρ.
Analog für Substitutionen σ, τ :
σ heißt allgemeiner als τ — geschrieben: σ ≤s τ — falls
σ(A) ≤s τ (A) für alle Atome A.
Achtung: ‘allgemeiner’ wird hier als ‘echt allgemeiner oder genauso
allgemein wie’ verstanden.
261
Definition:
ρ ist ein allgemeinster Unifikator (MGU) von {A1 , . . . , An }
falls ρ(A1 ) = . . . = ρ(An ) und ρ ≤s τ für alle Unifikatoren τ von
{A1 , . . . , An }.
Man schreibt: ρ = mgu{A1 , . . . , An }
(mgu steht für most general unifier)
Term-Gleichungssysteme
Das Finden eines (allgemeinsten) Unifikators (MGUs) ist ähnlich
dem Finden einer (allgemeinsten) Lösung eines arithmetischen
Gleichungssystems.
Beispiel: allgemeinste Unifikation von {A, B}, wobei
= P (g(g(u)), v)
A = P (g(x), f (x, z))
B
Reduktion auf das (Term-)Gleichungssystem
.
.
E1 = {g(x) = g(g(u)), v = f (x, z)}
Das bedeutet: Wir suchen eine Substitution (= Lösung) θ mit
θ(g(x)) = θ(g(g(u))), θ(v) = θ(f (x, z)),
sodass für alle anderen Lösungen η gilt: θ ≤s η.
263
Wichtige Eigenschaften der allgemeinsten Unifikation
• Allgemeinste Unifikatoren (MGUs) sind eindeutig, bis auf
Variablenumbenennungen.
Genauer: ρ = mgu{A1 , . . . , An } und ρ0 = mgu{A1 , . . . , An }
impliziert: ρ ≤s ρ0 und ρ0 ≤s ρ und daher ρ0 (A) = ν(ρ(A))
für eine Substitution ν die nur Variablennamen permutiert.
• Es gibt Unifikationsalgorithmen, die für jede Atommenge
{A1 , . . . , An } feststellen, ob diese Atome unifizierbar sind und
— im positiven Fall — eine entsprechende Substitution
ρ = mgu{A1 , . . . , An } ausgeben.
262
.
.
E1 = {g(x) = g(g(u)), v = f (x, z)}
{g(s), g(t)} ist unifizierbar gdw. {s, t} unifizierbar ist:
=⇒ E1 ist äquivalent zu
.
.
= {x = g(u), v = f (x, z)}.
E2
E2 kann als Substitution θ = {x ← g(u), v ← f (x, z)} interpretiert
werden; aber θ ist (noch) kein Unifikator: θ(A1 ) 6= θ(A2 )!
.
.
Wir müssen x = g(u) auf das System E2 − {x = g(u)} anwenden:
.
.
E3 = {x = g(u), v = f (g(u), z)}
.
In E3 ist jede Gleichung von der Form v = t, wobei die Variablen
auf den linken Seiten der Gleichungen nur einmal im ganzen
System vorkommen.
=⇒ E3 ist in gelöster Form und entspricht der Substitution:
σ = mgu{A, B} = {x ← g(u), v ← f (g(u), z)}
264
Unifikation als Term-Gleichungslösen
Ziel:
Suche MGU als allgemeinste Lösung eines
Term-Gleichungssystems E
Weg:
Schrittweise Transformation von E in gelöste Form
Terminologie
Ein Term-Gleichungssystem ist eine endliche Menge
.
.
E = {s1 = t1 , . . . , sn = tn }
wobei si , ti , für i = 1, . . . , n, Terme (∈ TΣ ) sind.
Eine Substitution θ heißt Lösung von E, wenn θ(si ) = θ(ti ) für alle
i = 1, . . . , n.
σ heißt allgemeinste Lösung von E, wenn für alle Lösungen θ
von E gilt: σ ≤s θ.
E ist in gelöster Form wenn:
1. {s1 , . . . , sn } ⊆ IVS
Nötig sind noch:
• Kriterien für Unlösbarkeit
268
Beispiel: Die Terme x und f (x) sind nicht unifizierbar.
.
Entsprechend gilt: {x = f (x)} ⇒ ⊥
E ⇒ ⊥
.
(occurs check) Wenn v = t ∈ E, wobei v ∈ IVS , v 6= t und
v ∈ V (t), dann
Beispiel: Die Terme a und f (x) sind nicht unifizierbar.
.
Entsprechend gilt: {a = f (x)} ⇒ ⊥
E ⇒ ⊥
Regeln zur Feststellung von Unlösbarkeit:
.
(clash) Wenn s = t ∈ E, wobei s und t mit verschiedenen
Funktions- oder Konstantensymbolen beginnen, dann
266
Zwei Systeme E1 und E2 heißen äquivalent, wenn sie die selbe
Menge von Lösungen besitzen.
2. jede Variable si kommt nur einmal in E vor
265
• garantierte Termination
Regeln zur Gleichungslösung
Ziel:
Reduktion von E auf gelöste Form oder ⊥ (falls unlösbar)
Regel zur Elimination von Redundanz:
.
(delete) Wenn s = s ∈ E dann
.
E ⇒ E − {s = s}
Regel zur Orientierung von Gleichungen:
.
(orient) Wenn t = v ∈ E, wobei v ∈ IVS und t 6∈ IVS dann
.
.
E ⇒ (E − {t = v}) ∪ {v = t}
267
s
t
Regel zur Entfernung gleicher Funktionssymbole:
}|
{ . z
}|
{
z
(decompose) Wenn f (s1 , . . . , sn ) = f (t1 , . . . , tn ) ∈ E, dann
Regel zur Substitution bereits bestimmter Variablen:
.
(eliminate) Wenn v = t ∈ E, wobei v ∈ IVS , v 6∈ V (t) und
.
v kommt auch in E − {v = t} vor, dann
.
.
E ⇒ ρ(E − {v = t}) ∪ {v = t},
wobei ρ = {v ← t}.
.
.
.
E ⇒ (E − {s = t}) ∪ {s1 = t1 , . . . , sn = tn }
Folgendes Beispiel macht klar, dass noch eine weitere Regel fehlt:
Beispiel (Fortsetzung)
.
.
E = {x = y, x = g(y)}
Anwendung von (eliminate):
270
v ∈ IVS , v ∈ V (E), v 6∈ V (t)
v ∈ IVS , t 6∈ IVS
• Wenn keine Regeln aus U R mehr auf System E anwendbar
sind, dann ist E entweder in gelöster Form oder ⊥.
f, g ∈ F S ∪ KS verschieden
v ∈ IVS , v 6= t, v ∈ V (t)
272
• Wenn E zu ⊥ transformierbar ist, dann ist E unlösbar.
.
.
• Wenn E zu einer gelösten Form {x1 = t1 , . . . , xn = tn }
transformierbar ist, dann ist {x1 ← t1 , . . . , xn ← tn } eine
allgemeinste Lösung von E und repräsentiert einen MGU.
• U R terminiert immer – die Regeln sind auf jedes
Term-Gleichungssystem nur endlich oft anwendbar.
Es gilt:
Unifikationstheorem
Eine anschließende Anwendung von (occurs check) liefert ⊥.
.
.
E ⇒ {y = g(y)} ∪ {x = y}
Beispiel
.
.
E = {x = y, x = g(y)} ist unlösbar:
Es existiert kein θ mit θ(x) = θ(y) und θ(x) = θ(g(y)), da ja sonst
θ(y) = θ(g(y)) gelten müsste.
Es ist aber keine der bisherigen Regeln auf E anwendbar!
.
Erst auf y = g(y) ist (occurs check) anwendbar.
269
Inferenzregelsystem U R für Unifikation
.
.
{s = s} ∪ E
(delete)
E
.
.
{f (s1 , . . . , sn ) = f (t1 , . . . , tn )} ∪ E
(decomp.)
.
.
{s1 = t1 , . . . , sn = tn } ∪ E
.
.
{t = v} ∪ E
(orient)
.
{v = t} ∪ E
.
.
{v = t} ∪ E
(eliminate)
.
{v = t} ∪ ({v ← t}(E))
.
.
{f (s1 , . . . , sm ) = g(t1 , . . . , tn } ∪ E
(clash)
⊥
.
.
{v = t} ∪ E
(occurs check)
⊥
271
Beispiel
Wir verwenden U R um die Atome A = P (g(a), x, g(x)) und
B = P (u, f (u, v), w) zu unifizieren.
Das entsprechende Term-Gleichungssystem lautet:
.
.
.
E = {g(a) = u, x = f (u, v), g(x) = w}
Wir erhalten schrittweise:
orient
.
.
.
E ⇒ {u = g(a), x = f (u, v), g(x) = w}
elim.
.
.
.
⇒ {u = g(a), x = f (g(a), v), g(x) = w}
elim.
.
.
.
⇒ {u = g(a), x = f (g(a), v), g(f (g(a), v)) = w}
.
.
.
{u = g(a), x = f (g(a), v), w = g(f (g(a), v))}
⇒
orient
Das letzte System ist in gelöster Form. Wir erhalten daraus
273
θ = mgu{A, B} = {u ← g(a), x ← f (g(a), v), w ← g(f (g(a), v))}
(Fortsetzung des Beispiels)
Es gibt zu
.
.
.
.
E = {g(b, x) = g(y, z), x = f (b), g(y, z) = u, f (b) = f (z)}
⇒
orient
.
.
.
.
{g(b, x) = g(y, z), x = f (b), u = g(y, z), f (b) = f (z)}
.
.
.
.
{x = f (b), g(b, f (b)) = g(y, z), u = g(y, z), f (b) = f (z)}
.
.
.
.
{x = f (b), g(b, f (b)) = g(y, z), u = g(y, z), b = z}
.
.
.
.
{x = f (b), g(b, f (b)) = g(y, z), u = g(y, z), z = b}
.
.
.
.
{z = b, x = f (b), g(b, f (b)) = g(y, b), u = g(y, b)}
.
.
.
.
.
{z = b, x = f (b), b = y, f (b) = b, u = g(y, b)}
⇒
elim.
clash
decoomp
⇒
orient
⇒
decomp.
⇒
elim.
⇒
⊥
auch andere Transformationsketten:
E
⇒
Das Ergebnis ist immer das selbe (Unifikationstheorem!)
275
Beispiel. Wir verwenden U R um zu testen ob
{Q(g(b, x), x), Q(g(y, z), f (b)), Q(u, f (z))} unifizierbar ist.
Ein entsprechendes Term-Gleichungssystem lautet:
.
.
.
.
E = {g(b, x) = g(y, z), x = f (b), g(y, z) = u, f (b) = f (z)}
⇒
decomp.
.
.
.
.
.
{b = y, x = z, x = f (b), g(y, z) = u, f (b) = f (z)}
.
.
.
.
.
{b = y, x = z, x = f (b), g(y, z) = u, b = z}
.
.
.
.
.
{x = z, b = y, z = f (b), g(y, z) = u, b = z}
.
.
.
.
.
{z = f (b), x = f (b), b = y, g(y, f (b)) = u, b = f (b)}
Beachte: Wir haben jeweils das erste bzw. zweite Argument des
ersten und zweiten, sowie des zweiten und dritten Atoms
gleichgesetzt. Das erste Atom wird damit auch dem dritten Atom
implizit gleichgesetzt.
E
⇒
⊥
elim.
⇒
elim.
⇒
decomp.
⇒
clash
274
Die Atome sind (paarweise, aber) nicht gemeinsam unifizierbar!
Der Resolutionskalkül
für allgemeine Klauselmengen
Zur Erinnerung:
Ziel ist die Ableitung der leeren Klausel als Nachweis der
Unerfüllbarkeit der Ausgangs-Klauselmenge.
PL-Resolution = AL-Resolution + Unifikation
Zusätzlich zu beachten:
• Variablenumbenennung
(vor jeder Anwendung der Resolutionsregel)
• Faktorisierung
(= Unifikation innerhalb von Klauseln)
276
= {Q(x), P (x)}
C2 = {¬P (f (x)), Q(x)}
?
Beispiel (Notwendigkeit der Umbenennung)
C1
– {P (x), P (f (x))} ist nicht unifizierbar:
.
– {x = f (x)} ist nicht lösbar (siehe ‘occurs check’)
Aber C2 repräsentiert
(∀x)[¬P (f (x)) ∨ Q(x)] =PL (∀y)[¬P (f (y)) ∨ Q(y)]
Wir müssen das Paar C1 , C20 = {¬P (f (y)), Q(y)} testen:
– {P (x), P (f (y))} ist unifizierbar:
.
– Die Lösung {x = f (y)} repräsentiert den MGU σ = {x ← f (y)}
Entsprechend ergibt sich folgende Inferenz (Resolutionsschritt):
277
C2 = {¬P (u), ¬P (v)}
Variante C20
C1
σ
σ
{Q(f (y)), P (f (y))}
{¬P (f (y)), Q(y)}
{Q(f (y)), Q(y)}
Motivation der Faktorisierung:
C1 = {P (x), P (y)}
Beachte: {C1 , C2 } ist unerfüllbar. C1 , C2 sind variablenfremd, aber
{} ist nicht durch ‘binäre’ Resolution ableitbar!
C3
= {P (x), ¬P (v)}
= {P (y), ¬P (v)}
C6
C4
=
=
{P (x), ¬P (u)}
{P (y), ¬P (u)}
Es gibt nur folgende Resolventen:
C5
Beobachtung: C3 – C6 sind Varianten von einander.
=⇒ Es gibt bis auf Umbenennung nur einen Resolventen C3 .
In der nächsten Generation:
C7 = {P (y), P (z)} von C10 = {P (x), P (z)} und C3
Auch alle weiteren Resolventen sind ebenfalls nur Varianten bereits
vorhandener Klauseln!
279
Beispiel (Umbenennung immer notwendig)
ohne Umbenennung (hier: korrekt, aber unzureichend!):
{¬P (f (y)), R(z, y)}
{R(x, y), P (x)}
σ
σ
{R(f (y), y), P (f (y))}
{¬P (f (y)), R(z, y)}
{R(f (y), y), R(z, y)}
wobei σ = mgu{P (x), P (f (y))} = {x ← f (y)}
mit Umbenennung (korrekt und hinreichend allgemein):
{¬P (f (y)), R(z, y)}
{R(x, u), P (x)}
σ
σ
{R(f (y), u), P (f (y))}
{¬P (f (y)), R(z, y)}
{R(f (y), u), R(z, y)}
{R(f (y), u), R(z, y)} ist allgemeiner als {R(f (y), y), R(z, y)}
=⇒ es sind immer variablenfremde Varianten zu resolvieren!
278
C2 = {¬P (u), ¬P (v)}
Lösung des Problems: Unifikation auch innerhalb von Klauseln
C1 = {P (x), P (y)}
Beachte: Aus C1 folgt bereits {P (x)}, aus C2 folgt bereits {¬P (u)}:
=⇒ Wende σ = mgu{P (x), P (y)} = {x ← y} auf C1 an.
Wende ρ = mgu{P (u), P (v)} = {u ← v} auf C2 an.
Die resultierenden Klauseln heißen Faktoren.
{}
{¬P (u), ¬P (v)}
ρ
{¬P (v)}
θ
{¬P (v)}
Leere Klausel durch Faktorisierung + AL-Resolution ableitbar:
{P (x), P (y)}
σ
{P (y)}
θ
{P (v)}
wobei θ = mgu{P (y), P (v)} = {y ← v}
Beachte:
Auch {{P (x), P (a)}, {¬P (u), ¬P (a)}} benötigt Faktorisierung.
280
Faktor, binärer Resolvent
Definition:
Die Klausel σ(C) heißt Faktor von Klausel C falls σ = mgu(D) für
eine Teil-Klausel D ⊆ C.
Beachte: Jede Klausel ist auch ein Faktor von sich selbst!
(= Randfall: Unifikation einer Singleton-Teil-Klausel)
.
Es seien C und D Klauseln die modulo Unifikation duale Literale
.
.
enthalten; d.h. C = C 0 ∪ {A} und D = D 0 ∪ {¬A0 }, wobei A und
A0 unifizierbar sind. Die binäre (PL-)Resolutionsregel lautet:
.
C 0 ∪ {A}
{¬A0 } ∪ D 0
θ(C 0 ∪ D 0 )
wobei θ = mgu{A, A0 }.
θ(C 0 ∪ D 0 ) heißt binärer Resolvent der Elternklauseln C und D.
Beispiel: Die Klauseln {P (x, g(y)), ¬P (f (y), x)} und
{¬P (f (u), v), P (u, u)} haben zwei binäre Resolventen:
{P (x, g(y)), ¬P (f (y), x)} {¬P (f (u), v), P (u, u)}
σ
{¬P (f (y), f (u)), P (u, u)}
mit σ = mgu{P (x, g(y)), P (f (u), v)} = {x ← f (u), v ← g(y)},
und
{P (x, g(y)), ¬P (f (y), x)} {¬P (f (u), v), P (u, u)}
ρ
{P (f (y), g(y)), ¬P (f (f (y)), v)}
mit ρ = mgu{P (f (y), x), P (u, u)} = {u ← f (y), x ← f (y)}
282
Resolutionsableitung
281
Robinson-Resolvent
.
Sei Π eine Klauselmenge.
Eine (Robinson-)Resolutionsableitung von Km aus Π ist eine
Folge von Klauseln
.
284
Wir schreiben Resolutionsableitungen auch in Baumform.
Eine Resolutionsableitung von {} aus Π heißt
Resolutionswiderlegung von Π.
• K` ist ein Robinson-Resolvent von variablenfremden
Varianten der (Eltern-)Klauseln Ki und Kj mit i, j < `.
• entweder K` ist eine Variante einer Klausel ∈ Π
(Kurzschreibweise: K` ∈0 Π),
sodass für alle 1 ≤ ` ≤ m gilt:
K1 , . . . , Km
Binäre Resolution und Faktorisierung lassen sich zu einer Regel
kombinieren:
C 0 ∪ {A , . . . , A }
{¬A10 , . . . , ¬An0 } ∪ D 0
1
m
θ(C 0 ∪ D 0 )
wobei θ = mgu{A1 , . . . , Am , A10 , . . . , An0 }.
θ(A1 ) = θ(A10 ) = θ(A2 ) = . . . = θ(An0 ) heißt resolviertes Atom.
θ(C 0 ∪ D 0 ) heißt Robinson-Resolvent von C und D.
(Nach John Alan Robinson, Erfinder des Resolutionsverfahrens.)
• Jeder binäre Resolvent ist auch ein Robinson-Resolvent.
• Robinson-Resolution ist zielgerichteter als binäre Resolution +
Faktorisierung:
Nicht alle Faktoren führen zu (binären) Resolventen.
283
Beispiel
Eine alternative Resolutionswiderlegung von Π:
Beispiel (Fortsetzung)
mit MGU σ = {x ← f (u), y ← f (u)},
resolviertes Atom: P (f (u))
288
• In der Praxis sind diverse (Beweis-)Strategien und
Redundanzeliminationen von großer Bedeutung
• Keine Axiome, eine Regel mit Unifikation als Sub-Routine;
gut automatisierbar
• Vollständigkeit: Relevant ist nur
Widerlegungsvollständigkeit: Aus unerfüllbaren Klauselmengen
ist die leere Klausel ableitbar
• Korrektheit: aus Π abgeleitete Klauseln folgen logisch aus Π
• Indirektes Verfahren: Suche nach Widerlegung
• Zweistufiges Verfahren:
KNF-Transformation (mit Skolemisierung)
+ Resolution (= AL-Resolution mit Unifikation)
• Basisobjekte: PL-Klauseln
Eigenschaften des Resolutionskalküls (PL)
286
resolviertes Atom: P (f (f (c)))
7. {} Robinson-Resolvent von 5, 6; mit MGU θ = {z ← c}
6. {¬P (f (f (z))} ∈0 Π
MGU ρ = {u ← c, v ← c}, resolviertes Atom: P (c)
5. {P (f (f (c)))} Robinson-Resolvent von 3, 4;
4. {P (c)} ∈0 Π
3. {¬P (u), ¬P (v), P (f (f (u)))} Robinson-Resolvent von 1, 2;
2. {¬P (u), ¬P (v), P (f (u))} ∈0 Π
1. {¬P (x), ¬P (y), P (f (x))} ∈0 Π
Π = {{P (c)}, {¬P (x), ¬P (y), P (f (x))}, {¬P (f (f (x))}} ist
unerfüllbar.
Resolutionswiderlegung:
1. {P (c)} ∈0 Π
2. {¬P (x), ¬P (y), P (f (x))} ∈0 Π
3. {P (f (c))} Robinson-Resolvent von 1, 2; MGU σ = {x ← c, y ← c}
resolviertes Atom: P (c)
4. {P (f (f (c)))} Robinson-Resolvent von 2, 3;
θ
MGU ρ = {x ← f (c), y ← f (c)}, resolviertes Atom: P (f (c))
5. {¬P (f (f (z))} ∈0 Π
6. {} Robinson-Resolvent von 4, 5; MGU θ = {z ← c}
285
resolviertes Atom: P (f (f (c)))
Beispiel (Fortsetzung)
{¬P (f (f (z)))}
Die erste Resolutionswiderlegung von Π in Baumform:
{P (c)}
{}
{¬P (x), ¬P (y), P (f (x))}
σ
{P (f (c))}
ρ
{P (f (f (c)))}
Die verwendeten MGUs:
σ = {x ← c, y ← c}
ρ = {x ← f (c), y ← f (c)}
θ = {z ← c}
287
Gesamtbeispiel zum Resolutionsverfahren (Forts.)
• cl(trans) = cl((∀x)(∀y)(∀z)[¬(R(x, y) ∧ R(y, z)) ∨ R(x, z)])
= {{¬R(x, y), ¬R(y, z), R(x, z)}}
Transformation in Klauselform:
Zeigen Sie mit dem Resolutionskalkül, dass jede nicht-triviale,
symmetrische und transitive Relation auch reflexiv ist.
Gesamtbeispiel zum Resolutionsverfahren
Also:
trans, sym, nontriv |= refl ,
292
θ = {z ← c}
σ = {v ← z, u ← z}
γ = {x ← z, y ← f (z)}
ρ = {x ← z, y ← f (z)}
wobei Ctrans = {¬R(x, y), ¬R(y, u), R(x, u)} und
{}
{R(z, f (z))}
Ctrans
γ
{¬R(x, y), R(y, x)} {R(z, f (z))}
{¬R(f (z), u), R(z, u)}
ρ
Variante
{R(f (z), z)}
{¬R(f (v), u), R(v, u)}
σ
{R(z, z)}
{¬R(c, c)}
Gesamtbeispiel zum Resolutionsverfahren (Baumform)
290
Wir erhalten die Klauselmenge Π = {C1 , C2 , C3 , C4 }, mit
C1 = {¬R(x, y), ¬R(y, z)), R(x, z)}
C2 = {¬R(x, y), R(y, x)}
C3 = {R(x, f (x))}
C4 = {¬R(c, c)}
• cl(¬refl) = cl(¬(∀x)R(x, x)) = cl((∃x)¬R(x, x)) = {{¬R(c, c)}}
• cl(nontriv) = cl((∀x)R(x, f (x))) = {{R(x, f (x))}}
• cl(sym) = cl((∀x)(∀y)[¬R(x, y) ∨ R(y, x)])
= {{¬R(x, y), R(y, x)}}
wobei
trans = (∀x)(∀y)(∀z)[(R(x, y) ∧ R(y, z)) ⊃ R(x, z)]
sym = (∀x)(∀y)[R(x, y) ⊃ R(y, x)]
nontriv = (∀x)(∃y)R(x, y)
refl = (∀x)R(x, x)
289
Gesamtbeispiel zum Resolutionsverfahren (Forts.)
Resolutionswiderlegung von Π:
1. {¬R(x, y), R(y, x)} ∈0 Π
2. {R(z, f (z))} ∈0 Π
3. {R(f (z), z)} von 1,2; MGU: {x ← z, y ← f (z)}
4. {¬R(x, y), ¬R(y, u), R(x, u)} ∈0 Π
5. {¬R(f (z), u), R(z, u)} von 2,4; MGU: {x ← z, y ← f (z)}
50 . {¬R(f (v), u), R(v, u)} Variante von 5
6. {R(z, z)} von 3,5’; MGU: {v ← z, u ← z}
7. {¬R(c, c)} ∈0 Π
8. {} von 6,7; MGU: {z ← c}
291
θ