¨Ubungen Naturwissenschaftliche Grundlagen – Physik – 10
Werbung
Prof. Dr. Mergel
C. Notthoff
H.Gollisch
Fachbereich Physik
Übungen Naturwissenschaftliche Grundlagen – Physik –
10.Übung, 25.06.08
Bitte bis zum 02.07.08 bearbeiten. !! Keine Abgabe !!
Die Lösung wir am Donnerstag Abend ins Netz gestellt.
http://www.uni-due.de/ddph/NWG2008.shtml
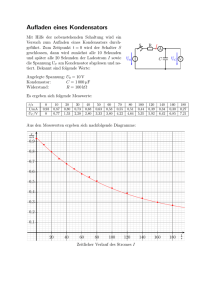
Aufgabe 1: Entladen eines Kondensators über einen Widerstand:
Zunächst wird der Kondensator (C = 1000 µF ) mit einer Spannung von U0 = 5 V
vollständig geladen. Im Anschluß wird der Kondensator entsprechend der Abbildung
über einen Widerstand R = 10 kΩ entladen. Berechnen Sie den zeitlichen Verlauf
des Entladestrom durch den Widerstand R und der Spannung am Kondensator und
skizzieren Sie diese, wenn zur Zeit t = 0 s der Schalter S geschlossen wird.
Tip: dtd (exp{a · t}) = a exp{a · t}
Lösung:
Nach schliessen des Schalters muss die Summe der beiden Spannungen UR = RI
verschwinden:
und UC = Q
C
Q
RI + C = 0.
erhalten wir also die Differentialgleichung
Mit I = dQ
dt
˙
I
1
˙
RI + C = 0 (1) oder II = − RC
, die durch den Ansatz:
I(t) = I0 exp{−τ · t} gelöst werden kann:
Einsetzen in (1) liefert
1
I0 exp{−τ · t} = RC τ I0 exp{−τ · t} ⇒ τ = RC
I0 ergibt sich aus der Anfangsbedingung:
I0 = R0 · U0 .
Analog kann U (t) bestimmt werden.
I = UR = −C · dU
dt
Damit ergibt sich U (t) zu
U (t) = U0 exp{−τ · t}.
(5)
Prof. Dr. Mergel
C. Notthoff
H.Gollisch
Fachbereich Physik
Übungen Naturwissenschaftliche Grundlagen – Physik –
10.Übung, 25.06.08
Bitte bis zum 02.07.08 bearbeiten. !! Keine Abgabe !!
Die Lösung wir am Donnerstag Abend ins Netz gestellt.
http://www.uni-due.de/ddph/NWG2008.shtml
Aufgabe 2: Laden eines Kondensators mit einer Konstantstromquelle:
Skizzieren Sie den zeitlichen Verlauf der Spannung am Kondensator in einem RCGlied, wenn eine konstant Stromquelle mit I = 10 mA angeschlossen wird und der
Kondensator zunächst vollständig entladen ist. Welche Spannung wird nach t = 10 s
erreicht?
Lösung:
Es gilt Q = CU ⇒ U =
Q
C
und dieses Differenziert
I
Q
I ·t
dU
=
bzw. U (t) =
=
dt
C
C
C
Damit ist die änderung der Spannung am Kondensator eine Grade mit der Steigung CI .
10 mA
Nach 10 s wird eine Spannung von U (t = 10 s) = 1000
= 10 V erreicht.
µF
(5)
Prof. Dr. Mergel
C. Notthoff
H.Gollisch
Fachbereich Physik
Übungen Naturwissenschaftliche Grundlagen – Physik –
10.Übung, 25.06.08
Bitte bis zum 02.07.08 bearbeiten. !! Keine Abgabe !!
Die Lösung wir am Donnerstag Abend ins Netz gestellt.
http://www.uni-due.de/ddph/NWG2008.shtml
Aufgabe 3: Entladen einer Spule über einen Widerstand:
Die Abbildung zeigt ein LR-Glied, welches in der Lage ist, beim Öffnen des Schalters
S sehr hohe Spannungen durch Selbstinduktion zu erzeugen. Dieses Prinzip findet
z.B. im Starter von Leuchtstoff-Lampen seine Anwendung.
Berechnen Sie den zeitlichen Verlauf der Spannung am Widerstand, wenn der Schalter
S zur Zeit t = 0 s geöffnet wird und skizzieren Sie den Verlauf.
U0 = 5 V , R = 10 M Ω , RL = 10 kΩ , und L = 0, 2 H ([L] = 1 VAs = 1 H)
Lösung:
Solange der Schalter S geschlossen ist fließt der Gesamtstrom Ig = RU0g = U0 RRLL+R
.
R
Der größte Teil fließt jedoch durch die Spule:
IL = RUL0 = 0, 5 mA (Parallelschaltung)
Wird der Schalter geöffnet fließt der Strom IL zunächst weiter und klingt Exponentiell ab. Es gilt
L
t}; mit I0 = RUL0 = IL .
L dIdtL = −(R + RL )IL ⇒ I(t) = I0 exp{− R+R
L
Da jetzt R und L in Reihe geschaltet sind muss der Strom in umgekehrter Richtung durch R fließen. Daher gilt für die Spannung am Widerstand U = RI =
L
−U0 RRL exp{− R∗R
t}
L
(5)