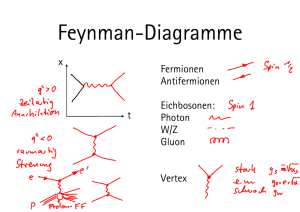
Bjorken-Skalenvariable x
Werbung

Kerne und Teilchen Physik VI Vorlesung # 08 6.5.2010 „Verlockend ist der äußre Schein, der Weise dringet tiefer ein“ (W. Busch) Guido Drexlin, Institut für Experimentelle Kernphysik Nukleonen - Streuung an Partonen - Strukturfunktionen im Partonenmodell - Callan-Gross Relation - Partonverteilungen (pdf) - Impulsverteilung des Nukleons - Gluonen & Masse des Nukleons KIT – University of the State of Baden-Württemberg and National Research Center of the Helmholtz Association www.kit.edu Nukleonen: Formfaktoren & Resonanzen Sachs-Formfaktoren des Nukleons: elektrischer (GE) & magnetischer (GM) Formfaktor des Nukleons - Q2 = 0: Proton: GE(0) = 1, GM(0) = 2.79, Neutron: GE(0) = 1, GM(0) = -1.91 anomale magnetische Momente gProton = 5.58, gNeutron = -3.82 - aus Q2-Abhängigkeit von G Ladungsverteilung r(r) der Nukleonen p, n Dipolformaktoren G(Q2): 2 2 2 W M 2 M Q 1 2 G(Q ) (1 1.41 Q 2 [GeV 2c 2 ]) 2 ´Kontinuum´ exponentieller Abfall r(r) qdr. Ladungsradius r ~ 0.8 fm Resonanzen: tiefinelastische Elektronstreuung Resonanzen 2M Q 2 0 Nukleon wird angeregt (D-Resonanz) 2 11.5.2010 G. Drexlin – VL08 W KIT-IEKP Nukleonen: tiefinelastische Streuung große invariante Masse W : - doppelt differentieller Wq. d2s/dW dE´ des e- wird unabhängig von Q2 - Streuung an punktförmigen Konstituenten des Nukleons Bjorken-Skalenvariable x : Hadronen 2 Q - Maß der Inelastizität der Streuung Proton ´bricht x auf´ 2M - elastisch: x = 1, inelastisch: 0 < x < 1 dimensionslose Strukturfunktionen : = Fouriertransformierte der Ladungsverteilung P´ p´ - magnetische Wechselwirkung: F1 ( x, Q 2 ) Mc 2 W1 (Q 2 , ) q P=(M,0) - elektrische Wechselwirkung: W > 2.5 GeV F2 ( x, Q ) W2 (Q , ) 2 2 Q2 Skaleninvarianz: F1, F2 unabhg. von Streuung an punktförmigen Partonen 3 11.5.2010 G. Drexlin – VL08 p Elektron Proton KIT-IEKP Partonen Parton-Modell des Nukleons R. Feynman (1969): - die inelastische ep-Streuung lässt sich darstellen als eine inkohärente Überlagerung von elastischen Elektron-Parton-Wechselwirkungen d.h. Stoßzeit des Elektrons ist kleiner als Wechselwirkungszeit der Partonen - kurze „Belichtungszeit“: Partonen sind in ihrem Zustand quasi „eingefroren“ spätere QCD-Wechselwirkung der Partonen lässt das Nukleon zerplatzen e 2 Q x X Bjorken-Variable x: 2M g (Hadronen) x = Bruchteil des Viererimpulses des Nukleons, der vom Parton Parton beim Stoßprozess getragen wird e bessere Diskussion der Kinematik durch Übergang vom Laborsystem Laborin das Breit-System Nukleon system 4 11.5.2010 G. Drexlin – VL08 KIT-IEKP Streuung an Partonen Kinematik im Breit-System: - in diesem schnell bewegten System sind die transversalen Impulse & Ruhemassen der Partonen vernachlässigbar [damit eigentlich: x = Anteil am longitudinalen Impuls des Nukleons] Gregory - das virtuelle Photon g überträgt nur Impuls, aber keine Energie Breit → q = (0, q) = (0, 2 x∙P) - das Parton wird zurückgestreut e wie an einer festen Wand Parton -x∙P 2x∙P (x∙P → -x∙P) „brick wall frame“ x∙P g P e B Nukleon2 (1-x)∙P Q Rest Nukleon Auflösung Breitsystem 5 11.5.2010 G. Drexlin – VL08 KIT-IEKP das Parton-Modell Nukleonen sind aus verschiedenen Quarktypen f mit der elektrischen Ladung zf ∙ e aufgebaut, Wq. für elektromagnet. Streuung ~ (zf)2 Proton uud Neutron udd Quantenzahlen durch ´Valenzquarks´ gegeben Nukleonen sind qqq Bindungszustände mit Spin s = ½ Ladung der Quarks Q(up) = +2/3, Q(down) = -1/3, da Baryonen D++ (uuu) mit Q = +2, D- (ddd) mit Q = -1 +2/3 e : 1/ 3 e : u (up ) d ( down ) c ( charm ) s ( strange ) t (top ) b(bottom ) die Quarks c, t, b sind so schwer, dass sie bei den erreichbaren Werten für Q² nur eine untergeordnete Rolle spielen & deshalb auch im Folgenden nicht weiter betrachtet werden müssen 6 11.5.2010 G. Drexlin – VL08 KIT-IEKP das Parton-Modell Nukleonen sind aus verschiedenen Quarktypen f mit der elektrischen Ladung zf ∙ e aufgebaut, Wq. für elektromagnet. Streuung ~ (zf)2 Proton uud Neutron udd Quantenzahlen durch ´Valenzquarks´ gegeben Nukleonen sind qqq Bindungszustände mit Spin s = ½ Ladung der Quarks Q(up) = +2/3, Q(down) = -1/3, da Baryonen D++ (uuu) mit Q = +2, D- (ddd) mit Q = -1 für die 3 Valenzquarks des Nukleons gelten folgende Summenregeln: 3 i 1 3 i 1 7 2 2 2 2 2 1 z 1 3 3 3 2 f 2 2 2 2 2 1 1 z 3 3 3 3 2 f 11.5.2010 G. Drexlin – VL08 für das Proton für das Neutron KIT-IEKP das Parton-Modell Nukleonen sind aus verschiedenen Quarktypen f mit der elektrischen Ladung zf ∙ e aufgebaut, Wq. für elektromagnet. Streuung ~ (zf)2 die einzelne Valenz-Quarks tragen jeweils einen Impulsanteil x Impuls-Verteilungsfunktion f(x): Zahl der Quarks mit Flavour f im Impulsintervall [x, x+dx] für eine Verteilungsfunktion f(x) eines geladenen Partons gilt: 1 f ( x) dx 1 0 Normierungsbedingung 8 11.5.2010 G. Drexlin – VL08 1 a 0 x f ( x) dx N bei N Partonen tragen diese einen Anteil a des Gesamt-Impulses des Nukleons KIT-IEKP Strukturfunktionen im Parton-Modell Strukturfunktion F2(x) beschreibt die ´elektrische´ Streuung an den Ladungen der Partonen (geladene Quarks) 1 0 3 F2 ( x) dx z 2f x i 1 1 3 a 2 F ( x ) dx z f 0 2 N i 1 =1 für das Proton = 2/3 für das Neutron mit N = 3 (Quarkmodell von M. Gell-Mann): Proton: ∫ = 1/3 und Neutron ∫ = 2/9 d.h. falls nur 3 geladene Quarks existieren die experimentellen Beobachtungen liegen ca. um einen Faktor 0.5 unter den Erwartungen, falls nur geladene Quarks den Impuls tragen: geladene Partonen tragen nur ca. 50% des Nukleonen-Impulses 9 11.5.2010 G. Drexlin – VL08 KIT-IEKP das erweiterte Parton-Modell das erweiterte Partonenmodell berücksichtigt das Vorhandensein von - neutralen Teilchen, die nicht an Photonen koppeln: Gluonen - eines Sees aus virtuellen Quark-Antiquark Paaren beide Komponenten können zur Streuung beitragen einzelne Quarkflavours werden mit unterschiedlichen Verteilungen vorkommen die einzelne Valenz-Quarks tragen jeweils einen Impulsanteil x Impuls-Verteilungsfunktion qf(x): Zahl der Quarks mit Flavour f im Impulsintervall [x, x+dx] zahlreiche See-Quarks (virtuelle Quark-Antiquark Paare): _ Impuls-Verteilungsfunktion qf(x): Zahl der Anti-Quarks mit f im Impulsintervall [x, x+dx] zahlreiche neutrale Konstituenten: Gluonen Impuls-Verteilungsfunktion g(x) 10 11.5.2010 G. Drexlin – VL08 KIT-IEKP Strukturfunktionen im Parton-Modell Isospinsymmetrie: Proton und Neutron können durch Vertauschen von u- und d-Quark ineinander übergeführt werden, Normierungsrelationen: n p p n p n qup qdown qup qdown qstrange qstrange Proton (uud) Neutron (udd) q q q q q q up qup dx 2 down qdown dx 1 strange qstrangedx 0 2 up Quarks, 1 down Quark up qup dx 1 down qdown dx 2 strange qstrangedx 0 1 up Quark, 2 down Quarks Verteilungen der Valenzquarks qV (qup, qdown) und Verteilungen der Seequarks qs: - Verteilungen der Antiquarks entsprechen denen der Seequarks 11 11.5.2010 G. Drexlin – VL08 KIT-IEKP Strukturfunktionen im Parton-Modell Strukturfunktion F2(x): Summe der mit x und (zf)2 gewichteten ImpulsVerteilungen (pro Nukleon) nochmals: bei der ep Streuung wechselwirken die Elektronen mit der Ladungsverteilung der Nukleonen (bzw. dem magnetischen Moment) F2 ( x) x z q f ( x) q f ( x) 2 f f q_f(x) : Quark-Impulsverteilung qf(x) : Antiquark-Impulsverteilung f : Quarkflavours (u,d,s) Berücksichtigung der Existenz von virtuellen Seequarks (Quark-Antiquark-Paare) wichtig: s-Quarks & alle Anti-Quarks kommen nur als See-Quarks im Nukleon vor 12 11.5.2010 G. Drexlin – VL08 KIT-IEKP Strukturfunktionen im Parton-Modell Strukturfunktionen von Proton und Neutron mit un(x) = dp(x): 4 p 1 p p F ( x) x u ( x) u ( x) d ( x) d p ( x) s ( x) s ( x) 9 9 ep 2 4 n 1 n n F ( x) x u ( x) u ( x) d ( x) d n ( x) s ( x) s ( x) 9 9 en 2 für die gemittelte F2(x) Strukturfunktion des Nukleons erhält man: eN 2 F 1 ( x) F2ep ( x) F2en ( x) ~ 0, nur Seequarks 2 Valenz- & Seequarks 1 5 x u ( x) u ( x) d ( x) d ( x) s ( x) s ( x) 9 18 mittlere quadrat. Ladung der up- und down-Quarks: 5/18 drittelzahlige Quark-Ladungen 13 11.5.2010 G. Drexlin – VL08 KIT-IEKP Strukturfunktionen im Parton-Modell Vergleich der Nukleon-Strukturfunktionen in eN und N Streuung: F2 , N x x q f x q f x f F2 ( x) x z 2f q f ( x) q f ( x) Neutrinos (´s) ´sehen´ nicht die elektrische Ladung qf identische Strukturfunktionen Quark-Ladungen für up: +2/3, down -1/3 F2(x) f x 1.2 x xx x x x 0.8 Elektron Neutrino F2N 18/5∙F2eN x xx x x 0.4 x Elektron Neutrino 14 11.5.2010 G. Drexlin – VL08 0 0.2 0.4 0.6 KIT-IEKP x Callan-Gross Relation die Streuung des Elektrons erfolgt an punktförmigen Spin ½ Teilchen, durch Vergleich des Wq. mit F1(x) & F2(x) mit dem spinabhängigen Mott-Wq. 2 x F1 ( x) erhält man folgende Relation: F2 ( x) F2 ( x) 2 x F1 ( x) Callan-Gross 1.5 Relation - die Strukturfunktion F1 entsteht durch magnetische Wechselwirkung, für Spin-0 Teilchen wäre F1(x) = 0 - die Callan-Gross Relation ist für das Nukleon gut erfüllt inelastische Streuung an punktförmigen Konstituenten mit Spin s = ½ 15 11.5.2010 G. Drexlin – VL08 1.5 < Q2 < 4 GeV2 5 < Q2 < 11 GeV2 12 < Q2 < 16 GeV2 1.0 0.5 0 0.5 1 Bjorken-Variable x = Q2/2M KIT-IEKP Messung der Strukturfunktionen - Strukturfunktionen von Proton und Neutron wurden an zahlreichen Orten gemessen (z.B. am DESY mit Eproton = 800 GeV, Eelektron = 30 GeV) - da keine freien Neutronentargets existieren, benutzt man für Neutronen leichte Kerne (z.B. Deuterium) als Targets Signaturen in Detektoren HERA-Beschleuniger 16 11.5.2010 G. Drexlin – VL08 KIT-IEKP Partonverteilungen (PDFs) q q q q x = 1 für nur 1 Konstituentenquark x mit Gluonen (S ~ ½ des Impulses) See q q q q q q _ q q x = ⅓ für 3 unabhängige Quarks 17 11.5.2010 G. Drexlin – VL08 kleine x: Gluonen, Quarks & Antiquarks KIT-IEKP Partonverteilungen - Nukleonimpuls bei der Integration über alle mit den Verteilungsfunktionen gewichteten Quarkimpulsen sollte gelten: 1 N F 2 ( x) dx 1 0 experimentelle Beobachtung: 1 1 18 e, N ,N 0 F2 x dx 5 0 F2 x dx 0,5 Quarks tragen nur ~ die Hälfte des Impulses, die andere Hälfte des Impulses kommt von den Gluonen (d.h. Teilchen die keine elektromagnet. bzw. schwache Ww. ausüben) 18 11.5.2010 G. Drexlin – VL08 KIT-IEKP Partonverteilungen - Nukleonimpuls bei der Integration über alle mit den Verteilungsfunktionen gewichteten Quarkimpulsen sollte gelten: 1 N F 2 ( x) dx 1 0 experimentelle Beobachtung: 1 1 18 e, N ,N 0 F2 x dx 5 0 F2 x dx 0,5 1 x d ( x) dx 0.18 down-Quarks 0 1 x u ( x) dx 0.36 up-Quarks 0 19 11.5.2010 G. Drexlin – VL08 KIT-IEKP Partonverteilungen - Nukleonaufbau Strukturfunktionen zeigen bei hohem Q2 einen deutlichen Effekt der See-Quarks: zahlreiche Quarks mit extrem kleinem Impulsanteil x große x: Hauptbeitrag durch Valenzquarks kleine x: Hauptbeitrag durch Gluonen und durch die von ihnen erzeugten Seequarks (Abstrahlung) führt zu einem steilen Anstieg der PDF bei kleinem x Seequarks durch Gluonen: 20 11.5.2010 G. Drexlin – VL08 KIT-IEKP Partonverteilungen - Nukleonaufbau Strukturfunktionen zeigen bei hohem Q2 einen deutlichen Effekt der See-Quarks: zahlreiche Quarks mit extrem kleinem Impulsanteil x 21 11.5.2010 G. Drexlin – VL08 KIT-IEKP Partonverteilungen - Nukleonaufbau Partondichte xf Partondichte-Verteilungen (pdf – parton density function) 50 Q2 = 100 GeV2 up-Quarks Gluonen 40 Q2 = 5000 GeV2 up-Quarks Gluonen 30 Gluonen & Seequarks dominant 20 Valenzquarks dominant 10 0 10-4 10-3 10-2 10-1 Impulsanteil x 22 11.5.2010 G. Drexlin – VL08 KIT-IEKP Partonverteilungen - Nukleonaufbau Gluonen spielen eine wichtige Rolle im Aufbau des Nukleons, sie tragen ~ 50% des Impulses Gluonen wurden zuerst am DESY nachgewiesen (1979): 3-Jet events bei PETRA 23 11.5.2010 G. Drexlin – VL08 KIT-IEKP Nukleonaufbau: woher kommt MN? Wbaryonisch Masse der Nukleonen p,n Masse des Protons (uud) Proton 938.27 MeV up-Quark ~ 1.5-3 MeV down-Quark ~ 3-7 MeV Masse des Protons (QCD) Proton ~ 940 MeV Quarks - Energie ~ 270 MeV Quarks - Masse ~ 160 MeV Gluonen - Energie ~ 320 MeV Anomalie-Term ~ 190 MeV 2008: baryonische Masse resultiert zu ~95% durch QCD-Vakuum-Effekte 24 11.5.2010 G. Drexlin – VL08 KIT-IEKP