Algorithmen auf Graphen

Kapitel 9: Graphen und Graph-Algorithmen
_________________________________
Graphen: Begriffe und Definitionen
Bewertete Graphen
Graphen-Implementierungen
Tiefen- und Breitensuche
Transitive Hülle
Kürzeste Wege
Traveling Salesman-Problem
PInf II 9.20
Graphen
Ein (gerichteter) Graph ist ein Paar G = <V, E>, wobei gilt:
•
V ist eine endliche Menge von Knoten (engl. Sg.:vertex) und
•
E ist eine zweistellige Relation auf V, d.h. E ⊆ V x V. Die Elemente
von E werden Kanten (engl. Sg.: edge) genannt.
•
Gilt G’ = <V’, E’> mit V’ ⊆ V und E’ ⊆ E, so heißt G’ Teilgraph von G.
Anwendungsbeispiele:
(1) V1 = Menge aller Flughäfen in Deutschland.
E1 = { (x,y) ∈ V1 x V1 | Es gibt einen Direktflug zwischen x und y }
(2) V2 = Menge der Einwohner von Marburg
E2 = { (x,y) ∈ V2 x V2 | x kennt y }
(3) V3 = Menge der Einwohner von Marburg
E3 = { (x,y) ∈ V3 x V3 | x ist verheiratet mit y }. V3 ist Teilgraph von V2
PInf II 9.30
Bildliche Darstellung von Graphen
Sei G= <V, E>:
•
Einen Knoten v ∈ V stellt man durch einen Punkt oder durch einen
kleinen Kreis dar.
•
Eine Kante (x,y) ∈ E stellt man durch einen Pfeil vom Knoten x zum
Knoten y dar.
Beispiel:
a
d
V = { a,b,c,d,e,f,g,h}
f
E = { (a,d), (d,a), (a,b),
(b,c), (c,a), (b,e),
(a,e), (f,g), (f,f)}.
b
h
g
c
e
PInf II 9.40
Ungerichtete Graphen
• Sei G = <V,E>. Falls für jedes e ∈ E mit e = (v1,v2) gilt: e’ = (v2,v1) ∈
E (E ist symmetrisch), so heißt G ungerichteter Graph, ansonsten
gerichteter Graph.
• Bei einem ungerichteten Graphen gehört zu jedem Pfeil von x nach y
auch ein Pfeil von y nach x. Daher läßt man die Pfeil-spitzen ganz weg
und zeichnet nur ungerichtete Kanten.
Beispiel:
V = einige Städte der
Umgebung
E = { (x,y) | Es gibt eine
direkte Bahnverbindung
zwischen x und y }
Köln
5
Marburg
4
Kassel
7
Gießen
0
Bonn
Mannheim 6
2 Fulda
3
1
Frankfurt
8
Würzburg
PInf II 9.50
Pfade, Zyklen und Gewichte
• Eine Kante k = (x,y) heißt inzident zu x und y.
• Ein Pfad (oder Weg) von x nach y ist eine Folge (x=a0 , a1, ... , ap=y)
von Knoten mit (ai , ai+1 ) ∈ E. p wird die Länge des Weges von x nach
y genannt.
• In einem einfachen Pfad kommt jeder Knoten höchstens einmal vor.
• Ein Pfad der Länge p ≥ 1 von x nach x, in dem außer x kein Knoten
mehr als einmal vorkommt, heißt Zyklus.
• Ein gerichteter Graph <V, E> heißt zyklenfrei oder gerichteter
azyklischer Graph (engl: directed acyclic graph, kurz: dag), wenn er
keine Zyklen enthält.
• Im ungerichteten Fall schließt man i.a. triviale Zyklen der Form (x,x)
oder (x,y,x) aus. Ein ungerichteter Graph ist zyklenfrei, wenn es
zwischen jedem Paar von Knoten (x,y) höchstens einen Pfad (ohne
triviale Zyklen) gibt.
PInf II 9.60
Beispiele
G = <V,E> sei wie oben definiert.
• (b,c,a,d,a) ist ein Pfad von b nach a.
a
d
• Er enthält einen Zyklus: (a,d,a).
f
• (c,a,b,e) ist einfacher Pfad
von c nach e.
b
h
• (f,f,f,g) ist ein Pfad.
• (a,b,c,a) und (a,d,a) und (f,f) sind die
einzigen Zyklen.
• (a,b,e,a) ist kein Pfad und kein
Zyklus.
• <{a,b,c,e}, {(a,b), (b,c), (b,e), (a,e)}>
ist ein azyklischer Teilgraph von G.
g
c
e
PInf II 9.70
Bewertete Graphen
Ein Graph G = <V, E> kann zu einem bewerteten Graphen
G = <V, E, gw(E)> erweitert werden, wenn man eine Gewichtsfunktion
gw: E → int (oder gw: E → float/double)
hinzunimmt, die jeder Kante e ∈ E ein (positives, ganzzahliges oder
reelles) Gewicht gw(e) zuordnet.
Für einen Weg w = (x=a0 , a1,
..., ap=y) heißt
len(w) = Σi=0 p-1 gw(ai, ai+1)
die bewertete Länge von w.
Beispiel:
len (Marburg, Gießen,
Frankfurt, Mannheim) = 184
Marburg 104
Köln
5 174
30 7
Gießen
106
34
3
0
181
66
104
Bonn
Frankfurt 1
224
88 136
6
Mannheim
4 Kassel
96
2 Fulda
93
8
Würzburg
PInf II 9.80
Ungerichtete Graphen und Zusammenhang
Ungerichtete Graphen sind Spezialfälle von gerichteten Graphen.
Zusätzlich soll für ungerichtete Graphen gelten:
• G heißt zusammenhängend, wenn es zwischen je zwei
(verschiedenen) Knoten einen Weg gibt.
• Ist G nicht zusammenhängend, so zerfällt er in eine Vereinigung
zusammenhängender Komponenten (auch Zusammenhangskomponenten genannt) .
• Ein zusammenhängender
zyklenfreier Graph ist ein Baum.
f
• Eine Gruppe paarweise nicht
zusammenhängender Bäume heißt
Wald. Jeder zyklenfreie ungerichtete
Graph ist also ein Wald.
Zusammenhangskomponenten von G
d
a
b
h
g
c
e
PInf II 9.90
Zusammenhang in gerichteten Graphen
Die Definitionen für Zusammenhang und Zusammenhangskomponenten
lassen sich für gerichteten Graphen ausdehnen:
Ein gerichteter Graph G heißt stark zusammenhängend, wenn es
zwischen je zwei (verschiedenen) Knoten einen Weg gibt. Für einen
beliebigen Graphen G kann man die Menge seiner starken
Zusammenhangskomponenten betrachten. Zwei Knoten a und b
liegen in der gleichen Komponente Z, wenn sowohl ein Weg von a nach
b als auch einer von b nach a in Z existiert.
• Ein gerichteter Graph G heißt
schwach zusammenhängend,
wenn der entsprechende
ungerichtete Graph, der aus G durch
Hinzunahme aller Rückwärtskanten
entsteht, zusammenhängend ist.
a
d
f
b
h
g
Beispiel:Starke Zusammenhangskomponenten von G
c
e
PInf II 9.100
Aufspannender Baum
• Ist G ungerichtet und zusammenhängend und R ein zusammenhängender, zyklenfreier Teilgraph von G, der alle Knoten von G enthält, so
heißt R ein (auf)spannender Baum (engl.: spanning tree) von G.
Rekursiver Algorithmus SpT zur Konstruktion
des (auf)spannen-den Baums für G:
• Markiere einen beliebigen Knoten v ∈ V
• Wiederhole für alle von v ausgehenden Kanten
e = (v,v') ∈ E:
Wenn v' unmarkiert, markiere v' und führe SpT
(v') aus, sonst lösche e (und gehe zur nächsten
Kante weiter).
Graph mit aufspannendem Baum
PInf II 9.110
Repräsentation von Graphen
Für die Repräsentation eines Graphen kommen in erster Linie zwei
Datenstrukturen in Frage:
• eine Boolesche Matrix (auch Adjazenzmatrix genannt)
• eine Liste oder ein Array von Listen (für die Knoten des Graphen und
deren jeweilige Verbindungen)
Repräsentation durch eine Adjazenzmatrix:
Ein Graph G = ( V, E) ist i.W. durch die Angabe seiner Kanten E ⊆ V x V
bestimmt.
• So wie Teilmengen von V durch Boolesche Arrays dargestellt werden
können, kann man Teilmengen von V × V durch Boolesche Matrizen
(sog. Adjazenzmatrizen) darstellen.
• Voraussetzung dafür ist, daß die Menge der Knoten durch einen
ordinalen Typ repräsentiert ist.
PInf II 9.120
Graphen: Java-Deklarationen
public
public class
class AGraph
AGraph {{
String[]
knoBez;
String[] knoBez;
int
int knAnz;
knAnz;
boolean[][]
boolean[][] aMx;
aMx;
//
// alle
alle Knoten-Bezeichner
Knoten-Bezeichner
//
Anzahl
// Anzahl der
der Knoten
Knoten
//
Adjazemnzmatrix
// Adjazemnzmatrix
AGraph
AGraph (String[]
(String[] knBez,
knBez, boolean[][]
boolean[][] kanten)
kanten) {{
...
... /*
/* Konstruktor,
Konstruktor, besetzt
besetzt Knoten-Bezeichner
Knoten-Bezeichner und
und
Kanten-Matrix
Kanten-Matrix mit
mit den
den gegebenen
gegebenen Parameter-Werten
Parameter-Werten */
*/
}}
}}
Die Klasse AGraph enthält als Basis-Definitionen für die
Repräsentation von Graphen durch Adjazentmatrizen:
• ein Datenfeld knBez des Typs Array of String für die Auflistung der
Knoten-Bezeichner,
• ein Datenfeld aMx des Typs Array of Array of boolean für die
Darstellung der Adjazenzmatrix. Für diese gilt:
aMx[u][v]== true <=> (u,v) ∈ E
PInf II 9.130
Adjazenzmatrix: Beispiel
//
// Konkretisierung
Konkretisierung zum
zum vorigen
vorigen Programm
Programm
String[]
knoBez
=
{"a","b","c","d","e","f","g","h"};
String[] knoBez = {"a","b","c","d","e","f","g","h"};
boolean[][]
boolean[][] kanten
kanten ==
{{false,
{{false, true,
true, false,
false, true,
true, true,
true, false,
false, false,
false, false},
false},
{false,
false,
true,
false,
true,
false,
false,
{false, false, true, false, true, false, false, false},
false},
...
//
};
...
// usw.
usw.
};
AGraph
gBsp
=
new
AGraph
(knoBez,
kanten)
;
AGraph gBsp = new AGraph (knoBez, kanten)
;
...
...
a
d
f
b
h
g
c
e
a b c d e f g h
a
x
x x
b
x
x
c x
d x
e
f
x x
g
h
( x = True, " " = False )
PInf II 9.140
Bewertete Adjazenzmatrizen
Die Idee der Adjazenzmatrix läßt sich leicht auf bewertete Graphen
ausdehnen. Statt eines booleschen Werts speichert man das Gewicht
gw (u,v) jeder Kante an der betreffenden Position M[u,v] der Matrix M.
Man setzt z.B.:
w, falls e =(u,v) ∈ E und gw(e) = w,
M[u,v] =
0, falls u=v und e =(u,u) ∈ E ,
∞ (bzw. MAX_VALUE) sonst
{
public
public class
class BGraph
BGraph {{
String[]
knoBez;
//
String[] knoBez;
// Alle
Alle Knoten-Bezeichner
Knoten-Bezeichner
int
knAnz;
//
Anzahl
int knAnz;
// Anzahl der
der Knoten
Knoten
int[][]
bMx;
//
Matrix
mit
Gewichten
int[][] bMx;
// Matrix mit Gewichten
BGraph
BGraph (String[]
(String[] knBez,
knBez, int[][]
int[][] kanten)
kanten) {{
...
/*
Konstruktor,
besetzt
...
/* Konstruktor, besetzt knoBez,
knoBez, knAnz
knAnz und
und
bMx
mit
den
gegebenen
Werten
*/;
bMx mit den gegebenen Werten */;
}} ...
...
}..
}..
PInf II 9.150
Bewertete Adjazenzmatrix: Beispiel
BN
BN FF FD
FD GI
GI KS
KS KK
BN
--- 34
BN 00 181
181 -34
FF
181
-181 00 104
104 66
66 -FD
FD -- 104
104 00 106
106 96
96 -GI
-66
-- 174
GI
66 106
106 00
174
KS
96
0
-KS
96
0
- steht für ∞
KK
34
-- 174
34 -174 -MA
--MA 224
224 88
88 -MR
--- 30
MR -30 104
104
WÜ
136
93
-WÜ 136 93
-
00
--
MA
MA
224
224
88
88
-----
--
00
--
--
--
MR
MR WÜ
WÜ
---136
136
--
93
93
--
30
30
104
104 -----
--
00
--
-00
Ist G ein ungerichteter Graph, so ist die Matrix symmetrisch - d.h.
man kommt im Prinzip mit einer Dreiecksmatrix aus.
PInf II 9.160
Bewertete Adjazenzmatrix: Initialisierung
String[]
String[] knBez
knBez == {"Bonn",
{"Bonn", "Frankfurt",
"Frankfurt", "Fulda",
"Fulda", "Gießen",
"Gießen",
"Kassel",
"Köln",
"Mannhem",
"Marburg",
"Würzburg"};
"Kassel", "Köln", "Mannhem", "Marburg", "Würzburg"};
int[][]
int[][] kanten
kanten == {{ {0,
{0, 181,
181, M,
M, M,
M, M,
M, 34,
34, 224,
224, M,
M, M},
M},
{181,
0,
104,
66,
M,
M,
88,
M,
136},
{181, 0, 104, 66, M, M, 88, M, 136},
...
...
{M,
{M, 136,
136, 93,
93, M,
M, M,
M, M,
M, M,
M, M,
M, 0}
0} };
};
BGraph
bahnNetz
=
new
BGraph
(knBez,
BGraph bahnNetz = new BGraph (knBez, kanten);
kanten);
M steht für ∞ (genauer für:
Integer.MAX_VALUE)
4 Kassel
Marburg 104
Köln
96
7
5 174
Gießen 30
106 2 Fulda
34
3
0
181
66
104
Bonn
93
Frankfurt 1
224
88 136
8
Würzburg
Mannheim 6
PInf II 9.170
Knoten- und Kantenzugriffe
Der Zugriff auf einzelne Knoten und Kanten ist mit Hilfe einfacher
Zugriffsfunktionen möglich:.
public
public class
class BGraph
BGraph {{ ...
...
String
gibKnoBez
String gibKnoBez (int
(int k)
k) {{
return
return knoBez[k];
knoBez[k];
}}
int
int kantenW
kantenW (int
(int u,
u, int
int v)
v) {{
return
bMx[u][v];
return bMx[u][v];
}}
//
// Forts.
Forts. von
von oben
oben
//
Knoten-Zugriff
// Knoten-Zugriff
//
// Kanten-Zugriff
Kanten-Zugriff
Beispiel:
bahnNetz.gibKnoBez(3);
bahnNetz.gibKnoBez(3);
bahnNetz.kantenW
bahnNetz.kantenW (3,7);
(3,7);
//
// Ergebnis:
Ergebnis: "Gießen"
"Gießen"
//
Ergebnis:
30
// Ergebnis: 30
PInf II 9.180
Adjazenzlisten (1)
Eine zweite (weniger speicheraufwendige) Möglichkeit zur Repräsentation eines Graphen besteht darin, jedem Knoten eine Liste seiner
Nachbarknoten - ggf. mit den zugehörigen Kantengewichten - zuzuordnen. Eine solche Liste wird auch Adjazenzliste genannt.
a
d
a
b
c
d
b
c
a
a
d
e
e
f
f
f
b
h
g
c
e
e
g
g
h
PInf II 9.190
Adjazenzlisten: Klassendefinitionen (1)
ziel
class
class VerbListe
VerbListe {{
int
//
int ziel;
ziel;
// Endpunkt-Nr
Endpunkt-Nr
int
//
int gew;
gew;
// Kanten-Gewicht
Kanten-Gewicht
VerbListe
VerbListe nx;
nx; //
// Nachfolger-Referenz
Nachfolger-Referenz
VerbListe
VerbListe (int
(int z,
z, int
int w,
w, VerbListe
VerbListe v)
v) {{
ziel
ziel == z;
z; gew
gew == w;
w; nx
nx == v;
v;
}}
}}
class
class LKnoten
LKnoten {{
String
String knBez;
knBez;
VerbListe
VerbListe nachbarn;
nachbarn;
LKnoten
LKnoten (String
(String s,
s, VerbListe
VerbListe v)
v) {{
knBez
=
s;
nachbarn
=
v;
knBez = s; nachbarn = v;
}}
}}
2
4
b
5
5
d
7
e
2
gew
a
5
2
4
5
b
d
e
7
2
knBez
nachbarn
PInf II 9.200
Adjazenzlisten: Klassendefinitionen (2)
public
public class
class LGraph
LGraph {{
static
final
static final int
int maxInt
maxInt == Integer.MAX_VALUE;
Integer.MAX_VALUE;
LKnoten[]
knoten;
//
LKnoten[] knoten;
// Array
Array von
von Knoten(-Referenzen)
Knoten(-Referenzen)
int
knAnz;
int knAnz;
LGraph
LGraph (LKnoten[]
(LKnoten[] knL)
knL) {{ //
// besetzt
besetzt Nachbarlisten
Nachbarlisten
knAnz
=
knL.length;
knAnz = knL.length;
knoten
knoten == new
new LKnoten[knAnz];
LKnoten[knAnz];
for
(int
i
for (int i == 0;
0; ii << knAnz;
knAnz; i++)
i++) knoten[i]
knoten[i] == knL[i];
knL[i];
}}
int
int kantenW
kantenW (int
(int u,
u, int
int v)
v) {{ /*
/* liefert
liefert gew,
gew, falls
falls
direkte
Verbindung,
sonst
maxInt
*/
direkte Verbindung, sonst maxInt */
if
if (u
(u ==
== v)
v) return
return 0;
0;
VerbListe
vLi
VerbListe vLi == knoten[u].nachbarn;
knoten[u].nachbarn;
while
while (vLi
(vLi !=
!= null)
null) {{
if
(vLi.ziel
if (vLi.ziel ==
== v)
v) return
return vLi.gew;
vLi.gew;
vLi
=
vLi.nx;
}
vLi = vLi.nx; }
String
String gibKnoBez
gibKnoBez (int
(int k)
k) {{
return
return maxInt;
maxInt;
return
knoten[k].knBez;
return knoten[k].knBez;
}} ...
...
}} ...
...
}}
PInf II 9.210
Adjazenzliste: Anwendung
Beispiel:
LKnoten[]
LKnoten[] knoten
knoten == {{ new
new LKnoten
LKnoten ("Bonn",
("Bonn",
new
VerbListe(1,
181,
new VerbListe(1, 181,
new
new VerbListe(5,
VerbListe(5, 34,
34,
4 Kassel
new
Marburg 104
new VerbListe(6,
VerbListe(6, 224,
224,
Köln
96
null
null )))),
)))),
5 174
30 7
....
106 2 Fulda
Gießen
....
34
3
//
usw.
// usw.
0
181
66
new
new LKnoten
LKnoten ("Würzburg",
("Würzburg",
104
Bonn
new
93
Frankfurt 1
new VerbListe(1,
VerbListe(1, 136,
136,
new
VerbListe(2,
93,
224
new VerbListe(2, 93,
88 136
null
8
null )))
)))
6
Würzburg
Mannheim
};
};
LGraph
LGraph bahnNetz
bahnNetz == new
new LGraph(knoten);
LGraph(knoten);
PInf II 9.220
Verkehrsnetz als Array von Adjazenzlisten
0
Bonn
1 181
5 34
6 224
nil
1
Frankfurt
0 181
2 104
3 66
6 88
8 136
nil
2
Fulda
1 104
3 106
4 96
8 93
nil
3
Gießen
1 66
2 106
5 174
7 30
nil
4
Kassel
2 96
7 104
nil
5
Köln
0 34
3 174
nil
6
Mannheim
0 224
1 88
nil
7
Marburg
3 30
4 104
nil
8
Würzburg
1 136
2 93
nil
PInf II 9.230
Implementierung durch Listen von Listen
Eine dritte Möglichkeit zur Implementierung von Graphen besteht
darin, auch die Folge der Knoten auf eine Liste abzubilden, d.h. der
gesamte Graph wird durch eine Liste von Listen dargestellt.
a
a
b
d
b
c
e
c
a
d
a
d
f
b
h
e
e
g
c
e
f
f
g
g
h
PInf II 9.240
Graph als Liste von Listen (1)
public
public class
class LLGraph
LLGraph {{
String
grBez;
//
String grBez;
// Graph-Bezeichner
Graph-Bezeichner
LLKnoten
kn;
//
LLKnoten kn;
// Liste
Liste der
der Knoten
Knoten des
des Graphen
Graphen
int
knAnz;
int knAnz;
LLGraph
LLGraph (String
(String bez)
bez) {{ //
// erzeugt
erzeugt Graphen
Graphen namens
namens bez
bez
grBez
=
bez;
grBez = bez;
kn
kn == null;
null;
knAnz
knAnz == 0;
0;
}}
public
public LLKnoten
LLKnoten fuegeKnEin
fuegeKnEin (String
(String knBez)
knBez) {{
//
// fügt
fügt Knoten
Knoten knBez
knBez in
in die
die Liste
Liste ein
ein
kn
kn == new
new LLKnoten
LLKnoten (knBez,
(knBez, kn);
kn);
knAnz
knAnz ++;
++;
return
return kn;
kn;
}}
//
// end
end fuegeKnEin
fuegeKnEin
....
//
....
// weiter
weiter s.
s. nächste
nächste Folie
Folie
PInf II 9.250
Graph als Liste von Listen (2)
//
// Forts.
Forts. von
von voriger
voriger Folie
Folie
public
class
LLKnoten
{
public class LLKnoten {
String
String knBez;
knBez;
NbListe
//
NbListe nachbarn;
nachbarn;
// Adjazenzliste
Adjazenzliste für
für ausg.
ausg. Kanten
Kanten
LLKnoten
//
LLKnoten nxKn;
nxKn;
// Ref.
Ref. auf
auf nächsten
nächsten Knoten
Knoten
LLKnoten
LLKnoten (String
(String s,
s, LLKnoten
LLKnoten nx)
nx) {{ //
// Konstruktor
Konstruktor
knBez
=
s;
knBez = s;
nachbarn
nachbarn == null;
null;
nxKn
nxKn == nx;
nx;
}} ...
//
...
// end
end Konstruktor
Konstruktor
public
public void
void fuegeNbEin
fuegeNbEin (LLKnoten
(LLKnoten ziel,
ziel, int
int gw)
gw) {{
//
// Kante
Kante vom
vom akt.
akt. Knoten
Knoten zu
zu Kn.
Kn. ziel
ziel mit
mit Gewicht
Gewicht gw
gw
nachbarn
=
new
NbListe
(ziel,
gw,
nachbarn);
nachbarn = new NbListe (ziel, gw, nachbarn);
}} ....
//
....
// end
end fuegeNbEin
fuegeNbEin
}}
//
end
// end LLKnoten
LLKnoten
PInf II 9.260
Graph als Liste von Listen (3)
//
// Forts.
Forts. von
von voriger
voriger Folie
Folie
public
public class
class NbListe
NbListe {{
LLKnoten
//
LLKnoten kn;
kn;
// Nachbarknoten,
Nachbarknoten, Ziel
Ziel einer
einer Kante
Kante
int
gw;
//
Kantengewicht
für
diese
int gw;
// Kantengewicht für diese Kante
Kante
NbListe
//
NbListe nxKn;
nxKn;
// Referenz
Referenz auf
auf nächsten
nächsten Nachbarn
Nachbarn
NbListe
NbListe (LLKnoten
(LLKnoten zi,
zi, int
int g,
g, NbListe
NbListe nx)
nx) {{
kn
kn == zi;
zi;
gw
gw == g;
g;
nxKn
nxKn == nx;
nx;
}...
//
}...
// end
end Konstruktor
Konstruktor
}}
//
end
NbListe
// end NbListe
Anwendungsbeispiel:
LLGraph
LLGraph bNetz
bNetz == new
new LLGraph
LLGraph ("Bahnnetz");
("Bahnnetz");
LLKnoten
LLKnoten bn
bn == bNetz.fuegeKnEin
bNetz.fuegeKnEin ("Bonn");
("Bonn");
LLKnoten
f
=
bNetz.fuegeKnEin
("Frankfurt");
LLKnoten f = bNetz.fuegeKnEin ("Frankfurt"); ...
...
bn.fuegeNbEin
bn.fuegeNbEin (f,
(f, 181);
181);
f.fuegeNbEin
f.fuegeNbEin (bn,
(bn, 181);
181); ...
...
PInf II 9.270
Vergleich der Implementierungen
Alle hier betrachteten Möglichkeiten zur Implementierung von
Graphen haben ihre spezifischen Vor- und Nachteile.
Seien n = Knotenzahl und m = Kantenzahl eines Graphen G.
Vorteile
Nachteile
Adjazenzmatrix
Berechnung der
Inzidenz mit O(1)
hoher Platzbedarf und teure
Initialisierung: beide O(n2)
Adjazenzliste
Platzbedarf beträgt
nur O(n+m)
Effizienz der Kantensuche
abhängig von Knotenordnung
Liste von
Listen
Knoten lassen sich
flexibel hinzufügen/
löschen
Effizienz von Knoten- und
Kantensuche abhängig von
Listenposition
PInf II 9.280
Traversieren von Graphen
• Viele Algorithmen auf Graphen beruhen darauf, daß man alle Knoten
(oder alle Kanten) des Graphen durchläuft (den Graphen traversiert).
• Solche Traversierungen funktionieren ähnlich wie entsprechende
Baum-Traversierungen, doch muß man bei Graphen darauf achten,
daß man nicht in Endlos-Schleifen gerät, wenn der Graph Zyklen hat.
Daher markiert man bereits besuchte Knoten.
Für die Traversierung betrachten wir die folgenden Strategien: :
Tiefensuche (depth first search)
Breitensuche (breadth first search)
• Tiefensuche entspricht der Baum-Traversierung in Vorordnung,
Breitensuche derjenigen in Ebenen-Ordnung.
• Alle folgenden Algorithmen können sowohl auf gerichtete als auch auf
ungerichtete Graphen angewendet werden. Dabei setzen wir voraus,
daß alle Graphen zusammenhängend sind.
Tiefensuche (1)
PInf II 9.290
Tiefensuche läßt sich am einfachsten implementieren: Wir betrachten
sowohl eine rekursive Implementierung als auch eine mit einem Stack.
Der folgende Algorithmus Depth-First-Visit besucht alle Knoten, die
von einem Ausgangsknoten mit der Nummer k aus erreichbar sind. Wir
setzen voraus, daß zu Beginn alle Knoten unmarkiert sind.
Programmgerüst:
void
void depFVisit
depFVisit (int
(int k)
k) {{
if
(
...)
//
k
if ( ...)
// k ist
ist noch
noch nicht
nicht markiert
markiert
markiere(k);
markiere(k);
bearbeite
bearbeite (k);
(k);
for
for (( ..
.. /*
/* alle
alle i,
i, die
die Nachbarn
Nachbarn von
von kk sind
sind */
*/ ))
depFVisit
(i);
depFVisit (i);
}}
Konkreter Code hängt von der
Graph-Implementierung ab.
Tiefensuche (2)
PInf II 9.300
Zum Markieren benutzen wir ein Feld der Länge knAnz. Als Typ der
Feldelemente wählen wir int, um den Algorithmus leicht auf
Mehrfachbesuche erweitern zu können.
void
void depFVisit
depFVisit (int
(int k)
k) {{
int[]
marken
=
new
int[] marken = new int
int [knAnz];
[knAnz];
for
(int
i
=
0;
i
<
for (int i = 0; i < knAnz;
knAnz; i++)
i++) marken
marken [i]
[i] == 0;
0;
//
initialisiere
// initialisiere Marken
Marken
rekDFVisit
rekDFVisit (marken,
(marken, k);
k);
}}
void
void rekDFVisit
rekDFVisit (int[]
(int[] marken,
marken, int
int k)
k) {{
if
if (marken[k]
(marken[k] << 1)
1) {{ //
// kk ist
ist noch
noch nicht
nicht markiert
markiert
marken
[k]
++;
marken [k] ++;
System.out.println
System.out.println (knoten[k].knBez);
(knoten[k].knBez);
//
// bezieht
bezieht sich
sich auf
auf Klasse
Klasse LGraph
LGraph
for
for (int
(int ii == 0;
0; ii << knAnz;
knAnz; i++)
i++)
if
if (kantenW
(kantenW (k,
(k, i)
i) << maxInt)
maxInt) //
// ii ist
ist Nachbar
Nachbar von
von kk
rekDFVisit
rekDFVisit (marken,
(marken, i);
i);
}}
}}
PInf II 9.310
Tiefensuche (Beispiel)
Marburg
Köln
5
4
Kassel
7
Gießen
2
3
Fulda
Frankfurt
Mannheim
depFVisit (0)
zur Ausgabe aller Städte in der
folgenden Reihenfolge :
0
Bonn
Falls wir die Nachbarn der
Knoten in alphabetischer Reihenfolge erzeugen, führt der Aufruf
1
8
6
Würzburg
Bonn, Frankfurt, Fulda, Gießen,
Köln, Marburg, Kassel,
Würzburg, Mannheim.
Der Aufruf
depFVisit (2)
führt zur Ausgabe :
Fulda, Frankfurt, Bonn, Köln, Gießen, Marburg, Kassel, Mannheim,
Würzburg.
Tiefensuche mit Stack
void
void dFSVisit
dFSVisit (int
(int k)
k) {{
Stack
st
=
new
Stack(knAnz);
Stack st = new Stack(knAnz);
markiere(k);
markiere(k); bearbeite
bearbeite (k);
(k);
st.push(k);
st.push(k);
while
Marburg
while (!
(! st.istLeer())
st.istLeer()) {{
Köln
int
akt
int akt == st.top();
st.top();
7
5
Gießen
if
if (( ...
... )) {{
/*
/* es
es existiert
existiert noch
noch nicht
nicht
3
mark.
mark. Nachbar
Nachbar jj von
von akt
akt */
*/
0
akt
akt == j;
j;
Bonn
Frankfurt 1
markiere(akt);
markiere(akt);
bearbeite(akt);
bearbeite(akt);
st.push(akt);
st.push(akt);
}}
Mannheim 6
else
st.pop();
else st.pop();
}}
}}
PInf II 9.320
4
Kassel
2
Fulda
8
Würzburg
Wenn Nachbarn in alphabetischer Reihenfolge erzeugt werden, führt
dFSVisit (7) zu Bearbeitung und push-Operationen in folgender
Reihenfolge: Marburg, Gießen, Frankfurt , Bonn, Köln, Mannheim, Fulda,
Kassel, Würzburg.
Breitensuche mit Queue
PInf II 9.330
Ähnlich wie bei der Baum-Traversierung in Ebenen-Ordnung wird eine
Warteschlange als Hilfsspeicher verwendet.
void
void bFVisit
bFVisit (int
(int k)
k) {{
Queue
q
=
new
Queue(knAnz);
Marburg
Queue q = new Queue(knAnz);
Köln
markiere(k);
markiere(k);
7
5
Gießen
q.enQueue(k);
q.enQueue(k);
while
while (!
(! q.istLeer())
q.istLeer()) {{
3
int
akt
0
int akt == q.top();
q.top();
q.deQueue();
q.deQueue();
Bonn
Frankfurt 1
bearbeite(akt);
bearbeite(akt);
for
(
/*
alle
noch
nicht
for ( /* alle noch nicht
mark.
mark. Nachbarn
Nachbarn jj von
von akt
akt */
*/ ))
Mannheim 6
{{ markiere(j);
markiere(j);
q.enQueue(j);
q.enQueue(j); }}
}}
4
Kassel
2
Fulda
8
Würzburg
}}
Wenn Nachbarn in alphabetischer Reihenfolge erzeugt werden, führt
BFVisit(Marburg) zur Reihenfolge:
Marburg, Gießen, Kassel, Frankfurt, Fulda, Köln, Bonn, Mannheim,
Würzburg.
Breitensuche mit Queue: Code
PInf II 9.340
Für die Markierung wird wieder ein int-Array Marken der Länge knAnz
verwendet:
void
void bFVisit
bFVisit (int
(int k)
k) {{
int[]
marken
=
new
int[] marken = new int
int [knAnz];
[knAnz];
for
(int
i
=
0;
i
<
for (int i = 0; i < knAnz;
knAnz; i++)
i++) marken[i]
marken[i] == 0;
0;
//
initialisiere
Marken
// initialisiere Marken
Queue
Queue qq == new
new Queue(knAnz);
Queue(knAnz);
marken[k]
++;
marken[k] ++;
q.enQueue(k);
q.enQueue(k);
while
while (!
(! q.istLeer())
q.istLeer()) {{
int
akt
int akt == q.top();
q.top();
q.deQueue();
q.deQueue();
System.out.println
System.out.println (knoten[akt].knBez);
(knoten[akt].knBez);
for
for (int
(int jj == 0;
0; jj << knAnz;
knAnz; j++)
j++)
if
if (kantenW(akt,
(kantenW(akt, j)
j) << maxInt
maxInt &&
&& marken[j]
marken[j] << 1)
1)
{{ marken[j]
marken[j] ++;
++; q.enQueue(j);
q.enQueue(j); }}
}}
}}
PInf II 9.350
Transitive Hülle
Eine zweistellige Relation R auf einer Menge V heißt transitiv, falls gilt :
∀ x, y, z ∈V : (x,y) ∈ R und (y,z) ∈ R → (x,z) ∈ R.
Die transitive Hülle t(R) einer zweistelligen Relation R auf V ist die
kleinste Relation Q, für die gilt: Q ist transitiv und R ⊆ Q.
Faßt man R als Kantenmenge eines Graphen G über V auf, so sei
t(G) = (V, t(R)) und es gilt:
• Es gibt in eine Kante (x,y) ∈ t(R) ↔ in G existiert ein Pfad von x nach y.
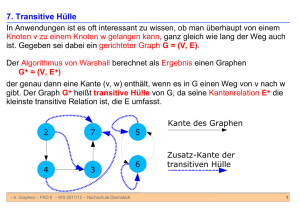
Das heißt, t(G) gibt direkt Auskunft darüber, zwischen welchen KnotenPaaren von G Pfade existieren. Wie kann man t(G) berechnen?
A
D
A
D
F
F
B
B
H
C
H
G
E
Ausgangsgraph G
C
E
G
transitive Hülle t(G)
PInf II 9.360
Warshall's Algorithmus
Warshall's Algorithmus berechnet die transitive Hülle einer Relation
(eines Graphen), die durch eine boolesche Adjazenzmatrix aMx
dargestellt ist. Die Matrix aMx wird dabei schrittweise zur transitiven
Hülle aufgefüllt:
void
void warshall
warshall ()
() {{ //
// berechnet
berechnet trans.
trans. Hülle
Hülle für
für Matrix
Matrix AMx
AMx
[u][v]:=
true
<=>
(u,v)
boolean[][]
aMx
=
{..//
aMx
E};
boolean[][] aMx = {..// aMx[u][v]:= true <=> (u,v) ∈∈ E};
for
for (int
(int yy == 0;
0; yy << knAnz;
knAnz; y++)
y++)
for
(int
x
=
0;
x
<
for (int x = 0; x < knAnz;
knAnz; x++)
x++)
if
if (aMx[x][y])
(aMx[x][y])
for
for (int
(int zz == 0;
0; zz << knAnz;
knAnz; z++)
z++)
if
(aMx[y][z])
aMx[x][z]
if (aMx[y][z]) aMx[x][z] == true;
true;
}}
Frage: Funktioniert dieser Algorithmus auch, wenn man so schachtelt :
for
for (int
(int xx == 0;
0; xx << knAnz;
knAnz; x++)
x++)
for
for (int
(int yy == 0;
0; yy << knAnz;
knAnz; y++)
y++) ....
....
?
PInf II 9.370
Korrektheit von Warshall's Algorithmus (1)
Die Korrektheit läßt sich in 3 Schritten nachweisen:
• Schritt 1 - Terminierung: Die 3 Schleifen laufen jeweils bis zu einer
festen, unveränderlichen Schranke → Terminierung i.O.
• Schritt 2 - Fundiertheit: Der Algorithmus stellt unter bestimmten
Voraussetzungen neue Kanten her. Da er nur dann eine neue Kante
(x,z) schafft (d.h. aMx[x,z] auf true setzt), wenn bereits (x,y) und
(y,z) ∈ R sind (d.h. aMx[x,y] = true und aMx[y,z] = true
gelten), tut er sicherlich nichts Falsches.
• Schritt 3 - Vollständigkeit: Es bleibt zu zeigen, daß er genug tut, d.h.
daß am Ende tatsächlich die (vollständige) transitive Hülle erzeugt
wurde.
Dieser Teil des Beweises nutzt vollständige Induktion über die
Mächtigkeit der Menge von Zwischenknoten auf dem Wege zwischen
zwei beliebigen Knoten u und v.
PInf II 9.380
Korrektheit von Warshall's Algorithmus (2)
• Für den Beweis der Vollständigkeit der erzeugten Verbindungen spielt
es eine ausschlaggebende Rolle, daß die äußere for-Schleife über den
Zwischenknoten y läuft.
• Wir formulieren die folgende Invariante der äußeren for-Schleife (in
Abhängigkeit von y, Knoten werden o.B.d.A. mit ihren Nummern
identifiziert).
I(y)
I(y)==“∀
“∀u,
u,vv∈∈VV::Wenn
Wennein
einWeg
Wegvon
vonuu nach
nachvvexistiert,
existiert,dessen
dessen
sämtliche
Zwischenknoten
in
Z
=
{0,
..
y-1}
sind,
dann
sämtliche Zwischenknoten in Z = {0, .. y-1} sind, danngilt:
gilt:
aMx[u,v]
=
true.”
aMx[u,v] = true.”
Der Beweis erfolgt durch Induktion über die Kardinalität n der Menge Z.
(1) Z = {}. Es existiert ein Weg von u nach v ohne Zwischenknoten →
aMx[u,v] = true.
(2) Die Behauptung gelte für Z = {0, .. y-1}
PInf II 9.390
Korrektheit von Warshall's Algorithmus (3)
Es sei ein beliebiger Weg von u nach v gegeben, dessen Zwischenknoten
alle in Z = {0, .. y} liegen.
Wenn y als Zwischenknoten nicht vorkommt, gilt nach I.V.: aMx[u,v] =
true.
Sei also y ein Zwischenknoten auf dem Weg von u nach v :
u . . ... .. . . . y . . ... .. .v
Aus I(y) folgt, daß bereits gilt :
aMx[u,y] und aMx[y,v]
alle Zwischenknoten mit Nr. < y
Beim nächsten Schleifendurchlauf (mit x=u, z=v) ...
... wird aMx[u,v]
for
auf true gesetzt und
for (int
(int xx == 0;
0; xx << knAnz;
knAnz; x++);
x++);
if
(aMx
[x][y])
if (aMx [x][y])
damit gilt : I(y+1)
for
for (int
(int zz == 0;
0; zz << knAnz;
knAnz; z++)
z++)
if
if (aMx
(aMx [y][z])
[y][z]) aMx
aMx [x][z]
[x][z] == true;
true;
PInf II 9.400
Wege in bewerteten Graphen
In einem bewerteten Graphen hatten wir bereits zu einem gegebenen
Weg zwischen zwei Knoten u und v die (bewertete) Länge des Weges
definiert:
W = (u=k0 , k1, ..., kp=v)
len(W) = gw(k0,k1) + ... + gw(kp-1,kp)
Für die Definition einer Entfernung ist diese Definition jedoch noch
unbefriedigend, da wir verschiedene Wege mit gleichem Anfang und
Ende haben können:
In unserem Beispiel gilt etwa:
len(Marburg, Gießen, Frankfurt, Mannheim) = 184 und:
len(Marburg, Gießen, Köln, Bonn, Mannheim) = 462
Als Entfernung für zwei Knoten u und v in einem bewerteten
zusammenhängenden Graphen definieren wir daher das Minimum der
Längen aller möglichen Wege, d.h. die Länge des kürzesten Weges.
PInf II 9.410
Kürzeste Wege
Ein
EinWeg
Weg(u
(u==aa00,,aa11,,...
...,,aapp==v)
v)zwischen
zwischenzwei
zweiKnoten
Knotenuuund
undvvheißt
heißt
gw(k
,
k
kürzester
Weg
,
wenn
seine
bewertete
Länge
Σ
i
i
minimalist.
ist.
kürzester Weg , wenn seine bewertete Länge Σ gw(k , ki+1))minimal
i
i
i+1
Dieser
DieserWert
Wertist
istdie
die(kürzeste)
(kürzeste)Entfernung
Entfernungvon
vonuunach
nachv.
v.
• Um die kürzeste Entfernung zwischen je zwei Knoten eines Graphen zu
finden (engl.: all pairs shortest path problem), kann man Warshall's
Algorithmus leicht verändern. Dieser Algorithmus wird gewöhnlich R.W.
Floyd zugeschrieben.
• Anstelle der booleschen Matrix verwenden wir jetzt wieder eine
bewertete Adjazenzmatrix bMx und setzen dabei gw (u,v) = ∞ (bzw. =
maxInt) , falls (u,v) ∉ E:
int[][]
int[][] bMx
bMx == {...
{... //
// bMx
bMx[u][v]:=
[u][v]:= gw(u,v)
gw(u,v) für
für (u,v)
(u,v) ∈∈ E,
E,
maxInt
sonst
};
maxInt sonst };
PInf II 9.420
Floyd's Algorithmus: Code
void
void kWegFloyd
kWegFloyd ()
() {{
//
// berechnet
berechnet kürzeste
kürzeste Wege
Wege für
für bewertete
bewertete Adj.-Matrix
Adj.-Matrix bMx
bMx
int[][]
//
int[][] bMx
bMx == {...
{... };
};
// vgl.
vgl. oben
oben
for
for (int
(int yy == 0;
0; yy << knAnz;
knAnz; y++);
y++);
for
(int
x
=
0;
x
<
for (int x = 0; x < knAnz;
knAnz; x++);
x++);
if
if (bMx[x][y]
(bMx[x][y] << M)
M)
for
for (int
(int zz == 0;
0; zz << knAnz
knAnz ;; z++)
z++)
if
((bMx[y][z]
<
M)
if ((bMx[y][z] < M) &&
&&
bMx[x][y]
bMx[x][y] ++ bMx[y][z]
bMx[y][z] << bMx[x][z])
bMx[x][z])
bMx[x][z]
bMx[x][z] == bMx[x][y]
bMx[x][y] ++ bMx[y][z];
bMx[y][z];
}}
Komplexität von Floyd's
Algorithmus: O (N3)
Invariante :
I(y)
I(y)=="∀
"∀ u,
u,vv∈V
∈V::bMx[u,v]
bMx[u,v]==Länge
Länge
des
deskürzesten
kürzestenWeges,
Weges,der
dernur
nur
Zwischenknoten
Zwischenknotenaus
aus{0
{0....y-1}
y-1}
benutzt.”
benutzt.”
PInf II 9.430
Dijkstra’s Algorithmus
Ein weiterer Algorithmus berechnet für einen vorgegebenen Knoten u die
kürzeste Entfernung zu allen anderen Knoten (engl.: single source
shortest path problem). Dieser Algorithmus stammt von E.W.Dijkstra
(1959). Ist man nur am kürzesten Weg zu einem bestimmten Knoten v
interessiert, so kann man i.a. vorzeitig abbrechen.
Grundidee des Algorithmus:
Eine Menge S ⊆ V (im Bild rechts grün
eingefärbt) beschreibt den jeweils
bereits bearbeiteten Teilgraphen
von G. Anfangs ist S = {u}
nk
G
S
k
u
k'
nk'
• S wird schrittweise um je einen Knoten erweitert, so daß für alle k ∈ S
gilt: Der kürzeste Weg von u nach k verläuft ausschließlich über Knoten
von S.
• NK = {nk | nk ist mit mindestens einem k ∈ S direkt verbunden} (im Bild
gelb eingefärbt) ist die Menge der Nachbar- oder Kandidatenknoten zur
Erweiterung von S. Aus K wird jeweils derjenige Knoten ausgewählt (und S
zugeschlagen), der minimalen Abstand zu u hat.
PInf II 9.440
Dijkstra’s Algorithmus: Programmgerüst
intSet
intSetSS=={u};
{u};
int
∞∞, ,∞∞, ,...,
int[knAnz]
[knAnz]minEntf
minEntf=={∞
{∞
...,∞∞};};
while
¬
while(¬
(¬
¬vv∈∈S)
S){{
Finde
Finde kk∈∈SSund
und nk
nk ∈∈(V
(V--S)
S)mit
mit
minEntf[k]
minEntf[k]++bMx[k,nk]
bMx[k,nk]ist
istminimal
minimal;;
minEntf[nk]
minEntf[nk]==minEntf[k]
minEntf[k]++bMx[k,nk];
bMx[k,nk];
SS==SS∪∪{nk
{nk};};
Invariante
Invariante::
∀∀ss∈∈SS:: minEntf[s]
minEntf[s]==kürzeste
kürzeste
Entfernung
Entfernung von
vonuu
nach
nachs.s.
}}
////minEntf[v]
minEntf[v]==Minimale
MinimaleDistanz
Distanzvon
vonuunach
nachvv
Komplexitätsbetrachtung:
Im ungünstigsten Fall wird die while-Schleife n = knAnz-mal durchlaufen.
Das Bestimmen des nächsten Knotens nk für S erfordert beim obigen (nicht
optimierten) Algorithmus einen Aufwand von O(N2). Damit liegt der Gesamtaufwand wieder bei O(N3). Dijkstra gibt allerdings eine Verbesserung seines
Algorithmus an, die den Aufwand im durchschnittlichen Fall auf O(N2) drückt.
PInf II 9.450
Implementierung von Dijkstra’s Algorithmus
Die Menge S wird mit Hilfe eines booleschen Array S der Länge knAnz
gespeichert. Es gilt S[k] = true ↔ k ∈ S.
Weiter wird ein int-Array minEntf der Länge anz zum Abspeichern der
kürzesten Entfernung zu u für alle Knoten von S benötigt. minEntf kann
mit 0 initialisiert werden, da später nur auf bereits in S liegende
Elemente zurückgegriffen wird.
Zu Beginn ist S = {u} und NK = {nk | es exisitiert eine Kante (u, nk) }
In jedem Schritt der äußeren (while-) Schleife wird ein Knotenpaar (k ∈
S, nk ∈ NK) so bestimmt, daß minEntf [k] + bMx [k][nk] minimal ist.
kNeu = nk ist ein neuer Knoten, zu dem die kürzeste Entfernung
kNeuEntf von u ermittelt wurde. kNeu wird zu S hinzugenommen und
kNeuEntf wird in minEntf [kNeu] aufgenommen.
Der Algorithmus terminiert, sobald kNeu der Zielknoten v ist.
Dijkstra’s Algorithmus: Code
PInf II 9.460
void
void kWegDijkstra
kWegDijkstra (int
(int u,
u, int
int v)
v) {{ //
// kürz.Weg
kürz.Weg von
von uu nach
nach vv
boolean[]
s
=
new
boolean[knAnz];
boolean[] s = new boolean[knAnz];
for
for (int
(int ii == 0;
0; ii << knAnz;
knAnz; i++)
i++) s[i]
s[i] == false;
false;
s[u]
s[u] == true;
true;
System.out.println("Kürzeste
System.out.println("Kürzeste Entfernung
Entfernung von
von "+
"+ knoBez[u]);
knoBez[u]);
int[]
int[] minEntf
minEntf == new
new int[knAnz];
int[knAnz];
minEntf[u]
minEntf[u] == 0;
0;
while
//
while (!
(! s[v])
s[v]) {{
// terminiert,
terminiert, wenn
wenn Ziel
Ziel vv erreicht
erreicht
int
int min
min == M;
M; int
int kNeu
kNeu == 0;
0;
for
for (int
(int kk == 0;
0; kk << knAnz;
knAnz; k++)
k++)
if
(s[k])
if (s[k])
for
for (int
(int nk
nk == 0;
0; nk
nk << knAnz;
knAnz; nk++)
nk++)
if
if (!
(! s[nk]
s[nk] &&
&& bMx[k][nk]
bMx[k][nk] << maxInt)
maxInt) {{
int
int kNeuEntf
kNeuEntf == minEntf[k]
minEntf[k] ++ bMx[k][nk]
bMx[k][nk] ;;
if
(kNeuEntf
<
min)
{min
=
kNeuEntf;
if (kNeuEntf < min) {min = kNeuEntf; kNeu
kNeu == nk;}
nk;}
}}
s[kNeu]
s[kNeu] == true;
true; //
// kNeu
kNeu wird
wird in
in SS aufgenommen
aufgenommen
minEntf[kNeu]
=
min;
minEntf[kNeu] = min;
System.out.println
System.out.println ("
(" nach
nach "" ++ knoBez[kNeu]
knoBez[kNeu] ++ "" ist
ist ""
++ min
min ++ "" km.");
km.");
}}
}}
PInf II 9.470
Beweis der Invarianten
∀x ∈S : minEntf[x] = kürzeste
Entfernung von u nach x.
Finde k ∈ S und nk ∈ (V - S) mit
minEntf[k] + BMx[k,nk] ist minimal ;
minEntf[nk] = minEntf[k] + BMx[k,nk];
∀ x ∈S ∪{nk} : minEntf[x] =
kürzeste Entfernung von
u nach x.
G
Angenommen, es gäbe eine kürzere
Verbindung u, ..., nk, dann sei k' der
letzte Zwischenknoten aus S auf
diesem Weg und nk' der nächste,
also u, ..., k', nk', ... , nk.
Dann wäre aber der Weg von u nach
nk' kürzer und statt nk wäre nk'
gefunden worden !
nk
k
nk'
S
u
k'
104
PInf II 9.480
4 Kassel
Marburg
Köln
96
30 7
174
5
106
Gießen
2 Fulda
34
3
0
181
66
104
Bonn
93
Frankfurt 1
224
88 136
8
Mannheim 6
Würzburg
S
Zu zeigen : Es kann keine kürzere
Verbindung von u zu nk geben als
die über k .
Beispiel: Kürzester Weg
von Bonn nach Kassel
minEntf
{0}
{0, 0, 0, 0, 0, 0, 0, 0, 0}
(1) {0}
{0, 0, 0, 0, 0, 0, 0, 0, 0}
(2) {0, 5}
{0, 0, 0, 0, 0, 34, 0, 0, 0}
(3) {0, 1, 5}
{0,181, 0, 0, 0, 34, 0, 0, 0}
(4) {0, 1, 3, 5}
{0,181, 0, 208, 0, 34, 0, 0, 0}
(5) {0, 1, 3, 5, 6}
{0,181, 0, 208, 0, 34, 224, 0, 0}
(6) {0, 1, 3, 5, 6, 7}
{0,181, 0, 208, 0, 34, 224, 238, 0}
(7) {0, 1, 2, 3, 5, 6, 7}
{0,181, 285, 208, 0, 34, 224, 238, 0}
(8) {0, 1, 2, 3, 5, 6, 7, 8} {0,181, 285, 208, 0, 34, 224, 238, 317}
(9) {0, 1, 2, 3, 4, 5, 6, 7, 8}
k
kNeu min
0
0
5
0
3
1
1
7
0
5
1
3
6
7
2
8
4
M
34
181
208
224
238
285
317
342
PInf II 9.490
Kürzester Weg und aufspannender Baum
Ist v der letzte (d.h. von u am weitesten entfernte) Knoten des Graphen
G (wie im vorangegangenen Beispiel) so liefert Dijkstra's Algorithmus
offenbar einen aufspannenden Baum für G - und zwar gerade
denjenigen, der für jeden Knoten k den kürzesten Weg von u nach k
darstellt.
34
96
7
30
174
Gießen
5
4 Kassel
104
Marburg
Köln
106
2 Fulda
3
0
181
66
104
Bonn
93
Frankfurt 1
224
88 136
8
Mannheim 6
Würzburg
PInf II 9.500
Bewertete Graphen: ein weiteres Beispiel
San Rafael
1
15
Richmond
2
18
San Francisco
15
12
0
Oakland
20
15
20
Pacifica 14
5 Hayward
San Mateo
15
Half Moon Bay
3
25
13
20
4
14
18
20
15
Palo Alto
6
15
10
50
10
10
12
7 Fremont
9
8 San Jose
Santa Clara
35
Scotts Valley
Santa Cruz
70
60
Watsonville
11
PInf II 9.510
Adjazenzmatrix für SFBay-Beispiel
0
5
6
7
8 9 10 11 12 13 14
0
0 18 - 12 20 -
1
18 0 15 -
2
-
1
2
3
4
-
-
-
-
-
-
-
- 15
-
-
-
-
-
-
-
-
-
-
-
15 0 15 -
-
-
-
-
-
-
-
-
-
-
20 -
-
-
-
-
-
-
-
-
3
12 -
4
20 -
15 0
-
-
-
-
-
-
-
-
5
-
-
- 20 20 0
0 20 18 - 14
-
-
-
-
-
-
-
6
-
-
-
- 18 -
0 15
- 10 -
-
-
-
-
7
-
-
-
-
-
-
-
-
-
8
-
-
-
-
-
60 -
-
-
14 15 0 20 -
-
- 20 0 15 -
9
-
-
-
-
-
- 10 -
10
-
-
-
-
-
-
-
-
11
-
-
-
-
-
-
-
-
12
-
-
-
-
-
-
-
-
-
-
13
-
-
-
- 25 -
-
-
-
-
-
- 50 0 15
15 -
-
-
-
-
-
-
-
-
14
-
-
15 0 35 - 35 0
60 -
-
-
25 -
-
-
- 10 -
-
0 70 -
-
10 70 0 50 -
15 0
Speicherung von Graphen als Array:SFBay-Beispiel
PInf II 9.520
private
private static
static final
final int
int MM == Integer.MAX_VALUE;
Integer.MAX_VALUE;
String[]
SFKn
=
{"San
String[] SFKn = {"San Francisco",
Francisco", "San
"San Rafael",
Rafael", "Richmond",
"Richmond", "Oakland",
"Oakland",
"San
"San Mateo","Hayward",
Mateo","Hayward", "Palo
"Palo Alto",
Alto", "Fremont",
"Fremont", "San
"San Jose",
Jose", "Santa
"Santa
Clara",
Clara", "Scotts
"Scotts Valley",
Valley", "Watsonville",
"Watsonville", "Santa
"Santa Cruz",
Cruz", "Half
"Half Moon
Moon
Bay",
Bay", "Pacifica"};
"Pacifica"};
int[][]
int[][] SFKanW
SFKanW == {{
{{ 0,
0, 18,
18, M,
M, 12,
12, 20,
20, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, 15},
15},
{18,
0,
15,
M,
M,
M,
M,
M,
M,
M,
M,
M,
M,
M,
{18, 0, 15, M, M, M, M, M, M, M, M, M, M, M, M},
M},
{{ M,
M, 15,
15, 0,
0, 15,
15, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M},
M},
{12,
{12, M,
M, 15,
15, 0,
0, M,
M, 20,
20, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M},
M},
{20,
{20, M,
M, M,
M, M,
M, 0,
0, 20,
20, 18,
18, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, 25,
25, M},
M},
{{ M,
M, M,
M, M,
M, 20,
20, 20,
20, 0,
0, M,
M, 14,
14, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M},
M},
{{ M,
M,
M,
M,
18,
M,
0,
15,
M,
10,
M,
M,
M,
M,
M, M, M, M, 18, M, 0, 15, M, 10, M, M, M, M, M},
M},
{{ M,
M, M,
M, M,
M, M,
M, M,
M, 14,
14, 15,
15, 0,
0, 20,
20, M,
M, M,
M, M,
M, M,
M, M,
M, M},
M},
{{ M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, 20,
20, 0,
0, 15,
15, M,
M, 60,
60, M,
M, M,
M, M},
M},
{{ M,
M,
M,
M,
M,
M,
10,
M,
15,
0,
35,
M,
M,
M,
M, M, M, M, M, M, 10, M, 15, 0, 35, M, M, M, M},
M},
{{ M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, 35,
35, 0,
0, M,
M, 10,
10, M,
M, M},
M},
{{ M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, 60,
60, M,
M, M,
M, 0,
0, 70,
70, M,
M, M},
M},
{{ M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, 10,
10, 70,
70, 0,
0, 50,
50, M},
M},
{{ M,
M, M,
M, M,
M, M,
M, 25,
25, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, 50,
50, 0,
0, 15},
15},
{15,
{15, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, M,
M, 15,
15, 0}};
0}};
BGraph
SFBayNetz
=
new
BGraph
(SFKn,
SFKanW);
BGraph SFBayNetz = new BGraph (SFKn, SFKanW);
PInf II 9.530
SFBay-Verkehrsnetz als Listenstruktur
0
San Francisco
18 1
12 3
20 4
1
San Rafael
18 0
15 2
nll
2
Richmond
15 1
15 3
nl
3
Oakland
12 0
15 2
20 5
nl
4
San Mateo
20 0
20 5
18 6
25 13
5
Hayward
20 3
20 4
14 7
nl
6
Palo Alto
18 4
15 7
10 9
nl
7
Fremont
14 5
15 6
20 8
nl
8
San Jose
20 7
15 9
60 11
nl
9
Santa Clara
10 6
15 8
35 10
nl
10 Scotts Valley
35 9
10 12
nl
11 Watsonville
60 8
70 12
nl
12 Santa Cruz
10 10
70 11
50 13
nl
13 Half Moon Bay
25 4
50 12
15 14
nl
14 Pacifica
15 0
15 13
nl
nl
15 14
nl
nl kurz für : null
PInf II 9.540
Kürzester Weg: SFBay-Beispiel
San Rafael
1
15
Richmond
2
18
San Francisco
15
12
0
Oakland
20
15
20
Pacifica 14
5 Hayward
20
San Mateo 4
15
Half Moon Bay
3
25
13
14
18
20
15
Palo Alto
6
15
10
50
10
10
12
7 Fremont
9
8 San Jose
Santa Clara
35
Scotts Valley
Santa Cruz
70
60
Watsonville
11
PInf II 9.550
Der Weg von San Rafael nach Scotts Valley
Min-Suche
Min-SucheAusgangsknoten:
Ausgangsknoten:San
SanRafael
Rafael
Zielknoten:
Scotts
Valley
Zielknoten: Scotts Valley
Die
Diekürzeste
kürzesteEntfernung
Entfernungvon
vonSan
SanRafael
Rafael
nach
Richmond
ist
15
km.
nach Richmond ist 15 km.
nach
nachSan
SanFrancisco
Franciscoist
ist18
18km.
km.
nach
nachOakland
Oaklandist
ist30
30km.
km.
nach
nachPacifica
Pacificaist
ist33
33km.
km.
nach
nachSan
SanMateo
Mateoist
ist38
38km.
km.
nach
nachHalf
HalfMoon
MoonBay
Bayist
ist48
48km.
km.
nach
nachHayward
Haywardist
ist50
50km.
km.
nach
nachPalo
PaloAlto
Altoist
ist56
56km.
km.
nach
nachFremont
Fremontist
ist64
64km.
km.
nach
nachSanta
SantaClara
Claraist
ist66
66km.
km.
nach
nachSan
SanJose
Joseist
ist81
81km.
km.
nach
nachSanta
SantaCruz
Cruzist
ist98
98km.
km.
nach
Scotts
Valley
ist
nach Scotts Valley ist101
101km.
km.
-------
PInf II 9.560
Traveling Salesman Problem
Ein
EinHandlungsreisender
Handlungsreisendermuß
mußeine
eineReihe
Reihevon
vonOrten
Ortenbesuchen.
besuchen. Er
Ermöchte
möchte
seine
seineTour
Tourso
soplanen,
planen,daß
daßder
derzurückzulegende
zurückzulegende Weg
Weg(=
(=Zyklus,
Zyklus,der
deralle
alle
Orte
Orteberührt)
berührt)minimal
minimalist.
ist.
Dies ist ein Problem über bewerteten Graphen. Die Knoten sind die zu besuchenden Orte, die (bewerteten) Kanten stellen die Entfernung (oder Fahrtkosten)
zwischen den Orten dar. Das Graphenproblem lautet also :
Finde
Findeinineinem
einemvorgegebenen
vorgegebenen
Graphen
Grapheneinen
einenZyklus
Zyklusminimaler
minimaler
Länge,
Länge,der
deralle
alleKnoten
Knotenenthält.
enthält.
Finden Sie eine TSP-Tour in dem
nebenstehenden Graphen!
KS Kassel
Marburg 104
Köln
96
MR
K 174
Gießen 30
106 FD Fulda
34
GI
BN
181
66
104
Bonn
93
Frankfurt F
224
88 136
WÜ
Mannheim MA
Würzburg
PInf II 9.570
Eigenschaften des TSP
Unser Beispielproblem läßt sich offenbar intuitiv auf einfache Weise (und
eindeutig!) lösen. Grundsätzlich ist das jedoch keineswegs der Fall.
(a) Oft gibt es überhaupt keine Lösung.
Beispiel: Wenn ein weiterer Knoten "Mainz" zwischen Bonn und
Frankfurt aufgenommen wird, ist das TSP nicht lösbar.
(b) Oft gibt es mehrere Zyklen, die alle zu besuchenden Knoten
enthalten. Dann kann der kürzeste Zyklus nur durch Ausprobieren
gefunden werden.
Kassel
Beispiel: Wenn zusätzlich eine
Verbindung Mainz-Mannheim
aufgenommen wird, gibt es
mehrere Zyklen.
KS
Marburg 104
Köln
96
K 174
30 MR
Gießen
106 FD Fulda
34
GI
BN 140
66
104
MZ 41
Bonn
93
F Frankfurt
71
224
88 136
WÜ
MA
Würzburg
Mannheim
PInf II 9.580
Lösungen des TSP
Bis heute ist keine effiziente Lösung des TSP bekannt. Alle bekannten
Lösungen sind von der Art :
Allgemeiner
AllgemeinerTSP-Algorithmus:
TSP-Algorithmus:
••
Erzeuge
Erzeugealle
allemöglichen
möglichenTouren;
Touren;
••
Berechne
Berechnedie
dieKosten
Kostenfür
fürjede
jedeTour;
Tour;
••
Wähle
Wähledie
diekostengünstigsteTour
kostengünstigsteTouraus.
aus.
Folgerung : Die Komplexität aller bekannten TSP-Algorithmen ist
O(cN), wobei N die Anzahl der Knoten und c die Maximalzahl der von
einem Knoten ausgehenden Kanten ist. Das heißt: Wenn wir einen
einzigen Knoten hinzunehmen, erhöht sich der Aufwand zur Lösung
des TSP um den Faktor c!
Beispiel: Hinzunahme des neuen Knotens Mainz im obenstehenden
Graphen.
PInf II 9.590
Varianten des TSP
Eine Verallgemeinerung des TSP besteht darin, auf die Rückkehr zum
Ausgangspunkt zu verzichten:
• TSP (u,v): Finde einen einfachen Weg von Knoten u nach Knoten v,
der alle Knoten von G enthält.
Offenbar stellt TSP(u,u) das ursprüngliche TSP-Problem dar.
Beispiel: TSP(Marburg, Gießen) ist (im ursprünglichen Graphen) eindeutig
lösbar, TSP (Marburg, Köln) ist nicht lösbar, für TSP (Marburg, Würzburg)
müssen im erweiterten Graphen mehrere mögliche Wege verglichen werden.
In einer weiteren Verallgemeinerung werden Mehrfachbesuche
einzelner Knoten bis zu einer Schranke maxB (= Maximalzahl zulässiger
Besuche) zugelassen.
• TSP (u,v,maxB): Finde einen Weg von Knoten u nach Knoten v, der
alle Knoten von G mindestens einmal und höchstens maxB-mal enthält.
Mit dieser Verallgemeinerung (und geeignetem maxB) ist das TSP
immer lösbar - allerdings mit noch erheblich gesteigerten Aufwand!
PInf II 9.600
TSP-Algorithmus: Erläuterung (1)
Der folgende Algorithmus für das Problem TSP (u,v,maxB) verfolgt eine
Tiefensuche (depth first)- Strategie mit Zurücksetzen (backtracking).
Er verwendet
• ein int-Array Marken der Länge knAnz zum Markieren der bereits
besuchten Knoten,
• ein int-Array MinWeg der Länge maxKnBes zum Speichern des (bisher)
minimalen Weges (mit maxKnBes = vorgegebene Schranke für die
Anzahl zu besuchender Knoten),
• eine rekursive Prozedur Besuche, die einen begonnenen Weg der
Tiefe t an der Stelle k mit dem Ziel z fortsetzt.
Ist der Weg noch keine vollständige Tour, und existiert zu k ein
Nachbarknoten k', der noch weniger als maxB-mal besucht wurde und
bei dessen Besuch die gesamte Weglänge unterhalb der WeglängenSchranke MinWegLen bleibt, wird der Weg bei k' mit Tiefe t+1
fortgesetzt (rekursiver Aufruf).
PInf II 9.610
TSP-Algorithmus: Erläuterung (2)
• Weiter wird durch eine boolesche Funktion TesteWeg geprüft,
- ob k bereits der Zielknoten v ist,
- ob alle Knoten besucht wurden.
• Ist ein Weg gefunden, so wird seine Länge (AktWegLen) mit der von
MinWeg (MinWegLen) verglichen. Falls er kürzer ist, wird er zum neuen
MinWeg und seine Länge wird als neue MinWegLen festgehalten. Der
Besuch wird abgebrochen.
• Beim Abbruch eines Besuchs wird zum vorherigen Knoten
zurückgekehrt (backtrack) und der nächste mit diesem verbundene
Knoten besucht. Wurden alle Wege durchprobiert und mindestens eine
Tour gefunden, so wird MinWeg, ansonsten eine Fehlermeldung
ausgegeben.
PInf II 9.620
TSP-Algorithmus: Programmgerüst
void
voidbesuche
besuche(int
(intk,k,int
int[ [] ]weg,
weg,int
inttiefe,
tiefe,int
int[ [] ]marken,
marken,int
intziel)
ziel){{
tiefe
+=
1;
weg
[tiefe]
=
k;
tiefe += 1; weg [tiefe] = k;
marken[k]
marken[k]+=
+=1;
1;int
intbishWegLen
bishWegLen==0;
0;
ifif(tiefe
(tiefe==
==0)
0)aktWegLen
aktWegLen=0
=0 ////Vorbesetzung
Vorbesetzung
else
else{bishWegLen
{bishWegLen==aktWegLen;
aktWegLen;
aktWegLen
aktWegLen+=
+=kantenW
kantenW(weg[tiefe-1],
(weg[tiefe-1],k);}
k);}
ifif(aktWegLen
<
minWegLen)
//
abbrechen,
(aktWegLen < minWegLen) // abbrechen,falls
fallskeine
keineVerbesserung
Verbesserung
ifif(testeWeg()
{
//
Weg
ist
eine
TSP-Tour)
(testeWeg() {
// Weg ist eine TSP-Tour)
int
int[ [] ]minWeg
minWeg == ...... ////Kopie
Kopievon
vonweg
wegbis
biszur
zurPosition
Positiontiefe;
tiefe;
minWegLen
minWegLen==aktWegLen;
aktWegLen;}}
else
////Weg
else
Wegist
istkeine
keineTSP-Tour
TSP-Tour
for
////alle
for....
alleNachbarknoten
Nachbarknotenj jvon
vonkkmit
mitMarken
Marken[j][j]<<maxB
maxB
besuche
besuche(j,
(j,weg,
weg,tiefe,
tiefe,marken,
marken,ziel);
ziel);
////ininallen
allenanderen
anderenFällen
FällenBesuch
Besuchzurücknehmen:
zurücknehmen:
aktWegLen
aktWegLen==bishWegLen;
bishWegLen;marken
marken[k]
[k]-=1;
-=1;
}}
Aufruf:
besuche
besuche(u,
(u,weg,
weg,-1,
-1,marken,
marken,v)v)
PInf II 9.630
Klassenerweiterung für TSP-Implementierung
Für die Implementierung des TSP-Algorithmus wird die Klasse Graph um
zur Klasse TSPGraph erweitert. Dazu werden einige zusätzlich benötigte
Datenfelder definiert. Die Operation TSPSuche ermittelt eine TSP-Tour.
Als Hilfsroutinen benutzt sie die Operationen besuche und testeWeg.
class
class TSPGraph
TSPGraph extends
extends BGraph
BGraph {{
private
int
schranke
;
//
private int schranke ;
// Abschätzung
Abschätzung für
für Weglänge
Weglänge
private
int
minWegLen
;
//
Länge
d.bish.minimalen
private int minWegLen ;
// Länge d.bish.minimalen Weges
Weges
private
private final
final int
int maxB
maxB == ...;
...; /*
/* Maximalzahl
Maximalzahl von
von Besuchen
Besuchen
pro
pro Knoten,
Knoten, z.B.
z.B. maxB
maxB == 22 */
*/
private
int
aktWegLen;
//
Länge
des
aktuellen
private int aktWegLen;
// Länge des aktuellen Weges
Weges
private
/*
private int
int maxKnBes;
maxKnBes;
/* Schranke
Schranke für
für die
die Anzahl
Anzahl
besuchter
Knoten
*/
besuchter Knoten */
private
//
private int[]
int[] minWeg;
minWeg;
// Bisher
Bisher minimaler
minimaler Weg
Weg
void
void TSPSuche
TSPSuche (int
(int st,
st, int
int zi)
zi) {{ //
// siehe
siehe nächste
nächste Folie
Folie
}} ...
...
}}
PInf II 9.640
TSPSuche: Java-Programm
void
void TSPSuche
TSPSuche (int
(int st,
st, int
int zi)
zi) {{ /*
/* sucht
sucht minimale
minimale TSP-Tour
TSP-Tour
von
st
nach
zi
*/
von st nach zi */
minWegLen
minWegLen == schranke;
schranke; //
// Abschätzung
Abschätzung nach
nach oben
oben
maxKnBes
=
...
;
/*
geeigneter
Wert
maxKnBes = ...
;
/* geeigneter Wert >> knAnz,
knAnz, z.B.
z.B.
(knAnz*maxB)
+1
*/
(knAnz*maxB) +1 */
weg
weg == new
new int[maxKnBes];
int[maxKnBes];
marken
marken == new
new int[knAnz];
int[knAnz];
for
for (int
(int kk == 0;
0; kk << knAnz;
knAnz; k++)
k++) marken[k]
marken[k] == 0;
0;
besuche
(st,
weg,
-1,
marken,
zi);
besuche (st, weg, -1, marken, zi);
if
if (minWegLen
(minWegLen ==
== schranke)
schranke)
System.out.println
System.out.println ("Kein
("Kein Weg
Weg gefunden!");
gefunden!");
else
{
else {
System.out.println
System.out.println ("Länge
("Länge des
des kürzesten
kürzesten Weges:
Weges: "" ++
minWegLen);
minWegLen);
System.out.println
System.out.println ("Besuchte
("Besuchte Knoten:
Knoten: ");
");
for
(int
k
=
0;
k
<
minWeg.length;
for (int k = 0; k < minWeg.length; k++)
k++)
System.out.println
System.out.println (knoBez[minWeg[k]]);
(knoBez[minWeg[k]]);
}}
}}
Operation besuche
PInf II 9.650
private
private void
void besuche
besuche (int
(int k,
k, int[]
int[] weg,
weg, int
int tiefe,
tiefe, int[]
int[]
marken,
int
zi)
{
/*
besucht
Knoten
k
mit
geg.
marken, int zi) { /* besucht Knoten k mit geg. Weg,
Weg,
Tiefe,
Tiefe, Markierung
Markierung und
und Ziel
Ziel */
*/
tiefe
++;
tiefe ++;
if
if (tiefe
(tiefe >=
>= maxKnBes)
maxKnBes) {{
System.out.println
System.out.println ("Zulässige
("Zulässige Knotenzahl
Knotenzahl im
im Weg
Weg
überschritten.");
};
überschritten."); return;
return;
};
weg[tiefe]
weg[tiefe] == k;
k;
marken[k]
marken[k] ++;
++;
int
int bishWegLen
bishWegLen == 0;
0;
if
(tiefe
//
if (tiefe ==
== 0)
0) aktWegLen
aktWegLen == 0;
0;
// Vorbesetzung
Vorbesetzung
else
{
else {
bishWegLen
bishWegLen == aktWegLen;
aktWegLen;
aktWegLen
aktWegLen +=
+= kantenW
kantenW (weg[tiefe-1],
(weg[tiefe-1], k);
k);
}}
if
if (aktWegLen
(aktWegLen << minWegLen)
minWegLen)
if
if (testeWeg(weg,
(testeWeg(weg, tiefe,
tiefe, marken,
marken, zi))
zi)) {{ //
// ist
ist TSP-Tour
TSP-Tour
minWeg
=
new
int[tiefe
+
1];
minWeg = new int[tiefe + 1];
System.arraycopy
System.arraycopy (weg,
(weg, 0,
0, minWeg,
minWeg, 0,
0, tiefe
tiefe ++ 1)
1) ;;
minWegLen
minWegLen == aktWegLen;
aktWegLen;
}}
else
//
siehe
else
//
siehe nächste
nächste Folie
Folie
PInf II 9.660
Hilfsoperationen für TSP (Forts.)
else
//
else
// Weg
Weg ist
ist keine
keine TSP-Tour
TSP-Tour
for
for (int
(int jj == 0;
0; jj << knAnz;
knAnz; j++)
j++)
//für
//für alle
alle Nachbarn
Nachbarn jj von
von kk mit
mit Marken[i]
Marken[i] << maxB
maxB
if
if (k
(k !=
!= jj &&
&& kantenW
kantenW (k,
(k, j)
j) << M)
M)
if
if (marken[j]
(marken[j] << maxB)
maxB)
besuche
besuche (j,
(j, weg,
weg, tiefe,
tiefe, marken,
marken, zi);
zi);
//
// in
in allen
allen anderen
anderen Fällen
Fällen Besuch
Besuch zurücknehmen:
zurücknehmen:
aktWegLen
aktWegLen == bishWegLen;
bishWegLen;
weg[tiefe]
weg[tiefe] == -1;
-1;
marken[k]
marken[k] --;
--;
}}
private
private boolean
boolean testeWeg
testeWeg (int[]
(int[] weg,
weg, int
int tiefe,
tiefe, int[]
int[]
marken,
marken, int
int zi)
zi) {{ //
// prüft
prüft gegebenen
gegebenen Weg
Weg auf
auf TSP-Tour
TSP-Tour
if
if (tiefe
(tiefe << knAnz-1
knAnz-1 |||| weg[tiefe]
weg[tiefe] !=
!= zi)
zi) return
return false;
false;
for
(int
k
=
0;
k
<
knAnz;
k++)
for (int k = 0; k < knAnz; k++)
if
if (marken[k]
(marken[k] ==
== 0)
0) return
return false;
false;
return
return true;
true;
}}
TSP von San Francisco nach San Rafael
PInf II 9.670
Länge des kürzesten Weges: 342
Besuchte Knoten:
San Francisco
Pacifica
Half Moon Bay
Eine
EineLösung
Lösungdes
desTSP
TSPvon
vonSan
SanFrancisco
Francisconach
nach
San Mateo
San
Rafael
ist
mit
einem
einfachen
Weg
möglich.
San Rafael ist mit einem einfachen Weg möglich.
Palo Alto
Santa Clara
Laufzeit
Laufzeit(auf
(auf33MHZ
33MHZ486
486PC)
PC)<<11sec
sec
Scotts Valley
Santa Cruz
Watsonville
San Jose
Fremont
Hayward
Oakland
Richmond
San Rafael
TSP von San Francisco nach San Mateo
PInf II 9.680
Länge des kürzesten Weges: 364.
Besuchte Knoten:
San Francisco
San Rafael
Richmond
Eine
EineLösung
Lösungdes
desTSP
TSPvon
vonSan
SanFrancisco
Francisconach
nach
Oakland
San
Mateo
gelingt
nur
mit
Mehrfachbesuchen.
San
Mateo
gelingt
nur
mit
Mehrfachbesuchen.
San Francisco
Pacifica
Laufzeit
Laufzeit(auf
(auf33MHZ
33MHZ486
486PC)
PC)ca.
ca.200
200sec
sec
Half Moon Bay
Santa Cruz
Scotts Valley
Santa Cruz
Watsonville
San Jose
Santa Clara
Palo Alto
Fremont
Hayward
San Mateo