7 Graphen - Ergänzung Floyd Warshall

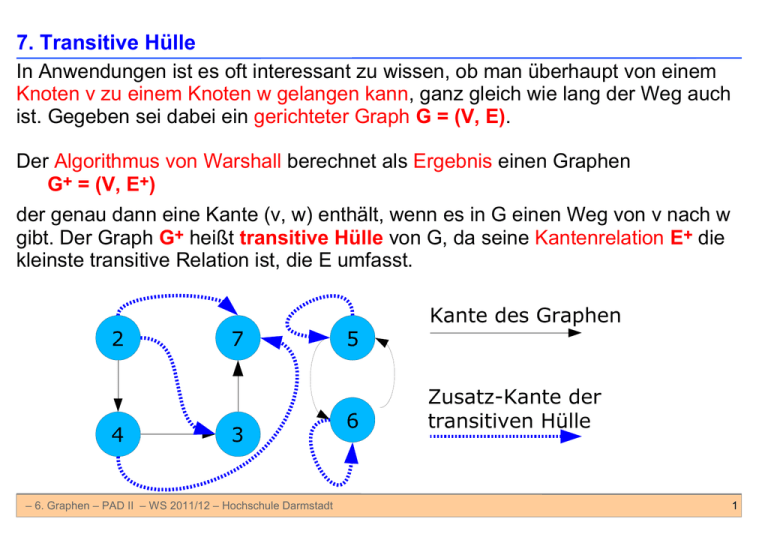
7. Transitive Hülle
In Anwendungen ist es oft interessant zu wissen, ob man überhaupt von einem
Knoten v zu einem Knoten w gelangen kann, ganz gleich wie lang der Weg auch
ist. Gegeben sei dabei ein gerichteter Graph G = (V, E).
Der Algorithmus von Warshall berechnet als Ergebnis einen Graphen
G+ = (V, E+)
der genau dann eine Kante (v, w) enthält, wenn es in G einen Weg von v nach w
gibt. Der Graph G+ heißt transitive Hülle von G, da seine Kantenrelation E+ die
kleinste transitive Relation ist, die E umfasst.
2
4
7
3
– 6.
Einführung
Graphen ––PAD
PG IIII –– SoSe
WS 2011/12
2009 ––Hochschule
HochschuleDarmstadt
Darmstadt
5
6
Kante des Graphen
Zusatz-Kante der
transitiven Hülle
1
7. Transitive Hülle
Der Graph G+ wird aus G entwickelt, indem schrittweise neue Kanten
hinzugenommen werden:
● In Schritt 0 kommt eine Kante (i, j) hinzu, wenn sich aus zwei Kanten ein
Weg von i nach j bilden lässt, der über den Knoten 0 führt (d.h. wenn (i, 0)
und (0, j) Kanten sind).
● In Schritt 1 kommt eine Kante (i, j) hinzu, wenn sich aus zwei Kanten ein
Weg von i nach j bilden lässt, der über den Knoten 1 führt; hierbei werden
die in Schritt 0 neu gefundenen Kanten mit berücksichtigt.
● Dieses Verfahren wird für alle Knoten fortgesetzt.
Warshall-Algorithmus
Warshall-Algorithmus
Eingabe:
Eingabe:Graph
GraphGG == (V,
(V, E)
E)mit
mitVV == {0,
{0, ...,
..., n-1}
n-1}
+
+
Ausgabe:
Ausgabe:Graph
GraphGG+ == (V,
(V, EE+))
+
Methode:
Methode: EE+ :=
:= EE
für
fürKnoten
Knotenkk == 0,
0, ...,
..., n-1
n-1
für
füralle
allePaare
Paarevon
vonKnoten
Knoten(i,
(i, j)
j)
++sind, dann
wenn
(i,
k)
und
(k,
j)
Kanten
in
E
wenn (i, k) und (k, j) Kanten in E sind, dann
+
erzeuge
erzeugeneue
neueKante
Kante(i,
(i, j)
j)ininEE+
– 6.
Einführung
Graphen ––PAD
PG IIII –– SoSe
WS 2011/12
2009 ––Hochschule
HochschuleDarmstadt
Darmstadt
2
7. Transitive Hülle
Beispiel:
– 6.
Einführung
Graphen ––PAD
PG IIII –– SoSe
WS 2011/12
2009 ––Hochschule
HochschuleDarmstadt
Darmstadt
3
7. Transitive Hülle
Implementierung:
● Man geht von der Adjazenzmatrix des Graphen G aus, d.h. H =A[i, j]
0
●
●
●
und ermittelt eine neue Matrix H1, die neue Wege zwischen Knoten angibt.
Das macht man solange, bis keine neuen Kanten mehr hinzugefügt werden
können.
Beim Übergang von Hk-1[i, j] nach Hk[i, j] entscheidet man:
➢
existiert eine Kante von i nach k und von k nach j, dann wird Hk[i, j]=1
➢
ansonsten bleibt Hk[i, j] unverändert
– 6.
Einführung
Graphen ––PAD
PG IIII –– SoSe
WS 2011/12
2009 ––Hochschule
HochschuleDarmstadt
Darmstadt
4
7. Transitive Hülle
template <class TV, int maxNodes>
bool *Warshall(Digraph<TV, maxNodes> g) {// berechnet transitive Hülle von g
bool *H = new bool[maxNodes*maxNodes];
for (int i=0; i<maxNodes; i++)
for (int j=0; j<maxNodes; j++)
H[i*maxNodes+j] = g.IsArc(i,j); // Initialisiere Feld H[i,j]
for (int k=0; k<maxNodes; k++)
for (int i=0; i<maxNodes; i++)
for (int j=0; j<maxNodes; j++)
H[i*maxNodes+j] = H[i*maxNodes+j] ||
H[i*maxNodes+k] && H[k*maxNodes+j];
}
return H;
Dies führt zu einem Verfahren mit Komplexität O(n3).
– 6.
Einführung
Graphen ––PAD
PG IIII –– SoSe
WS 2011/12
2009 ––Hochschule
HochschuleDarmstadt
Darmstadt
5
7. Transitive Hülle
Beispiel:
Adjazenz Matrix:
0
1
2
3
4
5
6
7
-------------------------------------------------0|
1|
2|
0
3|
0
4|
0
5|
0
6|
0
7|
Warshall Matrix:
0
1
2
3
4
5
6
7
-------------------------------------------------0|
0
0
0
0
0
0
0
0
1|
0
0
0
0
0
0
0
0
2|
0
0
0
1
1
0
0
1
3|
0
0
0
0
0
0
0
1
4|
0
0
0
1
0
0
0
1
5|
0
0
0
0
0
1
1
0
6|
0
0
0
0
0
1
1
0
7|
0
0
0
0
0
0
0
0
– 6.
Einführung
Graphen ––PAD
PG IIII –– SoSe
WS 2011/12
2009 ––Hochschule
HochschuleDarmstadt
Darmstadt
2
7
4
3
5
6
6
8. Kürzeste Wege
Bisher haben uns die Kantengewichte nicht interessiert. Nun wollen wird
Fragestellungen, wie etwa folgende beantworten können:
● Gegeben sei ein Graph, dessen Knoten Städte sind.
● Eine Kante führt von einem Knoten v nach w und ist mit x gewichtet, wenn
es eine befahrbare Straße der Länge x zwischen der Stadt v und w gibt.
● Frage: Wie ist die kürzeste Verbindung zwischen Stadt A und Stadt B?
●
Frage: Wie ist jeweils die kürzeste Verbindung zwischen je zwei von allen
Städten?
Lösung: Der Algorithmus von Floyd berechnet für alle Paare von Knoten (i, j)
die Länge des kürzesten Weges von i nach j. Der Algorithmus hat dieselbe
Struktur wie der Warshall-Algorithmus.
– 6.
Einführung
Graphen ––PAD
PG IIII –– SoSe
WS 2011/12
2009 ––Hochschule
HochschuleDarmstadt
Darmstadt
7
8. Kürzeste Wege
Algorithmus:
Man verwendet eine Kosten-Matrix C, in der die Summe der Kantengewichte
zwischen Knoten errechnet und gespeichert werden:
● Zu Beginn ist:
➢ C [i, i] = 0
0
➢
C0[i, j] = ∞∞, falls keine Kante von i nach j existiert
➢ C [i, j] = Kantengewicht von (i, j), falls eine Kante von i nach j existiert
0
●
beim Übergang von Ck-1 nach Ck wird unterschieden:
● C
k-1[i, j] = ∞, d.h. es wurde noch kein Weg von i nach j festgestellt,
aber es gibt einen Weg von i nach k und k nach j:
● dann setze C [i, j] = C
k
k-1[i, k] + Ck-1[k, j]
● C
k-1[i, j] != ∞, (d.h. es wurde ein Weg von i nach j festgestellt) und es
gibt einen kürzeren Weg über k (von i nach k und k nach j):
● dann setze C [i, j] = min(C [i, j], C
k
k
k-1[i, k] + Ck-1[k, j])
– 6.
Einführung
Graphen ––PAD
PG IIII –– SoSe
WS 2011/12
2009 ––Hochschule
HochschuleDarmstadt
Darmstadt
8
8. Kürzeste Wege
Beispiel:
1
4
4
2
2
3
6
2
Kostenmatrix
Kostenmatrix
Kostenmatrix
Schritt 1-3: C0
C3[1,2]=∞: 1,3,2
C4[1,2]=8: 1,4,2
1
2
3
4
1
0
∞
2
4
2
∞
0
∞
3
∞
6
4
∞
2
1
2
3
4
1
0
8
2
4
∞
2
∞
0
∞
0
∞
3
∞
6
∞
0
4
∞
2
– 6.
Einführung
Graphen ––PAD
PG IIII –– SoSe
WS 2011/12
2009 ––Hochschule
HochschuleDarmstadt
Darmstadt
1
2
3
4
1
0
6
2
4
∞
2
∞
0
∞
∞
0
∞
3
∞
6
0
∞
∞
0
4
∞
2
∞
0
9
8. Kürzeste Wege
template <class TV, int maxNodes>
float *Floyd(Digraph<TV, maxNodes> g) {
const float infinit = MAXFLOAT;
float *C = new float[maxNodes*maxNodes];
// (MAXFLOAT = unendlich)
// Kostenmatrix
for (int i=0; i<maxNodes; i++)
// Kostenmatrix initialisieren
for (int j=0; j<maxNodes; j++)
if (g.IsArc(i,j))
C[i*maxNodes+j] = g.GetArc(i,j);// C[i,j] mit Kantengew. belegen
else
C[i*maxNodes+j] = infinit;
// C[i,j] mit unendlich belegen
for (int i=0; i<maxNodes; i++)
// Kostenmatrix initialisieren
for (int j=0; j<maxNodes; j++)
if (i == j ) C[i*maxNodes+j] = 0;
// C[i,i] = 0
for (int k=0; k<maxNodes; k++)
for (int i=0; i<maxNodes; i++)
for (int j=0; j<maxNodes; j++)
if (C[i*maxNodes+j] > C[i*maxNodes+k] + C[k*maxNodes+j])
C[i*maxNodes+j] = C[i*maxNodes+k] + C[k*maxNodes+j];
return C;
Der
Algorithmus hat eine Laufzeit von O(n3).
}
– 6.
Einführung
Graphen ––PAD
PG IIII –– SoSe
WS 2011/12
2009 ––Hochschule
HochschuleDarmstadt
Darmstadt
10
8. Kürzeste Wege
Beispiel:
Adjazenz Matrix:
0
1
2
3
4
-------------------------------0|
1|
2
4
2|
3|
6
4|
2
Floyd Matrix:
0
1
2
3
4
-------------------------------0|
0
oo
oo
oo
oo
1|
oo
0
6
2
4
2|
oo
oo
0
oo
oo
3|
oo
oo
6
0
oo
4|
oo
oo
2
oo
0
1
4
2
2
3
4
6
2
Bemerkung: Der Algorithmus funktioniert nur für nicht-negative Zahlen. Will man
die längsten Wege berechnen, kann anstelle vom Minimum jeweils das
Maximum ermittelt und als Initialwert MINFLOAT verwendet werden.
– 6.
Einführung
Graphen ––PAD
PG IIII –– SoSe
WS 2011/12
2009 ––Hochschule
HochschuleDarmstadt
Darmstadt
11