"Lineare Modelle in der Statistik" und - Mathematik

Exkurse
zur Linearen Algebra, Wahrscheinlichkeitstheorie
und Statistik für die Skri pte
Lineare Modelle in der Statistik
Generaliserte Lineare Modelle
von
Gerhard Osius
0.4
0
2
0.2
0. 0 -~=:r::::.,__...,......:;::::....,......~~;=,-..,....::;:::::::;::=;=-;::::;::::::;:::=:;==;==-'I"""""T'".:::;:::;:::::;:::::;
-5
0
5
10
15
20
Dichten der t ('-y)-Verteilung für n = 5 und"(= 0, 2, 4 und 8.
n
Februar 2015
Fachbereich Mathematik/Informatik
Universität Bremen
Vorwort
Dies ist eine Zusammenstellung von Resultaten (vorwiegend aus der Wahrscheinlichkeitstheorie und der Linearen Algebra) die in meinen Skripten zu den Lehrveranstaltungen Lineare Modelle in der Statistik und Generalisierte Lineare Modelle verwendet werden. Die Exkurse behandeln unter anderem die univariaten Standardverteilungen von Teststatistiken (Chiquadrat-, t- und F- Verteilungen, auch nichtzentral), die multivariate Normalverteilung - deren Darstellung an Rao (1973) Linear
Statistical lnference and its Applications angelehnt ist - sowie Verteilungskonvergenz
in euklidischen Räumen - die weitgehend Billingsley (1968) Convergence of Probility
Measures und Billingsley (1979) Probability and Measure entnommen ist.
Die Beweise der Resultate die nicht als "Standardwissen" vorausgesetzt sind werden
am Ende des jeweiligen Exkurses mehr oder weniger vollständig zusammengestellt
oder es wird auf eine Literaturstelle verwiesen. Das "Standardwissen" kann in den
einschlägigen Lehrbüchern nachgelesen werden, z.B. wenn es sich um Verteilungen
handelt, bei Johnson und Kotz (1970-72) Distributions in Statistics.
Gegenüber der Auflage vom Februar 2014 sind nur gerinfügige Änderungen und
Korrekturen vorgenommen.
Bremen, im Februar 2015
Gerhard Osius
Inhaltsverzeichnis
27.2.15
Inhalt
1
(Seiten pro Kapitel)
Verteilungen
V
Die zentralen und nichtzentralen Chiquadrat-, tund F- Verteilungen
1
Die Chiquadrat-Verteilung
1.1 Die zentrale Chiquadrat-Verteilung
1.2 Die nichtzentrale Chiquadrat-Verteilung
1.3 Grenzwertsätze und Approximationen
(6)
2
Die t- Verteilung
2.1 Die zentrale t- Verteilung
2.2 Die nichtzentrale t- Verteilung
2.3 Approximationen der nichtzentralen t- Verteilung
(5)
3
Die F- Verteilung
3.1 Die zentrale F- Verteilung
3.2 Die F- Verteilung mit reellen Freiheitsgraden
3.3 Die nichtzentrale F- Verteilung
3.4 Approximationen der nichtzentralen F- Verteilung
(7)
Beweise
1
2
3
Die Chiquadrat-Verteilung
Die t- Verteilung
Die F- Verteilung
MN
Die multivariate Normalverteilung
1.
2.
3.
4.
5.
6.
Die eindimensionale Normalverteilung
Definition der multivariaten Normalverteilung
Eigenschaften der multivariaten Normalverteilung
Quadratische Formen von normalverteilten Variablen
Bedingte Normalverteilungen
Die zweidimensionale Normalverteilung
Beweise
3. Eigenschaften der multivariaten Normalverteilung
4. Quadratische Formen von normalverteilten Variablen
5. Bedingte Normalverteilungen
(7)
(7)
(6)
(17)
(15)
Inhaltsverzeichnis
27.2.15
M
Die Multinomialverteilung
1.
2.
3.
4.
5.
6.
7.
Definition
Auftreten
Randverteilungen, Erwartungswert, Covarianz
Erzeugende Funktionen
Multinomial-Grenzwertsatz
Darstellung als bedingte Poisson-Verteilung
Darstellung als Exponential-Familie
Q
1
2
(10)
(13)
Beweise
3.
4.
5.
6.
7.
2
Randverteilungen, Erwartungswert, Covarianz
Erzeugende Funktionen
Multinomial-Grenzwertsatz
Darstellung als bedingte Poisson-Verteilung
Darstellung als Exponential-Familie
Quantile von Verteilungen
(6)
Definition und elementare Eigenschaften
1.1 Binomialverteilung
1.2 Poisson-Verteilung
Verteilungskonvergenz und Quantile
Beweise
(8)
Inhaltsverzeichnis
27.2.15
3
Maß- und Wahrscheinlichkeitstheorie
CF
Charakteristische, Momente- und Kumulanten-erzeugende
Funktionen
1.
2.
3.
4.
5.
Definition der charakteristischen Funktion
Definition der Momente- und Kumulanten-erzeugenden Funktion
Die Eindeutigkeitssätze
Rechenregeln
Momente und Kumulanten eindimensionaler Verteilungen
5.1 Charakteristische Funktion und Momente
5.2 Moment-erzeugende Funktion und Momente
5.3 Kumulanten-erzeugende Funktion und Kumulanten
6.
Spezielle Verteilungen
6.1 Eindimensionale Normalverteilung
6.2 Multivariate Normalverteilung
6.3 Binomial-Verteilung
6.4 Multinomial-Verteilung
6.5 Poisson-Verteilung
Erwartungswert und Covarianzmatrix von Zufallsvektoren
7.
Beweise (noch unvollständig)
KV
1.
2
3
4
5
6
7
8
9
10
11
12
13
14
Konvergenz nach Verteilung in euklidischen Räumen
(11)
(1)
(12)
Definition der Verteilungskonvergenz
Konvergenz von Bildmaßen
Konvergenz von Produkt-Maßen
Konvergenz nach Wahrscheinlichkeit gegen eine Konstante
Rechenregeln von Slutzky über Konvergenz nach Verteilung
und Wahrscheinlichkeit
Die Reduktionsmethode von Cramer-Wald
Der Stetigkeitssatz für charakteristische Funktionen
Der Stetigkeitssatz für Moment-erzeugende Funktionen
Der Darstellungssatz von Skorohod
Stochastische Beschränktheit und der Satz von Prohorov
Konvergenz gegen Unendlich
Konvergenz von Wahrscheinlichkeiten
Konvergenz von Quantilen
Differenzierbare Transformation (Delta-Methode)
Beweise
(9)
Inhaltsverzeichnis
27.2.15
ZGS
Der zentrale Grenzwertsatz für reelle Zufallsvariablen
1.
2.
3.
4.
Die allgemeinen Resultate von Lindeberg und Ljapunov
Resultate für identische Verteilungen
Linearkombinationen unabhängiger Verteilungen
Die Ungleichung von Berry-Esseen
4
(9)
Beweise
(7)
BV
Bedingte Verteilungen
(9)
1.
Definition
1.1 Diskreter Fall
1.2 Allgemeiner Fall
2.
Methoden zur Bestimmung bedingter Verteilungen
2.1
2.2
2.3
2.4
3.
Stochastische Unabhängigkeit
Bildmaße bedingter Verteilungen
Unabhängigkeits-Transformationen
Bedingte Dichten
Erwartungswerte bedingter Verteilungen
3.1 Nicht-negative meßbare Abbildunden
3.2 Beliebige meßbare Abbildunden
Beweise
(2)
BEC Bedingte Erwartung und Covarianz-Matrix zufälliger Vektoren (3)
1.
2.
Grundlagen
Lineares Modell mit homogenen bedingten Covarianzen-
Beweise
COV Covarianz-Matrizen zufälliger Vektoren
Beweise
(2)
(1)
Inhaltsverzeichnis
27.2.15
5
WM Wurzeln positiv-semidefiniter Matrizen
(2)
Lineare Algebra
1.
2.
3.
Definition
Wurzeln positiv-definiter Matrizen
Die Cholesky-Wurzel
Beweise
(3)
SP
Skalarprodukte und orthogonale Projektionen
(5)
1.
2.
3.
Definitionen
Eigenschaften der Projektionen
Projektionen und Exponentialfunktion
Beweise
GI
Generalisierte Inverse einer Matrix
Beweise
(14)
(2)
(7)
Inhaltsverzeichnis
27.2.15
6
Statistik
MTK Multiple Tests und Konfidenzbereiche
2.
3.
Simultane Tests
Simultane Konfidenzbereiche
Sequentielle Tests
MS
Minimale und maximale gewichtete Streuung
1.
Problemstellung
Minimierung
Maximierung
Äquidistante Werte und konstante Gewichte
1.
2.
3.
4.
(6)
(7)
Beweise
(3)
CPR Cross-Product-Ratios
(5)
1.
2.
Der Cross-Product-Ratio einer 2x2-Tafel
Der Cross-Product-Ratio einer Tafel
Beweise
(2)
Exkurse
zur Linearen Algebra, Wahrscheinlichkeitstheorie
und Statistik für die Skri pte
Lineare Modelle in der Statistik
Generaliserte Lineare Modelle
von
Gerhard Osius
0.4
0
2
0.2
0. 0 -~=:r::::.,__...,......:;::::....,......~~;=,-..,....::;:::::::;::=;=-;::::;::::::;:::=:;==;==-'I"""""T'".:::;:::;:::::;:::::;
-5
0
5
10
15
20
Dichten der t ('-y)-Verteilung für n = 5 und"(= 0, 2, 4 und 8.
n
Februar 2014
Fachbereich Mathematik/Informatik
Universität Bremen
Vorwort
Dies ist eine Zusammenstellung von Resultaten (vorwiegend aus der Wahrscheinlichkeitstheorie und der Linearen Algebra) die in meinen Skripten zu den Lehrveranstaltungen Lineare Modelle in der Statistik und Generalisierte Lineare Modelle verwendet werden. Die Exkurse behandeln unter anderem die univariaten Standardverteilungen von Teststatistiken (Chiquadrat-, t- und F- Verteilungen, auch nichtzentral), die multivariate Normalverteilung - deren Darstellung an Rao (1973) Linear
Statistical lnference and its Applications angelehnt ist - sowie Verteilungskonvergenz
in euklidischen Räumen - die weitgehend Billingsley (1968) Convergence of Probility
Measures und Billingsley (1979) Probability and Measure entnommen ist.
Die Beweise der Resultate die nicht als "Standardwissen" vorausgesetzt sind werden
am Ende des jeweiligen Exkurses mehr oder weniger vollständig zusammengestellt
oder es wird auf eine Literaturstelle verwiesen. Das "Standardwissen" kann in den
einschlägigen Lehrbüchern nachgelesen werden, z.B. wenn es sich um Verteilungen
handelt, bei Johnson und Kotz (1970-72) Distributions in Statistics.
Gegenüber der Auflage vom Februar 2012 sind nur gerinfügige Änderungen und
Korrekturen vorgenommen.
Bremen, im Februar 2014
Gerhard Osius
Inhaltsverzeichnis
4.2.14
Inhalt
1
(Seiten pro Kapitel)
Verteilungen
V
Die zentralen und nichtzentralen Chiquadrat-, tund F- Verteilungen
1
Die Chiquadrat-Verteilung
1.1 Die zentrale Chiquadrat-Verteilung
1.2 Die nichtzentrale Chiquadrat-Verteilung
1.3 Grenzwertsätze und Approximationen
(6)
2
Die t- Verteilung
2.1 Die zentrale t- Verteilung
2.2 Die nichtzentrale t- Verteilung
2.3 Approximationen der nichtzentralen t- Verteilung
(5)
3
Die F- Verteilung
3.1 Die zentrale F- Verteilung
3.2 Die F- Verteilung mit reellen Freiheitsgraden
3.3 Die nichtzentrale F- Verteilung
3.4 Approximationen der nichtzentralen F- Verteilung
(7)
Beweise
1
2
3
Die Chiquadrat-Verteilung
Die t- Verteilung
Die F- Verteilung
MN
Die multivariate Normalverteilung
1.
2.
3.
4.
5.
6.
Die eindimensionale Normalverteilung
Definition der multivariaten Normalverteilung
Eigenschaften der multivariaten Normalverteilung
Quadratische Formen von normalverteilten Variablen
Bedingte Normalverteilungen
Die zweidimensionale Normalverteilung
Beweise
3. Eigenschaften der multivariaten Normalverteilung
4. Quadratische Formen von normalverteilten Variablen
5. Bedingte Normalverteilungen
(7)
(7)
(6)
(17)
(15)
Inhaltsverzeichnis
4.2.14
M
Die Multinomialverteilung
1.
2.
3.
4.
5.
6.
7.
Definition
Auftreten
Randverteilungen, Erwartungswert, Covarianz
Erzeugende Funktionen
Multinomial-Grenzwertsatz
Darstellung als bedingte Poisson-Verteilung
Darstellung als Exponential-Familie
Q
1
2
(10)
(13)
Beweise
3.
4.
5.
6.
7.
2
Randverteilungen, Erwartungswert, Covarianz
Erzeugende Funktionen
Multinomial-Grenzwertsatz
Darstellung als bedingte Poisson-Verteilung
Darstellung als Exponential-Familie
Quantile von Verteilungen
(6)
Definition und elementare Eigenschaften
1.1 Binomialverteilung
1.2 Poisson-Verteilung
Verteilungskonvergenz und Quantile
Beweise
(8)
Inhaltsverzeichnis
4.2.14
3
Maß- und Wahrscheinlichkeitstheorie
CF
Charakteristische, Momente- und Kumulanten-erzeugende
Funktionen
1.
2.
3.
4.
5.
Definition der charakteristischen Funktion
Definition der Momente- und Kumulanten-erzeugenden Funktion
Die Eindeutigkeitssätze
Rechenregeln
Momente und Kumulanten eindimensionaler Verteilungen
5.1 Charakteristische Funktion und Momente
5.2 Moment-erzeugende Funktion und Momente
5.3 Kumulanten-erzeugende Funktion und Kumulanten
6.
Spezielle Verteilungen
6.1 Eindimensionale Normalverteilung
6.2 Multivariate Normalverteilung
6.3 Binomial-Verteilung
6.4 Multinomial-Verteilung
6.5 Poisson-Verteilung
Erwartungswert und Covarianzmatrix von Zufallsvektoren
7.
(11)
Beweise (noch unvollständig)
KV
1.
2
3
4
5
6
7
8
9
10
11
12
13
14
Konvergenz nach Verteilung in euklidischen Räumen
(12)
Definition der Verteilungskonvergenz
Konvergenz von Bildmaßen
Konvergenz von Produkt-Maßen
Konvergenz nach Wahrscheinlichkeit gegen eine Konstante
Rechenregeln von Slutzky über Konvergenz nach Verteilung
und Wahrscheinlichkeit
Die Reduktionsmethode von Cramer-Wald
Der Stetigkeitssatz für charakteristische Funktionen
Der Stetigkeitssatz für Moment-erzeugende Funktionen
Der Darstellungssatz von Skorohod
Stochastische Beschränktheit und der Satz von Prohorov
Konvergenz gegen Unendlich
Konvergenz von Wahrscheinlichkeiten
Konvergenz von Quantilen
Differenzierbare Transformation (Delta- Methode)
Beweise
(9)
Inhaltsverzeichnis
4.2.14
ZGS
Der zentrale Grenzwertsatz für reelle Zufallsvariablen
1.
2.
3.
4.
Die allgemeinen Resultate von Lindeberg und Ljapunov
Resultate für identische Verteilungen
Linearkombinationen unabhängiger Verteilungen
Die Ungleichung von Berry-Esseen
4
(9)
Beweise
(7)
BV
Bedingte Verteilungen
(9)
1.
Definition
1.1 Diskreter Fall
1.2 Allgemeiner Fall
2.
Methoden zur Bestimmung bedingter Verteilungen
2.1
2.2
2.3
2.4
3.
Stochastische Unabhängigkeit
Bildmaße bedingter Verteilungen
Unabhängigkeits-Transformationen
Bedingte Dichten
Erwartungswerte bedingter Verteilungen
3.1 Nicht-negative meßbare Abbildunden
3.2 Beliebige meßbare Abbildunden
Beweise
(2)
BEC Bedingte Erwartung und Covarianz-Matrix zufälliger Vektoren (3)
1.
2.
Grundlagen
Lineares Modell mit homogenen bedingten Covarianzen-
Beweise
COV Covarianz-Matrizen zufälliger Vektoren
Beweise
(2)
(1)
Inhaltsverzeichnis
4.2.14
5
WM Wurzeln positiv-semidefiniter Matrizen
(2)
Lineare Algebra
1.
2.
3.
Definition
Wurzeln positiv-definiter Matrizen
Die Cholesky-Wurzel
Beweise
(3)
SP
Skalarprodukte und orthogonale Projektionen
(5)
1.
2.
3.
Definitionen
Eigenschaften der Projektionen
Projektionen und Exponentialfunktion
Beweise
GI
Generalisierte Inverse einer Matrix
Beweise
(14)
(2)
(7)
Inhaltsverzeichnis
4.2.14
6
Statistik
MTK Multiple Tests und Konfidenzbereiche
2.
3.
Simultane Tests
Simultane Konfidenzbereiche
Sequentielle Tests
MS
Minimale und maximale gewichtete Streuung
1.
Problemstellung
Minimierung
Maximierung
Äquidistante Werte und konstante Gewichte
1.
2.
3.
4.
(6)
(7)
Beweise
(3)
CPR Cross-Product-Ratios
(5)
1.
2.
Der Cross-Product-Ratio einer 2x2-Tafel
Der Cross-Product-Ratio einer Tafel
Beweise
(2)
V
Die zentralen und nichtzentralen Chiquadrat-,
t- und F-Verteilungen
Gerhard Osius
1
Die Chiquadrat-Verteilung
1.1
1.2
1.3
2
Die t- Verteilung
2.1
2.2
2.3
3
Die zentrale Chiquadrat-Verteilung
Die nichtzentrale Chiquadrat-Verteilung
Grenzwertsätze und Approximationen
Die zentrale t- Verteilung
Die nichtzentrale t- Verteilung
Approximationen der nichtzentralen t- Verteilung
Die F- Verteilung
3.1
3.2
3.3
3.4
Die zentrale F- Verteilung
Die F- Verteilung mit reellen Freiheitsgraden
Die nichtzentrale F- Verteilung
Approximationen der nichtzentralen F- Verteilung
V
Die zentralen und nichtzentralen Chiquadrat-,
t- und F-Verteilungen
Gerhard Osius
1
Die Chiquadrat-Verteilung
1.1
1.2
1.3
2
Die t- Verteilung
2.1
2.2
2.3
3
Die zentrale Chiquadrat-Verteilung
Die nichtzentrale Chiquadrat-Verteilung
Grenzwertsätze und Approximationen
Die zentrale t- Verteilung
Die nichtzentrale t- Verteilung
Approximationen der nichtzentralen t- Verteilung
Die F- Verteilung
3.1
3.2
3.3
3.4
Die zentrale F- Verteilung
Die F- Verteilung mit reellen Freiheitsgraden
Die nichtzentrale F- Verteilung
Approximationen der nichtzentralen F- Verteilung
G. Osius: Die Chiquadrat-Verteilung
8.7.10
1
Die Chiquadrat-Verteilung
1.1
Die zentrale Chiquadrat- Verteilung
V1-1
U = (U , ..., U ) sei ein n-dimensionaler Zufallsvektor, dessen Komponenten unab1
n
hängige reelle Zufallsvariablen mit Standard-Normalverteilung sind, d.h. L(U.)
Z
N(O, 1) für alle i = 1, ..., n. Die Verteilung der Quadratsumme
heißt eine zentrale Chiquadrat-Verteilung mit n Freiheitsgraden, die mit dem Symbol
2
X bezeichnet wird:
n
(2)
Da der Zufallsvektor U eine n-dimensionale Standard-Normalverteilung besitzt
n
(3)
L(U) = N (0,11 ) =
n
n
TI N(O, 1) ,
. 1
Z=
läßt sich die X2 -Verteilung auch suggestiv schreiben als das Normquadrat der n-din
mensionalen Standard-Normalverteilung
(4)
Die X2 - Verteilung besitzt eine Dichte cp , die nur auf den positiven Bereich (0,00)
n
n
konzentriert ist, und dort gegeben ist durch:
(5)
wobei
für
x> 0,
r die Eulersche Gamma/unktion ist:
00
(6)
r(a) = jtcx-1e-tdt.
o
Die Dichte cpn beschreibt auf (0,00) im Fall n < 2 eine fallende Kurve und im Fall
n> 2 eine schiefe Glockenkurve mit der Maximalstelle in x = n- 2 und zwei Wende-
punkten in x = (n- 2) ±
stelle.
J 2 (n -
2) also im Abstand
J 2 (n -
2) von der Maximal-
G. Osius: Die Chiquadrat-Verteilung
Vl-2
8.7.10
....Q)
..c
ü
(5
0.2
o. 0 +-Ä---.---.--....--,:::::;::::::::;:==;=-.,..::::;:::::::;::=r=;;;;;:=M=;=""T"'".,....-~:::;::=;=:;=;
o
5
10
15
20
25
2
Dichten der X -Verteilung jür die Freiheitsgrade m = 1,3,5 und 10.
m
Die Verteilungsjunktion P der X2 -Verteilung ist auf (0,00) streng monoton wachn
n
send und dort gegeben durch
x
(7)
Pn(x)
=P{x~ <x} =J cpn(u)du
für
x> o.
o
Das (obere) a-Quantil x~. et der x~ -Verteilung ist dann gegeben durch
,
(8)
X2
ni et
=p-1 (1-a)
n
bzw.
p{X 2 >X2
n-
Für den Freiheitsgrad n=l lassen sich P 1 bzw.
P bzw. das obere
~ -Quantil
}=a
ni et
xi.
et
fürO<a<1.
durch die Verteilungsfunktion
z et/2 = P- (1_ ~)' der Standard-Normalverteilung
1
N(O,l) beschreiben:
(9)
(10)
1- 2P(-JX)
für
x> 0,
für 0< a< 1.
Der Erwartungswert von X 2 ist der Freiheitsgrad n,und die Varianz ist der doppelte
n
Freiheitsgrad
(11)
G. Osius: Die Chiquadrat-Verteilung
8.7.10
Vl-3
Die Faltung von X2- Verteilungen ist wieder eine solche
2
xm
und X 2 stochastisch unabhängig
n
(12)
::::}
Für wachsenden Freiheitsgrad konvergiert die standardisierte X2 -Verteilung nach
n
Verteilung gegen die Standard-Normalverteilung
(x~ - n)/ y'2n ~ N(O,l)
(13)
für n ---+
00,
für n ---+
00.
und es folgt
x~/n
(14)
p)
1
Die X2 -Verteilung ist eine spezielle Gamma-Verteilung
n
X~ = Gam(~,2),
(15)
und hieraus kann man weitere (und teilweise auch obige) Eigenschaften der
X - Verteilungen herleiten. Eine Gamma-Verteilung der Form Garn ( ~, 2) mit belie2
bigem v> 0 wird daher auch als Chiquadrat-Verteilung mit Freiheitsgrad v bezeichnet:
Gam( ~,2)
(16)
1.2
für v> o.
Die nichtzentrale Chiquadrat-Verteilung
U = (U , ..., U ) sei ein n-dimensionale Zufallsvektor, dessen Komponenten unabhän1
n
gige reelle Zufallsvariablen mit folgneder Normalverteilung sind
(1)
L(U.)
z = N(fL·,l)
z
für i = 1,...,n.
Dann hängt die Verteilung der Quadratsumme
nur noch über die sogenannte Nichtzentralität
vom Vektor Jl = (fLl' ... ,fL ) der Erwartungswerte ab. Diese Verteilung
n
G. Osius: Die Chiquadrat-Verteilung
Vl-4
8.7.10
heißt die nichtzentrale X 2- Verteilung mit n Freiheitsgraden und Nichtzentraltität 8. Da
der Zufallsvektor U n-dimensional normalverteilt ist mit Erwartungsvektor Jl
n
(5)
cL'(U) = N (Jl,ll ) = TI N(Jlo,l) ,
n
n
i=l
z
läßt sich die X2 (8)- Verteilung auch suggestiv schreiben als
n
(6)
Für 8 =
mit
°bzw. Jl
2
= 0 liegt die zentrale X - Verteilung vor:
(7)
Die Faltung von nichtzentralen X2- Verteilungen ist wieder eine solche mit der
Summe der Freiheitsgerade bzw. Nichtzentralitäten als Freiheitsgrad bzw. Nichtzentralität:
Für den Freiheitsgrad n = 1 ist
und die Dichte <Pl6 bzw. Verteilungsfunktion P 1 6 von X; (8) ergeben sich aus der
,
,
Dichte 
2
2
fürx>O,
°
fürx>O.
2
Für n> 1 läßt sich die X (8) als Faltung von X (8) mit der zentralen X l-Verteilung
n
l
ndarstellen
(12)
X; (8) und X~-l unabhängig
Hieraus ergibt sich für die Dichte 0
J P1 6 (x- y) . 0, n > 1,
für x> 0, n > 1.
'
2
n,us: auf (0,00) positiv, und für die Verteilungsfunktion Pn,us: von Xn(8)
G. Osius: Die Chiquadrat-Verteilung
Vl-5
8.7.10
P s: ist streng wachsend auf (0,00).
(15)
n,u
Die Verteilungsfunktion hängt von der Nichtzentralität wie folgt ab
Pn 8(x) = P{X~(8) < x}
(16)
,
ist streng wachsend in x> 0
und streng fallend in 8>0 für x> O.
Für 8 ---+ 00 ergeben sich - aus (9) für n= 1 und mit (11) für nE W - die Grenzwerte
für 8 ---+ 00,
(17)
P n,oo (x) = 0
(18)
für x
> o.
Das obere a-Quantil von X2 (8) ist definiert durch
n
2
X
(19)
1
n,et
2
2
(8) = P- s:(1-a) bzw. P{X n > X n ,,,(8)} = a
n,u
,u-
für 0< a< 1,
und es gilt
(20)
X
2
n,et
(8) ist streng fallend in a und streng wachsend in 8
sowie (vgl. z.B. Agresti 1990, p.98)
(21)
Pn,8 (X~ ,et) = P{X~(8) < X~ ,et} ist streng wachsend in n.
Der Erwartungswert und die Varianz von X2 (8) lauten
n
2
(22)
Var{x (8)} = 2(n
n
+ 28) .
o
0.1
o. 0 ~r--T""---r--"'T"'""""""T---r-~.....----T----r----r--T"'"""""'T---':=:::;=::;:::=;:~~
o
5
10
15
20
Dichten der X2 (8)-Verteilung für n = 5 und Nichtzentralitäten 8 = 0, 1, 2 und 4.
n
G. Osius: Die Chiquadrat-Verteilung
Vl-6
8.7.10
Allgemeiner ist die k-te Kumulante von X2 (8) gegeben durch (vgl. Johnson-Kotz
n
1970-72, Chap. 28, Sec. 4):
Hieraus ergeben sich speziell die Kumulanten und zentralen Momente 3. und 4.
Ordnung zu
(24)
~3(X~( 8))
fL3(X~( 8)) = 8 (n- 38) ,
(25)
~iX~(8))
48 (n- 48) ,
(26)
fL3(X~( 8))
~4(X~(8)) + 3 (Var{x~(8)})2
1.3
48(n-48)
+ 12(n+28)2.
Grenzwertsätze und Approximationen
Die nichtzentrale X2 (8)-Verteilung ist nach 1.3 (8) die n-fache Faltung von
n
X~( Verteilungen. Hieraus ergibt sich mit dem Zentralen Grenzwertsatz die
%)-
asymptotische Normalverteilung der Standardisierung von X2 (8) für n---+ 00
n
X~(8) - (n+8)
(1)
J2(n + 28)
L
)
N(O, 1) ,
n-HX!
die für 8 = 0 zu 1.1 (13) reduziert. Für nicht zu kleines n erhält man hieraus die Normal-Approximation von X2 (8)
n
(2)
fL = n+8,
mit
a=
J 2(n + 28)
.
Eine andere Approximation, die auch für kleines n gilt, hat Patnaik (Biometrika 36,
1949, 202-232) vorgeschlagen. Hierbei wird die nichtzentrale Verteilung X2 (8) durch
n
2
das Vielfache c· X einer zentralen Verteilung approximiert, wobei c> 0 und v> 0
v
so gewählt werden, daß die ersten beiden Momente beider Verteilung übereinstimmen (vgl. auch Johnson-Kotz 1970-72, Ch. 28, Sec. 8)
n+28
(3)
c =
n
+8
(n+8)2
v =
n
+ 28
Hieraus ergibt sich die Gamma-Approximation von X2 (8)
n
(4)
mit der sich die Dichte und Verteilungsfunktion von X2 (8) approximieren lassen.
n
G. Osius: Die t- Verteilung
V2-1
8.7.10
2
Die t- Verteilung
2.1
Die zentrale t- Verteilung
Sind U und V unabhängige reelle Zufallsvariablen mit den Verteilungen
L(U) = N(O, 1L
(1)
L(V) =
X
2
n!
so heißt die Verteilung des Quotienten
(2)
T=
U
V1n V
eine zentrale t-Verteilung mit n Freiheitsgraden, die mit t bezeichnet wird
n
tn : = L(T) = cL( U/
(3)
V~ V ) .
Die t -Verteilung läßt sich suggestiv auch schreiben als
n
(4)
tn
:=
N(O,l)
/V1n X2n
für unabhängige N(O, 1) und X2 .
n
Die t -Verteilung besitzt auf IR folgende Dichte ep
n
n
x2 )-(n+ 1)/2
(5)
epn ( x ) = an ( 1 + -n
für x E IR ,
wobei die Konstante a unter Verwendung der Eulerschen-Gammafunktion
n
niert ist durch
(6)
a
n
r(n~1 ) / (r( ~ );:;;;-).
Die Dichte ep beschreibt eine um
n
depunkten in x = ± Jn/(n+2) .
Die Verteilungs/unktion P mit
n
x=o symmetrische Glockenkurve
mit den Wen-
x
Pn(x) =P{tn <x} =
-
(7)
r defi-
J epn(u)du
00
ist eine streng monoton wachsende sigmoide Kurve, die drehsymmetrisch im Punkt
(0,
(8)
+)
ist:
P (-x) = 1- P (x).
n
n
Das obere a-Quantil t
(9)
1
n,(X
der t -Verteilung ist dann gegeben durch
t : = p- (1- a)
n,(X
n
n
bzw.
P {t
>t
n- n,(X
}= a
für 0< a < 1.
G. Osius: Die t- Verteilung
V2-2
8.7.10
500
004
0.3
0.2
0.1
o. 0 ~"""""=;=::;::~T""'T"""T""T"""r-T""'1r-r-r"""T""'T""T""'T""T""T'""'T""T'""'T""T""T""'T"""T""'T"""T'""'T""'1r-r=:;==;=-r..,....;r::;
-4
-3
-1
-2
o
2
3
4
Dichten der t -Verteilung für die Freiheitsgrade n = 1, 2, 5 und 500.
n
Der Erwartungswert existiert nur für n> 1 und lautet
(10)
für n> 1.
E{tn } = 0
Und die Varianz existiert erst für n> 2 und ist dann
(11 )
Var {t } = n/ (n - 2)
n
>1
für n>2.
Für wachsenden Freiheitsgrad konvergiert die t
n
Verteilung gegen die Standard-
Normalverteilung
(12)
t
n
cf)
N(O,l)
für n
---+ 00,
d.h. es gilt
(13)
lim P (x) = P (x)
n
n---+oo
für alle x E IR
wobei P die Verteilungsfunktion von N(O,l) ist. Folglich konvergieren auch die zugehörigen Quantile
(14)
lim t
n---+oo
n,(X
= z
(X
für alle O<a<l,
wobei z(X = p-1 (1- a) das obere a-Quantil von N( 0,1) ist. Außerdem konvergieren
auch die Dichten cp punktweise gegen die Dichte cp von N(O,l):
n
(15)
lim
n---+oo
cp (x) = cp(x)
n
für alle xE IR.
G. Osius: Die t- Verteilung
2.2
V2-3
8.7.10
Die nichtzentrale t- Verteilung
Sind U und V unabhängige reelle Zufallsvariablen mit den Verteilungen
(1)
L(U) = Nb, 1),
so heißt die Verteilung des Quotienten
(2)
T=
U
V1n V
eine doppelt nichtzentrale t-Verteilung mit n Freiheitsgraden und den Nichtzentralitäten
"( und 8, die mit t ("(,8) bezeichnet wird
n
(3)
tn ("(,8):= L(T) =
4U / V~ V).
Die t ("(,8)-Verteilung läßt sich suggestiv auch schreiben als
n
2
(4)
für unabhängige N("( ,1) und X (8).
n
Für 8 = 0 ergibt sich die (einfach) nichtzentrale t b)- Verteilung mit Nichtzentralität "(
n
(5)
t ("() : = t ("(,0) = Nb, 1) /
n
n
V1n X2n
2
für unabhängige N("( ,1) und X .
n
Und für "( = 8 = 0 erhält man die zentrale t -Verteilung
n
(6)
t = t (0) = t (0,0).
n
n
n
0.4
0
0.2
o. 0 -k::::'-r4-,...4.---'---'~'T"""""r"::::;::::'=r=-';::::;::::;==:;:=;==-~:::;::::;:::::;=;
-5
o
5
10
15
20
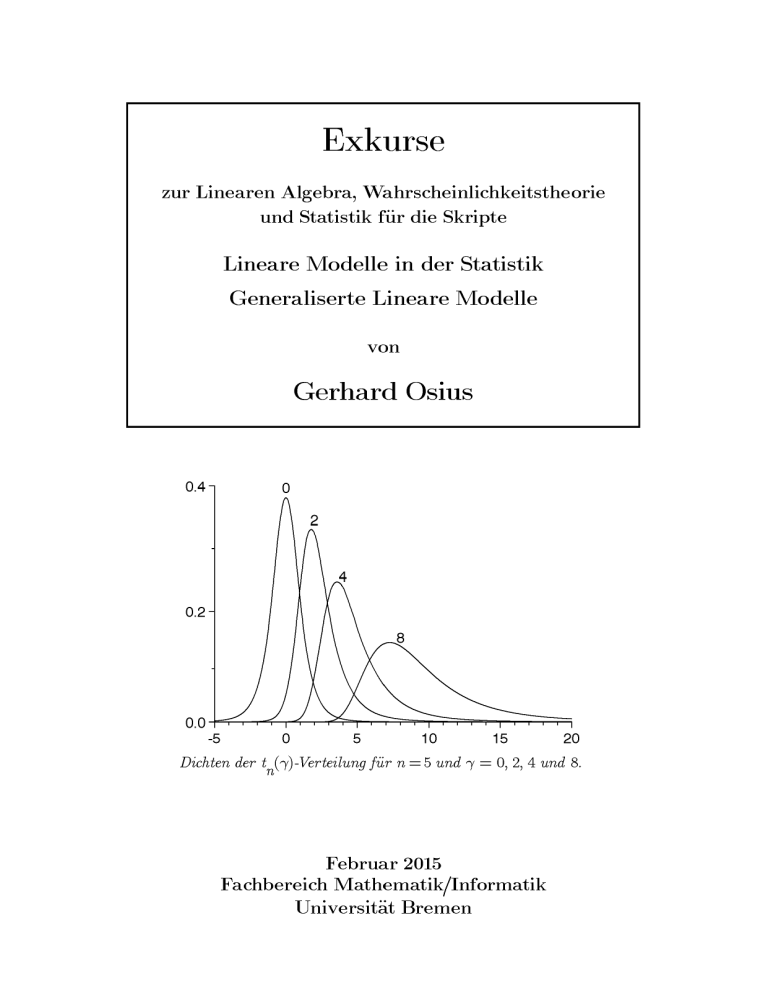
Dichten der t ("()-Verteilung für n = 5 und Nichtzentralitäten "( = 0, 2, 4 und 8.
n
G. Osius: Die t- Verteilung
Die Dichte cp
V2-4
8.7.10
, von t ("(,8) läßt sich unter Verwendung der Dichten cp von N( 0,1)
n,"f,V
n
2
und cp ,von X (8) angeben:
n,v
n
00
(7)
cp
n,"(,
8(x) =
2
2
J
2nw .cp(wx-"().cp 8(nw )dw >
0
n,
Und die Verteilungsfunktion P
0
für xEIR.
, von t ("(,8) ergibt sich
n,"(,v
n
(8)
für xEIR.
Im Zusammenhang mit Schärfebetrachtungen von Tests sind folgende MonotonieEigenschaften der Verteilungsfunktion von Interesse:
(9)
P n, "( , 8(x) ist streng monoton wachsend in x E IR,
(10)
Pn,"(, 8( x) ist streng monoton fallend in "(E IR,
(11)
Pn,"(, 8( x) ist für x> 0 streng monoton wachsend in 8> 0,
wobei sich für "( ---+
(12)
± 00 bzw. 8 ---+ 00 folgende Grenzwerte ergeben
P n,-oo, 8(x) = 1,
P n, +00, 8(x)=0
P n, "(,00 (x) = 1
für x> 0
für xE IR
weil
p
(13)
tn ("(, 8) -------+ ± 00
(14)
tn ("(, 8)
p
-------+
0
für "( ---+
± 00,
für 8 ---+
00.
Ein Vorzeichenwechsel der Nichtzentralität "( bewirkt eine Spiegelung der Verteilung um Null
(15)
tn (-"(,8) = - tn ("(,8),
und hieraus ergibt sich für die Verteilungsfunktion
(16)
P
,(x) = 1-pn,
n,-"(,v
,(-x)
für xEIR.
"(,v
Erwartungswert und Varianz der einfach nichtzentralen Verteilung lauten
(17)
"( .fiif2 . r ( n;-l )/ r ( ~ )
(18)
(1
+ "(2)n/(n-2)
- E{t ("()}2
n
für n> 1,
für n>2.
G. Osius: Die t- Verteilung
2.3
V2-5
8.7.10
Approximationen der nichtzentralen t- Verteilung
Wir betrachten die doppelt-nichtzentral-t-verteilte Zufallsvariable
(1)
U
Tn
mit stochastisch unabhängigen
)1 V
n n
(2)
Für n ---+ 00 gilt
(3)
)1n Vn
S :=
n
P
----+l
n---+ 00
1
und somit
(4)
Tn
L
n---+ 00
l
Nb,l)
bzw.
tn ('Y,8)
N( 'Y, 1)
n---+ 00
Die zugehörigen Approximationen
(5)
S
n
~
für großes n
1,
sind allerding relativ grob. Aus der asymptotischen Normalverteilung von S
(6)
n
mit
(7)
ergibt sich als Präzisierung von (3) die Normalapproximation
(8)
mit
f-L
n
-----+
a
1,
n
-----+
O.
Daraus erhält man folgende Approximation der doppelt-nicht-zentralen t- Verteilungsfunktion für nicht zu kleines n
(9)
<!>
n,
,(x)
"(,u
~
<!>(u)
mit
u
Für die einfach-nicht-zentrale t- Verteilung reduziert dies zur Approximation
(10)
<!>
n, "{,
o(x)
~
<!>(u)
mit
U
=
X-,
V 1+ 2n
x2
die auf Johnson & Welch (1940, Biometrika 31, 362-389) zurückgeht, vgl. auch
Scheffe (1959, The Analysis
1970-72, eh. 31, Sec. 6.
01 Variance)
problem IV.4, p. 415) sowie Johnson & Kotz
G. Osius: Die F- Verteilung
V3-1
8.7.10
3
Die F- Verteilung
3.1
Die zentrale F- Verteilung
Sind U und V unabhängige reelle Zufallsvariablen mit Chiquadrat-Verteilungen
2
(1)
L( V) = X2n ,
L(U) = X ,
m
so heißt die Verteilung des Quotienten
(2)
lU
m
F
lV
n
eine zentrale F-Verteilung mit Zähler-Freiheitsgrad m und Nenner-Freiheitsgrad n) die
mit F
m,n
(3)
bezeichnet wird
F
Die F
m,n
m,n
= L(F) = L((lU)/(lV)).
n
m
-Verteilung läßt sich suggestiv auch schreiben als
1
(4)
2
mXm
Fm,n
2
2
für unabhängige Xm und X n .
12
nXn
Die F
m,n
-Verteilung besitzt eine Dichte cp
m,n
,die nur auf dem positiven Bereich
(0,00) von Null verschieden ist, und dort gegeben ist durch
(x) = d
. ~1 (mx
(5)
cp
(6)
p = ~ m,
(7)
dm,n - m n . r(p). r(q) ,
wobei
m,n
m,n
_
+ n)-(p+q) >
°
q= ~ n
p q
mit
und
r(p+q)
r die Eulersche Gammafunktion ist.
Die Dichte cp mn beschreibt für positive Argumente x im Fall m
,
fallende Kurve und im Fall
··
- n(m-2) 1
f ur
x - m(n+2) < .
Die Verteilungsjunktion P
< 2 eine monoton
m> 2 eine
schiefe "Glockenkurve" mit einem Maximum
der F
-Verteilung ist auf (0,00) streng monoton
m,n
m,n
wachsend und dort gegeben durch
x
(8)
P m,n (x) =P{Fm,n <x} =
Das obere a-Quantil F
m,n;o:
der F
m,n
J cp m,n (u)du.
o
-Verteilung ist dann gegeben durch
G. Osius: Die F- Verteilung
F
(9)
:=
m,n;Oi
V3-2
8.7.10
p-l (1- a)
bzw.
m,n
P{Fmn>Fmn·Oi }=a
,
,,
für O<a<1.
Der Erwartungswert existiert nur für n> 2 und hängt nicht von m ab:
(10)
E{ Fm,n } = --.I!:-2
n-
>
für n> 2.
1
Und die Varianz existiert erst für n> 4 und ist dann
2
2n (m+n-2)
(11)
Var{F
m,n
} =
m (n-
2)
2
(n-
für n>4.
4)
Bei Vertauschen beider Freiheitsgrade ergibt sich
(12)
F
1
n,m
F
m,n
(13)
p
(14)
F
n,m
(x)=l-P m,n (1)
X
für x
1
n,m;Oi
> 0,
für 0 < a< 1.
F
m,n;l-Oi
Für den Zähler-Freiheitsgrad m = 1 ergeben sich folgende Zusammenhänge zur zentralen t -Verteilung und deren Verteilungsfunktion P :
n
n
2
(15)
F
(16)
Pl ,n ( x) = 1 - 2 P n (-
l,n
= t
n
JX)
für x
64
> 0,
64
m = 1, 4, 16, 64
m=8
n = 1, 4, 16, 64
n=8
0.5
0.5
o ...fL.r---.-T"""""T'"...,.....,---.-...,......,--.--,.......,...,..::;:::::;=:~;;;;=;;;;;;;;;;
o
2
Dichten der F
3
m,n
4
O-t-'-f'---r""--"""""'''''--'''''''''''--'--T"""""T"--r-T"""""T"--r-T""""T--r-.,.....,
o
2
3
-Verteilung für verschiedene Freiheitsgrade mund n.
4
G. Osius: Die F- Verteilung
2
F1,n;Ct = tn;Ct/2
(17)
V3-3
8.7.10
für
°< a<
Für wachsenden Nenner-Freiheitsgrad n konvergiert die F
m,n
skalierte X2- Verteilung:
(18)
ci:
Fm,n
1
2
-·X
m
m
-------+
1.
-Verteilung gegen eine
für n ---+ 00.
Im Zusammenhang mit der Konstruktion von Konfidenzintervallen ist noch folgende Monotonie der Quantile bzgl. des Zählerfreiheitsgrades von Interesse:
(19)
3.2
m· F
m,n,Ct
ist für
°< a< 1 streng monoton wachsend bzgl.
mElN.
Die F- Verteilung mit reellen Freiheitsgraden
Aus der Darstellung der Chiquadrat-Verteilung als Gamma-Verteilung
ergibt sich die zentrale F- Verteilung wie folgt
1. Gam(:0 1)
(2)
m
Fm,n
2'
für unabhängige Gam(!J], l)und Gam(%, 1).
1. Gam(!!:. 1)
n
2'
Ersetzt man die natürlichen Zahlen m, n durch positive reelle Zahlen r, s > 0, so erhält man die (zentrale) F -Verteilung mit reellen Freiheitsgraden r, s
r,s
(3)
1.
Gam(I...2' 1)
r
Fr,s
für unabhängige Gam(~, l)und Gam(~, 1).
1. Gam(~ 1)
2'
S
Die F -Verteilung besitzt eine Dichte cp ,die nur auf dem positiven Bereich
r~
r~
(0,00) von Null verschieden ist, und dort gegeben ist durch
d
. ~1 (rx
(5)
cpr/
, x)
(6)
P=2'
(7)
dr,s = "p sq. r(p+q)
r,s
r
+ s)-(p+q)
>
°
q=2..
mit
und
2
r(p)· r(q)
Die F- Verteilung läßt sich in eine Beta-Verteilung transformieren und umgekehrt.
Für die streng wachsende Funktion g: (0, (0)
-----+
(0,1)
G. Osius: Die F- Verteilung
(8)
1
1 + s/(rx)
rx
rx + s
g(x)
V3-4
8.7.10
ergibt sich
(9)
rFrs,
r Frs, + s
g(Fr,s)
1
1 + s/(r Fr ,s)
Insbesondere läßt sich die Verteilungsfunktion x}
,
r,s
'""-'
B(p, q) .
von F
r,s
wie folgt berechnen
P{ B(p, q) < g(x)} = I(g(x) p, q)
1
P{B(p,q) >g(x)} = I(l-g(x)lq,p)
mit 1(-1 p, q) als unvollständiger Beta-Quotienten-Funktion (vgl. Exkurs Beta-Vertei-
lung).
Die nichtzentrale F- Verteilung
3.3
Sind U und V unabhängige reelle Zufallsvariablen mit den Verteilungen
2
L(U) = Xm
(8),
(1)
so heißt die Verteilung des Quotienten
F =
(2)
lU
m
lV
n
eine (doppelt) nichtzentrale F- Verteilung mit dem Zähler- und Nenner-Freiheitsgrad m
und n, sowie den Zähler- und Nenner-Nichtzentralitäten 8 und c, die mit F
m,n
(8, c) be-
zeichnet wird:
(3)
Fm,n (8,c) = L(F) = L((lU)j(lV)).
m
n
Die F
m,n
(8, c)-Verteilung läßt sich suggestiv auch schreiben als
1
(4)
F
m,n
(8,c) =
2
(8)
X
;:
m
lX (c)
2
n n
Speziell für c = 0 ergibt sich die (einfach) nichtzentrale F
m,n
Nichtzentralität 8
2
für unabhängige Xm (8) und X n (c).
(8)-Verteilung mit der
G. Osius: Die F- Verteilung
(5)
2
Fm,n (8) = Fm,n (8,0) =
m,n
F
m,n
Die Dichte cp
cp
nf
2
m
= F
m,n
-Verteilung
(0) = F m,n (0,0).
s: von F
m,n,u,e
2
für unabhängige Xm (8) und Xn .
Und für 8 = c = 0 erhält man die zentrale F
(6)
V3-5
8.7.10
m,n
2
(8,c) läßt sich unter Verwendung der Dichten cp
s: und
m,u
von X (8) und X (c) angeben:
n
00
(7)
J mnv'cpm,us:(mvx)·cpn,e (nv)
cpm,n,u,e
s: (x) =
(8)
s: von X2 (8) zu
m,u
P
>
für
0
x> O.
o
Und die Verteilungsjunktion P
funktion P
dv
s: von F
m,n,u,e
m,n
(8,c) ergibt sich mit der Verteilungs-
m
m,n,b,e
(x)
P{ Fm,n(8,c) <x}
00
oJ n·P m, b(mvx).cpn,e (nv) dv
für
x> O.
Bei Vertauschen beider Freiheitsgrade und Nichtzentralitäten ergibt sich
(9)
1
Fn ,m(c,8) = F
(8 c)
m,n '
(10)
P
n,m,e,b
(x)=l-P
(1)
für x
m,n,b,e x
> 0,
m=8
n = 16
8 = 0, 1, 2, 4
0.5
o. 0 ~--r---r---r----r----r-----r-----r~---,-.----r--..----r--~--r---r---r----,
o
Dichten der F
m,n
1
(8)- Verteilung jür
2
m = 8)
3
n = 16 und verschiedene Nichtzentralitäten 8.
G. Osius: Die F- Verteilung
V3-6
8.7.10
Für den Zähler-Freiheitsgrad m = 1 erhält man folgenden Zusammenhang zur
nichtzentralen t- Verteilung:
(11)
F1,n (8,c)=t2n (j6,c).
Im Zusammenhang mit Schärfebetrachtungen von Tests sind folgende MonotonieEigenschaften der Verteilungsfunktion von Interesse:
(12)
p
s:
m,n,u,e
(x) ist
• streng wachsend in xE (0,00),
• streng wachsend in c> 0
für x> 0,
8 >0
für x> o.
• streng fallend in
(13)
p
s:
(~) ist für x>O streng monoton fallend in mElN.
m,n,u,e m
Für 8 ---+ 00 bzw. c ---+ 00 ergeben sich mit 1.2 (17) folgende Grenzwerte
(14)
F
P
(8,c) -------+
00
(15)
F
(8,c)
n,m
n,m
p
-------+
0
für 8 ---+ 00,
für c ---+ 00,
und somit insbesondere
(16)
p
p
s:
m,n,u,oo
m,n,oo,e
(x) = 1
für x >0,
(x) = 0
für x
> O.
G. Osius: Die F- Verteilung
3.4
V3-7
8.7.10
Approximationen der nichtzentralen F- Verteilung
Nach Severo & Zelen (1960, Biometrika 47, 411-416) läßt sich die Verteilungsfunktion
P
s: der (einfach) nichtzentralen F
(8)-Verteilung wie folgt durch die Verteim,n,u
m,n
lungsfunktion P von N(O,l) approximieren:
(1)
Pm,n,D (x) ~
p( u I JV)
mit
u = (1-~n)wl/3_(1-a),
a =
v = a
2 (m + 28)
9(m+8)2 '
2 3
+ 9n
2 w /
'
mx
m+8
w =--
Tiku (1966, Biometrika 52, 415-427) gibt eine Approximation der (einfach) nichtzen-
tralen F (8)-Verteilung durch eine zentrale F- Verteilung
m,n
(2)
[Fm,n (8)
+ c] /
b ~ Fr,n
(three-moment central-F approximation)!
wobei der reelle Freiheitsgrad r und die Parameter b, c so gewählt sind, daß die ersten drei Momente der beiden Verteilungen in (2) übereinstimmen:
(3)
r
~(n-2) h/1/(1-4K3IH2) -1],
(4)
b =
r·H
m K (2r + n - 2) ,
(5)
H= 2(m + 8)3
c =
n (b -1- 151m)
n-2
mit
+ 3 (m + 8)(m + 28)(n- 2) + (m + 38)(n- 2)2 ,
K= (m + 8)2 + (n- 2)(m + 28) .
Die Three-moment central-F approximation ist nach Tiku (1966, Biometrika 53, 606-610)
genauer als die Normalapproximation (1). Aus (2) ergibt sich nach 3.2 (10) folgende
Approximation der nicht-zentralen F (8)-Verteilungsfunktion durch die Verteim,n
lungsfunktion einer Beta-Verteilung bzw. durch die unvollständige Betaquotienten-Funktion I
(6)
(7)
P m,n, D(x) = P{Fmn
, (8) < x}
,.....,
,.....,
p{ B(%,%) < u}
I(ul%,%)
bzw.
P{Fmn
, (8) > x}
,.....,
,.....,
p{ B(%,%) > u}
I(l- u l%,%)
mit
u
1
l+ nbl(r[x+c]) ,
1- u
1+
1
r[x+c]/(nb)
Beweise zu: Chiquadrat-Verteilung
B V 1-1
11.8.06
Beweise zu:
1.1
Die zentrale Chiquadrat-Verteilung
Wir geben hier nur kurz die Beweisidee an, auf deren Grundlage man leicht einen
vollständigen Beweis erarbeiten kann. Die Reihenfolge entspricht hierbei aus beweisökonomischen Gründen nicht der Darstellung im Text.
Die Aussagen
(9)
(12)
für
x> 0,
2
xm
und x2 stochastisch unabhängig ::::}
n
sind bereits als Spezialfälle für 8 = 0 im Abschnitt 1.2 enthalten als
1.2 (10)
<P1 6(x) = <P( JX-/6)
-
<P( -JX- J6)
für
x>O,
'
1.2 (8)
und werden dort bewiesen.
Beweis von:
(5)
für
x> 0,
Der Beweis erfolgt durch Induktion über den Freiheitsgrad n. Der Induktionsanfang
n = 1 ergibt sich durch Differenzieren von (9). Und der Induktionsschritt n r----+ n + 1
verwendet (12) für m = 1 und n + 1 statt n.
Beweis von:
(10)
2
xl·a
'
(10) folgt direkt aus (9).
für 0 < a
< 1.
Beweise zu: Chiquadrat-Verteilung
11.8.06
B V 1-2
Beweis von:
(11)
Der Beweis erfolgt durch Induktion über den Freiheitsgrad n. Der Induktionsanfang
n = 1 verwendet das 2. und 4. Moment der Standard-Normalverteilung
E(N(0.1)
2
)
= 1,
Und der Induktionsschritt ergibt sich aus (12) in Verbindung mit den Rechenregeln
über Erwartungswert und Varianz.
Beweis von:
(13)
(x~-n)jy"'n ~ N(0,1)
für n ---+ oo ,
(14)
x~/n
für n ---+ oo .
_P----+ 1
(13) bzw. (14) folgen direkt aus der Darstellung (1) in Verbindung mit dem Zentralen Grenzwert bzw. dem Gesetz der großen Zahlen.
Beweise zu: Chiquadrat-Verteilung
B V 1-3
11.8.06
Beweise zu:
1.2 Die nichtzentrale Chiquadrat-Verteilung
Beweis von:
Dann hängt die Verteilung der Quadratsumme
nur noch über die sogenannte Nichtzentralität
(3)
2
8 = II llll = Jli
+... + Jl~
vom Vektor Jl = (Jll' ... ,Jln) der Erwartungswerte ab.
2
Zu zeigen ist, daß L(IIU 11 ) nur über 8 von Jl = (Jll' ... ,Jln) abhängt, wobei für Jl = 0
bzw. 8 = 0 nichts zu zeigen ist. Sei also Jl :;= 0. Wir zeigen erst, daß die Verteilung
von IIU 11 2 invariant ist gegenüber einer einer orthorrormalen Transformation. Für
eine orthorrormale Matrix C gilt
(i)
ccT = 11
also
IICUII2 = urcrcu = uru = IIUII2
(ii)
2
2
L(IIUII ) = L(IICUII ).
d.h.
n
und somit
Es genügt daher ein geeignetes C anzugeben, für das die Verteilung von CU nur
noch über 8 von Jl abhängt. Hierzu ergänzen wir den normierten Vektor ji
= llllii-1Jl
zu einer Orthonormal-Basis des IR n und betrachten die orthorrormale Matrix C deren Zeilen diese Orthonormal-Basis bilden. Da ji die erste Spalte von CT ist, folgt
für den ersten Einheitsvektor e = (1, 0, ... , 0)
1
(iii)
C -1 e 1 =
cT e
1
= ,,_-
bzw.
r
Die zentrierten Variablen
(iv)
Z. = U.- Jl·
z
z
z
mit
L(Z.)
= N(O, 1),
z
sind ebenfalls stochastisch unabhängig und daher gilt
(v)
L(Z) = N n (0, 11 n )
Aus der Darstellung
sow1e
L(CZ) = N n (0, CCT) = N n (0, 11 n )
Beweise zu: Chiquadrat-Verteilung
B V 1-4
11.8.06
(vi)
vgl. (iii)
ergibt sich dann mit (v), daß L(CU) nur noch über
IIJ.LII = J6 von J.L abhängt.
D
Beweis von (8)
Für stochastisch unabhängige reelle Zufallsvariablen V1' ... ,Vm' U1'" .. ,Un mit
L(V.) = N(.A.,1)
für j = 1, ... ,m.
L(U.)z = N(p,.,1)
z
für i = 1, ... ,n
J
J
gilt nach Definition der x2- Verteilung
Da I U
IIJ.LII 2,
mit
8=
mit
"f=II-AII 2 ,
mit
T
= IIJ.LII 2 + II-AII 2 = -A+8.
1 2 und I V 1 2 stochastisch unabhängig sind, folgt hieraus (8).
D
Beweis von (10) (11)
(10)
<P1 6(x) = <P( JX-/6)
-
<P( -JX- J6)
für x> 0,
'
Für x>O gilt:
P{xi(8)<x}
2
= P{N(J"6,1) < x}
= P{IN(J6))1
< Jx}
= P{-JX <N(J6,1) <)X}
=
P{ -JX -J6 <N(0,1) <
Jx -J6}
= <P(Jx -J6)- 0
D
Beweise zu: Chiquadrat-Verteilung
B V 1-5
11.8.06
Beweis von:
(12)
x~ (8) und x~_ 1 unabhängig
=?
xi (8) + X~+ 1 = X~ (8) .
Dies ist ein Spezialfall von (8).
D
Beweis von:
00
1 cp18(x-y)·cpn-1(y)dy
(13)
0
für x > 0, n > 1,
>0
'
00
1 p 1 8 (x- Y)
(14)
0
für x > 0, n > 1.
· cp n-1 ( Y) dY
'
Beide Integraldarstellungen folgen direkt aus der Faltungseigenschaft (12).
Die Ungleichung cp ,
n,u
> 0 auf dem Intervall (O,oo)
vgl. (11),
folgt aus den Ungleichungen
cpn-1
> O,
vgl. (15),
die ebenfalls beide auf dem Intervall (O,oo) gelten.
D
Beweis von:
(15)
P , ist streng wachsend auf (O,oo).
n,u
Die Behauptung folgt sofort aus cp ,( x) > 0 für x> 0, vgl. (13).
n,u
Beweis von:
(16)
P n 8(x) = P{x~(8) < x}
'
ist streng wachsend in x> 0
und streng fallend in 8> 0 für x > 0.
Der Beweis erfolgt durch Induktion über den Freiheitsgrad n.
Induktionsanfang: n = 1
Wegen
(i)
xi(8) =
2
N(c:,1) mit c: =
Pn,8(z
2
)
J6 ergibt sich für z =
2
P{xi (8) < z
}
P{ -z < N(c:,1) < z}
(z-c:)- <1>(-z-c:).
JX>O:
D
Beweise zu: Chiquadrat-Verteilung
B V 1-6
11.8.06
Differenzieren nach z bzw. c liefert mit cp = P 1 :
(ii)
8~
(iii)
2
;e p1 78(z )
P1,8( z
2
cp(z-E)
)
+ cp(z-E) > 0
- cp(z-E)
da cp> 0,
+ cp( -Z-E)
da cp symmetrisch.
- cp(lz-cl) + cp(lz+cl)
Für c > 0 gilt
-(z+c) < z-E <z+c
und somit
wobei die Gleichheit gerrau für c = 0 gilt. Da cp auf der positiven Achse (0, oo)
streng monoton fallend ist, folgt
(iv)
bzw.
wobei die Gleichheit gerrau für c = 0 gilt. Folglich ist P
sogar streng fallend für c > 0, also auch streng fallend in c
Und wegen (ii) ist P
16
16
(z2 ) fallend für c > 0, und
>0 und in 8
=
c2 .
(z2 ) streng wachsend in z > 0, also auch in x = z2 .
'
lnduktionsschritt: n
f-----t
n+ 1
Da X~t ( 8) die Faltung von
1
(v)
xi( 8) und X~ ist, gilt folgende Darstellung
i
P n+ 1, x) = P { U + V
< x}
= P { U < x- V} ,
wobei U, V stochastisch unabhängige Zufallsvariablen sind mit
L(V) = x2n .
Die Dichte cp von V ist nach Induktionsvoraussetzung (für 8 = 0) positiv auf (O,oo ),
n
und es gilt
X
P{U< x-V}
1 cpn(v) · P{U<x-v} dv
0
X
1 cpn(v) · 1,8 (x-v) dv.
0
Der Integrand ist für 0
send in x
send in x
<v<x
positiv und nach Induktionsanfang streng wach-
> 0 und streng fallend in 8 > 0. Damit ist auch das Integral streng wach> 0 und streng fallend in 8 > 0, und (16) ist für n + 1 gezeigt.
D
1108006
Beweise zu: Chiquadrat-Verteilung
B V 1-7
Beweise zu:
1.3 Grenzwertsätze und Approximationen
Beweis von:
(1)
N(O, 1),
n---+ oo
V2(n + 28)
Anwendung des Zentralen Grenzwertsatzes auf die zentrierte Dreiecksfolge Xnk mit
k = 1, 000, no
für
Wegen
a~ := Var(Xn1 )
und
E(X~ 1 ) = 48(n-4%) + 12(n+2%)
=
2(1 + 2%)
2
n---+oo
2
48n + 12 n 2
n---+ oo
ist die Ljapunov-Bedingung erfüllt (vgl. Exkurs Der Zentrale Grenzwertsatz für reelle
Zufallsvariablen, 2. Kriterium 2) und somit folgt (1), weil
Var(Xn+) = 2(n + 28) 0
D
Beweis von:
(3)
c
=
n + 28
n+8
V=
+ 8) 2
n + 28
(n
Gleichsetzen der ersten beiden Momente von x~ (8) und Garn ( ~, 2 c) liefert:
(i)
(ii)
E{Gam( ~,2c)},
cv
Var{x~ (8)} =
2(n + 28)
2vc
2
= Var{Gam( ~,2c)}
0
Einsetzen von (i) in (ii) ergibt 2(n + 28) = 2 (n+8) c und somit c aus (1)0 Aus (i)
ergibt sich weiter v = (n+8)/c und somit v aus (1)0
D
Beweise zu: t- Verteilung
B V 2-1
16.7.10
Beweise zu:
2.1 Die zentrale t- Verteilung
Beweis von:
(15)
cpn (x) = cp(x)
lim
n---+oo
Für festes x E IR ist für n
---+
für alle xE IR.
oo zu zeigen
Nun ist
cpn (x)
(21r)- 1/ 2 · b (c d )-1/ 2
bn
r ( n~1 ) [ r ( ~ )
cn
( 1 + ~x2r
dn
(1+ ~x
2
2
0
~l-1
).
d
für n---+ oo
Aus
c ---+ exp { x },
n
folgt
( c d )-1/2 -----+ exp {- 12 x2},
n
mit
n n n
n
---+
1
n
und für (i) bleibt nur noch zu zeigen
(ii)
b
n
-----+
1
für n ---+ oo .
Setzen wir z = ~ , so ist
Wir zeigen jetzt allgemeiner
(iii)
log T(z
+ ~)-log T(z)-
~ log(z)-----+ 0
für z---+ oo
woraus sich sofort log b ---+ 0 und somit (ii) ergibt. Der Nachweis von (iii) verwenn
det folgende Variante der Stirlingschen Formel- vgl. z.B. Abramowitz & Stegun (1970),
Handbook of Mathematical Functions, 6.1.40, p. 257) für z---+ oo:
(iv)
log T(z) = (z- ~) log(z)- z
Entsprechend ist
+~
log(27r)
+ o(1).
Beweise zu: t- Verteilung
B V 2-2
1607010
und somit folgt
+ ~) -log T(z) z [ log (z + ~ ) - log (z)] log T(z
~ log(z) =
~
+ o (1)
und für (iii) bleibt zu zeigen
(v)
z[log(z + ~) -log(z)]-----+ ~
für z---+ ooo
Nach dem Mittelwertsatz gibt es zu jedem z ein ~(z) E (z, z + ~) so daß
~) -log(z)
(vi)
log(z +
Wegen
z < ~(z) < z + ~
folgt
<
z
z
+ 1/2
_z_
~
(z)
=
~ ~~z)
<
...!.._
0
z
0
1.
Zusammen mit (vi) ergibt sich daher
1..
2
z/
0
z+ 1
2
< z (log (z + 12 ) -
log( z))
<
1
2
0
Wegen
z
z +1/2
folgt hieraus (v)o
für z---+ oo
D
Beweise zu: t- Verteilung
B V 2-3
1607010
Beweise zu:
2.2 Die nichtzentrale t- Verteilung
Beweis von:
00
(7)
cpn,'"'(,D (X)
1 2nw 2
0
(8)
p n,'"'(,D(x)
P{tn ( ')', 8) < x}
0
cp( wx -')') cp
0
n,cp
00
1 2nw
0
0
<!>( wx -')') cp
0
n,cp
(nw 2 ) dw
>
0
(nw 2 ) dw
für xEIRO
für xEIR
0
Die Verteilungsfunktion von W =~ergibt sich aus der von V bzwo x2 ( 8) mit
n
<~>w(w) = P{W<w} = P{V<nw 2 } = Px;(nw 2 )
für w>O,
und für die Dichte von W folgt
für w> 00
(i)
Zusammen mit der Dichte von U
für uEIR,
(ii)
ergibt sich daher die Dichte des Quotienten T= U /W (vgl. zo B. Skripte zur Stochastik
6.3 oder zur Maß- und Wahrscheinlichkeitstheorie 14)
00
cpT(x) =
1 wocpu(wx) ocpw(w) dwo
0
Mit (i) und (ii) ergibt sich hieraus (7), und (8) erhält man aus (7) wie folgt:
X
1 cpn,'"'(,D(t) dt
Pn,'"'(,D(x) =
-00
X
00
1 1 2nw 2
-00
0
J2nw 20
0
(
0
cp( wt -')') cp n,cp (nw 2 ) dw dt
0
Jcp(wt-')')dt) ocpn,cp (nw 2 )dw
-00
00
1
2nwo(wx-'Y)ocp (nw 2 )dwo
0
n,cp
D
Beweise zu: t- Verteilung
B V2-4
16.7.10
Beweise von:
(9)
P n,'"'(, 8 ( x) ist streng monoton wachsend in xE IR,
(10)
P n, , 8 ( x) ist streng monoton fallend in 'Y E IR,
1
(11)
P n,'"'(, 8 ( x) ist für x > 0 streng monoton wachsend in 8> 0,
Nach Definition der t (')',8)-Verteilung gilt folgende Darstellung
n
(i)
Pn,'"'(,u,(x) =P{tn ('Y,8)<x}
=P{Z+'Y<Vx},
wobei Z, V stochastisch unabhängige Zufallsvariable sind mit
L(Z) = N(O))
Mit den Dichten cp bzw. f von Z bzw. V ergibt sich daher
(ii)
<!>
,(x) =P{Z<Vx-'Y}
n,'"'(,u
J
f(v)·cp(z)d(v,z)
{z::::;vx-1}
VX-'"'(
00
=
J(f(v)· J
0
cp(z)dz)dv
-00
00
=
J (f(v)·(vx-'Y))dv.
0
ad (9-10}: Der Integrand f( v) · P (vx- 'Y) ist für jedes v > 0 positiv und
• streng wachsend in x,
• streng fallend in ')',
weil P streng wachsend ist. Damit hat auch das Integral P
,( x) dieselben Mono-
n,'"'(,u
tonie-Eigenschaften, d.h. (9) und (10) gelten.
ad {11):
Wir integrieren wir in (ii) erst über z und dann über
00
(iii)
J cp(z)·(
-oo
J
f(v)· dv)dz
{z::::;vx-1}
00
J cp(z) ·P{z<Vx-'Y} dz
-oo
v
Beweise zu: t- Verteilung
Nun ist für z >-
B V 2-5
16.7.10
r bzw. z + r > 0
P{z<Vx-r} = P{V>(z+r)/x}
=
P{ n V 2 > n(z + r) 2j x 2}
=
P{x~(8) > n (z + r) 2/ x 2}
= 1--r
und (z+r)/x}
1
für z <- ')'.
Damit ergibt sich aus (iii)
-'"'(
<P n,'"'(,u,(x) =
1
00
1 <p(z) ·(1-<Pn,8(h(z)))
<p(z) dz +
-oo
dz
-'"Y
00
+
<P(-r)
1 <p(z) ·(1-<Pn,8 (h(z)))
dz
1
-'"Y
und für (11) bleibt nur zu zeigen, daß das Integral
00
1 <p(z) ·(1-<Pn,8(h(z)))
dz
-'"Y
für x > 0 streng wachsend in 8 ist. Und dies ergibt sich daraus, daß der (positive) In-
tegrand <p(z) ·(1--8 und somit h(z)>O nach 1.2 (16) streng
7
wachsend in 8 ist.
D
Beweise von:
p
± oo
(13)
tn (')', 8)
(14)
tn (')',8) ~ 0
-----+
für 1'---+
± oo,
für 8---+ oo.
Die Behauptungen ergeben sich mit Exkurs KV 11 (1) und (5) aus
N(r,1) ~ ± oo
für 1' ---+ ± oo
x2n (8) ~ oo
für 8 ---+ oo ,
vgl. 1.2 (17).
D
Beweise zu: t- Verteilung
B V 2-6
16.7.10
Beweise zu:
2.3 Approximationen der nichtzentralen t- Verteilung
Beweis von:
(3)
sn ·-- ~
n n
(6)
(S -p, )ja
n
n
n
(7)
I-Ln
p
1
n---+ oo
L
n---+ oo
N(O, 1)
= (1+~//2
n
'
mit
a
2n
-
1.(1.+1)
n 2
n
Ausgangspunkt für (6) ist die asymptotische Normalverteilung von
s2 = 1. 2 ( 8)
n
(i)
c
z
c
n
(5 2-z )
n
n
L
n---+ oo
2
E(Sn )
n
n
d.h. (vgl. 1.3 (1))
nxn
= Var(s
1.(n+8)
n
r
2 112
n
N(O, 1)
n (2n + 48f1/ 2 =
mit
1+1
n
Vn (2 +
n---+ oo
~ 8f1/2
n---+ oo
1'
00
Für die Transformation F(x) = x1/ 2 mit F'(x) = ~ x - 1/ 2 ergibt sich aus (i) mit der
Delta-Methode (vgl. Exkurs Konvergenz nach Verteilung in euklidischen Räumen, Ab-
schnitt 14)
(ii)
cn(S;;p,n)
1-L
n
n:oo
F'(1) ·N(0,1)
N(o, ~)
mit
= z1/2 = (1 + 1)1/2 .
n
n
Hieraus erhält man (6) mit
Aus (ii) folgt mit c ---+ oo und p, ---+ 1 auch (3).
n
n
D
Beweise zu: t- Verteilung
B V 2-7
16.7.10
Beweis von:
(9)
mit
u
Für W '"'"'"'N(p, 1 a 2 ) stochastisch unabhängig von U'"'"'"' N('Y, 1) ergibt sich
n
n n
(i)

,(x) = P{ U/ Sn < x}
n, "(,u
~ P{U/Wn<x}
vgl. (8)
Wegen
folgt
P { U- x W n
< 0}
Xf-Ln -
u =
Mit (i) ergibt sich (9).
"(
wobei
= <!>( u)
X~
-
"(
D
Beweise zu: F- Verteilung
B V 3-1
8.7.10
Beweise zu:
3.1 Die zentrale F- Verteilung
Beweise von:
(5)
mit
1
1
(6)
p =2m,
(7)
P q F(p+q)
dm,n- m n . r(p). r(q).
und
q=2n
Vgl. den Beweis von 3.2 (5) für r = m und s = n.
D
Beweise von (10)-(18 ) fehlen noch!!!
Beweis von (19) unter Verwendung von 3.3 (13)
(19)
m ·F
m,n;o:
ist für 0 < a
< 1 streng monoton wachsend bzgl. mE W.
Für 1 < k < m ist zu zeigen
(i)
k·Fk,n;o: <m·Fm,n;o: .
Mit x = m · F
m,n;o:
> 0 ergibt sich
1- a = Pmn (Fmn·o: )
'
' '
nach 3.3 (13) mit 8=c:=0.
Da mit Pk
,n
auch Pk-1 streng monoton wachsend ist, folgt weiter
,n
1
Fk ,n,o:
. = P-k ,n (1- a)
< ;;
r;;
d.h. (i) gilt.
D
Beweise zu: F- Verteilung
B V 3-2
8.7.10
Beweise zu:
3.2 Die F- Verteilung mit reellen Freiheitsgraden
Beweise von:
(x) = d · ~ 1 (rx
r,s
(5)
cp
(6)
p = ~ r,
(7)
dr,s -
r,s
'I
0
mit
q= ~ s
v q
-
+ s)-(p+q) >
s
0
und
r(p +q)
r(p) r(q) '
0
Für stochastisch unabhängige X"' Gam(p, 1) und Y"' Gam(q, 1) mit Dichten
_ 1 p-1 -X
f X (X) - F(p) X e ,
(i)
f Y (Y) -
q-1 -y
1
r(q) Y
e
'
ergibt sich die Dichte des Quotienten Z =X/ Y zu (vgl. Skript ,,Stochastik", Kap. 6.3)
00
fz(z) =
J y -fx(zy) -fy(y) dy
0
00
1
r(p) . r(q) z
p- 1
J
o Y
p+q- 1 -y(1 +z) d
e
Y
Substitution:
1
y = (1+zr u
1
dy = (1+zr du
00
1
r(p) . r(q) z
p-1 (
1+ z
J u p+q-1 e-u du
)-p-q
u = y(1+z)
0
r(p + q) zP- 1(1 + zr(p+q)
r(p) · r(q)
Die Dichte von F
für z
>0
0
1
r,s
= (Xjp)j(Yjq)) = qp- Z ist daher (vgl. z.B. Skript ,,Stochastik",
Kap. 4.4)
cp
r,s
(x) = pq-1-f(pq-1x)
r(p + q)
-1 ( -1 )p-1 ( 1 + -1 )-(p+q)
r(p) . r(q) P q . P q x
Pq x
F(p+q) JJ -p. J!-1( -1( + ))-(p+q)
r(p) . r(q) Y q
q q Px
r(p + q) JJ q. xP-1( + ) -(p+q)
r(p) . r(q) Y q
q Px
r(p + q) (2p)P (2q)q. xP- 1(2q + 2p x) -(p+q)
r(p). r(q)
da r = 2p, s = 2q.
D
Beweise zu: F- Verteilung
B V 3-3
8.7.10
Beweise von:
(9)
g(Fr,s)
1
1 + sj(r Fr 8 )
rFrs
r Frs + s
'
,.....__
B(p, q).
'
Wir knüpfen an den Beweis von (5) an.
Aus
XjY = Z = pFr,s jq
folgt
g(Fr,s)
1
rFr,s / s
1
1 + sj(r Fr 8
'
)
1+ Y/X
X
X+Y
,.....__
B(p, q).
D
Beweise zu: F- Verteilung
B V 3-4
8.7.10
Beweise zu:
3.3 Die nicht-zentrale F- Verteilung
Beweise von:
00
(7)
cpmn 8 e(x) =
' ' '
(8)
<[>
1 m n v · cpm,u,(m v x) · cpn,e (n v) dv > 0
für x > 0.
0
(x)
m,n,87e
00
1 n·Pm, 8 (mvx) ·cpn,e (nv) dv
für x
> 0.
0
(9)
(10)
Fn,m (c:,8) = F
<[>
1
(b c)
m,n '
(x)=1-P
(l)
n7m7e78
m,n,87e x
für x
> 0,
(11)
Die Dichte und Verteilungsfunktion von X =.l U und Y =.l V ergeben sich aus (1):
m
n
(i)
x> 0,
fx(x) = m cpm,im x),
FX(x) = m,im x)
für
fy(Y) = ncpne(ny),
Fy(Y) = n e (n y)
für y > 0.
7
'
Hieraus erhält man die Dichte und Verteilungsfunktion des Quotienten F=X/Y
(vgl. z.B. Skript zur Stochastik 6.3)
00
(ii)
für
X
(iii)
<[>
m,n,8,e
(x)
x> 0
oo
1 1 v-fjvw) -fy(v) dv dw
für x > 0
0 0
l'[!
fjvw) v dw ]!y(v) dv
00
1 Fjvx) -fy(v) dv
0
Mit (i) ergeben sich (7) und (8) aus (ii) und (iii). (9) ergibt sich aus (4). (10) folgt aus
(9), da g(x) = 1/x eine streng fallende Funktion in x > 0 ist. Und (11) ergibt sich durch
quadrieren aus 2.2 (4).
D
Beweise zu: F- Verteilung
B V 3-5
807010
Beweise von:
(12)
P
,
m 7n 7u7e
(x) ist • streng wachsend in xE (O,oo ),
• streng wachsend in c > 0
• streng fallend in
Nach Definition der F
m,n
<!>
8
(8,c)-Verteilung gilt für
x> 0,
für x> 00
für
>0
x> 0 folgende
Darstellung
P{Fm,n (8,c) < x} = P{U < Vx},
, (x) =
m 7n 7u7e
wobei U, V stochastisch unabhängige Zufallsvariable sind L( U)
L( ~ V)
= x~( c )0 Mit der Dichte f von V ergibt sich
xm2 (8)
und
00
J f(v)
Pm,n,D,e (x) =
0
P{U<vx} dv
0
0
00
J f(v)
2
0 P{xm(8)
< vx} 0 dv
0
0
Für v > 0 ist f( v)
> 0 nach
1.2 (13) und somit ist auch der Integrand
>0
0
Nach 1.2
2
(16) ist der Integrand f( v) P{x m
( 8) < vx} und damit auch das Integral P
, (x)
m 7n 7u7e
streng wachsend in x > 0 und streng fallend in 80
0
Die Monotonie von P
nie bzgl. 80
, (x) bzgl. c folgt mit (10) aus der eben gezeigten Monoto-
m,n,u7e
D
Beweise zu: F- Verteilung
B V 3-6
807010
Beweis von:
(13)
<[>
(~)
ist für x > 0 streng monoton fallend in m E W
m,n,87e m
0
Für 1 < k < m und x > 0 ist zu zeigen
(i)
<[>
m,n,87e (~)<<!>
m
k,n,87e (~)0
k
Seien U, V, W stochastisch unabhängige Zufallsvariable mit folgenden Verteilungen
(ii)
L( U) = x~( 8),
L(V) =
x~-k'
L(W) = x~(c)jno
Wir setzen
(iii)
X
U/k
(iv)
y
(U+ V)/m
w
w
mit
L(X) =Fk ,n, 8 e ,
7
mit
L(Y) = Fm,n, 8 e
7
°
Dann gilt
(v)
<[>
(_E_)
P{kX <x}
k,n,87e k
P{U*<x}
(vi)

, (__E__) =
m 7n 7u 7e m
mit
U* == u jw,
mit
V*:=V/Wo
P{mY<x}
= P{U*+ V*<x}
Die Zufallsvariable U* hat auf (0, oo) eine Dichte f> 0 mit
nach (v),
und somit gilt
(vii)
p { U*
+ V* < X}
X
= J
j( U) p {V* < X- U} dU
o
o
0
Wegen L(V*j(m-k)) = Fm -k ,n, 0 e gilt
7
(viii)
P{V*< x-u} < P{V*< x}
p
(-X ) <
m-knOe m-k
1
für O<u<x,
'''
und somit folgt aus (vii) weiter
X
P{U*+V*<x} < P{V*<x} Jf(u)du = P{V*<x}P{U*<x} < P{U*<x}o
0
Zusammen mit (v), (vi) und (viii) ergibt sich jetzt (i) aus
(ix)
D
MN Die multivariate Normalverteilung
Gerhard Osius
1.
Die eindimensionale Normalverteilung
2.
Definition der multivariaten Normalverteilung
3.
Eigenschaften der multivariaten Normalverteilung
4.
Quadratische Formen von normalverteilten Variablen
5.
Bedingte Normalverteilungen
6.
Die zweidimensionale Normalverteilung
G. Osius: Multivariate Normalverteilung
1.
17.5.108
MN-2
Die eindimensionale Normalverteilung
Wir gehen aus von den eindimensionalen Normalverteilungen N(p"a 2) mit p,EIR,
17
> o. Für
17 ---+
0 konvergiert N(p"
(7
2
) nach Verteilung gegen die Einpunkt-Vertei-
lung mit Träger {p,}, die wir daher suggestiv mit N(p" 0) bezeichnen und auch als
(degenerierte) Normalverteilung ansehen. Die Klasse aller eindimensionalen Normalverteilungen ist clann
Diese Klasse ist abgeschlossen gegenüber affinen Transformationen und Faltungen,
cl.h. es gilt
JY;:,
cL'( aX + b) E JY;: .
(2)
cL'(X) E
(3)
Für stochastisch unabhängige X ,X gilt
a, bE IR
1
Durch Induktion ergibt sich, daß
JY;:
2
gegen "unabhängige Linearkombination" abge-
schlossen ist, cl.h. es gilt:
(4)
Für stochastisch unabhängige Xl'" ..,X gilt
J
cL'(X) E JY;: für alle j=l, ,J
cL'( t 1Xl
=*
+ + tJXJ ) E JY;:
Die charakteristische Funktion 'Y( -I p" (7 2 ) von N(p"
(5)
(7
2
) ist
für sEIR,
und die Moment-erzeugende Funktion M( -I p,,( 2 ) von N(p"a 2 ) lautet
(6)
für sEIR.
G. Osius: Multivariate Normalverteilung
2.
17.5.108
MN-3
Definition der multivariaten Normalverteilung
Wir geben drei verschiedene Definitionen der multivariaten Normalverteilung und
weisen anschließend deren Äquivalenz nach.
1. Definition: konstruktiv
Die erste Definition ist konstruktiv in dem Sinn, daß die multivariaten Normalverteilungen aus stochastisch unabhängigen (eindimensionalen) Standard-Normalverteilungen N (0,1) konstruiert werden. Hierzu seien Z1' ...,ZJ stochastisch unabhängige
1
Zufallsvariable mit
(0)
L(Zj) = N (0,1)
für alle j = 1, ..., J
1
Für eme beliebige IxJ- Matrix C mit Rang (C) = J < I und beliebiges fL E IRI betrachten wir die affine Einbettung G: IR] ---+ IRI mit
(1)
G(z) = Cz
·· zE IR] .
f ur
+ fL
Fassen wir Z = (Zl' ...,ZJ) Tals J-dimensionalen Zufallsvektor auf, so ist
(2)
X = G(Z) = C z
+ fL
eine I-dimensionale ZV. Die Verteilung von X hängt nur von C und Jl ab und wird
als eine I-dimensionale Normalverteilung vom Rang J wie folgt (vorläufig) bezeichnet
Formal gesehen ist N/fLl C) das Bildrnaß der Verteilung L(Z) unter G. Erwartungswert und Covarianzmatrix von X ergeben sich
(4)
(5)
E = Cov(X) = CC
T
mit
Rang(E) = Rang(C) = J.
Wir erweitern diese Definition noch, indem wir die Einpunktverteilungen auch als
Normalverteilungen vom Rang 0 auffassen und wie folgt bezeichnen
(6)
N/fL I0) = L(X)
falls
P{X=fL} = 1.
Es wird sich noch herausstellen, daß N/fL IC) nur noch über E von C abhängt.
Speziell für C = 11J (Einheitsmatrix), fL = 0 ist X = Z und somit ist
G. Osius: Multivariate Normalverteilung
MN-4
17.5.108
Aus der Verteilungsfunktion P von N( 0,1) ergibt sich sofort die Verteilungsfunktion
PJ und die Dichte cpJ von Z bzw. N/ü 1 11J)
J
(8)
TI
PJ(x) =
p(x.)
j=l
J
J
TI
cpi x )
cp(x.)
j=l
J
= (21r)-J/2. exp{ -
~ x T x}
für x = (xl' ...'xJ ) EIRJ .
2. Definition: Charakterisierung via Linearkombinationen
Die zweite Definition charakterisiert die multivariate Normalverteilung durch die
Verteilungen aller ihrer Linearkombinationen. Formal ist die Klasse
JVf aller I-di-
mensionalen Normalverteilungen definiert.
(9)
cL'(Y) E
JVf
{}
Y ist I-dimensionaler Zufallsvektor mit
cL'(tTy) E~
für alle tE IRI ,
bzw. mit Wahrscheinlichkeits-Maßen formuliert:
(10)
PE JVj
{}
Für jedes tE IRI ist das Bildmaß von P unter t T :IRI
---+
IR aus
~.
Für I-dimensionales Y = (Yl'" ..,Y )T mit cL'(Y) E JVj gilt speziell cL'(Y ) E ~ und
1
i
somit existieren alle Momente von Y. für i = 1, ,... ,1. Damit existieren auch Erwarz
tungsvektor und Covarianzmatrix von Y:
(11)
Jl = E(Y),
E= Cov(Y).
Für beliebiges tE IRI folgt dann
d.h. cL'(tTy) ist für jedes t bereits durch Jl und E festgelegt. Damit ist (nach dem
Eindeutigkeitssatz für mehrdimensionale Verteilungen) auch cL'(Y) bereits durch Jl
und E festgelegt und wird wie folgt bezeichnet
Der Rang der multivariaten Normalverteilung N/Jl,E) ist definiert als der Rang ihrer Covarianzmatrix E, d.h. als Rang (E) .
G. Osius: Multivariate Normalverteilung
MN-5
17.5.108
3. Definition: via charakteristischer Funktion
Die dritte Definition beschreibt die multivariate Normalverteilung durch ihre charakteristische Funktion (kurz: CF). Für beliebiges p, E IRI und eine (I x I) -Matrix E definieren wir eine Funktion "( ( -I p" E) : IRI ---+ <C durch
für tEIRI
(14)
und betrachten die Funktionenklasse
(15)
ß[ = {"(( -1p,E) 1
p,E IRI , E symmetrische, positiv-semidefinite (lxI) -Matrix}.
Nach der dritten Definition heißt eine I-dimensionale Zufallsvariable Y normalverteilt, falls ihre charakteristische Funktion CPy zu der Klasse ß[ gehört.
Äquivalenz der drei Definitionen
Es soll jetzt die Aquivalenz aller drei Definitionen nachgewiesen werden. Zuerst zeigen wir, daß die erste Definition die zweite impliziert, d.h. es ist zu zeigen
(16)
N[(p,1 C)
E
JVj.
Für cL'(X) =Nip,IC) mit X aus (2) und C vom Rang J> 0 ist
tTX = (CTt)T Z + t T p,
für jedes tEIRI .
Nach 1 (4) ist cL'{( CTt) TZ} E JV;:, also auch t TXE JV;:, und es folgt cL'(X) E JVj.
Für cL'(X) = Nip,1 0) ist X Einpunktverteilt in p, und somit ist cL'(t TX) eine Einpunktverteilt in t Tp" die ebenfalls zur Klasse
JV;: gehört. Und damit ist (16) gezeigt.
Als nächstes zeigen wir, daß aus der zweiten Definition die dritte folgt, d.h.
(17)
CPy = "(( -I p"E) E ß r
Hierzu bestimmen wir für beliebiges cL'(Y) = N/p" E) die charakteristische Funktion CPy von Y. Für beliebiges tE IRI ist cL'( t TY) = N (t Tp" t TE t) und unter Ver1
wendung der charakteristischen Funktion CPtTy von tTy gilt
cpt T y(l)
exp {i t TP, - ~ t TE t },
nach 1 (5).
G. Osius: Multivariate Normalverteilung
MN-6
17.5.108
Damit ist (17) gezeigt, und zuletzt zeigen wir, daß die dritte Definition die erste impliziert. Sei also Y eine I-dimensionale Zufallsvariable mit charakteristischer
I
Funktion 'P y = 'Y( -I Jl, E) für ein JlE IR und eine positiv-semidefinites Matrix E.
Für E= 0 ist 'Y( -I Jl,O) die charakteristische Funktion der Einpunktverteilung im
Punkt Jl, und wegen (6) folgt cL'(Y) =NI(JlI 0). Für E;= 0 ist J = Rang(E) > 0, und
es gibt eine (IxJ)-Matrix C vom Rang J mit E= CC T. Die charakteristische
Funktion 'P
X
von X = CZ + Jl aus (2) ergibt sich dann aus der charakteristischen
Funktion 'P von Z wie folgt
Z
T
'Px(t) = 'PCZ+JL(t) ='Pz(CTt). exp{it Jl}
für tE IRI .
Nach 1 (8) ist
'P
z(s)
= exp { -
~ s Ts }
·· sE IR],
f ur
und wegen E = C C T ergibt sich
für tE IRI .
Also ist 'P X = 'Y( -I Jl, E) und aus dem Eindeutigkeitssatz für charakteristische
Funktionen folgt cL'(X) = cL'(Y). Insgesamt gilt daher
(18)
cL'(Y) = N/JlI 0)
oder
cL'(Y) = N/JlI C).
Damit sind alle drei Definitionen äquivalent. Insesondere folgt, daß die Verteilung
T
von N/JlIC) nur noch über E = CC von C abhängt. Die provisorische Notation
N/JlI C) bzw. N/JlI 0) aus der ersten Definition wird daher nicht weiter verwendet.
G. Osius: Multivariate Normalverteilung
3.
MN-7
17.5.108
Eigenschaften der multivariaten Normalverteilung
Es sollen jetzt einige wichtige Eigenschaften der multivariaten Normalverteilung
zusammengestellt werden. Hierbei verwenden wir lediglich die charakterisierende
(zweite) Definition der Klasse
JV]-,
d.h. die Äquivalenz der anderen Definitionen
wird hier nicht ausgenutzt.
Affine Transformationen
Die erste wichtige Eigenschaft der normalverteilten Zufallsvektoren ist die Abgeschlossenheit gegenüber affinen Transformationen. Für einen I-dimensionalen Zufallsvektor, eine (JxI)-Matrix A und einen Vektor hEIR] gilt:
Produktmaße
Das Produktmaß von K Normalverteilungen der Dimensionen 1 , ..., IK ist eine Nor1
malverteilung der Dimension 1+ = 1 +...+ IK:
1
(2)
TIK
k=1
NI (Jlk ,Ek )
k
=NI+(Jl, E)
mit Jl
=:[~]
,
JlK
Schreibweise für die Block-Diagonal-Matrix:
Unter Verwendung von Zufallsvariablen läßt sich (2) äquivalent formulieren:
(2)'
Sind Xl' ..., X
K
stochastisch unabhängige Zufallsvektoren mit
cL'(X k ) = NI (Jlk ,Ek )
für alle k = 1) ...) K)
k
so folgt für den I +-dimensionalen Zufallsvektor X = (Xl' ..., X )
K
cL'(X) = NI (Jl,E)
mit Jl, E aus (2).
+
Speziell ergibt sich für Produktmaße eindimensionaler Normalverteilungen
(2) *
2
TII N1 (Jl.,a.)
i =1
Z
.
2
= N/Jl, Dlag{a })
Z
bzw unter Verwendung von Zufallsvariablen
·· Jl, a 2 E IRI .
f ur
G. Osius: Multivariate Normalverteilung
(2)*'
MN-8
17.5.108
Sind Xl' ..., XI stochastisch unabhängige Zufallsvariablen mit
cL'(X.) = N (p,. ,a~)
für alle i = 1) ...) I)
2
l 2 2
so folgt für den I-dimensionalen Zufallsvektor X = (Xl' ...,XI)
cL'(X) = N/p" Diag{ a 2 }) .
Die I-dimensionale Standard-Normalverteilung N/O, llI) ist daher das Produkt von I
eindimensionalen Standard-Normalverteilungen
I
Tl
N1 (0,1)
2=1
bzw unter Verwendung von Zufallsvariablen
(3)
N1(0, 111 ) =
(3)'
Sind Xl' ..., XI stochastisch unabhängige N (O,l)-verteilte Zufallsvariablen,
l
so hat der I-dimensionale Zufallsvektor X = (Xl' ...,XI) eine I-dimensionale Standard-Normalverteilung
cL'(X) = N/O,l1I) .
Unabhängigkeit und U nkorrreliertheit
Bei multivariater Normalverteilung ist Unkorreliertheit äquivalent zur Unabhängigkeit.
Für einen I-dimensionalen normalverteilten Zufallsvektor X, d.h.
mit
cL'(X) E ~ betrachten wir eine Zerlegung X = (Xl' ..., X K ) in K Teilvektoren X k
der Dimension I k (für alle k), wobei I = I+" Dann gilt
(4)
Xl' , X
K
sind stochastisch unabhängig
{}
Xl' , X K sind paarweise unkorreliert, d.h. Cov(X) =Diag{ Cov(X k )}
Rang und Standard-Darstellung
Für einen normalverteilten Zufallsvektor X mit cL'(X) = NI(p"E) wollen jetzt die
Bedeutung des Ranges der Verteilung, d.h. von Rang(E), studieren. Zunächst sind die
Normalverteilungen vom Rang 0 genau die Einpunktverteilungen:
(5)
Rang(E) = 0
E=O
P{X=p,} = 1.
Dieses Resultat soll jetzt verallgemeinert werden. Wir zeigen, daß die Verteilung
cL'(X) = NI (p" E) stets konzentriert ist auf den affinen Teilraum
(6)
p,
+ vft
= {p,+m I mEv«}
C IRJ,
wobei
G. Osius: Multivariate Normalverteilung
17.5.108
MN-9
(7)
der von den Spalten von E erzeugte lineare Teilraum ist mit der Dimension
(8)
J = Dim(c.4) = Rang(E).
Bezeichnet Pc4: lRI -----+ lRI die orthogonale Projektion auf den linearen Teilraum
c.4, so erhält man folgendes Resultat:
(9)
X stimmt P- fast-sicher überein mit
X = Jl + P~ X - Jl) , d.h.
P{X =X} = 1.
(10)
cL'(X) = N1(Jl,E) ist auf Jl + c.4 konzentriert, d.h.
P{XEIl+c.4} =P{X-Il Ec.4} = 1.
Wegen (9) kann man X bei allen wahrscheinlichkeitstheoretischen Betrachtungen
ohne Beschränkung der Allgemeinheit durch seine Standard-Darstellung X E Jl + c.4
ersetzen. Wir wollen diese Standard-Darstellung noch anders beschreiben.
Im trivialen Fall J = 0 bzw. c.4 = {O} ist Jl + c.4 = {Jl} einelementig und
X = Jl
hängt nicht mehr von X ab.
Im Fall J> 0 gibt es eine (I x J) - Matrix C mit
(11)
E=CC
T
,
Rang(C) = J,
und C besitzt die Linksinverse
c.4 wird dann auch von den Spalten von Cerzeugt
und die orthogonale Projektion auf c.4 ist darstellbar durch (vgl. Exkurs SP 2 (2))
Definieren wir nun den J-dimensionalen Zufallsvektor Z = (Z1' ...,ZJ) durch
dann gilt
(16)
Zl'"..,ZJ sind stochastisch unabhängig identisch N (0, l)-verteilt, d.h.
1
cL'(Z) = NjO, 11).
G. Osius: Multivariate Normalverteilung
MN-lO
17.5.108
Und für die Standard-Darstellung X erhält man die Darstellung
Damit ist gezeigt, daß sich jede Normalverteilung vom Rang J> 0 aus J unabhängigen eindimensionalen Standard-Normalverteilungen im Sinn der ersten Definition
aus Abschnitt 2 konstruieren läßt, d.h. N/Jl,E) = N/JlI C). Somit haben wir einen
(weiteren) Beweis für die Äquivalenz der ersten beiden Definitionen der multivariaten Normalverteilung aus Abschnitt 2, wobei sich der triviale Fall J = 0 mit
N/Jl, 0) = NI (JlI 0) wegen (5) ergibt.
Dichte
Wir wollen jetzt noch eine Dichte der multivariaten Normalverteilung N/Jl, E) angeben. Da die Verteilung N/Jl, E) auf den affinen Teilraum Jl
+ .At konzentriert
ist, kann sie höchstens dann eine Dichte bzgl. des Lebesgue-Maßes )/ besitzen,
wenn .At die maximale Dimension I hat, weil gilt
(18)
Rang(E) <I
)/(Jl+.At) = 0,
N/Jl, E) besitzt keine )/- Dichte.
Falls .At jedoch die maximale Dimension I hat, d.h. falls .At = IR] und somit auch
Jl +.At = IR] gilt, so besitzt NI(Jl,E) eine i-Dichte:
(19)
Für Rang(E) = I ist eine )/-Dichte von N/Jl,E) gegeben durch
I
xEIR ,
mit der quadratischen Form
I
xEIR .
Obwohl N/Jl,E) nach (18) im allgemeinen keine Dichte bzgl. des I-dimensionalen LeI
lEsgue-Maßes
auf IR besitzt, kann man eine Dichte bzgl. des Lebesgue-Maßes ).. JL+Jft
i
auf dem affinen Raum Jl +.At angeben. Diese auf Jl + .At konzentrierte Dichte ergibt sich unter Vewendung der Zerlegung (11) wie folgt:
G. Osius: Multivariate Normalverteilung
(20)
MN -11
17.5.108
Ist C eine lxl-Matrix vom Rang 1 mit E= CC T, so ist eine auf Jl + vft
konzentrierte /\.t+c4-Dichte von NiJl,E) gegeben durch
<pjxIJlIC) = [(27f)I. Det(CTC). exp{Q(x-Jl)}]-1/2,
XEJl+vft,
mit der auf vft definierten quadratischen Form
xE vft,
wobei E- eine beliebige generalisierte Inverse von Eist.
Die quadratische Form Q: vft -----+ IR hängt (auf vft) nicht von der
speziellen Wahl von Y ab!
Speziell für Jl =
°ist
<P j
-I 0
1
C) eine Dichte von Ni 0, E) bzgl. des Lebesgue-Maßes
Ac4 auf dem linearen Raum vft, und für beliebige Borel-Mengen Acvft gilt
(21)
P{N/O,E)EA} = j<pj-IOIC)dAc4 = P{N/Jl,E)EJl+A}.
A
Mit A = vft folgt hieraus
jdet(CTC) = (27f)-J/2.jexp{-~uTYu}dAc4(u).
c4
Da die rechte Seite nur noch von E, aber nicht mehr explizit von C abhängt, ist
(22)
dies auch für die linke Seite der Fall, d.h. die Determinante det (C TC) - und damit
die Dichte <P j
-I JlI C) -
hängt nicht von der speziellen Wahl der Matrix C ab.
Man beachte, daß (19) sich als Spezialfall aus (20) ergibt, denn es gilt
(23)
Rang(E) = l
T
det(C C) = det(E).
Moment-erzeugende Funktion
Die Moment-erzeugende Funktion M( -I Jl, E) von N/Jl, E) ist gegeben durch
(24)
M(tIJl,E) = exp{tTJl+ ~ tTEt}
K
fürtEIR .
G. Osius: Multivariate Normalverteilung
4.
17.5.108
MN -12
Quadratische Formen von normalverteilten
Variablen
Es sei X eine I-dimensionale Zufallsvariable mit Normalverteilung
(1)
cL'(X) = Nf(Jl,E),
(2)
J = Rang(E) .
Ferner sei E- eine beliebige generalisierte Inverse von E, d.h. es gilt
Für die zentrierte Variable X - Jl gilt dann
Setzen wir
so gilt für die Variable X - v
(6)
(X-v)TE-(X-v) ist X;(8)-verteilt mit
(7)
8 = JlT E Jl.
Hierbei ist X;( 8) für J = 0 als Einpunktverteilung in 8 anzusehen. Wir betrachten
noch zwei wichtige Spezialfälle·
SpezialfallI: Eist idempotent
Dann ist E selbst eine generalisierte Inverse (sogar die Moore-Penrose-Inverse) von
E. Ferner ist E = Pc4 auch die orthogonale Projektion auf den von E erzeugten
Teilraum .At. Man erhält dann aus (4), (6):
(8)
(X-Jl)T(X-Jl) und (X-Jl)T E(X-Jl) sind fast sicher gleich und
x}verteilt.
(9)
Die 3 Variablen
(XTX-vTv), (X-v)T(X-v),
(X-v)T E(X-v)
sind fast-sicher gleich und jeweils x'l8)-verteilt.
Ist zusätzlich Jl = EJl, d.h. JlE vft, so erhält man speziell:
G. Osius: Multivariate Normalverteilung
(10)
17.5.108
Für Jl=EJl sind XTX und X T EX fast sicher gleich und X;(8)-verteilt
. (
T
T",
mIt 0 = Jl Jl = Jl ilJl.
Spezialfall 2: Eist invertierbar
Dann ist J = I, Y = Yl, und ergänzend zu (6) hat man
(11)
MN -13
p-1X 1st
. XI2 (C)
·1· i'
T p-1 Jl.
X T il
0 -vertel t mIt 0 = Jl il
G. Osius: Multivariate Normalverteilung
5.
MN -14
17.5.108
Bedingte Normalverteilungen
Es seien Xl und X jeweils 1 - und I -dimensionale Zufallsvariablen und die I-di2
2
1
mensionale Variable X = (Xl' X 2) mit I = 11 +12 sei normalverteilt
(1)
cL'(X) = N/Jl,E)
(2)
~=(~) ,
mit
E= (E E
l1
12 )
E 21 E 22 '
wobei für k, 1 = 1, 2
(3)
Jlk =
E{X k },
E kl = Cov{Xk,X l }
(IkxIrMatrix ).
Um die bedingte Verteilung von X auf Xl zu bestimmen, sind einige Vorbereitun2
gen zu treffen. Bezeichnet
(4)
.
Ik
=
Blld(E
kl)
C
IR
kl
vft
den von den Spalten E kl erzeugten Teilraum, so sind die zentrierten Variablen
X - Jlk auf den Teilraum vft konzentriert. Der von der Covarianz-Matrix E erk
kk
12
zeugte Teilraum vft
12
läßt sich durch sein orthogonales Komplement vft1~ wie folgt
beschreiben:
Und analog ist
(6)
vft~l
T
= {dE IRI2 1 X ist von d X stochastisch unabhängig}.
1
2
Es gilt nun
(7)
Für eine beliebige generalisierte Inverse E ; von E
2
E 22 faktorisieren
Für die ll-dimensionale Variable
gilt dann
(10)
Y1 ist von X
2
stochastisch unabhängig,
22
läßt sich E
12
wie folgt über
MN -15
G. Osius: Multivariate Normalverteilung
17.5.108
(11)
Jl1 - 1712 172; Jl 2 '
Y1
ist normalverteilt mit:
1711 - 1711 172; 1721
.
Nach diesen Vorüberlegungen ergibt sich "die" bedingte Verteilung von Xl auf X
2
als eine Normalverteilung
(12)
mit
Jl1 (X 2) = Jl1 + 1712 172; (X 2 - Jl 2),
d.h. für jedes x EIR
2
I2
ist durch
eine reguläre bedingte Verteilung von Xl auf X definiert. Man beachte, daß nur
2
der Erwartungswert, aber nicht die Covarianzmatrix E
X = x abhängt.
2
2
rv
1
von der Bedingung
G. Osius: Multivariate Normalverteilung
6.
MN -16
17.5.108
Die zweidimensionale Normalverteilung
2
Für Jl=(Jl 1,Jl 2 ), a=(a 1,a 2 )EIR mit a 1,a 2 >0 sowie (2E IR mit -1<(2<1 ist die
2x2-Matrix
(1)
E _
eer1
;2]
[er;
ea 1a 2
a2
positiv-definit (d.h. x TEx> 0 für alle x E IR 2 mit x
(2)
E
=
--2
l-e
mit der Inversen
-2
1
-1
:;= 0)
a1
[
-1 -1
a
2
-e a 1
Die zweidimensionale Normalverteilung NiJl, E) (vom Rang 2) ist gegeben durch die
zweidimensionale stetige Wahrscheinlichkeitsdichte f: IR 2-----+ (0,00) mit (vgl. Abb. 1)
(3)
(4)
mit
für i = 1, 2.
± 1)
Die Cholesky-Wurzel von Eist (auch für (2 =
(5)
12
C = E /
=
o
[
a
VI
2
(22
].
Für cL'(Z) = N 2 ( 0, 11 2 ) ist daher
(6)
bzw.
x2
=
+ a2j
(2 a 2 Zl
(2a 2 [
]
~ X 1 - Jl 1
1 (22 Z2
+ Jl 2
+ a 2 V~
1-(2- Z2 + Jl 2
zweidimensional normalteilt: cL'(X) = NiJl, E).
Hierbei ist die zweite Komponente X
(2 a 2a ~1 [Xl -
Jl ] + Jl
1
normalverteilten
Var(c) =
a;
(1- (22).
2
2
die Summe emer linearen Funktion
der ersten Komponente Xl und einer davon unabhhängigen
"Fehlervariablen"
c = a 2(1- (22)1/2 Z2
mit
E( c) = 0
und
G. Osius: Multivariate Normalverteilung
17.5.108
e =- 0.8
e=- 0.6
e=O
e= + 0.6
MN -17
Abb. 1: Dichten f der zweidimensionalen Normalverteilung für verschiedene e bei
gleicher Achsen-Skalierung. Der Vorzeichenwechsel von e = - 0.6 zu e = + 0.6 entspricht einer 90°-Drehung bzw. einer Richtungsänderung der x1- oder xTAchse.
Für wachsendes lei wird die Glocke steiler und zieht sich stärker zusammen über
der Geraden x2 = !-L2 + 17 21711[xl - !-L1] für e > 0 bzw. x2 = !-L2 - 17 21711[xl - !-L1] für
e< o. Diese Geraden entsprechen den "Diagonalen" u1 = u2 bzw. u1 = - u2 für die
1
Standardisierungen u. = [x. - !-L .] 17-:- .
z
z z z
Beweise zu: Multivariate Normalverteilung
BMN-1
17.5.10
Beweise zu:
Eigenschaften der multivariaten Normalverteilung
3.
Beweis von
(1)
cL'(X) = N/Jl,E)
=*
T
cL'(AX + b) = NJ(AJl+ b, AEA ).
Übung!
Beweis von
(2)
mit
Es seien Xl'
00"
X
K
[
]
, E =
[171 ". .
JlK
0
0 ]
.
EK
stochastisch unabhängige Zufallsvektoren mit
cL'(X k ) = NI (Jlk,Ek )
k
Für X = (Xl'
~1
Jl = :
für alle k
X ) gilt dann
K
K
cL'(X) = TI NI (Jlk,Ek ) ,
(i)
00"
k=1 k
und zu zeigen ist cL'(X) = NI (Jl,E)! d.h.
+
(ii)
cL'(X) E JVj
und
+
(iii)
E(X) = Jl,
Cov(X) = E.
ad (ii):
k
I
Für beliebige tkETI/ mit k = 1, oo.,K und t = (tFOO!t K) E IR + gilt
T
T
t X = t l Xl
Da ttX1'
00"
+ 00. + t KT X K .
t~XK stochastisch unabhängig sind mit cL'(t[X k ) E JV;:, folgt
cL'(tTX)EJV;: mit 1(4). Und da t beliebig war, folgt (ii).
ad (iii):
Es ist
E(X) = (E(X l ) ,oo.,E(XK )) = (Jll"oo,JlK) = Jl.
Und für k;= m folgt aus der Unabhängigkeit von X und X
k
m
Beweise zu: Multivariate Normalverteilung
Cov(X k, X m ) = 0,
BMN-2
17.5.10
mit 0 als I k x Im -Nullmatrix.
Zusammen mit Cov(Xk,X k) = Cov(X k) = E k folgt Cov(X) = E.
D
Beweis von
(4)
(a)
Xl' , X
(b)
Xl' , X K sind paarweise unkorreliert, d.h. Cov(X) =Diag{ Cov(X k)}
K
sind stochastisch unabhängig
Da die Implikation ,,::::}" stets gilt, bleibt nur
daß die gemeinsame Verteilung von Xl' ...,X
K
,,~"
{}
zu zeigen. (a) ist äquivalent dazu,
das Produktmaß der Randverteilungen
cL'(Xl)r ..!cL'(X ) ist, d.h. zu zeigen ist
K
(a)'
cL'(X) =
TI
k
NI (Jlk,Ek)
mit
k
weil mit X nach (1) auch jedes X
Jlk := E(X k),
E k := Cov(X k),
k normalverteilt ist.
Nun ist cL'(X) = N1(Jl,E) mit Jl = (Jll, ... ,JlK ) und aus (b) folgt
E = Diag{(Ek)}
Zusammen mit (2) folgt daher (a)'.
D
Beweis von
(5)
Rang(E) = 0
E=O
P{X=Jl} = 1.
Die erste Äquivalenz ist trivial und die zweite ergibt sich wie folgt.
ad
,~":
ad ,,~":
Für jedes i = 1, .... I folgt Var(X.) = 0 und somit P{ X.= fL.} = 1.
z
z z
Also ist auchP{X=j.L} = 1.
(X - Jl) ist Einpunktverteilt in 0 E IR]
(X - Jl)(X - Jl)T ist Einpunktverteilt in 0 E IRJxJ
E = Cov(X) = E((X - Jl)(X - Jl)~ =
o.
D
Beweise zu: Multivariate Normalverteilung
BMN-3
17.5.10
Beweise von
(9)
X stimmt P-fast-sicher überein mit
X = p, + P~X - p,) , d.h.
P{X =X} = 1.
(10)
cL'(X) = N[(p"E) ist auf p, + vft konzentriert, d.h.
P{XEIl+vft} =P{X-Il Evft} = 1.
Für (9) ist zu zeigen
P{X-X=O} = 1
(i)
cL'(X-X) = N[(O,O).
Nun ist
X-X
bzw. mit (5)
(X-p,) - P (X-p,)
c4
(ll-Pc4) (X-p,)
Pc4_d X -p,)
wobei vftl.- das orthogonale Komplement von vft ist. Aus (1) folgt
und somit
cL'(X-p,) = N/O,E)
cL'(X-X) = N/O,~l.- E Pc4l.-).
Für beliebiges xE IRJ gilt Ex E vft, also Pc4l.- E x =
°somit folgt ~
folgt. (10) ergibt sich aus (9), weil nach Definition von
X =X
=*
XEIl+vft.
l.- E
=
°und (i)
X gilt
D
Beweis von
I
T
Aus (11) folgt E x = C C x für alle xE IR , und somit gilt die Inklusion "e" in (13).
Aus C-E = C T bzw. C = EC- T folgt Cy = EC-Ty für alle YEIRJ! und somit
gilt die Inklusion ,,::::>" in (13).
D
Beweise zu: Multivariate Normalverteilung
BMN-4
17.5.10
Beweise von
(16)
Zl'"..,ZJ sind stochastisch unabhängig identisch N (0, l)-verteilt, d.h.
1
cL'(Z) = N ja, 11).
X = J-L + P~X-J-L) =
(17)
CZ + J-L.
Übung!
Beweis von
(18)
Rang(E) <I
N/J-L, E) besitzt keine )/- Dichte.
)/(J-L+vft) = 0,
Wegen Dirn vft = Rang(E) <I hat der lineare Raum vft das Lebesgue-Maß Null,
d.h.i( vft) = 0 [vgl. z.B. Billingsley (1979), Sec. 12, p. 144]. Es folgt
(i)
I
I
A (J-L + vft) = A (vft) = o.
Da der Träger J-L +vft von N1(J-L, E) das Lebesgue-Maß Null hat, kann es keine
i- Dichte j geben, denn sonst müßte gelten
J
1
jdA =1
nach (9)
fL+ c4
im Widerspruch zu (i) .
D
Beweis von
(19)
Für Rang(E) = I ist eine AI-Dichte von N/J-L,E) gegeben durch
I
xEIR ,
mit der quadratischen Form
I
xEIR .
Es folgt sofort vft = IRI und somit J-L + vft = IRI . Weiter gibt es eine invertierbare
lxI-Matrix C mit E = CC T, d.h (10) gilt.
X=
Nach (17) genügt es zu zeigen, daß
CZ+J-L mit cL'(Z) = N/O, 11) die Dichte cpj-IJ-L!E) besitzt. Nach 2 (8) besitzt
Z die Dichte 'PI mit
Beweise zu: Multivariate Normalverteilung
'PI(z) =
BMN-5
17.5.10
" zE IR!
f ur
((2'71-/ exp(zTz ))-1/2,
= 'Piz I O! 11)
Aus der Wahrscheinlichkeitstheorie ist bekannt [vgl. z.B. Billingsley (1979), (17.14),
p. 193]' daß eine Dichte f von
X
wie folgt durch die Dichte 'PI von N (O,l1) gegeben
I
ist
(i)
f(x)
Q(x)
'PI (C- 1(X-Jl)) 'IDet(C-1)1,
" xE IRI
f ur
((27f/ exp(Q(x-Jl)t 1/ 2 ·IDet(C)I-1
mit
xT[C-1]T C-1 x.
x TE-l x,
da
Weiter folgt mit dem Determinanten-Produktsatz
Det(E) = Det (CC T) = Det(C)2
und somit
IDet(C) I = Det(E)1/2
Eingesetzt in (i) ergibt sich jetzt f(x) = 'Pix IJl! E).
D
Beweis von
(20)
Ist C eine lxl-Matrix vom Rang 1 mit E= CC T, so ist eine auf Jl + vft
konzentrierte /\.t+c4-Dichte von NiJl,E) gegeben durch
'PjxIJl!C):=
[(27fl· Det(CTC). exp{Q(x-Jl)}]-1/2,
XEJl+vft,
mit der auf vft definierten quadratischen Form
xE
vft,
wobei E- eine beliebige generalisierte Inverse von Eist.
Die quadratische Form Q: vft-----+ IR hängt (auf vft) nicht von der
speziellen Wahl von E- ab!
Wir können o.B.d.A. voraussetzen, daß X mit seiner Standard-Darstellung aus (17)
übereinstimmt, d.h. X = CZ + Jl, wobei cL'(Z) = N ( 0,11J) und C eine beliebige MaJ
trix ist mit
(i)
CC
T
= E,
Rang(C) = l.
Beweise zu: Multivariate Normalverteilung
BMN-6
17.5.10
Für die affine Einbettung G: IRJ -----+ IRI , definiert durch
(ii)
G(z) = Cz
·· zE IRJ
f ur
+ J-L
ist X = G(Z), und somit ist cL'(X) das Bildmaß von cL'(Z) unter G. G besitzt eine
Linksinverse G - : IRI
---+
IRJ, definiert durch
C - = (C TC) -1 C T,
mit
(iii)
d.h. es gilt
·· zE IRJ.
f ur
(iv)
Nach 2 (8) besitzt Z eine Dichte !.pJ bzgl. des Lebesgue-Maßes )/, und wir zeigen zuerst
(v)
G(Z) bzgl. des Bildmaßes AG :=)/G-1
!.pJo G- ist eine Dichte von X =
J
von A unter G.
Für beliebiges A E lBI gilt
J
(!.pJ o G-o G)
dA
J
G-l[A]
J
!.pJ
J
dA ,
vgl. (iv)
G-l[A]
= P{ZEG-1 [A]}
= P{G(Z)EA},
und damit ist (v) bewiesen. Weiterhin ist das Bild von G gerade
wobei .At durch (13) gegeben ist. Das Bildmaß AG ist daher auf J-L +.At konzentriert
und stimmt dort bis auf einen Faktor mit dem Lebesgue-Maß
\l+Jft
überein, d.h. es gilt (vgl. Exkurs "Das Lebesgue-Maß auf Unterräumen").
(vii)
(viii)
mit
f(x)
a . !.pJ ( C - (x - J-L) ) ,
([27f]J. det (C TC)
vgl. (iii)
r
12
/ . exp{ Q(x-J-L)},
vgl. 1 (8)
auf J-L +.At
Beweise zu: Multivariate Normalverteilung
BMN-7
17.5.10
mit
·· xE IRI.
f ur
(ix)
Nun ist [C-] TC- eine g-Inverse von E (sogar die Moore-Penrose-Inverse) weil
C CT[C-]TC - C C T
CC T
)
Mit der Wahl dieser g-Inversen ist dannf= <pj-IJ-L,C), und zu zeigen bleibt noch,
daß Q auf vft unabhängig von der Wahl der g-Inversen E- von E ist. Für xEvft
gibt es nach (13) ein vE IRI mit x = Ev, und
ist unabhängig von E - .
D
Beweis von
(23)
T
Rang(E) = I
det(C C) = det(E).
Für J = I gilt nach dem Determinanten-Produkt-Satz
det (C TC) = [det (C ) ] 2 = det (C C T)
= det(E),
vgl. (10).
D
Beweis von
(24)
Für X mit cL'(X) = NjJ-L, E) gilt
(i)
cL'(tTX) = N 1(t TJ-L, tTE t)
Und für die MGF von X folgt
(ii)
MX(t) = E( exp {tTX} )
= MtTx(l)
= exp{
t TJ-L + ~ tTEt}
vgl. 1 (6).
D
Beweise zu: Multivariate Normalverteilung
BMN-8
17.5.10
Beweise zu
4.
Quadratische Formen von normalverteilten
Variablen
Beweise von
(4)
(X-Jl)TE-(X-Jl) ist x~-verteilt.
(6)
(X-v)TE-(X-v) ist X;(8)-verteilt mit
Fall 1:
J= 0
Da X = Jl P-fast-sicher gilt, sei o.B.d.A. X = Jl. Dann ist
per Definition X~ - verteilt, d.h. (4) gilt, und
(X - v) TE- (X - v)
(Jl-v) TE- (Jl- v)
Jl TE E- EJl
nach Definition von v
= JlTEJl = 8
ist X~(8)-verteilt, d.h. (6) gilt.
Fall 2:
J> 0
Da X P- fast-sicher mit semer Standardisierung X übereinstimmt, seI o.B.d.A.
X= X, d.h. mit der Darstellung 3 (17) ist
(i)
mit
cL'(Z) = NJ(O,ll),
(ii)
mit
Rang (C) = J.
Aus (3) ergibt sich
CC T = CC T E-CC T
und da C eine Links-Inverse und C Teine Rechts-Inverse besitzt, folgt
Beweise zu: Multivariate Normalverteilung
BMN-9
17.5.10
(CZ) TL'-(CZ)
ZTCTL'-CZ
ZTZ
J
wegen (iii)
2
2: Z ..
j=1 J
Damit ergibt sich (4) aus der Definition der X}Verteilung. Weiter ist
x
= CZ
vgl. (i)
CZ+L'p,+v
vgl. Definition von v
CZ+CCTp,+v
vgl. (ii)
C(Z
Aus
+ P,
+ A) + v
mit A = CTp,.
X - v = C (Z + A)
folgt dann
(Z+A) CTL'-C(Z+A)
(Z + A) T(Z+A)
J
2:
j=1
Mit der Definition der nichtzentralen
2
(Z.+A.) .
J
J
X} Verteilung ergibt sich hieraus (6), wobei
D
Beweise zu: Multivariate Normalverteilung
B MN-lO
17.5.10
Beweis von
(8)
(X-Jl)T(X-Jl) und (X-Jl)T E(X-Jl) sind fast sicher gleich und
x}verteilt.
(9)
Die 3 Variablen
(XTX-vTv), (X-v)T(X-v),
(X-v)T E(X-v)
sind fast-sicher gleich und jeweils x'l8)-verteilt.
(10)
Für Jl=EJl sind XTX und X T EX fast sicher gleich und X;(8)-verteilt
. (
T
TE
mIt 0 = Jl Jl = Jl
Jl.
Die orthogonale Projektion auf den Raum .At ergibt sich nach 2.1(14) zu
da E idempotent und symmetrisch
E,
da E- eine g- Inverse von Eist.
Nach 3 (10) gilt
(i)
X- Jl E.At
P-fast sicher
=*
E(X-Jl) = ~(X-Jl) = X-Jl
P-fast sicher
=*
(X-Jl) TE(X-Jl) = (X-Jl)T(X-Jl)
P-fast sicher.
Wegen (4) ist damit (8) gezeigt.
Weiter folgt aus der Definition von v
und wegen (i) ist
(ii)
X-v = (X-Jl) +~JlE.At
P-fast sicher.
Also folgt
(iii)
IIXI1 2 = IIX-vI1 2 + IIvl1 2
bzw.
XTX - vTv = (X-v)T(X-v)
P-fast sicher.
Aus (ii) folgt wie oben (mit v statt Jl)
(X-v)TE(X-v) = (X-v)T(X-v)
P-fast sicher.
Beweise zu: Multivariate Normalverteilung
17.5.10
B MN-11
Zusammen mit (iii) ergibt sich jetzt (9) aus (6).
Und (10) folgt aus (9), weil zusätzlich v = 0 und 8 = Jl TEJl = Jl TJl gelten.
D
Beweis von
(11)
X
T Ip-1X
. XI2(c)
I
1st
u -vertel·1·
t mIt
ui' = Jl T Ip-1
I
Jl.
Es gibt eine invertierbare I xl-Matrix C mit E = C C T (z.B. die Cholesky-Zerlegung, vgl. Stoer (1983), (4.3.3), p. 155). Also
(i)
C -1 EC-1 T = 11 ,
E-1 = C- 1T C-1 .
Für X = C-1 X gilt cL'(X) = NI(iJ"
Also liefert (6) angewandt auf
E)
mit iJ, = C-1 Jl,
X, iJ" E =
E= C-1 EC-1T =11.
11, iJ = iJ,- EiJ, = 0 sofort:
(i) X T y1 X ist X;( 8) -verteilt
mit
D
Beweise zu: Multivariate Normalverteilung
B MN -12
17.5.10
Beweis zu
5.
Bedingte Normalverteilungen
Beweis von
(5)
...4t2 =
Für
...4t2 = {
c ..1...4
12
{cETIl1 c T X 1 ist von X 2 stochastisch unabhängig}.
1
eie ..1...412 } gilt:
T
{}
c 17
{}
c . Cov (Xl' X 2) = 0,
da ...412 = Bild(E12 )
= 0 ,
12
T
da Cov(X1,X 2 ) =1712
T
Cov( c X 1,X 2 ) = 0 ,
T
c Xl von X 2 unabhängig,
T
da (c Xl' X 2) normalverteilt.
D
Beweis von
(7)
Aus Symmetrie genügt es ...4 C...4
12
11
zu zeigen) und hierzu zeigen wir für die or-
thogonalen Komplemente: ...4~ C ...4~
cE...4cl
11
{}
c T 17 = 0
=*
Var {c Xl} = c 1711 c = 0
=*
c Xl ist Einpunkt-verteilt
=*
c Xl ist von X stochastisch unabhängig
=*
cl
cE...412
11
T
T
T
T
2
nach (5).
Beweis von
Nach (7) ist ...4 C ...4
21
22
und somit gibt es ein C mit
1721 = 1722 C,
also
17
12
= 17
T
21
C
T
17 .
22
D
Beweise zu: Multivariate Normalverteilung
B MN -13
17.5.10
D
Beweis von
(10)
Y 1 ist von X stochastisch unabhängig,
2
Cov((X1 - 1712 172; X 2 ), X 2 )
Es ist
Cov (Xl' X 2)
-
1712 172; Cov(X 2, X 2)
vgl. (8).
Da (Yl' X 2) normalverteilt ist, folgt die Behauptung.
D
Beweis von
(11)
Y ist normalverteilt mit:
Jl1 - 1712 172; Jl 2 '
1
1711 - 1711 172; 1721
.
Y 1 ist als lineare Funktion von (X 2, Xl) ebenfalls normalverteilt mit
E(X 1 ) - 1712 172; E(X 2 ),
nach Definition
JL1 - 1712 172; JL 2·
Cov(Y
)
1
Cov( Y 1 ' (Xl - 1712 172; XJ),
nach Definition
Cov(Y1 ' Xl) - 1712 172; . Cov(Y1 ' X 2)
Cov(Y1 ' Xl)
vgl. (10)
Cov((Xl - 1712 172; XJ ' Xl)
nach Definition
Cov(X ,X
1
1
) -
1712 172;. Cov(X 2,X1 )
1711 - 1712 172; 1721 .
D
Beweise zu: Multivariate Normalverteilung
B MN -14
17.5.10
Beweis von
(12)
mit
Jl1 (X 2) = Jl1 + 1712 172; (X 2 - Jl 2),
d.h. für jedes x EIR
2
I2
ist durch
Es genügt (13) zu zeigen und hierzu verwenden wir den Exkurs Bedingte Verteilungen
(2.3 Unabhängigkeits-Transformation).
Für die Abbildungen G+: IRI I X IRI 2 -------+ IRI 2 definiert durch
gelten
G+(G_(x F x 2 )!x 2)
(Xl - 1712 172; x 2)
und
GjG+(x F x 2 )!x 2)
(xl
+ 1712 172;
+ 1712 172;
x 2 = xl
x 2) - 1712 172; x 2 = xl
d.h. bei festem x 2 sind Gj-!x 2 ) und G+hx2) invers zueinander.
Da Y1 = GjX ,X ) nach (10) von X stochastisch unabhängig ist, folgt - vgl. Ex2
1 2
kurs Bedingte Verteilungen (2.3 Unabhängigkeits-Transformation) - für jedes x
2
Da G+ linear ist, folgt aus (11) sofort, daß G+(Y 1,x 2) normalverteilt ist mit
E(G+(Y 1,X 2 )) = G+(E(Y 1 ),x 2 )
(Jl 1 - 1712 172; JlJ
+ 1712 172;
x2
Jl1 + 1712 172; (x 2 - Jl 2 )
Jl1(x 2)
Cov(G+(Y1,x 2))
Cov(Y )
1
1711 - 1711 172; 1721
17 '"
1
Hieraus ergibt sich (13).
.
D
Beweise der Übungsaufgaben zu: Multivariate Normalverteilung
1.8.05
B MN - 15
..
Beweise der Ubungsaufgaben zu:
Eigenschaften der multivariaten Normalverteilung
3.
Beweis von
Aus
den
Rechenregeln über Erwartungswerte
und
Covarianzen folgt
für
Y=AX+b:
T
E(Y) = AJl + h,
Cov(Y) = AEA .
Zu zeigen bleibt also nur cL'(Y) E ~ bzw.
(i)
sT y E JV;:
Nun ist
sTy
für alle sE IRJ.
sTAX + sTh
(ATs)TX
+ sTh .
Wegen cL'(X) E JVf folgt cL'( (ATs )TX ) E JV;: und somit auch (i).
D
Beweis von
(16)
Zl'" ..,ZJ sind stochastisch unabhängig identisch N (0, l)-verteilt, d.h.
1
cL'(Z) = NjO, 11).
(17)
X = Jl + P~X-Jl) =
CZ + Jl.
Nach (1) ist cL'(Z) E ~ mit E(Z) = 0 und
Cov( Z) = C - E C - T
J
C - ce TC - T = (C - C) (C - C ) T = 11 J. 11 = 11J"
Also gilt (16), und (17) folgt aus
D
M
Die Multinomialverteilung
Gerhard Osius
1.
Definition
2.
Auftreten
3.
Randverteilungen, Erwartungswert, Covarianz
4.
Erzeugende Funktionen
5.
Multinomial-Grenzwertsatz
6.
Darstellung als bedingte Poisson-Verteilung
7.
Darstellung als Exponential-Familie
G. Osius: Die Multinomial-Verteilung
1.
M-2
8.1.13
Definition
Die Multinomial-Verteilung MK(N,p) mit K Klassen (wobei KE W, K> 1) vom Umfang
NE W und dem K-dimensionalen Wahrscheinlichkeitsvektor p E (0, 1)K, d.h. p += 1, ist
eine K-dimensionale diskrete Verteilung auf dem (von p unabhängigen) Träger
(1)
TN= {
xEW~ I x+ =N}
und der Zähldichte
(2)
!Jx I p)
N!
K
1
TI -, ·p
k=l xk.
X
k
k
Speziell für N = 1 besteht der Träger T gerrau aus denK Einheitsvektoren
1
(3)
Tl = { el' ... , eK}
(4)
ek = (ekl) E IRK
wobei
mit
ekl = 8kl
für alle k, l
( 8 = Kronecker-Symbol)
und die Zähldichte vereinfacht sich zu
(5)
für alle k = 1, ... , K.
Unter Verwendung der MK(1,p)-Verteilung vom Umfang 1 läßt sich die Verteilung
MK(N, p) für beliebiges N > 1 auch rekursiv über den Umfang N definieren als Faltung von MK(N -1,p) und MK(1,p), d.h. es gilt
(6)
wobei
MK(N,p) = MK(N -1,p)
* MK(1,p),
* den Faltungs-Operator bezeichnet.
Insbesondere ist MK(N,p) dieN-fache Faltung von MK(1,p).
G. Osius: Die Multinomial-Verteilung
2.
8.1.13
M-3
Auftreten
Bei einem Zufallsexperiment betrachten wir eine Zerlegung des Ergebnisraumes .f2
in K disjunkte Ereignisse A , ... , AK
1
K
(1)
.f2 = U Ak'
k=l
mit positiven Wahrscheinlichkeiten
FürNunabhängige Wiederholungen des Zufallsexperiments bezeichne Xk die Anzahl der Wiederholungen, bei denen das Ereignis Ak eingetreten ist. Dann bilden
diese Anzahlen einen K-dimensionalen Zufallsvektor X= (X1'" .. ,XK) mit einer Multinomial-Verteilung
und dem Wahrscheinlichkeitsvektor p = (p , ... , pK ).
1
3.
Randverteilungen, Erwartungswert, Covarianz
Die Eigenschaften der Multinomialverteilung formulieren wir unter Verwendung
von Zufallsvariablen, d.h. wir betrachten einen K-dimensionalen Zufallsvektor
X= (X1,... ,XK) mit der Multinomial-Verteilung
Die Randverteilung einer Komponente von X ist binomial-verteilt
(2)
für jedes k.
Speziell für K = 2 ist X = N- X (P- fast-sicher) und somit ist X bereits durch seine
2
1
erste (binomialverteilte) Komponente X eindeutig bestimmt. In diesem Sinn ent1
spricht eine Multinomialverteilung mit K = 2 Klassen stets einer Binomialverteilung.
Der Erwartungsvektor und die KxK Covarianzmatrix von X lauten
G. Osius: Die Multinomial-Verteilung
(3)
E (X)
Jl"·-
p
EP(Xk)
(4)
M-4
8.1.13
Np
bzw.
Npk'
N ( Diag{p}- p pT)
bzw.
Cov P(Xk,Xz)
- Npkpl
für k ;= l
Cov P(Xk,Xk)
N Pk (1- pk))
E == Cov p (X)
Insbesondere sind X , ... , XK nicht stochastisch unabhängig, es besteht sogarein line1
arer funktionaler Zusammenhang
(5)
X+:=X1 + ... +XK=N
(P-fast sicher).
Zur weiteren Untersuchung der Covarianzmatrix wollen wir diese zuerst anders
darstellen. Bezeichnet
den Diagonalraum (der aus allen konstanten Vektoren besteht) und
(7)
D = Diag {J.L} = N · Diag {p}
die Diagonalmatrix des Erwartungsvektors, so läßt sich die Covarianzmatrix unter
Verwendung der D-orthogonalen Projektion P~ schreiben als
(8)
E
= D · (ITK- P~)
-D·PD
-65
mit
Hieraus ergibt sich insbesondere der Rang der Covarianzmatrix zu
(9)
RangE= K -1,
was im Hinblick auf (5) nicht überrascht.
Der Spaltenraum von Eist das (übliche) orthogonale Komplement von f!25
Eine (symmetrische) generalisierte Inverse von Eist gegeben durch
(11)
und die Moore-Penrose-Inverse von E lautet (nach Tanabe und Sagae, J. Royal Statistical Society B1 54, 1992, p. 211-219)
Go Osius: Die Multinomial-Verteilung
M-5
801.13
(12)
wobei
(13)
4.
Erzeugende Funktionen
Für einen Zufallsvektor X= (Xl'"oo,XK) mit Multinomial-Verteilung MK(N, p) ist die
charakteristische Funktion cpX gegeben durch
Analog ist die Moment-erzeugende Funktion MX von X gegeben durch
(2)
und hieraus ergibt sich die Kumulanten-erzeugende Funktion KX von X zu
(3)
= N olog(pTexp(t))
Die Ableitungen der Kumulant-erzeugenden Funktion lauten
(4)
(5)
DKx(t)
N ( p T exp { t}) -l p T Diag {exp (t)}
v Kx(t)
N ( pT exp{ t} rlo Diag {p} exp(t)
2
D Kx(t)
0
0
N ( pT exp{ t} )-10 Diag {p} 0Diag {exp(t)}N ( pTexp{ t} r
Und für t
bzwo
0
20
pT 0Dial {exp(t)} 0p
= 0 ergeben sich der Erwartungswert und die Covarianzmatix von X (in
Übereinstimmung mit 3 (3-4):
(6)
EP(X)
(7)
Cov (X)
p
VKx(O) = Np,
2
D Kx (0) = N ( Diag{p}- p pT)
0
G. Osius: Die Multinomial-Verteilung
5.
M-6
8.1.13
Multinomial-Grenzwertsatz
Für eine Folge X n = (Xn 1,... ,Xn K) von Zufallsvektoren mit
(1)
L(X)
=MK(Nn ,p)
n
n
gelte für n ---+ oo
(2)
N
(3)
p
n
n
-----+
oo
-----+
p
Dann ist X
oo
(wachsende Umfänge)
E (0, l)K.
asymptotisch (multivariat) normalverteilt, gerrauer gilt der Multino-
n
mial-Grenzwertsatz
(4)
(5)
mit
E
00
= Diag{p } - p
00
00
pT .
00
Hierbei ist E 00 nach 3 die Covarianz-Matrix der Multinomialverteilung MK(l, p 00)
und läßt sich daher auch darstellen als
= D oo · (11K -
(6)
E oo
(7)
D 00 = Diag{p 00}.
pDoo)
qz;
mit
Die Verteilungskonvergenz (3) läßt sich noch wesentlich verschärfen. Es konvergieren sogar die zugehörigen Moment-erzeugenden Funktionen MU von U n punktn
weise gegen die Moment-erzeugende Funktion M U von U
(8)
MV (t)
n
für alle t E IRK_
G. Osius: Die Multinomial-Verteilung
6.
M-7
8.1.13
Darstellung als bedingte Poisson-Verteilung
Die Multinomialverteilungen läßt sich auch als bedingte Poisson-Verteilungen wie
folgt darstellen. Gerrauer gilt für einen Zufallsvektor X= (X1'" .. ,XK)
(1)
Sind X , ... ,XK stochastisch unabhängig und Poisson-verteilt, d.h.
1
L(X) = Pois(J.L)
mit
so ist für jedes NE W die auf X+= N bedingte Verteilung von X eine
Multinomialverteilung
mit
p
1
= -J.L
E (0,1) K.
1-L+
Damit läßt sich jede Multinomialverteilung MK(N, p) als bedingte Poisson-Verteilung darstellen - indem man (1) auf J.L =Np anwendet - und dies ermöglicht es, Resultate über Multinomialverteilungen zu zeigen, indem man die Resultate für die zugehörigen bedingten Poissonverteilungen zeigt.
Umgekehrt kann man aus einer Multinomialverteilung MK(N, p) auch wieder unabhängige Poissonverteilungen erhalten, indem man den Umfang N =X+ gemäß einer
Poissonverteilungen variieren läßt. Gerrauer gilt für den Zufallsvektor X folgende
"Umkehrung" von (1)
(2)
Ist für jedes NE W die auf X+= N bedingte Verteilung von X eine Multinomialverteilung, d.h.
L(XIX+ =N) = MK(N,p)
wobei p E (0, 1)K nicht von N abhängt, und ist zusätzlich die Summe X+
Poissonverteilt, d.h.
L(X+) = Pois(-A)
mit -AE(O,oo),
so sind X , ... ,XK stochastisch unabhängig und Poisson-verteilt, d.h.
1
L(X) = Pois(J.L)
mit
G. Osius: Die Multinomial-Verteilung
7.
8.1.13
M-8
Darstellung als Exponential-Familie
Ein MK(N,p)-verteilter Zufallsvektor X ist wegen X+ =N bereits durch K- 1 Komponenten eindeutig bestimmt - und das trifft wegen
scheinlichkietsvketor
7r
+= 1 auch
7r
auf den Wahr-
zu. Deshalb wollen wir bei den folgenden Betrachtungen je-
weils eine Komponente von X und
7r
fortlassen. Hierbei ist es notationsmäßig
zweckmäßig, mit einer MK+ (N, p)-Verteilung zu beginnen, wobei wir die Vektoren
1
xEIRK+l jetzt mit 0, ... , K (statt 1, ... , K+1) indizieren. Dann ist
(1)
und
p ist eindeutig durch p bestimmt, weil
(2)
mit
Der "verkürzte" Wahrscheinlichkeitsvektor liegt im Parameterraum
(3)
!?I[(== {pE(0,1)K I Pt <1} c
IRK
der offen und konvex ist. Eine zweckmäßige Umparametrisierung erhält man
durch die multivariate Logit-Transformation
(4)
logit:
!?I[(
mit
-----+
k = 1, ... , K.
logitk(p) = log(pk/(1-p+))
Diese Transformation ist bijektiv und ihre Inverse ist
(5)
. -1 : IRK
1og1t
fJAo
mit
K
K
logitk\"P) = exp(1/;k) / (1 +
2:: exp(1fz) ),
k = 1, ... , K.
l =1
Der Parameter '1/J = logit(p) hat den Vorteil gegenüber p, daß er über den ganzen
IRK variieren kann. Eine weitere Umparametrisierung ergibt sich aus der multivariate Odds-Transformation
(6)
odds:
!?I[(
oddsk(p)
und ihrer Inversen
(0, oo)K
pk/(1- p +),
mit
k= 1, ... ,K
G. Osius: Die Multinomial-Verteilung
fJAo
(7)
M-9
8.1.13
mit
K
K
+ 2:= wz),
oddsk\w) = wk / (1
k = 1, ... , K.
l =1
Zwischen beiden Umparametriserung besteht der Zusanmmenhang
(8)
logit(p) = log( odds(p)) ,
logiC\"P) = odds- 1( exp("P)) ,
wobei log(-) bzw. exp( -) die komponentenweise Fortsetzung der Logarithmus- bzw.
Exponentialfunktion auf (0, oo)K bzw. IRK bezeichne.
Ein Zufallsvektor
ist wegen X+ = N bereits eindeutig bestimmt durch
(10)
da
Wir zeigen jetzt, daß die Klasse aller Verteilung von X mit Parameter p E ff'j( eine
K-dimensionale Exponentialfamilie mit kanonischem Parameter "P = logit p E IRK
bilden. Der Träger dieser Verteilungsklasse ist
und die Familie der Dichten ist für x E TN gegeben durch
(12)
!(X I p) = N!
K
1
TI -,
k=O xk.
X
0
p k
k
mit
x0 =
N-x+'
p0 = 1-p+
Mit den Bezeichnungen
(13)
w
= odds(p),
"P = logit(p) = log(w)
ergibt sich dann für die log-Dichte
K
(14)
logf(xlp) =
2:= xklogpk +
(N-x+) log(1-p+)
+
d(x)
k=1
K
l:=xklog(pk/(1-p+))
+
Nlog(1-p+)
+
d(x)
k=1
mit
G. Osius: Die Multinomial-Verteilung
M-10
8.1.13
K
(15)
d(x) = log N! -
2:: log xk!
-log (N- x +)!.
k=l
Nun ist nach (5)
K
(16)
exp( 1/Jk)
I (1 + 2:: exp(1/Jz) ),
k = 1, ... , K.
l =1
K
(17)
p0 = 1 - p
+
= 1
I (1 + 2:: exp(1/Jz)),
l =1
und somit ergibt sich die Darstellung
(18)
logf(xlp) = '1/JTx-h("P) +d(x)
mit
K
(19)
h("P) = N log (1
+ 2:: exp(1/Jz)) .
l =1
Folglich bilden die Dichten eine K-parametrige Exponentialfamilie mit kanonischem Parameter
"P = logit(p) E IRK und der sogenannten Kumulanten-Funktion
h("P). Die Kumulanten-erzeugende Funktion von X ist daher gegeben durch
für t E IRK.
(20)
Insbesondere ergeben sich die (bereits im Abschnitt 3 bestimmten) Momente
(21)
E"p(X) = D h("P)T = \7 h('I/J) = Np.
(22)
Cov"p(X) = D h("P) = N ( Diag{p}- p pT).
2
Hierbei gilt
(23)
Cov"p(X) ist positiv-definit.
Dies ist kein Widerspruch zur Darstellung 3 (8), weil hier für den "verkürzten"
Wahrscheinlichkeitsvektor p +< 1 gilt. Und als Folgerung ergibt sich
(24)
h ist streng konvex ..
Beweise: Die Multinomial-Verteilung
MB-1
801.13
Beweise zu
3.
Randverteilungen, Erwartungswert, Covarianz
Beweis von
(2)
für jedes ko
Der Beweis erfolgt durch Induktion über N. Für N = 1 folgt die Behauptung wegen
Xk E {0, 1} aus
P{Xk=1} = P{X=ek} = pko
Der Induktionsschritt N
(i)
(ii)
f-----t
N + 1 ergibt sich aus den Faltungseigenschaften
MK(N + 1,p) = MK(N,p)
B(N + 1,p) =
B(N,p)
* MK(1,p),
*
B(1,p)o
D
Beweis von
(3)
Jl : =
E p (X) = Np
bzwo
EP(Xk) = N pk,
(4)
E == Cov (X) = N ( Diag(p)- p pT)
p
bzwo
für k ;= l
Covp(Xk,Xz) = -Npkpl
Cov P(Xk,Xk) = N pk (1- pk)
1
Der Beweis erfolgt durch Induktion über N. Für N = 1 folgt die Behauptung wegen
Xk ,Xl E {0, 1} aus
(i)
(ii)
vgl. (2)
E(Xk Xz)- E(Xk) E(Xz)
0
0
8k lo E(Xk Xk)- E(Xk) E(Xz),
0
0
8 = Kronecker-Symbol
8k lo E(Xk)- E(Xk) E(Xz)
0
vgl. (i)
Der Induktionsschritt N
f-----t
N + 1 ergibt sich aus der Faltungseigenschaft
Beweise: Die Multinomial-Verteilung
8.1.13
MB-2
und den Rechenregeln
(iv)
E(X+ Y)
(v)
Cov(X+ Y)
E(X) + E(Y)
Cov(X) + Cov(Y) + 2 Cov(X, Y)
Cov(X) + Cov(Y)
falls X, Y st. unabhängig.
D
Beweis von
(8)
E = D · (ITK- P~ ).
Wegen
E = N ( Diag{p}- p pT)
=
D
vgl. (4)
-1
T
-p,+JlJl,
da N = p, +
ist daher zu zeigen
(i)
Nun ist
-1
1-L
+ Jl Jl
T
e + ( e~D e +r
1
1
e + (p, +r
-1
e~D,
vgl. Exkurs SP 3 (3)
e~D
TD
0+ e+e+
und somit bleibt für (i) noch zu zeigen
(ii)
und dies folgt sofort aus D e += Jl·
D
Beweise: Die Multinornial-Verteilung
MB-3
8.1.13
Beweis von
(9)
RangE= K -1,
(10)
Es ist
(i)
Also ist
vgl. (8)
RangE = Rang P4'D =Dirn {jj' = K- Dirn f!25 = K -1,
d.h. (9) gilt.
D-1 [ 0j_ ]
Aus
{jj' =
folgt
BildE = D [Bild
vgl.Exkurs SP 2 (10)
P1J
vgl. (i)
D [ß]
D [ u-1 [ qz;j_ l]
d.h. (10) gilt.
D
Beweis von
(11)
Die Behauptung folgt aus
E-D-1 -E
D. pD. D-1. D. pD
4'
4'
vgl. (8)
u.pD.pD
4'
4'
D·PD
4'
= E.
D
Beweise: Die Multinomial-Verteilung
8.1.13
MB-4
Beweis von
(12)
Für
(o)
E
--
E+ =
(i)
D·PD
-65
P.®_L. u-1. P.®_L
mit
-0'= 0j_n = u-1 [0j_J
vgl. Exkurs SP 2 (10)
ist (nach Definition der Moore-Penrose-Inversen, vgl. Exkurs GI) zu zeigen
(ii)
~-E
ist symmetrisch
(iii)
E-~
ist symmetrisch
(iv)
E·~·E =E
(v)
~-E·~=~.
'
Der folgende Beweis verwendet nicht die spezielle Struktur von D und 0 sondern
gilt für jede positiv-definite Matrix D und jeden Teilraum 0, wenn E und E+
durch (o) definiert sind.
ad (ii):
(vi)
P.®_L. u-1. P.®_L
·E
P.®_L -D-1 -E
da
Bild(E) = D [ -0'] = 0j_
D
p.®_L p-65
0
(11- P.® )(11- P~)
D
+ p.® p.®D
D
+ P.®D
II- p.®- p.®
11- P.®- P.®
vgl. Exkurs SP 2 (11)
da
Bild(P~) = 0
II- p
.®
also gilt (ii).
Beweise: Die Multinomial-Verteilung
ad (iii):
MB-5
801.13
Zunächst ergibt sich - analog (vi) -
(vii)
(11-
P~)(11- Pq;)
vgl. Exkurs SP 2 (11)
D
D
D
+ Pq;
II- Pq; - Pq; + Pq; Pq;
11- Pq; - Pq;
II- pD
q;
und hiermit folgt
D0
(vi)
PJ
0
Pq;j_
0
u-10 Pq;j_
DOPDou-1op
-65
q]_l_
da
Bild(D-1 Pq; j_) = -0' nach (i)
0
also gilt (iii)
ad (iv):
E ·E+ ·E
0
vgl. (vi)
da
E
Bild(E) = D [ -0'] = 0j_
vgl. (vi)
Pq;j_ D-10 Pq;j_
0
0
Pq;j_
Pq;j_ D-10 Pq;j_
0
L'+o
D
Beweis von
(13)
Wegen 0 = span{ e +} ergibt sich mit Exkurs SP 2 (3)
1
Pq;= e+(e!e+f e!
T
e+e+=K.
wobei
D
Beweise: Die Multinomial-Verteilung
8.1.13
MB-6
Beweise zu
4.
Erzeugende Funktionen
Beweise von
K
(1)
'Px (t)
E( exp (i · tTX))
[ 2:=
pk exp (i tk) ]N
k=l
( p Texp (i t) ) N
K
(2)
Mx(t)
E( exp (tTX))
[ 2:=
pk exp (tk) ]N
k=l
(PT exp (t) )N
(3)
KX(t) = logMX(t)
= N ·log(pTexp(t))
für tEIRK,
für tEIRK.
Da MK(N,p) dieN-fache Faltung von MK(1,p) ist, genügt es, die Behauptungen für
N = 1 zu zeigen. Für N = 1 gilt (1) wegen
K
2:=
pk exp { i tTek}
k=l
K
=
2:=
k=l
pk exp { i tk}
(2) folgt analog (ohne "i") für N = 1, und (3) ergibt sich aus (2).
D
Beweise: Die Multinomial-Verteilung
MB-7
801.13
Beweise von
(4)
(5)
DKx(t)
N ( pT exp{ t} )-10 pT 0Diag {exp(t)}
v Kx(t)
N ( pT exp { t}) - 1 Diag {p} exp (t)
0
2
bzwo
0
N ( pT exp { t}) - 1 Diag {p} Diag {exp (t)} -
D Kx(t)
0
0
N ( pT exp{ t} )- 2 0 pT 0 Diag 2 {exp(t)} 0 p
Die erste Gleichung in (4) ergibt sich durch Differenzieren von (3), und die zweite
Gleichung ergibt sich mit der Identität
für a, b E IRKO
(i)
Erneutes Differenzieren liefert
(ii)
2
D Kx (t) = D \7 KX(t)
r 1 Diag {p} Diag {exp (t)} N ( pT exp{ t} r 2 pT Diag {exp(t)} Diag {p}
= N ( pT exp { t}
0
0
0
0
0
0 exp(t)
und hireraus ergibt sich (5) mit
Diag{p} exp(t) = Diag{exp(t)} p,
0
0
vgl. (i)o
D
Beweise: Die Multinomial-Verteilung
MB-8
801.13
Beweise zu
5.
M ultinomial-G renzwertsatz
Beweise von
(4)
U n :=
(5)
E
(8)
MV (t)
~(
n
= Diag{p } - p
00
mit
Xn - Pn) ------=.:=--------+
;
00
00
pT 0
00
MU(t) = exp { ~ tTE00 t}
n
für alle t E IRKo
Da die Verteilungskonvergenz (4) mit dem Stetigkeitssatz für Moment-erzeugende
Funktionen (vgl. Exkurs KV 8) aus (8) folgt, genügt es (8) zu zeigen bzwo
(i)
für alle t E IRKo
Ku (t) = log Mu (t)
n
n
Bezeichnet K(-1 p) die Kumulanten-erzeugende Funktion von MK(l, p), doho
(ii)
für alle t E IRK,
K(tlp) = log(pTexp(t))
so läßt sich die Kumulanten-erzeugende Funktion von
(iii)
wie folgt darstellen
(iv)
Ku (t) = Kx
n
n
(~ 11 2 t)- ~ OP! t
= Nn 0K(~1/2t I pn)-
~ opJ t
vgl. Exkurs CV 4
vgl. 4 (3)
Nach der Taylor-Formel (vgl. zoB. Dieudonne, 1960, 8.1403) gilt dann die Entwikklung 20 Ordnung von K( s I p) im Punkt 0:
(V)
K( s I p) = K( 0 I p)
+
D K( 0 I p) 0s
+ ~ s T 0D2K( 0 I p) 0s +
R( s I p)
mit dem Restglied
1
(vi)
R(slp) =
(J~(l-T) 20 D 3 K(Tslp)dT)o(s,s,s)o
0
Wegen
K(O I p) = 0
DK(Oip) =PT
D 2K(O I p) = Diag{p}- p pT
vgl. 4 (6)
vgl. 4 (7)
Beweise: Die Multinomial-Verteilung
MB-9
8.1.13
reduziert (v) zu
Zusammen mit (iv) ergibt sich daher
(viii)
12
Ku (t) = N . KI(!V 1 t 1 p ) - VIr_ ·pJ t
n
n
n
= N . [!V1/2 PT t
n
n
n
n
n
+ 12 !V1
tT(Diag{p } n
n
p p T) t+ R(!V1/2 t I p )]
nn
n
n
-lir_n ·pT
t
n
=
12 tT(Diag{p }-p PT)t+N ·R(!V1/2tlp ).
n
n
n
n
n
n
Wegen
bleibt für (i) nur noch zu zeigen
(ix)
N
n
°
R(!V112 t I p )
n
n
----+
0
0
Da die Funktion D3K( TS I p) stetig ist bzgl. TE [ 0, 1] und p E (0, l)K, folgt
(x)
3
C(s) = sup{IID K(Tslp n)IIITE[O,l],nEW}
<
oo,
und man erhält die Restglied-Abschätzung
1
(xi)
< I (J
0
~(1-T) 2 ·D 3 K(T~1/ 2 tlpn) dT )1·11~1/ 2 t11 3 .
1
< ( J~
IID3 K(T~1/2t I pn)ll dT)
-~3/2 ·II t113.
0
< ~
aus der sich (ix) ergibt.
C(t)
0
~ 3/ 2 ·II t11 3)
D
Beweise: Die Multinomial-Verteilung
MB-10
8.1.13
Beweise zu
6.
Darstellung als bedingte Poisson-Verteilung
Beweise von
(1)
Sind X , ... ,XK stochastisch unabhängig und Poisson-verteilt, d.h.
1
L(X) = Pois(J.L)
mit
so ist für jedes NE W die auf X+= N bedingte Verteilung von X eine
Multinomialverteilung
L(X IX+ =N) = MK(N, p)
(2)
mit
p
1
K
= -J.L
E (0,1) .
1-L+
Ist für jedes NE W die auf X+ = N bedingte Verteilung von X eine Multinomialverteilung, d.h.
L(XIX+ =N) = MK(N,p)
wobei p E (0, 1)K nicht von N abhängt, und ist zusätzlich die Summe X+
Poissonverteilt, d.h.
L(X+) = Pois(-A)
mit -AE(O,oo),
so sind X , ... ,XK stochastisch unabhängig und Poisson-verteilt, d.h.
1
L(X) = Pois(J.L)
mit
Bemerkung: Man kann in (1) und (2) auch NEW zulassen, wenn man MK(O,p)
0
als Einpunkt-Verteilung in 0 E T = {0} interpretiert.
0
Da die Faltung von Poisson-Verteilungen wieder eine solche ist, ergibt sich aus den
Voraussetzungen in (1) sofort
(i)
L(X+) = Pois(-A)
mit,\ E (O,oo),
wobei A = J.L + ist. Da (i) in (2) sogar vorausgesetzt wird, genügt es für (1) und (2) unter der Voraussetzung (i) die Äquivalenz der beiden Aussagen für beliebiges p
E (0, 1)K zu zeigen:
(P)
L(X) = Pois(J.L)
(M)
L(XIX+ =N) = MK(N,p)
mit
für jedes NE W.
Beweise: Die Multinomial-Verteilung
MB-11
8.1.13
Für jedes XE w~ gilt trivialerweise
(ii)
P{X=x} = P{X=xiX =x } P{X =x}
+ +
+ +'
weil P{X+ = x +} > 0 nach (i). Zwischen der Dichte von MK(N, p)
f Jx Ip)
(iii)
= N!
TI p:k I xk!
für x = (x1'" .. ,xK) E TN"
k
und der Dichte von Pois(J.L)
..
1\..TK
f ur x E 11~ 0
(iv)
wobei p ( -I -A) die Dichte von Pois(-A) ist. Wir zeigen jetzt (P) {} (M).
1
ad (P) => (M): Für jedes NE W und x E TN gilt
P{X=xiX+ =x+} = P{X=x}/P{X+ =x+}
= PK(x IJ.L)
I Pl(NI -A)
= JN(xlp)
vgl. (P), (i)
vgl. (v)
Also gilt (M).
ad (M) => (P): Für jedes NE W und x E TN gilt
(vi)
P{X=x} = P{X=xiX+ =x+} · P{X+ =x+},
= !N(xlp). pl(NI-A)
= pK(x I J.L)
Und für x = 0 gilt
vgl. (M), (i)
Beweise: Die Multinomial-Verteilung
(vii)
P{X=O}
8.1.13
MB-12
exp(--A)
TI exp(p,k)
k
= pK(O I J.L)
Folglich stimmt die Dichte von X mit pK( -I J.L) überein auf
W~ = {0} U U TN,
NElN
d.h. (P) gilt.
D
Beweise: Die Multinomial-Verteilung
MB-13
8.1.13
Beweise zu
7.
Darstellung als Exponential-Familie
Beweise von
h("P)T = \1 h( '1/J) = Np .
(21)
E"p(X) = D
(22)
Cov"p(X) = D h("P) = N ( Diag{p} - p pT).
(23)
Cov"p(X) ist positiv-definit.
2
ad {21}(22): Die jeweils erste Gleichung gilt generell für Exponential-Familien- vgl.
z.B. G. Osius (2006) Einführung in die Statistik1 9.2 (10-11). Und die jeweils letzte
Gleichung ergibt sich komponentenweise aus 3 (3) (4).
ad{23):
Wegen (22) reicht es, die Behauptung für N=2 zu zeigen. Für t E IRK mit
(der Index
"P wird im Beweis unterdrückt) ist zu zeigen
(i)
t Cov(X) t = 0
T
t=O.
Nun gilt mit Jl = E(X)
(ii)
T
T
0 = t Cov(X) t = Var(t X)
=>
t..lT -p,
2
t ..l span(T2 - J.L).
Für den k-ten Einheitsvektor ek E IRK gilt
und
ek,
2ek E T2 = {XE w~ I X+< 2}
ek
= (2ek -J.L)- (ek -J.L) E span(T2 -J.L)
Da dies für alle k = 1, ... , K gilt, ist span(T - Jl) = IRK, und aus (ii) folgt (i).
2
D
G. Osius: Quantile von Verteilungen
Q
9.7.10
Quantile von Verteilungen
Gerhard Osius
1
2
Definition und elementare Eigenschaften
1.1
Binomialverteilung
1.2
Poisson-Verteilung
Verteilungskonvergenz und Quantile
Q-l
G. Osius: Quantile von Verteilungen
1
Q-2
9.7.10
Definition und elementare Eigenschaften
X sei eine reelle Zufallsvariable mit Verteilungsfunktion F: IR -----+ [ 0,1]. Für vorgebenes 0< p < 1 heißt
~E IR
ein unteres p-Quantil oder oberes (1- p)-Quantil der Vertei-
lung cL'(X) bzw. Verteilungsfunktion F, falls gilt
(1)
P{ X <~} < P < P{ X < ~}
F(~-)
bzw.
< P < F(~) .
Hierbei ist
F(~-) = sup {F(x)
I x <~}
= P{ X <~}
der linksseitige Limes von F im Punkt
~.
Falls F in
~
stetig ist, so ist (1) äquivalent
zu p = F(~).
Ist F stetig und injektiv) so ist das untere p-Quantil eindeutig bestimmt und gegeben
durch F-\p)s.
Für beliebiges F dagegen ist die Menge der p-Quantile ein Intervall, dessen Randpunkte wir bestimmen. Hierzu betrachten wir die links- bzw. rechts-stetige (Quasi-)
Inverse F-: (0,1) -----+ IR bzw. F : (0,1) -----+ IR von F, die definiert sind durch
(2)
F-(p)
inf{xEIR I p::;F(x)}
(links-stetige Inverse))
(3)
F_(p) : = sup {xE IR I F(x)::;p }
(rechts-stetige Inverse).
:=
Für jesdes xE IR gelten dann die grundlegenden Eigenschaften
(4)
F(Fjp)-) < P < F(F-(p)) ,
(5)
F-(p) < x
{}
P ::; F(x) ,
(6)
x < F_(p)
{}
F(x-) < p.
Hieraus erhält man die Darstellungen
(7)
F-(p)
Min {XEIR I p ::; F(x)}
= Min{ xEIR I p::; P{X<x}} ,
(8)
F_(p)
Max{ xEIR I F(x-) ::; p} = Max { x E IR I P{ X < x} ::; p} .
und die folgende Charakterisierung von Quantilen:
(9)
~
ist ein p-Quantil von F
Folglich ist F-(p) das kleinste und Fjp) das größte p-Quantil von F.
G. Osius: Quantile von Verteilungen
Q-3
9.7.10
Ist Y = a + bX mit a, b E IR und b:;= 0 eine (nichttriviale) lineare Transformation von
X, so ergeben sich die Quantile von Y aus denen von X wie folgt:
(10)
~
ist ein p-Quantil von cL'(X)
(a + b~) ist ein
p-Quantil von cL'( a + bX)
{ (a + b~) ist ein (1- p)-Quantil von cL'( a + bX)
falls
b> 0 }.
falls
b<O
Ein p-Quantil für p = ~ wird auch als Median bezeichnet, d.h. ~ ist ein Median von
cL'(X) bzw. von F, falls gilt
(11)
P{ X <~} < ~ < P{ X <~}
F(~-) < ~ < F(~) .
bzw.
Der (genauer: ein) Median ist ein Lokationsparameter, weil nach (10) für b :;= 0 gilt
(12)
~
=*
ist ein Median von cL'(X)
(a + b~) ist ein Median von cL'(a + bX) .
Im Gegensatz zum Erwartungswert ist der Median (selbst wenn er eindeutig bestimmt ist) nicht jaltungskompatibel, d.h. für unabhängige Zufallsvariablen Xl' X ist
2
der Median von Xl + X 2 im allgemeinen nicht die Summe der Mediane von Xl und
X 2· Als Beispiel seien Xl' X 2 jeweils x;-verteilt mit Median ~1 = ~2 = Xi;50% ~ 0,455.
Dann ist Xl +X2 x;-verteilt mit Median X;.50%
, ~ 1,386. Ein weitereres Beispiel für
diskrete Zufallsvariablen findet sich in 1.1.
Falls X integrierbar ist, so hat jeder Median von X die Minimimierungseigenschaft
(13)
~
E(IX-~I) =
ist ein Median von cL'(X)
Min E(IX-cl),
cE lR
woraus insbesondere folgt
(14)
~ l' ~2 sind Mediane von cL'(X)
=*
Falls X nicht integrierbar ist, so gilt (13) immer noch, ist aber uninteressant, weil
dann alle Erwartungswerte in (13) unendlich sind.
G. Osius: Quantile von Verteilungen
9.7.10
Q-4
1.1 Binomialverteilung
Für cL'(X) = B(n, 7r) ergeben sich für 0< p < 1 die Werte der beiden Inversen von F zu
(1)
Min {kE{O, ,n} I p ~ P{X<k}},
(2)
Max{kE{O, ,n} IP{X<k} ~p}.
Die Werte F-(p) und Fjp) liegen also im Träger TX = {O, ..., n} von X und sind charakterisiert durch (man beachte den Wechsel von
< und <)
(3)
P{X<F-(p)-l}
<
P
<
P{X<F-(p)})
(4)
p{X< Fjp)-l}
<
P
<
P{X< Fjp)} .
Falls p nicht im Bild der Verteilungsfunktion F liegt, so stimmen F-(p) und F (p)
überein
(5)
p ;= P{ X <k}
für alle kE{O, ..., n}
und andernfalls unterscheiden sie sich um den Wert 1
(6)
p=P{X<k}
für ein kE{O, ...,n}
(1) - (6) gelten sogar für eine beliebige Verteilung cL'(X) mit Träger TX={O, ..., n}.
Beispiele: Der Median von X für 7r = 0,4.
Für n = 1 ist F-(~) =F)~) =
°der eindeutig bestimmte Median von X.
Und für n = 2 ist wegen F(O) = 0,36 und F(l) = 0,84 der eindeutig bestimmte Median
F-(~) =F)~) = 1. Dieser stimmt nicht mit der Summe der Mediane von B(l,p) überein, was ein weiteres Beispiel zur Faltungs-Inkompatibilität des Medians liefert.
G. Osius: Quantile von Verteilungen
9.7.10
Q-5
1.2 Poisson-Verteilung
Für cL'(X) = Pois(p,) ergeben sich für 0< p < 1 die Werte der beiden Inversen von P
zu
(1)
Min {k E Wo I p ~ P{ X <k} } ,
(2)
Max { k E Wo I P{ X < k} ~ p } .
Die Werte P-(p) und Pjp) liegen also im Träger TX = Wo von X und sind charakterisiert durch (man beachte den Wechsel von
< und <)
(3)
p{X<P-(p)-l}
<
P
<
p{X<P-(p)})
(4)
p{X<Pjp)-l}
<
P
<
p{X<Pjp)}.
Falls p nicht im Bild der Verteilungsfunktion P liegt, so stimmen P-(p) und P (p)
überein
(5)
p ;= P{ X <k}
für alle k E Wo
und andernfalls unterscheiden sie sich um den Wert 1
(6)
p = P{ X <k}
für ein k E Wo
(1) - (6) gelten sogar für eine beliebige Verteilung cL'(X) mit Träger TX = Wo·
G. Osius: Quantile von Verteilungen
2
Q-6
9.7.10
Verteilungskonvergenz und Quantile
Sei X ~ X verteilungskonvergent und F bzw. F sei die Verteilungsfunktion von
n
n
X bzw. F.
n
Falls F in a E IRstetig ist, so gilt für jede Folge a -----+ a
n
(1)
lim
< an } = P{ X <
n P{ X n- a}
bzw.
lim F (a ) = F( a) ,
(2)
lim P{ X
n < an } = P{ X < a}
bzw.
lim F (a -) = F(a-) .
n
n
n
n n
n n
Wir setzen jetzt weiter voraus, daß F stetig und injektiv ist. Dann konvergiert jede
Folge ( von p-Quantilen von F gegen das (eindeutig bestimmte) p-Quantil von F:
n
n
(3)
bzw.
Insbesondere konvergiert auch die rechts- bzw. links-stetige Inverse von F punktn
weise gegen die Inverse von F:
(4)
lim F (p) = F-\p) .
n n-
Das p-Quantil F-\p) wird daher auch als asymptotisches p-Quantil von F ben
zeichnet und in der Praxis oft als Approximation für ein "echtes" p-Quantil von F
n
verwendet.
Anwendungsbeispiele
• Die t -Verteilung ist für n ----+ 00 verteilungskonvergent gegen N(O, 1), und somit
n
konvergieren die oberen a-Quantile t
gegen das obere a-Quantil z .
n,Q
Q
• Die Standardisierung (B(n,p)-p'n)ja n der B(n,p)-Verteilung mit P,n=np und
a 2 =np(1-p) ist für n----+oo verteilungskonvergent gegen N(O,l). Folglich ist ein
n
asymptotisches oberes a-Quantil von B(n ,p) gegeben durch: p, n + zQ a n .
• Die Standardisierung (Pois(p,) - p,)j
JIL der Pois(p,)- Veteilung ist für p, ----+ 00 vertei-
lungskonvergent gegen N(O,l). Folglich ist ein asymptotisches oberes a-Quantil
von Pois(p,) gegeben durch: p, + zQ
JIL.
Beweise: Quantile von Verteilungen
Q B-1
9.7.10
Beweise zu:
1
Definition und elementare Eigenschaften
Beweis von
(2)
F-(p)
inf{xEIR I p::;F(x)}
(links-stetige Inverse)!
(3)
F_(p) : = sup {xE IR I F(x)::;p }
(rechts-stetige Inverse).
(4)
F(Fjp)-) < P < F(F-(p))
:=
Wir zeigen zuerst, daß F- (p) wohldefiniert ist, d.h in IR liegt. Wegen F( (0) = 1 und
p< 1 ist A : = {x E IR I p < F(p)}
;=
x
n
0 und es gibt eine Infimum-Folge x E A mit
n
1 inf A E [-00, (0)
Da F in inf A rechts-stetig ist (auch für inf A = - (0), folgt
(i)
p <
lim F(x n ) = F(infA) .
n---+oo
Wegen F(- (0) = 0 und p > 0 folgt inf A;= - 00. Also ist F-(p) = inf A E IR wohldefiniert und aus (i) ergibt sich die zweite Ungleichung in (4).
Jetzt zeigen wir, daß F (p) wohldefiniert ist, d.h in IR liegt. Wegen F(-oo) = 0 und
p> 0 ist B : = {xEIR I F(x)::;p}
;=
0 und es gibt eine Supremum-Folge Y EB mit
n
Y t supB E (-00,00]
n
Es folgt (auch für supB = (0)
(ii)
F((supB)-) = n---+oo
lim F(y n ) < P
Wegen F( 00 -) = F( (0) = 1 und p < 1 folgt su pB ;= 00. Also ist F (p) = supBE IR
wohldefiniert und aus (ii) ergibt sich die erste Ungleichung in (4).
D
Beweise: Quantile von Verteilungen
QB-2
9.7.10
Beweis von
(5)
F-(p) < x
(6)
x
ad (5)
p ~ F(x) ,
< F_(p)
,;~":
F(x-) < p.
Da F monoton wachsend ist, ergibt sich mit (4)
,,<;:=.": Ergibt sich aus der Definition von
ad (6)
,,~":
F-(p) als Infimum.
Da F(x-) = P{X< x} monoton wachsend in x ist, ergibt sich mit (4)
F(x-) < F(Fjp)-) < P
,,<;:=.": Für jedes
y< x gilt dann F(y) < F(x-) < P , und somit
x = sup (-00, x) < sup {yEIR I F(y) ~p} = F_(p) .
D
Beweis von
(7)
F-(p)
Min{ xEIR I p ~ F(x)}
(8)
F_(p)
Max{ xEIR I F(x-) ~ p} = Max { x E IR I P{ X < x} ~ p} .
(9)
~
ad (7):
F-(p)
Min { x E IR I F-(p)
ad (8):
F (p)
Max{ xEIR I x < Fjp)}
ad (9)
~
ist ein p-Quantil von F
ist ein p-Quantil von F
{}
< x}
= Min{ xEIR
I p ~ P{X<x}} ,
F-(p) < ~ < F_(p).
Min { x E IR I p ~ F(x) }
vgl. (5).
Max{ xEIR I F(x-) ~ p}
vgl. (6).
< P < F(~)
{}
F(~-)
{}
F-(p) < ~ < F_(p)
vgl. (5)(6). D
Beweise: Quantile von Verteilungen
QB-3
9.7.10
Beweis von
~
(10)
ist ein p-Quantil von cL'(X)
(a + b~) ist ein
p-Quantil von cL'( a + bX)
{ (a + b~) ist ein(l- p)-Quantil von cL'( a + bX)
falls
falls
b> 0 }
b< 0 .
Für b> 0 folgt die Behauptung aus
<
P{a+bX<a+b~} = P{X<~}
P
<
P{X<~} = P{a+bX<a+b~}
und für b< 0 folgt sie aus
P{a+bX <a+b~} =
P{X>~} = 1-P{X<~}
1- p < 1-P{X <~} =
<
1- p,
P{X>~} = P{a+bX<a+b~}.
Beweis von
~ ist ein Median von cL'(X)
(13)
=*
E(IX-~I) =
Min E(IX-cl),
cE lR
Für eine Zufallsvariable Y > 0 läßt sich der Erwartungswert darstellen als
00
E(Y) =
J
P{Y> y} dy
o
vgl. z.B. Billingsley (1986), Probability and Measure, (21.9), p. 282. Also gilt
H(c)
E( IX-
cl)
00
J P { IX- c I > y} dy
o
00
J [P{X-c<-y}+P{X-c>y}Jdy
o
00
00
J P{X <c-y} dy
+
o
J P{X>c+y} dy
0
c
00
JP {X < x} dx + J P {X > x} dx .
Für
~
-00
c
c
c
< c folgt:
H(c) -
H(~)
JP {X < x} dx
~
c
J[P {X < x } ~
-
JP {X > x} dx
~
P {X > x }J dx .
Substitution: x = c ± y
D
Beweise: Quantile von Verteilungen
Für ~ < x gilt:
QB-4
9.7.10
~ < P{ X <~} < P{ X < x} < P{ X < x}
=*
P{X<x} = I-P{X<x} < ~
=*
P{X<x}-P{X>x} > 0
und somit:
H(c) -
H(~)
>
für ~ < c .
0
Analog folgt für c < ~:
H( c) - H(~) =
~
JP {X > x} dx
c
~
-
JP {X < x} dx
c
c
=
J[P {X > x } -
P {X < x }] dx .
~
Für x < ~ gilt:
P{ X < x} < P{ X <~} < ~
=*
P{X>x} > P{X>x} = I-P{X<x} > ~
=*
P{X>x}-P{X<x} > 0
und somit:
H(c) -
H(~)
Insgesamt folgt H( c) - H(~)
>
0
für c < ~ .
> 0 für alle c, und die
Behauptung gilt.
D
Beweise: Quantile von Verteilungen
9.7.10
QB-5
Beweise zu:
1.1 Binomialverteilung
Die folgenden Beweise benutzen nur, daß X den Träger Tx= {O, ..., n} besitzt, aber
nicht die konkreten Binomial-Wahrscheinlichkeiten. Sie gelten deshalb auch für beliebiges cL'(X) mit diesem Träger.
Beweis von
(1)
Min {kE{O, ,n} I p ~ P{X<k}},
(2)
Max{kE{O, ,n} IP{X<k} ~p}.
ad (1):
Aus
P{X<x} = P{X<Int(x)}
folgt
P-(p) = Min{ kEZ I p ~ P{X<k}}
Mit
P{X<-l} =
°<
mit
P = P{X<n}
Int(x) = Max {kE Z I k<x}
vgl. 1 (7).
ergibt sich (1).
ad (2):
Aus
P{X<x} = P{X<Suc(x)}
folgt
P_(p) =
Mit
P{X< O} =
mit
Max{kEZIP{X<k}~p}
°<
P
<
1 = P{X<n+1}
Suc(x) = Min {kE Z I x< k}
vgl. 1 (8).
ergibt sich (2).
Beweis von
(5)
p ;= P{ X <k}
für alle kE{O, , n}
P-(p) = P (p) ,
(6)
p=P{X<k}
für ein kE{O, ,n}
P-(p) = k = P (p) - 1.
Die Behauptungen folgen direkt aus den Charakterisierungen (3) und (4).
D
Beweise: Quantile von Verteilungen
9.7.10
QB-6
Beweise zu:
1.2 Poisson-Verteilung
Die folgenden Beweise benutzen nur, daß X den Träger TX = Wo besitzt, aber nicht
die konkreten Poisson-Wahrscheinlichkeiten. Sie gelten deshalb auch für beliebiges
cL'(X) mit diesem Trägers, also z.B. für die negative Binomialverteilung.
Alle Beweise sind völlig analog zu denen aus 1.1 Binomialverteilung.
Beweis von
(1)
Min {k E Wo I p ~ P{ X <k} } ,
(2)
Max { k E Wo I P{ X < k} ~ p } .
ad (1):
Aus
P{X<x} = P{X<Int(x)}
folgt
P-(p) = Min{ kEZ I p ~ P{X<k}}
Mit
P{X<-l} = 0
<
mit
Int(x) = Max {kE Z I k<x}
vgl. 1 (7).
ergibt sich (1).
P
ad (2):
Aus
P{X<x} = P{X<Suc(x)}
mit
Suc(x) = Min {kE Z I x< k}
folgt
P_(p) = Max{kEZ IP{X<k}
~p}
vgl. 1 (8).
Mit
P{X< O} = 0
<
P
ergibt sich (2).
Beweis von
(5)
p ;= P{ X <k}
für alle k E Wo
P-(p) = P (p) ,
(6)
P = P{ X <k}
für ein k E Wo
P-(p) = k = P (p) - 1.
Die Behauptungen folgen direkt aus den Charakterisierungen (3) und (4).
D
Beweise: Quantile von Verteilungen
Q B-7
9.7.10
Beweise zu:
2 Verteilungskonvergenz und Quantile
Beweis von
(1)
lim
< an } = P{ X <
n P{ X n- a}
bzw.
lim F (a ) = F( a) ,
(2)
lim P{ X
< an } = P{ X < a}
bzw.
lim F (a -) = F(a-) .
ad (1):
1. Beweis. Seien c und d beliebige Stetigkeitsstellen von F mit c < a
n
Dann gilt
n
c
F (c)
n
<
a
n
<
< Fn (a n) <
n
n n
n
n n
d
für fast alle n
F (d)
für fast alle n
n
t
t
F(c)
F(d)
< d.
da F stetig in c, d
Es folgt
< lim n inf Fn (a n) < lim n sup Fn (a n) < F(d)
(i)
F(c)
Fall 1:
aEIR
Da F höchstens abzählbare viele Unstetigkeitsstellen hat, gibt es Folge c
k
dkt a mit ck < a
(iii)
ta
und
< dk und
F ist stetig in ck und dk.
vgl. (i)
Aus
und der Stetigkeit von F in a folgt
(iv)
lim F (a ) = F( a) ,
Fall 2:
a=oo
n
d.h. (7) gilt.
n n
Die Herleitung von (i) bleibt auch für d = a =
ck ta und eine konstante Folge dk = a =
00.
00
gültig. Wie im Fall 1 wählen wir
Da F in
00
stetig ist, ergibt sich (iv) wie
im Fall 1.
Fall 3:
a=-oo
Die Herleitung von (i) bleibt auch für c = a = -
dk ta und eine konstante Folge ck = a = wie im Fall 1.
00.
00
gültig. Wie im Fall 1 wählen wir
Da F in -
00
stetig ist, ergibt sich (iv)
Beweise: Quantile von Verteilungen
ad (1):
9.7.10
QB-8
2. Beweis. Die Behauptung folgt direkt aus dem Exkurs Konvergenz nach
Verteilung in Euklidischen Räumen) 12 (1) für Y = a .
n
ad (1):
D
n
3. Beweis für a E IR. Die Behauptung ergibt sich mit dem Exkurs Kon-
vergenz nach Verteilung in Euklidischen Räumen) 2 (2) angewandt auf die Funktionenfolge g (x) = x- a + a, die auf IR gleichmäßig gegen die Identität g(x) = x konvern
n
giert. Daher folgt
X n -a n +a = gn(X)
n
n---+ 00
g(X) = X
und weil F in a stetig ist, ergibt sich
P { X n < an} P { X n - an + a < a}
n---+
(0)
P { X < a}
D
Anwendung von (7) auf -X ~---+-X und -a ---+-a unter Berücksichn
n
tigung von
ad (2):
P{ X
< a}
= P{ - a < - X} = 1 - P{ - X
<- a}
D
Beweis von
(3)
bzw.
Zu zeigen ist, daß jeder Häufungspunkt a von (( ) das p-Quantil von Fist, d.h.
n
(i)
bzw.
F(a) =p.
Nun gibt es eine gegen a konvergente Teilfolge (k ---+ a. Aus
ergibt sich für k ---+ 00 mit (1) und (2)
F(a-) = P { X
< a} < p < P { X < a}
Da F in a stetig ist, folgt (i).
= F(a).
D
CF Charakteristische, Momente- und
Kumulanten-erzeugende Funktionen
Gerhard Osius
1.
Definition der charakteristischen Funktion
2.
Definition der Momente- und Kumulanten-erzeugenden
Funktion
3.
Die Eindeutigkeitssätze
4.
Rechenregeln für charakteristische und Momente- und
Kumulanten-erzeugende Funktionen
5.
Momente und Kumulanten eindimensionaler Verteilungen
5.1
5.2
5.3
6.
Spezielle Verteilungen
6.1
6.2
6.3
6.4
6.5
7.
Charakteristische Funktion und Momente
Moment-erzeugende Funktion und Momente
Kumulanten-erzeugende Funktion und
Kumulanten
Eindimensionale Normalverteilung
Multivariate Normalverteilung
Binomial-Verteilung
Multinomial-Verteilung
Poisson-Verteilung
Erwartungswert und Covarianzmatrix von Zufallsvektoren
Literatur
Billingsley, P., (1968): Convergence
01 Probability Measures.
New York: Wiley.
Billingsley, P., (1979): Probability and Measure. New York: Wiley
Gänssler, P., Stute, W. (1977): Wahrscheinlichkeitstheorie. Berlin: Springer.
G. Osius: Charakteristische und Momenten-erzeugende Funktion
1.
CF - 2
22.4.05
Definition der charakteristischen Funktion
Für ein Wahrscheinlichkeitsmaß P auf (IRK , IB K ) ist die charakteristische Funktion
K
(kurz: CF) 'Pp: IR
---+
<C definiert als
j exp{i .tTx} P(dx)
(1)
j cos{tTx} P(dx)
+ i -J sin{tTx} P(dx)
'Pp wird auch als Fourier-Transformierte von P bezeichnet.
Ist X eine Zufallsvariable mit cL'(X) = P so ist die CF von X definiert als
'P X
(2)
:=
'Pp' cl.h.
'P x (t)
E( exp{i· tTX})
E ( cos {i . t TX} )
+ i . E ( sin {i . t TX} )
Man beachte, daß 'Pp(t)E<C stets definiert ist, weil wegen Isinl, Icosl
< 1 die Erwar-
tungswerte stets existieren!
2.
Definition der Momente- und Kumulanten-erzeugenden
Funktion
Für ein Wahrscheinlichkeitsmaß P auf (IRK , IB K ) ist die Momente-erzeugende (geneK
rierende) Funktion (kurz: MGF) M : IR
(1)
---+
(0,00] definiert als
Mp(t) = jexp{tTx}P(dx) E(O,oo].
M p wird auch als Laplace-Transformierte von P bezeichnet.
Ist X eine Zufallsvariable mit cL'(X) = P, so ist die MGF von X definiert als
MX:=Mp , cl.h.
(2)
MX(t)
:=
E( exp{ tTX})
Die Kumulanten-erzeugende (generierende) Funktion (kurz: KGF) K p bzw. K
bzw. X ist der Logarithmus der MGF von P bzw. X, d.h.
(3)
log Mp(t)
E
(-00,00] ,
log MX(t) E(-oo,oo].
X
von P
G. Osius: Charakteristische und Momenten-erzeugende Funktion
22.4.05
CF - 3
Man beachte, daß Mp(t) E(O,oo] und Kp(t) E (-00,00] zwar stets existieren, aber nicht
notwendig endlich sind. Die MGF und KGF ist nur dort von Interesse, wo sie endlich ist. Trivialerweise ist
(4)
3.
Die Eindeutigkeitssätze
Ein Wahrscheinlichkeitsmaß ist durch die charakteristische Funktion eindeutig bestimmt, d.h. es gilt der
Eindeutigkeitssatz für charakteristische Funktionen: Für Wahrscheinlichkeitsmaße P und Q auf (IRK,IBK) mit charakteristischen Funktionen !.pp und !.pQ gilt:
!.pp = !.pQ
{}
P= Q.
Als Folgerung ergibt sich, daß die Verteilung cL'(X) einer K-dimensionalen Zufallsvariablen X eindeutig bestimmt ist durch die Klasse cL'( t T X) der Verteilungen aller Linearkombinationen tTX für jedes tE IRK , d.h. es gilt der
Eindeutigkeitssatz für Verteilungen: Für K-dimensionale Zufallsvektoren X und Y
gilt :
für alle t E IRK .
cL'(X) = cL'(Y)
Eine Verteilung, deren Momente-erzeugende Funktion in einer Umgebung U von 0
endlich ist, ist durch ihre Momente-erzeugende Funktion auf U bereits eindeutig be-
stimmt, d.h. es gilt der
Eindeutigkeitssatz für Momente-erzeugende Funktionen: Es seien P und Q Warscheinlichkeitsmaße auf (IRK,IB K)) deren Moment-erzeugende Funktionen M p und M Q
beide in einer Umgebung U von 0 E IRK endlich sind. Dann gilt:
P=Q.
Hieraus folgt natürlich sofort der entsprechende Eindeutigkeitssatz für Kumulanten-erzeugende Funktionen.
G. Osius: Charakteristische und Momenten-erzeugende Funktion
4.
22.4.05
CF - 4
Rechenregeln
X sei ein K-dimensionaler Zufallsvektor, A eine (ix K) -Matrix und bE IRJ.
Für die i-dimensionale transformierte Zufallsvariable AX + b lassen sich die charakteristische, Momente- und Kumulanten-erzeugende Funktion direkt aus der von
X berechnen:
(1)
'PAX+b(t)
(2)
MAX +b (t) = MX (A t)
(3)
KAX+b(t) = Kx(A t) + b t
'Px(ATt)
T
T
für alle tE IRJ,
exp{i.bTt}
T
für alle tE IRJ,
exp{ b t}
T
für alle tE IRJ,
Ist weiter Y ein L-dimensionaler Zufallsvektor, so lassen sich die charakteristische,
Momente- und Kumulanten-erzeugende Funktion des (K + L )-dimensionalen Zufallsvektors (X, Y) direkt angeben, falls X und Y stochastisch unabhängig sind:
(3)
L
Sind X und Y stochastisch unabhängig) so giltjür alle sEIRK,tEIR :
'P (X, Y) ( s , t)
'PX(s)
'Py(t) ,
M(X, y)(s, t)
Mx(s)
My(t) ,
K(X, Y) ( s , t)
Kx(s) + Ky(t) .
Unter Verwendung des Eindeutigkeitssatzes für charakteristische Funktionen erhält
man sogar die folgende Charakterisierung stochastischer Unabhängigkeit
(4)
X und Y sind stochastisch unabhängig
{}
jür alle sEIRK,tEIRL .
Ein entsprechendes Resultat gilt auch für die Momente- bzw. Kumulantenerzeugenden Funktionen von X, Y und (X, Y) sofern diese in einer Umgebung von
o endlich sind.
Speziell für K = L ergeben sich die charakteristische, Momente und Kumulanten-erzeugende Funktion der Faltung X + Y aus den entsprechenden Funktionen von X
und Y:
G. Osius: Charakteristische und Momenten-erzeugende Funktion
22.4.05
CF - 5
Faltungssatz für CF, MGF und KGF: Für stochastisch unabhängige K-dimensionale
Zujallsvektoren X und Y gilt jür alle tE IRK :
<Px+y(t)
<Px (t)
<Py(t) ,
MX+y(t)
MX (t)
My(t) ,
Kx+y(t)
KX(t)
+ Ky(t) .
5.
Momente und Kumulanten eindimensionaler Verteilungen
5.1
Charakteristische Funktion und Momente
Für eine reelle (d.h. eindimensionale) Zufallsvariable X lassen sich die Momente
E{ X k } - sofern sie existieren - auch aus den Ableitungen der charakteristischen
Funktion <P = <PX von X bestimmen:
n
Falls E{ IXl } <
(1)
ist, so ist <P n-mal stetig differenzierbar mit
<p(k)(t) = i k .E{ X k eitX }
für k = 0, ... , n und alle tEIR .
(a)
00
Speziell für t = 0 ergeben sich die Momente von X aus
für k = 0, ... , n .
Die folgende Bedingung ist hinreichend dafür, daß O gilt
Wenn (CFA) gilt, so läßt sich <P um jedes x E IRin eine Potenzreihe entwickeln
T
(2)
fürltl<r.
Speziell für x = 0 gilt
(3)
<p(t) =
f
(i t;k E{ X k }
k=O k.
für It I <r,
und somit ist <P dann bereits durch alle Momente von X eindeutig bestimmt.
G. Osius: Charakteristische und Momenten-erzeugende Funktion
5.2
22.4.05
CF - 6
Moment-erzeugende Funktion und Momente
Die Moment-erzeugende Funktion M = MX einer reellen Zufallsvariablen X ist nur
dort von Interesse, wo sie endlich ist, d.h. auf ihrem Endlichkeitsbreich
Endl(M) = {s EIR I M(s) <00 } .
(1)
Der Endlichkeitsbereich Endl(M) ist zusammenhängend - also ein Intervall -welches
stets die Null enthält, weil
(2)
M(O) = 1 .
Im (trivialen) Fall Endl(M) = {O} enthält die MGF keine detaillierten Information
über die Verteilung von X, und wir wollen daher im folgenden davon ausgehen, daß
der Endlichkeitsbereich ein nicht-degeneriertes Intervall ist, d.h. wir setzen für ein
r
> 0 voraus
(MGF)
T
M ist auf [-r, +r] endlich,
bzw.
[-r, +r] C Endl(M).
Hieraus folgt, daß alle absoluten Momente von X endlich sind
(3)
für alle k E W,
und es folgt die Bedingung (CFA) für die charakteristische Funktion. Weiter erT
hält man folgende Reihenentwicklung von M
00
(4)
M(t) =
k'fo
k
k!
k
E{X }
für It I <r.
M ist auf dem offenen Intervall ( -r, +r) beliebig oft differenzierbar mit
(5)
für alle kEWU{O} und
Itl < r.
Speziell für t = 0 ergeben sich die Momente von X aus den Ableitungen von M( und
darum heißt M auch die Moment-erzeugende Funktion)
(6)
für alle k E WU{O} .
Folglich stellt (4) die Taylor-Entwicklung der Funktion M im Nullpunkt dar.
G. Osius: Charakteristische und Momenten-erzeugende Funktion
5.3
22.4.05
CF - 7
Kumulanten-erzeugende Funktion und Kumulanten
Aus der Bedingung (MGF)
T
- die wir weiter voraussetzen - ergibt sich, daß auch
die Kumulanten-erzeugende Funktion K = log MX der reellen Zufallsvariablen X
X
auf dem abgeschlossenen Intervall [-r, +r] endlich und auf dem offenen Intervall
( -r , +r) beliebig oft differenzierbar ist.
Die Ableitungen von K X im Nullpunkt heißen Kumulanten von X und werden wie
folgt bezeichnet
(1)
k-te Kumulante von X,
kEWU{O}.
Die Kumulanten lassen sich aus den (zentralen) Momenten von X berechnen und
umgekehrt. Die Kumulanten bis zur Ordnung 4 lauten:
(2)
K;O(X) = 0
(3)
K;1 (X) = E(X)
(4)
K;2(X) = E([X-fL]2)
fL 2 (X)
(5)
K;iX)
E( [X - fL] 3)
fL 3 (X)
(6)
K;iX)
E( [X - fL] 4) - 3 fL~(X)
a
Var(X)
2
Die Kumulanten der transformierten Zufallvariablen U = aX + b ergeben sich direkt
aus den Kumulanten von X
(7)
K;1(aX + b) = aK;1(X)
+b
(8)
K; r (a X + b) = aT K; r (X)
bzw.
E(aX + b) = aE(X)
für
+b
r> 2.
Und die Kumulanten einer Faltung ergeben sich als Summe der entsprechenden Kumulanten
(9)
X und Y stochastisch unabhängig
K; r (X + Y) = K; r (X)
+ K; r (Y)
für alle r.
G. Osius: Charakteristische und Momenten-erzeugende Funktion
6.
Spezielle Verteilungen
6.1
Eindimensionale Normalverteilung
22.4.05
Für cL'(X) = N(p"a 2 ) mit p,E IR und 17 2 > 0 ist die charakteristische Funktion
(1)
für tEIR.
Die Momente und Kumulanten--erzeugende Funktion ist überall endlich mit
+ ~ t2 a 2 }
(2)
Mx( t) = exp {p,t
(3)
KX(t) = p,t + ~ t a
2 2
für tE IR,
für tE IR.
Aus den Ableitungen
(4)
K~(t)
P,
K~(t)
17
~2(t)
0
+ ta 2 ,
2
für
r> 2
ergeben sich die Kumulanten von X zu
(5)
;;;1 (X) = P, ,
;;;/X) = 0
6.2
für
r> 2.
Multivariate Normalverteilung
Für cL'( X) = NK (p" E) lautet die charakteristische Funktion
(1)
'P
T
T
X (t) = exp { i . t P, - ~ t E t}
K
für tE IR .
Die Momente und Kumulanten--erzeugende Funktion ist überall endlich mit
(2)
MX(t) = exp{tTp,+ ~ tTEt}
fürtEIR ,
(3)
KX(t) = tTp,+ ~ tTEt
fürtEIR .
K
K
CF - 8
G. Osius: Charakteristische und Momenten-erzeugende Funktion
6.3
22.4.05
CF - 9
Binomial-Verteilung
Für cL'(X) = B(N,p) ist die charakteristische Funktion
(1)
für tE IR.
Die Momente und Kumulanten--erzeugende Funktion ist überall endlich mit
(2)
MX(t) = (p et
(3)
KX(t) = N ·log(p et
6.4
+ 1- p)N
+ 1- p)
für tE IR,
für tE IR.
Multinomial-Verteilung
Für cL'(X) =MK(N,p) mit P=(Pk) E[O,l]K und P+ =1 ist die charakteristische
Funktion
(1)
Die Momente und Kumulanten--erzeugende Funktion ist überall endlich mit
(2)
(3)
G. Osius: Charakteristische und Momenten-erzeugende Funktion
6.5
22.4.05
CF - 10
Poisson-Verteilung
Für cL'(X) = Pois (p,) ist die charakteristische Funktion
(1)
't
!.pX( t) = exp {p, (e Z
-
I)}
für tE IR.
Die Momente und Kumulanten--erzeugende Funktion sind überall endlich mit
(2)
MX ( t) = exp {p, ( et - I)}
für tE IR,
(3)
KX(t) = p,(et -1)
für tE IR.
Aus den Ableitungen
(4)
für rE W
ergibt sich, daß alle Kumulanten von X mit dem Erwartungswert p, übereinstimmen:
(5)
K,
r
(X) = p,
für rE W .
G. Osius: Charakteristische und Momenten-erzeugende Funktion
7.
22.4.05
CF - 11
Erwartungswert und Covarianzmatrix von Zufallsvektoren
Für einen K-dimensionalen ZuJallsvektor X = (Xk) bzw. für eine JxK ZuJallsmatrix
Y = (Y ) ist der Erwartungswert komponentenweise definiert, d.h. als Vektor bzw.
jk
JxK Matrix der Erwartungswerte der Komponenten, sofern diese existieren:
(1)
bzw.
Wenn der Erwartungswert Jl: = E(X) E IRK existiert, so ist die KxK Covarianzmatrix von X als Matrix aller Covarianzen der Komponenten definiert durch
Die Diagonale der Covarianzmatrix enthält also die Varianzen Var(X ), und für
k
eindimensionales X ist daher Cov(X) = Var(X).
Wenn die Covarianzmatrix Cov(X) existiert, so gilt für eine JxK Matrix A:
(3)
Cov(AX) = A· Cov(X) .A T.
Wenn die Moment-erzeugende Funktion MX von X in einer Umgebung von 0 endlich ist, so ergeben sich der Erwartungswert und die Covarianzmatrix wie folgt aus
den Ableitungen der Kumulant-erzeugenden Funktion K
(4)
E(X)
(5)
Cov(X)
DKX(O)
2
T
D KX(O).
= \7 KX(O),
X
von X
Beweise zu: Charakteristische und Momenten-erzeugende Funktion
27.7.05
B CF - 1
Beweise zu:
Erwartungswert und Covarianzmatrix von
7
Zufallsvektoren
Beweis von:
(4)
(5)
E(X) = DKx(O)T = V Kx(O),
2
Cov(X) = D Kx(O).
Es gibt eine Kugel um 0 vom Radius r> 0, so daß KX(t) für 11 t
11
< r endlich ist. Für
festes (beliebiges) tE lRK - {O} ist die KGF von Z = tTX nach 4 (3) gegeben durch
und somit auch endlich für Is I < sO: = r
11 t 11-1. Differenzieren nach s liefert
(i)
=
DKx(st) = DKx(st).t = t T . V Kx(st)
fürlsl<so
(ii)
=
D(t T. V Kx(st)) = t T .D2Kx (st) . t
fürlsl<so·
Hieraus ergeben sich mit 5.3 (2) und (3)
(iii)
t T E(X)
(iv)
t T Cov(X) t = Var(tTX) = Var(Z) = K~(O) = t TD2Kx (O) t
=
E(tTX)
Dies gilt nicht nur für alle
c> 0)
11
t 11
=
E(Z)
=
K~(O)
=
tTV KX(O)
< r sondern (nach Multiplikation mit geeignetem
sogar für alle tE lRK . Damit ergeben sich die Behauptungen aus dem allge-
meinen Resultat für Vektoren u, v E lRK und symmetrische KxK-Matrizen A, B:
(v)
(vi)
tTu = tTv
t TAt = tTB t
für alle tElRK
u=v,
für alle tE lRK
A=B.
Zum Nachweis von (v) und (vi) erhält man mit t = e als k-tem Einheitsvektor
k
für alle k,
(vii)
Und für t = e
d.h.
u=v
für alle k
k
+ e z ergibt sich
für alle k, l
und mit (viii) erhält man A = B.
D
KV Konvergenz nach Verteilung in
euklidischen Räumen
Gerhard Osius
1
Definition der Verteilungskonvergenz
2
Konvergenz von Bildmaßen
3
Konvergenz von Produkt-Maßen
4
Konvergenz nach Wahrscheinlichkeit gegen eine Konstante
5
Rechenregeln von Slutzky über Konvergenz nach Verteilung
und Wahrscheinlichkeit
6
Die Reduktionsmethode von Cramer-Wold
7
Der Stetigkeitssatz für charakteristische Funktionen
8
Der Stetigkeitssatz für Moment-erzeugende Funktionen
9
Der Darstellungssatz von Skorohod
10
Stochastische Beschränktheit und der Satz von Prohorov
11
Konvergenz gegen Unendlich
12
Konvergenz von Wahrscheinlichkeiten
13
Konvergenz von Quantilen
14
Differenzierbare Transformation (Delta-Methode)
15
Konvergenz von quadratischen Formen
Literatur
Billingsley, P., (1968): Convergence of Probability Measures. New York: Wiley.
Billingsley, P., (1986): Probability and Measure. New York: Wiley
Gänssler, P., Stute, W. (1977): Wahrscheinlichkeitstheorie. Berlin: Springer.
G. Osius: Konvergenz nach Verteilung in euklidischen Räumen
1.
5.12.14
KV-2
Definition der Verteilungskonvergenz
Für Wahrscheinlichkeitsmaße (P )
1\.T
n nEm
sagen (VK)
0
-
und P auf (lRI, IBI) sind die folgenden Aus-
(VK) äquivalent
4
Für die Verteilungsfunktionen F und F von P und P gilt
(VK) 0
n
F stetig in a
=?
n
lim F (a) = F(a)
n
n
für jedes aElRI
Für jede beschränkte (gleichmäßig) stetige Funktion h: lR I---+ lR gilt:
lhm 1h dPn = 1h dP.
Für jedes BE IBI gilt ( BB ist der topalogische Rand von B):
(VK) 2
P(BB) = 0
(VK)
lim P (B) = P(B).
=?
P(B)
=?
lim sup P (B)
n---+ oo n
n
n
Für jedes BEIBI gilt:
3
B offen
(VK)
=?
< lim
inf P (B)·
n---+ oo n
Für jedes BE IBI gilt:
4
B abgeschlossen
< P(B).
Beweis: vgl. z.B. Billingsley (1968) Thm. 2.1, Billingsley (1986) Thm. 29.1.
D
In (VK) kann "gleichmäßig" äquivalent fortgelassen werden oder stehen bleiben.
1
Falls eine bzw. alle Bedingungen (VK) 0
-
(VK) 4 gelten, so heißt die Folge (Pn)
schwach konvergent gegen P und man schreibt hierfür:
P =?P
n
p~p
oder
(schwache Konvergenz)
n
Falls die Wahrscheinlichkeitsmaße P
X : .f2
n
n
-----+
lR I bzw. X: .f2
Pn = L(X)
n
-----+
bzw. P Verteilungen von Zufallsvektoren
n
lR I sind, d.h.
bzw.
P= L(X),
so heißt die Folge (Xn) verteilungskonvergent gegen X, falls für die Verteilungen gilt
L(Xn ) ~ L(X), und man schreibt kurz:
x~x
n
(Verteilungskonvergenz von Zufallsvariablen)
Die Wahrscheinlichkeitsmaße auf den zugrunde liegenden Wahrscheinlichkeitsräumen (Dn, dn,Pn) und (D, ~P) sind bei Betrachtungen der Verteilungen von Xn
G. Osius: Konvergenz nach Verteilung in euklidischen Räumen
KV-3
5.12.14
und X nur von untergeordneter Bedeutung. Die Bedingungen (VK)
0
-
(VK) lassen
4
sich unter Verwendung der Zufallsvektoren äquivalent umformulieren, z.B.
(VK1)1
Für jede beschränkte (gleichmäßig) stetige Funktion h: 1R1 ---+ lR gilt:
(VK);
lim E{ h(X )} = E{h(X)}.
n
n
Für jedes BE IB 1 gilt:
P{XEBB} = 0
lim P{X EB} = P(XEB}.
n
n
Obwohl sich hierbei die Erwartungswerte E {-} und die Wahrscheinlichkeiten
P{-} auf die entsprechenden Wahrscheinlichkeitsmaße P bzw. P des Definitionsn
bereichs der in {-} auftretenden Zufallsvektoren beziehen, wollen wir diese Abhängigkeit zur Vereinfachung nicht mit in die Notation einbeziehen.
Für die schwache Konvergenz gilt das elementare (aber wichtige)
Teilfolgenkriterium: P ~ P gilt genau dann 1 wenn jede Teilfolge (P
n
tere Teilfolge (P
n
11 )
enthält mit P
n
11
~ P.
n1
)
eine wei-
Der Beweis ergibt sich direkt aus dem entsprechenden Teilfolgenkriterium für die
Konvergenz reeller Zahlenfolgen x
2
n
-----+
x.
Konvergenz von Bildmaßen
Es sei g: 1R1 ---+ lRK eine meßbare Abbildung und D(g) = {xE1R1 Ig unstetig in x} die
Menge der Unstetigkeitsstellen von g. Dann ist D(g) eine Bore1-Menge und es gilt:
(1)
Ist g P- fast sicher stetig, d.h. P { D (g)} = 0, so folgt
L
p g-1
P g-1 -----+
n
0
Für die Zufallsvektoren lautet (1)
(1)*
P{XED(g)} = 0, Xn ~X
=?
g(Xn) ~ g(X).
Für stetiges g gilt stets D(g) = 0 und somit auch P{D(g)} = 0 = P{XED(g)}.
Allgemeiner gilt für eine Folge g : 1R1 ---+ lRK meßbarer Abbildungen, die auf jeder
n
kompakten Menge K C 1R1 gleichmäßig gegen g konvergiert:
(2)
P{D(g)} = 0,
p~p
n
L
p -1
P g -1 -----+
g
n n
0
G. Osius: Konvergenz nach Verteilung in euklidischen Räumen
(2) *
P{XED(g)} = 0,
x~x
5.12.14
KV-4
L
g (X ) -----+
g(X).
n
n
n
Für die konstante Folge g = gergibt sich (1) aus (2).
n
Beweis: Zu (1) vgl. z.B. Billingsley (1968) Thm. 5.1 oder (1986) Thm. 29.2. Und zu (2)
vgl. Billingsley (1968) Thm. 5.5 und die darauf folgenden Bemerkungen.
3
D
Konvergenz von Produkt-Maßen
Für Wahrscheinlichkeitsmaße P~, P' auf (1R1, IB 1 ) und P~, P" auf (lRK, IBK) gilt für
die Produktmaße
P'xP''
~P'xP'' {} P'~P'
P''~P''.
n
n
n
'
n
(1)
Für Zufallsvektoren X', X' und X", X" lautet (1):
n
n
Falls X', X" stochastisch unabhängig und
(1)*
X', X'' stochastisch unabhängig für jedes n, so gilt
n
n
X''){} X' ~X' X"~X".
(X'n' X")~(X'
n
'
n
' n
Beweis: Vgl. z.B. Billingsley (1968) Thm. 3.2.
4
D
Konvergenz nach Wahrscheinlichkeit gegen eine Konstante
von Zufallsvektoren mit Werten in 1R1 heißt nach Wahrscheinlichkeit
n
konvergent gegen a ElR1 (Schreibweise: X ~ a ), falls gilt
n
Eine Folge X
(KW)
Für jedes c > 0 gilt: li~ P{ll xn- a II
> c}
limP{IIX
-all < c}
n
n
bzw.
= 0
= 1,
oder in äquivalenter "topologischer" Formulierung
(KW)*
Für jede Umgebung U von a gilt:
lim P{ X
n
n
\t U}
= 0
bzw.
lim P{ X E U} = 1.
n
n
Fassen wir a E lR I als konstanten Zufallsvektor auf, so erhält man (elementar):
(1)
p
X -----+ a.
n
Für beliebige a E 1R1, aufgefaßt als konstante Zufallsvektoren, gilt offenbar:
n
G. Osius: Konvergenz nach Verteilung in euklidischen Räumen
(2)
L
a -----+ a
n
{}
a
n
p
-----+
a
{}
5.12.14
KV-5
lim a = a.
n n
X heißt eine stochastische Nullfolge falls X ~ 0 gilt. Man schreibt dann auch (in
n
n
Anlehnung an die Symbolik von Landau): X = o (1 ).
n
p
5
1
Rechenregeln von Slutzky über Konvergenz nach Verteilung
und Wahrscheinlichkeit
Seien X , X I-dimensionale und Y K-dimensionale Zufallsvektoren mit
n
n
(0)
Dann folgt:
L
(1)
(Xn ,Y)
n
(X,a).
(2)
Für I= K: [X ±Y]
n
n
(3)
Für K= 1: Y·X
n
n
L
L
[X±a],
<Xn ,Yn >
L
<X,a>.
a·X.
Man beachte insbesondere den Spezialfall a = 0.
Beweis: (1) folgt aus Billingsley (1968) Thm. 4.1, und (2- 3) ergeben sich aus (1)
und 2 (1) *" weil die Operatoren "± " < - , - > und " · " stetig sind.
6
D
Die Reduktionsmethode von Cramer-Wold
Sind X , X I-dimensionale Zufallsvektoren, so läßt sich die Verteilungskonvergenz
n
X ~X auf die Konvergenz aller Linearkombinationen <t,X >~<t,X> zun
n
rückführen:
X
n
L
X {}
< t,X >
n
L
<t,X> für alle tElR 1 .
1
O.B.d.A. kann man in (8) nur normierte Vektoren tElR zulassen, d.h.lltll = 1.
Beweis: Vgl. z.B. Billingsley (1968) Thm. 7.7 oder Billingsley (1986) Thm. 29.4.
D
G. Osius: Konvergenz nach Verteilung in euklidischen Räumen
7
KV-6
5.12.14
Der Stetigkeitssatz für charakteristische Funktionen
Für die charakteristischen Funktionen cp , cp: lRI ---+ <C der I-dimensionalen Zufallsn
vektoren X , X gilt:
n
lim cp = cp (punktweise) in 1R1
n
X
n
X.
n
Beweis: Vgl. z.B. Billingsley (1968) Thm. 7.6 oder Billingsley (1986) Sec. 29.
8
D
Der Stetigkeitssatz für Moment-erzeugende Funktionen
Sind die Moment-erzeugende Funktionen M , M: lR I ---+ [ 0, oo] der I-dimensionalen
n
Zufallsvektoren X , X in einer Umgebung U des Nullpunktes OE lRI endlich, so gilt:
n
lim M = M (punktweise) in U
n
n
=?
X
X.
n
Die Umkehrung gilt i.a. nicht.
Beweis: Für I = 1 vgl. z.B. Billingsley (1979) Sec. 30, und mit der Methode von
Cramer-Wold ergibt sich die Behauptung für beliebiges I.
9
D
Der Darstellungssatz von Skorohod
Für Wahrscheinlichkeitsmaße P , P auf ( 1R1, IB 1 ) gilt P ~ P dann und nur dann,
n
n
wenn es I-dimensionale Zufallsvektoren Y , Y auf einem gemeinsamen Wahrscheinn
lichkeitsraum ( D, d, P) gibt mit L(Y ) = P , L(Y) = P, so daß Y punktweise
n
n
n
gegen Y konvergiert: Y (w) -----+ Y ( w) für alle w E .f2.
n
Beweis: Vgl. z.B. Billingsley (1986) Thm. 29.6 .
10
D
Stochastische Beschränktheit und der Satz von Prohorov
Eine Folge P von Wahrscheinlichkeitsmaßen auf (lRI, IBI) heißt straff (engl.: tight ),
n
falls es für jedes c: > 0 eine kompakte Menge K C lR I gibt mit P (K) > 1- c: für alle n.
n
Für I-dimensionale Zufallsvektoren X ist P = L(X ) gerrau dann straff, wenn gilt
n
n
n
G. Osius: Konvergenz nach Verteilung in euklidischen Räumen
(SB)
Zu jedem
c: > 0
5.12.14
KV-7
gibt es ein M > 0, so daß für (fast) alle n E W gilt:
P{IIXnll > M} < c.
Falls (SB) gilt, so heißt X
n
auch stochastisch beschränkt, und man verwendet dafür
(in Anlehnung an das Landau'sche Symbol 0) die Schreibweise X = 0 (1). Verteip
n
lungskonvergente Folgen sind stochastisch beschränkt:
X
X
n
X = 0 (1).
n
p
=?
Allgemeiner gilt der
Satz von Prohorov: Für I-dimensionale Zufallsvektoren X
(i)
(ii)
n
sind äquivalent
X
ist stochastisch beschränkt.
n
Jede Teilfolge von X besitzt eine verteilungskonvergente Teilfolge.
n
Beweis: vgl. z.B. Billingsley (1968) Thm. 6.1-2.
11
D
Konvergenz gegen Unendlich
Eine Folge X
von reellen Zufallsvariablen heißt nach Wahrscheinlichkeit konvergent
n
gegen oo (Schreibweise: X
p
oo), falls gilt
n
Für jedes M> 0 gilt:
(KW) 00
lim
P{Xn<M} = 0.
n
Für positive Zufallsvariablen läßt sich dieses Konzept auf Konvergenz nach Wahrscheinlichkeit gegen Null zurückführen
(1)
Falls X
n
> 0 für allen, so gilt:
X _P----t oo
n
{}
x-n 1 -P----t 0.
Konvergenz von X nach Wahrscheinlichkeit gegen -oo ist analog definiert durch
n
(KW) -00 Für jedes M> 0 gilt:
lim
P{Xn>-M} = 0
n
d.h. es gilt
(2)
X
p
n
-oo
{}
-Xn
p
+oo.
Für weitere Zufallsvariablen Y und Y ergeben sich folgende Rechenregeln:
n
p
(3)
X -----+ + oo,
n
(4)
X -----+ ± oo,
p
n
X
p
< Y ?-fast-sicher für alle n
n- n
y = 0 (1)
n
p
y n-----+ + 00 '
=?
p
X n +Yn-----+±oo,
G. Osius: Konvergenz nach Verteilung in euklidischen Räumen
p
Y ~ Y, Y>O ?-fast-sicher
(5) X n-----+ ± oo,
(6)
X
n
p
p
X -----+ + oo,
n
y-----+
n
+ 00
::::}
KV-8
5.12.14
p
· Y -----+
n
n
± oo,
p
+ Y n-----+
+ oo,
n
p
X · Y -----+ + oo.
n
n
X
Für eine Folge a E lR interpretiert als Folge konstanter Zufallsvariablen gilt
n
(7)
12
p
lim a = oo
n
a -----+ oo.
n
n
Konvergenz von W ahrscheinlichkeiten
Für Zufallsvariablen X n, Y n, X und -oo <
- a<
- oo gilt
(1)
13
X
X,
n
p
Y ----+ a,
n
P{X=a} = 0
Konvergenz von Quantilen
Für eine reelle Zufallsvariable X mit Verteilungsfunktion F und 0 < a < 1 heißt
x E lR ein (oberes) a- Quantil der Verteilung P : = d: (X), wenn gilt
Ct
(1)
P(X <xa)
< 1-a < P(X < xa)
bzw.
F ( xa-) == lim F( x) < 1- a < F ( x) .
xixa
Das a-Quantil ist im allgemeinen nicht eindeutig bestimmt, und man kann zeigen,
daß die Menge der a-Quantile ein abgeschlossenes Intervall ist. Für stetiges Fist (1)
äquivalent zu F(x) = 1-a, d.h. jedes Urbild von 1-a unterFistein a-Quantil.
Es sei jetzt X
ablen und x
n
np
L
bzw. x
X eine verteilungskonvergente Folge von reellen Zufallsvaria
sei oberes a-Quantil von X
n
bzw. X. Dann erhält man für
die Quantilfolge folgendes Resultat
(2)
Ist die Verteilungsfunktion F von X stetig, und ist das a-Quantil
von F eindeutig, d.h. F-1 {1- a} = { x }, so gilt:
Ct
lim
n---+
00
X
n,et
=X
·
et
G. Osius: Konvergenz nach Verteilung in euklidischen Räumen
KV-9
5.12.14
14 Differenzierbare Transformation (Delta-Methode)
Y , Z seien I-dimensionale Zufallsvektoren, die nach Wahrscheinlichkeit gegen
n n
dasselbe a E lRI konvergieren:
(1)
y
p
n
zn
a,
p
a.
Ferner sei c > 0 eine reelle Skalierungsfolge, sodaß c [Y -Z ] nach Verteilung gen
n n n
gen einen I-dimensionalen Zufallsvektor U konvergiert :
(2)
c [Y -Z]
n n
n
U.
Weiter sei F: 1R1 -----+ lRK eine meßbare Transformation, die in einer Umgebung A
von a differenzierbar ist, und deren Ableitung DF auf A stetig ist. Dann läßt sich die
Verteilungskonverenz (2) mit F "transformieren" zu
(3)
c [F(Y) -F(Z )]
n
n
n
DF(a). U,
und es gilt die stochastische Taylor-Formel
(4)
c ( [F (Y ) - F (Z ) ] - DF ( a) · [ Y - Z ] )
n
n
n
n
n
p
0.
Ist G: 1R1 ---+ lRK eine weitere meßbare Transformation, die mit F in einer Umgebung von a übereinstimmt, so gilt weiter
(5)
c ( [F (Y ) - F (Z ) ] - [ G ( Y ) - G (Z ) ] )
n
n
n
n
n
p
0.
Zusatz 1: Wenn c -----+ oo gilt, dann folgt aus (2) bereits [ Y - Z ]
n
n
n
mit sind die beiden Konvergenzen in (1) zueinander äquivalent.
p
0 und so-
Zusatz 2: Die stochastische Taylor-Formel (4) folgt bereits, wenn statt der Verteilungskonvergenz
(2)*
(2) nur stochastische Beschränktheit vorausgesetzt wird:
c [Y -Z ] = 0 (1).
n
n
n
p
Spezialfall (asymptotische Normalverteilung): Bei normalverteiltem U, d.h.
(6)
L { U} = N/p,,E),
ist die Limesverteilung in (3) ebenfalls eine Normalverteilungg:
(7)
mit
D:=DF(a).
G. Osius: Konvergenz nach Verteilung in euklidischen Räumen
5.12.14
KV- 10
Anwendungen
Für eine reelle Zufallsvariable X mit p, = E(X) und a 2 = Var(X) E (0, oo) sei X eine
n
Folge stochastisch unabhängiger und wie X verteilter reeller Zufallsvariablen (also unabhängige Wiederholungen von X). Für den Mittelwert fi(n) =~X~) der ersten n Zufallsvariablen als Schätzer für p, gilt dann (Gesetz der großen Zahlen)
(8)
i/(n)
r
P
n---+ oo
1-L
und (Zentralen Grenzwertsatz)
(9)
n---+
oo
Für Y = fi(n\ Z = a = p, und c = JTi sind somit die Voraussetzungen (1) und (2)
n
n
n
2
sowie (6) mit I= 1 und a = E erfüllt. Wir betrachten jetzt einige spezielle Verteilungen von X und zugehörige interessierende Transformationen F.
Binomialverteilung: Für L(X) =B(1,p) ist a 2 = p(1-p) und neben dem Erwar-
tungswert p, = pistauch der "kanonische Parameter" 1/J = logit(p): = ln[p/(1-p)] von
Interesse. Da die logistische Funktion logit(p) nur für p E (0, 1) definiert ist, setzen
wir sie zu einer Funktion F auf ganz IR meßbar fort, indem wir sie auf dem Komplement IR\ (0, 1) beliebig (aber meßbar, also z.B. konstant Null) setzen. Mit der
Ableitung
F'(p) = logit'(p) = [p(1-p)]-1 = a -2
ergibt sich dann aus (9) bzw. (3) und (7) - mit
L
(10)
n---+ oo
p statt fi
N(O a- 2 )
'
Wegen (5) gilt (10) auch für jede andere meßbare Fortsetzung G der logistischen
Funktion logit: (0, 1) -----+IR und deshalb schreibt man (10) auch suggestiv als
(11)
Vn [logit(p(n)) - 1/J]
J n p (1- p)
[ logit(p(n)) -1/J J
n---+
oo
n---+
oo
N(O,a- 2 )
bzw.
N(0,1).
Somit ist die Schätzung {; = logit(p) von 1/J asymptotisch normalverteilt.
D
G. Osius: Konvergenz nach Verteilung in euklidischen Räumen
5.12.14
KV -11
Poissonverteilung: Für L(X) = Pois(p,) ist a 2 = p, und neben dem Erwartungswert
p, ist auch der "kanonische Parameter" 1/J = ln(p,) von Interesse. Da der Logarithmus
nur auf (0, oo) definiert ist, setzen wir ihn wieder zu einer Funktion F auf ganz lR
beliebig - aber meßbar - fort. Mit der Ableitung
ergibt sich dann aus (9) bzw. (3) und (7)
(12)
Vn [ln((L(n)) -1/J]
Vn; [ ln((L(n)) -1/J J
n---+ oo
n---+ oo
N(O,a- 2 )
bzw.
N(0,1),
wobei wir statt F suggestiv Zn geschrieben haben, weil es nach (5) nicht auf die konkrete Fortsetzung ankommt. Insgesamt ist die Schätzung {; = ln((L) von 1/J also
asymptotisch normalverteilt.
D
Exponentialverteilung: Für L(X) = Expo().) ist p, = ).- 1, a 2 = p, 2 = ).- 2 und neben
dem Erwartungswert ist auch der "kanonische Parameter" ). = p,- 1 von Interesse,
den man hier auch als Hazard bezeichnet. Mit F(x) = x- 1 für x :;= 0 (und beliebig für
x = 0) ergibt sich aus
-2
-a
analog (11) und (12) die asymptotische Normalverteilung des Schätzers ~ = (1,-1
(wieder in suggestiver Schreibweise)
(13)
n---+ oo
D
G. Osius: Konvergenz nach Verteilung in euklidischen Räumen
15
Konvergenz von quadratischen Formen
Für Folgen X , Y S-dimensionaler Zufallsvektoren gilt
n n
(1)
Xn = Op(1),
(2)
II
xn
2
11
(Xn- Y n) = op(1)
*
= Op(1)
xn =
=?
Op(1).
Für Folgen A , B von (SxS)- Zufallsmatrizen gilt:
n n
(3)
(A n -B)
= op(1)
n
(XT A X ) - (XTB X ) = op(1).
n
n
n
n
n
n
5.12.14
KV- 12
Beweise zu: Konvergenz nach Verteilung in euklidischen Räumen
5.12.14
B KV- 1
Beweise zu:
Konvergenz nach Verteilung in euklidischen Räumen
Beweise zu
11
Konvergenz gegen Unendlich
Beweis von
(1)
Falls X > 0 für alle n, so gilt: X
n
n
p
oo
{}
p
x-1
0.
n
Folgt direkt aus den Definitionen (KW), (KW) 00 da
X <M
n-
x-n 1 ->M-1.
{}
D
Beweis von
(3)
p
X -----+ + oo,
n
Wegen P{Xn
X
< Yn}
p
< Y n P-fast-sicher für alle n
n-
y n-----+ + 00 '
= 1 gilt für jedesM>O:
D
Beweis von
(4)
p
X n -----+ ± oo,
y = 0 (1)
n
p
::::}
p
X n + Y n-----+ ± oo ,
Es genügt den Fall "+ oo" zu beweisen, weil sich der Fall "- oo" hieraus durch Übergang auf- X ergibt.
n
Zu zeigen ist also X
(i)
P{Xn
+ Yn
n
p
+ oo, d.h. für beliebiges M> 0 gilt
+ Y n> M}-----+ 0.
Hierzu leiten wir für beliebiges c > 0 her:
Da Y stochastisch beschränkt ist, gibt es zu c > 0 ein K> 0 mit
n
Beweise zu: Konvergenz nach Verteilung in euklidischen Räumen
5.12.14
B KV- 2
für fast alle n.
(iii)
Nun gilt
(M+K) <X ,
n
-K<Y
n
M<(Xn +Y)
n
und somit
P{Xn + Yn <M} <
(iv)
P{Xn <M+K oder Yn <-K}
<
Wegen X
p
00
n
(v)
P{Xn <M+K} + P{Yn <-K}.
gilt
P{X <M +K}-----+ 0
und mit (iii) folgt (ii).
D
Beweis von
(5)
p
X -----+ ± oo,
n
Y ~ Y, Y>O P-fast-sicher
n
X
p
· Y -----+ ± oo,
n
n
Es genügt den Fall "+ oo" zu beweisen, weil sich der Fall "- oo" hieraus durch Übergang auf- X , - Y ergibt. Hierfür ist für beliebiges M, c > 0 zu zeigen:
n
n
(i)
limnsup P{Xn Yn <M} < c.
Nun gibt es höchstens abzählbar viele a E lR mit P { Y = a} > 0 - vgl. z.B. Billingsley
(1979) Thm. 10.2 (iv) -und folglich existiert eine fallende Folge 0 <Km l 0 mit
(ii)
P{Y=K } = 0
m
für allem.
Also gilt für jedes m:
für n ---+ oo, m fest.
(iii)
Aus K
(iv)
m
l 0 folgt andererseits für m ---+ oo
P{Y <Km} -----+ P{Y < 0} = 0,
Zu c>O gibt es daher ein m(c)EW mit
P{Y < Km(e)} < c
und für K =Km(e/olgt aus (iii)
da Y>O P-fast-sicher.
Beweise zu: Konvergenz nach Verteilung in euklidischen Räumen
(v)
5.12.14
B KV- 3
für fast alle n.
Aus
M/K<X,
n
folgt
P {Xn · Y n < M}
K<Y
n
<
M<X ·Y
n n
P {Xn < M / K oder Y n < K}
< P{Xn <MjK}
Wegen X
p
00
n
P{Xn
+
P{Yn <K}.
gilt
< MjK}-----+
0
und mit (v) folgt (i).
D
Beweis von
(6)
X
p
-----+
n
+ oo,
Y
p
-----+
n
+ oo
::::}
X
n
+Y
p
-----+
+ oo,
n p
X · Y-----+ +oo.
n
n
Für beliebiges M> 0 gilt
1<X,
n
M<Y
M<X +X,
n
n
n
M<X Y
n n
und somit folgt
(i)
P{Xn + Yn < M}
<
P{Xn < 1}
+ P{Yn <M}
(ii)
P{Xn · Yn < M}
<
P{Xn < 1}
+ P{Yn < M}.
Die rechten Seiten von (i) und (ii) konvergieren nach Voraussetzung gegen 0, und
da M beliebig war, folgt die Behauptung.
D
Beweise zu: Konvergenz nach Verteilung in euklidischen Räumen
5.12.14
B KV- 4
Beweise zu
12
Konvergenz von W ahrscheinlichkeiten
Beweis von
(1)
X
Fall 1:
- oo
X,
n
y
p
n
P{X=a} = 0
a,
< a < + oo .
Nach den Regeln von Slutzky 5 (2) gilt
X -Y
n
X-a
n
und wegen P{X-a = 0} = P{X=a}=O folgt hieraus
Fall 2:
P{Xn <Yn}
P{Xn- Yn
< 0} -----+ P{X- a < 0}
P{X<a},
P{Xn> Yn}
P{Xn-Yn>O}-----+ P{X-a>O}
P{X>a}.
a = oo. Es genügt, zu zeigen
P{X <Y }-----+1,
(i)
n
n
denn mit P{Xn < Y n } <
< Y n} folgt hieraus auch- P{Xn(ii)
P{Xn< Y n } -----+ 1.
Nach 10 ist mit der Folge X
n
auch die Folge -X stochastisch beschränkt, und
n
mit 11 (4) ergibt sich
(iii)
p
Y - X ----+ oo.
n
n
Also gilt P{Xn> Yn} = P{Yn -Xn < 0} -----+ 0,
Fall 3:
d.h. (i) gilt.
a = -oo.
Die Behauptung folgt aus Fall 2, angewendet auf- X , - Y , -X, - a, weil
n
n
-Xn
-X
'
-Yn
p
oo,
P {-X = -
a} =
0.
D
Beweise zu: Konvergenz nach Verteilung in euklidischen Räumen 5012014 B KV- 5
Beweise zu
13
Konvergenz von Quantilen
Beweis von
(2)
Ist die Verteilungsfunktion F von X stetig1 und ist das a-Quantil
von F eindeutig, doho F-1 {1- a} = { x }, so gilt:
Ct
lim
n---+
00
X
n,et
o
=X
et
Es genügt, für eine beliebige konvergente Teilfolge
x
m,a
-----+
zu zeigen: a = x
0
Ct
a E [ -oo, +oo J
für m---+ oo
Nach Definition des Quantils gilt:
P{Xm <xm,a }<1-a<P{X
<x }0
m - m,a
Da F stetig ist, gilt P {X= a} = 0 und aus 12 (1) mit Y
m
:= x
m,a
ergibt sich
P{X<a} < 1-a < P{X<a}
doho a ist ein a-Quantil von F. Und aus der Eindeutigkeit des a-Quantils von F folgt
dann a = x
0
Ct
D
Beweise zu: Konvergenz nach Verteilung in euklidischen Räumen
5.12.14
B KV- 6
Beweise zu
Differenzierbare Transformation (Delta-Methode)
14
Beweis zu "Differenzierbare Transformation"
L
DF(a). U,
(3)
c [F(Y) -F(Z )]
n
n
n
(4)
c ( [F (Y ) - F (Z ) ] - DF (a) · [Y - Z ] )
n
n
n
n
n
(5)
c ( [F (Y ) - F (Z ) ] - [G ( Y ) - G (Z ) ] )
n
n
n
n
n
p
p
0.
0.
ad (4) incl. Zusatz, d.h. mit (2)* statt (2):
Es gibt eine abgeschlossene Kugel B =
{ulll u-a I < r}
um a E lB mit Radius r > 0,
so daß F in B differenzierbar ist. Nach der Taylor-Formel gilt dann die Entwicklung
(vgl. z.B. Dieudonne, 1960, 8.14.3) :
(i)
F(y)- F(z) = H(y,z) · (y-z)
(ii)
H(y,z) =
für y, zEB
mit
1
J DF(z + t(y-z))dt
0
1
DF(a)
+ f [DF(z+t(y-z))- DF(a)] dt.
0
Also
(iii)
IIH(y,z)- DF( a) I < s(y,z) : =
sup
IIDF(z + t(y-z )) -
O<t<1
Definieren wir jetzt
(iv)
R(y,z) = F(y)-F(z)-DF(a)[y-z]
= [H(y,z)-DF(a)](y-z)
füry,zElR 1
für y, zEB
so ist für die stochastische Taylor-Formel (4) zu zeigen
(v)
c R(Y ,z )
n
n n
d.h. für beliebiges
c: > 0
p
ist zu zeigen
P { llcn R (Yn ,zn ) I
bzw. für beliebige
c: > 0
o,
> c:}-----+ 0,
und 71 > 0 ist zu zeigen
DF( a) II·
Beweise zu: Konvergenz nach Verteilung in euklidischen Räumen
P{llcn R(Yn ,zn )II > c:} < 3 71
(vi)
5.12.14
B KV- 7
für fast alle n.
Wegen (2)* gibt eine Schranke K> 0 mit
(vii)
p { II cn [ y n - zn ] II > K} < 7l
für fast alle n.
Da die Ableitung DF in a stetig ist, gibt es ein 0<8 = 8(c:,K) < r mit
(viii)
IIDF(u)- DF(a) II <; .
llu-all < 8
Die offene KugelB6 = {ulllu-all < 8} ist konvex, d.h.
y, zEB6
=?
z + t(y-z)
B6
für alle 0 < t< 1.
=?
II DF(z + t(y-z))- DF( a) II < ;
für alle tE [0,1]
=?
IIH(y,z)- DF( a) II < ;
vgl. (iii)
=?
II[H(y,z)- DF(a)] · (y-z) II < lly-zll· ~ .
*
IIR(y,z)ll < lly-zll· ;
E
Also folgt aus (viii)
II y-a II, llz-all < 8
vgl. (iv), da B6 cB.
und hieraus ergibt sich für alle n
IIYn -aii,IIZn -all<8,
bzw.
llcnR(Yn,Zn)ll>c:
=?
IIYn -all>8 oder IIZn -all > 8 oder llcn(Yn -Zn) II > K.
Für die Wahrscheinlichkeiten folgt daher (mit der Sub-Additivität)
(ix)
P{llcnR(Yn,Zn) II
> c:} <
P{IIYn -all>8} + P{IIZn -all>8} + P{llcn(Yn -Zn) II >K}.
Nach Voraussetzung (1) gilt
(x)
P{ll Yn -all > 8} < 7l
für fast alle n.
(xi)
P{IIZn -all > 8} < 7l
für fast alle n.
Aus (vii) und (ix)- (xi) folgt (vi), und somit ist (4) inclusive Zusatz 2 bewiesen.
D
Beweise zu: Konvergenz nach Verteilung in euklidischen Räumen 5012014 B KV- 8
ad (3):
Multiplikation von (2) mit der Kxl-Matrix DF(a) liefert
c DF(a)
n
0
[Yn - Z n ]
DF(a) 0U,
und Addition zu (4) ergibt (3)0
D
ad (5):
Nach Voraussetzung gilt DG(a) = DF(a) und (4) lautet mit G statt F:
p
c ([G(Y)- G(Z )]-DF(a) [Y -Z])
n
n
n
n
n
0,
0
und Subtraktion von (4) liefert dann (5)0
D
Beweis von Zusatz 1:
Multiplikation von (2) mit c-1 -----t 0 liefert [Y -Z ]
n
n
n
L
p
0 0 = 00
°
D
Beweis des "Spezialfalles":
Folgt sofort aus den Rechenregeln über Normalverteilungeno
D
Beweise zu: Konvergenz nach Verteilung in euklidischen Räumen 5012014 B KV- 9
Beweise von
15
Konvergenz von quadratischen Formen
(1)
Xn = Op(l),
(2)
I xn 1 2 =
(Xn- Y n) =
*
Op(l)
(3)
op(l)
=?
xn = Op(l)o
(A n -B)
= op(l)
n
(XT A X ) - (XTB X ) = op(l)o
n n n
n n n
Aus beiden Voraussetzungen folgt Y n = Op(l) und somit
ad (1):
IIXn 2 -IIY n
11
11
2
= xrx
_yry
n n
n n
= (X
n
+ Y n)T(Xn -Yn ),
= (Op(l)
ad (2):
ad (3):
+ Op(l) )T 0op(l))
daXTY = YTX
n n
n n
Op(l)T op(l) = op(l)o
0
IIXnll < 1 + 11Xn11 2
(XTA X )-(XTB X)= XT(A -B )X
nnn
nnn
n n
n
n
(2) ergibt sich aus der Abschätzung
= Op(l)
T
0
op(l) Op(l)= op(l)o
0
D
D
ZGS Der zentrale Grenzwertsatz für reelle
Zufallsvariablen
Gerhard Osius
1.
Die allgemeinen Resultate von Lindeberg und Ljapunov
2.
Resultate für identische Verteilungen
3.
Linearkombinationen unabhängiger Verteilungen
4.
Die Ungleichung von Berry-Esseen
G. Osius: Der Zentrale Grenzwertsatz für reelle Zufallsvariablen
1.
28.7.10
ZGS- 2
Die allgemeinen Resultate von Lindeberg und
Ljapunov
Für jedes n E W seien Xnk für k = 1, ...1 K(n) unabhängige reellwertige Zufallsvariablen mit
(1)
deren Summe
K(n)
(2)
X
n+
==l:Xk
k=l n
eine positive Varianz hat
(3)
a
K(n)
2
n+
2
Var(X ) - 2:: a k
n+
k= 1 n
:=
Theorem 1 (Lindeberg):
>
0.
Gilt für jedes c > 0 und n---+ oo
(4)
(Lindeberg-Bedingung)
so ist die Standardisierung von X n+ für n---+ oo verteilungskonvergent gegen die Standard-Normalverteilung
(5)
1
-X
an+
n+
n---+ oo
N(0,1).
Zusatz: Aus der Lindeberg-Bedingung folgt
(6)
Max
ank
1::; k::; K(n) an+
n---+ oo
0
und aus der FeZZer-Bedingung folgen weiter
K(n)
2::
(7)
n---+ oo
k=1
(8)
0,
lim K(n) = oo.
n---+oo
Folgerung: Wenn
(9)
a
2
n+
n---+oo
oo
gilt1 und es eine Schranke M > 0 gibt mit
(Feller-Bedingung).
G. Osius: Der Zentrale Grenzwertsatz für reelle Zufallsvariablen
28.7.10
ZGS- 3
für allen E Wund k = 1, ... , K(n),
(10)
so folgt die Lindeberg-Bedingung
(4) für alle c > 0 und die Verteilungskonvergenz (5).
Theorem 2 (Ljapunov): Gilt für irgendein 8 > 0 die Ljapunov-Bedingung
1
- 2+8
(Lih)
an+
K(n)
~
u
k=l
E{IXnk 12+8}
so folgt die Lindeberg-Bedingung
2.
----+
n---+ 00
0,
(4) für alle c > 0 und die Verteilungskonvergenz (5).
Resultate für identische Verteilungen
Für jedes n E W seien X nk für k = 1, ... , K( n) unabhängige und identisch verteilte reelle
Zufallsvariablen mit
(1)
0
< a n2 == Var{Xn k} < oo.
Die Varianz der Summe X n+ ist dann
(2)
und für die Gültigkeit der Lindeberg- bzw. Ljapunov-Bedingung hat man folgende
Kriterien.
Kriterium 1: Die folgenden drei Bedingungen zusammen implizieren die Lindeberg-Bedingung
(3)
lim K(n) = oo.
n---+oo
2
ist von Null wegbeschränkt1 d.h. a - 2 ist beschränkt.
n
(4)
a
(5)
(X~ ) n E lN ist gleichgradig integrierbar.
n
1
Umgekehrt folgt aus der Lindeberg-Bedingung auch
(6)
a
2
n
(5) falls zusätzlich gilt
1
ist beschränkt.
Insgesamt ist unter
Integrierbarkeit
(3) (4) und (6) die Lindeberg-Bedingung äquivalent zur gleichgradigen
1
(5) der quadrierten Variablen.
G. Osius: Der Zentrale Grenzwertsatz für reelle Zufallsvariablen
28.7.10
ZGS- 4
Kriterium 2: Aus den Bedingungen (3) 1 (4) und
(7)
E{1Xn1 12+8 } ist nach oben beschränkt.
für irgendein 8 > 01 folgt die Ljapunov-Bedingung (LI h) für dieses 8.
Theorem (Lindeberg-Levy): Sei X
n
eine Folge unabhängiger und identisch verteilter
reeller Zufallsvariablen mit
(8)
E{Xn } = p,,
0
< a 2 :=
Var {X } < oo,
n
und _X(n) sei der Mittelwert von X1'" .. ,Xn' d.h.
(9)
n
g(n) = 1. 2:: X ..
n .
z
z=l
Dann ist der standardisierte Mittelwert für n ---+ oo verteilungskonvergent gegen die
Standard-Normalverteilung:
(10)
n---+ oo
a
Binomial-Grenzwertsatz
(de
Moivre-Laplace):
N(0,1)
Es
sez
Y
n
ezne
Folge
B( n,p )-verteilter Zufallsvariablen mit
n
(11)
p ist von 0 und von 1 wegbeschränkt1 d.h.
n
p- 1 und (1- p ) - 1 sind beschränkt.
n
n
Dann ist die Standardisierung von Y
n
für n---+ oo verteilungskonvergent gegen die Stan-
dard-Normalverteilung
(12)
Yn- npn
Jnpn(1-pn)
n---+ oo
N(0,1).
Zusatz: Im Spezialfall p = p . für alle n besagt {11) nur1 daß 0 < p < 1 gilt.
n
z
G. Osius: Der Zentrale Grenzwertsatz für reelle Zufallsvariablen
28.7.10
ZGS- 5
Poisson-Grenzwertsatz: Es sei Y
eine Folge Poisson-verteilter Zufallsvariablen mit
n
0 : = E { Y } -----+ oo. Dann ist die Standardisierung von Y für n ---+ oo Verteilungsn
n
n
konvergent gegen die Standard-Normalverteilung
(13)
L
n---+ oo
3.
N(0,1).
Linearkombinationen unabhängiger Verteilungen
(Y)
sei eine Folge von stochastisch unabhängigen reellen Zufallsvariablen mit
n nEm
li.T
(1)
E{Y } = 0,
n
< T n2 : =
0
Var {Y }
n
< oo.
Für eine Dreiecksfolge (ank) reeller Zahlen mit n E W und k = 1, ... , K( n) und
K(n)
(2)
lla 112 == 2:=
a2k
k=l n
n
> 0
betrachten wir die Linearkombination
K(n)
(3)
(4)
S
=
n
2:= a kY.k
k=l n
E{Sn }=0,
mit
a
2
n
K(n)
:=Var{S }=
n
2:=
2 2
a kTk >0.
k=l n
Gesucht sind hinreichende Kriterien für die asymptotische Normalverteilung der
LinearkombinationS , d.h für die Verteilungskonvergenz
n
(ANL)
L
n---+ oo
N(0,1).
Satz 1: Ist (Yn2 ) nEm
li.T gleichgradig integrierbar und erfüllt die Folge (a k) die Kriterien
n
(5)
Max
l~k~K(n)
n---+ oo
0,
sup
nEW
2
llan11
a2n <
00'
so gilt die Lindeberg-Bedingung für die Variablen Xnk = ank Yk, und die Verteilungskonvergenz
(ANL)
gilt.
G. Osius: Der Zentrale Grenzwertsatz für reelle Zufallsvariablen
28.7.10
ZGS- 6
Zusatz 1: Die gleichgradige Integrierbarkeit der Folge (Y 2 ) impliziert die Beschräntktheit
n
der Folge (T 2 ). Wenn zusätzlich (T 2 ) von Null wegbeschränkt ist1 d.h. (T - 2) beschränkt
n
n
n
ist1 so ist die Bedingung
(6)
Max
a~k
1~k~K(n)
llanll 2
äquivalent zu
0,
n---+ oo
(5) und somit hinreichend für die Verteilungskonvergenz (ANL).
Zusatz 2: Ist die Folge (Y) identisch verteilt (und somit gleichgradig integrierbar) ist so
n
ist die Bedingung (6) hinreichend für die Verteilungskonvergenz (ANL).
1
Satz 2: Sei an k = ak unabhängig von n und K(n) = n für alle n. Ist (Yn2 ) nEm
-r-.T gleichgra2
dig integrierbar und (T ) von Null wegbeschränkt1 dann folgt aus
n
n
(7)
111
a
112
= l 2:= ak2
c E ( 0' oo) '
n n
nk
n---+ oo
=1
die Bedingung (6) und somit die Verteilungskonvergenz (ANL).
Folgerung:
Sei ank = ak unabhängig von n und K(n) = n für alle n. Ist die Folge
(Yn2) nEm-r-.T identisch verteilt wie Y mit
T
2
= Var(Y) 1 so folgt aus der Bedingung
(7) die
Verteilungskonvergenz (ANL) bzw. die äquivalente Aussage
(8)
Zum Beweis von Satz 2 werden noch zwei Resultate über reelle Folgen verwendet:
Lemma 1: Seien cn' yn
> 0,
n E W reelle Folgen1 und cn ---+ 0 sei nicht-wachsend. Dann
gilt
lim
n---+oo
c y = 0
lim
<=?
n n
n---+oo
c · Max { y , ... ,y } = 0.
n
1
n
B ezspze l e: c = n-1 , c = n-1/2 .
n
n
0
0
Lemma 2: Seien cn' yn
> 0,
nE W reelle Folgen1 und cn---+ 0 sei nicht-wachsend. Ferner
sei m: W ---+ W eine Abbildung mit m ( n)
11
< n für
alle n E W, d.h. m( n) repräsentiert eine
Auswahl 11 aus der Menge { l, ... ,n }. Dann gilt:
lim
n---+oo
c y = 0
n n
lim
n---+oo
cn ym (n ) = 0.
G. Osius: Der Zentrale Grenzwertsatz für reelle Zufallsvariablen
28.7.10
ZGS- 7
Beispiel: m(n)< n sei ein Index1 bei dem {y1' ... ,yn} sein Maximum annimmt1 d.h.
ym(n) = Max{yl' ... ,yn}. Der kleinste Index dieser Art läßt sich definieren durch:
m(n) == Min{ m<n I ym=Max{yl' ... ,yn}}.
G. Osius: Der Zentrale Grenzwertsatz für reelle Zufallsvariablen
4.
ZGS- 8
28.7.10
Die Ungleichung von Berry-Esseen
Die Verteilungskonvergenz der standardisierten Zufallsvariablen U gegen die Norn
malverteilung N(O, 1) im zentralen Grenzwertsatz bedeutet, daß die Verteilungsfunktion F von U punktweise gegen die Verteilungsfunktion P der Standard-Norn
n
malverteilung konvergiert:
(1)
lim F (x) = (x)
für alle x E IR.
n---+oo n
Unter zusätzlichen Voraussetzungen ist die Konvergenz sogar gleichmäßig und die
Konvergenzgeschwindigkeit der Differenz F - P gegen 0 kann abgeschätzt werden.
n
Bezeichnet
(2)
IIJII : =
sup IJ(x) I
<
00
XE 1R
die Supremums-Norm einer (nicht notwendig beschränkten) Funktion!: IR-----+ IR, so
läßt sich für beliebige VerteilungsfunktionenFund G die Norm II F- G II
< oo
unter
Verwendung der Ableitung G' und den zugehörigen charakteristischen Funktionen
cpF und cp G wie folgt abschätzen (vgl. z:B. Gänssler-Stute 1977, Lemma 4.2.5)
Fundamental-Ungleichung von Esseen: Für jedes T> 0 gilt
(2)
IIF-GII <
[frl cpp{x)~cpdx)
~
ldx
+
241~'11]
Man beachte, daß die Ungleichung trivialerweise gilt, wenn das Integral oder II G 'II
nicht endlich sind. Als Abschätzung der Konvergenzgeschwindigkeit im zentralen
Grenzwertsatz läßt sich zeigen (vgl. z:B. Gänssler-Stute 1977, Satz 4.2.10 und Korollar 4.2.12)
Satz von Berry-Esseen: Für k = 1r ...1 K seien X k unabhängige reelle Zufallsvariablen
mit E(Xk) = 0 und Varianz
ai = Var(Xk) < oo. Bezeichnet
K
(3)
U= ;
2:= Xk
a~
mit
+ k=l
K
=
2:=
k=l
ai =
Var(X+)
die Standardisierung der Summe X t = X + ... +XK) so gilt für die Verteilungsfunktion
1
Fvon
(4)
U
IIF-<PII
<
6
-3 .
CJ
K
2:= E{IXkl
+ k=l
3
}.
G. Osius: Der Zentrale Grenzwertsatz für reelle Zufallsvariablen
28.7.10
ZGS- 9
Zusatz 1: Die entsprechende Abschätzung gilt auch für die 1pbere 11 Verteilungsfunktion
d.h.
(5)
Zusatz 2: Falls die Varianzen und dritten absoluten Momente übereinstimmen
(6)
für alle k = 1, ... , K
(was bei identisch verteilten XF ...1 XK der Fall ist) 1 so ist a~ =K a
2
und die obere
Schranke vereinfacht sich zu
(7)
Man beachte, daß die Abschätzungen (4) und (5) trivialerweise gelten, wenn mindestens eins der absoluten Momente E { IXk } nicht endlich ist.
3
1
Beweise zu: Der Zentrale Grenzwertsatz
B ZGS -1
3.3.11
Beweise zu:
1.
Die allgemeinen Resultate von Lindeberg und
Ljapunov
Beweis von
Folgerung: Wenn
(9)
a
2
n+
n---+oo
oo
gilt1 und es eine Schranke M
> 0 gibt mit
für allen E Wund k = 1, ... , K(n),
(10)
so folgt die Lindeberg-Bedingung
(4) für alle c > 0 und die Verteilungskonvergenz (5).
Für jedes c > 0 gibt es wegen (9) ein n(c) E W mit c an+> M für allen> n(c).
Dann ist P { IXnm I> c a n +} <
- P { IXnm I> M} = 0
für allen> n(c),
und die Lindeberg-Bedingung folgt, weil die Integrale für n > n(c) verschwinden:
1
K(n)
a~
k=l
2:=
1
{IXnk I> eaJ
x~k dP
=
o
für allen> n(c).
D
Beweis von
Theorem 2 (Ljapunov): Gilt für irgendein 8 > 0 die Ljapunov-Bedingung
(Lih)
1 K(n)
- 2+8 u
~ E{IXnk 12+8} n---+
00
an+
o'
k=l
so folgt die Lindeberg-Bedingung
(4) für alle c > 0 und somit die Verteilungskonvergenz
(5).
Für jedes c > 0 ist die Lindeberg-Bedingung zu zeigen, wobei wir a : = a + setzen:
n
n
(4)
Wegen
1
K(n)
1
a~
k=l
{IXnkl>eaJ
2:=
2
0
Xnk dP
n---+oo
(Lindeberg-Bedingung)
Beweise zu: Der Zentrale Grenzwertsatz
a n D 1Xnk1 2 +D
x2
nk
IXnkl >can
a2
17
xnk
n
B ZGS- 2
3.3.11
2+D
<
n
1Xnk1 2 +D
1
CD
17
2+D
n
folgt
1
K(n)
a2n
k=l
2:
2
1
{IXnk I> eaJ
<
XnkdP
<
1
K(n)
cD a 2+D
n
k=l
1
K(n)
cD a 2+D
k=l
n
2:
2:
1
{IXnk I> eaJ
1Xnk12+DdP
E{IXnki 2+D}.
Der letzte Ausdruck konvergiert nach (L 16) gegen 0 und somit folgt (4).
D
Beweise zu:
3.
Linearkombinationen unabhängiger Verteilungen
Beweis von
Satz 1: Ist (Yn2 ) nEm
-r-.T gleichgradig integrierbar und erfüllt die Folge (a k) die Kriterien
n
(5)
Max
a~k
1 ~k ~K(n)
a,J
sup
nEW
0'
n----+oo
llanll 2
a,J
<
00'
so gilt die Lindeberg-Bedingung für die Variablen Xnk = ank Yk, und die Verteilungskonvergenz (ANL) gilt.
Nachzuweisen ist nur die Lindeberg-Bedingung d.h. für beliebiges c > 0 ist für
n---+ oo
zu ze1gen
(LB)
Setzen wir
(i)
so gilt
m
n ==
2
llan 11 max
=
2
Max
k a nk
>
0,
vgl. (2)
Beweise zu: Der Zentrale Grenzwertsatz
Iank Y k I > c CJ n
B ZGS- 3
3.3.11
2
2
2
2
>
c
mnYk
>
c
y2
>
a ·-
::::}
ank Yk
::::}
2
2
CJ
CJ
n
2
n
2
k
n
2
c an
mn
Hiermit ergibt sich die Abschätzung
(ii)
K(n)
1
2:
a2n
k=l
1
K(n)
a2
k=l
1
K(n)
a2
k=l
1
K(n)
a2
k=l
2:
n
n
1
2
lank Yk 1
dP
1
Y k2 dP
nk {Yf > ftJ
a
l an11
a2
1
{Yf > ftJ
a2
2:
lank Yk
{lank Yk I> c:aJ
2:
n
1
2
l an11
nE lN
a2
1
2
dP
<
<
Y 2 dP
k
<
. sup
1 Y 2 dP
k ElN {Yf > ftJ k
<
.
nk k ElN {Yf > ftJ
n
sup
sup
2
1
2
n
. sup
1 Y 2 dP
k ElN {Yf > ftJ k
Nach (5) ist das erste Suprememum endlich und es gilt a n ---+ oo. Da (Yn2 ) nEm
-r-.T
gleichgradig integrierbar ist, konvergiert das zweite Supremum gegen 0 und die
Lindeberg-Bedingung (LB) folgt.
D
Beweis von
Zusatz 1: Die gleichgradige Integrierbarkeit der Folge (Y 2 ) impliziert die Beschräntktheit
der Folge (T
2
).
Wenn zusätzlich (T
n
ist1 so ist die Bedingung
(6)
Max
a~k
l~k~K(n)
llanll 2
2
n
von Null wegbeschränkt ist1 d.h. (T - 2) beschränkt
n
n
)
n---+ oo
0,
äquivalent zu (5) und somit hinreichend für die Verteilungskonvergenz (ANL).
Beweise zu: Der Zentrale Grenzwertsatz
3.3.11
B ZGS- 4
Wenn (Y 2 ) gleichgradig integrierbar ist, so ist T 2 =E{Y 2 } beschränkt, vgl. z.B.
n
n
n
Nach Billingsley (1968), p.32 (5.1). Nach Voraussetzung gibt es Schranken u, v mit
(i)
Ü
<
U
<
2
Tk
<
V
<
für alle k.
00
und somit ist die zweite Bedingung von (5) erfüllt (das Supremum ist
< 1/u). Die
Äquivalenz der ersten Bedingung in (5) zu (6) ergibt sich aus den Abschätzungen
<
<
D
Beweis von
Zusatz 2: Ist die Folge (Y) identisch verteilt (und somit gleichgradig integrierbar) ist
n
so ist die Bedingung (6) hinreichend für die Verteilungskonvergenz (ANL).
1
Wenn alle Y identisch verteilt sind, dann ist die Folge (Y 2 ) trivialerweise
n
n
gleichgradig integrierbar und die Folge (T~) ist konstant. Damit sind die Voraussetzungen von Zusatz 1 erfüllt und somit folgt (ANL) aus (6).
D
Beweis von (mit Lemma 1)
Satz 2: Sei an k = ak unabhängig von n und K(n) = n für alle n. Ist (Yn2 ) nEm
-r-.T gleichgra2
dig integrierbar und (T ) von Null wegbeschränkt1 dann folgt aus
n
n
(7)
.lila
1 2 =1.n k2:=
n n
=1
ak2
cE
n---+ oo
(O,oo),
die Bedingung (6) und somit die Verteilungskonvergenz
Folgerung:
Sei ank = ak unabhängig von n und K(n) = n für alle n. Ist die Folge
(Yn2) nEm-r-.T identisch verteilt wie Y mit
Verteilungskonvergenz
(8)
(ANL).
T
2
= Var(Y) 1 so folgt aus der Bedingung
(ANL) bzw. die äquivalente Aussage
(7) die
Beweise zu: Der Zentrale Grenzwertsatz
B ZGS- 5
3.3.11
ad "Satz 2": Es ist nur (6) zu zeigen, und mit Satz 1, Zusatz 1 folgt dann (ANL). Aus
(7) folgt
llan112 n----+oo
(i)
oo
und somit ist c == lla 11-2 eine nicht-wachsende Nullfolge. Nach Lemma 1 (angen
n
2
wandt auf y : = a ist (6) in diesem Fall äquivalent zu
n
n
a2n
(ii)
2 - - - - + 0'
II anll
Aus
(iii)
n----+oo
n n
1 2
-a
n n
n-1
n
2:: a~ n k= z
1.. a 2 = 1..
1..
1
-----+
2:: a~
folgt mit (7)
n k= 1 z
c-c = 0,
und Division von (iii) durch (7) liefert (ii).
2 II anll 2· T 2und nach (7)
ad "Folgerung": In diesem Fall ist a n =
2
la
n n
(iv)
n----+oo
cT
gilt
2
.
Die Äquivalenz von (ANL) zu (8) ergibt sich durch Multipliaktion bzw. Division
durch die "Wurzel aus (iv)".
D
Beweis von Lemma 1 (mit Lemma 2)
Lemma 1: Seien cn' yn
> 0,
n E W reelle Folgen, und cn
---+
0 sei nicht-wachsend. Dann
gilt
lim
n----+oo
ad
,;~":
c y = 0
n n
lim
n----+oo
c · Max { y , ... ,y } = 0.
n
1
n
Folgt aus dem Beispiel zu Lemma 2.
D
Beweise zu: Der Zentrale Grenzwertsatz
3.3.11
B ZGS- 6
Beweis von
Lemma 2: Seien cn' yn
> 0,
nE W reelle Folgen1 und cn---+ 0 sei nicht-wachsend. Ferner
sei m: W ---+ W eine Abbildung mit m ( n)
< n für
alle n E W, d.h. m( n) repräsentiert eine
11
11
Auswahl aus der Menge { l, ... ,n }. Dann gilt:
lim
n---+oo
c y = 0
lim
n n
n---+oo
cn ym (n ) = 0.
Beispiel: m(n)< n sei ein Index1 bei dem {y1' ... ,yn} sein Maximum annimmt1 d.h.
ym(n) = Max{yl' ... ,yn}. Der kleinste Index dieser Art läßt sich definieren durch:
m(n) == Min{ m<n I ym=Max{yl' ... ,yn}}.
Fall1:
Die Folge (m(n))nElN besitzt eine obere Schranke MEW.
Dann ist cn y mn
() <
- cn Max {y 1,... ,yM}
Fall 2:
-----+
0
da c ---+ 0.
n
Die Folge (m(n))nElN ist unbeschränkt.
Da c nicht-wachsend ist, gilt c < c ( )' und statt c y ( ) ---+ 0 genügt es zu zeigen
n
n- mn
n mn
(i)
cm(n) . ym(n)-----+ 0.
Angenommen, (i) gilt nicht, d.h. es gibt ein c: > 0 sodaß cmn
( ) · ymn( ) > c: für unendlich
viele nE W gilt. Da m( n) unbeschränkt ist, folgt cky k > c: für unendlich viele k E W im
Widerspruch zu c y ---+ 0 .
n n
D
Beweise zu: Der Zentrale Grenzwertsatz
3.3.11
B ZGS -7
Beweise zu:
4.
Die Ungleichung von Berry-Esseen
Beweis von
Zusatz 1: Die entsprechende Abschätzung gilt auch für die ;pbere 11 Verteilungsfunktion
d.h.
(5)
Anwendung des Satzes auf Yk =- Xk für k = 1, ... , K liefert für die Verteilungsfunktion G der Standardisierung V=- U
(i)
Wegen
G(-x) = P{V<-x} = P{ U>x}
und
(-x) = P{N(O,l) >x}
folgt
sup IP{U>x}-P{N(O,l)>x}l
XE 1R
sup I G(- x)- <!>(- x) I
XE 1R
II G- II
und mit (i) folgt die Behauptung.
D
BV Bedingte Verteilungen
Gerhard Osius
1.
Definition
1.1
1.2
2.
Methode zur Bestimmung bedingter Verteilungen
2.1
2.2
2.3
2.4
3.
Diskreter Fall
Allgemeiner Fall
Stochastische Unabhängigkeit
Bildmaße bedingter Verteilungen
Unabhängigkeits-Transformationen
Bedingte Dichten
Erwartungswerte bedingter Verteilungen
3.1
3.2
Nicht-negative meßbare Abbildunden
Beliebige meßbare Abbildunden
Literatur
Billingsley, P., (1986): Probability and Measure) (2 nd Edition). New York: Wiley
Gänssler, P., Stute, W. (1977): Wahrscheinlichkeitstheorie. Berlin: Springer.
G. Osius: Bedingte Verteilungen
1.
BV-2
24.9.08
Definition
Für Zufallsvektoren X: (fl, d,P)
-----t
(IRm,IBm) und Y: (fl,d,P)
-----t
(IR n, IBn) soll
eine bedingte Verteilung von X bedingt auf Y definiert werden. Zur Motivation betrachten wir zunächst den Fall, daß Y diskret ist.
1.1
Diskreter Fall
Y sei eine diskrete Zufallsvariable mit dem (höchstens) abzählbaren Träger
Für jedes yE T y ist durch die bedingte Wahrscheinlichkeit
(2)
P{XEA I Y=y}
ein Wahrscheinlichkeitsmaß auf IBm definiert, die sogenannte bedingte Verteilung
cL'( X IY = y) von X unter der Bedingung Y = y. Erweitert man die Definition der
bedingten Wahrscheinlichkeit wie folgt
(3)
P(A IB) =
P(A nB)
P(B)
{
P(A)
falls
P(B) > 0
falls
P(B) = 0
so gilt stets
(4)
p(AnB) = P(AIB) . P(B).
Mit dieser Erweiterung läßt sich die bedingte Verteilung cL'(X IY = y) gemäß (2)
für beliebige y E IRn definieren, wobei gilt
(5)
cL'(XIY=y) = cL'(X).
Die gemeinsame Verteilung von X und Y ist durch die Verteilung P y von Y und
die Familie cL'(X IY) = (cL'(X IY = y))y E lRn aller bedingten Verteilungen von X
auf Y eindeutig bestimmt:
G. Osius: Bedingte Verteilungen
(6)
P{XEA, YEB}
24.9.08
2:=
BV-3
P{XEAIX=y}·P{Y=y}
yEBnS
J
P{XEA I X=y}· Py(dy)
B
1.2
Allgemeiner Fall
Für beliebiges (also nicht notwendig diskretes) Y hat die bedingte Wahrscheinlichkeit 1.1 (2) nicht mehr die gewünschte Eigenschaft 1.1 (6). Im allgemeinen Fall geben wir daher keine konstruktive, sondern eine charakterisierende Definition der
bedingten Verteilung von X auf Y (nach Gänsler-Stute 1997, 5.3), die sich aus der
fundamentalen Beziehung 1.1 (6) ergibt. Eine Funktion p,: IBmxIRn ---+ [0,1] mit
(1)
(A,y)
1----+
fL(A,y) =: P{XEAIY=y}
heißt eine reguläre bedingte Verteilung von X auf Y falls sie die folgenden drei Bedingungen erfüllt:
(BVO)
Für jedes AE IBm ist fL(A,y) = P {XEA I Y = y} eine meßbare Funktion in
yE IR n.
(BV1)
Für jedes AEIB m und jedes BE IBn gilt:
P{XEA, YEB} =
J P{XEA I Y=y}· Py(dy).
B
(BV2)
Für jedes yE IR n ist fL(A,y) = P {XEA IY = y} als Funktion in AE IBn
ein Wahrscheinlichkeitsmaß.
Die Bedingung (BVO ) ist technischer Natur, aber notwendig, damit das Integral in
(BV1) definiert ist. Nach (BV2) ist fL(- ,y) ein Wahrscheinlichkeitsmaß, das wir als
bedingte Verteilung von X unter der Bedingung Y = y interpretieren und wie folgt
bezeichnen
(2)
cL'(XIY=y) := fL(-,Y) = P{XE(-) I Y=y}.
Die entscheidende Bedingung (BV1 ) besagt dann, daß die gemeinsame Verteilung
von (X, Y) eindeutig bestimmt ist durch die Verteilung Py = cL'( Y) von Y und die
Familie cL'( X I Y) = (cL'(X I Y = y)) yE lRn aller bedingter Verteilungen.
G. Osius: Bedingte Verteilungen
24.9.08
BV-4
Betrachtet man für ein festes A E IBm das Maß v A auf IBn mit
(3)
so ist v A offenbar von P y dominiert. Die Bedingungen (BVO) und (BV1) besagen
gerade, daß ,u(A, - ) eine Dichte von vA bezüglich P y ist. Nach dem Satz von Radon-Nikodym ist damit die Existenz von ,u mit (BVO) und (BV1) gesichert. Man
kann zeigen, daß es stets eine reguläre bedingte Verteilung von X auf Y gibt, d.h.
die Dichten ,u(A, -) von vA bezüglich P y lassen sich derart wählen, daß auch (BV2)
gilt. Darüberhinaus ist die reguläre bedingte Verteilung im folgenden Sinn eindeutig:
Zu je zwei Versionen ,ul und ,u2 einer regulären bedingten Verteilung von
(4)
X auf Y gibt es eine Menge BQ E IBn mit:
(a)
P{Y EBQ} = 1
(b)
,ul (y, -) = ,u2(y, -)
für alle YEB o·
Einen Beweis für Existenz und Eindeutigkeit der regulären bedingten Verteilung
findet in Gänssler-Stute (1997), Abschnitt 5.3.
Für diskretes Y ist durch 1.1 (2) eine reguläre bedingte Verteilung von X auf Y definiert und für zwei Versionen ,u2' ,u2 gilt nach (4) ,ul (y, -) = ,u2 (y, - ) zumindest für
alle yETy ' d.h. für YET y ist cL'(XIY=y) eindeutig durch 1.1 (2) gegeben.
Beispiel: Y = X
Als triviales (aber wichtiges) Beispiel zeigen wir, daß die Verteilung von X unter
der Bedingung X = x die Einpunktverteilung (Dirac-Verteilung) im Punkt x ist
cL'(X IX=x) = Dirac(x) ,
d.h. die zugehörige reguläre bedingte Verteilung von X auf X ist definiert durch
,u(A,x) = P{XEA I X=x} :=IA(x),
mit I
A
als Indikatorfunktion von A. Die Bedingungen (BVO), (BV2) sind evident
und (BV1) ergibt sich aus
P{XEA, XEB}
J
AnB
dP X
D
G. Osius: Bedingte Verteilungen
2.
24.9.08
BV-5
Methoden zur Bestimmung bedingter Verteilungen
Wir betrachten jetzt einige spezielle Situationen, bei denen sich eine reguläre bedingte Verteilung von X auf Y explizit angeben läßt (wie es z.B. für diskretes Y
der Fall ist).
2.1
Stochastische Unabhängigkeit
Sind X und Y stochastisch unabhängig, so ist die bedingte Verteilung von X auf Y
gleich der Verteilung von X:
cL'(X IY) = cL'(X)
(1)
d.h. durch
(2)
P{XEA I X=y}:= P{XEA}
ist eine reguläre bedingte Verteilung von X auf Y definiert.
2.2
Bildmaße bedingter Verteilungen
Das Bildmaß einer regulären bedingten Verteilung cL'(XIY) von X auf Y unter einer meßbaren Transformation H: IRm
-----+
IR n ist eine reguläre bedingte Verteilung
von H(X) auf Y, also
(1)
cL'(H(X) I Y) = H- 1 cL'(X IY).
Gemeint ist damit, daß durch
(2)
P{H(X)ECI Y=y}:= P{XEH-1[C] I Y=y}
eine reguläre bedingte Wahrscheinlichkeit von H(X) bedingt auf Y definiert ist,
sofern P{XEA I X=y} eine reguläre bedingte Verteilung von X auf Y ist.
G. Osius: Bedingte Verteilungen
2.3
BV-6
24.9.08
U nabhängigkeits-Transformationen
Wir geben jetzt die bedingte Verteilung von X auf Y für den Fall an, daß es eine
geeignete Transformation U = G(X, Y) gibt, die von Y stochastisch unabhängig
ist. Hierzu betrachten wir meßbare Transformationen
die sich bei festgehaltenem zweiten Argument gegenseitig umkehren:
(1)
H(G(x,y),y) = x,
Die meßbare Abbildung
(2)
G(H(u,y),y) =
für alle x, y, u.
u
G: IRmxIRn -----+ IRkxIRn definiert durch
G(x,y) = (G(x,y),y)
ist daher bijektiv mit der meßbaren Umkehrabbildung
(3)
H(u,y) = (H(u,y),y).
Damit läßt sich das Paar (X,Y) umkehrbar-eindeutig zu G(X,Y) =(U,Y) mit
U = G(X,Y) transformieren. Wir setzen jetzt voraus
(4)
U und Y sind stochastisch unabhängig.
Dann ist die bedingte Verteilung von X auf Y = y durch die Verteilung von
H(U,y) gegeben, d.h.
(5)
cL'(XIY=y)
cL'(H(U,y))
für alle y.
Genauer ist durch
(6)
P{XEAIY=y}
P{H(U,y) EA}
P{U,y) EH-1 [A]}
eine reguläre bedingte Verteilung von X auf Y definiert.
für alle y, A
G. Osius: Bedingte Verteilungen
2.4
BV-7
24.9.08
Bedingte Dichte
Die Konstruktion der bedingten Verteilung von X auf Y unter Verwendung einer
bedingten Dichte ist dann möglich, wenn es Maße
V
x : IBm -----+ IR und v y :IBn -----+ IR
gibt, deren Produktmaß v = vXx v y die (gemeinsame) Verteilung des Paares
(X, Y) : (.f2, d) -----+ (IR m, IBm) X (IR n, IBm) dominiert. Dann besitzt cL'(X, Y) eme
v- Dichte p : IR m x IR m -----+ IR, deren Werte wir auch suggestiv schreiben als
(1)
p(X=x, Y=y):= p(x,y).
Damit definiert
(2)
p(Y =y) : = Py(y) : =
Jp(X=x, Y =y) vX(dx)
eine vy-Dichte von cL'(Y), und
{ Y E IR n I p(Y =
(3)
y) > 0 }
ist ein Träger von Y:
Wir definieren nun - analog zur bedingten Wahrscheinlichkeit 1.1 (3) - die bedingte
Dichte von X unter der Bedingung Y = y durch
(5)
p(X=x, Y =y)
p(X = x I Y =y) := PXly(x) : =
p(Y =y)
{
p(X=x)
falls p(Y =y) > 0,
falls p(Y =y) = 0 .
Für jedes y E IR n gilt dann
(6)
p(X=x, Y=y) = p(X=x I Y=y) ·p(Y=y)
vX-fast überall.
Wegen
(7)
JPXly(x) vX(dx) = 1
ist PXly: IR
m-----+ IR die vX-Dichte eines Wahrscheinlichkeitsmaßes p,(-, y) auf IBm.
Man überzeugt sich leicht davon, daß die Funktion p, die Bedingungen (BVO-2) aus
1.2 erfüllt, und somit eine reguläre bedingte Verteilung von X auf Y darstellt.
Insbesondere ist die bedingte Dichte PXly also eine vX-Dichte der bedingten VerteilungcL'(XIY=y) =p,(-,y).
G. Osius: Bedingte Verteilungen
3.
BV-8
24.9.08
Erwartungswerte bedingter Verteilungen
Bezeichne P X
Iy = ci:{X I Y
=
y} die (genauer: eine reguläre) bedingte Verteilung
von X unter Y = y. Für eine meßbare Abbildung H: IR m -----+ IR ist der Erwartungswert von H(X) bzgl. der bedingten Verteilungen P X
(1)
Iy
definiert als
E{H(X) IY=y}:= JH(x)· PX1y(dx)
(sofern das rechte Integral existiert), und wird auch als bedingter Erwartungswert
von H(X) unter der Bedingung Y = y bezeichnet. Wir leiten jetzt eine andere Charakterisierung des bedingten Erwartungswertes (1) her. Zunächst betrachten wir
den Fall, daß die Abbildung H nicht-negativ ist.
3.1
Nicht-negative meßbare Abbildungen
Betrachten wir 3 (1) als eine FunktionJ: IR n
(1)
---+
IR in y, d.h.
J(y):= JH(x) PX1y(dx),
so gilt
(2)
J ist meßbar.
Und für beliebiges BE IBn ist
(3)
JJ(y) . Py(dy)
B
J
H(X) dP
d.h.
{YEB}
wobei I C die Indikatorfunktion der Menge C bezeichnet. Speziell mit B = IR n läßt
sich der Erwartungswert von H(X) wie folgt darstellen:
(5)
E{H(X)} = E { E{H(X) I Y = (-)}} = E{J}.
Wegen H > 0 folgt hieraus
(6)
E{H(X)} < 00
J < 00
P y - fast-sicher.
G. Osius: Bedingte Verteilungen
3.2
24.9.08
BV-9
Beliebige meßbare Abbildungen
Wir setzen voraus, daß H(X) integrierbar bzgl. H ist, d.h.
(1)
E{IH(X)I}<oo.
Nach 3.1 (6) - angewandt auf
IHI - ist jetzt die
durch 3.1 (1) definierte Funktion f
nur Py-fast-sicher definiert, d.h. f ist definiert auf einer Menge TE IBn mit
(2)
P{YET}=1.
Setzt man f auf IR n fort durch
(3)
f(y) = 0
für y
\t T,
so ist f auf ganz IR n definiert und dort endlich. Die Beziehungen 3.1 (3 - 5) gelten
dann auch für beliebiges H, sofern die Bedingung (1) gilt.
Beweise: Bedingte Verteilungen
BBV -1
24.9.08
Beweise zu:
Bedingte Verteilungen
Beweise zu 2.1 - 2.3
Der Nachweis der Bedingungen (BVO) - (BV2) für die jeweils angegeben bedingten
Verteilungen ist "streight forward".
Beweise zu
2.4
Bedingte Dichten
Beweis von
(6)
p(X=x, Y=y) = p(X=x I Y=y) ·p(Y=y)
vX-fast überall.
Für p(Y = y) = 0 folgt aus (2)
p(X=x, Y =y) = 0
und somit gilt dann (6). Und für p(Y =y)
> 0 gilt (6)
sogar für alle xE IR m .
D
>0
folgt sie
Beweis von
(7)
JPXly(x) vX(dx) =
1
Für p(Y = y) = 0 gilt die Behauptung trivialerweise, und für p(Y = y)
aus den Definitionen (2) und (5).
D
Beweise: Bedingte Verteilungen
BBV-2
24.9.08
Beweis von (BVO-2)
(BVO) folgt aus der Meßbarkeit von p, und (BV2) ergibt sich aus (7). Zum Nachweis von (BV1) ist für beliebige A E lB
P{XEA, YEB} =
J fL(A,y)
m
n
und BE lB zu zeigen
. Py(dy)
bzw.
. Py(Y) . vy(dy)
bzw.
B
=
J fL(A,y)
B
=
=
1(j p(X I Y
1(1 p(X=x, Y
=x
Die letzte Formulierung gilt, da p eine
=y) . vx(dx) ) Py(Y) . Vy(dy)
=y) . vx(dx) ) . Vy(dy)
V
x xVy-Dichte von (X, Y)
bzw
wegen
ist..
(6).
D
G. Osius: Bedingte Erwartung und Covarianz-Matrix
BEC-1
4.2.14
BEC Bedingte Erwartung und
Covarianz-Matrix zufälliger Vektoren
Gerhard Osius
1.
Grundlagen
Für Zufallsvektoren X:(.f2,d,P)
-----t
(IRm,IBm) und Y:(.f2,d,P)
-----t
(IRn,IBn) wol-
len wir den Erwartungswert E(Y) und die Covarianz-Matrix Cov(Y) aus dem bedingten Erwartungswerten E(Y I X = x) und der bedingten Covarianz.Matrix
2
2
Cov(Y I X= x) bestimmen. Hierfür setzen wir voraus, daß E(ll Xll ) und E(ll Yll )
endlich sind, d.h. die folgenden Erwartungswerte und Covarianz-Matrizen existie-
ren:
(1)
1-Lx == E(X)
E
IRm,
EX:= Cov(X)
E
IRmxm,
1-Ly == E(Y)
E
IRn,
Ey: = Cov(Y)
E
IRnxn.
Dann existieren auch für jedes x E X[n] die bedingten Erwartungswerte und bedingten Covarianz-Matrizen
(2)
1-Lylx(x) : = E(Y I X= x) ,
(3)
EYIX(x): = Cov(Y I X= x)
= E(YYT I X= x) -p,YIX(x) 1-Lyljx)T
Aus den Eigenschaften bedingter Erwartungen ergibt sich sofort
(4)
(5)
1-Ly = 1E(Y I X= x) dP\x) = E(p,yljX)).
E(YYI) = 1E(YYT IX= x) dV(x)
= E( EYIX(X))
+ E(p,YIX(X) I-Lylx(X)1),
vgl. (3).
und somit
(6)
L'y = E(YYI)- 1-Lyi-LyT
= E( EYIX(X))
+ E(p,YIX(X) 1-Lylx(X) 1) -
= E( EYIX(X))
+ Cov(p,yljX)) .
E(p,YIX(X)) E(p,yljX)
l
G. Osius: Bedingte Erwartung und Covarianz-Matrix
2.
4.2.14
BEC-2
Lineares Modell mit homogenen bedingten Covarianzen
Für eine feste meßbare Funktion h: IR m-----+ R k betrachten wir jetzt den Zufallsvektor U = h(X) und setzen voraus, daß
(7)
Jlu := E(U) E IR k , Eu : = Cov(U) E IR kxk
existieren. Weiter setzen wir ein lineares Modell
(LM)
Jlylx(x) = a
+ ßTh(x)
mit den Parametern a E IR m und ß E IR mxn voraus. Mit (4) und (6) ergibt sich
T
(7)
Jly = a
(8)
Cov(J.LYIX(X)) = Cov(ßTU) = ßTEuß
(9)
Ey = E(EYIX(X))
+ ß Jlu·
+ ßTEuß.
Fordern wir noch die Homogenität der bedingten Covarianzen
für alle x
(HC)
so ergibt sich schließlich
(10)
Triviales Beispiel: Y =X
Dann ist L(Y I X= x) die Einpunkt-verteilung Dirac(x) und somit gilt
x,
Folglich liegt für h als Identität bzw. U = X das lineare Modell (LM) vor mit a
und ß als Einheitsmatrix. Da auch (HC) gilt, reduziert sich (10) zu Ey =EX
=0
G. Osius: Bedingte Erwartung und Covarianz-Matrix
Beweise zu:
4.2.14
BEC-3
1. Grundlagen
Zu zeigen ist nur die Existenz der bedingten Erwartunswerte in (2) und (3) sowie
die (jeweils erste) Darstellung in (4) und (5). Wir betrachten allgemeiner eine meßbare Funktion g :IR n-----+ R k für die der Erwartungswert von V = g(Y) existiert.
Nach Gänssler-Stute (Wahrscheinlichkeitstheorie) Springer Verlag 1970 S. 191) existiert
dann die bedingte Erwartung E(V I X= x) für x E X[D] und aus 5.2.20 Satz (i) folgt
(i)
E(V) = J E(V I X= x) dV(x)
Für V= Y bzw. V= yyT ergeben sich dann die Behauptungen. Es gibt noch einen
elementaren Beweis von (i), wenn wir voraussetzen, daß (X, Y) einen Träger der
Form .f2 = .f2xx.f2 y und eine positive Dichte f: .f2-----+ (0, oo) bzgl. eines Produktmaßes
v = vXX vY besitzt, wobei vX bzw. vY a-endliche Maße auf IR m bzw. IR n sind. Dann
sind auch die Randdichten
fy(y) = Jf(x,y) dv (x)
(ii)
X
positiv und fast-überall endlich, weshalb wir endliche Versionen wählen können und damit gilt (ii) nur fast-überall. Weiter ist
eine Dichte der bedingten Verteilung L(Y I X= x). Dann ist
(iii)
E(lg(Y)I) =
f lg(y)lfy(y) dvy(y)
= J lg(y)l UJ(x,y) dv)x)] dvy(Y)
= J lg(y)l UJ'X(y Ix)fx(x) dv)x)] dvy(y)
= J [Jig(y)IJ'X(y I x) dvy(y)] fx(x) dv x(x).
= J E(lg(Y)II X= x) fx(x) dv x(x)
= J E(lg(Y)II X= x) dV(x).
Da der Integrand nicht-negativ und das Integral nach Voraussetzung endlich ist, ist
auch der bedingte Erwartungswert E(lg(Y)II X= x) fast-überall endlich und somit
existiert der bedingte Erwartungswert E(g(Y) I X= x) fast-überall. Jetzt ergibt sich
(i) aus (iii) mit V statt lg(Y)I.
G. Osius: Covarianz-Matrizen von Zufallsvektoren
cav
20.3.02
COV-1
Covarianz-Matrizen zufälliger Vektoren
Gerhard Osius
Allgemein ist für einen I-dimensionalen Zufallsvektor U und einen i-dimensionalen
Zufallsvektor V die (Ixi)-Covarianzmatrix von U und V definiert als die Matrix
der Covarianzen aller Komponenten von U mit allen von V, d.h.
(1)
Cov(U, V) = (Cov(U., V.)) . ..
z ]
Z,]
Definiert man für eine (Ixi) Zufalls-Matrix Z den Erwartungswert komponentenwelse
(2)
E(Z) = (E(Z ..)) .. ,
ZJ
ZJ
so läßt sich die obige Covarianz-Matrix auch schreiben als
(3)
Cov(U,V)
E{(U-E(U)). (V-E(V ))T}
E{UVT} - E(U) E(V)T.
Für lineare Transformationen AU und BV von U und Vergibt sich die Covarianz
(4)
T
Cov(AU,BV) = A·Cov(U,V)·B ,
wobei A und B feste Matrizen geeigneten Formats sind.
Die Covarianz ist translationsinvariant, d.h. für beliebige aE IRI und bE IR] gilt
(5)
Cov(U +a, V + b) = Cov(U, V).
Speziell für U = Vergibt sich in (1) die Covarianz-Matrix von U
(6)
Cov(U) = Cov(U,U) = E{(U-E(U)).(U-E(U))T}.,
und die (4) und (5) entsprechenden Rechenregeln lauten
(7)
Cov(A U)
A· Cov(U)· AT,
(8)
Cov(U +a)
Cov(U).
Ferner gilt für den Erwartungswert
(9)
E(AZB
+ C)
= A·E(Z)·B
+ C,
G. Osius: Covarianz-Matrizen von Zufallsvektoren
20.3.02
COV-2
wobei A, Bund C beliebige feste Matrizen (vom richtigen Format) sind.
Für eine feste lxl-Matrix A läßt sich der Erwartungswert der Bilinearform
U TA V = V TATU unter Verwendung der Covarianzmatrix darstellen
(10)
E(U TA V)
Spur(A Cov(U,V)T)+ E(U)TA E(V)
Spur(Cov(U,V) A T) + E(V) TA T E(U).
Hieraus ergibt sich der Erwartungswert einer quadratischen Form U T Q U für eine
feste symmetrische lxI-Matrix Q zu
(11)
E(UTQU) = Spur(QCov(U)) + E(U)TQE(U).
Beweise: Covarianz-Matrizen von Zufallsvektoren
9.7.10
COVB 1
Beweise
Die Beweise von (3)-(5) und (9) ergeben sich direkt aus den Definitionen
und den Eigenschaften des Erwartungswertes.
Beweis von
(10)
Für
E(U TA V)
Spur(ACov(U,V)T)
+ E(U)TAE(V)
Spur(Cov(U,V) AT)
+ E(V) TAT E(U) .
JlU = E(U),
X = U - JlU
Jly = E(V),
Y = A(V - Jl y )
ist
E(X) = 0,
E(Y) = 0
und
E(XTy) = E(2: XY.) = 2: E(X.Y.)
.
Z
z z
.
z z
Z
= 2: Cov(X., Y.)
.
z z
z
Spur(Cov(X, Y))
Spur(Cov([U - Jlu]' A[V - Jl y ]))
Spur(Cov(U, V)A T)
Spur(A Cov(U, V) T).
Mit
E(XTy) = E([U - Jlu]TA[V - Jl y ])
T
E(U A V) - E(U)TAJly - JlJ AE(V)
+ JlJAJly
T
E(U A V) - JlJAJly
folgt die Behauptung.
D
G. Osius: Wurzeln positiv-semidefiniter Matrizen
4.6.10
WM-1
WM Wurzeln positiv-semidefiniter Matrizen
Gerhard Osius
1.
Definition einer Wurzel
Es seI A eine reelle symmetrische positiv-semi-definite I xl-Matrix. Eine I xIMatrix B heißt eine Wurzel von A, falls gilt
Eine Wurzel von A existiert stets, und kann durch Zusatzbedingungen sogar eindeutig bestimmt werden. So gibt es z.B. genau eine symmetrische positiv-semi-definite
Wurzel von A, die wir suggestiv mit ~ bezeichnen, vgl. z.B. Debnath & Mikusiriski
Introduetion to Hilbert Spaces with Applications (Academic Press, Boston 1990), The-
orem 4.6.5. Jede mit A kommutierende lxI-Matrix C kommutiert auch mit~, d.h.
(2)
~C=C~.
AC=CA
Falls C auch symmetrisch und positiv-semidefinit ist, so ist auch das Produkt AC
symmetrisch und positiv-semidefinit - vgl. z.B. Debnath & Mikusiriski (1990), Theorem 4.6.3 - und die Wurzel des Produkts ist das Produkt der Wurzeln
(3)
AC=CA
Eine beliebige Wurzel von A bezeichen wir suggestiv mit A 1/2 d.h. es gilt stets
(1) I
A = A 1/ 2 . A T/ 2
mit
Hieraus ergibt sich speziell
(4)
RangA
< Rang A 1/2 .
Weiter gilt für cE IR mit c > 0
(5)
~ A 1/2 ist eine Wurzel von cA,
und für die symmetrische Wurzel folgt
(6)
~ = ~JA.
Die Elemente einer Wurzel A 1/2 lassen sich durch die Diagonalelemente von A abschätzen:
G. Osius: Wurzeln positiv-semidefiniter Matrizen
(7)
IA~(21
<
~
Z)
zz
4.6.10
WM-2
i,j = 1, ... ,1.
für
Für eine Folge A mit einer zugehörigen Folge A 1/ 2 von Wurzeln gilt daher
n
n
(8)
(An1/1"T'>T
ist beschränkt.
nEll'I
=*
(A)"T'>T
ist beschränkt
n nEll'I
Hieraus ergibt sich die Stetigkeit der symmetrischen Wurzel:
(9)
2.
lim~=VA.
lim A = A
n
n
n
n
Wurzeln positiv-definiter Matrizen
Wenn A symmetrisch und positiv-definit - und somit invertierbar - ist, so folgt aus
1 (4), daß auch jede Wurzel A 1/2 invertierbar ist, und Inversion von 1 (1) I liefert
A-1 = A-T/2. A-1/2
(1)
mit
A-1/2 = (A1/ 2 )-1 ,
d.h. A -T/2 ist eine Wurzel der inversen Matrix A -1.
Speziell gilt für die symmetrische Wurzel
(2)
JIT =
(3)
j
3.
11
A-1 =
mit 11 als Einheitsmatrix,
[JA ]-1.
Die Cholesky-Wurzel
Wenn A symmetrisch und positiv-definit ist, so gibt es genau eine Wurzel von A,
die eine untere Dreiecksmatrix ist, die sogenannte Cholesky-Wurzel von A - vgl. z.B.
Stoer (1983), (4.3.3), Satz, S. 155. Für die Cholesky-Wurzel von cA gilt
(1)
(2)
für
A invertierbar
cEIR, c>O,
=*
Die Cholesky-Wurzel ist ein stetiger Operator, d.h. es gilt
(3)
lim A = A
n
n
lim A 1/ 2 = A 1/2 .
n
n
Beweise: Wurzeln positiv-semidefiniter Matrizen
28.7.06
BWM-1
Beweise zu:
1.
Definition einer Wurzel
Beweis von
(5)
~ A 1/2 ist eine Wurzel von cA,
(6)
~ = ~VA.
Wegen
cA = cA 1/2 A T/2 = ~ A 1/ 2 [~ A 1/ 2 JT
gilt (5).
Da mit VA auch ~ VA symmetrisch ist, ergibt sich (6) aus (5).
D
Beweis von
(7)
für
Für jedes i folgt aus (1):
A ..
und somit
~
V.f1
ii
n
i,j = 1, ... ,1.
=~B
j
2
..
zJ
>B 2..
-
zJ
>IB··I
Z)
D
Beweis von
(9)
lim~=VA.
lim A = A
n
n
n
n
Nach dem Teilfolgen-Kriterium ist zu zeigen, daß jede Teilfolge k = k(n)
weitere Teilfolge m = m(k)
---+ 00
enthält mit ~
m
---+
---+ 00
eine
VA . Wegen (8) ist die Folge
~ beschränkt, und somit enthält jede Teilfolge k ---+
n
---+ B.
00
eine konvergente Teilfolge
..r;cm
Aus
A
m
= ~ ~
m
m
-----t
BB
folgt
A = BB.
Nun ist B als Limes symmetrischer Matrizen wieder symmetrisch und somit ist
D
Beweise: Wurzeln positiv-semidefiniter Matrizen
BWM-2
28.7.06
Beweise zu:
3.
Die Cholesky-Wurzel
Beweis von
(1)
für
cEIR,
c>o.
· A 1/ 2 1st
. auc h c
.
1/2· A 1/ 2 eme
. k smatnx.
. W egen
M lt
untere D relec
C 1/ 2
.
A 1/2 . [ c 1/ 2 . A 1/2] T = cA 1/2 A T/2 = cA
ist daher c 1/2 . A 1/2 die (eindeutig bestimmte) Cholesky-Wurzel von cA.
D
Beweis von
(2)
A invertierbar
Nach 1 (4) ist A 1/2 invertierbar. Wegen
A = A 1/ 2 A T/ 2
bleibt nur zu zeigen, daß [A T/ 2 ]-1 eine untere bzw. [A1/ 2 ]-1 eine obere Dreiecksmatrix ist, und dies ergibt sich aus dem folgenden Lemma.
Lemma: Für eine invertierbare untere Dreiecksmatrix B ist die Inverse B-1 eine obere
Dreiecksmatrix.
1
Beweis des Lemmas: Ist B = (b ) eine nxn-Matrix mit C: = B- = (c
ij
kl
) und D =
det(B), so gilt - vgl. z.B. H.-i. Kowalsky (1972)) Lineare Algebra) 15.3 c = D-1 . (_l)k+l. det(BÄ) ,
kl
wobei die (n-l)x(n-l)-Matrix B*.. aus B durch Streichung der k-ten Zeile und l-ten
Z)
Spalte entsteht. Nach Voraussetzung gilt
(i)
i<j
und zu zeigen ist für 1 < l < k
(ii)
b.. = 0,
Z)
<n
bzw.
det(B'k l) =
o.
Beweise: Wurzeln positiv-semidefiniter Matrizen
Für festes l
<k
sei
B\ Z =
BWM-3
28.7.06
(brj ) und unter Verwendung der Indikatorfunktion IA
einer Menge A ergibt sich
(iii)
i*=i+I{i~k}'
mit
Zum Nachweis von (ii) genügt es zu zeigen, daß B*kZ eine untere Dreiecksmatrix ist,
die auf der Hauptdiagonalen eine 0 enthält, also
b~o =
(iv)
i<j
(v)
biz =
ad (iv):
Falls i
Und für k
< i ist l< k< i <j, also i* = i+1 <j+1 =j* und wieder b7j
ad (v):
Wegen l<k ist
Z)
0,
0.
<k
gilt, so ist i* = i
b7z = bZ(Z+1)
<j <
j*
-
und somit b~o = bo*o* = 0 nach (i).
Z)
Z]
= bi*j* =
o.
D
= 0 nach (iii) und (i).
Beweis von
(3)
Ern A 1/ 2 = A 1/2 .
n
n
Ern A = A
n
n
Nach dem Teilfolgen-Kriterium ist zu zeigen, daß jede Teilfolge k = k(n)
weitere Teilfolge m = m(k)
---+ 00
enthält mit A 1/2
m
---+
A 1/ 2 beschränkt, und somit enthält jede Teilfolge k ---+
n
1 2
A / ---+ B.
---+ 00
eine
A 1/2. Nach (3) ist die Folge
00
eine konvergente Teilfolge
m
folgt
A=BB
T
,
d.h. B ist eine Wurzel von A.
Nun ist B als Limes von unteren Dreiecksmatrizen wieder eine solche, und somit
ist B die Cholesky-Wurzel A 1/2 von A.
D
G. Osius: Skalarprodukte und orthogonale Projektionen
SP
SP-1
30.8.11
Skalarprodukte und orthogonale Projektionen
Gerhard Osius
1.
Definitionen
Das Standard-Skalarprodukt (-,-) auf IR] ist definiert durch
(1)
/u,v):= u Tv =
\
~
.
J
u.v ..
JJ
Unter Verwendung einer positiv-definiten symmetrischen ]
x] - Matrix
D läßt sich ein
Skalarprodukt bzgl. D definieren durch
(2)
(u,v)D:= uTDv = (u,Dv) = (Du,v).
Für D = 11J (Einheitsmatrix) ergibt sich wieder das Standard-Skalarprodukt. Für
eine beliebige Wurzel D 1/2 von D erhält man die Darstellung
(3)
T2
T2
(u,v)D = (D / u, D / v) .
Da D T/ 2 : IRJ
J
IR ein Isomorphismus ist, läßt sich das Skalarprodukt bzgl. D als
Modifikation des Standard-Skalarproduktes bzgl. des Isomorphismus D T/ 2 inter-----+
pretieren.
Die zugehörige Norm li-liD bzgl. D ist gegeben durch
(4)
T2 2
Ilullt:= (u,u)D = IID / uI1 .
Mit der Matrixnorm IIAII = sup IIAxl1 ergeben sich die Abschätzungen
Ilxll<1
(5)
Ilu liD
< IID
T2
/ 11·11 ull,
Folglich ist die Norm li-liD äquivalent zur Norm 11-11 und die von den Normen erzeugten Topologien stimmen überein.
Für einen linearen Teilraum vft ist die D-orthogonale Projektion
p! :IR
J
-----+
vft
auf vft definiert als die orthogonale Projektion bzgl. des Skalarproduktes (-, - )D'
d.h. für beliebiges y E IRJ ist
y wie folgt charakterisiert:
p!
(6)
v-pDy
-.At
{}
vEvft und [v - Y]..lD vft
{}
vEvft und (v - y, u)D = 0
für alle u Evft.
G. Osius: Skalarprodukte und orthogonale Projektionen
2.
SP- 2
30.8.11
Eigenschaften der Projektionen
Die D-orthogonale Projektion läßt sich auch durch die übliche orthgonale Projektion P T/2 [
D
T/2
D
] bzgl. des Standard-Skalarproduktes auf das isomorphe Bild
.At
[...4] von ...4 beschreiben:
(1)
Allgemeiner ist für eine beliebige KxJ-Matrix A vom Rang J die symmetrische
Matrix AT DA auch positiv-definit, und für den Bildraum A[...4] von ...4 unter der
Einbettung A: IRJ -----+ IRK gilt
(2)
A·
p~DA
=
p~[.At]. A.
Unter Verwendung einer JxS-Matrix X, deren Spalten den Raum...4 erzeugen, läßt
sich die D-orthogonale Projektion als JxJ-Matrix darstellen
(3)
J
X[XTDX]- XTD,
falls ...4 = X[IR ],
X [XTDXr1XTD ,
falls Rang X = Dim...4.
Hierbei ist [X TDXr eine beliebige verallgemeinerte Inverse von X TDX, die unter
der Bedingung Rang X = Dim...4, d.h. die Spalten von X bilden eine Basis von ...4,
die übliche inverse Matrix [XTDXr1 ist.
Beispiel: Eindimensionaler Raum vi(
Ein eindimensionaler Raum ...4 wird von jedem xE...4 - {O} aufgespannt, und die
JxJ-Projektionsmatrix ergibt sich zu
D
Die D-orthogonale Projektion ist idempotent, stellt aber als Matrix betrachtet im
allgemeinen keine symmetrische Matrix dar:
(4)
pD . pD = pD
.At
.At
.At
(5)
[p!]T =D.P! .D-1
(6)
. [DT/2]-1 _ P T ,/ 2
D T/2 . pD
.At
D / [.At]
(Idempotenz)
bzw.
[p!]T. D = D .
ist symmetrisch .
Für die Norm einer Projektion ergeben sich die Darstellungen
p!
G. Osius: Skalarprodukte und orthogonale Projektionen
(7)
IIP~ull~
(8)
IIP~ull~
30.8.11
SP- 3
UTDP~u
T 2
11
P DT/2[c4l D / u
2
11
·· uE IRJ
f ur
Das D-orthogonale Komplement .At~D von .At ist definiert als orthogonales Komplement bzgl. des Skalarproduktes ( -. - )D' d,h.
(9)
.At~D
{vEIRJI v..lD.At}
{vEIRJI (u,v)D = 0 für alle UE.At}.
Zwischen dem D-orthogonalen Komplement und dem üblichen Komplement .At~
bzgl. des Standard-Skalarproduktes besteht folgender Zusammenhang:
Für die D-orthogonalen Projektionen auf .At und .At~D gelten
für alle u E IRJ .
(11)
(12)
Weiter läßt sich die D-orthgonale Projektion auf .At~D auch durch die
D-1-orthogonale Projektion auf das übliche Komplement .At~beschreiben.
(13)
Für einen weiteren linearen Teilraum J'V C IR] gilt
(14)
Die D-orthogonale Projektion ist invariant gegenüber Multiplikation von D mit einer positiven Konstanten
für jedes cE IR, c> o.
(15)
Die D-orthogonale Projektion ist stetig bzgl. D, d.h. für eine Folge (D)
l\.T posin nEll'I
tiv-definiter symmetrischer 1 xl-Matrizen gilt
(16)
D
D
::::}
(17)
Spur(~)
Dim.At.
(18)
.At ..lD J'V
n
-----+
Weiter gelten:
::::}
G. Osius: Skalarprodukte und orthogonale Projektionen
3.
30.8.11
SP-4
Projektionen und Exponentialfunktion
Für einen linearen Teilraum vft C IRJ ist jedes y E IRI eindeutig bestimmt durch
seine beiden Projektionen Pc4 Y und Pc4...L y, und die resultierende lineare Abbildung (pc4 ,Pc4...L) : IRI -----+ vft x vft~ ist bijektiv. Für die komponentenweise definierte Exponentialfunktion exp : IRI -----+ (0,00 ist auch die Abbildung
l
I
((Pc4oexp),Pc4...L): IR -----+ Pc4 [(O,ooll
(1)
y
1------+
xvft~
(pc4 exp(y) , Pc4...L y)
noch bijektiv (Haberman 1974, Theorem 2.6). Wir wollen jetzt wir eine leichte Verallgemeinerung angeben, die darin besteht, daß wir D-orthogonale Projektionen
für eine Diagonalmatrix D betrachten. Hierzu zeigen wir zuerst das
Theorem: Sei D = Diag{ cl} mit cl E (0,00)1 gegeben und vft C IRI sei ein linearer Teilraum mit
l
JV vft~ D. Dann gibt es zu jedem u E (0,00
und v E JV genau ein
I
y = H(u, v) E IR mit
(i)
(ii)
Damit gibt es eine Funktion H: (0 , (0) Ix JV
-----+
IRI die implizit definiert ist durch
I
Die Funktion H ist surjektiv) weil für jedes y E IR gilt
(a)
H( exp(y), P~y) =
y.
Weiter ist H differenzierbar mit stetigen partiellen Ableitungen und für diese gelten
(c)
(Identität auf JV).
Zusatz: Die Bedingungen
(i) und (ii) zusammen sind äquivalent dazu) daß r, =
Maximalstelle der streng konkaven Funktion
(iii)
e: vft -----+ IR ist mit
e("l) = ~i d·(TJ·u.
- exp(v·+TJ·))
.
Z
Z Z
Z
Z
Als unmittelbare Folgerung ergibt sich dann das
y- v die
G. Osius: Skalarprodukte und orthogonale Projektionen
l
Korollar: Sei D = Diag{ cl} mit cl E (0,00
raum mit JV
30.8.11
gegeben und vft C IR! sei ein linearer Teil-
vft~ D. Dann ist die folgende Abbildung bijektiv
F = ((P~ 0 exp), P~) :IR
-----+
P~[(O,oo/l x.AI
y
r------+
F(y) = (P~ exp(y) , P~y) .
1
SP- 5
Beweise zu: Skalarprodukte und orthogonale Projektionen
30.8.11
B SP-l
Beweise zu:
1.
Definitionen
Beweis von
(D Tu, v).
(2)
(3)
(u, Y)D = (D T/ 2u, D T/ 2y) .
Es ist
u T D y = u T D 1/ 2 D T/ 2 y = (D T/ 2u, D T/ 2 y).
Nachzuweisen sind ferner die Eigenschaften eines Skalarproduktes:
(i)
(ii)
(iii)
(- ,- )D
(- ,- )D
(-, - )D
ist bilinear
ist symmetrisch
ist positiv-definit, d.h.
(u, u)D > 0 für u;= o.
(i) und (ii) folgen sofort aus (2), und (iii) ergibt sich mit (3) weil D T/ 2u;=O für
u;=o.
D
Beweis von
(5)
Ilu liD < IID T/ 2 11·11 ull ,
Es ist
Ilu liD = IID T/ 2 ull < IID T/ 2 11·11 ull
und
Ilu I < IID- T/ 2 11·11 ulI D·
D
Beweise zu: Skalarprodukte und orthogonale Projektionen
30.8.11
B SP- 2
Beweise zu:
2.
Eigenschaften der Projektionen
Beweis von
(1)
(2)
Wir beweisen zuerst (2) indem wir für beliebiges yE IR] zeigen
(i)
v:= A·
pi
DA
Y =
P~[c4l . Ay
Nach 1 (6) ist hierfür zu zeigen
(ii)
vE A[ Jt]
(iii)
(v-Ay, AU)D = 0 für alle uEJt.
Für
w:=P
gilt
v=Aw
ATDA
c4
yEJt
,
und (ii) folgt. Weiter ist
(v-Ay, AU}D
(Aw-Ay, AU}D
[Aw-Ay]TDAu
[w-y]TAT DAu
(w-y, U}ATDA
o
nach Definition von w
als Projektion von y
Also gilt auch (iii), und (2) ist gezeigt. Anwendung von (2) auf D = 11 und A = D T/ 2
liefert (1), weil D 1/ 2 . D T/ 2 = D.
D
Beweise zu: Skalarprodukte und orthogonale Projektionen
30.8.11
B SP- 3
1. Beweis von
(3)
J
x [XTDXrXTD,
falls .At = X[IR ],
X[XTDXrlXTD,
falls Rang X = Dim.At.
Das Resultat gilt für das Standard-Skalarprodukt, d.h. D = 11, nach Skript ))Lineare
Modelle" (Abschnitt 2.1), und wir führen den allgemeinen Fall darauf zurück. Für
DT/2[~ = D T/ 2X[IR J ] gilt daher:
[D T/ 2X] . ([D T/ 2X]T [D T/ 2X]t . [D T/ 2X]T
DT/2X(XTD1/2DT/2Xr X T D 1/ 2
DT/2X(XTDXt X T D 1/ 2
DT/2X(XTDXt X T D 1/ 2 D T/ 2 [D T/ 2]-1
DT/2X(XTDXt X T D [D T/ 2]-1
Zusammen mit (1) folgt hieraus (3)
D
2. Beweis von
(3)
J
X [XTDXrXTD,
falls .At = X[IR ],
X[XTDXrlXTD,
falls Rang X = Dim.At.
Für yE IRJ ist die orthogonale Projektion v = ~(y) charakterisiert durch
(i)
v E .At
(ii)
(y - v) ~D .At .
Da .At von den Spalten von X erzeugt wird, sind (i) und (ii) äquivalent zu
(i)'
Es gibt ein OEIRS mit v = XO.
(ii) ,
bzw.
Zum Beweis von (3) genügt es daher zu zeigen, daß
(iii)
w:=
X(XTDXrXTDy
ebenfalls die Bedingungen (i)' und (ii) , erfüllt, d.h. zu zeigen ist:
(iv)
Es gibt ein 0' E IRS mit w = XO'.
Beweise zu: Skalarprodukte und orthogonale Projektionen
30.8.11
B SP-4
= XTDw.
(v)
XTDy
ad (iv):
Gilt nach Definition von w für () = (XTDXrXTDy.
ad(v):
Nach (ii) , und (i)' gilt
(vi)
XTDy
= XTDv = XTDX()
und somit
XTDw = XTDX(XTDXrXTDy
= XTDX(XTDX)-XTDX()
nach (iii)
nach (vi)
= XTDX()
nach (vi)
= XTDy,
D
Beweis von
(4)
(Idempotenz)
Dies folgt sofort aus ~u = u für jedes uE.At.
Beweis von
(5)
bzw.
Für ein beliebiges X mit Rang X = Dim.At gilt:
[~lT = DX[XTDXrl X T
nach (3)
DX[XTDXrl XTDD- 1
D. pD. D- 1
":At
nach (3).
D
Beweise zu: Skalarprodukte und orthogonale Projektionen
30.8.11
B SP-5
Beweis von
(6)
. [DT/2j-l _ P T ,/ 2
D T/2 . pD
.At
- D / [.Atl
ist symmetrisch .
Die Gleichung in (6) folgt aus (1). Und P DT/2 [.Atl ist symmetrisch, weil orthogonale
Projektionen Pd (bzgl. des Standard-Skalarproduktes) auf beliebige Unterräume d
stets symmetrisch sind (dies folgt z.B. aus der zweiten Gleichheit in (3) für D = 11).
D
Beweis von
(7)
IIP~ull~
(8)
IIP~ull~
uTDP~u
11
T2
2
P DT/2[.Atl D / u 11
f"ur uE IRJ
(7) ergibt sich aus
IIP~ull~
uT[p~jT.D.P~u
u T D·P D .p D u
.At .At
nach (5)
uTD.P~u
nach (4).
Und (8) erhält man wie folgt:
IIP~ull~
11
11
. D T/ 2 u 11 2
DT/2[.Atl
D
T2
2
P DT/2[.Atl· D / u 11
[D T/ 2j-l P
nach (1)
nach 1 (4)
D
Beweis von
Für beliebiges vE IR] gilt
v E .At~D
{}
(u, v)D = (u,Dv) = 0
{}
Dv E.At~
für alle u E .At
D
Beweise zu: Skalarprodukte und orthogonale Projektionen
30.8.11
B SP- 6
Beweis von
(11)
d.h. y
Zu zeigen ist
d.h. nach 1 (5), angewandt auf.At
~
D,
(i)
bzw.
(ii)
(i) folgt aus 1 (5) angewandt auf.At, und (ii) ergibt sich aus ~ y E.At
D
Beweis von
(12)
Multiplikation von (11) mit ~ liefert
pD. pD
.At.At
pD
.At
+
+
pD. pD
.At.At ~ D
pD.pD
.At.At ~ D
nach (4)
und hieraus folgt (12).
D
Beweis von
(13)
Es ist
nach (10)
nach (2)
nach (5).
D
Beweise zu: Skalarprodukte und orthogonale Projektionen
30.8.11
B SP-7
Beweis von
(14)
pD. pD =
JtC JV
":At
JV
D
D
~.~.
~YEJtCJV
Für beliebiges y E IRJ gilt
D
~y.
und somit
Also folgt:
(i)
Einsetzen von
pJ
D-1 [ ~lTD,
nach (5)
in (i) liefert
D-1 [pJlT[~lTD = D-l[~lTD
und somit
[pJlT[~lT
=
[~lT
Transponieren hiervon liefert
(ii)
und zusammen mit (i) ist alles gezeigt.
D
Beweise zu: Skalarprodukte und orthogonale Projektionen
30.8.11
B SP- 8
Beweise von
(15)
für jedes cE IR, c> O.
~n ----t ~
(16)
Für eine Matrix X, deren Spalten eine Basis von .At bilden, gilt nach (3)
~D = X[X T cDXr 1 X T cD = X[XTDXr1XTD = ~
~n = X[XTDnXr1XTDn ----tX[X T DXr1 X T D = ~.
D
Beweise von
(17)
Spur(~)
(18)
.At..l D JV
ad (17):
Betrachte eine Jx5-Matrix B
Dim.At.
D
D
D
~+JV= ~ +~
= (bl' ... ,b5 ), deren Spalten b1, ... , b5 EIRJ
eine D-Orthonormal-Basis von .At bilden, wobei 5 = Dirn .At ist. Dann gilt
(i)
B T DB = 115,
und
pD_ BBTD
.At-
Also
D
Spur(~ ) =
vgl. (3).
J
2:= (BB
. 1
J=
J
=
5
T
D) ..
JJ
J
2:= 2:= 2:=
5
b. b. d .. =
j =1 s=1 i =1 JS zs zJ
J
J
2:= 2:= 2:=
b. b. d ..
s=1 j =1 i =1 JS zs ZJ
5
= 2:= Ilbsll~.
s=1
Wegen
IlbS II~= 1 für alle s= 1, ... ,5 folgt also Spur(P.At) = S.
ad (18):
Für y E IR! gibt es u E .At und v E JV; sodaß
D
~+JVy = u+v.
E fIt
pD
":At y
Analog ist
~ Y = v und somit
sog
-
(14)
pD (pD
)
":At ":At + JVY
u,
für alle y,
d.h. (18) gilt.
D
Beweise zu: Skalarprodukte und orthogonale Projektionen
30.8.11
B SP- 9
Beweise zu:
Projektionen und Exponentialfunktion
3.
Beweise von
Theorem: Sei D = Diag{ cl} mit cl E (0,00)1 gegeben und vft C IRI sei ein linearer Teilraum mit JV
vft~ D.
l
Dann gibt es zu jedem u E (0,00
und v E JV genau ein
I
y = H(u, v) E IR mit
(i)
(ii)
Damit gibt es eine Funktion H: (0 , (0) Ix JV
-----+
IRI die implizit definiert ist durch
I
Die Funktion H ist surjektiv) weil für jedes y E IR gilt
(a)
H( exp(y), P~y) = y.
Weiter ist H differenzierbar mit stetigen partiellen Ableitungen und für diese gelten
(c)
(Identität auf JV).
Zusatz: Die Bedingungen (i) und (ii) zusammen sind äquivalent dazu) daß
Maximalstelle der streng konkaven Funktion
(iii)
r, = y- v
die
e: vft -----+ IR ist mit
e("l) = ~i d·(TJ·u.
- exp(v·+TJ·))
.
Z
Z Z
Z
Z
Wir führen das Problem auf die Existenz und Eindeutigkeit der Maximum-Likelihood-Schätzung für log-lineare Poisson-Modelle (mit Gewichten) zurück und verwenden dabei Resultate aus dem Skript G. Osius 1998, Lineare Modelle in der Statistik, Teil II (Generalisierte Lineare Modelle), Teil III (Modelle für diskrete Daten) das
wir hier mit LM-Skript 11 bzw. III abkürzen.
Die Bedingungen (i) und (ii) lassen sich äquivalent formulieren als
(i) I
P~(exp(y) - u) = 0
bzw.
D( exp(y) - u) ~ vft
(ii)
y-vEvft
bzw.
yEv+vft
Setzen wir
Beweise zu: Skalarprodukte und orthogonale Projektionen
(iii)
r, =
also
y- v,
30.8.11
B SP-lO
y=v+r,
so bleibt zu zu zeigen, daß es genau ein "I E vft gibt mit
(iv)
D (exp(v +
r,) -
u) ~ .At.
Für die positiv-definite Diagonalmatrix
(v)
E(v) = Diag{ exp(v)}
(vi)
E(v) . exp(r,) = (exp(v.) . exp(r,.)). = exp(v + "I).
folgt
z
z z
Setzen wir noch
(vii)
E-\v).u
z(u, v)
=
(exp(-v.)z .U.).E
(O,ool
zz
= Diag(u)· exp(-v)
so läßt sich (iv) äquivalent schreiben als
(iv)'
D· E(v)· (exp(r,) - z(u, v)) ~ .At.
Mit der Diagonalmatrix
(viii)
W(v) = D· E(v) = Diag{w(v)},
w(v) = D· exp(v) =
mit
(d z.. exp(v.)).
E (O,ool
z z
ergibt sich als weitere Äquivalenz von (iv)'
(iv) "
(exp( r,)
-
z( u, v)) ~W(v) vft
p~(v) (exp(r,) - z(u, v)) = 0
bzw.
bzw.
P~(v) exp(r,) = P~(v) z(u, v) .
Dies entspricht der Normalengleichung für die Maximum-Likelihood-Schätzung eines log-linearen Poisson-Modells mit dem Modellraum vft (für den log-Erwartungsvektor "I = log Jl), dem Gewichtsvektor w> 0 und der "Beobachtung" z(u, v) > 0
(vgl. LM-Skript III, 2.3). Insbesondere ist das gesuchte r, E vft die (eindeutig) bestimmte Maximalstelle
mit
r,
des (streng konkaven) log-Likelihood-Kerns
e: vft--dR
Beweise zu: Skalarprodukte und orthogonale Projektionen
30.8.11
B SP-11
~ w. (71 . z .( v) - exp( 71 .))
i
Z
Z Z
Z
(ix)
~ d.· exp(v . ) (71 . u . exp(- v .) - exp(71 .))
i Z
Z
zz
Z
Z
~ d. (71 . u. - exp( v . + 71 .)).
i Z Z Z
Z
Z
Damit ist die Eindeutigkeit von
~
gezeigt, und die Existenz von
~
ergibt sich wegen
z(u, v) > 0 aus dem entsprechenden Existenzsatz für den Schätzer (vgl. LM-Skript II,
2.6.2 Existenzsatz 1 und 2.6.5). Unter Verwendung der Schätzfunktion ~(-,-) für t'( -)
ergibt sich dann
(x)
~ = ~(z(u, v), w(v)) = ~(Diag-l{exp(v)}. u, D· exp(v))
und das gesuchte y ist
(xi)
y = H(u,v)
v
+ ~(z(u, v), w(v))
v
+ ~(Diag-l{exp(v)}. u, D· exp(v))
Die Schätzfunktion ~(z, w) ist für z, w> 0 differenzierbar mit stetigen partiellen
Ableitungen vgl. LM-Skript 2.7.1 (9), (4) und 2.7 (22) (mit identischer Varianzfunktion)
(xii)
mit
(xiii)
b(z, w) = Diag{ w· exp(~(z, w))},
(xiv)
D2~(z,w) = Dl~(z,w).Diag{[z-exp(~(z,w))l/w}.
Folglich ist auch H differenzierbar mit stetigen partiellen Ableitungen, und Differenzieren von (i)H nach u bzw. von (ii)H nach v liefert (b) bzw. (c).
(a) ergibt sich daraus, daß y für u = exp(y) und v = P~y die Bedingungen (i) und
(ii) erfüllt.
Obwohl das Theorem jetzt schon bewiesen ist, wollen wir für die partiellen Ableitungen von H noch eine explizite Darstellung angeben. Partielles Differenzieren
von (xi) ergibt
(xv)
D1 H(u, v)
(xvi)
D2 H(u, v)
= I
D1 ~(z(u, v), w(v)) . D1z(u, v),
+ D1~(z( u, v), w( v)) . D2z( u, v) + D2~( z( u, v), w( v)) . D w( v)
.
Beweise zu: Skalarprodukte und orthogonale Projektionen
30.8.11
B SP -12
mit der lxI-Matrix I, die die Einbettung J'V-----+ IRJ darstellt. Nun ist
(xvii)
exp[r](z(u, v), w(v))] = exp[H(u,v)-v]
(xviii)
b(z(u, v), w(v))
Diag{ w(v) . exp(r](z(u, v), w(v)))}
Diag{ D . exp(v) . exp(H(u, v) -v)}
Diag{ D· exp(H(u, v)}
D· Diag{ exp(H(u, v)}
D(u, v)
und eingesetzt in (xii) ergibt sich
(xix)
D1r](z(u,v),w(v)) = Pj(u,v).Diag-1{exp[H(u,v)-v]}
Mit den Ableitungen
(xx)
D z(u, v)
1
E-\v) = Diag-1{exp(v)}
D2 z(u, v) = - Diag(u) . Diag{ exp(-v)} = - Diag(u) . Diag -l{ exp(v)}
(xxi)
D w(v) = D· Diag {exp(v)} = D· E(v)
erhält man weiter
Beweise zu: Skalarprodukte und orthogonale Projektionen
(xxii)
D H(u, v)
1
30.8.11
B SP -13
Pj(u,v). Diag-1{exp[H(u, v) -v]}. Diag-1{exp(v)}
= Pj(u, v) . Diag-1{exp[H(u, v)]}
(xxiii)
D1r7( z(u, v), w(v)) . D2z(u, v)
= - Pj(u, v) . Diag-1{exp[H(u, v) -v]}. Diag(u) . Diag -l{ exp(v)}
= - Pj(u,v). Diag-1{exp[H(u, v)]}. Diag(u)
(xxiv)
D2r7(z(u, v), w(v)) . Dw(v)
= - Pj(u, v) . Diag-1{exp[H(u, v) -v]}. Diag(u) . Diag -l{ exp(v)}
D1r7(z(u, v), w(v)) . Diag{[z(u, v) - exp(H(u, v) - v)] /w}. Dw(v)
D1H(u, v) . [D1z(v)r1 . Diag{[z(u, v) - exp(H(u, v) - v)] /w}. Dw(v)
D1H(u, v) . E(v) . Diag{[z(u, v) - exp(H(u, v) - v)] /w}. D· E(v)
D1H(u, v) . E 2(v) . Diag{[z(u, v) - exp(H(u, v) - v)] /w}. D ,
wobei im letzten Schritt die Kommutativität der Matrizenmultiplikation für Diagonalmatrizen verwendet wurde. Damit ergibt sich schließlich
(xxv)
D2 H(u, v) =
I - Pj(u,v). Diag-1{exp[H(u, v)]}. Diag(u)
+ D1H(u, v) . Dial(exp(v)) . Diag{[z(u, v) -
exp(H(u, v) - v)] /w} . D.
D
Beweise von
l
Korollar: Sei D = Diag{ cl} mit cl E (0,00
raum mit JV
gegeben und vft C IR! sei ein linearer Teil-
vft~ D. Dann ist die folgende Abbildung bijektiv
F = ((P~ 0 exp), P~) :IR
-----+
P~[(O,oo/] x JV
y
r------+
F(y) = (P~ exp(y) , P~y) .
1
Zu jedem ZEP~[(O,oo/] gibt es ein UE(O,oo/, sodaß z=P~u. Und nach dem
Theorem gibt es zu jedem v E JV ein y E IR! mit
also
F(y) = (z, v).
Beweise zu: Skalarprodukte und orthogonale Projektionen
30.8.11
B SP -14
Damit ist F surjektiv und wir zeigen jetzt die Injektivität. Aus F(y1) = F(y
D
D
Pc4 exp(Y1) = Pc4 exp(y 2)'
D
J folgt
D
PJV Y 1 = PJVY 2 =:
V
Für u = exp(y 2) erfüllen sowohl Y1 als auch y 2 die Bedingungen (i) und (ii) des
Theorems und somit folgt y 1 = Y2. Folglich ist F auch injektiv.
D
Beweise zu: Skalarprodukte und orthogonale Projektionen
30.8.11
B SP -14
Damit ist F surjektiv und wir zeigen jetzt die Injektivität. Aus F(y1) = F(y
D
D
Pc4 exp(Y1) = Pc4 exp(y 2)'
D
J folgt
D
PJV Y 1 = PJVY 2 =:
V
Für u = exp(y 2) erfüllen sowohl Y1 als auch y 2 die Bedingungen (i) und (ii) des
Theorems und somit folgt y 1 = Y2. Folglich ist F auch injektiv.
D
G. Osius: Generalisierte Inverse einer Matrix
GI-l
31.5.06
GI Generalisierte Inverse einer Matrix
Gerhard Osius
Es sei A eine Ixl-Matrix. Eine lxI-Matrix A- heißt eine generalisierte Inverse
(kurz: g-Inverse) von A, falls gilt
(G I)
A . A- . A = A.
Und eine lxI-Matrix A + heißt eine Moore-Penrose-Inverse (kurz: MP-Inverse) oder
Pseudo-Inverse von A, falls die folgenden 4 Bedingungen gelten
(MP1)
A . A +. A
(MP2)
A+ .A . A+ = A+
(d.h. A ist g-Inverse von A +)
(MP3)
A . A+
ist symmetrisch:
A·A+=A+T·AT !
(MP4)
A +. A
ist symmetrisch:
(d.h. A + ist g-Inverse von A)!
= A
!
Diese Bedingungen lassen sich unter Verwendung orthogonaler Projektionen interpretieren. Die beiden Bedingungen (MP1) und (MP3) zusammen sind äquivalent
zu
(MP1,3) A A + ist die orthogonale Projektion Pc4(A) auf den Spaltenraum
...4(A) = Bild A
c
IRf von A.
Analog sind beide Bedingungen (MP2) und (MP4) zusammen äquivalent zu
(MP2,4) A + A ist die orthogonale Projektion Pc4(A +) auf den Spaltenraum
...4(A +) = Bild A + c IR] von A +.
Wenn (MP1), (MP2) und (MP3) gelten, so ist (MP4) zu der folgenden Verschärfung äquivalent
(MP 4)*
A +A ist die orthogonale Projektion Pc4(A T) auf den Spaltenraum
...4(AT ) = Bild AT C IR] von AT.
Die Existenz- und Eindeutigkeitsfrage einer MP-Inversen klärt das folgende
Theorem: Zu jeder Matrix A gibt es genau eine Moore-Penrose-Inverse A +.
Der Nachweis des Theorems verwendet bereits einige der folgenden Eigenschaften
G. Osius: Generalisierte Inverse einer Matrix
A++ = A.
(1)
A ist die MP-Inverse von A +:
(2)
Für invertierbares A gilt:
(3)
Falls A vollen Zeilenrang hat, d.h. Rang(A) = I, so gilt:
(b)
(4)
(5)
AA+=II
GI- 2
31.5.06
d.h. A + ist eine Rechts-Inverse von A.
I'
Falls A vollen Spaltenrang hat, d.h. Rang(A) = J, so gilt:
(b)
d.h. A + ist eine Links-Inverse von A.
Für die Nullmatrix gilt:
0+ =
o.
(6)
(7)
Asymmetrisch
A + symmetrisch,
(8)
A positiv-semidefinit
A + positiv-semidefinit .
(9)
(cA)+ = c-1 A +
(10)
·· a EIst:
IR I .
Fur
A A + = A +A .
für jedes cE IR mit c :;=
(Diag {a})+ =
Diag { a +}
a:
-1
= {
~i
o.
wobei
falls ai :;= 0 }.
falls a. = 0
z
Für eine Folge A quadratischer IxI- Matrizen mit (beliebigen) g- Inversen A - gilt
n
n
(11)
lim A = A,
n---+oo
n
A ist invertierbar
Insbesondere ist die Moore-Penrose-Inverse stetig im Bereich der invertierbaren
Matrizen. Auf die Invertierbarkeit kann nicht verzichtet werden, wie das folgende
Beispiel zeigt.. Für reelle Zahlen (aufgefaßt als lxI-Matrizen) a = 1.. -----+ a = 0 folgt
n n
a + = n -----+ 00 :;= 0 = a + und somit ist die Moore-Penrose-Inverse im Punkt a = 0
n
nicht stetig.
Beweise: Generalisierte Inverse einer Matrix
28.7.06
B GI-l
Beweise zu:
Generalisierte In verse einer Matrix
Beweis der Äquivalenz (MP1) & (MP3) <=> (MP1,3)
(MP1,3) A A + ist die orthogonale Projektion Pc4(A) auf den Spaltenraum
...4(A) = Bild A
ad
c IRf von A.
,;~":
P = AA + ist nach (MP3) symmetrisch und wegen
AA +AA = AA +,
vgl. (MPl)
auch idempotent. Folglich ist P die orthogonale Projektion auf seinem Spaltenraum ...4(P) = Bild P. Wegen P = AA + ist
Bild P
c
Bild A
und aus (MP1) folgt
Bild A
c
Bild AA +
Bild P.
Insgesamt ist also
...4(A) = Bild A
Bild P
...4(P)
und (MP1,3) ist gezeigt.
ad ,,<;:=.":
Die Projektion P = AA + ist symmetrisch, d.h. (MP3) gilt.
Für jedes x E IR] ist Ax E ...4(A) und somit gilt
PAx= Ax
für alle x.
Hieraus folgt PA = A, d.h. (MP1) gilt.
D
Beweise: Generalisierte Inverse einer Matrix
28.7.06
B GI- 2
Beweis der Äquivalenz (MP2) & (MP4) <=> (MP2,4)
(MP2,4) A + A ist die orthogonale Projektion Pc4(A +) auf den Spaltenraum
...4(A +) = Bild A + c IR] von A +.
Der Beweis ergibt sich aus dem von ,,(MPl)&(MP3)<:>(MPl,3)" durch Vertauschen
von A mit A +.
D
Beweis der Äquivalenz (MP4) <=> (MP4)* unter (MPl-3)
(MP 4)* A +A ist die orthogonale Projektion Pc4(A T) auf den Spaltenraum
...4(AT ) = Bild AT C IR] von AT.
Da (MP4)* eine Verschärfung von (MP4) ist, genügt es die Implikation ,,::::}" zu zeigen, also (MP4)* aus (MPl-4) herzuleiten. Nach (MP2,4) ist
die orthogonale Projektion auf
(ii)
Bild A + = Bild P ,
und zu zeigen bleibt nur
(iii)
Bild AT = Bild P.
Aus (i) folgt zunächst
Bild P
c
Bild AT,
und aus
vgl. (MPl)
ergibt sich
Bild AT
c
Bild P.
D
Beweise: Generalisierte Inverse einer Matrix
BGI- 3
28.7.06
Beweis von
Theorem: Zu jeder Matrix A gibt es genau eine Moore-Penrose-Inverse A +.
Eindeutigkeit:
Ai und
At
(i)
seien Moore-Penrose-Inversen von A. Dann gilt
AA} =
Pc4(A)
z
für i = 1,2
vgl.. (MP1,3)
für i = 1,2
vgl.. (MP4)*
und somit
(ii)
AAt·
AA+
1
Analog folgt
(iii)
A}A
z
Pc4(A T )
A+A
At A.
und somit
(iv)
1
Damit ergibt sich
A+
1
A+ AA+
vgl. (MP2)
A+ AA+
vgl. (iv)
A+ AA+
vgl. (ii)
A+
vgl. (MP2).
1
2
2
1
1
2
2
D
Existenz unter Verwendung von (3) und (4):
Ist K = Rang A, so gibt es eine IxK-Matrix B und eine KxJ-Matric C mit
(*)
A=BC
,
Rang B = Rang C = K.
Obwohl dies aus der linearen Algebra bekannt sein sollte, geben wir hierfür unten
noch einen Beweis an.
Weil B+ = (B TBr1 B T eine Linksinverse von B ist, und C+ = C T(CC T)-l eme
Rechtsinverse von C ist, gilt
(i)
Beweise: Generalisierte Inverse einer Matrix
BGI-4
28.7.06
Aus den folgenden Eigenschaften ergibt sich nun, daß C+B+ eine MP-Inverse von
A=BC ist:
(B C)(C+B+)(B C)
B (CC+)(B+B) C
BC
vgl. (i),
(C+B+)(B C)(C+B+)
C+(B+B) (CC+)B+
C+B+
vgl. (i),
(BC)(C+B+)
B(CC+)B+
BB+
ist symmetrisch
vgl. (4),
(C+B+)(BC)
C+(B+B) C
C+C
ist symmetrisch
vgl. (3).
D
Beweis von (*):
Bezeichnet .At = .At(A) den Spaltenraum von A, und ist
(i)
K:= Dim.At = Rang A,
so gibt es eine IxK- Matrix B, deren Spalten eine Orthonormal-Basis von .At sind.
Daher ist
(ii)
und die orthogonale Projektion auf .At hat die Gestalt
(iii)
T
vgl. z.B. Exkurs SP 2.
Pc4 = BB ,
Da Pc4 auf .At die Identität repräsentiert, folgt
(iv)
für alle x,
Damit ist
(v)
A=Pc4 A=BBTA=BC
(vi)
C= BTA.
mit
Hieraus ergibt sich
(vii)
Rang A = Rang BC
< Rang C = Rang B TA < Rang A
und somit ist
(ix)
K = Rang A = Rang C .
D
Beweise: Generalisierte Inverse einer Matrix
28.7.06
B GI- 5
Beweis von
(1 )
A ist die MP-Inverse von A +:
A++ = A.
Die Bedingungen (MPl) - (MP4) sind "symmetrisch" in A und A +, d.h. durch Vertauschen von A mit A + gehen (MPl) bzw. (MP3) in (MP2) bzw. (MP4) über. Also
erfüllt A die definierenden Gleichungen für A ++.
D
Beweis von
(2 )
Für invertierbares A gilt:
Für invertierbares A erfüllt A + = A -1 die Bedingungen (MPl) - (MP4) trivialerwelse.
D
Beweis von
(3)
Falls A vollen Zeilenrang hat, d.h. Rang(A) = I, so gilt:
(b)
AA+=l1
I'
d.h. A + ist eine Rechts-Inverse von A.
Betrachtet man (a) als eine Definition von A + so folgt (b) sofort, und zu zeigen
bleiben die Bedingungen (MPl) - (MP4). Wegen (b) gelten (MPl) - (MP3) trivialerweise, und (MP 4) folgt aus A +A = A(A TA)-l AT.
D
Beweis von
(4)
Falls A vollen Spaltenrang hat, d.h. Rang(A)= J, so gilt:
(b)
d.h. A + ist eine Links-Inverse von A.
Betrachtet man (a) als eine Definition von A +, so folgt (b) sofort und zu zeigen
bleiben die Bedingungen (MPl) - (MP4). Wegen (b) gelten (MPl), (MP2), (MP4) trivialerweise, und (MP3) folgt aus AA + = A(AAT)-l AT.
D
Beweise: Generalisierte Inverse einer Matrix
BGI- 6
28.7.06
Beweis von
(5)
0+ = o.
Für die Nullmatrix gilt:
A + = 0 erfüllt die Bedingungen (MPI - (MP4) für A =
o.
D
Beweis von
(6)
A +T = A T+.
Transponieren von (MPl), (MP2) liefert
(MPl)T
AT. A +T. AT = AT,
(MP2)T
A+ T . AT. A+ T = A+ T,
und (MP3), (MP4) lassen sich schreiben als
(MP3)
A +T . AT ist symmetrisch,
(MP4)
AT. A +T ist symmetrisch.
Also erfüllt A +T die definierenden Gleichungen für die MP-Inverse von AT.
D
Beweis von
(7)
Asymmetrisch
::::}
A + symmetrisch,
(8)
A positiv-semidefinit
::::}
A + positiv-semidefinit .
ad (7):
(7) folgt direkt aus (6) und (MP3).
ad (8):
Nach (7) ist A + symmetrisch und für beliebiges tE IR! gilt nach (MP2)
tTA+t = tTA+ AA+t = (A+t)TA(A+t)
> o.
A A + = A +A .
D
Beweise: Generalisierte Inverse einer Matrix
BGI-7
28.7.06
Beweis von
(9)
für jedes cE IR mit c :;=
o.
Zu zeigen ist, daß c-1 A + die definierenden Gleichungen für die MP-Inverse von cA
erfüllt, und diese ergeben sich wie folgt
(i)
cA· c-1 A +.cA = c (AA TA) = cA,
vgl. (MP 1)
(ii)
c-1 A + . cA· c-1 A + = c-1 (A +AA +) = c-1 A +,
vgl (MP 2)
(iii)
cA· c-1 A + = AA + ist symmetrisch,
vgl. (MP 3)
(iv)
c-1 A + . cA = A +A ist symmetrisch,
vgl. (MP 4).
D
Beweis von
·· a EIst:
IR!·
P ur
(10)
(Diag {a})+ =
Diag { a +}
a:
wobei
-1
= {
~i
falls a i :;= 0 }.
falls a. = 0
z
Zu zeigen ist, daß Diag{ a +} die Bedingungen (MP1-4) erfüllt.
(MP1-2) folgen aus
a.a}- a. = a.,
z z z
für alle i.
z
Und (MP3-4) gelten, weil Produkte von (quadratischen) Diagonalmatrizen wieder
solche und somit auch symmetrisch sind.
D
Beweis von
(11)
A ist invertierbar
lim A n = A,
n---+oo
Wegen det(A
n
)
-----t
det(A)
:;=
0 gibt es ein n so daß für k > n gilt:
o
d.h.
Da die Matrixinversion in A stetig ist, folgt
k > n ' und hieraus ergibt sich die Behauptung.
O
o
A ist invertierbar.
k
Ai: = Ai:1
-----t
A -1 für die Teilfolge
D
G. Osius: Multiple Tests und Konfidenzbereiche
30.7.05
MTK -1
MTK Multiple Tests und Konfidenzbereiche
Gerhard Osius
1.
Simultane Tests
Bei vielen statistischen Analysen werden mehrere Tests durchgeführt. So ist z.B. bei
einem Modell mit Parametervektor () von Interesse, welche Parameterkomponenten
von
0
verschieden
sind,
und
hierzu
werden
Nullhypothesen
der
Form
HOT: () = 0 gegen ihre Alternative H T: () :;= 0 für verschiedene r = 1, ..., R getestet.
r
r
Zur Analyse dieser Situation betrachten wir allgemein R > 2 einzelne Testprobleme
einer Nullhypothese H~ gegen eine Alternative H T (die typischerweise die Negation
der Nullhypothese ist) für r = 1, ... ,R. Ferner sei für jedes r = 1, ... ,R eine Teststatistik T , ein Signifikanzbereich S und ein Testniveau a
r
r
r
gegeben, so daß für den
Einzeltest gilt
(1)
Ablehnung von HoT {} T ES .
r
r
(2)
Für jede Auswahl g'( C {l, ... ,R} können wir die Kombination aller Nullhypothesen
H~ mit rE g'( betrachten
(3)
Hi:: Für alle rE g'( gilt die Nullhypothese H~,
und diese gegen die Alternative testen
(4)
Hg(: Für mindestens ein rEg'( gilt die Alternative H T .
Es ist naheliegend, die kombinierte Nullhypothese Hr; abzulehnen, falls bei den
Einzeltests H~ für mindestens ein rE g'( abgelehnt wird, d.h.
(5)
Ablehnung von Hg(
{}
Es gibt rEg'( mit T ES .
r
Die Schärfe dieses simultanen Tests ist
(6)
"( g( = P{ Ablehnung von Hg'(} =
p{ T U {TTEST}}
Eg(
und läßt sich durch die Schärfe der Einzeltests
r
G. Osius: Multiple Tests und Konfidenzbereiche
MTK -2
30.7.05
r
(7)
"( = P{ Ablehnung von H } = P{T ES }
r
o
r
r
wegen der Monotonie und Subadditivität von Wahrscheinlichkeitsmaßen wie folgt
abschätzen:
(8)
Unter der kombinierten Nullhypothese Hg( ist "( g( das Fehlerrisiko 1. Art des simultanen Tests und läßt sich nach (2) durch die Summe der Fehlerrisiken 1. Art
der Einzeltests abschätzen
Will man für alle simultanen Tests ein Niveau eYg(
< eY erreichen, so kann man z.B.
alle Einzeltests zum gleichen Niveau eY = ~ durchführen (Bonferroni-Korrektur).
r
Wenn der zusätzliche Informationen über den Zusammenhang der Teststatistiken
Tl' ... ,T für die Einzeltests vorliegen, so läßt sich die Abschätzung (8) eventuell verR
bessern. Insbesondere ergibt sich bei stochastischer Unabhängigkeit der Teststatistiken statt der Abschätzung (8) sogar eine Gleichung:
(10)
2.
falls Tl' ... ,TR stochastisch unabhängig.
Simultane Konfidenzbereiche
Für die Konstruktion simultaner Konfidenzbereiche gelten analoge Überlegungen
2 Parameter er E IRSr
wie für simultane Tests. Hierzu betrachten wir allgemein R>
mit Konfidenzbereichen zur Sicherheit 1- eY , d.h. zufällige Bereiche C E IBSr mit
r
(1)
eY
r
r
=p{er tJ-C}
r
für r = 1, ..., R.
Das kartesiche Produkt dieser Konfidenzbereiche ist dann ein simultaner Konfidenzbereich für den Vektor () = (e , ..., eR) zum simultanen Niveau
l
R
(2)
eY.
szm
=
p{() tJ- r=l
TI Cr }
R
=
p{ r=l
U {e r tJ- cr }} .
Das simultane Niveau läßt sich wieder abschätzen durch
R
(3)
Max{eY l , ..., eYR }
<
eY
sim
<
2:
r=l
eY
r
·
G. Osius: Multiple Tests und Konfidenzbereiche
30.7.05
Um zu erreichen, daß das simultane Niveau a.
szm
nicht überschreitet, kann man z.B. gleiche Niveaus a
MTK -3
einen vorgegebenes Niveau a
r
= ~ wählen (Bonferroni-Kor-
rektur). Wenn der zusätzliche Informationen über den Zusammenhang der Konfi-
denzbereiche Cl' ... ,C der Komponenten vorliegen, so läßt sich die Abschätzung (3)
R
eventuell verbessern.
3.
Sequentielle Tests
Wir betrachten jetzt den Spezialfall, daß die R
> 2 Nullhypothesen
eine aufsteigende
Sequenz bilden, d.h. es gilt
(1)
1
H2O::::}···::::} H0R HO::::}
1
::::}
R
H0
'
(statt der Implikation ,,::::}" kann auch die Inklusion "e" stehen, wenn man die Hypothesen mit den zugehörigen Parametermengen bzw. Modellen identifiziert). Beim
sequentiellen Testproblem will man sich für genau eine sequentielle Hypothese der
Form
(2)
s Hr0 un d nzc. ht H0r- 1
Hr:
entscheiden, wobei r = 1, ..., R und formal
Hg als falsch
(bzw. leere Menge) gesetzt
wird. Man beachte, daß "nicht H~- L, nach (1) äquivalent ist zu "nicht H~ für alle
i<r"
Eine typische Anwendung für (1) ist ein parametrisches Modell mit Parametervektor () = (e l' ..., eR) und den Hypothesen
(3)
H~: er = ... = eR = 0 .
Die zugehörigen sequentiellen Hypothesen (2) lauten
Man beachte, daß diese sequentielle Hypothese wesentlich von der Reihenfolge der
Parameterkomponenten abhängt, die daher bei konkreten Anwendungen sinnvoll
gewählt sein sollte.
Wir gehen wieder davon aus, daß für jedes rein Einzeltest der Nullhypothese H~
gegen ihre Negation (nicht H~) als Alternative gegeben ist durch eine Teststatistik
T , ein Signifikanzbereich S und ein Testniveau a ,so daß gilt
r
r
r
G. Osius: Multiple Tests und Konfidenzbereiche
(5)
Ablehnung von HOT {} T ES .
(6)
Unter H~ gilt:
r
MTK -4
30.7.05
r
P{Tr ESr } <
- ar .
Führt man die Einzeltests aufsteigend für r = 1, 2, ... solange durch, bis erstmals die
Nullhypothese nicht abgelehnt wird, so ergibt sich folgendes Entscheidungskriterium für die
(7)
Aufsteigende sequentielle Testprozedur:
Entscheidung für H;
H~
und
Ablehnung von H5' .... , H~-l
{}
keine Ablehnung von
T t/:. S
{}
r
T. ES. für alle i < r.
und
r
z
z
Bei der aufsteigend sequentiellen Testsprozedur wird im r-ten Schritt die Nullhypothese H~ nur dann noch mit dem Einzeltest überprüft, wenn die vorangegangenen
Einzeltests die Nullhypothesen H~, .... ,H~-l bereits abgelehnt haben. Die zugehörige Schärfe der aufsteigendenden Prozedur im r-ten Schritt ist daher
(8)
"(
iT
= P{ Ablehnung von Hol, .... ,HOT} =
p{ .<n{T.ES.}} ,
Z
T
Z
Z
und läßt sich durch die Schärfe der Einzeltests
(9)
"(. = P{ Ablehnung von H
Z
o}
Z
= P{T.ES.}
Z
Z
wegen der Monotonie von Wahrscheinlichkeitsmaßen nach oben abschätzen:
(10)
"( iT <
Min T.
-.<
Z
Z
T
Im r-ten Schritt der aufsteigenden Prozedur besteht ein Fehler 1. Art darin, die
Nullhypothese H~ und zuvor alle vorangegangenen Nullhypothesen H~, .... ,H~-l
abzulehnen, obwohl irgendeine dieser r Nulhypothesen - und wegen (1) somit auch
HOT - zutrifft. Das zugehörige Fehlerrisiko 1. Art a jr ist daher durch die Schärfe "( jr
unter H~ gegeben und läßt sich nach (10) und (6) durch das Fehlerrisiko 1. Art des
zuletzt durchgeführten Einzeltests abschätzen
(11)
Unter HOT gilt: a
ir
=
'1!
<
'ir -
'1!
< ar .
'r -
Wenn man alle Einzeltests zum gleichen Niveau a = a durchführt, so hat auch die
r
aufsteigend sequentielle Prozedur ein Niveau von höchstens a - und zwar unabhängig davon, nach welchem Schritt r die Prozedur beendet ist. Im Gegensatz zu den
simultanen Tests ist bei der sequentiellen Testprozedur also keine (Bonferroni-)Kor-
G. Osius: Multiple Tests und Konfidenzbereiche
MTK -5
30.7.05
rektur des Niveaus der Einzeltests erforderlich. Dafür muß man sich von vorn herein auf eine feste Sequenz interessierender Hypothesen festlegen.
Bei der bisherigen betrachteten aufsteigenden Testprozedur werden die Einzeltests
aufsteigend für r = 1,2, ... durchgeführt. Wenn man die Einzeltest dagegen absteigend
für r = R, R-1, ... solange durchführt, bis erstmals die Nullhypothese abgelehnt wird,
so ergibt sich folgende
(12)
Absteigende sequentielle Testprozedur:
Entscheidung für H;
{}
Ablehnung von H~-l
keine Ablehnung von
{}
T
r-1
ES
r-1
und
und
H~, .... ,H~
T.dS. für alle i > r.
zv::. z
-
Bei der absteigenden Testsprozedur wird die Nullhypothese H~ nur dann noch mit
dem Einzeltest überprüft, wenn die vorangegangenen Einzeltests die Nullhypothesen H~+\ .... ,H~ nicht abgelehnt haben. Die zugehörige Schärfe der absteigendenden Prozedur ist dann
(13)
"(J-r = P{ Ablehnung von H~ und keine Ablehnung von H~+ , .... , H~ }
1
=P{{T ES}
r
r
n
n i>r{T.\tS.}}
Z
Z
und läßt sich durch die Schärfe des zuletzt durchgeführten Einzeltests nach oben
abschätzen:
Beim Test von H~ in der absteigenden Prozedur besteht ein Fehler 1. Art darin, die
Nullhypothese H~ abzulehnen - und zuvor alle vorher gestesten Nullhypothesen
H~+\ .... ,H~ anzunehmen -, obwohl H~ zutrifft. Das zugehörige Fehlerrisiko 1. Art
unter H r und läßt sich nach (14) durch das Fehlerrisiken 1.
o
J-r
Art des zuletzt durchgeführten Einzeltests abschätzen
ist daher die Schärfe "(
(15)
Unter H r gilt:
o
a
J-r =
'1!
I
a
J-r <
- '1!'r <
- r
.
Wenn man alle Einzeltests zum gleichen Niveau a = a durchführt, so hat auch
r
also auch die absteigende Prozedur ein Niveau von höchstens a - und zwar auch
wieder unabhängig davon, nach welchem Schritt die Prozedur beendet ist.
Beide sequentielle Testprozeduren kommen aber nicht notwendig zum gleichen Ergebnis, d.h zur gleichen sequentiellen Hypothese HS . Bezeichnet r bzw. r den jer
i
J-
G. Osius: Multiple Tests und Konfidenzbereiche
MTK -6
30.7.05
weiligen Index r bei sich die auf- bzw. absteigende Prozedur für HS entscheidet, so
r
wird H für r = r beim Einzeltest nach (12) nicht abgelehnt, und mit (7) folgt, daß
J-
r
dann r nicht kleiner als r j sein kann. Folglich gilt stets
(16)
rj
<
r J- .
-
Andererseits wird H für s = r -1 beim Einzeltest nach (12) abgelehnt und mit (7)
s
folgt r j
:;=
J-
s. Hieraus ergibt sich
(17)
Falls r j und r J- verschieden sind, so gibt es daher Indizes
t = rj
<
s = r -1
J-
<
r=r
J- '
bei denen für die zugehörigen Nullhypothesen
die Einzeltest die mittlere Nullhypothese H~ ablehnen, aber die beiden äußeren Hypothesen H~ und H~ nicht ablehnen. Dies erscheint zwar paradox, läßt sich aber unter den bisherigen sehr allgemeinen Voraussetzungen nicht ausschließen. Lediglich
im Fall R = 2 ergibt sich aus (16) und (17) stets die Gleichheit r j = r
f
Wenn in einer konkreten Situation beide sequentiellen Testprozeduren zu unterschiedlichen Resultaten gelangen, so muß von Fall zu Fall entschieden werden, welches Resultat "plausibler" ist.
G. Osius: Minimale und maximale gewichtete Streuung
10.3.06
MS-1
MS Minimale und maximale gewichtete Streuung
Gerhard Osius
1.
Problemstellung
Für K> 2 Beobachtungen xl' ..., x E IR mit positiven Gewichten w ' ..., w > 0 soll
K
1
K
die gewichtete Streuung
K
(1)
S(x I w) = 2: wk(xk - x)2
k=l
der x-Werte um ihr gewichtetes Mittel
K
_
1 K
mit
(2)
x =
2: wkxk
w+ = 2: w k ·
+k=l
k=l
w
untersucht werden. Hierbei betrachten wir den Gewichtsvektor w = (w l' ..., W K) als
fixiert und wollen S( x I w) bzgl. x minimieren und maximieren. Wegen
(3)
S(xlcw) = c·S(xlw)
fürc>O
können - und wollen wir zunächst auch - die Gewichte normieren durch
(4)
W
+ = 1,
so daß insbesondere w E (0, l)K gilt. Da S(x I w) invariant gegenüber einer Permutation der Indizes ist, setzen wir ohne Einschränkung der Allgemeinheit voraus
(5)
Für konstantes x ist S(x I w) = 0 und deshalb betrachten wir nur noch den Fall
(6)
Spannweite (Range) von x.
Für fixiertes xl und x
K
untersuchen wir S(x I w) jetzt als Funktion der restlichen x-
Werte, d.h. als Funktion in
Im Fall K = 2 ist S(x I w) bei fixiertem xl und x konstant und deshalb wollen wir
2
(8)
K> 3
voraussetzen. Zur Minimierung bzw. Maximierung von S(x I w) führen wir eine lineare Transformation der x-Werte durch
G. Osius: Minimale und maximale gewichtete Streuung
.l(x-x)
r
k
1
(9)
10.3.06
MS-2
bzw.
Dann gilt
(10)
S(x I w) = r 2 . S(u I w),
und statt S(x I w) können wir auch
K
(11)
S(ulw) = ~wk(uk-u)2
k=l
f
k=l
2
wku k -
[
f
k=l
WkU k ] 2
für fixiertes
(12)
als Funktion in
(13)
minimieren bzw. maximieren.
2.
Minimierung
Für die Minimierung von S(u I w) bzgl. u
geben wir zwei verschiedene Wege an.
Zunächst ergibt sich folgende Abschätzung - sogar auch für K = 2 -
(1)
S(ulw) > w1(u1-u)2+wK(uK-u)2
w u
1
2
1 (12)
+ wK(1-u)2
(w1 +wK )u 2 - 2wK u +
2
(WI
+wKl[u- Wl:~K] +WK[l- Wl:~K]
WK[l-Wl:~K]
>
wobei bei der ersten und letzten Abschätzung genau dann die Gleichheit gilt, wenn
(2)
u
k
= u
für alle 1 < k < K
und
U
=
W
K.
W +W
1
Definieren wir nun u'
(3)
u'
k
E (0,1)
für 1 < k
< K,
u~ = 0,
K
G. Osius: Minimale und maximale gewichtete Streuung
MS-3
10.3.06
so folgt
WK
li'
W +W
'
1
K
und somit erfüllt u' die Bedingung (1). Also ist u' eine Minimalstelle von S(u w)
1
und das zugehörige Minimum ist
(4)
S (u 'I w ) --
w
w1 K
W +W
1
_
-
(
K
wl +wK ) wKl (
1-w)
Kl
mit
w
K
W +W
wKl =
.
K
1
u' ist auch die einzige Minimalstelle, weil jede ander Minimalstelle u die Bedin-
gung (2) erfüllen muß, was nur für u = u' der Fall ist. Im Fall K = 2 ist S(u w) bei
1
fixiertem u und u konstant gleich dem in (4) angegebenen Wert.
l
2
Wir wollen jetzt die Minimalstelle alternativ unter Verwendung der Ableitungen
bestimmen, wobei wir K> 2 voraussetzen. Nach der zweiten Darstellung in 1 (11) ist
8
-8
S(ulw)
W
(5)
z
82
8 8
(6)
Wz
S(u w)
1
Wk
mit 8 als Kronecker-Symbol. Nun gilt
D S(ulw) = (Dl~S(ulw))l,k=2, ... ,K_l ist negativ-definit,
2
(7)
und somit ist S(u w) streng konkav bzgl. u . Für u' aus (3) gilt
1
(8)
für allel< l < K
u =u'
und es folgt erneut, daß u' die einzige Minimalstelle von S(u w) ist.
1
Insgesamt ist damit - auch für K = 2 - folgendes gezeigt:
und xl < x mit r = x - xl hat die Funktion
K
K
S(x 1 w) bzgl. x_ = (x 2' ... xK _ l ) E [xl' xK ]K-2 genau eine Minimalstelle in
Minimierungssatz: Für festes w
(8)
>0
für 1 < k < K,
mit
_
wKl -
wK
W +W
1
Das zugehörige Minimum in x' mit x~ = xl' xk = xK ist
Zuzsatz: Bei festem w
l
+ wK wird das Minimum (9) maximal bzgl. wKl für
wKl = ~ ,d.h. für w l =wK
.
K
G. Osius: Minimale und maximale gewichtete Streuung
3.
MS-4
10.3.06
Maximierung
Wir wollen jetzt S(u I w) bzgl. u_ maximieren. Da der Wertebereich [0, 1]K-2 von u_
kompakt ist, nimmt S(u I w) sein Maximum an. Allerdings kann die Maximalstelle
nicht in der offenen Menge (0,1)K-2 liegen, weil die Funktion (nach 2.) nur einen kritischen Wert besitzt, der eine Minimalstelle ist. Zur Bestimmung des Maximums betrachten wir erneut die partielle Ableitung aus 1 (5) für
(1)
wdu z-
2:
k
1< l < K
2: wku k]
wkuJ = wdu Z(l-w Z) -
k~Z
wZ(l-w Z)[u Z-u ]
m
(2)
um
Bei festem
= l_lwz
um
wachsend für
k"fz wkuk
ist S(u I w) in
U
mit
als gewichtetem Mittel von
U
z
daher streng fallend für
U
z
um =
m] und streng
E [0, U
zE [um' 1]. Folglich wird S(u I w) maximal für U z=
(uk)k~Z·
°oder
U
z= 1. Da
diese Überlegung für jedes l = 2, ..., K-1 gilt, folgt insgesamt, daß S(u I w) sein Maximum nur in u 2' ..., u K _ l E{O, I} annehmen kann.
Jedes solche u _ E {O, 1}K-2 bzw. das zugehörige u E {O, l}K ist von der Form u mit
1
falls
falls
(3)
kEI }
ktJ-I
für ein I C {I, ..., K -I} mit 1 EI.
Es folgt
(4)
(5)
U1 =
2: wk =
1- w(J)
mit
krfJ
S(uII w) =
~lWkUlk2 [k~lWkUlk
-
r liI
w(J) =
2: wk
kEI
Wk
-
[krI
2
Wk ]
uI(l-uI ) = w(J)[l-w(J)]
~- [w(J)- ~]2.
Die Maximierung von S(u I w) bzgl. u E{O, l}K ist also äquivalent zur Minimierung
von I w(J) - ~ I bzgl. I. Zur Bestimmung des Minimums von I w(J) - ~ I muß man prinzipiell für alle ~-2 verschiedenen Teilmengen I den Wert w(J) berechnen und diejenigen bestimmen, bei denen der Abstand zu ~ minimal ist. Eine explizite Angabe
des Minimums ist aber in Spezialfällen möglich, z.B. bei konstanten Gewichten.
G. Osius: Minimale und maximale gewichtete Streuung
MS-5
10.3.06
Spezialfall: Konstante Gewichte
Bei konstanten Gewichten
(6)
mit
w
+
=1
ist
(7)
= k# 1 .
w(I)
Für gerades Kund 10 = {I, ..., ~} ist w(Io) = ~ und 10 ist auch die einzige Minimal-
stelle von 1w(I) - ~
Damit ist u1 die einzige Maximimalstelle von S( U
o
zugehörigen Maximum
(8)
S( U I
o
1
k)
I·
=
~
k) mit dem
1
(für gerades K).
Für ungerades Kund 11 = {I, ..., K~1}, 12 = {I, ..., Kt1 } ist
und 11 und 11 sind die beiden einzigen Minimalstelle von 1w(I) - ~ I· Damit sind u1
1
und u1 die einzigen Maximalstellen von S( U
mit dem (gleichen) Maximum
1
2
(9)
k)
(für ungerades K).
D
G. Osius: Minimale und maximale gewichtete Streuung
10.3.06
MS-6
Insgesamt haben wir daher gezeigt
Maximierungssatz: Für festes
Funktion S(x
w> 0
und xl < x
K
mit r = x - xl nimmt die
K
I w) bzgl. x_ = (x 2' ... xK_ 1) E [xl' xK ]K-2 ihr Maximum auf der Menge
{xl' x }K-2 an. Das Maximum läßt sich dann ermitteln) indem man die für alle
K
verschiedenen Elemente xI E {xl' x }K-2 der Form
K
(10)
falls k EI }
falls k ItI
iK- 2
für ein I C {I, ..., K -I} mit 1 E 1.
den Funktionswert
berechnet und davon das Maximum bestimmt oder (äquivalent) das Minimum von
I w(l) - ~ I bzgl. I bestimmt.
Zusatz für konstante Gewichte: w1 = w 2 = ... = wK = w
Für gerades K besitzt S(x I w) genau eine Maximalstelle xI für 10 = {I, ..., ~} und das
o
zugehörige Maximum ist
(für gerades K).
(12)
Für ungerades K besitzt S(x I w) genau zwei Maximalstellen xI und xI für
1
2
1 = {I, ..., K~l} und 1 = {I, ..., Ki1 } 1 = {I, ..., ~} und das zugehörige Maximum ist
1
0
2
(13)
(für ungerades K).
G. Osius: Minimale und maximale gewichtete Streuung
4.
10.3.06
MS-7
Aquidistante Werte und konstante Gewichte
Neben dem Minumum und dem Maximum von S(x I w) bzw S(u I w) interessiert
O
uns auch der Wert für äquidistantes X bzw. uO, d.h. für
(1)
bzw.
oder explizit
(2)
für 1 < k
bzw.
Für konstante Gewichte
(3)
mit
W
+
=1
ergibt sich dann
K
(4)
U ° = K(l-l)
K
(5)
2
2: w k u k
k=l
K-l
2: (k-1)
k=l
1
= K(K-l)2
=
= K(l-l)
2: k
k=l
= K(l-l)
K
1
2: (k-1)2
= K(K-l)2
k=l
K(~-1)2 ~K(K-1)(2K-1)
-
(~)
1
2
K-l
2: k2
k=l
~~::::~)
und somit
(6)
K
'I\"
02
-02
u wk u k - u
6(K-l) - 4
12(~-1) [2(2K-1) - 3(K-1)]
K+l
12(K-l) .
2K-l
k=l
1
Für beliebige konstante Gewichte
(7)
erhalten wir dann
mit
w =Kw
+
<K
Beweise zu: Minimale und maximale gewichtete Streuung
28.7.06
B MS-l
Beweise zu:
1.
Problemstellung
Beweis von
(10)
2
S(x I w) = r ·S(u I w)
Es ist
x = r 2( u - -)2
U
.
(x k - -)2
k
und somit
D
Beweise zu:
2.
Minimierung
Beweis von
(7)
2
D S(ulw) =
(D Z2k S(U I w))Z,k=2, ... ,K-l ist negativ-definit.
Für beliebiges y_ = (Y 2, ..., YK - 1) setzten wir Y1 = YK = 0 und erhalten
- ~ y~D2S(ulw)y_ =
K-l K-l
2:= 2:=
Z=2k=2
wd8kZ -wJYZYk
K K
2:= 2:=
W
l =1 k=1
K
K
wkYk
2:=
wk (Yk - y)2
k=1
- ~ y~D2S(ulw)y_=O
ist D 2 S(u I w) negativ-definit.
{}
K
+ 2:= 2:=
2:=
k=1
K
Wegen
z [8 kZ - w k] Yz Yk
l=1k=1
wZwkYZYk
> o.
Y1 = ... =YK
D
Beweise zu: Minimale und maximale gewichtete Streuung
B MS-2
28.7.06
Beweis von
(8)
DzS(ulw) =0
Es gilt
DzS(ulw) =0
(i)
u = ... = u = u.
2
K
ad
,;~":
für allel< l < K
{}
u =u'
für alle 1 < l < K
Aus (i) folgt
K
U = 2: w k u k
k=l
WK
-
u
W
vgl. (i), (3).
u =u'
twK
1
ad ,,-{=": Für u = u' wurde bereits (2) gezeigt, und somit gilt auch (i).
D
Beweis von
Minimierungssatz: Für festes w
S(x I w)
>0
und xl < x
mit r = x - xl hat die Funktion
K
K
bzgl. x_ = (x ' ... x _ ) E [xl' x ]K-2 genau eine Minimalstelle in
2
K l
K
(8)
für 1 < k < K,
mit
_
w Kl -
wK
tw .
W
1
K
Das zugehörige Minimum in x' mit x~ = xl' xk = x ist
K
l + wK wird das Minimum (9) maximal bzgl. wKl für
Zuzsatz: Bei festem w
wKl = ~ ,cl.h. für w l =wK
Für w =
(i)
~ w ist W t = 1, und für u aus 1 (9) gilt
+
2
S( x I w) = W t S( x I w) = W t r . S( u I w) ,
vgl. 1 (10).
Nun ist u' mit u~=wKl =wKl für l<k<K die einzige Minimalstelle von S(ulw).
Also ist das zugehörige x' mit x~ = xl + r u ~ die einzige Minimalstelle von S( x I w)
und somit von S(x I w). Das resultierende Minimum ergibt sich mit (i) und (4) zu
W
+r 2 . (w l + wK) wKl (1- wKl )
2
r . (w
l
+ wK) wKl (1- W Kl ),
da wKl = wKl"
Der Zusatz folgt, weil f( x) = x(l- x) ein globales Maximum in x = ~ hat.
D
Beweise zu: Minimale und maximale gewichtete Streuung
28.7.06
BMS-3
Beweise zu:
3.
Maximierung
Beweis von
Maximierungssatz: Für festes
w> 0
und xl < x
K
mit r = x - xl nimmt die
K
Funktion S(x I w) bzgl. x_ = (x ' ... x _ ) E [xl' x ]K-2 ihr Maximum auf der Menge
2
K 1
K
{xl' x }K-2 an. Das Maximum läßt sich dann ermitteln) indem man die für alle iK- 2
K
verschiedenen Elemente xI E {xl' x }K-2 der Form
K
falls k EI }
falls k ItI
(10)
für ein I C {I, ..., K -I} mit 1 E 1.
den Funktionswert
berechnet und davon das Maximum bestimmt oder (äquivalent) das Minimum von
I w(l) - ~ I bzgl. I bestimmt.
Zusatz für konstante Gewichte: w1 = w 2 = ... = wK = w
Für gerades K besitzt S(x I w) genau eine Maximalstelle xI für 10 = {I, ..., ~} und das
o
zugehörige Maximum ist
(für gerades K).
(12)
Für ungerades K besitzt S(x I w) genau zwei Maximalstellen xI und xI für
1
2
1 = {I, ..., K~l} und 1 = {I, ..., Ki1 } 1 = {I, ..., ~} und das zugehörige Maximum ist
2
1
0
(für ungerades K).
(13)
Für w =
(i)
~ w ist w += 1, und für u aus 1 (9) gilt
+
2
S( x I w) = w +S( x I w) = w +r .S( u I w) ,
vgl.
1 (10).
Der Satz ergibt sich aus den Betrachtungen für S(u I w), da obiges xI das zu u geI
D
hörige Argument nach 1 (9) ist. Und der Zusatz folgt, weil dort w + = K w ist.
CPR Cross-Product-Ratios
Gerhard Osius
1.
Der Cross-Produet-Ratio einer 2x2- Tafel
2.
Die Cross-Produet-Ratio-Matrix einer Tafel
G Osius: Der Cross-Produet-Ratio (CPR) einer 2x2-Tafel
1.
CPR 1- 2
2.8.01
Der Cross-Product-Ratio einer 2X2-Tafel
Für eine 2x2-Matrix Jl= (J-Ljk) E (0,00)2X2 mit positiven Komponenten ist der CrossProduet-Ratio (kurz: CPR) oder das Kreuzverhältnis von Jl definiert als
(1)
Die elementaren Eigenschaften des CPR sind:
(2)
Der CPR ist invariant gegenüber Matrix-Transposition:
(3)
Der CPR ist invariant gegenüber Multiplikation von Zeilen und Spalten mit positiven Faktoren Cj' dk > 0:
(4)
Vertauschen der Zeilen oder Spalten invertiert den CPR:
CPR (J1 21 J1 22 ) = 1/ CPR( (J-L
J-L n J-L 12
]k
0
))
= CPR (J1 12 J1 n
J-L 22 J-L 21
).
Eine 2x2-Matrix Il> 0 ist durch ihre Zeilen- und Spaltensummen sowie ihren CPR
bereits eindeutig bestimmt. Genauer gilt:
(5)
Für beliebig vorgegebene "Zeilensummen" z1' z2 E (0,00) und "Spaltensummen"
s1' s2E(0,00) mit z+ =s+ gibt es zu jedem
e>o
genau eine 2x2-Matrix
Jl= (J-Ljk) E (0,00)2X2 mit
(a)
J-L °t = z °
für j = 1, 2 ,
(b)
J-L+k = sk
für k = 1, 2 ,
(c)
]
CPR(Jl) =
]
e.
Diese Matrix Jl ist nach (a) und (b) eindeutig gegeben durch J-L
!Ln = zl s/ s+
falls
e= 1
J-L
falls
e:;= 1,
n =l(J(l-b)
2a
a = 1-e ,
n mit
wobei
2
d=b -4ac.
G Osius: Der Cross-Produet-Ratio (CPR) einer 2x2-Tafel
2.
2.8.01
CPR 1- 3
Die Cross-Product-Ratio-Matrix einer Tafel
Für eine JxK-Matrix Jl= (J-Ljk) E (O,oo/xK mit positiven Komponenten ist die CrossProduet-Ratio-Matrix (kurz: CPR-Matrix) definiert als die JxK-Matrix () = CPR(Jl)
deren Komponenten ()jk gerade die Cross-Produet-Ratios der 2x2-Teiltafeln von Jl
mit den beiden Zeilen 1, j und den beiden Spalten 1, k, d.h. es gilt:
fl n . fl ik
(1)
für alle j, k.
fl1k . flj1
1
....
k
· ...
K
1
@
· ...
@
· ...
fl 1K
J
6Y
· ...
@
· ...
fljK
J
fl
· ...
fl
· ...
fl
J1
Jk
JK
1
k
K
1
1
1
1
J
1
(9
(JjK
J
1
(JJk
(JJK
Tabelle 1: Das markierte Element ()jk der CPR-Matrix () (unten) ist der CPR
der markierten 2x2-Teiltafel der Matrix Jl (oben).
G Osius: Der Cross-Produet-Ratio (CPR) einer 2x2-Tafel
2.8.01
CPR 1- 4
Durch die CPR-Matrix () sind bereits die Cross-Produet-Ratios aller 2x2-Teiltafeln
bestimmt, denn für je zwei beliebige Zeilen i j E {I, ... ,i} und Spalten k, l E {I, ... ,K}
gilt:
(2)
Die erste Zeile und erste Spalte der CPR-Matrix ist konstant =1, d.h.
(3)
()lk =
für alle j, k,
1,
und damit ist die CPR-Matrix bereits durch die (i -l)x(K -l)-Untermatrix
(4)
vollständig bestimmt. Folglich könnte man die CPR-Matrix auch von vornherein
durch die (i-l)x(K -l)-Matrix (4) definieren, aber die hier gewählte Definition mit
der redundanten ersten Zeile und ersten Spalte ist für viele Formulierungen praktischer.
Aus den elemetaren Eigenschaften des CPR einer 2x2-Matrix ergeben sich sofort
die entsprechenden Eigenschaften der CPR-Matrix:
(5)
Die CPR-Matrix von Jl ist invariant gegenüber Transposition von Jl
(6)
Die CPR-Matrix von Jl ist invariant gegenüber Multiplikation von Zeilen und
Spalten der Matrix Jl mit positiven Faktoren Cj' dk > 0:
(7)
Der CPR-Matrix-Operator ist idempotent:
CPR ( CPR (Jl) ) = CPR(Jl) .
Eine ix K- Matrix Il> 0 ist durch ihre Zeilen- und Spaltensummen sowie ihre CPRMatrix bereits eindeutig bestimmt. Genauer gilt:
G Osius: Der Cross-Produet-Ratio (CPR) einer 2x2-Tafel
Theorem: Für beliebig vorgegebene )ßeilensummen 11
S
Z
2.8.01
CPR 1- 5
E (O,oo)J und )ßpaltensummen 11
E (0 ,oo)K mit z + = s+ gibt es zu jeder J x K-Matrix () E (0,00/xK, deren erste Zeile und
Spalte konstant =1 ist (d.h. (3) giltJ) genau eine JxK-Matrix p,E (0 , oo)JxK mit
(b)
= Zj
jt
J.L +k = sk
(c)
CPR(p,) = () .
(a)
J.L
für j = 1, , J,
für k = 1, , K,
Einen elementaren Beweis hierfür findet man in R. Sinkhorn (Diagonal equivalence
to matrices with prescribed row and column sums. Amer. Math. Mon. 74, 1967,
402-405). Das Theorem ergibt sich auch aus Resultaten von S. Haberman (The Analysis Of Frequency Data University of Chicago Press 1974, Theorem 2.6) über die Exi-
stenz von Maximum-Likehood-Schätzungen in bedingten Poisson-Modelle.
Beweise: Der Cross-Produet-Ratio (CPR) einer 2x2-Tafel
12.8.05
CPR B 1-1
Beweise zu:
1.
Der Cross-Product-Ratio einer 2X2-Tafel
ad (2)-(4): Die Behauptungen ergeben sich dirket aus der Definition des CPR.
ad (5):
Wenn die Zeilen- und Spaltensummen von Jl durch (a) und (b) vorgegeben sind, so
ist die Matrix Jl bereits durch Jl
n eindeutig bestimmt, weil
Wegen Jljk> 0 muß zusätzlich gelten
(ii)
A := max { 0 , (z1 - s2)}
<
!Ln
< E: =
min { z1' s1} .
Unter (a) und (b) lautet daher die Bedingung (c)
(iii)
Zu zeigen ist also, daß (iii) genau eine Lösung !Ln im Bereich (ii) besitzt, aus der
sich dann mit (i) die gesuchte Matrix Jl ergibt. Definieren wir das Polynom 2. Grades durch
so ist (iii) äquivalent zu f(!L
n ) = o.
Zu zeigen bleibt also, daß die Funktion f im offe-
nen Intervall (A ,E) genau eine Nullstelle !Ln besitzt. Nun ist
f(O)
- ß·z ·s
f(z1 - s2)
- ß . s2 . (s +- z1) = - ß ·s2 . (z +- z1)
f(z1)
z1· s2
f(s1)
s1·(s+ -z1) = s1·(z+ -z1) = s1· z2
und somit auch f(A)
1
1
< 0 und f(E) > o.
<
-ß·s 2 ·z2 <
>
>
0,
0,
0,
0,
Folglich hat die Funktion f im Intervall (A ,E)
zunächst mindestens eine Nullstelle, und weil es sich um ein Polynom 2. Grades handelt, hat sie auch genau eine Nullstelle im Intervall (A ,E). Zur expliziten Bestim-
Beweise: Der Cross-Produet-Ratio (CPR) einer 2x2-Tafel
12.8.05
CPR B 1- 2
mung dieser Nullstelle ,u11 E (A ,E) schreiben wir f in der Form
f( x) = a x 2 + bx
a = 1-e
+C
mit
,
C
= - e zlsl= (a-1) zlsr
s+ -sl-zl +e(zl +sl)
= s+ -a(zj+sk)·
e
Für = 1 bzw. a = 0 ist f eine lineare Funktion und die Nullstelle lautet
(iv)
für
e= 1 bzw. a = 0
Für e:;= 1 bzw. a:;= 0 hat f die beiden Nullstellen
x
1,2
=-l(b+va)
2a-
d = b2 - 4ac.
mit
Für a> 0 ist max { xl' x 2 } und für a< 0 ist min{ xl' x 2 } die gesuchte Nullstelle in
(A ,E), d.h. in beiden Fällen gilt
(v)
,u
11
= -
l2a ( b - va)
für
e:;= 1 bzw. a :;= 0 .
Man kann anolog (iv) bzw. (v) auch eme explizte Darstellung von ,ujk für jedes
j, k = 1, 2 erhalten:
(vi)
,ujk = z/k/ S +
(vii)
,u0k = _1_
J
2a
jk
für
(~- b k )
o
J
J
e= 1,
für e:;= 1,
mit
_
(_l)j+k
ajk - 1-e
,
bjk = s+ -ajk(Zj+Sk) '
cjk = (ajk -1) z/k'
d = b2 - 4 a c .
jk
jk
jk jk
Zum Beweis von (vi) bzw. (vii) wende man jeweils (iv) bzw. (v) auf diejenige Tafel
an, bei der man die Zeilen und/oder die Spalten vertauscht hat, wobei nach (4) ggf.
e in e- 1 übergeht.
Beweise zu:
2.
Die Cross-Product-Ratio-Matrix
ad (5)-(7): Die Behauptungen ergeben sich direkt aus der Definition des CPR.
D