Aufgabe 3.1 Zur Ermittlung der Stoßziffer ε wird der skizzierte

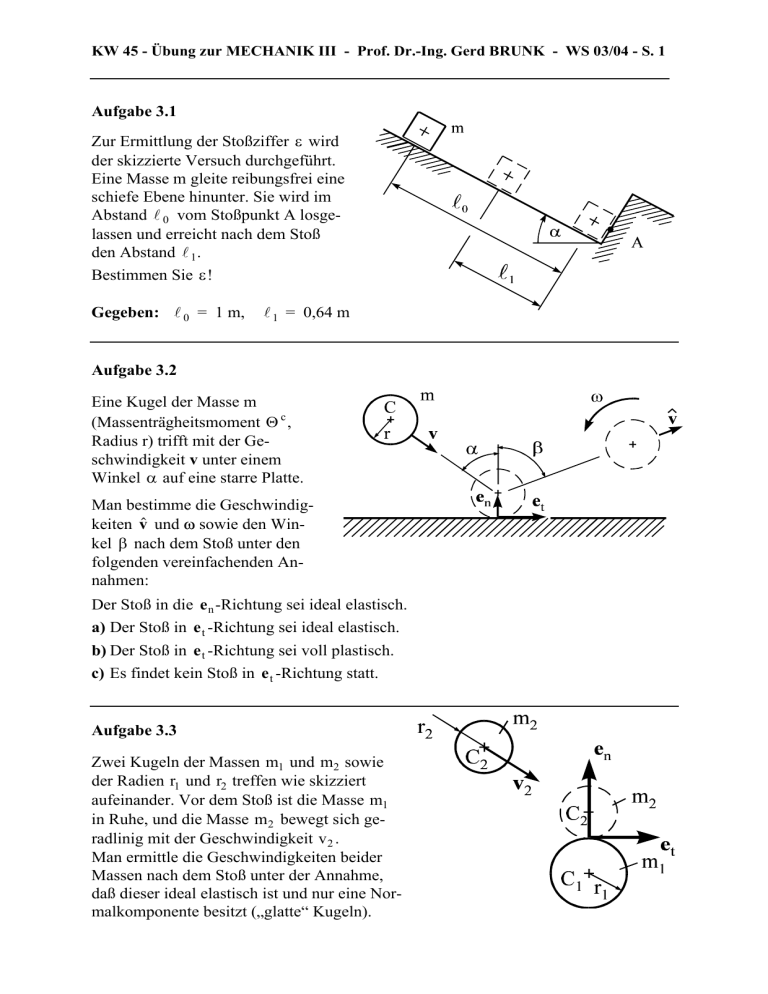
KW 45 - Übung zur MECHANIK III - Prof. Dr.-Ing. Gerd BRUNK - WS 03/04 - S. 1
Aufgabe 3.1
Zur Ermittlung der Stoßziffer ε wird
der skizzierte Versuch durchgeführt.
Eine Masse m gleite reibungsfrei eine
schiefe Ebene hinunter. Sie wird im
Abstand l 0 vom Stoßpunkt A losgelassen und erreicht nach dem Stoß
den Abstand l 1 .
Bestimmen Sie ε !
Gegeben: l 0 = 1 m,
l 1 = 0,64 m
Aufgabe 3.2
Eine Kugel der Masse m
(Massenträgheitsmoment Θ c ,
Radius r) trifft mit der Geschwindigkeit v unter einem
Winkel α auf eine starre Platte.
Man bestimme die Geschwindigkeiten v$ und ω sowie den Winkel β nach dem Stoß unter den
folgenden vereinfachenden Annahmen:
Der Stoß in die e n -Richtung sei ideal elastisch.
a) Der Stoß in e t -Richtung sei ideal elastisch.
b) Der Stoß in e t -Richtung sei voll plastisch.
c) Es findet kein Stoß in e t -Richtung statt.
Aufgabe 3.3
Zwei Kugeln der Massen m1 und m2 sowie
der Radien r1 und r2 treffen wie skizziert
aufeinander. Vor dem Stoß ist die Masse m1
in Ruhe, und die Masse m2 bewegt sich geradlinig mit der Geschwindigkeit v 2 .
Man ermittle die Geschwindigkeiten beider
Massen nach dem Stoß unter der Annahme,
daß dieser ideal elastisch ist und nur eine Normalkomponente besitzt („glatte“ Kugeln).
KW 45 - Übung zur MECHANIK III - Prof. Dr.-Ing. Gerd BRUNK - WS 03/04 - S. 2
Aufgabe 3.4
Das skizzierte Spielzeug besteht aus fünf einzelnen Pendeln in einer Ebene. Es hängen
fünf Kugeln (jeweils der Masse m und des Radius a) so an fünf Fäden, daß der
Abstand der Massenmittelpunkte zur Aufhängung jeweils l beträgt.
Man bestimme die Geschwindigkeiten aller Kugeln nach einem Stoß, wenn anfangs
a) die erste Kugel um 5°,
b) Kugel 1 und Kugel 2 um 5° und
c) Kugel 1, 2, 3 um 5° ausgelenkt
werden.
Der Abstand δ zwischen den Kugeln
soll sehr klein, aber nicht Null sein.
Die Fäden seien masselos.
Gegeben: l = 1 m,
a = 0,01 m,
m = 0,01 kg,
ε ≈1
Aufgabe 3.5
Eine Masse m1 trifft mit einem elastischen Stoß auf ein ruhendes Pendel der Länge l .
a) Man bestimme die Winkelgeschwindigkeit des Pendels nach dem Stoß.
b) Man bestimme die Länge a so, daß
im Lager A keine Kräfte infolge des
Stoßvorganges auftreten.
c) Welcher Bewegungszustand stellt sich
ein, wenn das Pendel nicht gelagert ist,
und wie wirkt sich die Bedingung b
dann aus?
Lösungen
zu 2.1:
ε = 0,8
________________________________________________________________
zu 2.2:
a)
v = vn en + vt et
v$ = − v n e n +
mr 2 − Θc
vt et ,
mr 2 + Θc
ω = −
2
Θ
+1
mr 2
c
vt
r
KW 45 - Übung zur MECHANIK III - Prof. Dr.-Ing. Gerd BRUNK - WS 03/04 - S. 3
b)
mr 2
v$ = − v n e n +
vt et ,
mr 2 + Θc
ω = −
c)
v$ = − v n e n + v t e t
ω = 0
,
1
Θ
+1
mr 2
c
vt
r
v$ t
v$ n
________________________________________________________________
Berechnung des Winkels β aus tan β =
zu 2.3:
v$ 1 = v n 2
2 m2
e
m1 + m2 n
m2 − m1
e + v t2 e t
m1 + m2 n
________________________________________________________________
v$ 2 = v n 2
zu 2.4:
Trifft eine um ϕ = 5° ausgelenkte Kugel auf eine ruhende Kugel, so hat nach
dem Stoß die erste Kugel die Geschwindigkeit v$ 1 = 0 und die zweite die Geschwindigkeit v$ 2 = v1 ≈ 0,276 m s.
(Ausführliche Besprechung im Tutorium)
________________________________________________________________
zu 2.5:
v1
a
2 m1
a)
$ =
ω
b)
ΘA
a = 2
l m2
c)
v$ 2 =
$ =
ω
ΘA
+ m1
a2
;
l2
Θ := Θ + m2
4
A
c
„Stoßmittelpunkt“
8 m1 Θc
4 Θc ( m1 + m2 ) + m1 m2 ( 2a − l)
2
4 m2 m1 ( 2a − l)
4 Θc ( m1 + m2 ) + m1 m2 ( 2a − l)
mit a aus b): ω =
2
4 m1 m2 l
v1
m 22 l 2 + 4 m1 Θ A
v1
v1