E-TM-WS1.DOC - Bildungsportal Sachsen

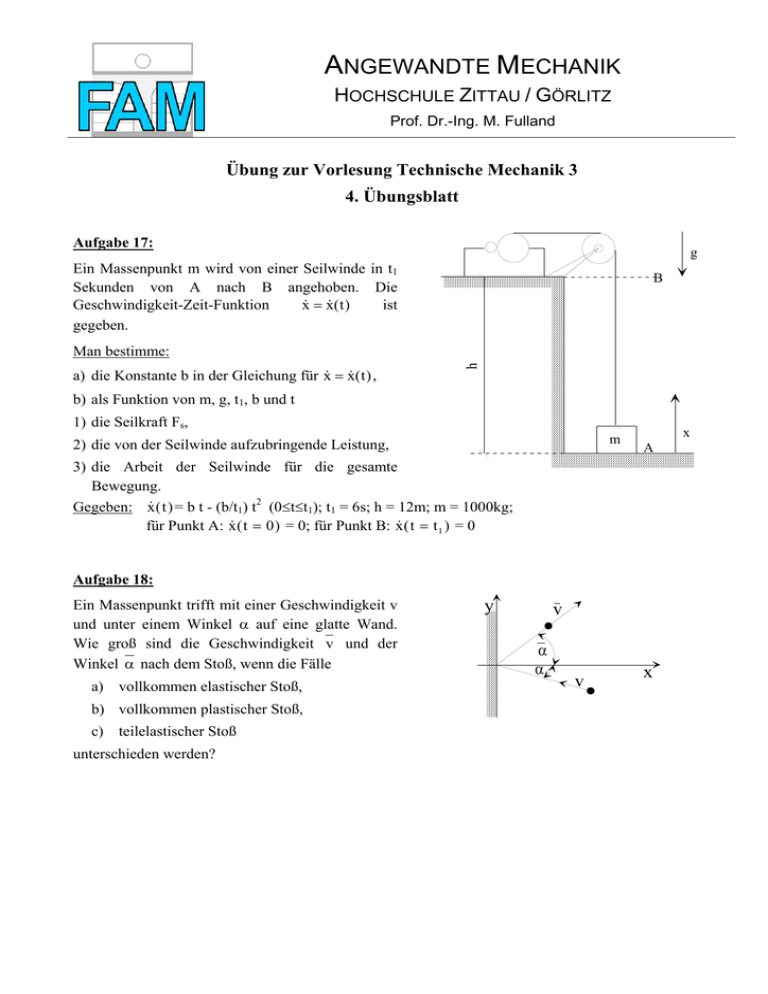
ANGEWANDTE MECHANIK
HOCHSCHULE ZITTAU / GÖRLITZ
Prof. Dr.-Ing. M. Fulland
Übung zur Vorlesung Technische Mechanik 3
4. Übungsblatt
Aufgabe 17:
g
Ein Massenpunkt m wird von einer Seilwinde in t1
Sekunden von A nach B angehoben. Die
x& = x& ( t )
Geschwindigkeit-Zeit-Funktion
ist
gegeben.
B
a) die Konstante b in der Gleichung für x& = x& ( t ) ,
h
Man bestimme:
b) als Funktion von m, g, t1, b und t
1) die Seilkraft Fs,
m
2) die von der Seilwinde aufzubringende Leistung,
x
A
3) die Arbeit der Seilwinde für die gesamte
Bewegung.
Gegeben: x& ( t ) = b t - (b/t1) t2 (0≤t≤t1); t1 = 6s; h = 12m; m = 1000kg;
für Punkt A: x& ( t = 0) = 0; für Punkt B: x& ( t = t 1 ) = 0
Aufgabe 18:
Ein Massenpunkt trifft mit einer Geschwindigkeit v
und unter einem Winkel α auf eine glatte Wand.
Wie groß sind die Geschwindigkeit v und der
Winkel α nach dem Stoß, wenn die Fälle
a) vollkommen elastischer Stoß,
b) vollkommen plastischer Stoß,
c) teilelastischer Stoß
unterschieden werden?
y
v
α
α
v
x
ANGEWANDTE MECHANIK
HOCHSCHULE ZITTAU / GÖRLITZ
Prof. Dr.-Ing. M. Fulland
Aufgabe 19:
Ein Körper der Masse m1 und der Geschwindigkeit v1 stößt „vollkommen plastisch“ (Stoßzahl e = 0) mit
einer Kugel der Masse m2 zusammen und bleibt an ihr haften. Die Kugel ist an einem als masselos zu
betrachtenden Pendelstab der Länge h2 befestigt. Nach dem Stoß bewegen sich die Massen m1 und m2 auf
einer Kreisbahn um Punkt D und stoßen im Punkt B zentral und vollkommen elastisch mit einer zweiten
frei aufliegenden Kugel der Masse m3 zusammen. Diese folgt nun einer widerstandsfreien Flugbahn und
stößt im Punkt C gegen eine Wand.
Berechnen Sie:
b) die Geschwindigkeit v3 der Masse m3 unmittelbar nach dem Stoß,
c) die Höhe h3 des Punktes C,
g
D
a) die Geschwindigkeit vB, mit der das Pendel im
Punkt B gegen die Masse m3 stößt,
h2
m1
v1
C
m3
m2
h3
B h1
A
l
d) die Größe und Richtung der Geschwindigkeit,
mit der die Kugel im Punkt C aufschlägt.
Gegeben: m1 = m = 1 kg; m2 = 2 m; m3 = 1,5 m; v1 = 30 m/s; h1 = 0,5 m; h2 = 2 h; l = 3 m
Aufgabe 20:
Eine Kreisscheibe (Radius R) ist in ihrem Mittelpunkt auf einem Arm (Länge l) gelagert, der sich
mit der Winkelgeschwindigkeit ω1 = ϕ& um eine
feste Achse durch O dreht. Die Scheibe dreht sich
um eine Achse durch A mit der Winkelgeschwindigkeit ω2 = α& gegen ein festes Bezugssystem.
Man bestimme die momentane Geschwindigkeit
und Beschleunigung eines Punktes P auf dem
Kreisumfang.
y
P
A α
ϕ
R
l
O
x