Löcher im Universum

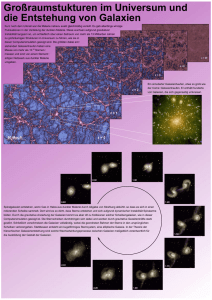
Löcher im Universum
Bei der Suche nach Löchern (als leere Räume) im Universum muss in den Zwischenräumen der
sichtbaren Strukturen analysiert werden, ob dort vorher unsichtbare Materie liegt:
Zwischen den Sternen:
•
•
Im sichtbaren Wellenlängen kaum Materie
Aber: Infrarot- und Gammastrahlen zeigen: interstellares Medium (dünnes Gas)
Zwischen Galaxien:
•
•
•
Wo Galaxien sind auch andere oftmals  Galaxienhaufen und Superhaufen
Genau Struktur und damit Zwischenräume schwer zu sagen, da unser Blick auf das Universum
nur eine 2D-Projektion der dreidimensionalen Verteilung ist
Räumliche Position Messen  Entfernung über Rotverschiebung nach Hubble bei weit
entfernten Galaxien durch Expansion des Universums
𝑣 = 𝑧𝑐 = 𝐻0 𝑟; 𝑧 = 𝑅𝑜𝑡𝑣𝑒𝑟𝑠𝑐ℎ𝑖𝑒𝑏𝑢𝑛𝑔 𝐻0 = (67,74 ± 0,46)
•
𝑘𝑚
𝑠𝑀𝑝𝑐
Erstellen auf Grundlage von ca.250.000 Galaxiendaten der 3D Darstellung 
Bereiche mit nahezu keiner MaterieVoids (75% des Universums sind Voids):
•
•
Galaxienhaufen sind die Wände der Lehrräume (meist 75 Mio Lj)
Woher kommt diese Struktur?
o Nach Urknall ist Materie recht gleichmäßig verteilt
o geringe Dichteschwankungen potenzieren sich
o  entleeren den weniger dichten Raume und füllen diese wo schon mehr Materie war
o  größere Dichteschwankung  positiver Feedbackloop
•
•
•
•
Voids sind plausible, denn
Mittlere/kritische Dichte im Universerum: 1 Proton pro m² &
Mittler Dichte in Galaxie: 1 Mio Teilchen pro m²
 es muss ganz dünne Gebiete geben, um den Mittelwert von 1 Teilchen pro m² zu erlangen
Dunkle Materie erzeugt Strukur:
•
Kalte dunkle Materie (observierbar in der kosmischen Hintergrundstrahlung) 
Galaxien/Galaxienhaufen
Abbildung 1: Verteilung sichtbarer Materie (links) und dunkler Materie (rechts)
•
Heiße dunkle Materie  leichte Materie die sich schnell bewegt und dadurch die Blasen
erzeugt bzw. stabilisiert
Abbildung 2:
Oben: Simulation der Struktur in heißer (links), warmer (mitte), und kalt (rechts) dunkler
Materie im Universum am Anfang (starke Rotverschiebung)
Unten: gleich wie oben nur in der Jetztzeit (z=0)