Physik 1: Wellen und Thermodynamik Übungsblatt 2

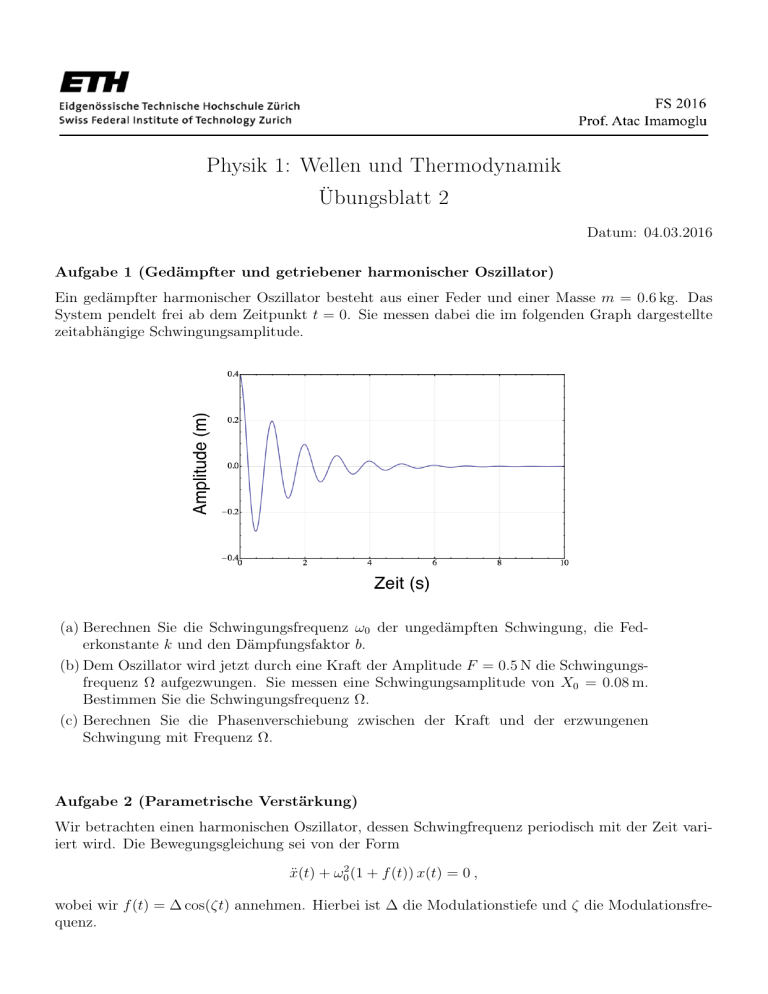
Physik 1: Wellen und Thermodynamik
Übungsblatt 2
Datum: 04.03.2016
Aufgabe 1 (Gedämpfter und getriebener harmonischer Oszillator)
Ein gedämpfter harmonischer Oszillator besteht aus einer Feder und einer Masse m = 0.6 kg. Das
System pendelt frei ab dem Zeitpunkt t = 0. Sie messen dabei die im folgenden Graph dargestellte
zeitabhängige Schwingungsamplitude.
(a) Berechnen Sie die Schwingungsfrequenz ω0 der ungedämpften Schwingung, die Federkonstante k und den Dämpfungsfaktor b.
(b) Dem Oszillator wird jetzt durch eine Kraft der Amplitude F = 0.5 N die Schwingungsfrequenz Ω aufgezwungen. Sie messen eine Schwingungsamplitude von X0 = 0.08 m.
Bestimmen Sie die Schwingungsfrequenz Ω.
(c) Berechnen Sie die Phasenverschiebung zwischen der Kraft und der erzwungenen
Schwingung mit Frequenz Ω.
Aufgabe 2 (Parametrische Verstärkung)
Wir betrachten einen harmonischen Oszillator, dessen Schwingfrequenz periodisch mit der Zeit variiert wird. Die Bewegungsgleichung sei von der Form
ẍ(t) + ω02 (1 + f (t)) x(t) = 0 ,
wobei wir f (t) = ∆ cos(ζt) annehmen. Hierbei ist ∆ die Modulationstiefe und ζ die Modulationsfrequenz.
(a) Nennen Sie zwei Beispiele, wie ein solches System physikalisch realisiert werden kann.
(b) Wie muss die Modulationsfrequenz ζ gewählt werden, damit eine mit der Frequenz ω0
oszillierende Kraft entsteht, die die (bereits vorhandene) Schwingung verstärkt?
(c) Bonusaufgabe. Wie suchen eine exponentiell anwachsende Lösung der Form
x(t) = X0 exp(γt/2) cos(ω0 t + φ)
mit dem Verstärkungsfaktor γ ω0 und der Phase φ. Bestimmen Sie die Verstärkung
pro Periode für eine Modulationstiefe von ∆ = 0.1.
Aufgabe 3 (Massensensor)
Kleine mechanische Schwingungssysteme können heutzutage als extrem sensitive Massensensoren
eingesetzt werden. Eine Massenänderung des Systems, z.B. durch Anlagerung von Partikeln, kann
hierbei in eine Frequenzänderung der mechanischen Oszillation überführt werden.
Wir betrachten eine Struktur mit quaderförmiger Geometrie (Länge L, Breite W , Höhe H), die an
einer Seite fest und an der gegenüberliegenden Seite frei ist (ganz ähnlich zu einem freischwingenden
Balken). Die fundamentale Schwingung dieses System (Biegeschwingung aus der Ebene) kann man
3
und Masse meff = 16
m0 betrachten. Für
als harmonischen Oszillator mit Federkonstante keff = 3EI
L3
3
2
9
das Elastizitätsmodul gelte E = 170 · 10 N/m , das Flächenträgheitsmoment ist I = H12W , und m0
bezeichne die Masse des Quaders. Die Dichte des Materials betrage ρ = 2320 kg/m3 .
(a) Leiten Sie einen Ausdruck für die kleinste noch auflösbare Massenänderung des Quaders
in Abhängigkeit von der kleinsten noch auflösbaren Frequenzänderung her. Nehmen
Sie an, dass die Massenänderung klein gegenüber der ursprünglichen Masse ist.
(b) Die kleinste noch detektierbare Frequenzänderung betrage 25 Hz. Was ist die kleinste
Masse, die wir mit einer Struktur der Länge L = 120 µm, Breite W = 50 µm und Höhe
H = 200 nm noch auflösen können?