Wiederholungskurs zu den Grundlagen der

Wiederholungskurs zu den Grundlagen der
Diskreten Optimierung
von Dipl.-Math. Wolfgang Kinzner
im Wintersemester 2008/2009
Zentrum für Mathematik
Technische Universität München
30. April 2009
Inhaltsverzeichnis
1 Grundlagen der Graphentheorie
2
2 Kürzeste Wege
7
3 Matroide und minimal aufspannende Bäume
12
4 Flüsse
17
5 Matchings
25
1
1
Grundlagen der Graphentheorie
Landau-Notation
Definition 1
Es seien f, g : N → R+
0 zwei Funktionen. Wir schreiben
f (n) = O(g(n))
:⇔
∃c ∈ R+ ∃n0 ∈ N ∀n ≥ n0 : f (n) ≤ cg(n),
f (n) = Ω(g(n)) :⇔
f (n) = Θ(g(n)) :⇔
∃c ∈ R+ ∃n0 ∈ N ∀n ≥ n0 : f (n) ≥ cg(n),
∃c1 , c2 ∈ R+ ∃n0 ∈ N ∀n ≥ n0 : c1 g(n) ≤ f (n) ≤ c2 g(n),
f (n) = o(g(n)) :⇔
f (n) = ω(g(n)) :⇔
∀c ∈ R+ ∃n0 ∈ N ∀n ≥ n0 : f (n) ≤ cg(n),
∀c ∈ R+ ∃n0 ∈ N ∀n ≥ n0 : f (n) ≥ cg(n).
Bemerkung 1 Es gelten:
f (n)
n→∞ g(n)
1. f (n) = o(g(n)) ⇔ lim
2. f (n) = O(g(n))
=
lim f (n)
n→∞ g(n)
existiert.
3. f (n) = O(g(n)) ⇔ g(n) =
4. f (n) = Θ(g(n) ⇔ f (n) =
und f (n) =
Übung 1.1
Welche der folgenden Aussagen ist richtig?
(a)
(i) 5n2 + 9n + 7 = O(n2 ).
(ii) 5n2 + 9n + 7 = Θ(n2 ).
(iii) 5n2 + 9n + 7 = o(n2 ).
(iv) 5n2 + 9n + 7 = o(n3 ).
(v) 5n2 + 9n + 7 = Θ(n3 ).
(vi) log(n2 ) = Θ(log(n3 ))
(vii) log n = Θ(ln n)
(viii) ∀ǫ ∈ R+ ∀k ∈ N : (log n)k = o(nǫ )
(ix) 10log n = O(2n ).
(x) 10
√
n
= O(2n ).
(xi) 10n = O(2n ).
(b) Es gibt zwei Funktionen f, g, für die weder f (n) = O(g(n)) noch g(n) =
O(f (n) gilt.
2
Repräsentation von Graphen
Allgemeine Voraussetzung ab jetzt (wenn nicht anders erwähnt): G = (V, E) ist
ein ungerichteter ungewichteter Graph mit V = [n] (d.h. |V | = n) und |E| = m.
(1) Adjazenzliste Feld von n Listen, eine für jeden Knoten in V .
1 → ...
..
..
..
.
.
.
v → v1 → v2 → . . . →
..
..
..
.
.
.
n → ...
mit N (v) = {v1 , v2 , . . . , vk }.
vk
Vorteil: Kompakte Darstellung mit
Speicher.
Nachteil: Test, ob {v, w} Kante ist, kostet in schlechtestem Fall
Zeit.
(2) Adjazenzmatrix:
n × n Matrix A = (aij )1≤i,j≤n
mit aij =


. . . a1n
.. 
..
.
. 
. . . ann
a11
 ..
= .
an1
Vorteil: Test, ob {v, w} Kante ist, kostet
Nachteil: Adjazenzmatrix erfordert
Zeit.
Speicher.
Übung 1.2
Gegeben sei der folgende ungerichtete, ungewichtete Graph G:
1
4
2
3
(a) Geben Sie die Adjazenzliste und die Adjazenzmatrix A von G an.
(b) Geben Sie A2 an, ohne das Matrixprodukt (algebraisch) zu berechnen. Wie
kann man an A und A2 erkennen, das G Dreiecke enthält? Ist A2 Adjazenzmatrix eines Graphen?
3
Breiten- und Tiefensuche
Funktionsweise Breitensuche:
•
•
•
•
•
Laufzeit:
Algorithmus 1
Input: Graph G = (V, E), Knoten u ∈ V
Output: Fnkten bekannt : V → {0, 1}, abst : V → N0 ∪ {∞},
vor : V \ {u} → V
BFS∗ (G, u)
(1)
Enqueue (Q, u)
(2)
bekannt[u] := 1; abst[u] := 0;
(3)
foreach w ∈ V \ {u} do bekannt[w] := 0; abst[w] :=
∞
(4)
while Q 6= ∅
(5)
v:= Dequeue (Q)
(6)
foreach w ∈ N (v) and bekannt[w] = 0
(7)
Enqueue (Q, w)
(8)
bekannt[w] := 1
(9)
abst[w] := abst[v] + 1
(10)
vor[w] := v
4
Modifikationen:
• Test auf Bipartitheit:
– Es gilt: G bipartit ⇐⇒ G hat 2-Färbung.
– Färbe Startknoten mit Farbe 0, seine Nachbarknoten mit Farbe 1,
deren Nachbarknoten wieder mit 0 usw.
– Bekommt Knoten dieselbe Farbe wie einer seiner Nachbarknoten ⇒
2-Färbung nicht möglich ⇒ G nicht bipartit.
– BFS fertig, dann überprüfe, ob bekannt(v) = 1 ∀v ∈ V .
∗ Ja, dann ist G bipartit.
∗ Nein, dann setze Verfahren mit neuem Knoten von anderer Zusammenhangskomponente fort.
Laufzeit:
• Test auf Zusammenhang:
– Nach Ausführung von BFS bekannt(v) = 1 für alle v ∈ V ⇒ G
zusammenhängend.
– Gibt es noch Knoten in Q mit bekannt(v) = 0 ⇒ G nicht zusammenhängend.
Laufzeit:
• Test auf Kreisfreiheit:
– Für jedes v, aus Warteschlange entnommen, teste zusätzlich, ob v
Nachbarknoten w hat, der nicht Vorgängerknoten ist und trotzdem
bekannt ist.
– Wenn der Fall ⇒ Kreis gefunden.
– Wenn BFS gesamten Graphen (d.h. alle ZHK) durchläuft, ohne einen
Kreis zu finden ⇒ G kreisfrei.
Laufzeit:
• Test, ob Graph Baum ist:
– Es gilt: G ist Baum ⇔ ist zusammenhängend und kreisfrei.
– Teste also G auf die beiden Eigenschaften wie oben beschrieben.
Laufzeit:
5
Übung 1.3
Welche der folgende Aussagen richtig?
n
(a) Auf einer n-elementigen Knotenmenge gibt es genau 2( 2 ) verschiedene
Graphen.
(b) Ist G nicht zusammenhängend, dann gilt immer n > m.
(c) Ein Graph ist genau dann ein Baum, wenn je zwei Knoten durch genau
einen Pfad verbunden sind.
(d) Bäume sind immer bipartit.
(e) Man kann dist(v, w) für v, w ∈ V unter Verwendung von BFS in O(n+m)
bestimmen.
(f ) Man kann dist(v, w) für v, w ∈ V unter Verwendung von DFS in O(n+m)
bestimmen.
(g) Ist G zusammenhängend, so haben BFS und DFS eine Laufzeit von O(n).
(h) Ist G zusammenhängend, aber kein Baum, so sind die durch BFS und
DFS, vom selben Startknoten aus, konstruierten Spannbäume immer verschieden.
Übung 1.4
Sei G = (V, E) ein Graph, dann bezeichnet G := (V,
V
2
\ E) sein Komplement.
(a) Die Bildung von G kostet Θ(n2 ) Zeit. (Bei Darstellung über über Adjazenzmatrix)
(b) Zeigen sie: Ein bipartiter Graph auf n Knoten hat höchstens
n2
4
Kanten.
(c) Wie läßt sich in O(n + m) Zeit testen, ob das Komplement eines Graphen
mit n Knoten und m Kanten bipartit ist.
Übung 1.5
Sei G = (V, E) ein ungerichteter Graph ohne Schleifen. Mit δ(G) := min d(v)
v∈V
werde der Minimalgrad von G bezeichnet.
Zeigen Sie: Gilt δ(G) ≥ 2, dann hat G einen Kreis, dessen Länge mindestens
δ(G) + 1 ist.
6
2
Kürzeste Wege
Der Dijkstra-Algorithmus
Funktionsweise:
•
•
•
•
Laufzeit:
Algorithmus 2 (Dijkstra)
~ = (V, E,
~ ℓ) mit Längenfunktion ℓ : E → R+ ,
Input: Graph G
Knoten s ∈ V
Output: Funktion abst : V → R ∪ {∞}
Dijkstra(G, ℓ, s)
(1)
foreach x ∈ V \ {s} do abst[x] := ∞
(2)
abst[s] := 0
(3)
Q := V
(4)
while Q 6= ∅
(5)
x := Knoten in Q mit kleinstem abst[.]-Wert
(6)
Q := Q \ {x}
~
(7)
foreach y ∈ Q mit (x, y) ∈ E
(8)
abst[y] := min{abst[y], abst[x] + ℓ(x, y))
Modifikation:
Berechnung der kürzesten Pfade durch Speicherung des Vorgängers jedes Knotens.
Algorithmus 3
~ = (V, E,
~ ℓ) mit Längenfunktion ℓ : E → R+ ,
Input: Graph G
Knoten s ∈ V
Output: Funktion abst : V → R ∪ {∞}
Dijkstra*(G, ℓ, s)
(1)-(8) wie oben
(9)
if abst[x] + ℓ(x, y) < abst[y]
(10)
then abst[y] = abst[x] + ℓ(x, y)
(11)
vor[y] = x
(12) foreach v ∈ V
(13)
A[v, 1] = v
(14)
for i = 2 to n
(15)
A[v, i] = vor(A[v, i − 1])
7
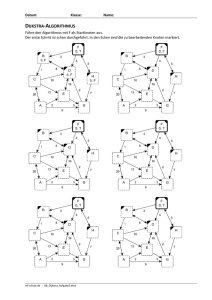
Übung 2.1
Für einen Graphen G = (V, E) betrachten wir die Reihenfolge v1 , v2 , ..., vn mit
vi ∈ V , in der die Knoten von G im Dijkstra-Algorithmus aus Q gelöscht werden
(Zeile 6). Wir sagen dann, dass v1 , v2 , ..., vn eine (mögliche) Besuchsreihenfolge
für Dijkstra(G, v1 ) ist.
Sei G der folgende Graph mit Gewichtsfunktion ℓ wie angegeben:
u3
u9
111111
000000
0000000
1111111
00
11
00
11
00
11
00000011001111111
111111
0000000
00
11
00
11
000000
111111
000000
111111
00
11
00
11
00
11
000
111
000000
111111
000000
111111
110011001111111
1111111110011111111111111
0000000
10111111
00000000000000
0000000
000
111
000000
00000000000000
11111111111111
0000000
1111111
10111111
000
111
000000
0000000
1111111
000000
000000010111111
1111111
3
1
u4
1
3
4
u8
2
u5
1
3
u2
1
2
u7
3
2
2
4
5
u6
u1
Welche der folgenden Aussagen sind richtig?
(a) Eine Besuchsreihenfolge für Dijkstra(G, ℓ, u1 ) ist u1 , u4 , u9 , u8 , u6 , u5 , u2 , u7 , u3 .
(b) Eine Besuchsreihenfolge für Dijkstra(G, ℓ, u7 ) ist u7 , u6 , u8 , u5 , u9 , u4 , u2 , u1 , u3 .
(c) Beim Ausführen von Dijkstra(G, ℓ, u9 ) ist abst[u9 ] stets echt kleiner als
abst[u2 ]. (“stets“ bedeutet, sobald abst[v] < ∞ für den besagten Knoten
v.)
(d) Beim Ausführen von Dijkstra(G, ℓ, u1 ) ist abst[u3 ] stets echt kleiner als
abst[u8 ].
(e) Beim Ausführen von Dijkstra(G, ℓ, u7 ) ist abst[u8 ] stets echt kleiner als
abst[u9 ].
(f ) Beim Ausführen von Dijkstra*(G, ℓ, u7 ) enthält ein kürzester u7 , u9 Pfad immer die Kante {u6 , u9 }.
(g) Beim Ausführen von Dijkstra*(G, ℓ, u1 ) enthält ein kürzester u1 , u2 Pfad immer die Kante {u5 , u2 }.
8
Übung 2.2
Welche der folgenden Aussagen sind richtig?
(a) Seien v1 , v2 , ..., vn eine mögliche Besuchsreihenfolge für Dijkstra(G, v1 ).
Dann gilt am Ende des Algorithmus abst[v1 ] ≤ abst[v2 ] ≤ · · · ≤ abst[vn ].
(b) Ist man beim Aufruf von Dijkstra(G, ℓ, s) nur an dem Abstand von s
zu einem festen Knoten t interessiert, so kann man abbrechen, sobald
abst[t] < ∞.
(c) Ist man beim Aufruf von Dijkstra(G, ℓ, s) nur an dem Abstand von s zu
einem festen Knoten t interessiert, so kann man abbrechen, sobald t aus
Q gelöscht wird.
(d) Sei G ein ungerichteter, ungewichteter Graph. Dann findet der DijkstraAlgorithmus einen kürzesten Weg von s nach t in O(n + m) Schritten.
(e) Berechnet man mit dem Dijkstra*-Algorithmus mit einem Durchlauf die
kürzesten Pfade von einem Startknoten zu allen anderen Knoten, so bildet
die Vereinigung dieser Pfade einen Spannbaum von G bzw. der Zusammenhangskomponente des Startknotens.
(f ) Nehmen wir an, in G existieren negative Kantengewichte und sei −C das
kleinste dieser Gewichte. Der kürzeste Weg zwischen zwei Knoten in einem
solchen Graphen kann bestimmt werden, indem zunächst jedes Gewicht um
(C + 1) erhöht und dann der Dijkstra-Algorithmus verwendet wird.
(g) Ist G ein gerichteter Graph ohne negative Zyklen, in dem nur Kanten am
Startknoten negative Gewichte haben dürfen. Dann liefert der DijkstraAlgorithmus richtige Ergebnisse.
(h) Nehmen wir an, G sei ungerichtet und habe genau eine Kante e mit negativem Gewicht, aber keine negativen Zyklen. Dann kann ein kürzester
s-t-Weg durch zweimaliges Aufrufen des Dijkstra-Algorithmus auf einem
Subgraphen von G gefunden werden.
9
Der Floyd-Warshall-Algorithmus
Lemma 1
~ = (V, E),
~ ℓ:E
~ → R und i, j ∈ [n] und k ∈ [0, n]. Weiter seien
Seien G
k
Pi,j
:= {P = (v1 , . . . , vr ) :
:=
dki,j =
dki,j
P ist gerichteter i, j-Pfad und v2 , . . . , vr−1 ∈ [k]} und
k
min{ℓ(P ) : P ∈ Pi,j
}
∞
:
:
k
falls Pi,j
6= ∅,
sonst.
Dann gilt:
Funktionsweise:
•
•
•
Laufzeit:
Algorithmus 4
~ = (V, E),
~ Längenfunktion ℓ : E → R
Input: Graph G
Output: n × n Matrix D
Floyd–Warshall(G, ℓ)
(1)
for i = 1 to n
(2)
for j = 1 to n
(3)
dˆ0i,j := ℓ(i, j)
(4)
for k = 1 to n
(5)
for i = 1 to n
(6)
for j = 1 to n
k−1 ˆk−1
k−1
, di,k + dˆk,j
}
(7)
dˆki,j := min{dˆi,j
n
(8)
return D := (dˆ )1≤i,j≤n
i,j
10
Modifikationen:
• Berechnung von kürzesten Pfaden.
k
k
Sei wi,j
der Vorgänger von j auf einem Pfad P ∈ Pi,j
mit ℓ(P ) = dki,j .
Dann gilt
−
→
: falls i 6= j und (i, j) ∈ E ,
0
k = 0 : wi,j :=
: sonst.
(
k−1
k−1
k−1
wenn di,j
≤ di,k
+ dk,j
k
wi,j
=
k−1
k−1
k−1
wenn di,j > di,k + dk,j .
Modifizierter Algorithmus gibt schließlich die Matrix der kürzesten Pfade
n
W = (wij
)1≤i,j≤n aus.
• Erkennen von negativen Zyklen.
Es gilt:
Es gibt einen Zyklus negativer Länge ⇐⇒
Übung 2.3
Gegeben sei der folgende gerichtete, gewichtete Graph G = (V, E, ℓ) mit V =
{v1 , ..., v6 } und E = {e1 , ..., e8 }.
v2
3
v4
2
2
v1
-3
v6
-2
5
1
v3
1
v5
(a) Berechnen Sie mithilfe des Floyd-Warshall-Algorithmus einen kürzesten
Weg von v1 nach v6 und dessen Länge.
(b) Zeigen Sie, dass der Dijkstra-Algorithmus für das gleiche Problem unbrauchbar ist.
Übung 2.4
Was passiert beim Floyd-Warshall Algorithmus zur Bestimmung kürzester s, tWege, wenn es zwar einen Zyklus negativer Länge gibt, dieser jedoch nicht von
s aus erreichbar ist oder t nicht von diesem erreicht werden kann? Geben Sie
eine direkte Modifikation des Algorithmus an, so dass ein kürzester s, t-Weg
gefunden wird.
11
3
Matroide und minimal aufspannende Bäume
Der Algorithmus von Prim
Funktionsweise.
Laufzeit:
Algorithmus 5 (Algorithmus von Prim)
Input: Graph G = (V, E), Längenfunktion ℓ : E → R≥0
Output: Baum T = (V, F )
Prim(G, ℓ)
(1)
Wähle beliebigen Knoten s ∈ V
(2)
W := {s}, F := ∅, σ[s] := 0
(3)
foreach v ∈ N (s) do vor[v] := s, σ[v] := ℓ(s, v)
(4)
foreach v ∈ V \ (N (s) ∪ {s}) do vor[v] := N IL,
(5)
(6)
(7)
(8)
(9)
(10)
σ[v] := ∞
while W 6= V
y := Knoten mit minimalem σ[.]-Wert in V \ W
W := W ∪ {y}, F := F ∪ {vor[y], y}
foreach z ∈ N (y) ∩ (V \ W ) mit σ[z] > ℓ(y, z)
σ(z) := ℓ(y, z)
vor[z] := y
Der Algorithmus von Kruskal
Funktionsweise:
Laufzeit:
Algorithmus 6 (Algorithmus von Kruskal)
Input: Graph G = (V, E), Längenfunktion ℓ : E → R+
Output: Baum T = (V, F )
Kruskal(G, ℓ)
(1)
Sortiere alle Kanten in E so, daß ℓ(e1 ) ≤ · · · ≤ ℓ(em );
(2)
F := ∅;
(3)
for i = 1 to m
(4)
if (V, F ∪ {ei }) kreisfrei then F := F ∪ {ei }
12
Übung 3.1
Sei G = (V, E) der folgende Graph mit Gewichtsfunktion ℓ wie angegeben:
u3
u9
11001100
111111
000000
0000000
1111111
00
11
00000011001111111
111111
0000000
1100110011001100
000000
111111
000000
111111
00
11
000
111
000000
111111
000000110011111111111111
111111
110011001111111
10111111
1111111
0000000
00000000000000
0000000
000
111
000000
10111111
00000000000000
11111111111111
0000000
1111111
000
111
000000
0000000
1111111
000000
000000010111111
1111111
3
u4
1
1
3
4
u8
2
u5
1
3
u2
1
5
u7
3
2
2
4
5
u6
u1
Welche der folgenden Aussagen sind richtig?
(a) Eine gültige Reihenfolge beim Ablaufen der Knoten im Prim-Algorithmus
ist
u5 , u4 , u9 , u8 , u1 , u6 , u3 , u7 , u2 .
(b) Im Algorithmus von Prim wird der Knoten u2 stets als Letzter in den
spannenden Baum eingebunden.
(c) Im Algorithmus von Kruskal existieren unmittelbar vor dem letzten Schritt
stets die Komponenten {u2 } und V − u2 .
(d) Kein minimal spannender Baum enthält die Kanten {u1 , u5 } und {u4 , u5 }
gleichzeitig.
13
Matroide
Definition 2 (Unabhängigkeitssystem, Matroid)
• Ein Unabhängigkeitssystem ist ein Paar (E, I), wobei E eine endliche
Menge ist und
I ⊆
mit
(M1)
(M2)
• E heißt Grundmenge, die Mengen A ⊆ E mit A ∈ I heißen unabhängig und die Mengen B ⊆ E mit B 6∈ I heißen abhängig.
• Eine Menge A ∈ I heißt Basis, wenn sie
Falls A inklusionsminimal abhängig ist, so heißt A
• Ein Unabhängigkeitssystem heißt Matroid, wenn außerdem noch die folgende Eigenschaft gilt:
(M3)
Wichtige Beispiele 1
(1) Vektorraummatroid:
Sei V ein Vektorraum, E eine Menge von Vektoren in V . Außerdem sei
I := {F ⊆ E : F ist linear unabhängige Familie von Vektoren in V } ⊆ P(V ).
Dann ist (E, I) ein Matroid.
(2) Graphischer Matroid oder Kreismatroid:
Sei G = (V, E) ein Graph und sei
I :=
Dann ist (E, I) ein Matroid.
Unabhängige Mengen:
Basen:
(3) Sei G = (V, E) ein Graph mit E 6= ∅. Wir definieren
I := {M ⊆ E : M Matching}.
Dann ist U := (E, I)
Basen:
14
Übung 3.2
Sei (E, I) das Kreismatroid des Graphen G aus Aufgabe 3.1.
Sind die folgenden Aussagen richtig?
(a) {u6 , u7 } ist in jedem Element von I enthalten.
(b) {u6 , u7 } ist in einem Element von I enthalten.
(c) {u6 , u7 } ist in genau einem Element von I enthalten.
Übung 3.3
Sei E eine endliche Menge, k ∈ N, (E1 , E2 , . . . , Ek ) eine Partition von E,
b1 , b2 , . . . bk ∈ N0 und I := {I ⊆ E : |I ∩ Ei | ≤ bi , i = 1, . . . k}.
Zeigen Sie: (E, T ) ist ein Matroid.
Übung 3.4
Eine Hilfsorganisation hat aus weihnachtlichen Spenden n Ladungen mit Lebensmitteln zur Verfügung. Für jede Ladung i ∈ [n] wurde ein Nährwert wi ∈ N
und ein Verfalldatum ti ∈ N0 ermittelt. Täglich kann nur eine Ladung in das
Krisengebiet gebracht werden. Ziel der Helfer ist es, eine Auswahl F ⊆ [n] von
Ladungen zu treffen (nach dem Verfallsdatum sortiert), so dass keine Ladung
i ∈ F nach ihrem Verfalldatum geliefert wird und der Nährwert aller gelieferten
Ladungen maximiert wird. Zeigen Sie, dass dem Problem ein Matroid und ein
Maximierungsproblem über diesem zu Grunde liegt.
Übung 3.5
(a) Sei (E, I) ein Unabhängigkeitssystem. Zeigen Sie:
(E, I) ist genau dann ein Matroid, wenn die folgende Bedingung erfüllt
ist:
(M3)´ Wenn X ⊆ E und I1 , I2 ∈ {I : I ∈ I, I ⊆ X} maximal unabhängig
bezüglich X sind (d.h. ∀x ∈ X \ Ii (i = 1, 2) : Ii ∪ {x} ∈
/ I), dann gilt
|I1 | = |I2 |.
(b) Sei (E, I) ein Matroid, I ∈ I, e ∈ E und I ∪{e} ∈
/ I. Dann enthält I ∪{e}
genau einen Kreis.
Übung 3.6
Zeigen Sie:
(a) Seien (E1 , I1 ), (E2 , I2 ) Matroide mit E1 ∩ E2 = ∅. Dann ist auch (E1 ∪
E2 , I) mit I = {I1 ∪ I2 : I1 ∈ I1 , I2 ∈ I2 } ein Matroid.
(b) Seien (E, I1 ), (E, I2 ) Matroide. Dann ist (E, I1 ∩I1 ) im Allgemeinen kein
Matroid.
15
Maximierungsprobleme über Unabhängigkeitssystemen
Definition 3
Ein Maximierungsproblem über einem Unabhängigkeitssystem (E, I) ist gegeben durch eine GewichtsfunktionP
ℓ : E → R+
0 (und der Vereinbraung, dass für
Mengen A ∈ I wieder ℓ(A) := e∈A ℓ(e) sein soll). Gesucht ist eine Menge
A∗ ∈ I mit
ℓ(A∗ ) = max ℓ(A).
A∈I
Algorithmus 7 (Greedy-Algo. zur Max. über Unabhsys.)
Input: Unabhängigkeitssystem (E, I), Gewichtsfunktion ℓ : E →
R+
Output: Ag ∈ I
Greedy–Max(E, I, ℓ)
(1)
Sortiere E = {e1 , . . . , em } so, daß ℓ(e1 ) ≥ . . . ≥ ℓ(em );
(2)
Ag := ∅;
(3)
for i = 1 to m
(4)
if Ag ∪ {ei } ∈ I then Ag := Ag ∪ {ei }
Satz 1
Sei U = (E, I) ein Unabhängigkeitssystem. Dann gilt:
U ist genau dann Matroid,
Definition 4 (Approximationsgüte)
Ist Ag die vom Greedy-Algorithmus gefundene maximale Lösung und A∗ die
g
tatsächliche maximale Lösung der Maximierungsaufgabe, so nennt man A
A∗ die
Approximationsgüte des Greedy-Algorithmus.
Übung 3.7 (Klausuraufgabe 6)
Sei G = (V, E) ein Graph mit V = {v1 , . . . , vn } und Maximalgrad ∆. Der folgende Algorithmus M SN hat das Ziel, eine möglichst große stabile Menge in G
zu finden:
Algorithmus 8 (Maximale stabile Menge MSN)
(1)
S := ∅
(2)
for i = 1 to n
(3)
if G[S ∪ {vi }] enthält KEINE Kante then S := S ∪
{vi }
(4)
return S
(a) Für ein bestimmtes Unabhängigkeitssystem U und eine Gewichtsfunktion
c auf der Grundmenge von U ist M SN ein Greedy-Algorithmus für ein
Maximierungsproblem über U . Geben Sie U und c an, und begründen Sie,
warum U ein Unabhängigkeitssystem ist.
(b) Zeigen Sie: M SN hat Approximationsgüte mindestens
16
1
∆.
4
Flüsse
Netzwerke
Definition 5 (Netzwerk, Fluss)
~ s, t, c), wobei G = (V, E)
~ ein ge• Ein Netzwerk ist ein Tupel N = (V, E,
richteter Graph ist, s, t ∈ V zwei ausgezeichnetene Knoten benennen und
~ → R+ eine Kapazitätsfunktion. Die Knoten s bzw. t werden Quelle
c:E
0
bzw. Senke genannt. Für einen Knoten v ∈ V schreiben wir
~
N + (v) := {w ∈ V : ∃(v, w) ∈ E}
und
~
N − (v) := {w ∈ V : ∃(w, v) ∈ E}.
~ → R+ heisst s-t-Fluss (engl. flow) in N , wenn
• Eine Abbildung f : E
0
–
–
wobei wir im Folgenden der Einfachheit halber immer nur noch f (x, y)
statt f ((x, y)) und c(x, y) statt c((x, y)) schreiben werden.
• Der Wert von f ist definiert als
val(f ) =
Ein Fluss f hat maximalen Wert in N , falls val(f ) ≥ val(f ′ ) für alle
Flüsse f ′ in N gilt.
Übung 4.1
In Brutopia ist der Diktator Brutus I. auf Druck des Auslands zurückgetreten, jetzt soll eine Demokratie in dem Land eingeführt werden. Die m verschiedenen gesellschaftlichen Gruppierungen (Widerstandsgruppen, Gewerkschaften,
religiöse Gruppen, einflußreiche Verbände usw.) haben sich darauf geeinigt, ein
Übergangsparlament zu bilden, in das jede Gruppe einen Vertreter entsendet (das
Parlament hat also genau m Mitglieder). Um von Anfang an Gleichberechtigung
zu demonstrieren, soll dabei der Anteil von Frauen und Männern ausgewogen
sein. Man entschließt sich daher, Obergrenzen bF und bM (jeweils etwas mehr
als m
2 , um die Parlamentsbildung leichter zu machen) für die Anzahl von Frauen bzw. Männern im Parlament festzusetzen.
Können Sie dem brutopischen Volk helfen, ein Übergangsparlament zu bestimmen, indem Sie das Problem als Netzwerkflussproblem formulieren? Beachten
Sie, dass jeder Brutopier Mitglied mehrerer gesellschaftlicher Gruppierungen
sein kann.
17
MaxFlowMinCut-Theorem
Definition 6 (Schnitt, Kapazität)
Eine Menge X ⊆ V mit s ∈ X und t ∈ V \ X heißt s-t-Schnitt (engl. cut).
Die Kapazität von X ist definiert durch
cap(X) =
Lemma 2
Sei N ein Netzwerk und f ein Fluß in N und X ein beliebiger s-t-Schnitt. Dann
gilt
val(f ) =
Satz 2 (MaxFlowMinCut-Theorem)
Sei N ein Netzwerk. Dann gilt:
Übung 4.2
Bestimmen Sie einen minimalen Schnitt im folgenden Graphen. Wie groß ist
der maximale s,t-Fluss? Können Sie anhand eines oder mehrerer minimaler
Schnitte einen maximalen s,t-Fluss bestimmen?
2
v1
2
v4
1
7
5
s
v3
3
4
t
4
5
6
6
v2
v5
3
18
Der Algorithmus von Ford-Fulkerson
Definition 7 (Restnetzwerk)
~ s, t, c) ein Netzwerk und f ein Fluss in N .
Sei N = (V, E,
~ f , s, t, cf ),
Das Restnetzwerk von N bezüglich f ist definiert als Nf := (V, E
~
wobei wir zunächst die Kapazitätsfunktion c mittels c(x, y) := 0 für (x, y) ∈
/ E
auf ganz V × V erweitern. Dann setzen wir

falls f (x, y) > 0

falls f (y, x) > 0
cf (x, y) :=

sonst
~ f := {(x, y) : cf (x, y) > 0}.
sowie E
Lemma 3
Wenn f ein Fluss in N und W ein gerichteter Pfad im Restnetzerk Nf sind,
dann sei 0 < δ := mine∈W cf (e) und definiere f ′ wie folgt:
1. Falls (x, y) ∈ W und δ < f (y, x), setze f ′ (x, y) := 0 und f ′ (y, x) :=
f (y, x) − δ.
2. Falls (x, y) ∈ W und δ ≥ f (y, x), setze f ′ (x, y) := f (x, y) + δ − f (y, x)
und f ′ (y, x) := 0.
3. Falls (x, y) 6∈ W und (y, x) 6∈ W , setze f ′ (x, y) := f (x, y).
Dann ist f ′ ein Fluss in N mit val(f ′ ) > val(f ). (Wir sagen, dass wir f ′ aus
f durch Augmentieren von f entlang von W erhalten haben.)
Algorithmus 9 (Ford-Fulkerson)
~ s, t, c)
Input: Netzwerk N = (V, E,
Output: Fluss f
~ s, t, c))
Ford-Fulkerson(N = (V, E,
(1)
f := 0
(2)
while ∃ s-t-Pfad W in Nf
(3)
Satz 3
Sei N ein Netzwerk mit Kapazitäten aus
. Dann terminiert Algorithmus 9
nach höchstens
Schritten mit einem Fluss maximalen Werts.
19
Übung 4.3
Betrachten sie das folgende Netzwerk N mit den angegebenen Flusskapazitäten:
12
v1
v4
20
16
s
4
10
9
t
7
4
13
v2
v3
14
Berechnen Sie mit Hilfe des Algorithmus von Ford-Fulkerson einen maximalen Fluss von N . Geben Sie dabei in jedem Schritt das Restnetzwerk und den
augmentierenden Pfad an.
20
Schichtnetzwerk und der Algorithmus von Dinic
Definition 8 (Saturiert, Schichtnetzwerk, Durchsatz)
~ s, t, c) ein Netzwerk und f ein Fluss in N .
Sei N = (V, E,
• Der Fluss f heißt saturiert,
~ f , s, t, cf )
• Das geschichtete Restnetzwerk ist definiert als GNf = (V ′ , GE
mit
k := distNf (s, t),
V0 := {s},
V ′ := V0 ∪ · · · ∪ Vk ,
Vk := {t},
Vi := {x ∈ V : distNf (s, x) = i},
~ f :=
GE
• Der Durchsatz eines Knotens v 6∈ {s, t} ist definiert als
DS(v) =
für s bzw. t setzen wir
DS(s) =
und
Funktionsweise Dinic:
•
•
•
•
•
•
Laufzeit:
21
DS(t) =
Algorithmus 10
~ f , s, t, cf ), Knoten v, Fluss g
Input: GNf = (V ′ , GE
Output: Fluss g
PushFlow(v, g)
(1)
Q := {v}, push[v] := DS(v)
(2)
foreach x ∈ V ′ \ {v} do push[x] := 0
(3)
while Q 6= {t}
(4)
v:=Dequeue (Q)
(5)
while push[v] 6= 0
~f
(6)
wähle Kante (v, x) ∈ GE
(7)
if cf (v, x) ≥ push[v] then
(8)
push[x] := push[x] + push[v]
(9)
g(v, x) := g(v, x) + push[v]
(10)
push[v] := 0
(11)
else
(12)
push[x] := push[x] + cf (v, x)
(13)
g(v, x) := g(v, x) + cf (v, x)
(14)
push[v] := push[v] − cf (v, x)
(15)
if x 6∈ Q then Enqueue (Q, x)
(16)
return g
Algorithmus 11
~ f , s, t, cf )
Input: GNf = (V ′ , GE
Output: Fluss g
~ f , s, t, cf ))
MaxFlow(GNf = (V ′ , GE
(1)
g := 0
(2)
while es gibt s-t-Pfad in GNf
(3)
v:=Knoten mit minimalem Durchsatz
(4)
g := PushFlow (GNf , v, g)
(5)
g := PullFlow (GNf , v, g)
(6)
aktualisiere Kapazitäten in GNf
(7)
entferne rekursiv Knoten von Durchsatz 0 und
(8)
Kanten mit Kapazitäten 0 aus GNf
(9)
(aber berechne kein neues Restnetzwerk)
Algorithmus 12
~ s, t, c))
Dinic(N = (V, E,
(1)
f := 0
(2)
while es gibt s-t-Pfad in GNf
(3)
f := f + MaxFlow (GNf )
(4)
berechne GNf neu
22
Übung 4.4
Welche der folgenden Aussagen sind richtig?
(a) Im nebenstehenden geschichteten Netzwerk wird durch einmaligen Aufruf
von PushFlow und PullFlow ein Fluss mit Wert 9 erzeugt.
00000
11111
111111
000000
000000
111111
111111
000000
000000
111111
00000
11111
00000000000000
111111
11111111
000000
111111
000000
111111
0000
1111
00000
11111
000000
111111
0000000
1111111
000000
111111
000000
111111
0000
1111
00000
11111
000000
111111
0000000 1111
1111111
1111111111
00000000000000
4
4
5
4
4
4
s
5
5
5
t
4
(b) Im nebenstehenden geschichteten Netzwerk wird durch einmaligen Aufruf
von PushFlow und PullFlow ein Fluss mit Wert 1 erzeugt.
1
1
1
1
s
1
1
1
t
1
1
1
(c) Im nebenstehenden geschichteten Netzwerk wird durch einmaligen Aufruf
von PushFlow und PullFlow ein Fluss mit Wert 2 erzeugt.
1
2
s
3
2
1
t
3
1
2
2
1
1
(d) Das nebenstehenden Netzwerk stimmt mit seinem geschichteten Restnetzwerk zum Fluss mit Wert 0 überein.
1
1
s
1
1
1
1
1
1
1
1
t
1
1
23
Übung 4.5
Welche der folgenden Aussagen sind richtig?
(a) Das Restnetzwerk eines Graphen zu gegebenem Fluss ist eindeutig.
(b) Das geschichtete Restnetzwerke eines Graphen zu gegebenem Fluss ist eindeutig.
(c) Ein Fluss hat genau dann maximalen Wert, wenn er saturiert ist.
(d) Es kann in einem Netzwerk zwei saturierte Flüsse mit unterschiedlichem,
nicht-maximalen Wert geben.
(e) In den Restnetzwerken, die im Dinic-Algorithmus erzeugt werden, wächst
die Distanz von s zu t stets streng.
Übung 4.6
Betrachten Sie das nachfolgend abgebildete Netzwerk.
Die Kapazitäten der Kanten stehen in den Kreisen, die anderen Zahlen geben
den derzeitigen Fluss f an. Bestimmen Sie mithilfe des Algorithmus von Dinic
einen maximalen Fluss. Geben Sie dabei die entsprechenden Restnetzwerke und
die darin enthaltenen saturierenden Flüsse an.
24
5
Matchings
Grundlegendes
Definition 9 (Matching, maximales, größtes, perfektes, Matchingzahl)
Sei G = (V, E) ein Graph.
• Eine Menge M ⊆ E heißt Matching, falls
• M heißt
– maximales Matching, wenn
– größtes Matching, wenn
– perfektes Matching, wenn
• Die Matchingzahl ist definiert als
• Ein Knoten v heißt überdeckt von M , wenn es eine Kante e ∈ M mit
v ∈ e gibt.
Bemerkungen 1
1. Es gilt:
M maximales Matching
M größtes Matching
M perfektes Matching
2. Sei
τ (G) := min{ℓ ∈ N : es gibt eine Knotenüberdeckung der Größe ℓ in G}.
die Knotenüberdeckungszahl.
(a) Dann gilt: ν(G) ≤ τ (G) ≤ 2ν(G)
(b) Ist G = (A ∪ B, E) bipartit, dann gilt:
25
Übung 5.1
Sei G ein beliebiger Graph auf n Knoten. Welche der folgenden Aussagen sind
richtig? (α(G) := max{k ∈ N : ∃k-stabile Menge in G} (Stabilitätszahl))
(a) α(G) ≤ τ (G).
(b) α(G) ≤ n − τ (G).
(c) α(G) ≥ n − τ (G).
Sei G = (A ∪ B, E) ein bipartiter Graph auf 2n Knoten. Welche der folgenden
Aussagen sind richtig, welche falsch?
(d) Wenn α(G) = n ist, so besitzt G ein perfektes Matching.
(e) Wenn G ein perfektes Matching besitzt, so ist α(G) = n.
26
Der Flussalgorithmus
Funktionsweise:
• Überführe den bipartiten Graphen G = (A ∪ B, E) in ein Netzwerk N =
~ s, t, c) wie folgt
(V ∪ {s, t}, E,
• Dann gilt
•
•
Laufzeit:
Übung 5.2
Bestimmen Sie mit Hilfe des Flussalgorithmus ein maximales Matching im folgenden Graphen:
8
6
7
3
4
1
2
27
9
5
Augmentierende Pfade und der Algorithmus von Hopcraft
und Karp
Definition 10 (Alternierende und Augmentierende Pfade)
Sei M ein Matching in G = (V, E).
• Ein Pfad in G heißt M -alternierend, wenn
• Ein Pfad in G der Länge ≥ 1 heißt M -augmentierend, wenn
Definition 11 Sei M ein Matching in G. Dann sei
∞
falls M größtes Matching
ℓ(M ) :=
min{ℓ(P ) : P ist M -augm. Pfad}
sonst
Algorithmus 13 (Hopcroft-Karp)
Input: Graph G = (A ∪ B, E)
Output: Matching M
Hopcroft–Karp(G = (A ∪ B, E))
(1)
M := ∅
(2)
while ℓ(M ) < ∞
(3)
S:= nicht von M -überdeckte Knoten in A
(4)
T := Knoten, die von S aus über M -augmentierende
Pfade der Länge ℓ(M ) erreichbar sind.
(5)
bestimme mittels DFS ausgehend von den Knoten in
T eine inklusionsmaximale Menge knotendisjunkter
M -augmentierender Pfade der Länge ℓ(M )
(6)
Satz 4
Algorithmus 13 findet in einem bipartiten Graphen ein größtes Matching und
lässt sich mit einer Laufzeit von
Schritten implementieren.
Übung 5.3
Gegeben sei der folgende Graph:
(a) Gibt es eine Möglichkeit für HopkroftKarp, nach einer Augmentationsphase ein größtes Matching in G gefunden zu haben?
(b) Gibt es eine Möglichkeit für HopkroftKarp, mehere Augmentationsphasen zu brauchen, um in G ein größtes Matching zu finden?
28
Der Satz von Hall
Satz 5 (Heiratssatz von Hall)
Sei G = (A ∪ B, E) ein bipartiter Graph. Dann gilt: G hat genau dann ein
perfektes Matching, wenn
(i)
(ii)
wobei NG (S) die Menge aller Knoten in B ist, die mindestens einen Nachbarn
in der Menge S haben.
Übung 5.4 (Ein unendliches Gegenbeispiel zum Satz von Hall)
Finden Sie einen bipartiten Graphen G = (A ∪ B, E) mit unendlichen Knotenmengen A und B und der Eigenschaft |Γ(S)| ≥ |S| für jedes endliche S ⊆ A
und jedes endliche S ⊆ B, sodass G kein perfektes Matching enthält.
Übung 5.5
Bei einer Weihnachtsfeier soll jedes Kind genau vier Geschenke erhalten. Es
gibt daher viermal so viele Geschenke wie Kinder. Natürlich darf ein Kind dabei nur solche Geschenke bekommen, die es mag, sonst fängt es an zu weinen.
Geben Sie eine hinreichende und notwendige Bedingung dafür an, dass alle Geschenke verteilt werden und kein Kind weint, und beweisen Sie deren Korrektheit.
Übung 5.6
Welche der folgenden Aussagen sind richtig?
(a) Jeder 2-reguläre Graph mit perfektem Matching ist bipartit.
(b) Jeder r-reguläre bipartite Graph besitzt ein perfektes Matching.
(c) Jeder 3-reguläre Graph besitzt ein perfektes Matching.
29