Fortgeschrittenenpraktikum Versuch F23 Gewinnmessung nach

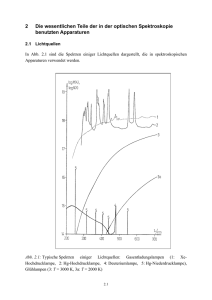
Fortgeschrittenenpraktikum
Versuch F23
Gewinnmessung nach Hakki und Paoli
Inhaltsverzeichnis
Einleitung
Hintergrund
Gewinn in Halbleitern
Die Halbleiterlaserdiode
Messung des Gewinns
Messung des Spektrums
Ein paar Worte zum Einfluss der endlichen Instrumentenauflösung
Aufgabenstellung und Versuchsdurchführung
Zusammenfassung
Bestimmung des Schwellstroms bei verschiedenen Temperaturen
Bestimmung des Brechungsindex des verwendeten Lasermaterials
Justieren der Laserdiode gegenüber dem Monochromator
Bestimmung der Gewinnspektren
Literatur
3
4
4
7
8
10
11
14
14
14
14
14
15
15
Einleitung
In diesem Versuch soll das temperatur- und ladungsträgerabhängige Gewinnspektrum von
Halbleiter-Laserdioden bestimmt werden.
In der Vorbereitung zum Versuch sollen Sie sich Kenntnisse in Halbleiterphysik und Optik
aneignen.
Insbesondere sind Kenntnisse auf folgenden Feldern verlangt:
• Bandstruktur und Bandlücke von Halbleitern
• Absorption und Verstärkung optischer Strahlung in Halbleitern
• Aufbau und Funktionsweise einer Halbleiterlaserdiode
• Funktionsweise und Auflösung eines optischen Gitters bzw. Gittermonochromators
• Gewinnmessung nach Hakki und Paoli
Im Anhang zu dieser Versuchsanleitung sind verschiedene Zeitschriftenartikel und Ausschnitte
aus Lehrbüchern zusammengestellt, um weiterführende und speziellere Erläuterungen zum
Versuch zu geben. Grundlegendere Kenntnisse, beispielsweise der Halbleiterphysik oder der
Optik, müssen Sie sich gegebenenfalls selbst mit Hilfe weiterer Lehrbücher aneignen.
Hintergrund
Hier kann und soll nur eine extrem kurze Zusammenfassung der wichtigsten Aspekte des
Hintergrundes des Versuchs gegeben werden. Ein ausführliches Studium der angegebenen
Lehrbuchliteratur ist unbedingt notwendig, um alles zu verstehen.
Als bekannt werden vorausgesetzt: (parabolische) Bandstruktur eines direkten Halbleiters,
Zustandsdichte, Funktionsweise einer pn-Diode
Gewinn in Halbleitern
Strahlende elektronische Übergänge zwischen den einzelnen Bändern eines Halbleiters sind
vergleichbar mit denen zwischen den elektronischen Niveaus eines Atoms. In beiden Fällen
können unter anderem die folgenden, für diesen Versuch interessierenden Prozesse stattfinden
(siehe Abb. 1):
vorher
nachher
vorher
nachher
vorher
nachher
Leitungsband
Valenzband
spontane Emission
Absorption
stimulierte Emission
Abb. 1: Mögliche Emissions-/Absorptionsprozesse im Halbleiter
Spontane Emission: Ein Elektron aus dem Leitungsband rekombiniert spontan mit einem Loch
im Valenzband (man sagt auch, das Elektron fällt vom Leitungsband ins Valenzband). Die
entsprechende Energiedifferenz wird dabei in Form eines Photons abgegeben.
Absorption: Ein einfallendes Photon regt ein Elektron aus dem Valenzband in das Leitungsband
an, wobei ein Loch im Valenzband zurückbleibt. Die gesamte Energie des Photons wird dabei
exakt auf das Elektron übertragen, d.h. das Photon wird „vernichtet“, bzw. das Licht wird
abgeschwächt.
Stimulierte Emission: Ein einfallendes Photon stimuliert ein Elektron-Loch-Paar zur
Rekombination. Das beim Rekombinationsprozess emittierte Photon hat dann genau die gleiche
Energie (bzw. Wellenlänge), Phase und Polarisationsrichtung wie das einfallende Photon, das
dabei natürlich nicht verloren geht. Man kann also sagen, dass das Licht verstärkt wird. Auf
diesem Prinzip beruhen die Laser.
Natürlich können noch viele weitere, kompliziertere Prozesse (z.B. Zwei-Photonen-Prozesse,
Störstellen-, Auger- oder Exzitonenprozesse) stattfinden. In den folgenden Betrachtungen
werden aber nur die drei oben genannten „einfachen“ Prozesse betrachtet.
Bei genauerer Betrachtung sieht man, dass natürlich nicht jedes beliebige Photon emittiert oder
absorbiert werden kann, sondern nur Photonen der passenden Energie. D.h., die Energie des
Photons muss genau (innerhalb des Rahmens der Unschärferelation) der Energie, die bei der
Rekombination von Elektron und Loch frei wird, entsprechen (Energieerhaltung!). Prozesse, an
denen weitere Teilchen (z.B. Phononen) beteiligt sind, die zusätzlich zur Energie- oder
Impulsbilanz beitragen könnten, werden hier ebenfalls nicht weiter berücksichtigt.
Im Gegensatz zum Atom sind im Halbleiter die beteiligten Niveaus nicht scharf, sondern es
handelt sich um breite sogenannte Bänder, insbesondere um das Leitungsband und das
Valenzband.
Wovon hängt es nun ab, welcher der drei Prozesse stattfindet? Insbesondere ist die Frage
interessant, wovon es abhängt, ob bei Einfall eines Photons nun Absorption oder Emission
stattfindet.
Für ein 2-Niveau-System lässt sich diese Frage relativ leicht beantworten, die entsprechenden
Berechnungen finden Sie im Anhang als Kopie aus dem Bergmann-Schäfer, Band Optik.
Für den Halbleiter stellt sich die Lage etwas komplizierter dar, da die Niveaus nicht scharf sind,
sondern sich über einen breiten Energiebereich erstrecken. Zudem ist die
Besetzungswahrscheinlichkeit nicht konstant über diesen Bereich.
Es lassen sich jedoch vorab erst einmal folgende prinzipielle Überlegungen anstellen.
Die Anzahl der Elektronen ist proportional zum Produkt aus der Zustandsdichte D(E) des
jeweiligen Bandes und der Besetzungswahrscheinlichkeit f(E) (Fermifunktion).
Sowohl Zustandsdichte als auch Besetzungswahrscheinlichkeit sind eine Funktion der Energie.
Die entsprechenden Graphen der Funktion sind in Abb. 2 dargestellt.
Abb. 2: Fermifunktion, Zustandsdichte und Elektronen- bzw. Lochkonzentration im Leitungs- bzw.
Valenzband (aus [1]).
Wie man sieht, fängt die Anzahl der Elektronen (und der Löcher) für kleine Energien bei Null
an, durchläuft dann ein Maximum, um zu hohen Energien wieder auf Null hin abzufallen.
Die Wahrscheinlichkeit für stimulierte Emission (als Funktion der Photonenenergie), die ja
proportional zum Produkt der Anzahl der Löcher im Valenzband und der Elektronen im
Leitungsband ist, wird also ebenfalls bei Null Anfangen, ein Maximum durchlaufen und dann
wieder auf Null abfallen. Qualitativ ist die Funktion in Abb. 3 dargestellt.
Wahrscheinl. stim. Emiss. [w.E.]
0
Energie [w.E]
Abb. 3: Qualitativer Verlauf der photonenenergieabhängigen Wahrscheinlichkeit für die stimulierte
Emission alleine (ohne Absorption)
Absorptionswahrscheinlichkeit [w.E.]
Der zweite interessante Fall ist die Absorption. Hier kann man eine Betrachtung analog zum
Fall der stimulierten Emission durchführen. Die Absorptionswahrscheinlichkeit ist proportional
zur Anzahl der passenden Elektronen im Valenzband (Elektron = fehlendes Loch,
Besetzungswahrscheinlichkeit = 1-fVB,Löcher(E) ) und zur Anzahl der freien Zustände im
Leitungsband (Besetzungswahrscheinlichkeit = 1-fLB,Elektronen(E) ). Qualitativ ergibt sich damit
die in Abb. 4 gezeigte Funktion.
0
Eg
Energie [w.E]
Abb. 4: Qualitativer Verlauf der photonenenergieabhängigen Wahrscheinlichkeit für die Absorption alleine
(ohne stimulierte Emission)
In der Realität finden nun beide Prozesse gleichzeitig statt, für die Nettoverstärkung (oder
-abschwächung) kommt es also auf die Differenz zwischen beiden Größen an. Das
Übergangsmatrixelement ist für beide Vorgänge gleich, ebenso die beteiligten Zustandsdichten,
so dass sich die Rechnung im Prinzip recht einfach gestaltet.
Der exakte Verlauf der beiden Kurven hängt dabei vor allem von der Zustandsdichte und der
Fermiverteilung ab. Die Zustandsdichte hängt vor allem von der Temperatur ab (wegen der
Temperaturabhängigkeit der Bandlückenenergie) und die Fermiverteilung hängt sowohl von der
Temperatur als auch von der z.B. durch anlegen eines Stromes variierbaren Ladungsträgerdichte
in den Bändern ab.
Anmerkung: Eine Diode, durch die durch Anlegen einer Spannung ein Strom fließt, befindet
sich nicht mehr im thermodynamischen Gleichgewicht. Dementsprechend gibt es auch kein
Ferminiveau mehr in diesem Halbleiter. Allerdings kann man (unter bestimmten, meistens
erfüllten Voraussetzungen) noch sogenannte „Quasi-Ferminiveaus“ einführen, die getrennt für
die Elektronen im Leitungsband und die Löcher im Valenzband jeweils wieder die
Besetzungswahrscheinlichkeit mit Hilfe der Fermifunktion berechenbar machen. Diese QuasiFerminiveaus sind dann allerdings nicht mehr ortsunabhängig für den gesamten
Halbleiterkristall, sondern können über den Ort im Kristall variieren.
Je höher die Stromdichte in der aktive Zone der Laserdiode ist, desto mehr freie Ladungsträger
werden in das Valenz- und Leitungsband injiziert. Damit sind mehr Zustände in den
entsprechenden Bändern mit den jeweiligen Ladungsträgern besetzt und die stimulierte
Emission wird immer wahrscheinlicher, während die Absorption immer unwahrscheinlicher
wird. Dementsprechend steigt der Gewinn immer mehr an.
Ein Beispiel für berechnete Gewinnkurven für verschiedene Ladungsträgerdichten sind in der
folgenden Abb. 5 dargestellt.
Abb. 5: Berechnete Abhängigkeit des Gewinns von GaAs für verschiedene Ladungsträgerdichten (aus [2]).
In Abb. 5 ist der Gewinn in Abhängigkeit der Photonenenergie dargestellt, wie es unter
Physikern, die sich mit dem Halbleiter selbst befassen, üblich ist. Ansonsten wird
normalerweise, wenn man sich mehr mit dem emittierten Licht selbst beschäftigt, die
Darstellung in Abhängigkeit der Wellenlänge des Lichtes gewählt. Da Photonenenergie und
Lichtfrequenz über E = hν fest miteinander verknüpft sind, und außerdem c = λν gilt, lassen
sich Photonenenergie und Wellenlänge leicht ineinander umrechnen. Dabei entspricht die
Energie von 1 eV der Energie, die ein Elektronen beim Durchlaufen eines elektrischen Feldes
von 1 V aufnimmt, also 1 eV = 1,6022·10-19 J.
Die Halbleiterlaserdiode
Aus dem oben gesagten ist es bereits ersichtlich, dass man bei Erreichen einer genügend hohen
Ladungsträgerdichte in einem Halbleiter eine optische Verstärkung erzielen kann. Falls man
nun dieses Material in einen geeigneten Resonator einbringt, könnte damit prinzipiell ein Laser
gebaut werden.
Aufbau und Funktionsweise einer Laserdiode sind im beiliegenden Auszug aus dem Buch
„Optoelektronische Halbleiterbauelemente“ erläutert.
Messung des Gewinns
Intensität [w.E.]
Es gibt verschiedene Arten, den Gewinn von Halbleitermaterialien zu messen. Die zunächst
scheinbar einfachste wäre, einfach Licht verschiedener Wellenlänge durch einen
entsprechenden Halbleiter zu strahlen und die optische Leistung vor und hinter dem Material zu
bestimmen. Dieses Verfahren kann (und wird auch) prinzipiell angewandt werden, stößt jedoch
gerade bei Laserdiodenstrukturen auf Probleme.
Laserdioden bestehen prinzipiell aus einem pn-Übergang überlagert von einer
Doppelheterostruktur und somit aus einer nur sehr dünnen Schicht, die optischen Gewinn
aufweist. Daher müsste man bei der Durchstrahlmethode den Lichtstrahl in diese (und nur
diese) Schicht einkoppeln, was nicht ohne Probleme geht. Deshalb wurden andere Verfahren
zur Bestimmung des Gewinns der optisch aktiven Zone entwickelt.
Eines dieser Verfahren ist die Methode nach Hakki und Paoli, die diese im Jahre 1975 erstmals
ausführlich zur Untersuchung von Laserdioden anwandten (siehe auch beigefügten
Zeitschriftenartikel).
Bei der Messung wird folgendermaßen vorgegangen. Es wird das Spektrum der verstärkten
spontanen Emission (Abb. 6) unterhalb der Laserschwelle gemessen.
8
6
4
2
0
1500
1520
1540
1560
1580
1600
Wellenlänge [nm]
Abb. 6: Spektrum einer Laserdiode unter der Schwelle
Die Minima und Maxima in Abb. 6 werden durch destruktive bzw. konstruktive Interferenz der
zwischen den Laserfacetten mehrfach hin und her reflektierten Lichtwellen verursacht und
werden wie folgt berechnet.
Man betrachtet das Feld, das vom Inneren der Laserdiode her auf eine der beiden Facetten,
beispielsweise die linke, trifft. Dieses habe die Feldstärke F. Wenn R die Reflektivität der
Facette (gemessen für die Intensität des Lichtes) sei, dann ist r = R1/2 der Reflektionswert für
die Feldstärke. Von der Facette aus nach rechts wird sich also das Licht mit der Feldstärke
F1,l − r = r ⋅ F
(1)
ausbreiten und durch den Laser laufen. Im Laser selbst erfahre es die (für verschiedene optische
Frequenzen ν verschiedene) Verstärkung g(ν) durch den stromdurchflossenen Halbleiter (g
kann auch negativ sein, dann wird das Feld abgeschwächt!). Zusätzlich wird das Feld durch die
ladungsträgerdichteunabhängigen Verluste α abgeschwächt. Nach dem Durchlaufen eines
Stückes Halbleiter der Länge L (= Laserlänge) hat das Feld die Intensität
F2,l − r = F1,l − r ⋅ e
g (ν ) −α
L
2
= r ⋅ F ⋅e
g (ν ) −α
L
2
.
(2)
Im Exponenten der e-Funktion steht der Faktor ½, da hier die Feldstärke und nicht die Intensität
des Lichtes berechnet wird.
Dieses Feld wird reflektiert (Faktor r) und läuft zurück durch die Laserdiode zur linken Facette.
An der linken Facette kommt also Licht mit der Feldstärke
F3, r −l = F2,l − r ⋅ r ⋅ e
g (ν ) −α
L
2
= r ⋅ F ⋅e
g (ν ) −α
L
2
⋅r ⋅e
g (ν ) −α
L
2
= F ⋅ r 2 ⋅ e( g (ν ) −α ) L
(3)
an.
Im Falle konstruktiver Interferenz, die ja die Maxima des in Abb. 6 gezeigten Spektrums bilden,
überlagern sich beide Feldstärken (und die aller weiteren Umläufe) additiv, so dass sich für die
Gesamtfeldstärke
F + = F + F ⋅ r 2 ⋅ e( g (ν ) −α ) L + F ⋅ r 4 ⋅ e 2( g (ν ) −α ) L + ...
(4)
ergibt. Mit R=r2 ergibt sich
∞
F + = F ∑ R n ⋅ e n ( g (ν ) −α ) L .
(5)
x = R ⋅ e ( g (ν ) −α ) L
(6)
n =0
Diese Gleichung lässt sich mit
umschreiben zu
∞
F + = F ∑ xn .
(7)
n =0
Die Summe lässt sich leicht ausrechnen. Für x < 1 gilt
∞
∑x
n =0
n
=
1
1− x
(8)
und es ergibt sich somit
F + (ν ) =
F
1 − R ⋅ e(
g (ν ) −α ) L
.
(9)
An dieser Stelle sieht man auch gleich, dass dieses Verfahren nur unterhalb der Laserschwelle
gilt. Der Faktor R·e(g(ν)-α)L, mit dem das optische Feld nach jedem Umlauf multipliziert wird,
muss kleiner als 1 sein. Das bedeutet, dass keine Lasertätigkeit stattfindet.
Die analoge Rechnung lässt sich für die Minima durchführen. Zu beachten ist hier, dass sich die
Feldstärken nach einem Umlauf in der Laserkavität destruktiv überlagen, und erst nach zwei
Umläufen wieder eine konstruktive Überlagerung stattfindet. Somit ergibt sich die zu Gl. 4
analoge Gleichung für die Feldstärke in den Minima zu
F − = F − F ⋅ r 2 ⋅ e( g (ν ) −α ) L + F ⋅ r 4 ⋅ e 2( g (ν ) −α ) L − F ⋅ r 6 ⋅ e3( g (ν ) −α ) L + F ⋅ r 8 ⋅ e 4( g (ν ) −α ) L − ...
(10)
F − = F (1 − r 2 ⋅ e( g (ν ) −α ) L )(1 + r 4 ⋅ e 2( g (ν )−α ) L + r 8 ⋅ e 4( g (ν ) −α ) L + r12 ⋅ e6( g (ν )−α ) L + ...) .
(11)
bzw.
Die Summe lässt sich genau wie die vorherige ausrechnen, und es ergibt sich
F − (ν ) =
bzw.
F ⋅ (1 − R ⋅ e(
1− R ⋅ e
2
g (ν ) −α ) L
2( g (ν ) −α ) L
)
(12)
F − (ν ) =
F ⋅ (1 − R ⋅ e(
(1 − R ⋅ e
( g (ν ) −α ) L
g (ν ) −α ) L
)(1 + R ⋅ e
)
( g (ν ) −α ) L
)
=
F
1 + R ⋅ e(
g (ν ) −α ) L
.
(13)
In der (Max/Min-) Methode von Hakki und Paoli wird aus dem Verhältnis der Lichtleistung
(~Feldstärke2) am Maximum zur Lichtleistung im benachbarten Minimum der Gewinn
berechnet. Dabei wird davon ausgegangen, dass sich sowohl F als auch g nur wenig mit der
Lichtfrequenz ändern und über einen Modenabstand als konstant angesehen werden können.
Somit ergibt sich nach kurzer Rechnung (bitte selbst nachvollziehen!)
g (ν ) − α =
1 ⎛ P+ − P− ⎞
1
ln ⎜
⎟+
L ⎜⎝ P + + P − ⎠⎟ L ⋅ ln( R)
(14)
wobei P+/- die optischen Leistungen in den Maxima und Minima der FP-Moden sind.
Damit ist es im Prinzip also recht einfach möglich, den wellenlängenabhängigen (bzw.
frequenzabhängigen) Gewinn einer Laserdiode zu messen.
Die Länge L in Gl. (14) lässt sich einfach, beispielsweise unter einem Mikroskop, ausmessen.
Die Reflektivitäten der Facette lassen sich auch relativ einfach bestimmen. Aus der Länge L
und dem Abstand der einzelnen FP-Moden lässt sich sofort der Brechungsindex des Materials
bestimmen, und mit Hilfe des Brechungsindex kann man dann die Reflektivität (senkrechter
Einfall) der Grenzfläche Luft-Halbleiter bestimmen.
Schwieriger ist es mit den Wellenleiterverlusten in der Laserkavität (α). Diese ließen sich
bestimmen, wenn man gleiche Laserdioden verschiedener Länge zur Verfügung hätte, was in
diesem Versuch aber leider nicht gegeben ist. Für die Auswertung reicht es, wenn man hier
einen typischen Wert von α = 3 cm-1 annimmt.
Messung des Spektrums
Das optische Spektrum, das von der Laserdiode emittiert wird, wird in diesem Versuch mit
einem Gittermonochromator vermessen. Der Aufbau und die Funktionsweise eines
Gittermonochromators werden als bekannt vorausgesetzt bzw. können bei Bedarf z.B. im Skript
zum Praktikum „Methoden der Angewandten Physik“, Versuch „Emissionsspektroskopie“
nachgelesen werden (http://sol.physik.tu-berlin.de/htm_group/teaching/scripte/emspek.pdf).
Zur Detektion des durch den Monochromator in seine spektralen Anteile zerlegten Lichts wird
ein Diodenzeile, häufig auch Reticon genannt, verwendet.
Ein Reticon besteht aus vielen nebeneinander angeordneten Photodioden, so dass Licht
verschiedener Wellenlängen, das ja im Monochromator räumlich separiert wird, auf
verschiedene Dioden trifft. Auf diese Weise kann das Spektrum schneller gemessen werden, als
wenn durch Drehen des Gitters die verschiedenen Wellenlängen nacheinander auf den
Ausgangsspalt und dann auf einen einzigen Detektor fallen würde (parallele statt serieller
Verarbeitung). Nachteilig ist jedoch die häufig schlechtere Empfindlichkeit und vor allem die
Tatsachen, dass die „Ausgangsspaltbreite“ durch die Geometrie der Dioden festgelegt ist und
nicht mehr variabel dem Messproblem entsprechend angepasst werden kann.
Der Strahlenverlauf im Inneren des Monochromators für z.B. drei verschiedene Wellenlängen
ist in der folgenden Abb. 7 skizziert.
Parabol-Spiegel
Schwenkbarer
Spiegel
Eingangsspalt
Gitter
Reticon
Parabol-Spiegel
Schwenkbarer
Spiegel
Abb. 7: Strahlenverlauf im Inneren des Monochromators, skizziert für drei verschiedene Wellenlängen
Wie man aus der Abbildung sieht, wird der Eingangsspalt für verschiedene Wellenlängen auf
verschiedene Positionen am Ausgang abgebildet. Durch Auswertung mit dem Reticon können
so die Intensitäten der verschiedenen Wellenlängen gleichzeitig aufgenommen werden. Dabei
wird jedem Reticonkanal eine andere Wellenlänge zugeordnet.
Ein paar Worte zum Einfluss der endlichen Instrumentenauflösung
Bei diesem Experiment, wie auch bei fast allen anderen, ist es wichtig, sich Gedanken über die
endliche Instrumentenauflösung zu machen.
Mit der endlichen Instrumentenauflösung ist die Tatsache gemeint, dass man unterhalb einer
bestimmten Differenz zweier Messgrößen diese mit einem entsprechenden Messinstrument
nicht mehr getrennt registrieren kann. Dabei kann es sich beispielsweise um
Längenunterschiede (Ortsauflösung), Zeitunterschiede (Zeitauflösung) oder aber, wie beim
Monochromator, um Wellenlängenunterschiede (Wellenlängenauflösung) handeln. Unter dem
Auflösungsvermögen versteht man die kleinste Differenz zweier Größen, die von einem
entsprechenden Messinstrument noch getrennt registriert werden kann.
Diese „Ungenauigkeit“ des Messergebnisses, die durch die endliche Auflösung hervorgerufen
wurde, darf man jedoch nicht mit Messfehlern bedingt durch statistische Schwankungen, durch
systematische Fehler, durch Rauschen oder anderes verwechseln. Die Auflösung lässt sich, im
Gegensatz zu den Fehlern, durch geeignete mathematische Methoden (sogenannte Entfaltung)
nach der Messung herauskorrigieren, sofern die genaue Funktion der durch die endliche
Auflösung bedingten Veränderungen genügend genau bekannt ist.
Der Einfluss der Auflösung auf das Messergebnis soll für diesen Versuch kurz erläutert werden,
eine Berücksichtigung im Rahmen der Auswertung würde jedoch zu weit führen und ist deshalb
nicht verlangt.
Das Auflösevermögen des Monochromators kann man in erster Näherung als gaußförmig
annehmen. D.h., falls Licht mit einer (gedachten) unendlich scharfen Wellenlänge mit dem
Monochromator gemessen wird, wird auf dem Reticon (und damit auf den verschiedenen
„Wellenlängenkanälen“) eine gaußförmige Verteilung der Energie entstehen, siehe Abb. 8.
Um es hier noch einmal ganz deutlich zu sagen: Das Licht, das nach Durchgang durch den
Monochromator auf das Reticon fällt, hat natürlich immer noch nur eine einzige, unendliche
scharfe Wellenlänge. Durch die endliche Auflösung des Monochromators werden keine neuen
Wellenlängen erzeugt! Das Licht fällt jedoch nicht auf einen einzigen Punkt am Ausgang,
sondern wird örtlich „verschmiert“ und damit bei der Interpretation der Messung als eine
Wellenlängenverteilung gedeutet. Bzw., genauer gesagt, es lässt sich nicht mehr ohne weiteres
genau sagen, welche Wellenlänge eigentlich ursprünglich auf den Monochromator fiel. Durch
die gaußförmige Verteilung wird „vorgegaukelt“, dass die gedachte Wellenlänge nicht
unendlich scharf ist, sondern die Form einer Gaußkurve hat. (An diesem Beispiel sieht man
auch gleich, dass man die endliche Instrumentenauflösung auch prinzipiell wieder
herausrechnen könnte. Wenn man weiß, dass die Instrumentenauflösung eine Gaußkurve mit
der Breite ∆λ ist, und man dann eine Gaußkurve mit der Breite ∆λ misst, kann diese nur von
einer unendlich scharfen Laserlinie mit der Wellenlänge genau im Mittelpunkt der Gaußkurve
erzeugt worden sein.)
Monochromatoreingang
Monochromatorausgang
Intensität
Intensität
hohe Auflösung
Wellenlänge
geringe Auflösung
Ort
Abb. 8: Schematische Darstellung der Signale am Eingang und Ausgang des Monochromators
Die entscheidende Frage ist: Stellt dieses ein Problem für die Auswertung in diesem Versuch
dar?
Durch die Verteilung der Energie auf einen breiteren Bereich werden die gemessenen
Maximalwerte kleiner als die wirklichen Werte. Da dieses aber für alle Wellenlängen in der
gleichen Weise geschieht, und in der Auswertung die absolute Stärke des Signals keine Rolle
spielt, würde das erst einmal keinerlei Einfluss auf die Genauigkeit der Auswertung haben.
Das Problem in diesem Versuch ergibt sich erst dadurch, dass hier ein kontinuierliches
Spektrum gemessen wird. Zum Messwert der Energie für eine Wellenlänge tragen auch die
benachbarten Wellenlängen bei, deren gaußförmige Auflösung zum Teil ja auch in den
betrachteten Wellenlängenkanal fällt. In den Maxima des Spektrums ist die Energie in den
benachbarten Wellenlängen jedoch geringer als die der nominell gemessenen Wellenlänge,
während in den Minima diese Energie höher als bei der nominell gemessenen ist. Dadurch
werden die Maxima weniger stark erhöht als die Minima. Das gemessene Verhältnis der
Maxima und Minima zueinander ist also kleiner als in Wirklichkeit, und die Auswertung ergibt
dadurch falsche Ergebnisse.
Dem Problem der begrenzten Auflösung kann mal auf vielerlei Arten begegnen.
1) Bessere (bzw. passende) Auflösung wählen
Man kann natürlich versuchen, ein Messinstrument mit einer höheren Auflösung zu verwenden.
Da dieses jedoch praktisch immer mit höheren (und meistens sogar exponentiell ansteigenden)
Kosten verbunden ist, muss dieser Schritt in der Regel vorher genau überlegt werden.
Wenn die Auflösung deutlich (Faktor 3-10) besser als die kleinsten zu messenden Strukturen (in
diesem Versuch beispielsweise die Breite der einzelnen FP-Moden) ist, kann in den meisten
Fällen der Einfluss der Auflösung vernachlässigt werden, da er von der Größe her unter die
Größe der anderen Fehlerquellen fällt.
Manchmal gibt es jedoch auch gar keine Instrumente mit noch besserer Auflösung als die, die
einem bereits zur Verfügung stehen.
2) Nachträgliche Entfaltung
Wenn man die Auflösefunktion des verwendeten Instruments kennt (oder messen kann), so
kann man normalerweise durch Entfaltung die Messergebnisse den „wahren“ Werten annähern.
Da jedoch sowohl die eigentliche Messung selbst als auch die Instrumentenauflösung fehlerhaft
und verrauscht sind, geht dieses nicht unendlich gut. Trotzdem ist dieses ein vielfach
verwendetes Verfahren zur Verbesserung der „Auflösung“ der Messinstrumente, wobei häufig
die wahre Instrumentenauflösung durch eine Gaußfunktion angenähert wird (und schon hat man
wieder die erste Ungenauigkeit in Form eines systematischen Fehlers hineingebracht!)
3) Andere geeignete Auswerteverfahren
Manchmal gibt es auch Verfahren, um bei der Auswertung der Messergebnisse bessere
Ergebnisse zu erzielen. Bei der Hakki-Paoli-Methode beispielsweise gibt es ein
(komplizierteres) Auswerteverfahren, was (bei Benutzung der gleichen Messdaten) bessere
Ergebnisse liefert, ohne explizit die wahre, verwendete Instrumentenauflösung zu verwenden.
Dieses Verfahren geht zum Beispiel davon aus, dass aufgrund der endlichen Auflösung die
Energie (ohne verloren zu gehen) nur umverteilt wird, ohne explizit von der exakten Form der
Umverteilung gebrauch zu machen, und berechnet daraus durch geschickte Integralbildung
dann den Gewinn.
Einzelheiten dieser Methode würden jedoch den Rahmen des Praktikums sprengen und werden
deshalb weder in der Vorsprache noch in der Auswertung verlangt. Für Interessierte ist der
entsprechende Artikel „Technique for measurement of the gain spectra of semiconductor diode
lasers“ von D.T. Cassidy jedoch im Anhang beigelegt.
4) Ignorieren
Etwas, was man nie tun sollte, was aber leider doch zu oft gemacht wird.
Es ist eigentlich bei allen Experimenten immer extrem wichtig, sich vor der Messung (oder
wenigstens während der Auswertung) Gedanken über die Auflösung der verwendeten
Messgeräte und deren Einfluss auf die Ergebnisse zu machen. Wenigstens Punkt 1) sollte
immer bedacht werden.
Aufgabenstellung und Versuchsdurchführung
Zusammenfassung
Der Praktikumsversuch gliedert sich in mehrere Teilaufgaben
1. Bestimmung des Schwellstroms der Laserdiode bei verschiedenen Temperaturen
2. Bestimmung des Brechungsindex des verwendeten Lasermaterials
3. Justieren der Laserdiode gegenüber dem Monochromator
4. Bestimmung der Gewinnspektren des Halbleitermaterials bei verschiedenen
Temperaturen und Strömen
Bestimmung des Schwellstroms bei verschiedenen Temperaturen
Nehmen Sie die (qualitative) Lichtleistungs-Strom-Kennlinie (P-I-Kennlinie) der Laserdiode
bei den Temperaturen 20°C und 80°C auf.
Die Temperaturstabilisierung der Laserdiode wird auf die entsprechende Temperatur gesetzt.
Nachdem sich die korrekte Temperatur eingestellt hat, wird für verschiedene Ströme (typ. 0 mA
bis 60 mA) die Lichtleistung durch Messung des Stromes an einem vor die Laserdiode
gehaltenen Photodetektor gemessen. Da die absolute Lichtleistung in diesem Versuch
uninteressant ist, kann auf eine Kalibrierung des Detektors verzichtet werden. Durch
Auftragung der Messergebnisse in einem Diagramm kann der Schwellstrom für die
verschiedenen Temperaturen abgelesen werden.
Bestimmung des Brechungsindex des verwendeten Lasermaterials
Aus der Formel für ein Fabry-Perot-Filter lässt sich bei bekannter Länge und bekanntem
spektralen Abstand der einzelnen sogenannten FP-Moden der Brechungsindex berechnen, was
hier geschehen soll. Als erstes wird die Länge der Laserdiode unter dem Mikroskop
ausgemessen. Aus dem (im späteren Versuchsteil) gemessenen Spektrum kann dann der
Modenabstand und somit der Brechungsindex bestimmt werden. Länge und Brechungsindex
werden für die spätere Auswertung benötigt.
Justieren der Laserdiode gegenüber dem Monochromator
Der schwierigste Teil der Versuchsdurchführung ist die Justage der Laserdiode und der Linse
vor dem Monochromator. Hier muss iterativ vorgegangen werden. Mit etwas Glück ist die
Wellenlänge der Laserdiode (zumindest in etwa) bekannt, so dass der Monochromator erst
einmal auf diese Wellenlänge gefahren werden kann. Der Eingangsspalt des Monochromators
wird auf maximale Breite eingestellt. Anschließend sind die Laserdiode und die Linsen zuerst
per Hand und in späteren Schritten mit Hilfe der Feinjustage so zu justieren, dass maximales
Signal auf dem Detektor entsteht. Danach sind im ständigen Wechsel die Position von Linse
und Laserdiode zu variieren sowie sukzessive die Schlitze zu verengen (bis zu einer minimalen
Schlitzbreite von ca. 10 µm.
ACHTUNG!!! Intuitiv würde man das ganze bei möglichst starkem optischen Signal, also bei
einem Diodenstrom oberhalb der Laserschwelle, machen. Das Reticon ist jedoch empfindlich
gegenüber zu hohen Lichtleistungen und kann dabei sehr schnell zerstört werden! Daher ist erst
der Monochromator (bei ausgeschaltetem Laser) auf die entsprechende Mittenwellenlänge zu
fahren, um danach vorsichtig unter ständiger Beobachtung des Signals des Reticons den
Diodenstrom zu erhöhen. Dann kann die Justage per Hand erfolgen. Sollte es nötig sein, noch
einmal den Monochromator weit zu verfahren, ist vorher wieder die Laserdiode auszuschalten.
Bestimmung der Gewinnspektren
Anschließend sind die optischen Spektren unterhalb der eigentlichen Laserschwelle
aufzunehmen. Dabei sollen Sie zwei verschiedene Serien aufnehmen. Eine Serie (bei ca.
Zimmertemperatur) mit 5 verschiedenen Strömen sowie für einen konstanten Strom bei 4
verschiedenen Temperaturen (20°C, 40°C, 60°C und 80°C). Achten Sie bei der zweiten Serie
(am zweckmäßigsten bereits vor der ersten Messung) darauf, dass sich die Laserdiode für alle
Temperaturen beim gewählten Strom unterhalb der Schwelle befindet.
Für die Auswertung sind die jeweiligen Gewinnspektren aus den einzelnen Messungen zu
berechnen und für jede Serie in ein Diagramm zu zeichnen. (Hilfe: Origin bietet unter „tools“
die Funktion „pick peaks“, die bei korrekter Anwendung sehr hilfreich ist.)
Wie verschiebt sich das Gewinnmaximum mit der Temperatur bzw. mit dem Strom?
Literatur
[1] H. Ibach und H. Lüth, Festkörperphysik - Eine Einführung in die Grundlagen, Springer
Verlag, 1981
[2] G.H.B. Thompson, Physics of Semiconductor Laser Devices, Verlag John Wiley & Sons,
1980