1.1 Zeichen, Begriffe und Tafeln

1 MATHEMATIK
1.1 Zeichen, Begriffe und Tafeln
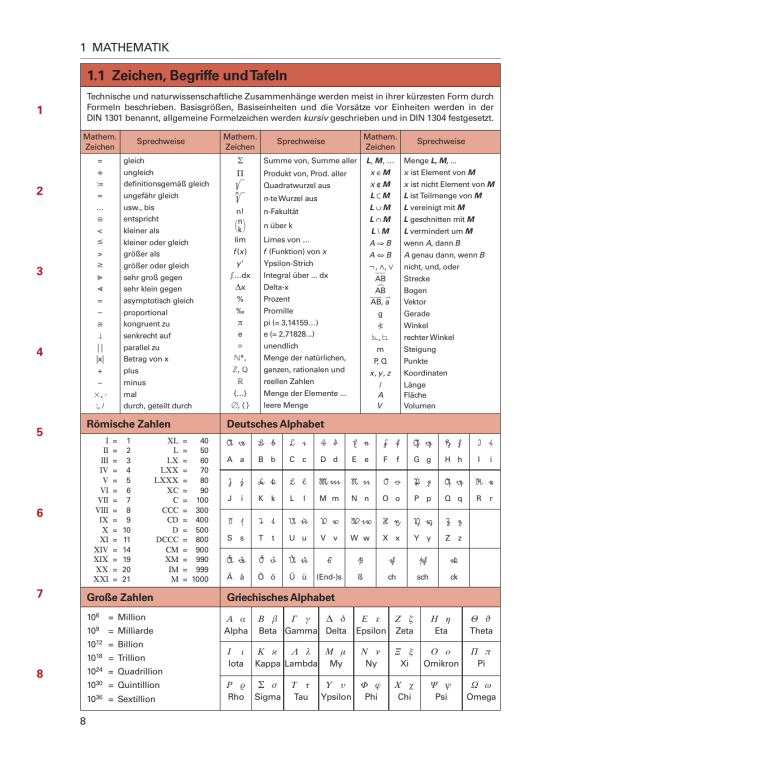
Technische und naturwissenschaftliche Zusammenhänge werden meist in ihrer kürzesten Form durch
Formeln beschrieben. Basisgrößen, Basiseinheiten und die Vorsätze vor Einheiten werden in der
DIN 1301 benannt, allgemeine Formelzeichen werden kursiv geschrieben und in DIN 1304 festgesetzt.
1
Mathem.
Zeichen
2
3
4
Sprechweise
gleich
Í
Summe von, Summe aller
L, M, …
Menge L, M, ...
ungleich
∏
Produkt von, Prod. aller
x ist EIement von M
y苶
y苶
Quadratwurzel aus
n-Fakultät
xBM
xCM
LIM
LrM
LRM
L\M
A⇒B
A⇔B
C, @, 3
苶
苶
AB
+
A
B
៮៬
៮៬
AB, a
:=
definitionsgemäß gleich
$
ungefähr gleich
…
usw., bis
≠
entspricht
<
kleiner als
à
kleiner oder gleich
n!
n
k
lim
f(x)
n
f (Funktion) von x
>
größer als
größer oder gleich
ñ
sehr groß gegen
Ÿ…dx
ï
sehr klein gegen
¤x
Delta-x
G
asymptotisch gleich
%
Prozent
ã
proportional
‰
Promille
¯
kongruent zu
π
pi (= 3,14159…)
a
r, R
Ypsilon-Strich
y’
Integral über ... dx
=
senkrecht auf
e
e (= 2,71828...)
parallel zu
∞
unendlich
|x|
Betrag von x
⺞*,
Menge der natürlichen,
+
plus
⺪, ⺡
ganzen, rationalen und
–
minus
{…}
mal
durch, geteilt durch
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
1
2
3
4
5
6
7
8
9
10
11
14
19
20
21
()
)
)(
)((
)(((
(_
_
___
_+
+
+___
_|
(|
&|
|
106
= Million
109
= Milliarde
1012 = Billion
1018 = Trillion
1024
= Quadrillion
1030 = Quintillion
1036 = Sextillion
L vermindert um M
wenn A, dann B
A genau dann, wenn B
nicht, und, oder
Strecke
Bogen
Vektor
Gerade
Winkel
rechter Winkel
Steigung
Punkte
Koordinaten
Länge
Fläche
Volumen
m
x, y, z
§
A
V
Menge der Elemente ...
⭋, { }
L vereinigt mit M
L geschnitten mit M
P, Q
reellen Zahlen
⺢
x ist nicht Element von M
L ist Teilmenge von M
g
||
Große Zahlen
8
n über k
Limes von …
á
&
&&
&&&
&*
*
*&
*&&
*&&&
&(
(
(&
(&*
(&(
((
((&
8
n-te Wurzel aus
冢冣
Römische Zahlen
7
Sprechweise
=
:, /
6
Mathem.
Zeichen
Sprechweise
7
⳯, ·
5
Mathem.
Zeichen
leere Menge
Deutsches Alphabet
=
40
=
50
=
60
=
70
=
80
=
90
= 100
= 300
= 400
= 500
= 800
= 900
= 990
= 999
= 1000
A a
B b
C c
D d
E e
F f
G g
H h
I i
A a
B b
C c
D d
E e
F
f
G g
H h
I
i
J j
K k
L l
Mm
N n
O o
P p
Q q
R r
J
i
K k
L
l
M m
N n
O o
P p
Q q
R
S
s
T t
U u
V v
Ww
X x
Y y
Z z
S s
T
t
U u
V v
W w
X x
Y y
Z
Ä ä
Ö ö
Ü ü
%
ß
£
s£
§
Ä ä
Ö ö
Ü ü
(End-)s
ß
ch
sch
ck
r
z
Griechisches Alphabet
Å å
Alpha
‹ ∫
Ì ©
¤ ∂
Beta Gamma Delta
Û ⁄
lota
ˆ Δ
fl ¬
˘ μ
Kappa Lambda My
› ~
Ny
¸ ®
Rho
Í ‚
Sigma
Ï ƒ
Phi
˝ †
Tau
Á ¨
Ypsilon
‰ ™
ˇ Ω
Epsilon Zeta
Ó ª
Eta
ı «
Theta
Ù ≈
Xi
Ø ø
Omikron
∏ π
Pi
Ç ç
Chi
‡ ¥
Psi
„ ∑
Omega
1.1 Zeichen, Begriffe und Tafeln
Umwandlungstabellen
Längeneinheiten
⇒
1 km = 1000 m
⳯ 10
1m
0,1 m
0,01 m
0,001 m
⳯ 10
10 dm
1 dm
0,1 dm
0,01 dm
: 10
⳯ 100
1 m2
0,01 m2
0,0001 m2
0,000 001 m2
⳯ 100
100 dm2
1 dm2
0,01 dm2
0,0 001 dm2
: 100
⳯ 1000
m3
1
0,001 m3
0,000 001 m3
0,000 000 001 m3
⇐
2
⳯ 100
10 000 cm2
100 cm2
1 cm2
0,01 cm2
: 100
1 000 000 mm2
10 000 mm2
100 mm2
1 mm2
: 100
⇐
1 km3 = 1 000 000 000 m3
Volumeneinheiten
⇒
1
1 000 mm
100 mm
10 mm
1 mm
: 10
1km2 = 1 000 000 m2
Flächeneinheiten
⇒
⳯ 10
100 cm
10 cm
1 cm
0,1 cm
: 10
⳯ 1000
dm3
1 000
1 dm3
0,001 dm3
0,000 001 dm3
: 1000
3
⳯ 1000
1 000 000
1 000 cm3
1 cm3
0,001 cm3
: 1000
cm3
mm3
1 000 000 000
1 000 000 mm3
1 000 mm3
1 mm3
: 1000
⇐
Masseeinheiten
⇒
⳯ 1000
1t
0,001 t
0,000 001 t
0,000 000 001 t
⳯ 1000
1 000 000 000 mg
1 000 000 mg
1 000 mg
1 mg
: 1000
1 000 000 g
1 000 g
1g
0,001 g
: 1000
1000 kg
1 kg
0,001 kg
0,000 001 kg
: 1000
Krafteinheiten
⇒
⳯ 1000
1 000 kN
1 kN
0,001 kN
: 1000
Winkeleinheiten
(Grad)
1° = 60’
(Minute) 1’ = 60”
(Sekunde) 1”
5
1 000 000 N
1 000 N
1N
: 1000
⇐
1 Pa
1 MN/m2
1 kN/cm2
1 kN/m2
=
=
=
=
1 N/m2
1 N/mm2
10 N/mm2
0,001 N/mm2
1 kg ≠ 9,81 N (Im Bauwesen darf 9,81 auf 10 aufgerundet werden.)
Masse-/Krafteinheiten
0,1 kg
1 kg
10 kg
100 kg
1000 kg (1 t)
⇐
Einheiten der Spannung
⳯ 1000
1 MN
0,001 MN
0,000 001 MN
4
⳯ 1000
alte Einheiten:
1 Pfd. = 0,5 kg
1 Ztr. = 50 kg
1 dz = 100 kg
1N
10 N
100 N
1 000 N (1 kN)
10 000 N (10 kN)
180° entspricht 200gon
1 rad = (180/π)°
1gon = (9/10)°
1°
= (10/9)gon
(1 Pfund)
(1 Zentner)
(1 Doppelzentner)
Zeiteinheiten
(Jahr) 1 a = 365 d
(Tag)
1 d = 24 h
(Stunde) 1 h = 60’
Besondere Flächeneinheiten
Besondere Volumeneinheiten
1 Zoll (”)
1 inch
1 mile
1 mil
1 ft
1 yd
1 km2
1 ha
1a
1 Morgen
1 sq in
1 sq ft
1 hî
1 barrel
1 gallone
1î
1 cu in
= 100 ha
= 100 a
= 100 m2
= 25 a
= 6,452 cm2
= 0,0929 m2
7
(Minute) 1’ = 60”
(Sekunde) 1” = (1/60)’
(Monat) 1 m = (1/12) a
Besondere Längeneinheiten
= 2,5400 cm
= 1 Zoll
= 1609 m
= 0,0245 mm
= 0,3048 m (foot)
= 0,9144 m (yard)
6
= 100 î
= 1,59 hî
= 4,546 î
= 1 dm3
= 16,39 cm3 (cubic
inch)
8
9
1.1 Zeichen, Begriffe und Tafeln
1
Interpolation
Aufrunden und Abrunden
Tabellen z.B. enthalten immer nur eine Auswahl
von einander zugeordneten Zahlen- oder Funktionswerten (der Funktionswert y1 wird dem
Argument x1 zugeordnet).
Aufrunden: Die letzte Ziffer einer gerundeten Zahl
ist um 1 zu erhöhen, wenn die nächste Ziffer der
nichtgerundeten Zahl 5 oder größer ist.
y = Funktionswert
Abrunden: Die letzte Ziffer einer gerundeten Zahl
bleibt unverändert, wenn die nächste Ziffer der
nichtgerundeten Zahl kleiner als 5 ist.
Beispiele
y1
π = 3,14159265 … wird durch
2
x = Argument
x1
3
Werte zwischen zwei bekannten Größen lassen
sich durch lineare Interpolation bestimmen,
wenn vorausgesetzt wird, dass der Zuwachs der
Funktionswerte y proportional zum Zuwachs der
Argumente x erfolgt.
(y1 – y0) · (x – x0)
y = y0 + ᎏᎏ
x1 – x0
x
x1
x
Für Tabellen gegenläufiger Tendenz von Argument und Funktionswert gilt:
(y0 – y1) · (x1 – x)
y = y1 + ᎏᎏ
ᎏ
x1 – x0
y0 220
y
y1 195
x0 < x < x1
y0 > y > y1
3,30
x0
x1
x
Gesucht ist der Wasserbedarf w für die Körnungsziffer Δ = 3,95.
Bezugswert
Δ
Funktionswert
w in Liter
x1
4,20
195
y1
x0
3,30
220
y0
(220 – 195) · (4,20 – 3,95)
y = 195 + ᎏᎏᎏ = 201,9
4,20 – 3,30
10
=
=
=
=
10–1 Dezi
Beispiel
8
0,001
0,01
0,1
1
10–3
10–2
10–1
100
1000
100
10
1
= 106
= 107
= 108
= 109
=
=
=
=
103
102
101
100
= 1 Million
= 10 Millionen
= 100 Millionen
= 1 Milliarde
Vorsätze vor Einheiten
4,20
x
143,257 zu 143
4 339 111 zu 4 340 000
Zehnerpotenzen
1 000 000
10 000 000
100 000 000
1 000 000 000
y
7
Im Bauwesen genügt häufig eine Bestimmung
von Zahlenwerten auf drei Stellen genau
(Rechenschiebergenauigkeit). Dabei wird nach
den vorgenannten Regeln auf- oder abgerundet.
3,14159… zu 3,14
344 600 zu 345 000
x0 < x < x1
y0 < y < y1
x0
6
Signifikante Stellen
Bei drei signifikanten Stellen wird
y1
y
y0
5
aufgerundet auf Zehntausendstel,
aufgerundet auf Tausendstel,
abgerundet auf Hundertstel,
abgerundet auf Zehntel.
Beispiele
y
4
3,1416
3,142
3,14
3,1
(d) 1 Dezimeter
10–2 Centi (c)
10–3 Milli
1 Zentimeter
(m) 1 Millimeter
= (1/10) m
= 10 cm
= (1/100) m
= 1 cm
= (1/1000) m
= 1 mm
10–6 Mikro (µ) 1 Mikrometer
= 1-millionstel
Meter
10–9 Nano (n) 1 Nanometer
= 10–9 m
10–12 Pico
= 10–12 m
(p) 1 Picometer
Beispiel
10–4 = 0,0001
1 ist die vierte Stelle hinter dem
Komma
1.1 Zeichen, Begriffe und Tafeln
Trigonometrische Funktionen
䊳
0° … 45°
ƒ
0° … 45°
ƒ
in Grad
sin ƒ
tan ƒ
0
0,000 0
0,000 0
1
2
3
4
5
0,017 5
0,034 9
0,052 3
0,069 8
0,087 2
0,017 5
0,034 9
0,052 4
0,069 9
0,087 5
6
7
8
9
10
0,104 5
0,121 9
0,139 2
0,156 4
0,173 6
11
12
13
14
15
S. 28
1
in Grad
sin ƒ
90
45
0,707 1
1,000 0
45
89
88
87
86
85
46
47
48
49
50
0,719 3
0,731 4
0,743 1
0,754 7
0,766 0
1,035 5
1,072 4
1,110 6
1,150 4
1,191 8
44
43
42
41
40
0,105 1
0,122 8
0,140 5
0,158 4
0,176 3
84
83
82
81
80
51
52
53
54
55
0,777 1
0,788 0
0,798 6
0,809 0
0,819 2
1,234 9
1,279 9
1,327 0
1,376 4
1,428 1
39
38
37
36
35
0,190 8
0,207 9
0,225 0
0,241 9
0,258 8
0,194 4
0,212 6
0,230 9
0,249 3
0,267 9
79
78
77
76
75
56
57
58
59
60
0,829 0
0,838 7
0,848 0
0,857 2
0,866 0
1,482 6
1,539 9
1,600 3
1,664 3
1,732 1
34
33
32
31
30
16
17
18
19
20
0,275 6
0,292 4
0,309 0
0,325 6
0,342 0
0,286 7
0,305 7
0,324 9
0,344 3
0,364 0
74
73
72
71
70
61
62
63
64
65
0,874 6
0,882 9
0,891 0
0,898 8
0,906 3
1,804 1
1,880 7
1,962 6
2,050 3
2,144 5
29
28
27
26
25
21
22
23
24
25
0,358 4
0,374 6
0,390 7
0,406 7
0,422 6
0,383 9
0,404 0
0,424 5
0,445 2
0,466 3
69
68
67
66
65
66
67
68
69
70
0,913 5
0,920 5
0,927 2
0,933 6
0,939 7
2,246 0
2,355 9
2,475 1
2,605 1
2,747 5
24
23
22
21
20
26
27
28
29
30
0,438 4
0,454 0
0,469 5
0,484 8
0,500 0
0,487 7
0,509 5
0,531 7
0,554 3
0,577 4
64
63
62
61
60
71
72
73
74
75
0,945 5
0,951 1
0,956 3
0,961 3
0,965 9
2,904 2
3,077 7
3,270 9
3,487 4
3,732 1
19
18
17
16
15
31
32
33
34
35
0,515 0
0,529 9
0,544 6
0,559 2
0,573 6
0,600 9
0,624 9
0,649 4
0,674 5
0,700 2
59
58
57
56
55
76
77
78
79
80
0,970 3
0,974 4
0,978 1
0,981 6
0,984 8
4,010 8
4,331 5
4,704 6
5,144 6
5,671 3
14
13
12
11
10
36
37
38
39
40
0,587 8
0,601 8
0,615 7
0,629 3
0,642 8
0,726 5
0,753 6
0,781 3
0,809 8
0,839 1
54
53
52
51
50
81
82
83
84
85
0,987 7
0,990 3
0,992 5
0,994 5
0,996 2
6,313 8
7,115 4
8,144 4
9,514 4
11,430 1
9
8
7
6
5
41
42
43
44
45
0,656 1
0,669 1
0,682 0
0,694 7
0,707 1
0,869 3
0,900 4
0,932 5
0,965 7
1,000 0
49
48
47
46
45
86
87
88
89
90
0,997 6
0,998 6
0,999 4
0,999 85
1,000 0
14,300 7
19,081 1
28,636 3
57,290 0
,∞
4
3
2
1
0
cos ƒ
cot ƒ
ƒ
cos ƒ
cot ƒ
ƒ
45° … 90°
in Grad
tan ƒ
45° … 90°
2
3
4
5
6
7
8
in Grad
11
1.1 Zeichen, Begriffe und Tafeln
Bestimmungsstücke eines Kreisabschnitts
2
3
4
5
6
7
8
12
Grad
h
ᎏᎏ
r
s
ᎏᎏ
r
A
ᎏᎏ2
r
1
2
3
4
5
0,017 5
0,034 9
0,052 4
0,069 8
0,087 3
0,000 0
0,000 2
0,000 3
0,000 6
0,001 0
0,017 5
0,034 9
0,052 4
0,069 8
0,087 2
0,000 00
0,000 00
0,000 01
0,000 03
0,000 06
6
7
8
9
10
11
12
13
14
15
0,104 7
0,122 2
0,139 6
0,157 1
0,174 5
0,192 0
0,209 4
0,226 9
0,244 3
0,261 8
0,001 4
0,001 9
0,002 4
0,003 1
0,003 8
0,004 6
0,005 5
0,006 4
0,007 5
0,008 6
0,104 7
0,122 1
0,139 5
0,156 9
0,174 3
0,191 7
0,209 1
0,226 4
0,243 7
0,261 1
0,000 10
0,000 15
0,000 23
0,000 32
0,000 44
0,000 59
0,000 76
0,000 97
0,001 21
0,001 49
16
17
18
19
20
21
22
23
24
25
0,279 3
0,296 7
0,314 2
0,331 6
0,349 1
0,366 5
0,384 0
0,401 4
0,418 9
0,436 3
0,009 7
0,011 0
0,012 3
0,013 7
0,015 2
0,016 7
0,018 4
0,020 1
0,021 9
0,023 7
0,278 3
0,295 6
0,312 9
0,330 1
0,347 3
0,364 5
0,381 6
0,398 7
0,415 8
0,432 9
0,001 81
0,002 17
0,002 57
0,003 02
0,003 52
0,004 08
0,004 68
0,005 35
0,006 07
0,006 86
26
27
28
29
30
31
32
33
34
35
0,453 8
0,471 2
0,488 7
0,506 1
0,523 6
0,541 1
0,558 5
0,576 0
0,593 4
0,610 9
0,025 6
0,027 6
0,029 7
0,031 9
0,034 1
0,036 4
0,038 7
0,041 2
0,043 7
0,046 3
0,449 9
0,466 9
0,483 8
0,500 8
0,517 6
0,534 5
0,551 3
0,568 0
0,584 7
0,601 4
0,007 71
0,008 62
0,009 61
0,010 67
0,011 80
0,013 01
0,014 29
0,015 66
0,017 11
0,018 64
36
37
38
39
40
41
42
43
44
45
0,628 3
0,645 8
0,663 2
0,680 7
0,698 1
0,715 6
0,733 0
0,750 5
0,767 9
0,785 4
0,048 9
0,051 7
0,054 5
0,057 4
0,060 3
0,063 3
0,066 4
0,069 6
0,072 8
0,076 1
0,618 0
0,634 6
0,651 1
0,667 6
0,684 0
0,700 4
0,716 7
0,733 0
0,749 2
0,765 4
0,020 27
0,021 98
0,023 78
0,025 68
0,027 67
0,029 76
0,031 95
0,034 25
0,036 64
0,039 15
46
47
48
49
50
51
52
53
54
55
0,802 9
0,820 3
0,837 8
0,855 2
0,872 7
0,890 1
0,907 6
0,925 0
0,942 5
0,959 9
0,079 5
0,082 9
0,086 5
0,090 0
0,093 7
0,097 4
0,101 2
0,105 1
0,109 0
0,113 0
0,781 5
0,797 5
0,813 5
0,829 4
0,845 2
0,861 0
0,876 7
0,892 4
0,908 0
0,923 5
0,041 76
0,044 48
0,047 31
0,050 25
0,053 31
0,056 49
0,059 78
0,063 19
0,066 73
0,070 39
A
Halbmesser
Bogenlänge
Bogenhöhe
Sehnenlänge
Fläche des
Kreisabschnitts
ƒ Bogenmaß
ƒ° Zentriwinkel
(in Grad)
s
f
S. 23
r
b
h
s
A
b
h
1
b
ᎏᎏ
r
r
ƒ in
䊳
䊳
S. 13
ƒ°
b = r · π · ᎏᎏ
180°
ƒ
s = 2 r · sin ᎏᎏ
2
ƒ
h = 2 r · sin2 ᎏᎏ
4
ƒ°
r2
A = ᎏᎏ · π · ᎏᎏ – sin ƒ
2
180°
冢 冣
ƒ in
冢 冣
冢
冣
Grad
b
ᎏᎏ
r
h
ᎏᎏ
r
s
ᎏᎏ
r
A
ᎏᎏ2
r
56
57
58
59
60
61
62
63
64
65
0,977 4
0,994 8
1,012 3
1,029 7
1,047 2
1,064 7
1,082 1
1,099 6
1,117 0
1,134 5
0,117 1
0,121 2
0,125 4
0,129 6
0,134 0
0,138 4
0,142 8
0,147 4
0,152 0
0,156 6
0,938 9
0,954 3
0,969 6
0,984 8
1,000 0
1,015 1
1,030 1
1,045 0
1,059 8
1,074 6
0,074 17
0,078 08
0,082 12
0,086 29
0,090 59
0,095 02
0,099 58
0,104 28
0,109 11
0,114 08
66
67
68
69
70
71
72
73
74
75
1,151 9
1,169 4
1,186 8
1,204 3
1,221 7
1,239 2
1,256 6
1,274 1
1,291 5
1,309 0
0,161 3
0,166 1
0,171 0
0,175 9
0,180 8
0,185 9
0,191 0
0,196 1
0,201 4
0,206 6
1,089 3
1,103 9
1,118 4
1,132 8
1,147 2
1,161 4
1,175 6
1,189 6
1,203 6
1,217 5
0,119 19
0,124 43
0,129 82
0,135 35
0,141 02
0,146 83
0,152 79
0,158 89
0,165 14
0,171 54
76
77
78
79
80
81
82
83
84
85
1,326 5
1,343 9
1,361 4
1,378 8
1,396 3
1,413 7
1,431 2
1,448 6
1,466 1
1,483 5
0,212 0
0,217 4
0,222 9
0,228 4
0,234 0
0,239 6
0,245 3
0,251 0
0,256 9
0,262 7
1,231 3
1,245 0
1,258 6
1,272 2
1,285 6
1,298 9
1,312 1
1,325 2
1,338 3
1,351 2
0,178 08
0,184 77
0,191 60
0,198 59
0,205 73
0,213 01
0,220 45
0,228 04
0,235 78
0,243 67
86
87
88
89
90
1,501 0
1,518 4
1,535 9
1,553 3
1,570 8
0,268 6
0,274 6
0,280 7
0,286 7
0,292 9
1,364 0
1,376 7
1,389 3
1,401 8
1,414 2
0,251 71
0,259 90
0,268 25
0,276 75
0,285 40
1.1 Zeichen, Begriffe und Tafeln
Zahlentabellen
Exponential-, Hyperbel-,
Logarithmusfunktionen
x
ex
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,6
3,6
3,7
3,8
3,9
4,0
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
5,0
1,000
1,105
1,221
1,350
1,492
1,649
1,822
2,014
2,226
2,460
2,718
3,004
3,320
3,669
4,055
4,482
4,953
5,474
6,050
6,686
7,389
8,166
9,025
9,974
11,023
12,182
13,464
14,880
16,445
18,174
20,086
22,198
24,533
27,113
29,964
33,115
36,598
40,447
44,701
49,402
54,598
60,340
66,686
73,700
81,451
90,017
99,484
109,947
121,510
134,290
148,413
sinh (x) cosh (x)
0,000
0,100
0,201
0,305
0,411
0,521
0,637
0,759
0,888
1,027
1,175
1,336
1,509
1,698
1,904
2,129
2,376
2,646
2,942
3,268
3,627
4,022
4,457
4,937
5,466
6,050
6,695
7,406
8,192
9,060
10,018
11,076
12,246
13,538
14,965
16,543
18,285
20,211
22,339
24,691
27,290
30,162
33,336
36,843
40,719
45,003
49,737
54,969
60,751
67,141
74,203
1,000
1,005
1,020
1,045
1,081
1,128
1,185
1,255
1,337
1,433
1,543
1,669
1,811
1,971
2,151
2,352
2,577
2,828
3,107
3,418
3,762
4,144
4,568
5,037
5,557
6,132
6,769
7,473
8,253
9,115
10,068
11,122
12,287
13,575
14,999
16,573
18,313
20,236
22,362
24,711
27,308
30,178
33,351
36,857
40,732
45,014
49,747
54,978
60,759
67,149
74,210
Konstanten (gerundet)
ln (x)
lg (x)
,–
– 2,303
– 1,609
– 1,204
– 0,916
– 0,693
– 0,511
– 0,357
– 0,223
– 0,105
0,000
0,095
0,182
0,262
0,336
0,405
0,470
0,531
0,588
0,642
0,693
0,742
0,788
0,833
0,875
0,916
0,956
0,993
1,030
1,065
1,099
1,131
1,163
1,194
1,224
1,253
1,281
1,308
1,335
1,361
1,386
1,411
1,435
1,459
1,482
1,504
1,526
1,548
1,569
1,589
1,609
,–
– 1,000
– 0,699
– 0,523
– 0,398
– 0,301
– 0,222
– 0,155
– 0,097
– 0,046
0,000
0,041
0,079
0,114
0,146
0,176
0,204
0,230
0,255
0,279
0,301
0,322
0,342
0,362
0,380
0,398
0,415
0,431
0,447
0,462
0,477
0,491
0,505
0,519
0,531
0,544
0,556
0,568
0,580
0,591
0,602
0,613
0,623
0,633
0,643
0,653
0,663
0,672
0,681
0,690
0,699
Größe
Zahlenwert
1
Größe
Zahlenwert
π
3,141 593
e
2π
6,283 185
e2
2,718 282
7,389 056
3π
9,424 778
e3
20,085 537
y苶
e
1,648 721
y苶
e
1,395 612
π:3
1,047 198
π:4
0,785 398
π : 180
0,017 453
eπ
23,140 693
π2
9,869 604
e2 π
535,491 656
3
π3
31,006 277
eπ/2
4,810 477
y苶
π
1,772 454
e– π
0,043 214
3
y苶
π
1,464 592
1:e
0,367 879
1:π
0,318 310
1 : e2
0,135 335
180 : π
57,295 780
y1/e
苶
0,606 531
1 : π2
0,101 321
ee
15,154 262
y苶
1/π
0,564 190
πe
22,459 158
In π
1,144 730
In 10
2,302 585
lg π
0,497 150
lg e
0,434 294
y苶
2
1,414 214
y苶
3
1,732 051
y苶
5
2,236 068
y苶
6
2,449 490
y苶
7
2,645751
y10
苶
3,162 278
2
3
4
Umrechnungstabelle
Grad – Gon – Rad (Bogenmaß)
Grad
Rad
Gon
5
Rad
Rad
Grad
Gon
1
2
3
4
5
0,0175
0,0349
0,0524
0,0698
0,0873
1
2
3
4
5
0,0157
0,0314
0,0471
0,0628
0,0785
0,1
0,2
0,3
0,4
0,5
5,73
11,46
17,19
22,92
28,65
6,37
12,73
19,10
25,46
31,83
6
7
8
9
0,1047
0,1222
0,1396
0,1571
6
7
8
9
0,0942
0,1100
0,1257
0,1414
0,6
0,7
0,8
0,9
34,38
40,11
45,84
51,57
38,20
44,56
50,93
57,30
10
20
30
40
50
0,1745
0,3491
0,5236
0,6981
0,8727
10
20
30
40
50
0,1571
0,3142
0,4712
0,6283
0,7854
1,0
1,2
1,4
1,6
1,8
57,30 63,66
68,75 76,39
80,21 89,13
91,67 101,9
103,1
114,6
60
70
80
90
1,0472
1,2217
1,3963
1,5708
60
70
80
90
0,9425
1,0996
1,2566
1,4137
2,0
2,2
2,4
2,6
114,6
126,1
137,5
149,0
127,3
140,1
152,8
165,5
100
120
140
160
180
1,7453
2,0944
2,4435
2,7925
3,1416
100
126
150
175
200
1,5708
1,9635
2,3562
2,7489
3,1416
2,8
3,0
3,2
3,4
3,6
160,4
171,9
183,3
194,8
206,3
178,3
191,0
203,7
216,5
229,2
6
7
8
13
1 MATHEMATIK
1.2 Rechenarten
Grundrechenarten
1
Rechenart
Addition
Sonstige Rechenarten
a
b
Beispiel
a+b=c
Minuend
Subtrahend
Beispiel
a–b=c
Multiplikation
Faktor
Faktor
Beispiel
a·b=c
Division
Dividend
Divisor
Beispiel
a:b=c
Subtraktion
2
3
c
Summand Summand Summenwert
Differenzwert
Assoziativität
4
Distributivität
Produktwert
Quotientenwert
a+b = b+a
ab = ba
(a + b) + c = a + (b + c)
(ab) c = a (bc)
(a + b) c = ac + bc
a (b + c) = ab + ac
Stufen der Rechenarten
Stufe 1
Addition, Subtraktion
Stufe 2
Multiplikation, Division
Stufe 3
Potenzierung, Radizierung,
Logarithmierung
5
6
7
Beispiele Addition, Subtraktion
a+0 = 0+a = a
a + (b – c) = a + b – c
a – (b + c) = a – b – c
a – (b – c) = a – b + c
a – 0 = a aber 0 – a = – a
a + (– b) = a – b
a – (– b) = a + b
– (a + b) = – a – b
– (a – b) = – a + b = b – a
Beispiele Multiplikation
● Schreibweise: a · b = ab, 2 · a = 2 a, ab = ba
abc = acb = bac = bca = cab = cba
a·0=0·a=0a=0
a·1=1·a=1a=a
8
● Gleiche Vorzeichen ergeben plus,
ungleiche Vorzeichen ergeben minus:
(+ a) (+ b) = (– a) (– b) = + ab = ab
(+ a) (– b) = (– a) (+ b) = – ab
14
Potenzierung
Radizierung
a
b
c
Basis
Exponent
Potenzwert
Beispiel
ab = c
Radikand
Wurzelexponent
Beispiel
Addition und Multiplikation
Kommutativität
Rechenart
Logarithmierung
Wurzelwert
b
y苶
a=c
Logarithmand
Basis
Beispiel
logb a = c
Logarithmuswert
Rechenregeln ohne Klammern
Gleichstufige Rechenarten werden von links nach
rechts ausgeführt.
Beispiel 8 – 2 + 3
= 6 + 3
= 9
Bei ungleichstufigen Rechenarten wird die Rechenart höherer Stufe zuerst ausgeführt.
Beispiel 8 – 2 · 3
= 8 – 6
20 : 5 + 3 · 7 = 4 + 21
14 + 3 · 23
= 2
= 25
= 14 + 3 · 8 = 38
Klammerregeln
Die Rechnung innerhalb einer Klammer wird
stets vor der Rechnung außerhalb der Klammer
ausgeführt.
Beispiel (2 + 9) · 6
= 11 · 6 = 66
Bei mehrfacher Klammerung werden von innen
nach außen runde, eckige und geschweifte Klammern benutzt. Die Klammern werden von innen
nach außen aufgelöst.
Beispiel 2 · {3 + 4 · [26 – 2 · (3 + 4)] : 3}
2 · {3 + 4 · [26 – 2 · 7] : 3}
2 · {3 + 4 · 12 : 3}
2 · 19
=
=
=
= 38
Auflösen der Klammer mit PLUS (+) vor der
Klammer ⇒ Klammer kann entfallen
Auflösen der Klammer mit MINUS (–) vor der
Klammer ⇒ Klammer kann entfallen, wenn alle
Vorzeichen in der Klammer umgekehrt werden
Faktor vor der Klammer mit Summanden ⇒
Jeder Wert in der Klammer wird mit dem Faktor
mutipliziert.
Beispiele
(a +
(a –
(a +
(a –
(a –
b) (c
b) (c
b) (c
b) (c
b) c
+ d)
+ d)
– d)
– d)
=
=
=
=
=
c (a – b) = ac – bc
ac + ad + bc + bd
ac + ad – bc – bd
ac – ad + bc – bd
ac – ad – bc + bd
1.2 Rechenarten
Bruchrechnung
Rechenart,
Rechenoperation
Formeln und Rechenregeln
Beispiele
Erweitern
Multiplikation von Zähler und Nenner
mit gleicher Zahl. Wert bleibt gleich
a a n a·n
ᎏᎏ = ᎏᎏ · ᎏᎏ = ᎏᎏ
b b n b·n
2 2 7 2 · 7 14
ᎏᎏ = ᎏᎏ · ᎏᎏ = ᎏᎏ = ᎏᎏ
3 3 7 3 · 7 21
Kürzen
Division von Zähler und Nenner durch
die gleiche Zahl. Wert bleibt gleich
a a n a :n
ᎏᎏ = ᎏᎏ : ᎏᎏ = ᎏᎏ
b b n b:n
14 14 7 14 : 7 2
ᎏᎏ = ᎏᎏ : ᎏᎏ = ᎏᎏ = ᎏᎏ
21 21 7 21 : 7 3
Hauptnenner (HN)
bestimmen
Der Hauptnenner ist das kleinste
gemeinsame Vielfache (KgV) der
Nenner. Berechnung durch Zerlegung
der Nenner in Primfaktoren.
1 2 1 1
Hauptnenner von ᎏᎏ; ᎏᎏ; ᎏᎏ; ᎏᎏ
4 5 6 30
4 = 2·2
5 = 5
HN = 2 · 2 · 5 · 3 = 60
6 = 2·3
30 = 2 · 3 · 5
Addition
a c a+c
ᎏᎏ + ᎏᎏ = ᎏᎏ
b
b b
5 3 5+3 8
ᎏᎏ + ᎏᎏ = ᎏᎏ = ᎏᎏ = 1
8
8 8
8
a c a · d c · b (a · d) + (c · b)
ᎏᎏ + ᎏᎏ = ᎏᎏ + ᎏᎏ = ᎏᎏ
b·d
b d b·d d·b
oder nach vorheriger Ermittlung des
Hauptnenners.
2 1 2 · 5 1 · 3 10
13
3
ᎏᎏ + ᎏᎏ = ᎏᎏ + ᎏᎏ = ᎏᎏ + ᎏᎏ = ᎏᎏ
3 5 3 · 5 5 · 3 15 15 15
1 2 1 1 15 24 10 2
51
ᎏᎏ + ᎏᎏ + ᎏᎏ + ᎏᎏ = ᎏᎏ + ᎏᎏ + ᎏᎏ + ᎏᎏ = ᎏᎏ
4 5 6 30 60 60 60 60 60
a c a–c
ᎏᎏ – ᎏᎏ = ᎏᎏ
b
b b
5 3 2 1
ᎏᎏ – ᎏᎏ = ᎏᎏ = ᎏᎏ
8 8 8 4
a c a · d c · b (a · d) – (c · b)
ᎏᎏ – ᎏᎏ = ᎏᎏ – ᎏᎏ = ᎏ ᎏ
b·d
b d b·d d·b
oder nach vorheriger Ermittlung des
Hauptnenners.
2 1 2 · 5 1 · 3 10 3
7
ᎏᎏ – ᎏᎏ = ᎏᎏ – ᎏᎏ = ᎏᎏ – ᎏᎏ = ᎏᎏ
3 5 3 · 5 5 · 3 15 15 15
1 2 1 1 15 24 10 2
1
ᎏᎏ – ᎏᎏ + ᎏᎏ – ᎏᎏ = ᎏᎏ – ᎏᎏ + ᎏᎏ – ᎏᎏ = – ᎏᎏ
4 5 6 30 60 60 60 60
60
Bruch mit Zahl
a·n
a
ᎏᎏ · n = ᎏᎏ
b
b
3
3 · 5 15
7
ᎏᎏ · 5 = ᎏᎏ = ᎏᎏ = 1 ᎏᎏ
8
8
8
8
Bruch mit Bruch
a c a·c
ᎏᎏ · ᎏᎏ = ᎏᎏ
b d b·d
3 2 3·2
6
3
ᎏᎏ · ᎏᎏ = ᎏᎏ = ᎏᎏ = ᎏᎏ
8 5 8 · 5 40 20
Bruch durch Zahl
a
a
ᎏᎏ : n = ᎏᎏ
b
b·n
3
3
3
ᎏᎏ : 5 = ᎏᎏ = ᎏᎏ
8
8 · 5 40
Bruch durch Bruch
a c a d a·d
ᎏᎏ : ᎏᎏ = ᎏᎏ · ᎏᎏ = ᎏᎏ
b d b c b·c
3 2 3 5 15
ᎏᎏ : ᎏᎏ = ᎏᎏ · ᎏᎏ = ᎏᎏ
8 5 8 2 16
übliches Teilen des Zählers durch den
Nenner
8
ᎏᎏ = 8 : 3 = 2,66…
3
苶
= 2,6
gleichnamige Brüche
ungleichnamige Brüche
Subtraktion
gleichnamige Brüche
ungleichnamige Brüche
Multiplikation
Division
Umwandeln
gemeiner Bruch
in Dezimalzahl
2
3
ᎏᎏ = 3 : 8 = 0,375
8
Umwandeln
endliche Dezimalbrüche
reinperiodische
Dezimalbrüche
unreinperiodische
Dezimalbrüche
Vorzeichenregeln
beim Dividieren
Division durch 0
Erweitern mit 10, 100, 1000 usw.,
gegebenenfalls anschließend kürzen



Rechnung gemäß Beispiel
für unreinperiodische Dezimalbrüche
a
(+ a) : (+ b) = + a : b = + ᎏᎏ
b
a
(+ a) : (– b) = – a : b = – ᎏᎏ
b
a
(– a) : (– b) = + a : b = + ᎏᎏ
b
b70
b70
b70
1
3
4
5
8 : 3 = 2,66…
– ᎏᎏᎏ
6
20
periodische
–ᎏ
1ᎏᎏ
8
Wieder20
holung
0,375 · 1000
0,375 = ᎏᎏ =
1000
苶 = ᎏ3ᎏ
0,3
9
3 · 125 3
375
ᎏᎏ = ᎏᎏ = ᎏᎏ
1000 8 ·125 8
42
苶苶
0,4
2 = ᎏᎏ
99
苶苶
x = 2,34
2
2319
x = ᎏᎏ
990
苶苶
1000 · x = 2342,4
2
苶苶
– 10 · x = – 23,4
2
6
7
990 · x = 2319,00
3
(+ 3) : (+ 8) = + 3 : 8 = + ᎏᎏ
8
3
(+ 3) : (– 8) = – 3 : 8 = – ᎏᎏ
8
3
(– 3) : (– 8) = + 3 : 8 = + ᎏᎏ
8
8
Eine Division durch 0 ist unzulässig.
+ ∞ bzw. – ∞ sind keine reellen Zahlen.
15
1.2 Rechenarten
Dreisatzrechnung
Verhältnisse beim Dreisatz
1
direkter Dreisatz
1. Aussagesatz
x⇒y
x⇒y
2. Einheitssatz
y
1 ⇒ ᎏᎏ
x
1⇒y·x
y · x1
x1 ⇒ ᎏᎏ
x
3. Schlusssatz
2
indirekter Dreisatz
y·x
x1 ⇒ ᎏᎏ
x1
Dreisatz mit geradem Verhältnis (direkt oder proportional)
Beispiel
Kosten
8 000
4 000
2 000
3
0
0
1
2 3 m3
Volumen
5
4,50 m3 Eichenholz kosten 7875,00 €.
Wieviel kosten 3,00 m3 Eichenholz?
1. 4,50 m3 Eichenholz kosten
7875,00 €
2. 1,00 m3 Eichenholz kosten
7875,00 €
ᎏ
ᎏ
4,50 m3
3. 3,00 m3 Eichenholz kosten
7875,00 € · 3,00 m3 = 5250,00 €
ᎏ
ᎏᎏ
ᎏ
4,50 m3
Dreisatz mit umgekehrtem Verhältnis (indirekt oder antiproportional)
Beispiel
200
Stunden
4
150
100
50
0
5
0
2
4 6 8
Maurer
10
5 Maurer benötigen für eine Montagearbeit 80 Stunden. Wie lange dauert die Montage, wenn 8 Maurer zur
Verfügung stehen?
1. 5 Maurer benötigen
80 h
2. 1 Maurer benötigt
5 · 80 h
3. 8 Maurer benötigen
5 · 80 h
ᎏᎏ = 50 h
8
Zusammengesetzter Dreisatz (doppelter Dreisatz)
Es werden 3 Größen gegenübergestellt. Die gesuchte
Größe wird stufenweise errechnet. In jeder Stufe wird
nur eine Größe verändert.
Beispiel
6 Zimmerer verlegen bei 8-stündiger Arbeitszeit pro
Tag 210 m2 Parkett. Wieviel m2 Parkett verlegen 5 Zimmerer bei einer Arbeitszeit von 9 h/Tag?
1. Dreisatz: 6 Zimmerer verlegen in 8 h
210 m2
1 Zimmerer verlegt in 8 h
210 m2
ᎏᎏ
6
5 Zimmerer verlegen in 8 h
210 m2 · 5
ᎏᎏ
6
2. Dreisatz: 5 Zimmerer verlegen in 1 h
210 m2 · 5
ᎏᎏ
6·8
6
5 Zimmerer verlegen in 9 h
7
210 m2 · 5 · 9
ᎏᎏ = 196,875 m2
6·8
Verhältnisgleichung, Proportionen
Zwei Verhältnisse mit gleichen Werten können gleichgesetzt und als Gleichung geschrieben werden.
Das Verhältnis (eine Proportion) kann auch als Bruchgleichung geschrieben werden.
Außenglieder
8
a:b = 3:4
Innenglieder
16
oder
3
a
ᎏᎏ = ᎏᎏ
4
b
Bruchgleichung
Eine Verhältnisgleichung kann als Produktengleichung
geschrieben werden.
a:b = 3:4
oder
3·b = 4·a
Innenglied ⳯ Innenglied = Außenglied ⳯ Außenglied
1.2 Rechenarten
Potenzen
Wurzeln
an
Definition
(Sprechweise:
a hoch n)
=a·a·a·…·a
n Faktoren
Spezialfälle
a1 = a; a0 = 1
(für a 7 0 und n B ⺞*) 1n = 1; 0n = 0
Potenzen mit
negativen
Exponenten
1
1
a– 1 = ᎏᎏ; a– n = ᎏᎏ
a
an
Vorzeichen beim
Potenzieren
(für n B ⺞*)
(+ a)n = +an für alle n
(– a)n = + an für gerade n
(– a)n = – an für unger. n
Summe und
Differenz
von Potenzen
2 a3 + 3 a3 – a3 = 4 a3
3 a4 + 4 a2 – 2 a2 =
= 3 a4 + 2 a2
Produkt
von Potenzen
am an = am + n
an bn = (ab)n
(am)n = am n
Quotient
von Potenzen
am : an
am : bm
Darstellung mit
Bruchpotenzen
(für a ≥ 0)
n
n
冢y苶a冣
= a
y苶
a
= y苶
a
n
2
1
ᎏᎏ
y苶
a
= an
m
ya
苶
= an
n
n
1
n
= y苶
a
y苶
y苶
a = ya苶
m
m
冢 冣
m
ᎏᎏ
n
1
ᎏmᎏ
1
ᎏᎏ
= a mn
2
n
Produkte von Wurzeln ny ny
苶
b = y苶
a 苶
ab
(für a ≥ 0 und b ≥ 0)
m+q
n
n
ᎏᎏ
m ya
ya
苶
苶q = a n
Eindeutigkeit
von Wurzeln
(für a ≥ 0)
n
ya苶n
y4
苶
3
y苶
27
= a≥0
= +2
= +3
3
● Wurzeln positiver Radianten sind positiv.
● Wurzeln negativer Radikanden sind für den
reellen Zahlenbereich nicht definiert.
= am – n
= (a : b)m
Fakultät, Binomialkoeffizient
Fakultät: n! = 1 · 2 · 3 · … · n.
Definition
(für a ≥ 0 und n B ⺞*)
Es gilt 0! = 1
y苶
– 5 nicht definiert
● Wurzel aus Null ist gleich Null
y苶
0=0
4
Beispiel (Hinweis auf ± Zeichen)
Sei x2 = 3
Binomialkoeffizient:
n!
n
ᎏ mit 0 ≤ k ≤ n
k = ᎏ
k! (n – k)!
冢 冣
3 = ± 1,7321…)
(nicht x = y苶
Binomische Formeln
Logarithmen
x = ± y苶
3 = ± 1,7321…
5
1. binomische Formel
(a + b)2 = a2 + 2 ab + b2
2. binomische Formel
(a – b)2 = a2 – 2 ab + b2
3. binomische Formel
(a + b) (a – b) = a2 – b2
Höhere Potenzen
(a + b)3 = a3 + 3 a2 b + 3 ab2 + b3
(a – b)3 = a3 – 3 a2 b + 3 ab2 – b3
n
冢冣
Definition
logb a = c, wenn bc = a
für b > 0 und a > 0
Brigg’scher (dekadischer) Logarithmus
lg a
natürlicher Logarithmus (logarithmus
naturalis)
ln a = loge a
mit e = 2,71828…
Spezialfälle
lg 1 = 0; ln 1 = 0
logb 1 = 0; logb b= 1
lg 10 = 1; ln e = 1
Logarithmengesetze
(für alle Basen b > 0)
log (ac)
a
log ᎏᎏ
c
log (an)
n
log y苶
a
n
冢冣
(a ± b)n = an ± 1 an – 1 b + 2 an –2 b2
n
± 3 an – 3 b3 + … ± …
冢冣
Spezialfälle
a3 + b3 = (a + b) (a2 – ab + b2)
a3 – b3 = (a – b) (a2 + ab + b2)
a4 – b4 = (a2 + b2) (a2 – b2)
an – bn = (a – b) (an – 1 + an – 2 b + an – 3 b2
+ … + abn – 2 + … + bn – 1)
Umrechnungen
= log10 a
6
= log a + log c
7
= log a – log c
= n log a
1
= ᎏᎏ log a
n
ln a
= ln 10 · lg a
lg a
= lg e · ln a
lg e
= M = 0,4343…
1
ln 10
= ᎏᎏ = 2,3026…
M
log
a
b b
= a
logb (bn) = n
17
8
1.2 Rechenarten
1
Zahlenmengen, Verknüpfungen
Priorität der Verknüpfungen
Für einige Zahlenmengen, die in der Mathematik eine besondere Bedeutung haben, hat man
eigene Symbole gebildet.
Treten in einem Ausdruck (Aussage, Term) unterschiedliche Verknüpfungen auf, so werden die
Verknüpfungen höherer Priorität vor denen geringerer Priorität abgearbeitet. Bei Verknüpfungen gleicher Priorität erfolgt die Abarbeitung von
links nach rechts.
Es gelten die Klammerregeln.
[0]; 1; 2; 3 ; ...
2
Priorität
... ; -3; -2; -1; 0; 1; ...
Verknüpfung
Potenzierung, Radizierung,
Logarithmierung, Funktionen
hoch
z. B.: -7,25 ; -1/2 ; 2 3/4
z. B.: p; e;
3
·, :
>, ≥, =, ≤, <, 7
(relationale Operatoren)
2
z. B.: 5 + 3i ; 4 - 5i ; 6 +7i
(nicht)
#
(und)
3
(oder)
⇒, ⇔
⺞*, ⺪*, ⺡*, ⺢* sind Zahlenmengen ohne Null
Aussagen
Die Menge, die keine Elemente enthält, heißt
leere Menge und wird mit ∅ oder { } bezeichnet.
A, B, C, ... sind Leerstellen für wahre (w) oder
falsche (f) Aussagen.
Die Lösungsmenge wird mit L benannt.
Symbol
5
6
Zahlenmenge
Menge aller …
⺞
Natürliche
Zahlen
positiven ganzen
Zahlen
⺪
Ganze
Zahlen
positiven und negativen ganzen Zahlen
⺡
Rationale
Zahlen
endlichen und periodischen Dezimalzahlen
⺢
Reelle
Zahlen
endlichen und unendlichen Dezimalzahlen
⺓
Komplexe
Zahlen
imaginäre Einheit
i2 = – 1
Die nicht in ⺡ liegenden Zahlen von ⺢ heißen
苶, die Kreiszahl π, die
irrationale Zahlen, z. B. y2
Euler’sche Zahl e = 2,71828…
7
C
niedrig
⺞ I ⺪ I ⺡ I ⺢ I ⺓
4
(Punktrechnung)
+, – (Strichrechnung)
Zahlenmengen heißen abgeschlossen bezüglich
ihrer Rechenoparationen, wenn das Ergebnis
wieder in der selben Zahlenmenge liegt.
Symbol
⺞
⺒
⺪
⺡
⺢
8
18
Abgeschlossenheit
Beispiel
+,·
2+5=7
+,·,:
1/2 + 1/5 = 7/10
+,·,–
2–5=–3
+ , –, · , :
2 : 5 = 2/5
+ , –, · , :
y5
苶 · y2
苶 = y10
苶
Beispiele
= Deutschland liegt in Europa!
= 12 ist eine Primzahl!
= Es regnet!
= Die Erde wird nass!
= Aus C folgt D!
= b > grün
A
B
C
D
E
F
(w)
(f)
(w oder f)
(w oder f)
(w)
(keine Aussage)
Aussagenverknüpfungen
C
Negation
CA
nicht A
@
Konjunktion
A@B
A und B
3
Disjunktion
A3B
A oder B
⇒
Implikation
A⇒B
aus A folgt B
(wenn A, dann B)
⇔
Äquivalenz
A⇔B
A genau dann,
wenn B
Eine Tautologie ist eine aussagenlogische Verknüpfung, die nur den Wahrheitswert w annehmen kann.
Axiome (ursprünglich Sätze), die unmittelbar
einleuchten, brauchen nicht bewiesen zu werden
und dienen als Grundlage der Beweisführung.
Wahrheitstafel
A
B
CA
A@B
w
w
f
f
w
f
w
f
f
f
w
w
w
f
f
f
A3B A⇒B A⇔B
w
w
w
f
w
f
w
w
w
f
f
w
1 MATHEMATIK
1.3 Prozentrechnung und Zinsrechnung
Prozentrechnung
1
Rechnen mit reinem Grundwert
PW · 100%
= ᎏᎏ
p
G·p
PW = ᎏᎏ
100%
PW · 100%
p = ᎏᎏ
G
● Prozent % v 1/100
G
● Grundwert G
● Prozentwert PW
● Prozentsatz p (%)
Beispiel
Eiche hat einen tangentialen Schwindverlust von 8,9%. Um wie viel mm
schwindet ein Seitenbrett mit einer
Breite b = 320 mm?
Lösung
320 mm ⭈ 8,9 %
PW = ᎏ ᎏ = 28,48 mm
100%
2
Rechnen mit vermindertem Grundwert
● Verminderter Grundwert Gmin
Gmin = G – PW
Verminderter
Grundwert
Prozentwert
(PW )
100 % – p %
p%
G
Gmin · 100%
= ᎏᎏ
100% – p
100 % = Grundwert (G)
Beispiel
Ein Kunde bezahlt wegen mangelhafter Arbeit 10% des Bruttopreises weniger und überweist
16 500,00 €. Wie hoch war der Bruttopreis?
Lösung
16 500,00 € ⭈ 100%
ᎏ = 18 333,33 €
G = ᎏᎏ
100% – 10%
Rechnen mit vermehrtem Grundwert
4
● Vermehrter Grundwert Gmehr
Gmehr = G + PW
Grundwert
(G)
Prozentwert
(PW )
100 %
p%
3
Gmehr · 100%
G = ᎏᎏ
100% + p
100 % + p % = vermehrter Grundwert
Beispiel
Ein Arbeiter erhält nach der Lohnerhöhung von 3,5% einen Stundenlohn von 13,40 €. Errechnen Sie den
vorherigen Lohn?
Lösung
13,40 € ⭈ 100%
ᎏ
ᎏ = 12,95 €
G=ᎏ
100% + 3,5%
5
Beispiel
Ein Betrieb erhält einen Kredit über
40 000,00 € mit Zinssatz von 8,5%.
a) Berechnen Sie die Zinsen.
b) Wie hoch wäre der Zinssatz, wenn
bei gleicher Laufzeit 3 700,00 €
Zinsen anfallen würden?
Lösung
6
Zinsrechnung
●
●
●
●
●
●
Kapital
Zinsen
Zinssatz
Laufzeit
1 Zinsjahr
1 Zinsmonat
K (€)
Z (€)
p (%/Jahr)
t (Jahre)
360 Tage
30 Tage
Kapital
Z · 100%
K = ᎏᎏ
p·t
K·p·t
Z = ᎏᎏ
100%
Z
Mit dem Zinssatz werden die Zinsen
für ein Jahr berechnet.
Z · 100%
p = ᎏᎏ
K· t
40 000,00 € ⭈ 8,5%
ᎏ = 3 400,00 €
Z = ᎏᎏ
100%
Z · 100%
t = ᎏᎏ
K· p
3 700,00 € ⭈ 100%
ᎏ = 9,25 %
p = ᎏᎏ
40 000,00 €
7
Zinseszinsrechnung
Die Zinsen werden dem Kapital zugerechnet und mitverzinst.
Kapital nach
n Jahren:
● Anzahl der Jahre n
p
Kn = K 1 ⴙ ᎏᎏ
100
(
)
n
Beispiel
Ein Zimmerer legt 5000,00 € festverzinslich mit 4,5 % an. Wie hoch ist
sein Kapital nach 10 Jahren?
Lösung
4,5% 10
K10 = 5000,00 € · 1 ⴙ ᎏᎏ =
1
00%
K10 = 7764,85 €
^
&
19
8
1 MATHEMATIK
1.4 Längen und Winkel
Längenteilung
1
Teilen der Gesamtlänge in gleiche Abstände
e
e
e
e
e
§
e = ᎏᎏ
n+1
z=n+1
ö
2
e
a
e
e
§ – (a + b)
e=ᎏ
ᎏ
n–1
b
ö
e
b2
e
b3
e
b4
e
b5
Randabstände
Gesamtlänge, Teilungsstrecke
Länge der Abstände
Anzahl der Teilungselemente
b1, …, bn
§
e
n
§ – (b1 + … + bn)
e = ᎏᎏ
n–1
ö
Unterbrechungen
Gesamtlänge, Teilungsstrecke
Länge der Abstände
Anzahl der Teilungselemente
Winkel
Winkelarten
Winkeleinheiten
b4
a3
a4
b3
Zwei von einem Punkt ausgehende Halbgeraden
bilden einen Winkel. Die Benennung erfolgt mit
griechischen Buchstaben å, ∫, ©.
Schenkel
b1
Scheitelwinkel sind gleich groß.
Scheitelwinkel liegen am Winkelscheitel einander
gegenüber.
6
å1 = å2
|
å3 = å4
Wechselwinkel sind gleich groß.
Wechselwinkel an geschnittenen Parallelen liegen dem Winkel auf der anderen Seite gegenüber.
å1 = å4
|
Stufenwinkel sind gleich groß.
Stufenwinkel liegen auf der anderen Stufe der
gleichen Seite der Geraden.
|
∫1 = ∫3
Nebenwinkel ergänzen sich zu 180°.
Nebenwinkel sind Nachbarwinkel auf der selben
Seite der Parallelen.
å1 + ∫1 = 180°
20
|
S
A
Die Einheiten der Winkel sind Grad (°), Minuten (’)
und Sekunden (’’). Es gelten die selben Regeln
wie bei Zeiteinheiten.
Umrechnung
1° = 60’
0,56666° = 0,56666° · 60’ / je 1°
21’ = 21’ : 60’ / je 1°
1’ = 60’’
→
→
34’
0,35°
Winkelbenennungen
∫1 = ∫4
7
å1 = å3
B
a
a2
a
b2
a1
a oder A ASB
el
nk
he
Sc
Scheitelpunkt
5
8
a, b
§
e
n
Teilen der Gesamtlänge in gleiche Abstände mit Unterbrechungen
b1
4
Gesamtlänge, Teilungsstrecke
Länge der Abstände
Anzahl der Teilungselemente
Anzahl der Abstände
Teilen der Gesamtlänge in gleiche Abstände mit Randabstand
e
3
§
e
n
z
å4 + ∫4 = 180°
a
a < 90°
Spitzer Winkel
90° < a < 180°
a = 90°
Rechter Winkel (R)
a
a
Stumpfer Winkel
Überstumpfer
Winkel