Script

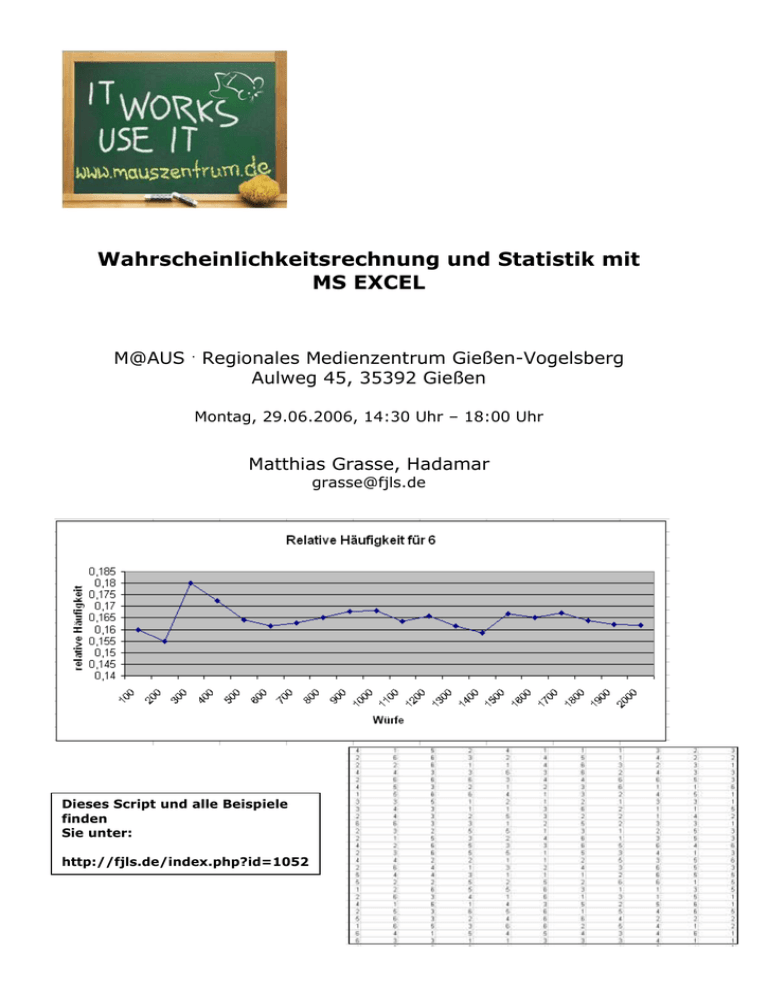
Wahrscheinlichkeitsrechnung und Statistik mit
MS EXCEL
M@AUS . Regionales Medienzentrum Gießen-Vogelsberg
Aulweg 45, 35392 Gießen
Montag, 29.06.2006, 14:30 Uhr – 18:00 Uhr
Matthias Grasse, Hadamar
[email protected]
Dieses Script und alle Beispiele
finden
Sie unter:
http://fjls.de/index.php?id=1052
Zeitplan:
14:30 Uhr
0. Meine Koordinaten
1. Grundlagen anhand des Mittelwertes (6. Schuljahr)
2. Relative Häufigkeiten (6. Schuljahr)
3. Wahrscheinlichkeiten – Simulation von Zufallsexperimenten
(8. Schuljahr)
- Zusatzaufgabe I
- Zusatzaufgabe II
16:00 Uhr
Kaffeepause
16:15 Uhr
4. Das Stabilwerden der relativen Häufigkeiten (8. Schuljahr)
5. Kombinatorik (10. Schuljahr)
6. Erwartungswert – Varianz – Standardabweichung
(9. Schuljahr)
7. Binomialverteilung (10. Schuljahr)
17:45 Uhr
8. Rückblick/ Auswertung des Workshops
Kenntnisse
Profi
gut
wenig
schon
mal
gehört
Anwendung
im
Unterricht
0
selten
regelmäßig
Workshop „Stochastik/Statistik mit MS EXCEL“
oft
2/16
Hinweis: Zur besseren Lesbarkeit wird ausschließlich die männliche Form verwendet.
Grundsätzlich ist dabei immer die weibliche und männliche Form gemeint.
1. Ein wenig Statistik (6. Schuljahr) – Datei Mittelwert Kaffee.xls
aus Lambach-Schweizer, 6. Schuljahr, S. 214, Nr. 2
1
kg abgepackt. Bei einer Kontrolle von mehreren Paketen wird die
2
Kaffeemenge nachgewogen und das genaue Gewicht notiert.
Wie viel g Kaffee sind durchschnittlich in einem Paket?
Kaffee wird in Paketen zu
Probe
Gewicht
in g
1
2
3
4
5
6
7
8
502
495
510
498
488
506
504
497
1. Starten sie MS Excel durch Doppelklick auf:
2. Geben Sie die Werte in das leere Tabellenblatt ein. Das
Ausfüllen der ‚Probennummer’ nimmt MS EXCEL
halbautomatisch vor. Markieren Sie dazu die Zellen A4
und A5. An der rechten unteren Ecke entsteht ein kleines
schwarzes Quadrat. Klicken Sie mit der linken Maustaste
darauf und ziehen Sie
die Werte nach unten.
3. Stellen Sie die Werte in einem
Diagramm dar. Markieren Sie dazu
die Werte in der Spalte B und klicken
Sie auf
(Diagramm – Einfügen).
Wählen Sie SÄULE und klicken Sie
auf FERTIG STELLEN.
Das Diagramm wird eingefügt. Die
Legende rechts können Sie mit einem
rechten Mausklick löschen oder Ihren
Wünschen anpassen.
Workshop „Stochastik/Statistik mit MS EXCEL“
3/16
Falls Sie die Darstellung der y-Achse bei ‚0’
beginnend wünschen, gehen Sie wie folgt vor:
Klicken Sie mit der rechten Maustaste auf die yAchse. Wählen Sie ACHSE FORMATIEREN.
Passen Sie auf der zweiten Karteikarte SKALIERUNG
die Werte nach Ihren Wünschen an. Wenn Sie die
Häkchen bei AUTOMATISCH entfernen, können Sie
die Werte manuell eingeben.
4. Berechnung des Mittelwertes
Sie können den Mittelwerte bilden durch
Summe aller Werte
(1) oder mit der eingebauten
Anzahl
Funktion von EXCEL (2).
Zu (1): Bilden Sie die Summe der Zellen B4 – B11. Markieren Sie
dazu diese Zellen und klicken Sie auf
Summe eingetragen.
. In der Zelle B12 wird die
Den Mittelwert berechnen Sie in Zelle B13: =B12/8.
Dieser Wert kann jetzt noch im Diagramm dargestellt werden (ist leider etwas kompliziert.)
Dazu wird im Prinzip eine weitere Datenreihe als Liniendiagramm mit dem (konstanten)
Mittelwert eingetragen.
a) Wir übertragen den Mittelwert an eine ‚etwas abgelegene Stelle’ des
Arbeitsblattes und zwar 8x. (hier: Zellen: J4 – J11).
b) Durch rechten Mausklick auf eine Säule im Diagramm (Auswahl:
DATENQUELLE) hat man die Möglichkeit, weitere Datenreihen
hinzuzufügen.
Workshop „Stochastik/Statistik mit MS EXCEL“
4/16
Klick auf HINZUFÜGEN – dann unter WERTE
den Bereich J4-J11 auswählen.
Es wird ein zweites Säulendiagramm eingefügt. Klicken Sie auf OK.
Klicken Sie mit der rechten Maustaste auf eine Säule des der neuen Datenreihe und wählen
Sie DIAGRAMMTYP. Entscheiden Sie sich für LINIENDIAGRAMM. Mit einem weiteren rechten
Mausklick auf die Linie können Sie noch die Stärke und die Farbe der Linie verändern.
Das fertige Diagramm sollte dann so aussehen:
Mit dieser Tabelle haben Sie jetzt eine universelle Möglichkeit, Daten darzustellen und den
Mittelwert zu bestimmen. Eventuell muss noch die Anzahl der Werte angepasst werden.
Workshop „Stochastik/Statistik mit MS EXCEL“
5/16
Zu (2): Berechnung des Mittelwertes durch die interne Funktion von EXCEL.
Der Befehl heißt einfach Mittelwert(Zahl1; Zahl2; …).
Geben Sie in Zelle B14 ein:
fertig!
Hinweis: Leider bietet EXCEL nicht die Möglichkeit der Erstellung von BOXPLOTS. Die
Quartile, Median, Minimum und Maximum einer Liste können aber berechnet werden. Die
Befehle heißen genau so. Näheres finden Sie in der Hilfe oder unter:
http://www.learn-line.nrw.de/angebote/eda/medio/tipps/installation.htm
Hier ein Screenshot des V200, der solche BOXPLOT beherrscht:
2. Relative Häufigkeiten (6. Schuljahr) – Datei Vögel im Winter.xls
Um Häufigkeiten zu vergleichen, betrachtet man ihren jeweiligen Anteil an der Gesamtzahl.
Diesen Anteil nennt man relative Häufigkeit.
Will man den Unterschied zwischen Häufigkeit und relativer Häufigkeit betonen, so spricht
man von absoluter Häufigkeit und relativer Häufigkeit.
Relative Häufigkeit =
absolute Häufigkeit
Gesamtzahl
aus Lambach-Schweizer, 6. Schuljahr, S. 211, Beispiel
Patrick hat an zwei Wintertagen die Vögel, die sein Futterhäuschen im Garten anflogen,
beobachtet und gezählt.
1. Tag
2. Tag
Kohlmeise
15
10
Blaumeise
9
12
Sperling
Amsel
Buchfink
Sonstige
27
6
3
15
6
4
0
3
a) Bestimme für jeden Tag jeweils die relativen Häufigkeiten der einzelnen Vogelarten.
b) Zeichne ein Balkendiagramm der relativen Häufigkeiten.
Zunächst muss die Tabelle in Excel übertragen werden.
Workshop „Stochastik/Statistik mit MS EXCEL“
6/16
Die Tabelle wird ergänzt durch die Summen und die relativen Häufigkeiten.
In der Zelle B6 wird die relative Häufigkeit eingetragen.
Diesen Quotienten können Sie jetzt wieder nach rechts zeihen, dazu
müssen Sie allerdings die Zelle H4 absolut adressieren, da diese sich
nicht ändern soll.
Verfahren Sie genau so für den 2. Tag.
Erstellen des Diagramms:
Markieren Sie die Zellen B6-G7. Wählen Sie ein Säulendiagramm aus. Formatieren Sie es
nach Ihren Wünschen.
3. Wahrscheinlichkeiten – Simulation von Zufallsexperimenten (8. Schuljahr)
- Datei Würfeln.xls
Ein Experiment, bei dem man das Ergebnis nicht sicher vorhersagen kann, heißt
Zufallsexperiment. Den einzelnen Ergebnissen kann man Wahrscheinlichkeiten zuordnen,
die zusammen 1 ergeben müssen.
Laplace-Wahrscheinlichkeiten
Es gibt Experimente, bei denen man annehmen kann, dass alle Ergebnisse eines
Zufallsversuchs gleich wahrscheinlich sind. Bei n Ergebnissen beträgt die Wahrscheinlichkeit
1
jedes Ergebnisses . Man spricht in solchen Fällen von einer Laplace-Annahme und von
n
Laplace-Wahrscheinlichkeiten.
Simulation eines Würfels
Der Befehl zum Erzeugen einer
(Pseudo-)Zufallszahl lautet
ZUFALLSZAHL(). EXCEL erzeugt eine Zufallszahl im Bereich von 0 bis 1.
Workshop „Stochastik/Statistik mit MS EXCEL“
7/16
Hinweis: Es gibt auch den Befehl
ZUFALLSBEREICH(untere Grenze; obere
Grenze). Dieser Befehl gibt eine ganze
Zufallszahl zwischen unterer und oberer
Grenze aus. Leider muss dazu das ‚AnalyseTool’ auf dem PC installiert sein. Sie
installieren das Analyse-Tool (falls Sie
Administratoren-Rechte haben und/oder keine
Wächterkarte eingebaut ist und Sie eventuell
die Office-CD zur Hand haben – oder einen
sehr guten Draht zum PC-Betreuer Ihrer
Schule), indem Sie auf EXTRAS – ADD INS
gehen und den Haken bei ANALYSE-TOOLS
setzten. Jetzt warten …
Aber auch mit dem Befehl ZUFALLSZAHL(), können Sie eine
Zufallszahl im gewünschten Bereich erzeugen.
GANZZAHL(ZUFALLSZAHL()*6)+1 erzeugt eine Zufallszahl
zwischen 1 und 6.
Durch Drücken von F9 können Sie nacheinander eine beliebige
Anzahl von Zufallszahlen erzeugen.
Dieses einfache Arbeitblatt bietet jetzt die Möglichkeit zu
ersten statistischen Auswertungen, etwa von 100 Würfen.
Dazu zieht man die Zelle B4 einfach 100x nach unten.
Das Zählen übernimmt Excel auch.
Legen Sie eine Auswertungstabelle an:
Die Funktion heißt ZÄHLENWENN. Dazu nutzt man am besten
die Eingabehilfe von EXCEL. Klicken Sie auf:
folgendes Fenster:
Workshop „Stochastik/Statistik mit MS EXCEL“
. Es öffnet sich
8/16
Geben Sie unter ‚Funktion suchen’:
ZÄHLENWENN ein. Klicken Sie OK.
Folgendes Fenster
erscheint. Füllen Sie
es wie angegeben
aus.
Wenn Sie den Bereich absolut Adressieren, können Sie für die Zahlen 2-6 jetzt einfach die
Kopierfunktion benutzten.
Fertig inkl. Diagramm sieht das Ergebnis dann so aus:
Workshop „Stochastik/Statistik mit MS EXCEL“
9/16
Zusatzaufgabe I: - Datei: Summe von zwei Würfeln.xls
Entwerfen Sie ein Arbeitsblatt, das 500-mal mit zwei Würfeln würfelt. Bilden Sie die Summe
der Würfe und stellen Sie die absoluten oder relativen Häufigkeiten in einem Diagramm dar.
Handelt es sich um einen LAPLACE-VERSUCH?
Mögliche Lösung:
Zusatzaufgabe II: - Datei: Auswahl Lernkontrolle.xls
Entwerfen Sie ein Arbeitsblatt das zufällig auswählt, wer aus der Klasse zur Lernkontrolle an
die Tafel muss.
Legen Sie auf dem 2. Tabellenblatt
eine Liste mit den Namen Ihrer
Klasse an und ermitteln Sie in einem
anderen Feld eine Zufallszahl, die
zwischen 1 und der Anzahl Ihrer
Schüler liegt.
Auf dem ersten Tabellenblatt wählen
Sie jetzt den hier 10. Schüler aus der
Liste aus. Dazu dient der
Befehl SVERWEIS.
Klicken Sie dazu wieder
auf
und suchen Sie
SVERWEIS. Ausgefüllt
sollte das Fenster dann
etwa so aussehen.
Workshop „Stochastik/Statistik mit MS EXCEL“
10/16
4. Das Stabilwerden der relativen Häufigkeiten (10. Schuljahr)
Datei: relative Häufigkeit - Wahrscheinlichkeit
Mit zunehmender Anzahl von Durchführungen eines Zufallsexperimentes stabilisiert sich der
Wert der relativen Häufigkeit. Diesen Wert nennt man Wahrscheinlichkeit. Eine TK eignet
sich sehr gut, diesen Vorgang zu visualisieren.
Das fertige Arbeitsblatt könnte etwa so aussehen:
Das ‚Geheimnis’ dieses Blattes sind die
2000 Zufallszahlen, die auf einem
zweiten Tabellenblatt erzeugt werden.
Auf dem ersten Tabellenblatt wird die
relative Häufigkeit der Zahl 6 bestimmt.
Dazu werden zunächst nur die ersten
100 Zahlen ausgewertet. Das Vorgehen
dazu ist unter 3. ausführlich beschrieben.
Dann werden die ersten 200
Zufallszahlen ausgewertet usw.
Sehr schön kann man sehen, wie sich der
Wert der relativen Häufigkeit um den
Erwartungswert ( 0,16 ) stabilisiert.
5. Kombinatorik (8. Schuljahr)
In der Kombinatorik dient die TK insbesondere als Rechenwerkzeug für die zum Teil
aufwendigen Berechnungen. Dadurch, dass der PC insbesondere die
Binomialkoeffizienten/Fakultäten problemlos berechnet, kann dieses Thema auch schon in der
Mittelstufe behandelt werden.
Workshop „Stochastik/Statistik mit MS EXCEL“
11/16
In der Literatur findet man die Übersicht meist in Tabellenform:
Hier: LS, Stochastik, Leistungskurs
n Kugeln
k Ziehungen
Geordnete Stichprobe
Ungeordnete Stichprobe
mit Zurücklegen
ohne Zurücklegen
nk
 n  k  1


k


n · (n-1) · … · (n-k+1)
n
 
k 
n
n!
mit:   
k
!
·
(
n
 k)!
k
 
Das Tabellenblatt selbst ist
unspektakulär:
Die vier möglichen Fälle
werden durch Eingabe der
Gesamtzahl und dem
Umfang der Stichprobe
ermittelt.
Hier ein Arbeitsblatt meiner
Schüler.
Folgendes steht in den Zellen:
B7:
B8:
C7:
C8:
Anbei auch noch die Erklärung für die einzelnen Fälle:
Geordnete Stichprobe mit Zurücklegen:
Die Reihenfolge der gezogenen Kugeln aus der Urne ist entscheidend, wobei nach jedem
Zug die gezogene Kugel zurückgelegt wird.
Klassisches Beispiel: PIN - Nummer beim Handy
Formel: n^k, n = Mögliche Zahlen für jede der k Stellen.
Geordnete Stichprobe ohne Zurücklegen:
Die Reihenfolge der gezogenen Kugeln aus der Urne ist entscheidend, wobei nach jedem
Zug die gezogene Kugel nicht zurückgelegt wird.
Klassisches Beispiel: Einlauf beim Pferderennen
Formel: n!/(n-k)!
Spezialfall: Vollerhebung ( Permutation) : n!
Ungeordnete Stichprobe ohne Zurücklegen:
Die Reihenfolge der gezogenen Kugeln aus der Urne ist nicht entscheidend, wobei nach
jedem Zug die gezogene Kugel nicht zurückgelegt wird.
Klassisches Beispiel: Lotto 6 aus 49
Formel: n!/(n-k)!*k! => 49! / 43! * 6!
Ungeordnete Stichprobe mit Zurücklegen:
Die Reihenfolge der gezogenen Kugeln aus der Urne ist nicht entscheidend, wobei nach
jedem Zug die gezogene Kugel zurückgelegt wird.
Klassisches Beispiel: Kombikiste (k =) 12 Flaschen (n = ) à 4 Sorten
Formel: (n+k-1)!/(n-1)!*k! => 15!/ (12! * 3!)
Workshop „Stochastik/Statistik mit MS EXCEL“
12/16
Weitere Beispiele finden Sie auf: http://www.fjls.de/133.0.html
6. Erwartungswert – Varianz – Standardabweichung (9. Schuljahr)
Datei: Erwartungswert.xls
Zur Auswertung von Daten und Tabellen dienen neben den o.g. Größen (Mittelwert, Median,
Quartile, Maximum, Minimum) auch die Größen Erwartungswert, Varianz und
Standardabweichung.
Nach der theoretischen Einführung dieser Größen im Unterricht kann man sich ein
universellen Rechenblatt anlegen, da die Bestimmung dieser Werte sehr aufwendig aber
formal ist.
Hier die Definitionen:
1. Ist X eine Zufallsvariable, welche die Werte x1, …, xn annehmen kann, so heißt die reelle
Zahl E(X) mit E(X) =
n
 x i · P(X  x i ) Erwartungswert der Zufallsvariablen X.
i 1
Analog heißt
2. … V(X) =
n
 (xi  E(X))2 · P(X  xi ) Varianz und
V(X) heißt Standardabweichung.
i 1
Die Berechnung erfolgt am besten in einer Tabelle:
Workshop „Stochastik/Statistik mit MS EXCEL“
13/16
Dabei werden lediglich die Anzahl der Ereignisse, die Werte der Zufallsvariablen (Spalte C)
und die Wahrscheinlichkeiten (Spalte D) eingegeben. Die Berechnungen in den anderen Zellen
sind sehr einfach und erklären sich über die Überschrift.
Hinweis: MS EXCEL liefert natürlich auch fertige Funktionen zur Berechnung dieser Werte.
7. Binomialverteilung (10. Schuljahr) – Datei: Binomialverteilung.xls
aus LS 10. Schuljahr, S. 211 oben
Wird ein Bernoulli-Experiment (Anm. hat nur zwei Ergebnisse) n-mal ausgeführt und hat das
Ergebnis X stets die Wahrscheinlichkeit p, so ist die Wahrscheinlichkeit dafür, dass X genau kn
mal auftritt: P(X=k) =   · pk · (1-p)n-k (*)
k 
Hinweis: Die Verteilung der Wahrscheinlichkeiten bei Bernoulli-Experimenten hängt
n
wesentlich von dem Binomialkoeffizienten   ab. Man spricht daher auch von einer
k 
Binomialverteilung.
Beispiel 1: Ein Spielwürfel wird 5-mal geworfen. Wie groß ist die Wahrscheinlichkeit, dass die
Sechs genau 2-mal auftritt?
2
5
1
1
1

n=5, p= , k=2  P(X=2) =   ·   · 1  
6
6
6

2
52
 0,161
Zur Berechnung legt man sich am besten ein universelles Arbeitsblatt an, welches auch nach
und nach entwickelt werden kann.
In der Tabelle ist hier das Beispiel eingestellt. Variabel sind nur die Wahrscheinlichkeit p (hier
auf 0,17 gerundet) und die Anzahl der Durchführungen n (hier 5). EXCEL verfügt über die
wichtigsten Funktionen zur Berechnung.
In der Spalte B wurde die Formel (*) verwendet.
In der Spalte C wurde direkt auf die Funktion zugegriffen:
Workshop „Stochastik/Statistik mit MS EXCEL“
14/16
Der Vergleich ergibt im Prinzip keine Abweichungen. Den im Beispiel gesuchten Wert findet
man in der Zelle B12 bzw. C12.
In den Spalten E-G sind noch die Summenfunktionen notiert, für die sonst aufwendig Tabellen
gewälzt werden müssen.
In Zelle E10 steht:
Man sieht, wenn man den letzten Parameter von FALSCH auf WAHR setzt, wird die summierte
Binomialverteilung gebildet.
Die Berechnung der beiden anderen Spalten erfolgt durch Differenzbildung:
F10:
und G11:
.
Beispiel 2: LS, 10. Schuljahr, S.211, Nr. 6
„Thorsten steckt 10 Saatbohnen in einen Blumenkasten. Die Wahrscheinlichkeit, dass die
Bohnen keimen, beträgt 0,8. Mit welcher Wahrscheinlichkeit keimen
a) alle 10 Bohnen b) genau 8 Bohnen c) mindesten 8 Bohnen“
Der Tabelle kann entnommen werden:
a) Zelle B10: 10,7 %
b) Zelle B18: 30,2 %
c) Zelle E18: 62,4 %.
Weitere Anregungen finden Sie unter: http://www.fjls.de/133.0.html
Workshop „Stochastik/Statistik mit MS EXCEL“
15/16
b) einige Internetadressen
[1]
http://www.kohorstlemgo.de/index.html?/helmut/stoch.html
Beispiele aus der SII
[2] http://www.fh-lueneburg.de/mathelehramt/stochastik/stochastik.htm
Immer eine ‚Reise wert’. Die Seite von
Frau Haftendorn.
[3] http://www.landratlucas.de/mint/stochastik/stochastik.html
Unzählige, liebevoll und professionelle
Arbeitsblätter.
[4] http://www.learnline.nrw.de/angebote/neuemedien/medio/
softuebl/daten/geda.htm
Ein Ausblick auch auf andere Programme,
die in der Stochastik/Statistik genutzt
werden können
Workshop „Stochastik/Statistik mit MS EXCEL“
16/16