SNT Übung 1

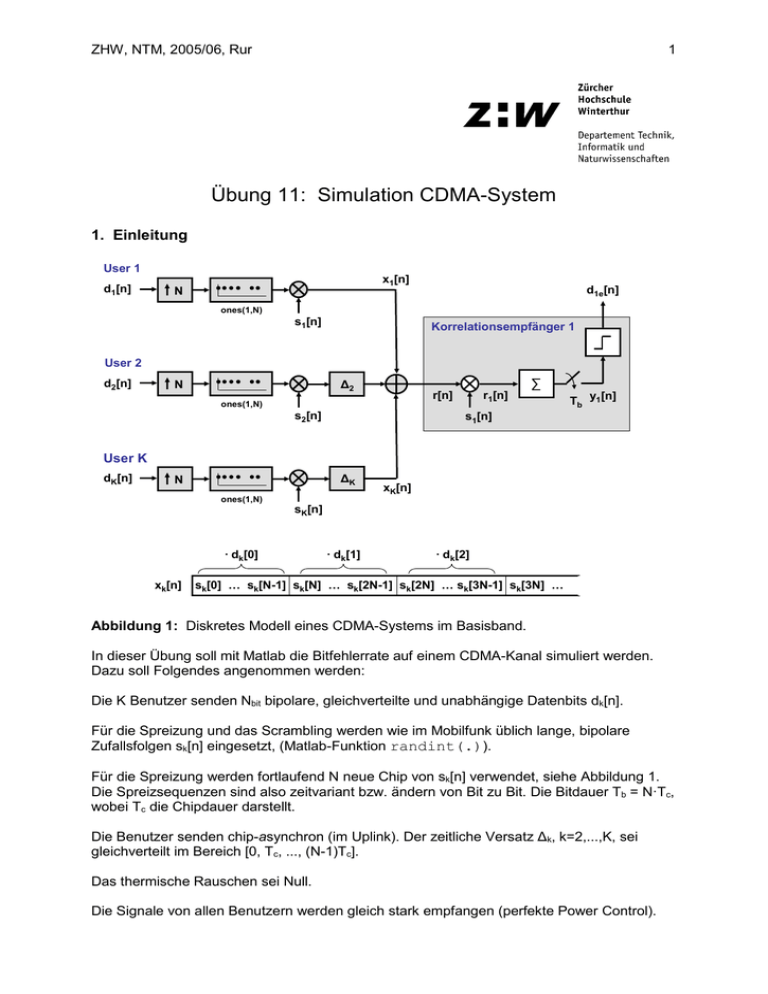
ZHW, NTM, 2005/06, Rur
1
Übung 11: Simulation CDMA-System
1. Einleitung
User 1
d1[n]
x1[n]
N
d1e[n]
ones(1,N)
s1[n]
Korrelationsempfänger 1
User 2
d2[n]
∑
Δ2
N
r[n]
ones(1,N)
s2[n]
r1[n]
Tb y1[n]
s1[n]
User K
dK[n]
ΔK
N
xK[n]
ones(1,N)
sK[n]
· dk[0]
xk[n]
· dk[1]
· dk[2]
sk[0] … sk[N-1] sk[N] … sk[2N-1] sk[2N] … sk[3N-1] sk[3N] …
Abbildung 1: Diskretes Modell eines CDMA-Systems im Basisband.
In dieser Übung soll mit Matlab die Bitfehlerrate auf einem CDMA-Kanal simuliert werden.
Dazu soll Folgendes angenommen werden:
Die K Benutzer senden Nbit bipolare, gleichverteilte und unabhängige Datenbits dk[n].
Für die Spreizung und das Scrambling werden wie im Mobilfunk üblich lange, bipolare
Zufallsfolgen sk[n] eingesetzt, (Matlab-Funktion randint(.)).
Für die Spreizung werden fortlaufend N neue Chip von sk[n] verwendet, siehe Abbildung 1.
Die Spreizsequenzen sind also zeitvariant bzw. ändern von Bit zu Bit. Die Bitdauer Tb = N·Tc,
wobei Tc die Chipdauer darstellt.
Die Benutzer senden chip-asynchron (im Uplink). Der zeitliche Versatz Δk, k=2,...,K, sei
gleichverteilt im Bereich [0, Tc, ..., (N-1)Tc].
Das thermische Rauschen sei Null.
Die Signale von allen Benutzern werden gleich stark empfangen (perfekte Power Control).
ZHW, NTM, 2005/06, Rur
2
2. Aufgabenstellung
1. Erstellen Sie mit Hilfe der Vorlage ntmueb11.m ein Programm, mit dem Sie die BER1
für Benutzer 1 in Funktion der Anzahl Benutzer K im CDMA-System simulieren können.
Wählen Sie K=2, N=5 und Nbit=3 und verifizieren Sie die Signale r[n], r1[n], y1[n] und
d1e[n].
2. Simulieren Sie für die Parameter K = 2,...,10, N = 31 und Nbit = 10’000 die Bitfehlerrate
BER1 in Funktion der Anzahl Benutzer.
Wie hängt BER1 vom zeitlichen Versatz Δk der Benutzer ab?
Bestimmen Sie das Carrier-to-Interference-Ratio C/I = Eb/I0 für K =2,...,10 und
verfizieren Sie die Performance an Hand der Figur 5.46 im Skript (Datenübertragung
über einen AWGN-Kanal im Basisband).
Achtung: Bitte initialisieren Sie alle Matrizen und Vektoren vor der Verarbeitung, damit
die Simulationszeit < 5s bleibt.
3. Benutzen Sie für die Spreizung statt zufälliger Folgen Ausschnitte aus einer sehr langen
PN-Folge (z.B. Schieberegister mit Feedback-Polynom X28+X3+1). Geben Sie jedem Benutzer einen zufälligen Startwert (seed).
Benutzen Sie für Testzwecke zuerst ein kurze PN-Sequenz (z.B. Schieberegister mit
Feedback-Polynom X3+X1+1).
ZHW, NTM, 2005/06, Rur
3
Musterlösung
Aufgabe 1
Verifikation der Signale (Code siehe unten):
d1 = [ 1 -1 -1]
d2 = [-1 1 1]
s1=[ 1 1 -1 1 -1
s2=[-1 1 -1 1 1
1 -1 1 -1 -1
-1 -1 -1 1 1
-1 -1 -1 -1 -1]
-1 -1 -1 1 1]
x1=[ 1 1 -1 1 -1
x2=[ 1 -1 1 -1 -1
-1 1 -1 1 1
-1 -1 -1 1 1
1 1 1 1 1]
-1 -1 -1 1 1]
r = [ 2 0 0 0 -2
-2 0 -2 2 2
0 0 0 2 2]
r1= [ 2 0 0 0 2
-2 0 -2 -2 -2
0 0 0 -2 -2]
-8
-1
-4
-1
y1= [
d1e= [
4
1
]
]
Aufgabe 2
Der zeitliche Versatz zwischen den Aussendungen der einzelnen Benutzer hat dank
dem Scrambling keinen Einfluss auf die BER-Performance eines einzelnen Benutzers.
Wenn 2 Benutzer einmal eine „schlechte“ Kreuzkorrelation haben, haben sie kurze Zeit
später vielleicht wieder eine „gute“ Kreuzkorrelation.
Simulationsresultate für N=31 und Nbit=10000:
Die mit * bezeichneten BER-Werte sind statistisch zu wenig signifikant
(zu wenig Bits übertragen bzw. zu wenig Fehler detektiert).
**: Für wenige „Interferer“ ist die AWGN-Approximation, die der SNR- bzw. C/I-Formel
zu Grund liegt, nicht mehr gerechtfertigt.
K
2
3
4
5
6
7
8
9
10
BER1
0*
0*
0.0004*
0.0023*
0.0063
0.0127
0.0175
0.0216
0.0326
C/I = N / (K-1)
**
11.9 dB
10.1 dB
8.9 dB
7.9 dB
7.1 dB
6.5 dB
5.9 dB
5.4 dB
Je grösser die Anzahl Benutzer K in der CDMA-Zelle in Abbildung 1 ist, desto grösser ist
die Interferenz und damit die Bitfehlerrate BER. Die Interferenz wirkt sich genau gleich
aus wie das thermische Rauschen auf einem AWGN-Kanal. Die BER-Werte liegen exakt
auf der BER-Performance-Kurve für bipolare Datenübertragung über einen AWGN-Kanal
(siehe Figur 5.46 im Skript).
ZHW, NTM, 2005/06, Rur
Aufgabe 3
Es gibt keinen Performance-Unterschied, wenn statt der Zufallsfolgen sk[n] sehr lange
PN-Folgen eingesetzt werden, solange nur kurze, N Chip lange Ausschnitte für die
Spreizung verwendet werden (im Code unten nicht implementiert).
Matlab-Code:
% Parameter
% =====================================================
K=10;
% Anzahl Benutzer
N=31;
% Spreizfaktor
Nbit=10000;
% Anzahl übertragene Bit pro Teilnehmer
% Generierung Datenfolge
% =====================================================
d=(-1).^randint(K,Nbit);
% Generierung Chipfolge
% =====================================================
s=(-1).^randint(K,Nbit*N);
x=zeros(K,N*Nbit);
for k=1:K,
for n=1:Nbit,
x(k,(n-1)*N+1:n*N)=d(k,n)*s(k,(n-1)*N+1:n*N);
end
end
% Generierung Empfangsvektor
% =====================================================
delta=randint(1,K,N);
delta(1)=0; % Benutzer 1 hat Versatz 0 Chip (Referenz)
r=x(1,:);
for k=2:K,
r=r+[zeros(1,delta(k)) x(k,1:Nbit*N-delta(k))];
end
% Korrelationsempfänger 1
% =====================================================
r1=s(1,:).*r;
% Entspreizung
y1=zeros(1,Nbit);
% Integrate and Dump
for n=1:Nbit,
y1(n)=sum(r1((n-1)*N+1:n*N));
end
d1=zeros(1,Nbit);
% Entscheider = BPSK-Demodulator
for n=1:Nbit,
d1(n)=sign(y1(n));
if d1(n)==0,
d1(n)=1;
end
end
% Bestimmung BER
BER=sum(abs(d(1,:)-d1)/2)/Nbit
4