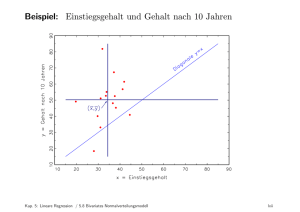
Okonometrie Organisatorisches I

Ökonometrie
Vorlesung an der Universität des Saarlandes
Dr. Martin Becker
Sommersemester 2014
Ökonometrie (SS 2014)
1 Einleitung
Folie 1
Organisatorisches 1.1
Organisatorisches I
Vorlesung: Mittwoch, 08:30-10:00 Uhr, Gebäude B4 1, HS 0.18
Übung: Dienstag, 12:15-13:45 Uhr, Gebäude B4 1, HS 0.18, Beginn: 22.04.
Prüfung: 2-stündige Klausur nach Semesterende (1. Prüfungszeitraum)
Anmeldung im ViPa nur vom 12.05. (8 Uhr) – 26.05. (15 Uhr)!
(Abmeldung im ViPa bis 10.07., 12 Uhr)
Hilfsmittel für Klausur
I
I
I
Moderat“ programmierbarer Taschenrechner, auch mit Grafikfähigkeit
”
2 beliebig gestaltete DIN A 4–Blätter (bzw. 4, falls nur einseitig)
Benötigte Tabellen werden gestellt, aber keine weitere Formelsammlung!
Durchgefallen — was dann?
I
I
Nachprüfung“ Ende März/Anfang April 2015 (2. Prüfungszeitraum)
”
ab Sommersemester 2015: ???
Ökonometrie (SS 2014)
Folie 2
1 Einleitung
Organisatorisches 1.1
Organisatorisches II
Informationen und Materialien unter
http://www.lehrstab-statistik.de
bzw. genauer
http://www.lehrstab-statistik.de/oekoss2014.html .
Kontakt: Dr. Martin Becker
Geb. C3 1, 2. OG, Zi. 2.17
e-Mail: [email protected]
Sprechstunde nach Vereinbarung (Terminabstimmung per e-Mail)
Vorlesungsunterlagen
I
I
I
Diese Vorlesungsfolien (Ergänzung im Laufe des Semesters)
Eventuell Vorlesungsfolien der Veranstaltung von Prof. Friedmann aus SS 2013
Download spätestens Dienstags, 19:00 Uhr, vor der Vorlesung möglich
Ökonometrie (SS 2014)
1 Einleitung
Folie 3
Organisatorisches 1.1
Organisatorisches III
Übungsunterlagen
I
I
I
I
Übungsblätter (i.d.R. wöchentlich)
Download i.d.R. nach der Vorlesung im Laufe des Mittwochs möglich
Besprechung der Übungsblätter in der Übung der folgenden Woche.
Übungsaufgaben sollten unbedingt vorher selbst bearbeitet werden!
Im Sommersemester 2014 sehr spezielle Situation (Makro...)
I
I
I
I
I
Beginn ausnahmsweise mit Wiederholung statistischer Grundlagen.
Dadurch Wegfall einiger regulärer Inhalte.
Alte Klausuren nur eingeschränkt relevant.
Wiederholung nur lückenhaft und wenig formal möglich!
Je nach Kenntnisstand: Eigene Wiederholung statistischer Grundlagen
z.B. aus den jeweiligen Veranstaltungsfolien nötig!
Ökonometrie (SS 2014)
Folie 4
2 Wiederholung statistischer Grundlagen
Deskriptive Statistik 2.1
Inhaltsverzeichnis
(Ausschnitt)
2
Wiederholung statistischer Grundlagen
Deskriptive Statistik
Wahrscheinlichkeitsrechnung
Schließende Statistik
Ökonometrie (SS 2014)
Folie 5
2 Wiederholung statistischer Grundlagen
Deskriptive Statistik 2.1
Lage- und Streuungsmaße eindimensionaler Daten
Betrachte zunächst ein kardinalskaliertes Merkmal X mit Urliste (Daten)
x1 , . . . , xn der Länge n.
Daten sollen auf wenige Kennzahlen“ verdichtet werden.
”
Übliches Lagemaß: klassische“ Mittelung der Merkmalswerte, also
”
arithmetisches Mittel“ x mit:
”
n
1
1X
x := (x1 + x2 + · · · + xn ) =
xi
n
n
i=1
Übliche Streuungsmaße: Mittlere quadrierte Differenz zwischen
Merkmalswerten und arithmetischem Mittel (empirische Varianz) sX2 sowie
deren (positive) Wurzel (empirische Standardabweichung) sX mit:
!
n
n
X
X
p
1
1
2 !
sX2 :=
(xi − x) =
xi2 − x 2 =: x 2 − x 2 ,
sX = + sX2
n
n
i=1
i=1
Standardabweichung sX hat dieselbe Dimension wie die Merkmalswerte,
daher i.d.R. besser zu interpretieren als Varianz sX2 .
Ökonometrie (SS 2014)
Folie 6
2 Wiederholung statistischer Grundlagen
Deskriptive Statistik 2.1
Abhängigkeitsmaße zweidimensionaler Daten I
Nehme nun an, dass den Merkmalsträgern zu zwei kardinalskalierten
Merkmalen X und Y Merkmalswerte zugeordnet werden, also eine Urliste der
Länge n (also n Datenpaare)
(x1 , y1 ), (x2 , y2 ), . . . , (xn , yn )
zu einem zweidimensionalen Merkmal (X , Y ) vorliegt.
Unverzichtbare Eigenschaft der Urliste ist, dass die Paare von
Merkmalswerten jeweils demselben Merkmalsträger zuzuordnen sind!
Mit den zugehörigen Lage- und Streuungsmaßen x, y , sX und sY der
eindimensionalen Merkmale definiert man als Abhängigkeitsmaße zunächst
die empirische Kovarianz sX ,Y mit:
!
n
n
X
1X
1
!
sX ,Y :=
(xi − x)(yi − y ) =
xi · yi − x · y =: xy − x · y
n
n
i=1
i=1
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 7
Deskriptive Statistik 2.1
Abhängigkeitsmaße zweidimensionaler Daten II
Als standardisiertes, skalenunabhängiges Abhängigkeitsmaß definiert man
darauf aufbauend den empirischen (Bravais-)Pearsonschen
Korrelationskoeffizienten rX ,Y mit:
sX ,Y
rX ,Y :=
sX · sY
Es gilt stets −1 ≤ rX ,Y ≤ 1.
rX ,Y misst lineare Zusammenhänge, spezieller gilt
I
I
I
rX ,Y > 0 bei positiver Steigung“ ( X und Y sind positiv korreliert“),
”
”
rX ,Y < 0 bei negativer Steigung“ ( X und Y sind negativ korreliert“),
”
”
|rX ,Y | = 1, falls alle (xi , yi ) auf einer Geraden (mit Steigung 6= 0) liegen.
rX ,Y ist nur definiert, wenn X und Y jeweils mindestens zwei verschiedene
Merkmalsausprägungen besitzen.
Ökonometrie (SS 2014)
Folie 8
2 Wiederholung statistischer Grundlagen
Deskriptive Statistik 2.1
Beispiel: Empirischer Pearsonscher Korrelationskoeffizient
rX, Y = 0
20
●
●
●
●
●
●
●
●
●
●
●
8
15
●
●
●
80
●
●
●
●
●
●
●
●
●
4
●
●
●
40
●
●
6
●
Y
●
●
●
●
●
Y
●
10
●
60
●
●
Y
rX, Y = −1
10
100
rX, Y = 1
●
●
●
●
●
●
●
●
0
5
10
15
20
5
●
●
15
20
10
15
rX, Y = 0.9652
rX, Y = 0.1103
rX, Y = −0.837
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
4
●
●
●
4.0
●
●
● ●
●
●
●
●
8
●
Y
10
●
●
●
●
Y
5.0
15
●
●
●
●
●
●
10
●
●
●
●
●
●
●
2
●
3.0
●
●
5
10
15
20
20
●
●
6
●
6.0
20
●
12
X
●
0
5
X
●
Y
●
●
10
●
5
● ● ●
X
●
●
●
●
●
●
●
●
●
2
●
5
●
20
●
●
5
10
X
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
X
15
20
●
●
●
5
10
15
●
20
X
Folie 9
Wahrscheinlichkeitsrechnung 2.2
Inhaltsverzeichnis
(Ausschnitt)
2
Wiederholung statistischer Grundlagen
Deskriptive Statistik
Wahrscheinlichkeitsrechnung
Schließende Statistik
Ökonometrie (SS 2014)
Folie 10
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Eindimensionale Zufallsvariablen I
(Eindimensionale) Zufallsvariablen X entstehen formal als (Borel-messbare)
Abbildungen X : Ω → R von Ergebnismengen Ω eines
Wahrscheinlichkeitsraums (Ω, F, P) in die reellen Zahlen.
Auf eine Wiederholung der grundlegenden Konzepte von Zufallsexperimenten
bzw. Wahrscheinlichkeitsräumen muss aus Zeitgründen allerdings verzichtet
werden.
Wir fassen eine Zufallsvariable auf als eine Variable“,
”
I
I
I
die (i.d.R. mehrere verschiedene) numerische Werte annehmen kann,
deren Werte ( Realisationen“) nicht vorherbestimt sind, sondern von einem
”
zufälligen, meist wiederholbarem Vorgang abhängen,
über deren Werteverteilung“ man allerdings Kenntnisse hat
”
( Wahrscheinlichkeitsrechnung) oder Kenntnisse erlangen möchte
( Schließende Statistik).
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 11
Wahrscheinlichkeitsrechnung 2.2
Eindimensionale Zufallsvariablen II
Unterteilung von Zufallsvariablen X (abhängig von Werteverteilung) in
mehrere Typen
Diskrete Zufallsvariablen X :
I
I
Können nur endlich viele oder abzählbar unendlich viele verschiedene Werte
annehmen.
Werteverteilung kann durch eine Wahrscheinlichkeitsfunktion pX spezifiziert
werden, die jeder reellen Zahl die Wahrscheinlichkeit des Auftretens zuordnet.
Stetige Zufallsvariablen X :
I
I
I
Können überabzählbar viele Werte (in einem Kontinuum reeller Zahlen)
annehmen.
Werteverteilung kann durch eine Dichtefunktion fX spezifiziert werden, mit
deren Hilfe man zum Beispiel Wahrscheinlichkeiten dafür ausrechnen kann,
dass der Wert der Zufallsvariablen in einem bestimmten Intervall liegt.
Einzelne reelle Zahlen (alle!) werden mit Wahrscheinlichkeit 0 angenommen!
Außerdem existieren (hier nicht betrachtete) Misch-/Sonderformen.
Ökonometrie (SS 2014)
Folie 12
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Eindimensionale Zufallsvariablen III
Wahrscheinlichkeiten P{X ∈ A} = PX (A) dafür, dass eine Zufallsvariable X
Werte in einer bestimmten Menge A annimmt, können konkreter
I
bei diskreten Zufallsvariablen X für endliche oder abzählbar unendliche
Mengen A mit Hilfe der Wahrscheinlichkeitsfunktion pX durch
X
P{X ∈ A} =
pX (xi )
xi ∈A
I
bei stetigen Zufallsvariablen X für Intervalle A = [a, b], A = (a, b), A = (a, b]
oder(!) A = [a, b) (mit a < b) mit Hilfe einer(!) zugehörigen Dichtefunktion fX
durch
Z
b
P{X ∈ A} =
fX (x)dx
a
berechnet werden.
Werteverteilungen von Zufallsvariablen sind bereits eindeutig durch alle
Wahrscheinlichkeiten der Form P{X ≤ x} := P{X ∈ (−∞, x]} für x ∈ R
festgelegt.
Die zugehörige Funktion FX : R → R; FX (x) = P{X ≤ x} heißt
Verteilungsfunktion von X .
Ökonometrie (SS 2014)
Folie 13
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Momente eindimensionaler Zufallsvariablen I
Lage- und Streuungsmaßen von Merkmalen (aus deskriptiver Statistik)
entsprechen Momente von Zufallsvariablen.
Momente von Zufallsvariablen sind also Kennzahlen, die die Werteverteilung
auf einzelne Zahlenwerte verdichten. (Diese Kennzahlen müssen nicht
existieren, Existenzfragen hier aber vollkommen ausgeklammert!)
Kennzahl für die Lage der (Werte-)Verteilung einer Zufallsvariablen X :
Erwartungswert bzw. auch Mittelwert µX := E(X )
I
Berechnung bei diskreter Zufallsvariablen X durch:
X
E(X ) =
xi · pX (xi )
xi ∈T (X )
I
(wobei T (X ) := {x ∈ R | pX (xi ) > 0} den Träger von X bezeichnet).
Berechnung bei stetiger Zufallsvariablen X durch:
Z ∞
E(X ) =
x · fX (x)dx
−∞
Ökonometrie (SS 2014)
Folie 14
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Momente eindimensionaler Zufallsvariablen II
Kennzahl für die Streuung der (Werte-)Verteilung einer Zufallsvariablen
p X:
2
Varianz σX := Var(X ) von X und deren (positive) Wurzel σX = + Var(X ),
die sog. Standardabweichung von X , mit
h
i
!
2
Var(X ) = E (X − E(X )) = E(X 2 ) − [E(X )]2
I
Berechnung von E(X 2 ) für diskrete Zufallsvariable X durch:
X 2
E(X 2 ) =
xi · pX (xi )
xi ∈T (X )
I
Berechnung von E(X 2 ) bei stetiger Zufallsvariablen X durch:
Z ∞
2
E(X ) =
x 2 · fX (x)dx
−∞
Ökonometrie (SS 2014)
Folie 15
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Momente eindimensionaler Zufallsvariablen III
Für eine Zufallsvariable X und reelle Zahlen a, b gilt:
I
I
E(aX + b) = a E(X ) + b
Var(aX + b) = a2 Var(X )
Allgemeiner gilt ( Linearität des Erwartungswerts“) für eine
”
(eindimensionale) Zufallsvariable X , reelle Zahlen a, b und (messbare)
Abbildungen G : R → R und H : R → R:
E(aG (X ) + bH(X )) = a E(G (X )) + b E(H(X ))
Ist X eine Zufallsvariable mit
p Erwartungswert µX = E(X ) und
Standardabweichung σX = Var(X ), so erhält man mit
X − E(X )
X − µX
Z := p
=
σX
Var(X )
eine neue Zufallsvariable mit E(Z ) = 0 und Var(Z ) = 1.
Man nennt Z dann eine standardisierte Zufallsvariable.
Ökonometrie (SS 2014)
Folie 16
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Momente eindimensionaler Zufallsvariablen IV
Weiteres Lagemaß für Zufallsvariablen: p-Quantile
Für p ∈ (0, 1) ist xp ein p-Quantil der Zufallsvariablen X , wenn gilt:
P{X ≤ xp } ≥ p
und
P{X ≥ xp } ≥ 1 − p
Quantile sind nicht immer eindeutig bestimmt, für stetige Zufallsvariablen mit
streng monoton wachsender Verteilungsfunktion lassen sich Quantile aber
eindeutig durch Lösung der Gleichung
FX (xp ) = p
bzw. unter Verwendung der Umkehrfunktion FX−1 der Verteilungsfunktion FX
(auch Quantilsfunktion genannt) direkt durch
xp = FX−1 (p)
bestimmen.
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 17
Wahrscheinlichkeitsrechnung 2.2
Spezielle parametrische Verteilungsfamilien
Parametrische Verteilungsfamilien fassen ähnliche Verteilungen zusammen.
Genaue Verteilung innerhalb dieser Familien wird durch einen oder wenige
(reelle) Parameter (bzw. einen ein- oder mehrdimensionalen
Parametervektor) eineindeutig festgelegt, also
I
I
legt der Parameter(vektor) die Verteilung vollständig fest und
gehören zu verschiedenen Parameter(vektore)n auch jeweils unterschiedliche
Verteilungen ( Identifizierbarkeit“).
”
Die Menge der zulässigen Parameter(vektoren) heißt Parameterraum.
Im Folgenden: Exemplarische Wiederholung je zweier diskreter und stetiger
Verteilungsfamilien.
Ökonometrie (SS 2014)
Folie 18
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Bernoulli-/Alternativverteilung
Verwendung:
I
I
I
I
Modellierung eines Zufallsexperiments (Ω, F, P), in dem nur das Eintreten
bzw. Nichteintreten eines einzigen Ereignisses A von Interesse ist.
Eintreten des Ereignisses A wird oft als Erfolg“ interpretiert, Nichteintreten
”
(bzw. Eintreten von A) als Misserfolg“.
”
Zufallsvariable soll im Erfolgsfall Wert 1 annehmen, im Misserfolgsfall Wert 0,
es sei also
1 falls ω ∈ A
X (ω) :=
0 falls ω ∈ A
Beispiel: Werfen eines fairen Würfels, Ereignis A: 6 gewürfelt“ mit P(A) = 61 .
”
Verteilung von X hängt damit nur von Erfolgswahrscheinlichkeit“ p := P(A)
”
ab; p ist also einziger Parameter der Verteilungsfamilie.
Um triviale Fälle auszuschließen, betrachtet man nur Ereignisse mit p ∈ (0, 1)
Der Träger der Verteilung ist dann T (X ) = {0, 1}, die
Punktwahrscheinlichkeiten sind pX (0) = 1 − p und pX (1) = p.
Symbolschreibweise für Bernoulli-Verteilung mit Parameter p: B(1, p)
Ist X also Bernoulli-verteilt mit Parameter p, so schreibt man X ∼ B(1, p).
Ökonometrie (SS 2014)
Folie 19
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
für x < 0
für 0 ≤ x < 1
für x ≥ 1
Ökonometrie (SS 2014)
=
0.8
0.6
0.4
0.2
0.0
−1.0
−0.5
0.0
0.5
1.0
1.5
2.0
1.5
2.0
x
FX
●
p = 0.4
●
−1.0
−0.5
0.0
0.5
1.0
x
Momente: E (X ) = p
γ(X )
pX
p = 0.4
0.0 0.2 0.4 0.6 0.8 1.0
Verteilungsfunktion:

 0
1−p
FX (x) =

1
pX(x)
Träger: T (X ) = {0, 1}
Wahrscheinlichkeitsfunktion:

 1 − p für x = 0
p
für x = 1
pX (x) =

0
sonst
Parameter:
p ∈ (0, 1)
FX(x)
Bernoulli-/Alternativverteilung
B(1, p)
Var(X )
√1−2p
p(1−p)
κ(X )
= p · (1 − p)
=
1−3p(1−p)
p(1−p)
Folie 20
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Binomialverteilung
Verallgemeinerung der Bernoulli-Verteilung
Verwendung:
I
I
I
I
I
Modellierung der unabhängigen, wiederholten Durchführung eines
Zufallsexperiments, in dem nur die Häufigkeit des Eintretens bzw.
Nichteintretens eines Ereignisses A interessiert ( Bernoulli-Experiment“).
”
Eintreten des Ereignisses A wird auch hier oft als Erfolg“ interpretiert,
”
Nichteintreten (bzw. Eintreten von A) als Misserfolg“.
”
Zufallsvariable X soll die Anzahl der Erfolge bei einer vorgegebenen Anzahl
von n Wiederholungen des Experiments zählen.
Nimmt Xi für i ∈ {1, . . . , n} im Erfolgsfall (für DurchfP
ührung i) den Wert 1
an, im Misserfolgsfall den Wert 0, dann gilt also X = ni=1 Xi .
Beispiel: 5-faches Werfen eines fairen Würfels, Anzahl der Zahlen kleiner 3.
n = 5, p = 1/3.
Verteilung von X hängt damit nur von Erfolgswahrscheinlichkeit“ p := P(A)
”
sowie der Anzahl der Durchführungen n des Experiments ab.
Um triviale Fälle auszuschließen, betrachtet man nur die Fälle n ∈ N und
p ∈ (0, 1). Träger der Verteilung ist dann T (X ) = {0, 1, . . . , n}.
Symbolschreibweise für Binomialverteilung mit Parameter n und p: B(n, p)
Übereinstimmung mit Bernoulli-Verteilung (mit Parameter p) für n = 1.
Ökonometrie (SS 2014)
Folie 21
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Binomialverteilung
B(n, p)
0.0 0.1 0.2 0.3 0.4 0.5
Träger: T (X ) = {0, 1, . . . , n}
Wahrscheinlichkeitsfunktion: pX (x)
  n x
p (1 − p)n−x für x ∈ T (X )
=
x

0
sonst
pX(x)
Parameter:
n ∈ N, p ∈ (0, 1)
pX
n = 5, p = 0.4
−1
0
1
2
3
4
5
●
●
4
5
6
x
FX (x) =
X
pX (xi )
xi ∈T (X )
xi ≤x
FX(x)
Verteilungsfunktion:
0.0 0.2 0.4 0.6 0.8 1.0
FX
n = 5, p = 0.4
●
●
●
●
−1
0
1
2
3
6
x
Momente: E (X ) = n · p
γ(X ) =
Ökonometrie (SS 2014)
√ 1−2p
np(1−p)
Var(X )
κ(X )
= n · p · (1 − p)
=
1+(3n−6)p(1−p)
np(1−p)
Folie 22
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Stetige Gleichverteilung
Einfachste stetige Verteilungsfamilie:
Stetige Gleichverteilung auf Intervall [a, b]
Modellierung einer stetigen Verteilung, in der alle Realisationen in einem
Intervall [a, b] als gleichwahrscheinlich“ angenommen werden.
”
Verteilung hängt von den beiden Parametern a, b ∈ R mit a < b ab.
Dichtefunktion fX einer gleichverteilten Zufallsvariablen X kann auf Intervall
1
[a, b] konstant zu b−a
gewählt werden.
Träger der Verteilung: T (X ) = [a, b]
Symbolschreibweise für stetige Gleichverteilung auf [a, b]: X ∼ Unif(a, b)
Ökonometrie (SS 2014)
Folie 23
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Stetige Gleichverteilung
Unif(a, b)
Parameter:
a, b ∈ R mit a < b
fX
a = 1, b = 3
0.4
0.0
0.2
fX(x)
0.6
Träger: T (X ) = [a, b]
Dichtefunktion: fX : R → R;
( 1
für a ≤ x ≤ b
b−a
fX (x) =
0
sonst
0
1
2
3
4
3
4
x
Momente: E (X ) = a+b
2
γ(X ) = 0
Ökonometrie (SS 2014)
Var(X )
κ(X )
0.0 0.2 0.4 0.6 0.8 1.0
Verteilungsfunktion: FX : R → R;

für x < a

 0
x−a
für a ≤ x ≤ b
FX (x) =
b−a


1
für x > b
FX(x)
FX
a = 1, b = 3
0
1
2
x
=
=
(b−a)2
12
9
5
Folie 24
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Normalverteilung
Verteilung entsteht als Grenzverteilung bei Durchschnittsbildung vieler
(unabhängiger) Zufallsvariablen (später mehr!)
Einsatz für Näherungen
Familie der Normalverteilungen hat Lageparameter µ ∈ R, der mit
Erwartungswert übereinstimmt, und Streuungsparameter σ 2 >√0, der mit
Varianz übereinstimmt, Standardabweichung ist dann σ := + σ 2 .
Verteilungsfunktion von Normalverteilungen schwierig zu handhaben,
Berechnung muss i.d.R. mit Software/Tabellen erfolgen.
Wichtige Eigenschaft der Normalverteilungsfamilie:
Ist X normalverteilt mit Parameter µ = 0 und σ 2 = 1, dann ist
aX + b für a, b ∈ R normalverteilt mit Parameter µ = b und σ 2 = a2 .
Zurückführung allgemeiner Normalverteilungen auf den Fall der
Standardnormalverteilung (Gauß-Verteilung) mit Parameter µ = 0 und
σ 2 = 1, Tabellen/Algorithmen für Standardnormalverteilung damit einsetzbar.
Dichtefunktion der Standardnormalverteilung: ϕ, Verteilungsfunktion: Φ.
Träger aller Normalverteilungen ist T (X ) = R.
Symbolschreibweise für Normalverteilung mit Parameter µ, σ 2 : X ∼ N(µ, σ 2 )
Ökonometrie (SS 2014)
Folie 25
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Normalverteilung
N(µ, σ 2 )
(x−µ)2
1
1
fX (x) = √
e − 2σ2 = ϕ
σ
2πσ
x −µ
σ
0.00 0.05 0.10 0.15 0.20
Träger: T (X ) = R
Dichtefunktion: fX : R → R;
fX(x)
Parameter:
µ ∈ R, σ 2 > 0
fX
µ = 5, σ2 = 4
0
5
10
x
FX : R → R; FX (x) = Φ
x −µ
σ
FX(x)
Verteilungsfunktion:
0.0 0.2 0.4 0.6 0.8 1.0
FX
µ = 5, σ2 = 4
0
5
10
x
Momente: E (X ) = µ
γ(X ) = 0
Ökonometrie (SS 2014)
Var(X )
κ(X )
= σ2
= 3
Folie 26
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Arbeiten mit Normalverteilungen
Problem (nicht nur) bei normalverteilten Zufallsvariablen X ∼ N(µ, σ 2 ):
Verteilungsfunktion FX und Quantilsfunktion FX−1 schlecht handhabbar bzw.
nicht leicht auszuwerten!
Traditionelle Lösung: Tabellierung der entsprechenden Funktionswerte
Lösung nicht mehr zeitgemäß: (kostenlose) PC-Software für alle benötigten
Verteilungsfunktionen verfügbar, zum Beispiel Statistik-Software R
(http://www.r-project.org)
Aber: In Klausur keine PCs verfügbar, daher dort Rückgriff auf (dort zur
Verfügung gestellte) Tabellen.
Wegen der Symmetrie der Standardnormalverteilung um 0 gilt nicht nur
ϕ(x) = ϕ(−x) für alle x ∈ R, sondern auch
Φ(x) = 1 − Φ(−x)
für alle x ∈ R .
Daher werden Tabellen für Φ(x) in der Regel nur für x ∈ R+ erstellt.
Ökonometrie (SS 2014)
Folie 27
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Ausschnitt aus Tabelle für Φ(x)
0.0
0.1
0.2
0.3
0.4
0.00
0.5000
0.5398
0.5793
0.6179
0.6554
0.01
0.5040
0.5438
0.5832
0.6217
0.6591
0.02
0.5080
0.5478
0.5871
0.6255
0.6628
0.03
0.5120
0.5517
0.5910
0.6293
0.6664
0.04
0.5160
0.5557
0.5948
0.6331
0.6700
0.05
0.5199
0.5596
0.5987
0.6368
0.6736
0.06
0.5239
0.5636
0.6026
0.6406
0.6772
0.07
0.5279
0.5675
0.6064
0.6443
0.6808
0.08
0.5319
0.5714
0.6103
0.6480
0.6844
0.09
0.5359
0.5753
0.6141
0.6517
0.6879
0.5
0.6
0.7
0.8
0.9
0.6915
0.7257
0.7580
0.7881
0.8159
0.6950
0.7291
0.7611
0.7910
0.8186
0.6985
0.7324
0.7642
0.7939
0.8212
0.7019
0.7357
0.7673
0.7967
0.8238
0.7054
0.7389
0.7704
0.7995
0.8264
0.7088
0.7422
0.7734
0.8023
0.8289
0.7123
0.7454
0.7764
0.8051
0.8315
0.7157
0.7486
0.7794
0.8078
0.8340
0.7190
0.7517
0.7823
0.8106
0.8365
0.7224
0.7549
0.7852
0.8133
0.8389
1.0
1.1
1.2
1.3
1.4
0.8413
0.8643
0.8849
0.9032
0.9192
0.8438
0.8665
0.8869
0.9049
0.9207
0.8461
0.8686
0.8888
0.9066
0.9222
0.8485
0.8708
0.8907
0.9082
0.9236
0.8508
0.8729
0.8925
0.9099
0.9251
0.8531
0.8749
0.8944
0.9115
0.9265
0.8554
0.8770
0.8962
0.9131
0.9279
0.8577
0.8790
0.8980
0.9147
0.9292
0.8599
0.8810
0.8997
0.9162
0.9306
0.8621
0.8830
0.9015
0.9177
0.9319
1.5
1.6
1.7
1.8
1.9
0.9332
0.9452
0.9554
0.9641
0.9713
0.9345
0.9463
0.9564
0.9649
0.9719
0.9357
0.9474
0.9573
0.9656
0.9726
0.9370
0.9484
0.9582
0.9664
0.9732
0.9382
0.9495
0.9591
0.9671
0.9738
0.9394
0.9505
0.9599
0.9678
0.9744
0.9406
0.9515
0.9608
0.9686
0.9750
0.9418
0.9525
0.9616
0.9693
0.9756
0.9429
0.9535
0.9625
0.9699
0.9761
0.9441
0.9545
0.9633
0.9706
0.9767
2.0
2.1
2.2
2.3
2.4
0.9772
0.9821
0.9861
0.9893
0.9918
0.9778
0.9826
0.9864
0.9896
0.9920
0.9783
0.9830
0.9868
0.9898
0.9922
0.9788
0.9834
0.9871
0.9901
0.9925
0.9793
0.9838
0.9875
0.9904
0.9927
0.9798
0.9842
0.9878
0.9906
0.9929
0.9803
0.9846
0.9881
0.9909
0.9931
0.9808
0.9850
0.9884
0.9911
0.9932
0.9812
0.9854
0.9887
0.9913
0.9934
0.9817
0.9857
0.9890
0.9916
0.9936
Ökonometrie (SS 2014)
Folie 28
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Beispiel: Arbeiten mit Normalverteilungstabelle
0.02
0.04
µ = 100, σ2 = 82
0.00
fN(100, 82)(x)
Frage: Mit welcher Wahrscheinlichkeit nimmt eine N(100, 82 )-verteilte
Zufallsvariable Werte kleiner als 90 an? (Wie groß ist die schraffierte Fläche?)
70
80
90
100
110
120
130
x
Antwort: Ist X ∼ N(100, 82 ), so gilt:
P{X < 90}
90 − 100
= FN(100,82 ) (90) = Φ
8
= Φ(−1.25) = 1 − Φ(1.25) = 1 − 0.8944 = 0.1056
Die gesuchte Wahrscheinlichkeit ist 0.1056 = 10.56%.
Ökonometrie (SS 2014)
Folie 29
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
0.04
µ = 100, σ2 = 82
0.02
2.5%
0.00
fN(100, 82)(x)
Frage: Welchen Wert x überschreitet eine N(100, 82 )-verteilte Zufallsvariable
nur mit 2.5% Wahrscheinlichkeit? (Welche linke Grenze x führt bei der
schraffierten Fläche zu einem Flächeninhalt von 0.025?)
70
80
90
100
110
<− | −>
?
120
130
Antwort: Ist X ∼ N(100, 82 ), so ist das 97.5%- bzw. 0.975-Quantil von X
gesucht. Mit
x − 100
FX (x) = FN(100,82 ) (x) = Φ
8
und der Abkürzung Np für das p-Quantil der N(0, 1)-Verteilung erhält man
x − 100 !
x − 100
Φ
= 0.975 ⇔
= Φ−1 (0.975) = N0.975 = 1.96
8
8
⇒ x = 8 · 1.96 + 100 = 115.68
Ökonometrie (SS 2014)
Folie 30
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Beispiel: Arbeiten mit Statistik-Software R
Beantwortung der Fragen (noch) einfacher mit Statistik-Software R:
Frage: Mit welcher Wahrscheinlichkeit nimmt eine N(100, 82 )-verteilte
Zufallsvariable Werte kleiner als 90 an?
Antwort:
> pnorm(90,mean=100,sd=8)
[1] 0.1056498
Frage: Welchen Wert x überschreitet eine N(100, 82 )-verteilte Zufallsvariable
nur mit 2.5% Wahrscheinlichkeit?
Antwort:
> qnorm(0.975,mean=100,sd=8)
[1] 115.6797
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 31
Wahrscheinlichkeitsrechnung 2.2
Mehrdimensionale Zufallsvariablen/Zufallsvektoren I
Simultane Betrachtung mehrerer (endlich vieler) Zufallsvariablen zur
Untersuchung von Abhängigkeiten möglich (und für die Ökonometrie später
erforderlich!)
Ist n ∈ N die Anzahl der betrachteten Zufallsvariablen, so fasst man die n
Zufallsvariablen X1 , . . . , Xn auch in einem n-dimensionalen Vektor
X = (X1 , . . . , Xn )0 zusammen und befasst sich dann mit der gemeinsamen
Verteilung von X .
Die meisten bekannten Konzepte eindimensionaler Zufallsvariablen sind leicht
übertragbar, nur technisch etwas anspruchsvoller.
Zwei Spezialfälle: Diskrete Zufallsvektoren und stetige Zufallsvektoren
Ökonometrie (SS 2014)
Folie 32
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Mehrdimensionale Zufallsvariablen/Zufallsvektoren II
Die gemeinsame Verteilung eines diskreten Zufallsvektors kann durch eine
(mehrdimensionale) gemeinsame Wahrscheinlichkeitsfunktion pX : Rn → R
mit pX (x) := P{X = x} für x ∈ Rn festgelegt werden.
Wahrscheinlichkeiten P{X ∈ A} dafür, dass X Werte in der Menge A
annimmt, können dann wiederum durch Aufsummieren der
Punktwahrscheinlichkeiten aller Trägerpunkte xi mit xi ∈ A berechnet
werden:
X
P{X ∈ A} =
pX (xi )
xi ∈A∩T (X)
Die gemeinsame Verteilung eines stetigen Zufallsvektors kann durch
Angabe einer gemeinsamen Dichtefunktion fX : Rn → R spezifiziert
werden, mit deren Hilfe sich Wahrscheinlichkeiten von Quadern im Rn (über
Mehrfachintegrale) ausrechnen lassen:
PX (A) =
Z
b1
a1
···
Z
bn
an
fX (t1 , . . . , tn )dtn · · · dt1
für A = (a1 , b1 ] × · · · × (an , bn ] ⊂ Rn mit a1 ≤ b1 , . . . , an ≤ bn
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 33
Wahrscheinlichkeitsrechnung 2.2
Mehrdimensionale Zufallsvariablen/Zufallsvektoren III
Die Verteilungen der einzelnen Zufallsvariablen X1 , . . . , Xn eines
n-dimensionalen Zufallsvektors nennt man auch Randverteilungen.
Bei diskreten Zufallsvektoren sind auch die einzelnen Zufallsvariablen
X1 , . . . , Xn diskret, die zugehörigen Wahrscheinlichkeitsfunktionen
pX1 , . . . , pXn nennt man dann auch Randwahrscheinlichkeitsfunktionen.
Bei stetigen Zufallsvektoren sind auch die einzelnen Zufallsvariablen
X1 , . . . , Xn stetig, zugehörige Dichtefunktionen fX1 , . . . , fXn nennt man dann
auch Randdichte(funktione)n.
Randwahrscheinlichkeits- bzw. Randdichtefunktionen können durch
(Mehrfach)summen bzw. (Mehrfach)integrale aus der gemeinsamen
Wahrscheinlichkeits- bzw. Dichtefunktion gewonnen werden (siehe Folien
Wahrscheinlichkeitsrechnung).
Ökonometrie (SS 2014)
Folie 34
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Unabhängigkeit von Zufallsvariablen, Abhängigkeitmaße I
Diskrete bzw. stetige Zufallsvektoren heißen (stochastisch) unabhängig,
wenn man ihre gemeinsame Wahrscheinlichkeits- bzw. Dichtefunktion als
Produkt der jeweiligen Randwahrscheinlichkeits- bzw. Randdichtefunktionen
pX (x) =
n
Y
i=1
bzw.
fX (x) =
pXi (xi ) = pX1 (x1 ) · . . . · pXn (xn )
n
Y
i=1
fXi (xi ) = fX1 (x1 ) · . . . · fXn (xn )
für alle x = (x1 , . . . , xn ) ∈ Rn gewinnen kann.
(Im stetigen Fall: siehe Folien WR für exakte“ bzw. korrekte“ Formulierung!)
”
”
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 35
Wahrscheinlichkeitsrechnung 2.2
Unabhängigkeit von Zufallsvariablen, Abhängigkeitmaße II
Bei fehlender Unabhängigkeit: Betrachtung bedingter Verteilungen und
(paarweise) linearer Abhängigkeiten interessant!
Bedingte Verteilungen:
Was weiß man über die Verteilung einer Zufallsvariablen (konkreter), wenn
man die Realisation (einer oder mehrerer) anderer Zufallsvariablen bereits
kennt?
Lineare Abhängigkeiten:
Treten besonders große Realisation einer Zufallsvariablen häufig im
Zusammenhang mit besondere großen (oder besonders kleinen) Realisationen
einer anderen Zufallsvariablen auf (mit einem entsprechenden Zusammenhang
für besonders kleine Realisationen der ersten Zufallsvariablen);
lässt sich dieser Zusammenhang gut durch eine Gerade beschreiben?
Ökonometrie (SS 2014)
Folie 36
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Unabhängigkeit von Zufallsvariablen, Abhängigkeitmaße III
Zur einfacheren Darstellung: Bezeichnung X bzw. Y statt Xi und Xj für zwei
Zufallsvariablen (aus einem Zufallsvektor).
Maß für lineare Abhängigkeit zweier Zufallsvariablen X und Y : Kovarianz
!
σXY := Cov(X , Y ) := E [(X − E(X )) · (Y − E(Y ))] = E(X · Y ) − E(X ) · E(Y )
(Zur Berechnung von E(X · Y ) siehe Folien WR!)
Rechenregeln für Kovarianzen (X , Y , Z Zufallsvariablen aus Zufallsvektor,
a, b ∈ R):
1
2
3
4
5
6
Cov(aX , bY ) = ab Cov(X , Y )
Cov(X + a, Y + b) = Cov(X , Y )
(Translationsinvarianz)
Cov(X , Y ) = Cov(Y , X )
(Symmetrie)
Cov(X + Z , Y ) = Cov(X , Y ) + Cov(Z , Y )
Cov(X , X ) = Var(X )
X , Y stochastisch unabhängig ⇒ Cov(X , Y ) = 0
Ökonometrie (SS 2014)
Folie 37
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Unabhängigkeit von Zufallsvariablen, Abhängigkeitmaße IV
Nachteil“ der Kovarianz:
”
Erreichbare Werte hängen nicht nur von Stärke der linearen Abhängigkeit,
sondern (wie z.B. aus Rechenregel 1 von Folie 37 ersichtlich) auch von der
Streuung von X bzw. Y ab.
Wie in deskriptiver Statistik: Alternatives Abhängigkeitsmaß mit normiertem
Wertebereich“, welches invariant gegenüber Skalierung von X bzw. Y ist.
”
Hierzu Standardisierung der Kovarianz über Division durch
Standardabweichungen von X und Y (falls σX > 0 und σY > 0!).
Man erhält so den Pearsonschen Korrelationskoeffizienten:
ρXY := Korr(X , Y ) :=
Ökonometrie (SS 2014)
Cov(X , Y )
σXY
= p
σX · σY
+ Var(X ) · Var(Y )
Folie 38
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Unabhängigkeit von Zufallsvariablen, Abhängigkeitmaße V
Rechenregeln: Sind X und Y Zufallsvariablen aus einem Zufallsvektor mit
σX > 0, σY > 0 und a, b ∈ R, so gilt:
1
2
3
4
5
6
7
Korr(aX , bY ) =
(
Korr(X , Y )
falls a · b > 0
− Korr(X , Y ) falls a · b < 0
Korr(X + a, Y + b) = Korr(X , Y )
(Translationsinvarianz)
Korr(X , Y ) = Korr(Y , X )
(Symmetrie)
−1 ≤ Korr(X , Y ) ≤ 1
Korr(X , X ) = 1
Korr(X , Y ) =
1
a>0
genau dann, wenn Y = aX + b mit
Korr(X , Y ) = −1
a<0
X , Y stochastisch unabhängig ⇒ Korr(X , Y ) = 0
Zufallsvariablen X , Y mit Cov(X , Y ) = 0 (!) heißen unkorreliert.
Ökonometrie (SS 2014)
Folie 39
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Beispiel: Zweidimensionale Normalverteilung I
Wichtige mehrdimensionale stetige Verteilung: mehrdimensionale
(multivariate) Normalverteilung
Spezifikation am Beispiel der zweidimensionalen (bivariaten)
Normalverteilung durch Angabe einer Dichtefunktion
fX ,Y (x, y ) =
1√
2πσX σY
1−ρ
e
2
−
1
2(1−ρ2 )
x−µX
σX
2
−2ρ
x−µX
σX
y −µY
σY
y −µY 2
+ σ
Y
abhängig von den Parametern µX , µY ∈ R, σX , σY > 0, ρ ∈ (−1, 1).
Man kann zeigen, dass die Randverteilungen von (X , Y ) dann wieder
(eindimensionale) Normalverteilungen sind, genauer gilt X ∼ N(µX , σX2 ) und
Y ∼ N(µY , σY2 )
Außerdem kann der Zusammenhang Korr(X , Y ) = ρ gezeigt werden.
Ökonometrie (SS 2014)
Folie 40
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Beispiel: Zweidimensionale Normalverteilung II
Sind fX bzw. fY die wie auf Folie 26 definierten Dichtefunktionen zur
N(µX , σX2 )- bzw. N(µY , σY2 )-Verteilung, so gilt (genau) im Fall ρ = 0
für alle x, y ∈ R ,
fX ,Y (x, y ) = fX (x) · fY (y )
also sind X und Y (genau) für ρ = 0 stochastisch unabhängig.
Auch für ρ 6= 0 sind die bedingten Verteilungen von X |Y = y und Y |X = x
wieder Normalverteilungen, es gilt genauer:
ρσX
X |Y = y ∼ N µX +
(y − µY ), σX2 (1 − ρ2 )
σY
bzw.
Y |X = x
ρσY
N µY +
(x − µX ), σY2 (1 − ρ2 )
σX
∼
Ökonometrie (SS 2014)
Folie 41
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Beispiel: Zweidimensionale Normalverteilung III
Dichtefunktion der mehrdimensionalen Normalverteilung
0.06
0.04
f(x,y)
0.02
0.00
6
4
6
y
4
2
2
0
0
−2
x
−4
µX = 1, µY = 3, σ2X = 4, σ2Y = 2, ρ = 0.5
Ökonometrie (SS 2014)
Folie 42
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Beispiel: Zweidimensionale Normalverteilung IV
Isohöhenlinien der mehrdimensionalen Normalverteilungsdichte
6
0.005
0.02
0.03
4
0.04
0.05
y
0.06
2
0.055
0.045
0.035
0.025
0.015
0
0.01
−4
−2
0
2
4
6
x
µX = 1, µY = 3, σ2X = 4, σ2Y = 2, ρ = 0.5
Ökonometrie (SS 2014)
Folie 43
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Beispiel: Zweidimensionale Normalverteilung V
Dichtefunktion der mehrdimensionalen Normalverteilung
0.15
f(x,y)
0.10
0.05
3
2
1
3
0
y
2
1
−1
0
−1
−2
x
−2
−3 −3
µX = 0, µY = 0, σ2X = 1, σ2Y = 1, ρ = 0
Ökonometrie (SS 2014)
Folie 44
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Beispiel: Zweidimensionale Normalverteilung VI
3
Isohöhenlinien der mehrdimensionalen Normalverteilungsdichte
2
0.02
0.04
0.06
1
0.08
0.1
0
y
0.14
−3
−2
−1
0.12
−3
−2
−1
0
1
2
3
x
µX = 0, µY = 0, σ2X = 1, σ2Y = 1, ρ = 0
Ökonometrie (SS 2014)
Folie 45
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Beispiel: Zweidimensionale Normalverteilung VII
Dichtefunktion der mehrdimensionalen Normalverteilung
0.10
f(x,y)
0.05
0.00
16
14
12
16
10
y
14
12
8
8
6
10
x
6
4
4
µX = 10, µY = 10, σ2X = 4, σ2Y = 4, ρ = −0.95
Ökonometrie (SS 2014)
Folie 46
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Beispiel: Zweidimensionale Normalverteilung VIII
14
16
Isohöhenlinien der mehrdimensionalen Normalverteilungsdichte
0.02
0.03
12
0.05
0.07
0.09
10
y
0.11
0.12
0.1
8
0.08
0.06
6
0.04
4
0.01
4
6
8
10
12
14
16
x
µX = 10, µY = 10, σ2X = 4, σ2Y = 4, ρ = −0.95
Ökonometrie (SS 2014)
Folie 47
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Momente von Summen von Zufallsvariablen I
Sind X und Y zwei Zufallsvariablen aus einem Zufallsvektor und a, b, c ∈ R,
so gilt:
E(a · X + b · Y + c) = a · E(X ) + b · E(Y ) + c
und
Var(aX + bY + c) = a2 Var(X ) + 2ab Cov(X , Y ) + b2 Var(Y )
Dies kann für mehr als zwei Zufallsvariablen X1 , . . . , Xn eines Zufallsvektors
weiter verallgemeinert werden!
Ökonometrie (SS 2014)
Folie 48
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Momente von Summen von Zufallsvariablen II
Für einen n-dimensionalen Zufallsvektor X = (X1 , . . . , Xn )0 heißt der
n-dimensionale Vektor
E(X) := [E(X1 ), . . . , E(Xn )]0
Erwartungswertvektor von X und die n × n-Matrix
0
V(X) := E (X − E(X)) · (X − E(X))


E[(X1 − E(X1 )) · (X1 − E(X1 ))] · · · E[(X1 − E(X1 )) · (Xn − E(Xn ))]


..
..
..
:= 

.
.
.
E[(Xn − E(Xn )) · (X1 − E(X1 ))] · · · E[(Xn − E(Xn )) · (Xn − E(Xn ))]


Var(X1 )
Cov(X1 , X2 )
· · · Cov(X1 , Xn−1 )
Cov(X1 , Xn )
 Cov(X2 , X1 )
Var(X2 )
· · · Cov(X2 , Xn−1 )
Cov(X2 , Xn ) 




.
.
.
.
.
.
.
.
.
.
= 

.
.
.
.
.


 Cov(Xn−1 , X1 ) Cov(Xn−1 , X2 ) · · ·
Var(Xn−1 )
Cov(Xn−1 , Xn ) 
Cov(Xn , X1 )
Cov(Xn , X2 ) · · · Cov(Xn , Xn−1 )
Var(Xn )
(Varianz-)Kovarianzmatrix von X.
Ökonometrie (SS 2014)
Folie 49
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Momente von Summen von Zufallsvariablen III
In Verallgemeinerung von Folie 48 erhält man für eine gewichtete Summe
n
X
i=1
n
X
den Erwartungswert E
i=1
die Varianz
Var
n
X
i=1
wi · Xi
!
=
wi · Xi
n X
n
X
i=1 j=1
=
n
X
i=1
0
wi2
!
=
n
X
i=1
wi · E(Xi ) = w0 E(X)
wi · wj · Cov(Xi , Xj )
· Var(Xi ) + 2
= w V(X)w
Ökonometrie (SS 2014)
(w = (w1 , . . . , wn )0 ∈ Rn )
wi · Xi = w1 · X1 + · · · + wn · Xn
n−1 X
n
X
i=1 j=i+1
wi · wj · Cov(Xi , Xj )
Folie 50
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Summen unabhängig identisch verteilter Zufallsvariablen I
Sind für n ∈ N die Zufallsvariablen X1 , . . . , Xn eines n-dimensionalen
Zufallsvektors stochastisch unabhängig (damit unkorreliert!) und identisch
verteilt ( u.i.v.“ oder Pi.i.d.“) mit E(Xi ) ≡ µX und Var(Xi ) ≡ σX2 , dann gilt
”
”n
für die Summe Yn := i=1 Xi also
E(Yn ) = n · µX
Var(Yn ) = n · σX2
sowie
und man erhält durch
Zn :=
Yn − nµX
√
=
σX n
1
n
X
i=1 i − µX √
n
σX
Pn
standardisierte Zufallsvariablen (mit E(Zn ) = 0 und Var(Zn ) = 1).
Zentraler Grenzwertsatz:
Verteilung von Zn konvergiert für n → ∞ gegen eine N(0, 1)-Verteilung
(Standardnormalverteilung).
iid
Gilt sogar Xi ∼ N(µX , σX2 ), so gilt (exakt!) Zn ∼ N(0, 1) für alle n ∈ N.
Ökonometrie (SS 2014)
Folie 51
2 Wiederholung statistischer Grundlagen
Wahrscheinlichkeitsrechnung 2.2
Summen unabhängig identisch verteilter Zufallsvariablen II
Anwendung des zentralen Grenzwertsatzes z.B. dadurch, dass man
näherungsweise (auch falls Xi nicht normalverteilt ist) für
hinreichend großes n ∈ N
I
die
N(nµX , nσX2 )-Verteilung
für Yn :=
n
X
Xi oder
i=1
I
Yn − nµX
√
die Standardnormalverteilung für Zn :=
=
σX n
verwendet.
1
n
Pn
Xi − µX √
n
σX
i=1
Leicht zu merken:
Man verwendet näherungsweise die Normalverteilung mit
passendem“ Erwartungswert und passender“ Varianz!
”
”
Ökonometrie (SS 2014)
Folie 52
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Inhaltsverzeichnis
(Ausschnitt)
2
Wiederholung statistischer Grundlagen
Deskriptive Statistik
Wahrscheinlichkeitsrechnung
Schließende Statistik
Ökonometrie (SS 2014)
Folie 53
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Grundidee der schließenden Statistik
Ziel der schließenden Statistik/induktiven Statistik:
Ziehen von Rückschlüssen auf die
Verteilung einer (größeren) Grundgesamtheit auf Grundlage der
Beobachtung einer (kleineren) Stichprobe.
Rückschlüsse auf die Verteilung können sich auch beschränken auf spezielle
Eigenschaften/Kennzahlen der Verteilung, z.B. den Erwartungswert.
Fundament“: Drei Grundannahmen
”
1
2
3
Der interessierende Umweltausschnitt kann durch eine (ein- oder
mehrdimensionale) Zufallsvariable Y beschrieben werden.
Man kann eine Menge W von Wahrscheinlichkeitsverteilungen angeben, zu der
die unbekannte wahre Verteilung von Y gehört.
Man beobachtet Realisationen x1 , . . . , xn von (Stichproben-)Zufallsvariablen
X1 , . . . , Xn , deren gemeinsame Verteilung in vollständig bekannter Weise von
der Verteilung von Y abhängt.
Ziel ist es also, aus der Beobachtung der n Werte x1 , . . . , xn mit Hilfe des
bekannten Zusammenhangs zwischen den Verteilungen von X1 , . . . , Xn und Y
Aussagen über die Verteilung von Y zu treffen.
Ökonometrie (SS 2014)
Folie 54
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Veranschaulichung“ der schließenden Statistik
”
Grundgesamtheit
Ziehungsverfahren
induziert
Zufallsvariable Y
Verteilung von
Stichprobe
Zufallsvariablen
X1, …, Xn
(konkrete)
Auswahl der
führt
Rückschluss auf
Verteilung/Kenngrößen
Ziehung/
Stichprobe
zu
Realisationen
x1, …, xn
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 55
Schließende Statistik 2.3
Bemerkungen zu den 3 Grundannahmen
Die 1. Grundannahme umfasst insbesondere die Situation, in der die
Zufallsvariable Y einem numerischen Merkmal auf einer endlichen Menge von
Merkmalsträgern entspricht, wenn man mit der Zufallsvariable Y das
Feststellen des Merkmalswerts eines rein zufällig (gleichwahrscheinlich)
ausgewählten Merkmalsträgers beschreibt.
In diesem Fall interessiert man sich häufig für bestimmte Kennzahlen von Y ,
z.B. den Erwartungswert von Y , der dann mit dem arithmetischen Mittel
aller Merkmalswerte übereinstimmt.
Die Menge W von Verteilungen aus der 2. Grundannahme ist häufig eine
parametrische Verteilungsfamilie, zum Beispiel die Menge aller
Normalverteilungen mit Varianz σ 2 = 22 .
Wir beschränken uns auf sehr einfache Zusammenhänge zwischen der
Verteilung der interessierenden Zufallsvariablen Y und der Verteilung der
Zufallsvariablen X1 , . . . , Xn .
Ökonometrie (SS 2014)
Folie 56
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Einfache (Zufalls-)Stichprobe
Einfachster“ Zusammenhang zwischen X1 , . . . , Xn und Y :
”
I
I
Alle Zufallsvariablen X1 , . . . , Xn haben dieselbe Verteilung wie Y .
Die Zufallsvariablen X1 , . . . , Xn sind stochastisch unabhängig.
Zufallsvariablen X1 , . . . , Xn mit diesen beiden Eigenschaften nennt man eine
einfache (Zufalls-)Stichprobe vom Umfang n zu Y .
Eine Stichprobenrealisation x1 , . . . , xn einer solchen einfachen Stichprobe
vom Umfang n erhält man z.B., wenn
I
I
Y das Werfen eines bestimmten Würfels beschreibt und x1 , . . . , xn die
erhaltenen Punktzahlen sind, wenn man den Würfel n Mal geworfen hat.
Y das Feststellen des Merkmalswerts eines rein zufällig (gleichwahrscheinlich)
ausgewählten Merkmalsträgers beschreibt und x1 , . . . , xn die Merkmalswerte
sind, die man bei n-maliger rein zufälliger Auswahl eines Merkmalsträgers als
zugehörige Merkmalswerte erhalten hat, wobei die Mehrfachauswahl desselben
Merkmalsträgers nicht ausgeschlossen wird.
Ökonometrie (SS 2014)
Folie 57
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Stichprobenfunktionen
Die Realisation x1 , . . . , xn einer Stichprobe hat große Ähnlichkeit mit einer
Urliste zu einem Merkmal aus der deskriptiven Statistik.
Die Information aus einer Stichprobe wird in der Regel zunächst mit
sogenannten Stichprobenfunktionen weiter aggregiert; auch diese haben oft
(große) Ähnlichkeit mit Funktionen, die in der deskriptiven Statistik zur
Aggregierung von Urlisten eingesetzt werden.
Interessant sind nicht nur die Anwendung dieser Stichprobenfunktionen auf
bereits vorliegende Stichprobenrealisationen x1 , . . . , xn , sondern auch auf die
Stichprobenzufallsvariablen X1 , . . . , Xn selbst, was dann zu einer neuen
Zufallsvariablen führt!
Bekannteste“ Stichprobenfunktion:
”
n
1X
X :=
Xi
bzw.
n
i=1
Ökonometrie (SS 2014)
n
1X
x :=
xi
n
i=1
Folie 58
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Illustration: Realisationen x von X
Beispiel: Verschiedene Realisationen x von X , wenn Y die Punktzahl eines
fairen Würfels beschreibt und wiederholt Stichprobenrealisationen x1 , . . . , x5
vom Umfang n = 5 (durch jeweils 5-maliges Würfeln mit diesem Würfel)
generiert werden:
x
Stichprobe Nr. x1 x2 x3 x4 x5
1
2
3
4
5
6
7
8
9
..
.
2
6
2
3
6
3
3
5
5
..
.
3
6
2
5
2
1
4
5
4
..
.
4
4
5
6
4
3
3
1
5
..
.
6
4
3
3
1
6
2
5
4
..
.
2
1
5
5
2
3
5
3
4
..
.
3.4
4.2
3.4
4.4
3
3.2
3.4
3.8
4.4
..
.
..
.
Ökonometrie (SS 2014)
Folie 59
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Visualisierung Verteilung X / Zentraler Grenzwertsatz
im Würfelbeispiel“ mit einfachen Stichproben vom Umfang n
”
3
4
5
6
0.12
0.08
pX(xi)
0.06
0.00
0.02
0.04
0.05
0.00
0.00
2
1
2
3
4
5
6
1
2
3
xi
xi
xi
n=4
n=5
n=6
4
5
6
4
5
6
1
1.75
2.75
3.75
xi
Ökonometrie (SS 2014)
4.75
5.75
0.08
0.06
pX(xi)
0.02
0.04
0.06
0.00
0.00
0.00
0.02
0.02
0.04
0.04
0.06
pX(xi)
0.08
0.08
0.10
0.10
0.12
1
pX(xi)
0.10
pX(xi)
0.10
0.05
pX(xi)
0.15
0.10
0.20
n=3
0.14
n=2
0.15
n=1
1
1.8
2.6
3.4
xi
4.2
5
5.8
1
2
3
xi
Folie 60
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Bemerkungen
Für Augenzahl Y eines fairen Würfels gilt: E(Y ) = 3.5.
Realisationen x aus Realisationen einer einfachen Stichprobe vom Umfang n
zu Y schwanken offensichtlich um den Erwartungswert von Y .
Genauer kann leicht gezeigt werden (vgl. Übungsaufgabe!), dass (generell!)
E(X ) = E(Y ) gilt.
Je größer der Stichprobenumfang n ist, desto näher liegen tendenziell die
Realisation von x am Erwartungswert.
Genauer kann leicht gezeigt werden (vgl. Übungsaufgabe!), dass (generell!)
σY
σX = √ gilt und sich somit die Standardabweichung von X halbiert, wenn
n
n vervierfacht wird.
Offensichtlich wird die Näherung der Werteverteilung von X durch eine
Normalverteilung ( Zentraler Grenzwertsatz) immer besser, je größer der
Stichprobenumfang n ist.
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 61
Schließende Statistik 2.3
(Punkt-)Schätzfunktionen
Mit den beschriebenen Eigenschaften scheint X sehr gut geeignet, um auf
Grundlage einer Stichprobenrealisation Aussagen über den Erwartungswert
von Y zu machen (wenn dieser – anders als im Beispiel – unbekannt ist).
Unbekannt wäre der Erwartungswert zum Beispiel auch beim Würfeln
gewesen, wenn man nicht gewusst hätte, ob der Würfel fair ist!
X bzw. x können so unmittelbar zur Schätzung von µY := E(Y ) oder p
bzw. µ verwendet werden; in diesem Zusammenhang nennt man X dann
(Punkt-)Schätzfunktion oder (Punkt-)Schätzer, x die zugehörige
Realisation oder den Schätzwert.
Wegen der Zusammenhänge zwischen Erwartungswert und
Verteilungsparameter (vgl. Folien 20 bzw. 26) können so auch Aussagen über
den Parameter p der Alternativ- bzw. den Parameter µ der Normalverteilung
gewonnen werden. X wird dann auch Parameter(punkt)schätzer genannt.
Ökonometrie (SS 2014)
Folie 62
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
(Qualitäts-)Eigenschaften von Schätzfunktionen I
Im Beispiel offensichtlich: Wer schätzt, macht Fehler!
Zur Untersuchung der Qualität von Punktschätzfunktionen:
Untersuchung der Verteilung (!) des Schätzfehlers
Zur Vereinheitlichung der Schreibweise: Bezeichnung“
”
b
I
I
θ für die Schätzfunktion
θ für die zu schätzende Größe
Schätzfehler damit also: θb − θ
Offensichtlich wünschenswert: Verteilung des Schätzfehlers nahe bei Null
Gängige Konkretisierung von nahe bei Null“: Erwartete quadratische
”
Abweichung (Englisch: Mean Square Error, MSE)
2 b := E θb − θ
MSE(θ)
soll möglichst klein sein.
Ökonometrie (SS 2014)
Folie 63
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
(Qualitäts-)Eigenschaften von Schätzfunktionen II
Man kann leicht zeigen:
h
i
2
b
b
MSE(θ) = E (θ − θ) = Var(θb − θ) +[ E(θb − θ) ]2
| {z } | {z }
b
=Var(θ)
b
=:Bias(θ)
b = E(θb − θ) = E(θ)
b − θ wird also die systematische Abweichung
Mit Bias(θ)
(Abweichung im Mittel, Verzerrung) eines Schätzers von der zu schätzenden
Größe bezeichnet.
b = 0 für alle
Gibt es keine solche systematische Abweichung (gilt also Bias(θ)
denkbaren Werte von θ), so nennt man θb erwartungstreu für θ.
q
b wird auch Standardfehler oder Stichprobenfehler von θb genannt.
Var(θ)
Bei Schätzung von E(Y ) mit X gilt:
σY2
2 E(X )=E(Y )
2
MSE(X ) = E (X − E(Y ))
=
Var(X ) = σX =
n
Ökonometrie (SS 2014)
Folie 64
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
(Qualitäts-)Eigenschaften von Schätzfunktionen III
Naheliegende Mindestanforderung“: Mit wachsendem Stichprobenumfang n
”
sollte der MSE einer vernünftigen Schätzfunktion gegen Null gehen.
Schätzfunktionen θb für θ, die diese Forderung erfüllen, heißen konsistent im
quadratischen Mittel oder MSE-konsistent für θ.
Wegen MSE(X ) =
σY2
n
ist X offensichtlich MSE-konsistent für E(Y ).
Mit der Zerlegung (vgl. Folie 64)
b = Var(θ)
b + [Bias(θ)]
b 2
MSE(θ)
ist θb also genau dann konsistent im quadratischen Mittel für θ, wenn jeweils
für alle denkbaren Werte von θ sowohl
1
2
die Varianz von θb gegen Null geht als auch
der Bias von θb gegen Null geht
(diese Eigenschaft heißt auch asymptotische Erwartungstreue).
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 65
Schließende Statistik 2.3
(Qualitäts-)Eigenschaften von Schätzfunktionen IV
Beim Vergleich mehrerer Schätzfunktionen ist es gängig, die Schätzfunktion
vorzuziehen, die den kleineren“ MSE hat.
”
Damit zieht man bei erwartungstreuen Schätzfunktionen die mit geringerer“
”
Varianz vor.
Wichtig hierbei ist, dass man universelle“ Vergleiche zu ziehen hat, also nicht
nur spezielle Situationen (also”spezielle θ) betrachtet. Bei erwartungstreuen
Schätzfunktionen θb und θe heißt
1
2
e wenn Var(θ)
b ≤ Var(θ)
e für alle denkbaren
θb mindestens so wirksam wie θ,
Werte von θ gilt, und
e wenn darüberhinaus Var(θ)
b < Var(θ)
e für mindestens einen
θb wirksamer als θ,
denkbaren Wert von θ gilt.
Eine Schätzfunktion, die in einer vorgegebenen Menge von Schätzfunktionen
mindestens so wirksam ist wie alle anderen Schätzfunktionen, heißt effizient
in dieser Menge von Schätzfunktionen.
Ökonometrie (SS 2014)
Folie 66
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Schätzung von Var(Y )
Naheliegender Ansatz zur Schätzung der Varianz σY2 = Var(Y ) aus einer
einfachen Stichprobe X1 , . . . , Xn vom Umfang n zu Y : Verwendung der
empirischen Varianz
n
1X
(Xi − X )2
n
bzw.
i=1
n
1X
(xi − x)2
n
i=1
Man kann allerdings zeigen, dass diese Schätzfunktion nicht erwartungstreu
für die Varianz von Y ist!
Bei dieser Rechnung wird allerdings klar, dass man mit der leichten
Anpassung
n
1 X
S :=
(Xi − X )2
n−1
2
n
bzw.
i=1
1 X
s :=
(xi − x)2
n−1
2
i=1
eine erwartungstreue Schätzfunktion für σY2 erhält.
Ökonometrie (SS 2014)
Folie 67
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Intervallschätzung von µY := E(Y )
(Realisation der) Punktschätzfunktion X für µY beinhaltet (zunächst) keine
Information über die Qualität der Schätzung (bzw. über den zu erwartenden
Schätzfehler).
Bisher: Varianz σX2 := Var(X ) (hier gleich mit MSE!) bzw. Standardfehler
q
σX = Var(X ) zur Quantifizierung der Schätzunsicherheit verwendet.
Weitergehender Ansatz:
Nicht nur Momente von X (hier: Varianz), sondern komplette Verteilung
berücksichtigen!
Erinnerung: X entsteht als (durch n dividierte) Summe unabhängig
identisch verteilter
Zufallsvariablen.
X ist N µY ,
2
σY
n
-verteilt, falls Xi (bzw. Y ) normalverteilt
(Wahrscheinlichkeitsrechnung!).
X kann näherungsweise als N µY ,
2
σY
n
-verteilt angesehen, falls Xi (bzw. Y )
nicht normalverteilt (Zentraler Grenzwertsatz!).
Ökonometrie (SS 2014)
Folie 68
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Die Qualität der Näherung durch eine Normalverteilung wird mit
zunehmendem Stichprobenumfang größer, hängt aber ganz entscheidend
von der Verteilung von Y ab!
Pauschale Kriterien an den Stichprobenumfang n ( Daumenregeln“, z.B.
”
n ≥ 30) finden sich häufig in der Literatur, sind aber nicht ganz unkritisch.
•
σ2
σ2
Verteilungseigenschaft X ∼ N µ, n bzw. X ∼ N µ, n wird meistens
(äquivalent!) in der (auch aus dem zentralen Grenzwertsatz bekannten)
Gestalt
X − µ√
n ∼ N(0, 1)
σ
X − µ√ •
n ∼ N(0, 1)
σ
bzw.
verwendet, da dann Verwendung von Tabellen zur Standardnormalverteilung
möglich.
Ökonometrie (SS 2014)
Folie 69
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Beispiel: Näherung für
X −µ √
n,
σ
0.3
0.4
N(0,1)
n=4
0.0
0.1
0.2
f(x)
0.2
0.0
0.1
f(x)
0.3
0.4
N(0,1)
n=2
falls Y ∼ Unif(20, 50)
−4
−2
0
2
4
−4
−2
x
2
4
x
0.2
0.3
0.4
N(0,1)
n=12
0.0
0.0
0.1
0.2
f(x)
0.3
0.4
N(0,1)
n=7
0.1
f(x)
0
−4
−2
0
x
Ökonometrie (SS 2014)
2
4
−4
−2
0
2
4
x
Folie 70
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Beispiel: Näherung für
X −µ √
n,
σ
0.3
0.4
N(0,1)
n=10
0.0
0.1
0.2
f(x)
0.2
0.0
0.1
f(x)
0.3
0.4
N(0,1)
n=3
falls Y ∼ Exp(2)
−4
−2
0
2
4
−4
−2
x
2
4
x
0.2
0.3
0.4
N(0,1)
n=250
0.0
0.0
0.1
0.2
f(x)
0.3
0.4
N(0,1)
n=30
0.1
f(x)
0
−4
−2
0
2
4
−4
−2
x
0
2
4
x
Ökonometrie (SS 2014)
Folie 71
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Beispiel: Näherung für
X −µ √
n,
σ
0.3
0.4
N(0,1)
n=10
0.0
0.1
0.2
f(x)
0.2
0.0
0.1
f(x)
0.3
0.4
N(0,1)
n=3
falls Y ∼ B(1, 0.5)
−4
−2
0
2
4
−4
−2
x
2
4
x
0.2
0.3
0.4
N(0,1)
n=250
0.0
0.0
0.1
0.2
f(x)
0.3
0.4
N(0,1)
n=30
0.1
f(x)
0
−4
−2
0
x
Ökonometrie (SS 2014)
2
4
−4
−2
0
2
4
x
Folie 72
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Beispiel: Näherung für
X −µ √
n,
σ
0.3
0.4
N(0,1)
n=10
0.0
0.1
0.2
f(x)
0.2
0.0
0.1
f(x)
0.3
0.4
N(0,1)
n=3
falls Y ∼ B(1, 0.05)
−4
−2
0
2
4
−4
−2
x
2
4
x
0.2
0.3
0.4
N(0,1)
n=250
0.0
0.0
0.1
0.2
f(x)
0.3
0.4
N(0,1)
n=30
0.1
f(x)
0
−4
−2
0
2
4
x
−4
−2
0
2
4
x
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 73
Schließende Statistik 2.3
Schwankungsintervalle für X I
Kennt man die Verteilung von X (oder eine geeignete Näherung), kann man
beispielsweise Intervalle angeben, in denen die Realisationen von X (ggf.
näherungsweise) mit einer vorgegebenen Wahrscheinlichkeit liegen.
Sucht man zum Beispiel ein Intervall, aus welchem die Realisationen einer
Zufallsvariablen nur mit einer Wahrscheinlichkeit von 0 < α < 1 herausfallen,
bietet sich
I
I
die Verwendung des α2 -Quantils, welches nur mit Wahrscheinlichkeit α2
unterschritten wird, als untere Grenze sowie
die Verwendung des 1 − α2 -Quantils, welches nur mit Wahrscheinlichkeit
überschritten wird, als obere Grenze
α
2
an (vgl. Übungsaufgabe 2 (c)).
Ökonometrie (SS 2014)
Folie 74
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Schwankungsintervalle für X II
Für N(µ,
σ 2 )-verteilte Zufallsvariablen lässt sich in Abhängigkeit des
1 − α2 -Quantils N α2 bzw. N1− α2 der N(0, 1)-Verteilung
I
I
α
2-
bzw.
das α2 -Quantil durch µ + σ · N α2 und
das 1 − α2 -Quantil durch µ + σ · N1− α2
berechnen (vgl. auch Folien 26 und 30).
Unter Verwendung der Symmetrieeigenschaft
Nα = −N1−α
bzw. hier
N α2 = −N1− α2
für Quantile der Standardnormalverteilung erhält man so die Darstellung
µ − σ · N1− α2 , µ + σ · N1− α2
eines um den Erwartungswert µ symmetrischen Intervalls, in dem die
Realisationen der Zufallsvariablen mit Wahrscheinlichkeit 1 − α liegen bzw.
mit Wahrscheinlichkeit α nicht enthalten sind.
Ökonometrie (SS 2014)
Folie 75
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Schwankungsintervalle für X III
Ist X1 , . . . , Xn eine einfache Stichprobe zumpUmfang n zu Y , und sind
µY = E(Y ) der Erwartungswert und σY = Var(Y ) die Standardabweichung
σ2
von Y , so erhält man also unter Verwendung von X ∼ N µY , nY (exakt
oder näherungsweise!) für vorgegebenes 0 < α < 1
σY
σY
P X ∈ µY − √ · N1− α2 , µY + √ · N1− α2
=1−α
n
n
und damit das (symmetrische) (1 − α)-Schwankungsintervall
σY
σY
µY − √ · N1− α2 , µY + √ · N1− α2
n
n
von X .
Ökonometrie (SS 2014)
Folie 76
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Beispiel: Schwankungsintervall
Aufgabenstellung:
I
I
I
Es gelte Y ∼ N(50, 102 ).
Zu Y liege eine einfache Stichprobe X1 , . . . , X25 der Länge n = 25 vor.
Gesucht ist ein 1 − α = 0.95-Schwankungsintervall für X .
Lösung:
I
I
I
I
Es gilt also µY = 50, σY2 = 102 , n = 25 und α = 0.05.
Zur Berechnung des Schwankungsintervalls
σY
σY
µY − √ · N1− α2 , µY + √ · N1− α2
n
n
benötigt man also nur noch das 1 − α2 = 0.975-Quantil N0.975 der
Standardnormalverteilung. Dies erhält man mit geeigneter Software (oder aus
geeigneten Tabellen) als N0.975 = 1.96.
Insgesamt erhält man also das Schwankungsintervall
10
10
50 − √ · 1.96, 50 + √ · 1.96 = [46.08, 53.92] .
25
25
Eine Stichprobenziehung führt also mit einer Wahrscheinlichkeit von 95% zu
einer Realisation x von X im Intervall [46.08, 53.92].
Ökonometrie (SS 2014)
Folie 77
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Beispiel: Schwankungsintervall
(Grafische Darstellung)
102
25
, α = 0.05
X
0.10
α 2 = 0.025
α 2 = 0.025
1 − α = 0.95
0.00
0.05
fX(x)
0.15
0.20
Im Beispiel: X ∼ N 50,
µY −
Ökonometrie (SS 2014)
σY
n
N1−α
2
µY
µY +
σY
n
N1−α
2
Folie 78
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Konfidenzintervalle für den Erwartungswert I
bei bekannter Varianz σ 2
In der Praxis interessanter als Schwankungsintervalle für X :
Intervallschätzungen für unbekannte Erwartungswerte µ := µY = E(Y ).
Zunächst: Annahme, dass die Varianz von σ 2 := σY2 = Var(Y ) (und damit
auch Var(X )) bekannt ist.
Für 0 < α < 1 kann die Wahrscheinlichkeitsaussage
σ
σ
P X ∈ µ − √ · N1− α2 , µ + √ · N1− α2
=1−α
n
n
umgestellt werden zu einer Wahrscheinlichkeitsaussage der Form
σ
σ
=1−α .
P µ ∈ X − √ · N1− α2 , X + √ · N1− α2
n
n
Dies liefert sogenannte Konfidenzintervalle
σ
σ
X − √ · N1− α2 , X + √ · N1− α2
n
n
für µ zur Vertrauenswahrscheinlichkeit bzw. zum Konfidenzniveau 1 − α.
Ökonometrie (SS 2014)
Folie 79
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Konfidenzintervalle für den Erwartungswert II
bei bekannter Varianz σ 2
In der resultierenden Wahrscheinlichkeitsaussage
σ
σ
P µ ∈ X − √ · N1− α2 , X + √ · N1− α2
=1−α .
n
n
sind die Intervallgrenzen
σ
X − √ · N1− α2
n
und
σ
X + √ · N1− α2
n
des Konfidenzintervalls zufällig (nicht etwa µ!).
Ziehung einer Stichprobenrealisation liefert also Realisationen der
Intervallgrenzen und damit ein konkretes Konfidenzintervall, welches den
wahren (unbekannten) Erwartungswert µ entweder überdeckt oder nicht.
Die Wahrscheinlichkeitsaussage für Konfidenzintervalle zum Konfidenzniveau
1 − α ist also so zu verstehen, dass man bei der Ziehung der Stichprobe mit
einer Wahrscheinlichkeit von 1 − α ein Stichprobenergebnis erhält, welches zu
einem realisierten Konfidenzintervall führt, das den wahren Erwartungswert
überdeckt.
Ökonometrie (SS 2014)
Folie 80
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Beispiel: Konfidenzintervall bei bekannter Varianz σ 2
Die Zufallsvariable Y sei normalverteilt mit unbekanntem Erwartungswert
und bekannter Varianz σ 2 = 22 .
Gesucht: Konfidenzintervall für µ zum Konfidenzniveau 1 − α = 0.99.
Als Realisation x1 , . . . , x16 einer einfachen Stichprobe X1 , . . . , X16 vom
Umfang n = 16 zu Y liefere die Stichprobenziehung
18.75, 20.37, 18.33, 23.19, 20.66, 18.36, 20.97, 21.48, 21.15, 19.39, 23.02,
20.78, 18.76, 15.57, 22.25, 19.91 ,
was zur Realisationen x = 20.184 von X führt.
Als Realisation des Konfidenzintervalls für µ zum Konfidenzniveau
1 − α = 0.99 erhält man damit insgesamt
σ
σ
x − √ · N1− α2 , x + √ · N1− α2
n
n
2
2
= 20.184 − √ · 2.576, 20.184 + √ · 2.576
16
16
= [18.896, 21.472] .
Ökonometrie (SS 2014)
Folie 81
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Verteilung von X bei unbekanntem σ 2
Wie kann man vorgehen, falls die Varianz σ 2 von Y unbekannt ist?
Naheliegender Ansatz: Ersetzen von σ 2 durch eine geeignete Schätzfunktion.
Erwartungstreue Schätzfunktion für σ 2 bereits bekannt:
n
1 X
S =
(Xi − X )2
n−1
2
i=1
Ersetzen von σ durch S =
√
S 2 möglich, Verteilung ändert sich aber:
Satz 2.1
Seien Y ∼ N(µ,
σ 2 ), X1 , . . . , Xn eine einfache Stichprobe zu Y . Dann gilt mit
q
√
Pn
1
2
S := S 2 = n−1
i=1 (Xi − X )
X − µ√
n ∼ t(n − 1) ,
S
wobei t(n − 1) die t-Verteilung mit n − 1 Freiheitsgraden bezeichnet.
Ökonometrie (SS 2014)
Folie 82
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Die Familie der t(n)-Verteilungen
Die Familie der t(n)-Verteilungen mit n > 0 ist eine spezielle Familie stetiger
Verteilungen. Der Parameter n wird meist Anzahl der Freiheitsgrade“
”
( degrees of freedom“) genannt.
”
t-Verteilungen werden (vor allem in englischsprachiger Literatur) oft auch als
Student’s t distribution“ bezeichnet; Student“ war das Pseudonym, unter
”
”
dem William Gosset die erste Arbeit zur t-Verteilung in englischer Sprache
veröffentlichte.
t(n)-Verteilungen sind für alle n > 0 symmetrisch um 0. Entsprechend gilt für
p-Quantile der t(n)-Verteilung, die wir im Folgendem mit tn;p abkürzen,
analog zu Standardnormalverteilungsquantilen
tn;p = −tn;1−p
bzw.
tn;1−p = −tn;p
für alle p ∈ (0, 1)
Für wachsendes n nähert sich die t(n)-Verteilung der
Standardnormalverteilung an.
Ökonometrie (SS 2014)
Folie 83
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Grafische Darstellung einiger t(n)-Verteilungen
für n ∈ {2, 5, 10, 25, 100}
0.0
0.1
0.2
f(x)
0.3
0.4
N(0,1)
t(2)
t(5)
t(10)
t(25)
t(100)
−4
−2
0
2
4
x
Ökonometrie (SS 2014)
Folie 84
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Konfidenzintervalle für den Erwartungswert I
bei unbekannter Varianz σ 2
Konstruktion von Konfidenzintervallen für µ bei unbekannter Varianz
σ 2 = Var(Y ) ganz analog zur Situation mit bekannter Varianz, lediglich
√
S2
=
q
1
Ersetzen von σ durch S =
2
Ersetzen von N1− α2 durch tn−1;1− α2
1
n−1
Pn
i=1 (Xi
− X )2
erforderlich.
Resultierendes Konfidenzintervall für µ zur Vertrauenswahrscheinlichkeit
bzw. zum Konfidenzniveau 1 − α:
S
S
X − √ · tn−1;1− α2 , X + √ · tn−1;1− α2
n
n
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 85
Schließende Statistik 2.3
Konfidenzintervalle für den Erwartungswert II
bei unbekannter Varianz σ 2
Benötigte Quantile tn−1;1− α2 können ähnlich wie bei der
Standardnormalverteilung z.B. mit der Statistik-Software R ausgerechnet
werden oder aus geeigneten Tabellen abgelesen werden.
Mit R erhält man z.B. t15;0.975 durch
> qt(0.975,15)
[1] 2.13145
Mit zunehmendem n werden die Quantile der t(n)-Verteilungen betragsmäßig
kleiner und nähern sich den Quantilen der Standardnormalverteilung an.
Ist Y und sind damit die Xi nicht normalverteilt, erlaubt der zentrale
Grenzwertsatz dennoch die näherungsweise Verwendung einer
√
t(n − 1)-Verteilung für X −µ
n und damit auch die Berechnung von
S
(approximativen) Konfidenzintervallen.
Ökonometrie (SS 2014)
Folie 86
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Quantile der t-Verteilungen: tn;p
n\p
0.85
0.90
0.95
0.975
0.99
0.995
0.9995
1
2
3
4
5
1.963
1.386
1.250
1.190
1.156
3.078
1.886
1.638
1.533
1.476
6.314
2.920
2.353
2.132
2.015
12.706
4.303
3.182
2.776
2.571
31.821
6.965
4.541
3.747
3.365
63.657
9.925
5.841
4.604
4.032
636.619
31.599
12.924
8.610
6.869
6
7
8
9
10
1.134
1.119
1.108
1.100
1.093
1.440
1.415
1.397
1.383
1.372
1.943
1.895
1.860
1.833
1.812
2.447
2.365
2.306
2.262
2.228
3.143
2.998
2.896
2.821
2.764
3.707
3.499
3.355
3.250
3.169
5.959
5.408
5.041
4.781
4.587
11
12
13
14
15
1.088
1.083
1.079
1.076
1.074
1.363
1.356
1.350
1.345
1.341
1.796
1.782
1.771
1.761
1.753
2.201
2.179
2.160
2.145
2.131
2.718
2.681
2.650
2.624
2.602
3.106
3.055
3.012
2.977
2.947
4.437
4.318
4.221
4.140
4.073
20
25
30
40
50
1.064
1.058
1.055
1.050
1.047
1.325
1.316
1.310
1.303
1.299
1.725
1.708
1.697
1.684
1.676
2.086
2.060
2.042
2.021
2.009
2.528
2.485
2.457
2.423
2.403
2.845
2.787
2.750
2.704
2.678
3.850
3.725
3.646
3.551
3.496
100
200
500
1000
5000
1.042
1.039
1.038
1.037
1.037
1.290
1.286
1.283
1.282
1.282
1.660
1.653
1.648
1.646
1.645
1.984
1.972
1.965
1.962
1.960
2.364
2.345
2.334
2.330
2.327
2.626
2.601
2.586
2.581
2.577
3.390
3.340
3.310
3.300
3.292
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 87
Schließende Statistik 2.3
Beispiel: Konfidenzintervall bei unbekanntem σ 2
Die Zufallsvariable Y sei normalverteilt mit unbekanntem Erwartungswert
und unbekannter Varianz.
Gesucht: Konfidenzintervall für µ zum Konfidenzniveau 1 − α = 0.95.
Als Realisation x1 , . . . , x9 einer einfachen Stichprobe X1 , . . . , X9 vom Umfang
n = 9 zu Y liefere die Stichprobenziehung
28.12, 30.55, 27.49, 34.79, 30.99, 27.54, 31.46, 32.21, 31.73 ,
was zur
√ Realisationen x = 30.542 von X und zur Realisation s = 2.436 von
S = S 2 führt.
Als Realisation des Konfidenzintervalls für µ zum Konfidenzniveau
1 − α = 0.95 erhält man damit insgesamt
s
s
x − √ · tn−1;1− α2 , x + √ · tn−1;1− α2
n
n
2.436
2.436
= 30.542 − √ · 2.306, 30.542 + √ · 2.306
9
9
= [28.67, 32.414] .
Ökonometrie (SS 2014)
Folie 88
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Hypothesentests
Bisher betrachtet:
Punkt- bzw. Intervallschätzung des unbekannten Mittelwerts
Hierzu: Verwendung der
1
2
theoretischen Information über Verteilung von X
empirischen Information aus Stichprobenrealisation x von X
zur Konstruktion einer
I
I
Punktschätzung
Intervallschätzung, bei der jede Stichprobenziehung mit einer vorgegebenen
Chance ein realisiertes (Konfidenz-)Intervall liefert, welches den (wahren)
Mittelwert (Erwartungswert) enthält.
Nächste Anwendung (am Beispiel des Erwartungswerts): Hypothesentests:
Entscheidung, ob der (unbekannte!) Erwartungswert von Y in einer
vorgegebenen Teilmenge der denkbaren Erwartungswerte liegt
( Nullhypothese“ H0 ) oder nicht ( Gegenhypothese/Alternative“ H1 ).
”
”
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 89
Schließende Statistik 2.3
Einführendes Beispiel I
Interessierende Zufallsvariable Y :
Von einer speziellen Abfüllmaschine abgefüllte Inhaltsmenge von
Müslipackungen mit Soll-Inhalt µ0 = 500 (in [g ]).
Verteilungsannahme:
Y ∼ N(µ, 42 ) mit unbekanntem Erwartungswert µ = E (Y ).
Es liege eine Realisation x1 , . . . , x16 einer einfachen Stichprobe X1 , . . . , X16
vom Umfang n = 16 zu Y vor.
Ziel: Verwendung der Stichprobeninformation (über X bzw. x), um zu
entscheiden, ob die tatsächliche mittlere Füllmenge (also der wahre,
unbekannte Parameter µ) mit dem Soll-Inhalt µ0 = 500 übereinstimmt
(H0 : µ = µ0 = 500) oder nicht (H1 : µ 6= µ0 = 500).
Ökonometrie (SS 2014)
Folie 90
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Einführendes Beispiel II
Offensichlich gilt:
I
I
I
X schwankt um den wahren Mittelwert µ; selbst wenn H0 : µ = 500 gilt, wird
X praktisch nie genau den Wert x = 500 annehmen!
Realisationen x in der Nähe“ von 500 sprechen eher dafür, dass H0 : µ = 500
”
gilt.
Realisationen x weit weg“ von 500 sprechen eher dagegen, dass H0 : µ = 500
”
gilt.
Also: Entscheidung für Nullhypothese H0 : µ = 500, wenn x nahe bei 500,
und gegen H0 : µ = 500 (also für die Gegenhypothese H1 : µ 6= 500), wenn x
weit weg von 500.
Aber: Wo ist die Grenze zwischen in der Nähe“ und weit weg“? Wie kann
”
”
eine geeignete“ Entscheidungsregel konstruiert werden?
”
Ökonometrie (SS 2014)
Folie 91
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Verteilungen von X
0.4
für verschiedene Erwartungswerte µ bei σ = 4 und n = 16
0.2
0.0
0.1
fX(x|µ)
0.3
µ = 500
µ = 494
µ = 499
µ = 503
494
496
498
500
502
504
506
x
Ökonometrie (SS 2014)
Folie 92
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Entscheidungsproblem
Fällen einer Entscheidung zwischen H0 : µ = 500 und H1 : µ 6= 500 führt zu
genau einer der folgenden vier verschiedenen Situationen:
Entscheidung
für H0 (µ = 500)
Entscheidung
für H1 (µ 6= 500)
Tatsächliche Situation:
H0 wahr (µ = 500)
richtige
Entscheidung
Fehler
1. Art
Tatsächliche Situation:
H1 wahr (µ 6= 500)
Fehler
2. Art
richtige
Entscheidung
Wünschenswert:
Sowohl Fehler 1. Art“ als auch Fehler 2. Art“ möglichst selten begehen.
”
”
Aber: Zielkonflikt vorhanden:
Je näher Grenze zwischen in der Nähe“ und weit weg“ an µ0 = 500, desto
”
”
I
I
seltener Fehler 2. Art
häufiger Fehler 1. Art
und umgekehrt für fernere Grenzen zwischen in der Nähe“ und weit weg“.
”
”
Ökonometrie (SS 2014)
Folie 93
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
0.4
Beispiel für nahe“ Grenze
”
Für µ 6= 500 (gegen µ = 500) entscheiden, wenn Abstand zwischen x und 500 größer als 1
0.2
0.0
0.1
fX(x|µ)
0.3
µ = 500
µ = 494
µ = 499
µ = 503
494
496
498
500
502
504
506
x
Ökonometrie (SS 2014)
Folie 94
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
0.4
Beispiel für ferne“ Grenze
”
Für µ 6= 500 (gegen µ = 500) entscheiden, wenn Abstand zwischen x und 500 größer als 3
0.2
0.0
0.1
fX(x|µ)
0.3
µ = 500
µ = 494
µ = 499
µ = 503
494
496
498
500
502
504
506
x
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 95
Schließende Statistik 2.3
Konstruktion einer Entscheidungsregel I
Unmöglich, Wahrscheinlichkeiten der Fehler 1. Art und 2. Art gleichzeitig für
alle möglichen Situationen (also alle denkbaren µ) zu verringern.
Übliche Vorgehensweise: Fehler(wahrscheinlichkeit) 1. Art kontrollieren!
Also: Vorgabe einer kleinen Schranke α ( Signifikanzniveau“) für die
”
Wahrscheinlichkeit, mit der man einen Fehler 1. Art (also eine Entscheidung
gegen H0 , obwohl H0 wahr ist) begehen darf.
Festlegung der Grenze zwischen in der Nähe“ und weit weg“ so, dass man
”
”
den Fehler 1. Art nur mit Wahrscheinlichkeit α begeht, also die Realisation x
bei Gültigkeit von µ = µ0 = 500 nur mit einer Wahrscheinlichkeit von α
jenseits der Grenzen liegt, bis zu denen man sich für µ = µ0 = 500
entscheidet!
Ökonometrie (SS 2014)
Folie 96
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Konstruktion einer Entscheidungsregel II
Gesucht ist also ein Bereich, in dem sich X bei Gültigkeit von
H0 : µ = µ0 = 500 mit einer Wahrscheinlichkeit von 1 − α realisiert (und
damit nur mit Wahrscheinlichkeit α außerhalb liegt!).
Gilt tatsächlich µ = µ0 , dann natürlich auch E(X ) = µ0 , und man erhält
den gesuchten Bereich gerade als Schwankungsintervall (vgl. Folie 76)
σ
σ
µ0 − √ · N1− α2 , µ0 + √ · N1− α2
n
n
mit
σ
σ
P X ∈ µ0 − √ · N1− α2 , µ0 + √ · N1− α2
=1−α .
n
n
Ökonometrie (SS 2014)
Folie 97
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Beispiel für Grenze zum Signifikanzniveau α = 0.05
0.4
Grenzen aus Schwankungsintervall zur Sicherheitswahrscheinlichkeit 1 − α = 0.95
0.2
0.0
0.1
fX(x|µ)
0.3
µ = 500
µ = 494
µ = 499
µ = 503
494
496
498
500
502
504
506
x
Ökonometrie (SS 2014)
Folie 98
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Entscheidung im Beispiel I
Bei einem Signifikanzniveau von α = 0.05 entscheidet man sich im Beispiel
also für H0 : µ = µ0 = 500 genau dann, wenn die Realisation x von X im
Intervall
4
4
500 − √ · N0.975 , 500 + √ · N0.975 = [498.04, 501.96] ,
16
16
dem sog. Annahmebereich des Hypothesentests, liegt.
Entsprechend fällt die Entscheidung für H1 : µ 6= 500 (bzw. gegen
H0 : µ = 500) aus, wenn die Realisation x von X in der Menge
(−∞, 498.04) ∪ (501.96, ∞) ,
dem sog. Ablehnungsbereich oder kritischen Bereich des Hypothesentests,
liegt.
Durch Angabe eines dieser Bereiche ist die Entscheidungsregel offensichtlich
schon vollständig spezifiziert!
Ökonometrie (SS 2014)
Folie 99
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Entscheidung im Beispiel II
Statt Entscheidungsregel auf Grundlage der Realisation x von X (unter
2
Verwendung der Eigenschaft X ∼ N(µ0 , σn ) falls µ = µ0 ) üblicher:
Äquivalente Entscheidungsregel auf Basis der sog. Testgröße oder
Teststatistik
X − µ0 √
N :=
n.
σ
Bei Gültigkeit von H0 : µ = µ0 ensteht N als Standardisierung von X und
ist daher daher (für µ = µ0 ) standardnormalverteilt:
X − µ0 √
n ∼ N(0, 1)
σ
Ökonometrie (SS 2014)
falls µ = µ0
Folie 100
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Entscheidung im Beispiel III
Man rechnet leicht nach:
σ
σ
X − µ0 √
X ∈ µ0 − √ · N1− α2 , µ0 + √ · N1− α2 ⇔
n ∈ −N1− α2 , N1− α2
σ
n
n
X −µ0 √
Als
Annahmebereich
A
f
ür
die
Testgr
öße
N
=
n erhält man also
σ
−N1− α2 , N1− α2 , als kritischen Bereich K entsprechend
K = R\A = −∞, −N1− α2 ∪ N1− α2 , ∞
und damit eine Formulierung der Entscheidungsregel auf Grundlage von N.
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 101
Schließende Statistik 2.3
Entscheidung im Beispiel IV
Man kann ( Veranstaltung Schließende Statistik“) die Verteilung von X
”
bzw. N auch in der Situation µ 6= µ0 (also bei Verletzung von H0 ) näher
untersuchen. Damit lassen sich dann auch (von µ abhängige!)
Fehlerwahrscheinlichkeiten 2. Art berechnen.
Im Beispiel erhält man so zu den betrachteten Szenarien (also
unterschiedlichen wahren Parametern µ):
Wahrscheinlichkeit der
Wahrscheinlichkeit der
Annahme von µ = 500 Ablehnung von µ = 500
P{N ∈ A}
P{N ∈ K }
µ = 500
0.95
0.05
µ = 494
0
1
µ = 499
0.8299
0.1701
µ = 503
0.1492
0.8508
(Fettgedruckte Wahrscheinlichkeiten entsprechen korrekter Entscheidung.)
Test aus dem Beispiel heißt auch zweiseitiger Gauß-Test für den
”
Erwartungswert einer Zufallsvariablen mit bekannter Varianz“.
Ökonometrie (SS 2014)
Folie 102
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Zweiseitiger Gauß-Test für den Ewartungswert
bei bekannter Varianz
Anwendung
als exakter Test, falls Y normalverteilt und Var(Y ) = σ 2 bekannt,
als approximativer Test, falls Y beliebig verteilt mit bekannter Varianz σ 2 .
Testrezept“ des zweiseitigen Tests:
”
1
Hypothesen: H0 : µ = µ0 gegen H1 : µ 6= µ0 für ein vorgegebenes µ0 ∈ R.
2
Teststatistik:
N :=
3
4
5
X − µ0 √
•
n mit N ∼ N(0, 1) (bzw. N ∼ N(0, 1)), falls H0 gilt (µ = µ0 ).
σ
Kritischer Bereich zum Signifikanzniveau α:
K = −∞, −N1− α2 ∪ N1− α2 , ∞
Berechnung der realisierten Teststatistik N
Entscheidung: H0 ablehnen ⇔ N ∈ K .
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 103
Schließende Statistik 2.3
Beispiel: Qualitätskontrolle (Länge von Stahlstiften)
Untersuchungsgegenstand: Weicht die mittlere Länge der von einer
bestimmten Maschine produzierten Stahlstifte von der Solllänge µ0 = 10 (in
[cm]) ab, so dass die Produktion gestoppt werden muss?
Annahmen: Für Länge Y der produzierten Stahlstifte gilt: Y ∼ N(µ, 0.42 )
Stichprobeninformation: Realisation einer einfachen Stichprobe vom Umfang
n = 64 zu Y liefert Stichprobenmittel x = 9.7.
Gewünschtes Signifikanzniveau (max. Fehlerwahrscheinlichkeit 1. Art):
α = 0.05
Geeigneter Test:
(Exakter) Gauß-Test für den Mittelwert bei bekannter Varianz
1
Hypothesen: H0 : µ = µ0 = 10 gegen H1 : µ 6= µ0 = 10
√
0
2
Teststatistik: N = X −µ
n ∼ N(0, 1), falls H0 gilt (µ = µ0 )
σ
3
Kritischer Bereich zum Niveau α = 0.05:
K = (−∞, −N0.975 ) ∪ (N0.975 , ∞) = (−∞, −1.96) ∪ (1.96, ∞)
√
4
Realisierter Wert der Teststatistik: N = 9.7−10
64 = −6
0.4
5
Entscheidung: N ∈ K
H0 wird abgelehnt und die Produktion gestoppt.
Ökonometrie (SS 2014)
Folie 104
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Einseitige Gauß-Tests für den Ewartungswert I
bei bekannter Varianz
Neben zweiseitigem Test auch zwei einseitige Varianten:
H0 : µ ≤ µ0
H0 : µ ≥ µ0
gegen
H1 : µ > µ0
(rechtsseitiger Test)
gegen
H1 : µ < µ0
(linksseitiger Test)
Konstruktion der Tests beschränkt Wahrscheinlichkeit, H0 fälschlicherweise
abzulehnen, auf das Signifikanzniveau α.
Entscheidung zwischen beiden Varianten daher wie folgt:
H0 : Nullhypothese ist in der Regel die Aussage, die von vornherein als
glaubwürdig gilt und die man beibehält, wenn das Stichprobenergebnis bei
Gültigkeit von H0 nicht sehr untypisch bzw. überraschend ist.
H1 : Gegenhypothese ist in der Regel die Aussage, die man statistisch absichern
möchte und für deren Akzeptanz man hohe Evidenz fordert.
Die Entscheidung für H1 hat typischerweise erhebliche Konsequenzen, so dass
man das Risiko einer fälschlichen Ablehnung von H0 zugunsten von H1
kontrollieren will.
Ökonometrie (SS 2014)
Folie 105
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Einseitige Gauß-Tests für den Ewartungswert II
bei bekannter Varianz
Auch für einseitige Tests fasst Teststatistik
N=
X − µ0 √
n
σ
die empirische Information über den Erwartungswert µ geeignet zusammen.
Allerdings gilt nun offensichtlich
I
im Falle des rechtsseitigen Tests von
H0 : µ ≤ µ0
I
gegen
H1 : µ > µ0 ,
dass große (insbesondere positive) Realisationen von N gegen H0 und für H1
sprechen, sowie
im Falle des linksseitigen Tests von
H0 : µ ≥ µ0
gegen
H1 : µ < µ0 ,
dass kleine (insbesondere negative) Realisationen von N gegen H0 und für
H1 sprechen.
Ökonometrie (SS 2014)
Folie 106
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Rechtsseitiger Gauß-Test für den Ewartungswert I
bei bekannter Varianz
Noch nötig zur Konstruktion der Tests:
Geeignetes Verfahren zur Wahl der kritischen Bereiche so, dass
Wahrscheinlichkeit für Fehler 1. Art durch vorgegebenes Signifikanzniveau α
beschränkt bleibt.
Konkreter sucht man bei rechtsseitigen Tests einen Wert kα mit
P{N ∈ (kα , ∞)} ≤ α für alle µ ≤ µ0 .
Offensichtlich wird P{N ∈ (kα , ∞)} mit wachsendem µ größer, es genügt
also, die Einhaltung der Bedingung P{N ∈ (kα , ∞)} ≤ α für das
größtmögliche µ mit der Eigenschaft µ ≤ µ0 , also µ = µ0 , zu gewährleisten.
Um die Fehlerwahrscheinlichkeit 2. Art unter Einhaltung der Bedingung an
die Fehlerwahrscheinlichkeit 1. Art möglichst klein zu halten, wird kα gerade
so gewählt, dass P{N ∈ (kα , ∞)} = α für µ = µ0 gilt.
Man rechnet leicht nach, dass kα = N1−α gelten muss, und erhält damit
insgesamt den kritischen Bereich K = (N1−α , ∞) für den rechtsseitigen Test.
Ökonometrie (SS 2014)
Folie 107
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Beispiel für Verteilungen von N
µ = 500
µ = 499
µ = 502
µ = 504
0.2
0.0
0.1
fN(x|µ)
0.3
0.4
Rechtsseitiger Test (µ0 = 500) zum Signifikanzniveau α = 0.05
−6
−4
−2
0
2
4
6
x
Ökonometrie (SS 2014)
Folie 108
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Rechtsseitiger Gauß-Test für den Ewartungswert II
bei bekannter Varianz
Anwendung
als exakter Test, falls Y normalverteilt und Var(Y ) = σ 2 bekannt,
als approximativer Test, falls Y beliebig verteilt mit bekannter Varianz σ 2 .
Testrezept“ des rechtsseitigen Tests:
”
1
Hypothesen: H0 : µ ≤ µ0 gegen H1 : µ > µ0 für ein vorgegebenes µ0 ∈ R.
2
Teststatistik:
N :=
3
X − µ0 √
•
n mit N ∼ N(0, 1) (N ∼ N(0, 1)), falls H0 gilt (mit µ = µ0 ).
σ
Kritischer Bereich zum Signifikanzniveau α:
K = (N1−α , ∞)
4
Berechnung der realisierten Teststatistik N
5
Entscheidung: H0 ablehnen ⇔ N ∈ K .
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 109
Schließende Statistik 2.3
Linksseitiger Gauß-Test für den Ewartungswert I
bei bekannter Varianz
Für linksseitigen Test muss zur Konstruktion des kritischen Bereichs ein
kritischer Wert bestimmt werden, den die Teststatistik N im Fall der
Gültigkeit von H0 maximal mit einer Wahrscheinlichkeit von α unterschreitet.
Gesucht ist also ein Wert kα mit P{N ∈ (−∞, kα )} ≤ α für alle µ ≥ µ0 .
Offensichtlich wird P{N ∈ (−∞, kα )} mit fallendem µ größer, es genügt
also, die Einhaltung der Bedingung P{N ∈ (−∞, kα )} ≤ α für das
kleinstmögliche µ mit µ ≥ µ0 , also µ = µ0 , zu gewährleisten.
Um die Fehlerwahrscheinlichkeit 2. Art unter Einhaltung der Bedingung an
die Fehlerwahrscheinlichkeit 1. Art möglichst klein zu halten, wird kα gerade
so gewählt, dass P{N ∈ (−∞, kα )} = α für µ = µ0 gilt.
Man rechnet leicht nach, dass kα = Nα = −N1−α gelten muss, und erhält
damit insgesamt den kritischen Bereich K = (−∞, −N1−α ) für den
linksseitigen Test.
Ökonometrie (SS 2014)
Folie 110
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Beispiel für Verteilungen von N
0.4
Linksseitiger Test (µ0 = 500) zum Signifikanzniveau α = 0.05
0.2
0.0
0.1
fN(x|µ)
0.3
µ = 500
µ = 496
µ = 498
µ = 501
−6
−4
−2
0
2
4
6
x
Ökonometrie (SS 2014)
Folie 111
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Linksseitiger Gauß-Test für den Ewartungswert II
bei bekannter Varianz
Anwendung
als exakter Test, falls Y normalverteilt und Var(Y ) = σ 2 bekannt,
als approximativer Test, falls Y beliebig verteilt mit bekannter Varianz σ 2 .
Testrezept“ des linksseitigen Tests:
”
1
Hypothesen: H0 : µ ≥ µ0 gegen H1 : µ < µ0 für ein vorgegebenes µ0 ∈ R.
2
Teststatistik:
N :=
3
X − µ0 √
•
n mit N ∼ N(0, 1) (N ∼ N(0, 1)), falls H0 gilt (mit µ = µ0 ).
σ
Kritischer Bereich zum Signifikanzniveau α:
K = (−∞, −N1−α )
4
Berechnung der realisierten Teststatistik N
5
Entscheidung: H0 ablehnen ⇔ N ∈ K .
Ökonometrie (SS 2014)
Folie 112
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Interpretation von Testergebnissen I
Durch die Asymmetrie in den Fehlerwahrscheinlichkeiten 1. und 2. Art ist
Vorsicht bei der Interpretation von Testergebnissen geboten, es besteht ein
großer Unterschied zwischen dem Aussagegehalt einer Ablehnung von H0
und dem Aussagegehalt einer Annahme von H0 :
Fällt die Testentscheidung gegen H0 aus, so hat man — sollte H0 tatsächlich
erfüllt sein — wegen der Beschränkung der Fehlerwahrscheinlichkeit 1. Art
durch das Signifikanzniveau α nur mit einer typischerweise geringen
Wahrscheinlichkeit ≤ α eine Stichprobenrealisation erhalten, die
fälschlicherweise zur Ablehnung von H0 geführt hat.
Aber: Vorsicht vor Über“interpretation als Evidenz für Gültigkeit von H1 :
”
Aussagen der Form Wenn H0 abgelehnt wird, dann gilt H1 mit
”
Wahrscheinlichkeit von mindestens 1 − α“ sind unsinnig!
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 113
Schließende Statistik 2.3
Interpretation von Testergebnissen II
Fällt die Testentscheidung jedoch für H0 aus, so ist dies meist ein
vergleichsweise schwächeres Indiz“ für die Gültigkeit von H0 , da die
”
Fehlerwahrscheinlichkeit 2. Art nicht kontrolliert ist und typischerweise große
Werte (bis 1 − α) annehmen kann.
Gilt also tatsächlich H1 , ist es dennoch mit einer oft – meist abhängig vom
Grad“ der Verletzung von H0 – sehr großen Wahrscheinlichkeit möglich, eine
”
Stichprobenrealisation zu erhalten, die fälschlicherweise nicht zur
Ablehnung von H0 führt.
Aus diesem Grund sagt man auch häufig statt H0 wird angenommen“ eher
”
H0 kann nicht verworfen werden“.
”
Ökonometrie (SS 2014)
Folie 114
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Interpretation von Testergebnissen III
Die Ablehnung von H0 als Ergebnis eines statistischen Tests wird häufig als
I
I
I
signifikante Veränderung (zweiseitiger Test),
signifikante Verringerung (linksseitiger Test) oder
signifikante Erhöhung (rechtsseitiger Test)
einer Größe bezeichnet. Konstruktionsbedingt kann das Ergebnis einer
statistischen Untersuchung — auch im Fall einer Ablehnung von H0 — aber
niemals als zweifelsfreier Beweis für die Veränderung/Verringerung/Erhöhung
einer Größe dienen!
Vorsicht vor Publication Bias“:
”
I
I
Bei einem Signifikanzniveau von α = 0.05 resultiert im Mittel 1 von 20
statistischen Untersuchungen, bei denen H0 wahr ist, konstruktionsbedingt in
einer Ablehnung von H0 .
Gefahr von Fehlinterpretationen, wenn die Untersuchungen, bei denen H0 nicht
verworfen wurde, verschwiegen bzw. nicht publiziert werden!
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 115
Schließende Statistik 2.3
Interpretation von Testergebnissen IV
Ein signifikanter“ Unterschied ist noch lange kein deutlicher“ Unterschied!
”
”
Problem: Fluch des großen Stichprobenumfangs“
”
Beispiel: Abfüllmaschine soll Flaschen mit 1000 ml Inhalt abfüllen.
I
I
Abfüllmenge schwankt zufällig, Verteilung sei Normalverteilung mit bekannter
Standardabweichung σ = 0.5 ml, d.h. in ca. 95% der Fälle liegt Abfüllmenge
im Bereich ±1 ml um den (tatsächlichen) Mittelwert.
Statistischer Test zum Niveau α = 0.05 zur Überprüfung, ob mittlere
Abfüllmenge (Erwartungswert) von 1000 ml abweicht.
Tatsächlicher Mittelwert sei 1000.1 ml, Test auf Grundlage von 500 Flaschen.
Wahrscheinlichkeit, die Abweichung von 0.1 ml zu erkennen: 99.4%
Systematische Abweichung der Abfüllmenge von 0.1 ml also zwar mit hoher
Wahrscheinlichkeit (99.4%) signifikant, im Vergleich zur (ohnehin
vorhandenen) zufälligen Schwankung mit σ = 0.5 ml aber keinesfalls deutlich!
Fazit: Durch wissenschaftliche Studien belegte signifikante Verbesserungen“
”
können vernachlässigbar klein sein ( Werbung...)
Ökonometrie (SS 2014)
Folie 116
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Der p-Wert
Hypothesentests komprimieren“ Stichprobeninformation zur Entscheidung
”
zwischen H0 und H1 zu einem vorgegebenen Signifikanzniveau α.
Testentscheidung hängt von α ausschließlich über kritischen Bereich Kα ab!
Genauere Betrachtung (Gauß-Test für den Erwartungswert) offenbart:
I
I
Je kleiner α, desto kleiner (im Sinne von ⊂“) der kritische Bereich.
Zu jeder realisierten Teststatistik N findet” man sowohl
F
F
große“ Signifikanzniveaus, deren zugehörige kritische Bereiche
”
N enthalten ( Ablehnung von H0 ), als auch
kleine“ Signifikanzniveaus, deren zugehörige kritische Bereiche
”
N nicht enthalten ( Annahme von H0 ).
Es gibt also zu jeder realisierten Teststatistik N ein sogenanntes
empirisches (marginales) Signifikanzniveau, häufiger p-Wert genannt,
welches die Grenze zwischen Annahme und Ablehnung von H0 widerspiegelt.
Ökonometrie (SS 2014)
Folie 117
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
p-Wert bei Gauß-Tests
für den Erwartungswert bei bekannter Varianz
Der Wechsel zwischen N ∈ Kα“ und N ∈
/ Kα“ findet bei den diskutierten
”
”
Gauß-Tests offensichtlich dort statt, wo die realisierte Teststatistik N gerade
mit (einer) der Grenze(n) des kritischen Bereichs übereinstimmt, d.h.
I
I
I
bei rechtsseitigen Tests mit Kα = (N1−α , ∞) für N = N1−α ,
bei linksseitigen Tests mit Kα = (−∞, −N1−α ) für N = −N1−α ,
bei zweiseitigen Tests mit Kα = (−∞, −N1− α2 ) ∪ (N1− α2 , ∞) für
N=
−N1− α2
N1− α2
falls N < 0
falls N ≥ 0
.
Durch Auflösen nach α erhält man
I
I
I
für rechtsseitige Tests den p-Wert 1 − Φ(N),
für linksseitige Tests den p-Wert Φ(N),
für zweiseitige Tests den p-Wert
2 · Φ(N) = 2 · (1 − Φ(−N))
2 · (1 − Φ(N))
Ökonometrie (SS 2014)
falls N < 0
falls N ≥ 0
= 2 · (1 − Φ(|N|)) .
Folie 118
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Beispiel: p-Werte bei rechtsseitigem Gauß-Test (Grafik)
0.2
fN(0, 1)(x)
0.3
0.4
Realisierte Teststatistik N = 1.6, p-Wert: 0.0548
p = 0.0548
0.0
0.1
1 − p = 0.9452
N0.85 N = 1.6 N0.99
x
Ökonometrie (SS 2014)
Folie 119
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Beispiel: p-Werte bei zweiseitigem Gauß-Test (Grafik)
0.2
fN(0, 1)(x)
0.3
0.4
Realisierte Teststatistik N = −1.8, p-Wert: 0.0719
2
= 0.03595
1 − p = 0.9281
p
2
= 0.03595
0.0
0.1
p
− N0.995 N = − 1.8 − N0.85
N0.85
N0.995
x
Ökonometrie (SS 2014)
Folie 120
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Entscheidung mit p-Wert
Offensichtlich erhält man auf der Grundlage des p-Werts p zur beobachteten
Stichprobenrealisation die einfache Entscheidungsregel
H0 ablehnen
⇔
p<α
für Hypothesentests zum Signifikanzniveau α.
Sehr niedrige p-Werte bedeuten also, dass man beim zugehörigen
Hypothesentest H0 auch dann ablehnen würde, wenn man die maximale
Fehlerwahrscheinlichkeit 1. Art sehr klein wählen würde.
Kleinere p-Werte liefern also stärkere Indizien für die Gültigkeit von H1 als
größere, aber (wieder) Vorsicht vor Überinterpretation: Aussagen der Art
Der p-Wert gibt die Wahrscheinlichkeit für die Gültigkeit von H0 an“ sind
”
unsinnig!
Warnung!
Bei der Entscheidung von statistischen Tests mit Hilfe des p-Werts ist es
unbedingt erforderlich, das Signifikanzniveau α vor Berechnung des p-Werts
festzulegen, um nicht der Versuchung zu erliegen, α im Nachhinein so zu wählen,
dass man die bevorzugte“ Testentscheidung erhält!
”
Ökonometrie (SS 2014)
2 Wiederholung statistischer Grundlagen
Folie 121
Schließende Statistik 2.3
Tests und Konfidenzintervalle
Enger Zusammenhang zwischen zweiseitigem Gauß-Test und (symmetrischen)
Konfidenzintervallen für den Erwartungswert bei bekannter Varianz.
Für Konfidenzintervalle zur Vertrauenswahrscheinlichkeit 1 − α gilt:
σ
σ
µ
e ∈ X − √ · N1− α2 , X + √ · N1− α2
n
n
σ
σ
⇔
µ
e − X ∈ − √ · N1− α2 , √ · N1− α2
n
n
µ
e−X√
⇔
n ∈ −N1− α2 , N1− α2
σ
X −µ
e√
⇔
n ∈ −N1− α2 , N1− α2
σ
Damit ist µ
e also genau dann im Konfidenzintervall zur
Sicherheitswahrscheinlichkeit 1 − α enthalten, wenn ein zweiseitiger
Gauß-Test zum Signifikanzniveau α die Nullhypothese H0 : µ = µ
e nicht
verwerfen würde.
Ökonometrie (SS 2014)
Folie 122
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Zusammenfassung: Gauß-Test für den Mittelwert
bei bekannter Varianz
Anwendungsvoraussetzungen
Nullhypothese
Gegenhypothese
exakt: Y ∼ N(µ, σ 2 ) mit µ ∈ R unbekannt, σ 2 bekannt
approximativ: E (Y ) = µ ∈ R unbekannt, Var(Y ) = σ 2 bekannt
X1 , . . . , Xn einfache Stichprobe zu Y
Teststatistik
Verteilung (H0 )
Benötigte Größen
Kritischer Bereich
zum Niveau α
H0 : µ ≤ µ0
H1 : µ > µ0
H0 : µ = µ0
H1 : µ 6= µ0
N=
X − µ0 √
n
σ
N für µ = µ0 (näherungsweise) N(0, 1)-verteilt
n
1X
Xi
X =
n i=1
(−∞, −N1− α2 )
∪(N1− α2 , ∞)
2 · (1 − Φ(|N|))
p-Wert
H0 : µ ≥ µ0
H1 : µ < µ0
(N1−α , ∞)
(−∞, −N1−α )
1 − Φ(N)
Φ(N)
Ökonometrie (SS 2014)
Folie 123
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
t-Test für den Mittel-/Erwartungswert I
bei unbekannter Varianz
Konstruktion des (exakten) Gauß-Tests für den Mittelwert bei bekannter
Varianz durch Verteilungsaussage
N :=
X − µ√
n ∼ N(0, 1) ,
σ
falls X1 , . . . , Xn einfache Stichprobe zu normalverteilter ZV Y .
Analog zur Konstruktion von Konfidenzintervallen für den Mittelwert bei
unbekannter Varianz: Verwendung der Verteilungsaussage
v
u
n
u 1 X
X − µ√
t :=
n ∼ t(n − 1)
mit
S =t
(Xi − X )2 ,
S
n−1
i=1
falls X1 , . . . , Xn einfache Stichprobe zu normalverteilter ZV Y , um geeigneten
Hypothesentest für den Mittelwert µ zu entwickeln.
Test lässt sich genauso wie Gauß-Test herleiten, lediglich
I
I
Verwendung von S statt σ,
Verwendung von t(n − 1) statt N(0, 1).
Ökonometrie (SS 2014)
Folie 124
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
t-Test für den Mittel-/Erwartungswert II
bei unbekannter Varianz
Beziehung zwischen symmetrischen Konfidenzintervallen und zweiseitigen
Tests bleibt wie beim Gauß-Test erhalten.
Wegen Symmetrie der t(n − 1)-Verteilung bleiben auch alle entsprechenden
Vereinfachungen“ bei der Bestimmung von kritischen Bereichen und
”
p-Werten gültig.
p-Werte können mit Hilfe der Verteilungsfunktion Ft(n−1) der
t(n − 1)-Verteilung bestimmt werden. In der Statistik-Software R erhält man
Ft(n−1) (t) beispielsweise mit dem Befehl pt(t,df=n-1).
Zur Berechnung von p-Werten für große n: Näherung der t(n − 1)-Verteilung
durch Standardnormalverteilung möglich.
Analog zu Konfidenzintervallen:
Ist Y nicht normalverteilt, kann der t-Test auf den Mittelwert bei
unbekannter Varianz immer noch als approximativer (näherungsweiser) Test
verwendet werden.
Ökonometrie (SS 2014)
Folie 125
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Zusammenfassung: t-Test für den Mittelwert
bei unbekannter Varianz
Anwendungsvoraussetzungen
Nullhypothese
Gegenhypothese
exakt: Y ∼ N(µ, σ 2 ) mit µ ∈ R, σ 2 ∈ R++ unbekannt
approximativ: E (Y ) = µ ∈ R, Var(Y ) = σ 2 ∈ R++ unbekannt
X1 , . . . , Xn einfache Stichprobe zu Y
Teststatistik
Verteilung (H0 )
Benötigte Größen
Kritischer Bereich
zum Niveau α
p-Wert
Ökonometrie (SS 2014)
H0 : µ ≤ µ0
H1 : µ > µ0
H0 : µ = µ0
H1 : µ 6= µ0
t=
H0 : µ ≥ µ0
H1 : µ < µ0
X − µ0 √
n
S
t für µ = µ0 (näherungsweise) t(n − 1)-verteilt
n
1X
X =
Xi
n i=1
v
v
!
u
u
n
n
X
u 1
u 1 X
2
S =t
(Xi − X )2 = t
Xi2 − nX
n − 1 i=1
n − 1 i=1
(−∞, −tn−1;1− α2 )
∪(tn−1;1− α2 , ∞)
2 · (1 − Ft(n−1) (|t|))
(tn−1;1−α , ∞)
(−∞, −tn−1;1−α )
1 − Ft(n−1) (t)
Ft(n−1) (t)
Folie 126
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Beispiel: Durchschnittliche Wohnfläche
Untersuchungsgegenstand: Hat sich die durchschnittliche Wohnfläche pro
Haushalt in einer bestimmten Stadt gegenüber dem aus dem Jahr 1998
stammenden Wert von 71.2 (in [m2 ]) erhöht?
Annahmen: Verteilung der Wohnfläche Y im Jahr 2009 unbekannt.
Stichprobeninformation: Realisation einer einfachen Stichprobe vom Umfang
n = 400 zu Y liefert Stichprobenmittel x = 73.452 und
Stichprobenstandardabweichung s = 24.239.
Gewünschtes Signifikanzniveau (max. Fehlerwahrscheinlichkeit 1. Art):
α = 0.05
Geeigneter Test:
Rechtsseitiger approx. t-Test für den Mittelwert bei unbekannter Varianz
1
Hypothesen: H0 : µ ≤ µ0 = 71.2 gegen H1 : µ > µ0 = 71.2
√ •
0
2
Teststatistik: t = X −µ
n ∼ t(399), falls H0 gilt (µ = µ0 )
S
3
Kritischer Bereich zum Niveau α = 0.05: K = (t399;0.95
√ , ∞) = (1.649, ∞)
73.452−71.2
4
Realisierter Wert der Teststatistik: t = 24.239
400 = 1.858
5
Entscheidung: t ∈ K
H0 wird abgelehnt; Test kommt zur Entscheidung,
dass sich durchschnittliche Wohnfläche gegenüber 1998 erhöht hat.
Ökonometrie (SS 2014)
Folie 127
2 Wiederholung statistischer Grundlagen
Schließende Statistik 2.3
Beispiel: p-Wert bei rechtsseitigem t-Test (Grafik)
0.2
1 − p = 0.968
p = 0.032
0.0
0.1
ft(399)(x)
0.3
0.4
Wohnflächenbeispiel, realisierte Teststatistik t = 1.858, p-Wert: 0.032
t399, 0.8
t = 1.858
t399, 0.999
x
Ökonometrie (SS 2014)
Folie 128
3 Einfache lineare Regression
Deskriptiver Ansatz 3.1
Inhaltsverzeichnis
(Ausschnitt)
3
Einfache lineare Regression
Deskriptiver Ansatz
Statistisches Modell
Parameterschätzung
Konfidenzintervalle und Tests
Punkt- und Intervallprognosen
Einfache lineare Modelle mit R
Ökonometrie (SS 2014)
3 Einfache lineare Regression
Folie 129
Deskriptiver Ansatz 3.1
Deskriptive Beschreibung linearer Zusammenhänge I
Aus deskriptiver Statistik bekannt: Pearsonscher Korrelationskoeffizient als
Maß der Stärke des linearen Zusammenhangs zwischen zwei
(kardinalskalierten) Merkmalen X und Y .
Nun: Ausführlichere Betrachtung linearer Zusammenhänge zwischen
Merkmalen (zunächst rein deskriptiv!):
Liegt ein linearer Zusammenhang zwischen zwei Merkmalen X und Y nahe,
ist nicht nur die Stärke dieses Zusammenhangs interessant, sondern auch die
genauere Form“ des Zusammenhangs.
”
Form“ linearer Zusammenhänge kann durch Geraden(gleichungen)
”
spezifiziert werden.
Ökonometrie (SS 2014)
Folie 130
3 Einfache lineare Regression
Deskriptiver Ansatz 3.1
Deskriptive Beschreibung linearer Zusammenhänge II
Problemstellung: Wie kann zu einer Urliste (x1 , y1 ), . . . , (xn , yn ) der Länge n
zu (X , Y ) eine sog. Regressiongerade (auch: Ausgleichsgerade) gefunden
werden, die den linearen Zusammenhang zwischen X und Y möglichst gut“
”
widerspiegelt?
Wichtig: Was soll möglichst gut“ überhaupt bedeuten?
”
Hier: Summe der quadrierten Abstände von der Geraden zu den
Datenpunkten (xi , yi ) in vertikaler Richtung soll möglichst gering sein.
(Begründung für Verwendung dieses Qualitätskriteriums“ wird nachgeliefert!)
”
Ökonometrie (SS 2014)
Folie 131
3 Einfache lineare Regression
Deskriptiver Ansatz 3.1
Deskriptive Beschreibung linearer Zusammenhänge III
Geraden (eindeutig) bestimmt (zum Beispiel) durch Absolutglied a und
Steigung b in der bekannten Darstellung
y = fa,b (x) := a + b · x .
Für den i-ten Datenpunkt (xi , yi ) erhält man damit den vertikalen Abstand
ui (a, b) := yi − fa,b (xi ) = yi − (a + b · xi )
von der Geraden mit Absolutglied a und Steigung b.
Ökonometrie (SS 2014)
Folie 132
3 Einfache lineare Regression
Deskriptiver Ansatz 3.1
Deskriptive Beschreibung linearer Zusammenhänge IV
Gesucht werden a und b so, dass die Summe der quadrierten vertikalen
Abstände der Punktwolke“ (xi , yi ) von der durch a und b festgelegten
”
Geraden,
n
X
2
(ui (a, b)) =
i=1
n
X
i=1
2
(yi − fa,b (xi )) =
n
X
i=1
(yi − (a + b · xi ))2 ,
möglichst klein wird.
Verwendung dieses Kriteriums heißt auch Methode der kleinsten Quadrate
(KQ-Methode) oder Least-Squares-Methode (LS-Methode).
Ökonometrie (SS 2014)
Folie 133
3 Einfache lineare Regression
Deskriptiver Ansatz 3.1
15
Beispiel: Punktwolke“
”
aus n = 10 Paaren (xi , yi )
●
●
●
●
10
●
●
yi
●
●
5
●
0
●
0
2
4
6
8
xi
Ökonometrie (SS 2014)
Folie 134
3 Einfache lineare Regression
Deskriptiver Ansatz 3.1
15
Beispiel: P
Punktwolke“ und verschiedene Geraden I
”
a = 1, b = 0.8, ni=1 (ui (a, b))2 = 180.32
●
●
●
●
10
●
●
ui(a, b)
yi
●
●
5
●
●
b = 0.8
0
a=1 1
0
2
4
6
8
xi
Ökonometrie (SS 2014)
Folie 135
3 Einfache lineare Regression
Deskriptiver Ansatz 3.1
15
Beispiel: P
Punktwolke“ und verschiedene Geraden II
”
a = 5, b = 0.8, ni=1 (ui (a, b))2 = 33.71
●
●
●
●
●
10
ui(a, b)
yi
●
●
●
●
5
b = 0.8
1
●
0
a=5
0
2
4
6
8
xi
Ökonometrie (SS 2014)
Folie 136
3 Einfache lineare Regression
Deskriptiver Ansatz 3.1
15
Beispiel: Punktwolke“
und verschiedene Geraden III
Pn
”
a = −1, b = 1.9, i=1 (ui (a, b))2 = 33.89
●
●
10
●
●
●
ui(a, b)
yi
●
●
●
5
●
●
0
b = 1.9
a = −1
1
0
2
4
6
8
xi
Ökonometrie (SS 2014)
Folie 137
3 Einfache lineare Regression
Deskriptiver Ansatz 3.1
Rechnerische Bestimmung der Regressionsgeraden I
Gesucht sind also b
a, b
b ∈ R mit
n
n
X
X
2
(yi − (b
a+b
bxi )) = min
(yi − (a + bxi ))2
a,b∈R
i=1
i=1
Lösung dieses Optimierungsproblems durch Nullsetzen des Gradienten, also
Pn
n
X
∂ i=1 (yi − (a + bxi ))2
!
= −2
(yi − a − bxi ) = 0
∂a
i=1
Pn
n
X
∂ i=1 (yi − (a + bxi ))2
!
= −2
(yi − a − bxi )xi = 0 ,
∂b
i=1
führt zu sogenannten Normalgleichungen:
!
n
n
X
X
!
na +
xi b =
yi
n
X
i=1
Ökonometrie (SS 2014)
xi
!
a+
i=1
n
X
i=1
xi2
!
!
b=
i=1
n
X
xi yi
i=1
Folie 138
3 Einfache lineare Regression
Deskriptiver Ansatz 3.1
Rechnerische Bestimmung der Regressionsgeraden II
Aufgelöst nach a und b erhält man die Lösungen
Pn
Pn
Pn
n
x
y
−
x
·
y
i
i
i
i
i=1
i=1
i=1
b
b=
2
Pn
Pn
2
n
i=1 xi −
i=1 xi
P
P
n
n
1
b
a = n1
y
−
x
·b
b
i
i
i=1
i=1
n
oder kürzer mit den aus der deskr. Statistik bekannten Bezeichnungen
Pn
Pn
Pn
Pn
x = n1 i=1 xi , x 2 = n1 i=1 xi2 , y = n1 i=1 yi und xy = n1 i=1 xi yi
bzw. den empirischen Momenten sX ,Y = xy − x · y und sX2 = x 2 − x 2 :
xy − x · y
sX ,Y
b
b=
=
sX2
x2 − x2
b
a = y − xb
b
Die erhaltenen Werte b
a und b
b minimieren tatsächlich die Summe der
quadrierten vertikalen Abstände, da die Hesse-Matrix positiv definit ist.
Ökonometrie (SS 2014)
3 Einfache lineare Regression
Folie 139
Deskriptiver Ansatz 3.1
Beispiel: Punktwolke“ und Regressionsgerade
” P
b
a = 2.03, b
b = 1.35, n (ui (b
a, b
b))2 = 22.25
15
i=1
●
●
10
yi
^
^, b
ui(a
)
●
●
●
●
●
●
5
●
^ ●
b = 1.35
0
1
^ = 2.03
a
0
2
4
6
8
xi
Ökonometrie (SS 2014)
Folie 140
3 Einfache lineare Regression
Deskriptiver Ansatz 3.1
Eigenschaften der KQ-Methode I
Zu b
a und b
b kann man offensichtlich die folgende, durch die Regressionsgerade
erzeugte Zerlegung der Merkmalswerte yi betrachten:
a+b
b · xi )
yi = b
a+b
b · x + y − (b
| {z }i |i
{z
}
=:b
yi
=ui (b
a,b
b)=:b
ui
Aus den Normalgleichungen lassen sich leicht einige Eigenschaften für die so
bi und ybi herleiten, insbesondere:
definierten u
I
I
I
Pn
Pn
Pn
Pn
1
b
b
bi .
b
u
=
0
und
damit
y
=
y
bzw.
y
=
y
:=
i
i
i
i=1 y
i=1
i=1
n
Pni=1
b = 0.
xu
i=1
P
Pin i
P
bi = 0 und ni=1 xi u
bi = 0 folgt auch ni=1 ybi u
bi = 0.
Mit i=1 u
Ökonometrie (SS 2014)
Folie 141
3 Einfache lineare Regression
Deskriptiver Ansatz 3.1
Eigenschaften der KQ-Methode II
Mit diesen Eigenschaften erhält man die folgende Varianzzerlegung:
n
n
1X
1X
2
(yi − y ) =
(b
yi − yb)2 +
n
n
i=1
i=1
|
{z
}
|
{z
}
Gesamtvarianz der yi
erklärte Varianz
n
1X 2
bi
u
n
i=1
| {z }
unerklärte Varianz
Die als Anteil der erklärten Varianz an der Gesamtvarianz gemessene Stärke
des linearen Zusammenhangs steht in engem Zusammenhang mit rX ,Y ; es gilt:
rX2 ,Y =
Ökonometrie (SS 2014)
1
n
1
n
Pn
yi − yb)2
i=1 (b
Pn
2
i=1 (yi − y )
Folie 142
3 Einfache lineare Regression
Deskriptiver Ansatz 3.1
Beispiel: Regressionsgerade mit Zerlegung yi = b
yi + b
ui
15
P
b
a = 2.03, b
b = 1.35, ni=1 b
ui2 = 22.25
y = y^
x
●
●
●
●
● ●
●
10
●
^
u
i
●
●
yi
●
●
●
●
●
5
yi
●
●
●
^
b
1
0
^
a
y^i
●
0
2
4
6
8
xi
Ökonometrie (SS 2014)
Folie 143
3 Einfache lineare Regression
Deskriptiver Ansatz 3.1
Beispiel: Berechnung von b
a und b
b
Daten im Beispiel:
i
xi
yi
1
2.51
6.57
2
8.27
12.44
3
4.46
10.7
4
3.95
5.51
5
6.42
12.95
6
6.44
8.95
7
2.12
3.86
8
3.65
6.22
9
6.2
10.7
10
6.68
10.98
Berechnete (deskriptive/empirische) Größen:
x = 5.0703
sX2 = 3.665
y = 8.8889
sY2 = 8.927
x 2 = 29.3729
sX ,Y = 4.956
y 2 = 87.9398
rX ,Y = 0.866
Damit erhält man Absolutglied b
a und Steigung b
b als
sX ,Y
4.956
b
b= 2 =
= 1.352
3.665
sX
b
a =y −b
b · x = 8.8889 − 1.352 · 5.0703 = 2.03
und damit die Regressionsgerade
y = f (x) = 2.03 + 1.352 · x .
Ökonometrie (SS 2014)
Folie 144
3 Einfache lineare Regression
Statistisches Modell 3.2
Das einfache lineare Regressionsmodell I
Bisher: rein deskriptive Betrachtung linearer Zusammenhänge
Bereits erläutert/bekannt: Korrelation 6= Kausalität:
Aus einem beobachteten (linearen) Zusammenhang zwischen zwei Merkmalen
lässt sich nicht schließen, dass der Wert eines Merkmals den des anderen
beeinflusst.
Bereits durch die Symmetrieeigenschaft rX ,Y = rY ,X bei der Berechnung von
Pearsonschen Korrelationskoeffizienten wird klar, dass diese Kennzahl alleine
auch keine Wirkungsrichtung erkennen lassen kann.
Nun: statistische Modelle für lineare Zusammenhänge
Ökonometrie (SS 2014)
3 Einfache lineare Regression
Folie 145
Statistisches Modell 3.2
Das einfache lineare Regressionsmodell II
Keine symmetrische Behandlung von X und Y mehr, sondern:
I
I
Interpretation von X ( Regressor“) als erklärende deterministische Variable.
”
Interpretation von Y ( Regressand“) als abhängige, zu erklärende
”
(Zufalls-)Variable.
Es wird angenommen, dass Y in linearer Form von X abhängt, diese
Abhängigkeit jedoch nicht perfekt“ ist, sondern durch zufällige Einflüsse
”
gestört“ wird.
”
Anwendung in Experimenten: Festlegung von X durch Versuchsplaner,
Untersuchung des Effekts auf Y
Damit auch Kausalitätsanalysen möglich!
Ökonometrie (SS 2014)
Folie 146
3 Einfache lineare Regression
Statistisches Modell 3.2
Das einfache lineare Regressionsmodell III
Es wird genauer angenommen, dass für i ∈ {1, . . . , n} die Beziehung
yi = β0 + β1 · xi + ui
gilt, wobei
I
I
I
u1 , . . . , un (Realisationen von) Zufallsvariablen mit E(ui ) = 0, Var(ui ) = σ 2
(unbekannt) und Cov(ui , uj ) = 0 für i 6= j sind, die zufällige Störungen der
linearen Beziehung ( Störgrößen“) beschreiben,
P
”
x1 , . . . , xn deterministisch sind mit sX2 = n1 ni=1 (xi − x)2 > 0
(d.h. nicht alle xi sind gleich),
β0 , β1 feste, unbekannte reelle Parameter sind.
Man nimmt an, dass man neben x1 , . . . , xn auch y1 , . . . , yn beobachtet, die
wegen der Abhängigkeit von den Zufallsvariablen u1 , . . . , un ebenfalls
(Realisationen von) Zufallsvariablen sind. Dies bedeutet nicht, dass man auch
(Realisationen von) u1 , . . . , un beobachten kann (β0 und β1 unbekannt!).
Ökonometrie (SS 2014)
Folie 147
3 Einfache lineare Regression
Parameterschätzung 3.3
Parameterschätzung I
Das durch die getroffenen Annahmen beschriebene Modell heißt auch
einfaches lineares Regressionsmodell.
Im einfachen linearen Regressionsmodell sind also (neben σ 2 ) insbesondere β0
und β1 Parameter, deren Schätzung für die Quantifizierung des linearen
Zusammenhangs zwischen xi und yi nötig ist.
Die Schätzung dieser beiden Parameter führt wieder zum Problem der Suche
nach Absolutglied und Steigung einer geeigneten Geradengleichung
y = fβ0 ,β1 (x) = β0 + β1 · x .
Achtung!
Die Bezeichnung der Parameter hat sich gegenüber der Veranstaltung
Schließende Statistik“ geändert, aus β1 wird β0 , aus β2 wird β1 !
”
Ökonometrie (SS 2014)
Folie 148
3 Einfache lineare Regression
Parameterschätzung 3.3
Parameterschätzung II
Satz 3.1 (Satz von Gauß-Markov)
Unter den getroffenen Annahmen liefert die aus dem deskriptiven Ansatz bekannte
Verwendung der KQ-Methode, also die Minimierung der Summe der quadrierten
vertikalen Abstände zur durch β0 und β1 bestimmten Geraden, in Zeichen
n
n
X
X
!
2
(yi − (βb0 + βb1 · xi )) = min
(yi − (β0 + β1 · xi ))2 ,
β0 ,β1 ∈R
i=1
i=1
die beste (varianzminimale) lineare (in yi ) erwartungstreue Schätzfunktion βb0
für β0 bzw. βb1 für β1 .
Dies rechtfertigt letztendlich die Verwendung des Optimalitätskriteriums
Minimierung der quadrierten vertikalen Abstände“ (KQ-Methode).
”
Ökonometrie (SS 2014)
Folie 149
3 Einfache lineare Regression
Parameterschätzung 3.3
Parameterschätzung III
Man erhält also — ganz analog zum deskriptiven Ansatz — die folgenden
Parameterschätzer:
Parameterschätzer im einfachen linearen Regressionsmodell
βb1 =
Vorsicht!
n
Pn
Pn
x
y
−
x
·
y
xy − x · y
sX ,Y
i
i
i
i
i=1
i=1
i=1
=
=
,
Pn
P
2
2
n
2 − x2
2
s
x
n
X
i=1 xi −
i=1 xi
1 Pn
Pn
b
b
βb0 = n1
y
−
x
i=1 i
i=1 i · β1 = y − x β1 .
n
Pn
sX2 , sY2 sowie sX ,Y bezeichnen in diesem Kapitel die empirischen Größen
Pn
Pn
sX2 = n1 i=1 (xi − x)2 = x 2 − x 2 ,
sY2 = n1 i=1 (yi − y )2 = y 2 − y 2
Pn
und sX ,Y = n1 i=1 (xi − x) · (yi − y ) = xy − x · y .
Ökonometrie (SS 2014)
Folie 150
3 Einfache lineare Regression
Parameterschätzung 3.3
Parameterschätzung IV
bi := yi − (βb0 + βb1 · xi ) = yi − ybi
Die resultierenden vertikalen Abweichungen u
der yi von den auf der Regressionsgeraden liegenden Werten ybi := βb0 + βb1 · xi
nennt man Residuen.
Wie im deskriptiven Ansatz gelten die Beziehungen
Pn
Pn
Pn
Pn
bi = 0,
b
b
y
,
y
=
u
=
0,
i=1 xi u
i=1 i
i=1 i
i=1 i
Pn
bi
bi u
i=1 y
die Streuungszerlegung
n
X
(yi − y )2
i=1
|
{z
}
Total Sum of Squares
=
n
X
i=1
|
(b
yi − yb)
{z
}
Explained Sum of Squares
bzw. die Varianzzerlegung
Pn
1
2
i=1 (yi − y ) =
n
Ökonometrie (SS 2014)
2
1
n
Pn
n
X
+
i=1
bi2
u
| {z }
Residual Sum of Squares
yi − yb)2 +
i=1 (b
3 Einfache lineare Regression
=0
1
n
Pn
i=1
bi2 .
u
Folie 151
Parameterschätzung 3.3
Das (multiple) Bestimmtheitsmaß R 2
Auch im linearen Regressionsmodell wird die Stärke des linearen
Zusammenhangs mit dem Anteil der erklärten Varianz an der Gesamtvarianz
gemessen und mit
Pn
Pn
2
b
bi2
(b
y
−
y
)
ESS
RSS
2
i=1 i
i=1 u
P
P
R = n
=
1
−
=
=
1
−
n
2
2
TSS
TSS
i=1 (yi − y )
i=1 (yi − y )
bezeichnet. R 2 wird auch (multiples) Bestimmtheitsmaß genannt.
Es gilt 0 ≤ R 2 ≤ 1 sowie der (bekannte) Zusammenhang R 2 = rX2 ,Y =
sX2 ,Y
sX2 ·sY2
.
Größere Werte von R 2 (in der Nähe von 1) sprechen für eine hohe
Modellgüte, niedrige Werte (in der Nähe von 0) für eine geringe Modellgüte.
Ökonometrie (SS 2014)
Folie 152
3 Einfache lineare Regression
Parameterschätzung 3.3
Beispiel: Ausgaben in Abhängigkeit vom Einkommen I
Es wird angenommen, dass die Ausgaben eines Haushalts für Nahrungs- und
Genussmittel yi linear vom jeweiligen Haushaltseinkommen xi (jeweils in 100
e) in der Form
iid
ui ∼ N(0, σ 2 ),
yi = β0 + β1 · xi + ui ,
i ∈ {1, . . . , n}
abhängen. Für n = 7 Haushalte beobachte man nun neben dem Einkommen
xi auch die (Realisation der) Ausgaben für Nahrungs- und Genussmittel yi
wie folgt:
Haushalt i
Einkommen xi
NuG-Ausgaben yi
1
35
9
2
49
15
3
21
7
4
39
11
5
15
5
6
28
8
7
25
9
Mit Hilfe dieser Stichprobeninformation sollen nun die Parameter β0 und β1
bi
der linearen Modellbeziehung geschätzt sowie die Werte ybi , die Residuen u
und das Bestimmtheitsmaß R 2 bestimmt werden.
Ökonometrie (SS 2014)
Folie 153
3 Einfache lineare Regression
Parameterschätzung 3.3
Berechnete (deskriptive/empirische) Größen:
x = 30.28571
sX2 = 114.4901
y = 9.14286
sY2 = 8.6938
x 2 = 1031.71429
sX ,Y = 30.2449
y 2 = 92.28571
rX ,Y = 0.9587
Damit erhält man die Parameterschätzer βb0 und βb1 als
sX ,Y
30.2449
βb1 = 2 =
= 0.26417
114.4901
sX
βb0 = y − βb1 · x = 9.14286 − 0.26417 · 30.28571 = 1.14228 .
Als Bestimmtheitsmaß erhält man R 2 = rX2 ,Y = 0.95872 = 0.9191.
bi erhält man durch Einsetzen (b
bi = yi − ybi ):
Für ybi und u
yi = βb0 + βb1 · xi , u
Ökonometrie (SS 2014)
i
xi
yi
ybi
bi
u
1
35
9
10.39
−1.39
2
49
15
14.09
0.91
3
21
7
6.69
0.31
4
39
11
11.44
−0.44
5
15
5
5.1
−0.1
6
28
8
8.54
−0.54
7
25
9
7.75
1.25
Folie 154
3 Einfache lineare Regression
Parameterschätzung 3.3
Grafik: Ausgaben in Abhängigkeit vom Einkommen
15
βb0 = 1.14228, βb1 = 0.26417, R 2 = 0.9191
●
y = y^
x
●
●
●
10
●
^
u
i
●
●
●
●
yi
●
●
●
5
●
●
yi
0
y^i
0
10
20
30
40
50
xi
Ökonometrie (SS 2014)
Folie 155
3 Einfache lineare Regression
Parameterschätzung 3.3
Eigenschaften der Schätzfunktionen βb0 und βb1 I
Wegen der Abhängigkeit von yi handelt es sich bei βb0 und βb1 (wie in der
schließenden Statistik gewohnt) um (Realisationen von) Zufallsvariablen.
βb0 und βb1 sind linear in yi , man kann genauer zeigen:
βb0 =
Ökonometrie (SS 2014)
n
X
x 2 − x · xi
· yi
n · sX2
i=1
und
βb1 =
n
X
xi − x
· yi
n · sX2
i=1
Folie 156
3 Einfache lineare Regression
Parameterschätzung 3.3
Eigenschaften der Schätzfunktionen βb0 und βb1 II
βb0 und βb1 sind erwartungstreu für β0 und β1 , denn wegen E(ui ) = 0 gilt
I
I
I
E(yi ) = β0 +P
β1 · xi +
) = β0 + β1 · xi ,P
E(u1 i P
n
1
E(y ) = E n i=1 yi = n ni=1 E(yi ) = n1 ni=1 (β0 + β1 · xi ) = β0 + β1 · x,
P
P
E(xy ) = E n1 ni=1 xi yi = n1 ni=1 xi (β0 + β1 · xi ) = β0 · x + β1 · x 2
und damit
E(βb1 ) = E
=
xy − x · y
=
E(xy ) − x · E(y )
x2 − x2
x2 − x2
β0 · x + β1 · x 2 − x · (β0 + β1 · x)
x2 − x2
=
β1 · (x 2 − x 2 )
x2 − x2
= β1
sowie
E(βb0 ) = E(y − x βb1 ) = E(y ) − x E(βb1 ) = β0 + β1 · x − x · β1 = β0 .
Diese beiden Eigenschaften folgen bereits mit dem Satz von Gauß-Markov.
Ökonometrie (SS 2014)
Folie 157
3 Einfache lineare Regression
Parameterschätzung 3.3
Eigenschaften der Schätzfunktionen βb0 und βb1 III
Für die Varianzen der Schätzfunktionen erhält man (mit der Darstellung aus
Folie 156):
Var(βb1 ) =
σ2
n · sX2
sowie
σ2 · x 2
b
Var(β0 ) =
n · sX2
Diese hängen von der unbekannten Varianz σ 2 der ui ab.
Eine erwartungstreue Schätzfunktion für σ 2 ist gegeben durch
n
1 X 2
bi
u
n−2
i=1
n
n
=
· sY2 · (1 − R 2 ) =
· (sY2 − βb1 · sX ,Y )
n−2
n−2
p
c2 dieser Schätzfunktion heißt auch
Die positive Wurzel σ
b=+ σ
Standard Error of the Regression (SER) oder residual standard error.
c2 := Var(u
\i ) =
σ
Ökonometrie (SS 2014)
Folie 158
3 Einfache lineare Regression
Parameterschätzung 3.3
Eigenschaften der Schätzfunktionen βb0 und βb1 IV
c2 für σ 2 liefert die geschätzten Varianzen der
Einsetzen des Schätzers σ
Parameterschätzer
\
c2 b := Var(
σ
βb1 ) =
β1
c2
sY2 − βb1 · sX ,Y
σ
=
n · sX2
(n − 2) · sX2
und
c2 · x 2
σ
(sY2 − βb1 · sX ,Y ) · x 2
\
c
2
b
σ βb0 := Var(β0 ) =
=
.
n · sX2
(n − 2) · sX2
q
q
c
c2 b dieser geschätzten
2
Die positiven Wurzeln σ
bβb0 = σ βb0 und σ
bβb1 = σ
β1
Varianzen werden wie üblich als (geschätzte) Standardfehler von βb0 und βb1
bezeichnet.
Ökonometrie (SS 2014)
Folie 159
3 Einfache lineare Regression
Konfidenzintervalle und Tests 3.4
Konfidenzintervalle und Tests
unter Normalverteilungsannahme für ui
Häufig nimmt man weitergehend für die Störgrößen an, dass speziell
iid
ui ∼ N(0, σ 2 )
gilt, d.h. dass alle ui (für i ∈ {1, . . . , n}) unabhängig identisch normalverteilt
sind mit Erwartungswert 0 und (unbekannter) Varianz σ 2 .
In diesem Fall sind offensichtlich auch y1 , . . . , yn stochastisch unabhängig und
jeweils normalverteilt mit Erwartungswert E(yi ) = β0 + β1 · xi und Varianz
Var(yi ) = σ 2 .
Da βb0 und βb1 linear in yi sind, folgt insgesamt mit den bereits berechneten
Momenten von βb0 und βb1 :
!
2
2
2
σ
·
x
σ
βb0 ∼ N β0 ,
und
βb1 ∼ N β1 ,
2
n · sX
n · sX2
Ökonometrie (SS 2014)
Folie 160
3 Einfache lineare Regression
Konfidenzintervalle und Tests 3.4
Konfidenzintervalle
unter Normalverteilungsannahme für ui
Da σ 2 unbekannt ist, ist für Anwendungen wesentlich relevanter, dass im
Falle unabhängig identisch normalverteilter Störgrößen ui mit den
c2 b für Var(βb0 ) und σ
c2 b für Var(βb1 ) gilt:
Schätzfunktionen σ
β0
β1
βb0 − β0
∼ t(n − 2)
σ
bβb0
und
βb1 − β1
∼ t(n − 2)
σ
bβb1
Hieraus erhält man unmittelbar die Formeln“
”
h
i
b
b
α
α
β0 − tn−2;1− 2 · σ
bβb0 , β0 + tn−2;1− 2 · σ
bβb0
für (symmetrische) Konfidenzintervalle zur Vertrauenswahrscheinlichkeit
1 − α für β0 bzw.
h
i
b
b
α
α
β1 − tn−2;1− 2 · σ
bβb1 , β1 + tn−2;1− 2 · σ
bβb1
für (symmetrische) Konfidenzintervalle zur Vertrauenswahrscheinlichkeit
1 − α für β1 .
Ökonometrie (SS 2014)
3 Einfache lineare Regression
Folie 161
Konfidenzintervalle und Tests 3.4
Beispiel: Ausgaben in Abhängigkeit vom Einkommen II
Im bereits erläuterten Beispiel erhält man als Schätzwert für σ 2 :
n · (sY2 − βb1 · sX ,Y )
7 · (8.6938 − 0.26417 · 30.2449)
c
2
σ =
=
= 0.9856
n−2
7−2
Die (geschätzten) Standardfehler für βb0 und βb1 sind damit
s
r
c2 · x 2
0.9856 · 1031.71429
σ
σ
bβb0 =
=
= 1.1264 ,
7 · 114.4901
n · sX2
s
r
c2
σ
0.9856
σ
bβb1 =
=
= 0.0351 .
2
7 · 114.4901
n · sX
Für α = 0.05 erhält man mit tn−2;1− α2 = t5;0.975 = 2.571 für β0 also
[1.14228 − 2.571 · 1.1264, 1.14228 + 2.571 · 1.1264] = [−1.7537, 4.0383]
als Konfidenzintervall zur Vertrauenswahrscheinlichkeit 1 − α = 0.95 bzw.
[0.26417 − 2.571 · 0.0351, 0.26417 + 2.571 · 0.0351] = [0.1739, 0.3544]
als Konfidenzintervall zur Vertrauenswahrscheinlichkeit 1 − α = 0.95 für β1 .
Ökonometrie (SS 2014)
Folie 162
3 Einfache lineare Regression
Konfidenzintervalle und Tests 3.4
Hypothesentests
unter Normalverteilungsannahme für ui
Genauso lassen sich unter der Normalverteilungsannahme (exakte) t-Tests für
die Parameter β0 und β1 konstruieren.
Trotz unterschiedlicher Problemstellung weisen die Tests Ähnlichkeiten zum
t-Test für den Mittelwert einer normalverteilten Zufallsvariablen bei
unbekannter Varianz auf.
Untersucht werden können die Hypothesenpaare
bzw.
H0 : β0 = β00
gegen
H1 : β0 6= β00
H0 : β0 ≤ β00
gegen
H1 : β0 > β00
H0 : β0 ≥ β00
gegen
H1 : β0 < β00
H0 : β1 = β10
gegen
H1 : β1 6= β10
H0 : β1 ≤ β10
gegen
H1 : β1 > β10
H0 : β1 ≥ β10
gegen
H1 : β1 < β10
Besonders anwendungsrelevant sind Tests auf die Signifikanz“ der Parameter
”
(insbesondere β1 ), die den zweiseitigen Tests mit β00 = 0 bzw. β10 = 0
entsprechen.
Ökonometrie (SS 2014)
Folie 163
3 Einfache lineare Regression
Konfidenzintervalle und Tests 3.4
Zusammenfassung: t-Test für den Parameter β0
im einfachen linearen Regressionsmodell mit Normalverteilungsannahme
Anwendungsvoraussetzungen
Nullhypothese
Gegenhypothese
iid
exakt: yi = β0 + β1 · xi + ui mit ui ∼ N(0, σ 2 ) für i ∈ {1, . . . , n},
σ 2 unbekannt, x1 , . . . , xn deterministisch und bekannt,
Realisation y1 , . . . , yn beobachtet
H0 : β0 = β00
H1 : β0 6= β00
Teststatistik
Verteilung (H0 )
Benötigte Größen
Kritischer Bereich
zum Niveau α
p-Wert
Ökonometrie (SS 2014)
sX ,Y
βb1 = 2
sX
H0 : β0 ≤ β00
H1 : β0 > β00
H0 : β0 ≥ β00
H1 : β0 < β00
βb0 − β00
t=
σ
bβc0
t für β0 = β00 t(n − 2)-verteilt
s
(sY2 − βb1 · sX ,Y ) · x 2
, βb0 = y − βb1 · x, σ
bβc0 =
(n − 2) · sX2
(−∞, −tn−2;1− α2 )
∪(tn−2;1− α2 , ∞)
2 · (1 − Ft(n−2) (|t|))
(tn−2;1−α , ∞)
(−∞, −tn−2;1−α )
1 − Ft(n−2) (t)
Ft(n−2) (t)
Folie 164
3 Einfache lineare Regression
Konfidenzintervalle und Tests 3.4
Zusammenfassung: t-Test für den Parameter β1
im einfachen linearen Regressionsmodell mit Normalverteilungsannahme
Anwendungsvoraussetzungen
iid
exakt: yi = β0 + β1 · xi + ui mit ui ∼ N(0, σ 2 ) für i ∈ {1, . . . , n},
σ 2 unbekannt, x1 , . . . , xn deterministisch und bekannt,
Realisation y1 , . . . , yn beobachtet
H0 : β1 = β10
H1 : β1 6= β10
Nullhypothese
Gegenhypothese
Teststatistik
t=
Verteilung (H0 )
Benötigte Größen
Kritischer Bereich
zum Niveau α
H0 : β1 ≤ β10
H1 : β1 > β10
sX ,Y
βb1 = 2 , σ
bβc1
sX
βb1 − β10
σ
bβc1
t für β1 = β10 t(n − 2)-verteilt
s
sY2 − βb1 · sX ,Y
=
(n − 2) · sX2
(−∞, −tn−2;1− α2 )
∪(tn−2;1− α2 , ∞)
2 · (1 − Ft(n−2) (|t|))
p-Wert
H0 : β1 ≥ β10
H1 : β1 < β10
(tn−2;1−α , ∞)
(−∞, −tn−2;1−α )
1 − Ft(n−2) (t)
Ft(n−2) (t)
Ökonometrie (SS 2014)
3 Einfache lineare Regression
Folie 165
Konfidenzintervalle und Tests 3.4
Beispiel: Ausgaben in Abhängigkeit vom Einkommen III
Im bereits erläuterten Beispiel soll zum Signifikanzniveau α = 0.05 getestet
werden, ob β0 signifikant von Null verschieden ist. Geeigneter Test:
t-Test für den Regressionsparameter β0
1
2
3
4
5
Hypothesen:
H0 : β0 = 0
gegen
H1 : β0 6= 0
Teststatistik:
βb0 − 0
t=
ist unter H0 (für β0 = 0) t(n − 2)-verteilt.
σ
bβc0
Kritischer Bereich zum Niveau α = 0.05:
K = (−∞, −tn−2;1− α2 ) ∪ (tn−2;1− α2 , +∞) = (−∞, −t5;0.975 ) ∪ (t5;0.975 , +∞)
= (−∞, −2.571) ∪ (2.571, +∞)
Berechnung der realisierten Teststatistik:
βb0 − 0
1.14228 − 0
t=
=
= 1.014
σ
bβc0
1.1264
Entscheidung:
t = 1.014 ∈
/ (−∞, −2.571) ∪ (2.571, +∞) = K ⇒ H0 wird nicht abgelehnt!
(p-Wert: 2 − 2 · Ft(5) (|t|) = 2 − 2 · Ft(5) (|1.014|) = 2 − 2 · 0.8215 = 0.357)
Der Test kann für β0 keine signifikante Abweichung von Null feststellen.
Ökonometrie (SS 2014)
Folie 166
3 Einfache lineare Regression
Konfidenzintervalle und Tests 3.4
Beispiel: Ausgaben in Abhängigkeit vom Einkommen IV
Nun soll zum Signifikanzniveau α = 0.01 getestet werden, ob β1 positiv ist.
Geeigneter Test:
t-Test für den Regressionsparameter β1
1
2
3
4
5
Hypothesen:
H0 : β1 ≤ 0
gegen
H1 : β1 > 0
Teststatistik:
βb1 − 0
ist unter H0 (für β1 = 0) t(n − 2)-verteilt.
t=
σ
bβc1
Kritischer Bereich zum Niveau α = 0.01:
K = (tn−2;1−α , +∞) = (t5;0.99 , +∞) = (3.365, +∞)
Berechnung der realisierten Teststatistik:
βb1 − 0
0.26417 − 0
t=
=
= 7.5262
σ
bβc1
0.0351
Entscheidung:
t = 7.5262 ∈ (3.365, +∞) = K
⇒
H0 wird abgelehnt!
(p-Wert: 1 − Ft(5) (t) = 1 − Ft(5) (7.5262) = 1 − 0.9997 = 0.0003)
Der Test stellt fest, dass β1 signifikant positiv ist.
Ökonometrie (SS 2014)
Folie 167
3 Einfache lineare Regression
Punkt- und Intervallprognosen 3.5
Punkt- und Intervallprognosen
im einfachen linearen Regressionsmodell mit Normalverteilungsannahme
Neben Konfidenzintervallen und Tests für die Parameter β0 und β1 in linearen
Regressionsmodellen vor allem Prognosen wichtige Anwendung.
Zur Erstellung von Prognosen: Erweiterung der Modellannahme
yi = β0 + β1 · xi + ui ,
iid
ui ∼ N(0, σ 2 ),
i ∈ {1, . . . , n}
auf (zumindest) einen weiteren, hier mit (x0 , y0 ) bezeichneten Datenpunkt,
bei dem jedoch y0 nicht beobachtet wird, sondern lediglich der Wert des
Regressors x0 bekannt ist.
Ziel: Schätzung“ (Prognose) von y0 = β0 + β1 · x0 + u0 bzw.
”
E(y0 ) = β0 + β1 · x0 auf Grundlage von x0 .
Wegen E(u0 ) = 0 und der Erwartungstreue von βb0 für β0 bzw. βb1 für β1 ist
[
yb0 := βb0 + βb1 · x0 =: E(y
0)
offensichtlich erwartungstreu für y0 bzw. E(y0 ) gegeben x0 .
[
yb0 bzw. E(y
0 ) wird auch (bedingte) Punktprognose für y0 bzw. E(y0 )
gegeben x0 genannt.
Ökonometrie (SS 2014)
Folie 168
3 Einfache lineare Regression
Punkt- und Intervallprognosen 3.5
Prognosefehler
Zur Beurteilung der Genauigkeit der Prognosen:
Untersuchung der sogenannten Prognosefehler
yb0 − y0
bzw.
[
E(y
0 ) − E(y0 ) .
Qualitativer Unterschied:
I
Prognosefehler
[
b
b
b
b
E(y
0 ) − E(y0 ) = β0 + β1 · x0 − (β0 + β1 · x0 ) = (β0 − β0 ) + (β1 − β1 ) · x0
I
resultiert nur aus Fehler bei der Schätzung von β0 bzw. β1 durch βb0 bzw. βb1 .
Prognosefehler
yb0 − y0 = βb0 + βb1 · x0 − (β0 + β1 · x0 + u0 ) = (βb0 − β0 ) + (βb1 − β1 ) · x0 − u0
ist Kombination von Schätzfehlern (für β0 und β1 ) sowie zufälliger
Schwankung von u0 ∼ N(0, σ 2 ).
[
Zunächst: Untersuchung von eE := E(y
0 ) − E(y0 )
Ökonometrie (SS 2014)
Folie 169
3 Einfache lineare Regression
Punkt- und Intervallprognosen 3.5
Wegen der Erwartungstreue stimmen mittlerer quadratischer (Prognose-)
[
Fehler und Varianz von eE = E(y
0 ) − E(y0 ) überein und man erhält
[
[
b
b
Var(E(y
0 ) − E(y0 )) = Var(E(y0 )) = Var(β0 + β1 · x0 )
= Var(βb0 ) + x 2 Var(βb1 ) + 2 · x0 · Cov(βb0 , βb1 ).
0
Es kann gezeigt werden, dass für die Kovarianz von βb0 und βb1 gilt:
x
x
2
Cov(βb0 , βb1 ) = −σ 2 · Pn
=
−σ
·
2
n · sX2
i=1 (xi − x)
Insgesamt berechnet man so die Varianz des Prognosefehlers
σe2E
σ2 · x 2
σ2
σ2 · x
2
:= Var(eE ) =
+ x0 ·
− 2 · x0 ·
n · sX2
n · sX2
n · sX2
x 2 + x02 − 2 · x0 · x
=σ ·
n · sX2
2
(x 2 − x 2 ) + (x 2 + x02 − 2 · x0 · x)
=σ ·
n · sX2
2
2
2
s
+
(x
−
(x
−
x)
1
x)
0
0
= σ2 · X
= σ2 ·
+
.
2
n
n · sX
n · sX2
2
Ökonometrie (SS 2014)
Folie 170
3 Einfache lineare Regression
Punkt- und Intervallprognosen 3.5
Die Linearität von βb0 und βb1 (in yi ) überträgt sich (natürlich) auch auf
[
E(y
0 ), damit gilt offensichtlich
2
[
eE = E(y
0 ) − E(y0 ) ∼ N 0, σeE
bzw.
[
E(y
0 ) − E(y0 )
∼ N(0, 1) .
σeE
Da σ 2 unbekannt ist, erhält man durch Ersetzen von σ 2 durch die
c2 die geschätzte Varianz
erwartungstreue Schätzfunktion σ
c2 e := Var(e
c2 ·
d E) = σ
σ
E
1 (x0 − x)2
+
n
n · sX2
[
von E(y
0 ) und damit die praktisch wesentlich relevantere Verteilungsaussage
[
eE
E(y
0 ) − E(y0 )
=
∼ t(n − 2) ,
σ
beE
σ
beE
aus der sich in bekannter Weise (symmetrische) Konfidenzintervalle (und
Tests) konstruieren lassen.
Ökonometrie (SS 2014)
Folie 171
3 Einfache lineare Regression
Punkt- und Intervallprognosen 3.5
Prognoseintervalle für E(y0 ) gegeben x0
Intervallprognosen zur Vertrauenswahrscheinlichkeit 1 − α erhält man also als
Konfidenzintervalle zum Konfidenzniveau 1 − α für E(y0 ) in der Form
h
[
[
E(y
·σ
beE , E(y
·σ
beE
0 ) + tn−2;1− α
0 ) − tn−2;1− α
2
2
i
i
h
b
b
b
b
= (β0 + β1 · x0 ) − tn−2;1− α2 · σ
beE , (β0 + β1 · x0 ) + tn−2;1− α2 · σ
beE .
Im Beispiel (Ausgaben in Abhängigkeit vom Einkommen) erhält man zu
gegebenem x0 = 38 (in 100 e)
2
2
1
(x
−
x)
1
(38
−
30.28571)
0
c2 e = σ
c2 ·
σ
+
= 0.9856 ·
+
= 0.214
E
n
7
7 · 114.4901
n · sX2
[
b
b
die Punktprognose E(y
0 ) = β0 + β1 · x0 = 1.14228 + 0.26417 · 38 = 11.1807
(in 100 e) sowie die Intervallprognose zur Vertrauenswahrscheinlichkeit 0.95
h
i
√
√
11.1807 − 2.571 · 0.214 , 11.1807 + 2.571 · 0.214
= [9.9914 , 12.37] (in 100 e) .
Ökonometrie (SS 2014)
Folie 172
3 Einfache lineare Regression
Punkt- und Intervallprognosen 3.5
Prognosefehler e0 := yb0 − y0
Nun: Untersuchung des Prognosefehlers e0 := yb0 − y0
Offensichtlich gilt für e0 = yb0 − y0 die Zerlegung
yb0 − y0 = (βb0 + βb1 · x0 ) −(β0 + β1 · x0 +u0 )
{z
}
|
{z
} |
[
=E(y
0)
=
=E(y0 )
[
E(y
0 ) − E(y0 )
|
{z
}
−
Fehler aus Schätzung von
β0 und β1
u0
|{z}
.
zufällige Schwankung
der Störgröße
[
b
b
E(y
0 ) hängt nur von u1 , . . . , un ab (über y1 , . . . , yn bzw. β0 und β1 ) und ist
iid
wegen der Annahme ui ∼ N(0, σ 2 ) unabhängig von u0 .
Damit sind die beiden Bestandteile des Prognosefehlers insbesondere auch
unkorreliert und man erhält:
[
σe20 := Var(yb0 − y0 ) = Var(E(y
0 ) − E(y0 )) + Var(u0 )
2
2
(x
−
x)
1
(x
−
x)
1
0
0
+
+ σ2 = σ2 · 1 + +
= σ2 ·
2
n
n
n · sX
n · sX2
Ökonometrie (SS 2014)
Folie 173
3 Einfache lineare Regression
Punkt- und Intervallprognosen 3.5
Aus der Unkorreliertheit der beiden Komponenten des Prognosefehlers folgt
auch sofort die Normalverteilungseigenschaft des Prognosefehlers
e0 = y0 − yb0 , genauer gilt:
e0 = yb0 − y0 ∼ N 0, σe20
bzw.
yb0 − y0
∼ N(0, 1) .
σe0
c2 ersetzt werden, um mit Hilfe der geschätzen
Wieder muss σ 2 durch σ
Varianz
2
1
(x
−
x)
0
c2 e := Var(
c2 · 1 + +
d yb0 − y0 ) = σ
σ
0
n
n · sX2
des Prognosefehlers die für die Praxis relevante Verteilungsaussage
yb0 − y0
e0
=
∼ t(n − 2) ,
σ
be0
σ
be0
zu erhalten, aus der sich dann wieder Prognoseintervalle konstruieren lassen.
Ökonometrie (SS 2014)
Folie 174
3 Einfache lineare Regression
Punkt- und Intervallprognosen 3.5
Prognoseintervalle für y0 gegeben x0
Intervallprognosen für y0 zur Vertrauenswahrscheinlichkeit 1 − α erhält man
also analog zu den Intervallprognosen für E(y0 ) in der Form
yb0 − tn−2;1− α2 · σ
be0 , yb0 + tn−2;1− α2 · σ
be0
i
h
b
b
b
b
be0 , (β0 + β1 · x0 ) + tn−2;1− α2 · σ
be0 .
= (β0 + β1 · x0 ) − tn−2;1− α2 · σ
Im Beispiel (Ausgaben in Abhängigkeit vom Einkommen) erhält man zu
gegebenem x0 = 38 (in 100 e)
(x0 − x)2
(38 − 30.28571)2
1
1
c
c
2
2
= 1.1996
σ e0 = σ · 1 + +
= 0.9856· 1 + +
n
7
7 · 114.4901
n · sX2
[
mit der bereits berechneten Punktprognose yb0 = E(y
0 ) = 11.1807 (in 100 e)
die zugehörige Intervallprognose für y0 zur Vertrauenswahrscheinlichkeit 0.95
i
h
√
√
11.1807 − 2.571 · 1.1996 , 11.1807 + 2.571 · 1.1996
= [8.3648 , 13.9966] (in 100 e) .
Ökonometrie (SS 2014)
Folie 175
3 Einfache lineare Regression
Punkt- und Intervallprognosen 3.5
Prognose: Ausgaben in Abhängigkeit vom Einkommen
15
βb0 = 1.14228, βb1 = 0.26417, x0 = 38, yb0 = 11.1807, 1 − α = 0.95
●
y = y^
x
10
●
●
●
yi
●
●
0
5
●
0
10
20
30
40
50
xi
Ökonometrie (SS 2014)
Folie 176
Einfache lineare Modelle mit R 3.6
3 Einfache lineare Regression
Einfache lineare Modelle mit Statistik-Software R
Beispiel (Ausgaben in Abhängigkeit vom Einkommen)
> summary(lm(y~x))
Call:
lm(formula = y ~ x)
Residuals:
1
2
-1.3882 0.9134
3
4
5
6
0.3102 -0.4449 -0.1048 -0.5390
7
1.2535
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.14225
1.12645
1.014 0.357100
x
0.26417
0.03507
7.533 0.000653 ***
--Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9928 on 5 degrees of freedom
Multiple R-squared: 0.919, Adjusted R-squared: 0.9028
F-statistic: 56.74 on 1 and 5 DF, p-value: 0.0006529
Ökonometrie (SS 2014)
Folie 177
Einfache lineare Modelle mit R 3.6
3 Einfache lineare Regression
Interpretation des Outputs I
c2 und R 2
Residuen, σ
Residuals:
1
2
-1.3882 0.9134
3
4
5
6
0.3102 -0.4449 -0.1048 -0.5390
Coefficients:
Estimate Std. Error t value
(Intercept) 1.14225
1.12645
1.014
x
0.26417
0.03507
7.533
-Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01
7
1.2535
Pr(>|t|)
0.357100
0.000653 ***
‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.9928 on 5 degrees of freedom
Multiple R-squared: 0.919, Adjusted R-squared: 0.9028
F-statistic: 56.74 on 1 and 5 DF, p-value: 0.0006529
bi
Auflistung bzw. Zusammenfassung der Residuen u
p
c2 , hier: σ
c2 = 0.9857
SER σ
b= σ
b = 0.9928 ⇒ σ
Anzahl Freiheitsgrade n − 2, hier: n − 2 = 5 ⇒ n = 7
(Multiples) Bestimmtheitsmaß R 2 , hier: R 2 = 0.919
Ökonometrie (SS 2014)
Folie 178
Einfache lineare Modelle mit R 3.6
3 Einfache lineare Regression
Interpretation des Outputs II
Ergebnisse zur Schätzung von β0 und β1
Residuals:
1
2
-1.3882 0.9134
3
4
5
6
0.3102 -0.4449 -0.1048 -0.5390
Coefficients:
Estimate Std. Error t value
(Intercept) 1.14225
1.12645
1.014
x
0.26417
0.03507
7.533
-Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01
7
1.2535
Pr(>|t|)
0.357100
0.000653 ***
‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.9928 on 5 degrees of freedom
Multiple R-squared: 0.919, Adjusted R-squared: 0.9028
F-statistic: 56.74 on 1 and 5 DF, p-value: 0.0006529
Realisationen von βb0 , βb1 , hier: βb0 = 1.14225, βb1 = 0.26417
Standardfehler von βb0 , βb1 , hier: σ
bβc0 = 1.12645, σ
bβc1 = 0.03507
t-Statistiken zu Tests auf Signifikanz, hier: zu β0 : t = 1.014, zu β1 : t = 7.533
p-Werte zu Tests auf Signifikanz, hier: zu β0 : p = 0.3571, zu β1 : p = 0.000653
Ökonometrie (SS 2014)
3 Einfache lineare Regression
Folie 179
Einfache lineare Modelle mit R 3.6
Zusammenhang zwischen p-Werten
zu zweiseitigen und einseitigen Tests bei unter H0 (um Null) symmetrisch verteilter Teststatistik
Erinnerung: t(n)- sowie N(0, 1)-Verteilung sind symmetrisch um Null, für die
zugehörigen Verteilungsfunktionen F gilt also F (x) = 1 − F (−x) für alle
x ∈ R und F (0) = 0.5, F (x) < 0.5 für x < 0 sowie F (x) > 0.5 für x > 0.
Für die p-Werte pz der zweiseitigen Tests auf den Mittelwert bei bekannter
(Gauß-Test) sowie unbekannter (t-Test) Varianz gilt daher bekanntlich
2 · F (x)
falls x < 0
pz = 2 · min{F (x), 1 − F (x)} =
,
2 · (1 − F (x)) falls x ≥ 0
wobei x den realisierten Wert der Teststatistik sowie F die
Verteilungsfunktion der Teststatistik unter H0 bezeichne.
Für die p-Werte pl = F (x) zum linksseitigen sowie pr = 1 − F (x) zum
rechtsseitigen Test bei realisierter Teststatistik x gelten demnach die
folgenden Zusammenhänge:
 p

z

 1 − pz falls x < 0
falls x < 0
2
2
pl =
sowie
pr =
 1 − pz falls x ≥ 0
 pz
falls x ≥ 0
2
2
Somit auch p-Werte zu einseitigen Tests aus R-Output bestimmbar!
Ökonometrie (SS 2014)
.
Folie 180
4 Multiple lineare Regression
Multiples lineares Modell 4.1
Zusammenfassung: Einfache lineare Regression I
Bisher: Annahme der Gültigkeit eines einfachen linearen Modells
yi = β0 + β1 · xi + ui ,
i ∈ {1, . . . , n},
mit
I
I
der abhängigen Variablen (Regressand) yi ,
einer unabhängigen, erklärenden Variablen (Regressor) xi , wobei
1
2
I
xi als deterministisch angenommen wird und
sX2 > 0 gelten muss,
der Störgröße ui , wobei
1
2
3
4
E(ui ) ≡ 0,
Var(ui ) ≡ σ 2 > 0,
Cov(ui , uj ) = 0 für alle i, j mit i 6= j sowie meist darüberhinaus eine
gemeinsame Normalverteilung der ui ,
iid
damit insgesamt ui ∼ N(0, σ 2 ) angenommen wird.
Ökonometrie (SS 2014)
4 Multiple lineare Regression
Folie 181
Multiples lineares Modell 4.1
Zusammenfassung: Einfache lineare Regression II
Auf Grundlage dieses Annahmen-Komplexes:
I
I
I
Verwendung der KQ-Methode, um eine geschätze Regressionsgerade
y = βb0 + βb1 · x mit den zugehörigen KQ-Prognosen ybi = βb0 + βb1 · xi und den
bi = yi − ybi zu bestimmen.
zugehörigen KQ-Residuen u
Bestimmung von Konfidenzintervallen und Durchführung von Hypothesentests
für die Regressionsparameter β0 und β1 .
Bestimmung von bedingten Punktprognosen und Prognoseintervallen für die
abhängige Variable y zu neuen“ Werten der unabhängigen, erklärenden
”
Variablen x.
Problem: (Perfekte) Validität der Ergebnisse nur, wenn Modell korrekt und
Annahmen-Komplex erfüllt ist!
Im Folgenden:
I
I
I
Erweiterung des einfachen linearen Regressionsmodells zum multiplen linearen
Regressionsmodell
Untersuchung der Konsequenz von Annahmeverletzungen
Geeignete Reaktion auf bzw. geeignete Verfahren im Fall von
Annahmeverletzungen
Ökonometrie (SS 2014)
Folie 182
4 Multiple lineare Regression
Multiples lineares Modell 4.1
Konsequenz bei weggelassener erklärender Variablen I
Der omitted variable bias“
”
Eine Möglichkeit der Verletzung der Annahmen des einfachen linearen
Modells: Modell ist tatsächlich komplexer, yi hänge auch von einer weiteren
erklärenden Variablen e
xi linear in der Gestalt
yi = β0 + β1 · xi + β2 · e
xi + i ,
i ∈ {1, . . . , n},
mit β2 6= 0 ab, wobei die üblichen Annahmen für die Störgrößen i
(insbesondere E(i ) ≡ 0) gelten sollen.
Wird statt des komplexeren Modells die Gültigkeit eines einfachen linearen
Modells angenommen, ist die Abhängigkeit von e
xi offensichtlich in der
Störgröße ui subsummiert, man erhält die Darstellung
yi = β0 + β1 · xi + β2 · e
x + i ,
}
| {zi
i ∈ {1, . . . , n}.
ui
Damit gilt im einfachen Modell jedoch E(ui ) = β2 · e
xi , die Annahme E(ui ) ≡ 0
ist also verletzt, sobald e
xi 6= 0 für mindestens ein i ∈ {1, . . . , n} gilt!
Ökonometrie (SS 2014)
Folie 183
4 Multiple lineare Regression
Multiples lineares Modell 4.1
Konsequenz bei weggelassener erklärender Variablen II
Der omitted variable bias“
”
Werden trotz dieser Annahmenverletzung Parameterschätzer im einfachen
linearen Modell bestimmt, so erhält man beispielsweise für βb1
βb1 =
n
n
X
X
(xi − x)
(xi − x)
·
y
=
· (β0 + β1 · xi + β2 · e
xi + i )
i
nsX2
nsX2
i=1
= β0
n
X
i=1
|
i=1
n
X
n
n
X
(xi − x)e
(xi − x)
(xi − x)xi
xi X (xi − x)i
+β1
+β2
+
nsX2
nsX2
nsX2
nsX2
i=1
i=1
i=1
{z
}
|
{z
}
|
{z
}
=0
und damit E(βb1 ) = β1 + β2
(sX ,Xe
!
=1
e
! sX ,X
s2
X
=
sX ,Xe
.
sX2
e .)
bezeichnet wie üblich die empirische Kovarianz zwischen X und X
Damit ist βb1 nicht mehr erwartungstreu für β1 , falls sX ,Xe 6= 0 gilt, auch
Konfidenzintervalle und Tests werden dann unbrauchbar!
Ökonometrie (SS 2014)
Folie 184
4 Multiple lineare Regression
Multiples lineares Modell 4.1
Das multiple lineare Regressionsmodell I
Lösung des Problems durch Schaffung der Möglichkeit, weitere erklärende
Variablen einzubeziehen.
Erweiterung des einfachen linearen Modells um zusätzliche Regressoren
x2i , . . . , xKi zum multiplen linearen Modell
yi = β0 + β1 x1i + . . . + βK xKi + ui ,
i ∈ {1, . . . , n},
bzw. in Matrixschreibweise
y = Xβ + u
mit
 
y1
 
y =  ...  ,
yn

1

X =  ...
1
x11
..
.
···
x1n
···

xK 1
..  ,
. 
xKn


β0
 β1 
 
β =  . ,
 .. 
βK
 
u1
 
u =  ...  .
un
Ökonometrie (SS 2014)
Folie 185
4 Multiple lineare Regression
Multiples lineares Modell 4.1
Das multiple lineare Regressionsmodell II
Modellannahmen im multiplen linearen Regressionsmodell übertragen sich (zum
Teil verallgemeinert) aus einfachem linearen Modell:
Für die K unabhängigen, erklärenden Variablen (Regressoren) x1i , . . . , xKi
wird angenommen, dass
1
2
die xki deterministisch sind (für i ∈ {1, . . . , n}, k ∈ {1, . . . , K }) und dass
sich für kein k ∈ {1, . . . , K } der Regressor xki als (für alle i ∈ {1, . . . , n} feste)
Linearkombination einer Konstanten und der übrigen Regressoren darstellen
lässt. Äquivalent dazu:
F
F
Die Regressormatrix X hat vollen (Spalten-)Rang K + 1.
x1i lässt sich nicht als Linearkombination einer Konstanten und der übrigen
Regressoren x2i , . . . , xKi darstellen.
Für die Störgrößen ui wird
1
2
3
4
E(ui ) ≡ 0 bzw. E(u) = 0 mit dem Nullvektor 0 := (0, . . . , 0)0 ,
Var(ui ) ≡ σ 2 > 0,
Cov(ui , uj ) = 0 für alle i, j mit i 6= j sowie meist darüberhinaus eine
gemeinsame Normalverteilung der ui ,
iid
damit insgesamt ui ∼ N(0, σ 2 ) bzw. u ∼ N(0, σ 2 In ) mit der
(n × n)-Einheitsmatrix In angenommen.
Ökonometrie (SS 2014)
Folie 186
4 Multiple lineare Regression
Multiples lineares Modell 4.1
Das multiple lineare Regressionsmodell III
Für den Erwartungswert von yi gilt nun
E (yi ) = β0 + β1 x1i + . . . + βK xKi ,
i ∈ {1, . . . , n},
die Regressionsgerade aus dem einfachen linearen Modell wird also nun zu
einer Regressionsebene, beschrieben durch die Regressions-Parameter
β0 , . . . , β K .
Der Regressionsparameter (und Steigungskoeffizient) βk gibt nun für
k ∈ {1, . . . , K } die erwartete Änderung (ohne den Einfluss der Störgröße ui )
von yi an, die aus der Erhöhung des Regressors xki um eine Einheit resultiert,
wenn alle anderen Regressoren konstant gehalten werden.
Zur Schätzung der Parameter des multiplen Regressionsmodells wird
wiederum die Methode der Kleinsten Quadrate (Least Squares, auch
Ordinary Least Squares) verwendet.
Ökonometrie (SS 2014)
Folie 187
4 Multiple lineare Regression
Parameterschätzung 4.2
Schätzung im multiplen linearen Modell I
Die Anwendung der KQ-Methode im multiplen linearen Modell führt zur
Suche nach βb0 , βb1 , . . . , βbK ∈ R mit
n
X
(yi − (βb0 + βb1 xi1 + . . . + βbK xKi ))2
i=1
!
=
min
β0 ,β1 ,...,βK ∈R
n
X
i=1
(yi − (β0 + β1 xi1 + . . . + βK xKi ))2 .
In Matrixschreibweise ist also der Vektor βb = (βb0 , βb1 , . . . , βbK )0 ∈ RK +1
gesucht mit
!
b 0 (y − Xβ)
b =
(y − Xβ)
min (y − Xβ)0 (y − Xβ) .
β∈RK +1
(Zu Matrizen A bzw. Vektoren b seien hier und im Folgenden wie üblich mit
A0 bzw. b0 jeweils die transponierten Matrizen bzw. Vektoren bezeichnet.)
Ökonometrie (SS 2014)
Folie 188
4 Multiple lineare Regression
Parameterschätzung 4.2
Schätzung im multiplen linearen Modell II
Die Matrixdarstellung erlaubt eine kompakte Lösung der Optimierung:
Für die zu minimierende Funktion
f (β) := (y − Xβ)0 (y − Xβ) = y0 y − β 0 X0 y − y0 Xβ + β 0 X0 Xβ
= y0 y − 2β 0 X0 y + β 0 X0 Xβ
erhält man den Gradienten
∂f (β)
= −2X0 y + 2X0 Xβ = 2(X0 Xβ − X0 y)
∂β
und damit wegen der Invertierbarkeit (!) von X0 X als Lösung von
∂f (β) !
=0
∂β
βb = (X0 X)−1 X0 y ,
die wegen der positiven Definitheit (!) von X0 X auch (einzige) Lösung des
Minimierungsproblems ist.
Ökonometrie (SS 2014)
4 Multiple lineare Regression
Folie 189
Parameterschätzung 4.2
Schätzung im multiplen linearen Modell III
Die Invertierbarkeit von X0 X ist gewährleistet, da nach Annahme die
(n × (K + 1))-Matrix X vollen (Spalten-)Rang K + 1 und damit auch die
((K + 1) × (K + 1))-Matrix X0 X vollen Rang K + 1 hat.
Da X vollen (Spalten-)Rang besitzt, ist X0 X außerdem positiv definit.
Eine Verletzung der getroffenen Annahme, dass X vollen (Spalten-)Rang
besitzt, bezeichnet man auch als perfekte Multikollinearität der
Regressormatrix X.
Bei Vorliegen von perfekter Multikollinearität ist die KQ-Methode zwar immer
noch (allerdings nicht wie eben beschrieben!) durchführbar, der optimale
Vektor βb ist allerdings nicht mehr eindeutig bestimmt, der zugehörige
Parametervektor β damit nicht mehr identifiziert.
Perfekte Multikollinearität kann durch (zum Teil offensichtliche)
Unachtsamkeiten bei der Zusammenstellung der Regressoren entstehen
(später mehr!).
Ökonometrie (SS 2014)
Folie 190
4 Multiple lineare Regression
Parameterschätzung 4.2
Schätzung im multiplen linearen Modell IV
Eine andere Darstellung des KQ-Schätzers βb ist gegeben durch

 
βb1
s11
 ..   ..
 . = .
sK 1
βbK
und
s12
..
.
···
sK 2
···
−1 

s1K
s1Y
..   .. 
.   . 
sKK
sKY
βb0 = y − (βb1 x 1 + . . . + βbK x K )
mit
n
1X
xk =
xki ,
n
y=
1
n
i=1
n
X
n
1X
skj =
(xki − x k )(xji − x j ),
n
yi ,
skY =
i=1
1
n
i=1
n
X
i=1
(xki − x k )(yi − y )
für k, j ∈ {1, . . . , K }.
Ökonometrie (SS 2014)
Folie 191
4 Multiple lineare Regression
Parameterschätzung 4.2
Schätzung im multiplen linearen Modell V
Offensichtlich erhält man für K = 1 hiermit die – abgesehen von der leicht
abweichenden Notation – zum KQ-Schätzer im einfachen linearen Modell
übereinstimmende Darstellung
s1Y
βb1 =
s11
sowie
Für K = 2 lässt sich die Darstellung
s22 s1Y − s12 s2Y
,
βb1 =
2
s11 s22 − s12
s11 s2Y − s12 s1Y
βb2 =
,
2
s11 s22 − s12
für die KQ-Schätzer ableiten.
Ökonometrie (SS 2014)
βb0 = y − βb1 x 1 .
βb0 = y − (βb1 x 1 + βb2 x 2 )
Folie 192
4 Multiple lineare Regression
Parameterschätzung 4.2
Schätzung im multiplen linearen Modell VI
Wie im einfachen linearen Regressionsmodell definiert man zu den
KQ/OLS-geschätzten Parametern βb = (βb0 , βb1 , . . . , βbK )0 mit
ybi := βb0 + βb1 x1i + . . . βbK xKi ,
i ∈ {1, . . . , n}
bzw.
b
y := Xβb
die vom (geschätzten) Modell prognostizierten Werte der abhängigen
Variablen auf der geschätzten Regressionsebene sowie mit
bi := yi − ybi ,
u
i ∈ {1, . . . , n}
b := y − b
u
y
bzw.
die Residuen, also die Abstände (in y -Richtung) der beobachteten Werte der
abhängigen Variablen von den progostizierten Werten auf der geschätzten
Regressionsebene.
Pn
P
bi = 0 sowie ni=1 xki u
bi = 0 für k ∈ {1, . . . , K } bzw.
Es gilt (analog) i=1 u
b = X0 (y − b
X0 u
y) = X0 y − X0 Xβb = X0 y − X0 X(X0 X)−1 X0 y = 0 .
Ökonometrie (SS 2014)
Folie 193
4 Multiple lineare Regression
Parameterschätzung 4.2
Schätzung im multiplen linearen Modell VII
0 0b
b 0u
b = (Xβ)
b = βbP
Damit
y0 u
X u = 0 sowie
Pn mit
Pb
Pngilt weiter
n
n
bi = i=1 (yi − ybi ) auch i=1 yi = i=1 ybi ⇐⇒ y = yb.
0 = i=1 u
So erhält man
b +b
b
b)0 (b
b) = b
b0 b
y0 y = (b
y+u
y+u
y0 b
y+ u
y +b
y0 u
u0 u
|{z} |{z}
=0
=0
2
und durch Subtraktion von ny 2 = nb
y auf beiden Seiten
2
b0 u
b
y0 y − ny 2 = b
y0 b
y − nb
y +u
und damit insgesamt die bekannte Streuungszerlegung
n
X
(yi − y )2
i=1
|
{z
}
Total Sum of Squares
Ökonometrie (SS 2014)
=
n
X
(b
yi − yb)2
i=1
|
{z
}
Explained Sum of Squares
+
n
X
i=1
bi2
u
.
| {z }
Residual Sum of Squares
Folie 194
4 Multiple lineare Regression
Parameterschätzung 4.2
Schätzung im multiplen linearen Modell VIII
Wie im einfachen linearen Modell misst das multiple Bestimmtheitsmaß
Pn
Pn
2
b
u
(b
yi − yb)2
RSS
ESS
2
i
i=1
i=1
P
R = 1 − Pn
=
=
=
1
−
n
2
2
TSS
TSS
i=1 (yi − y )
i=1 (yi − y )
den Anteil der durch den (geschätzten) linearen Zusammenhang erklärten
Streuung an der gesamten Streuung der abhängigen Variablen.
Es gilt weiterhin 0 ≤ R 2 ≤ 1.
Bei der Hinzunahme weiterer erklärender Variablen (Regressoren) in ein
bestehendes lineares Modell kann sich im Laufe der
ätzung der
Pn KQ/OLS-Sch
2
bi , offensichtlich
Zielfunktionswert an der Minimumstelle, RSS = i=1 u
höchstens weiter verringern.
Damit führt die Hinzunahme weiterer (auch eigentlich irrelevanter)
Regressoren höchstens zu einer Zunahme des multiplen Bestimmtheitsmaßes
R 2.
Ökonometrie (SS 2014)
Folie 195
4 Multiple lineare Regression
Parameterschätzung 4.2
Schätzung im multiplen linearen Modell IX
Um einen aussagekräftigeren Vergleich der Bestimmtheitmaße eines
ursprünglichen und eines erweiterten Modells durchführen zu können, kann
das adjustierte Bestimmtheitsmaß
2
R := 1 −
1
n−(K +1) · RSS
1
n−1 · TSS
=1−
n−1
RSS
n − (K + 1) TSS
verwendet werden.
Dieses kann sich bei Erweiterung eines Modells um zusätzliche Regressoren
auch verringern (und sogar negativ werden).
Es gilt (offensichtlich) stets
2
R ≤ R2 ≤ 1 .
Ökonometrie (SS 2014)
Folie 196
4 Multiple lineare Regression
Parameterschätzung 4.2
Schätzung im multiplen linearen Modell X
2
Bei der Berechnung von R wird die für σ 2 = Var(ui ) erwartungstreue
Schätzfunktion
n
X
b0 u
b
u
RSS
1
2
c
2
bi =
u
=
σ =
n − (K + 1)
n − (K + 1)
n − (K + 1)
i=1
verwendet.
p
c2 dieser
Wie im einfachen linearen Modell wird die positive Wurzel + σ
Schätzfunktion als Standard Error of the Regression (SER) oder residual
standard error bezeichnet.
Die Korrektur um K + 1 Freiheitsgrade erklärt sich dadurch, dass nun K + 1
Beobachtungen nötig sind, um die Regressionsebene (eindeutig) bestimmen
zu können.
Ökonometrie (SS 2014)
Folie 197
4 Multiple lineare Regression
Parameterschätzung 4.2
Schätzung im multiplen linearen Modell XI
Die Schätzfunktion βb = (X0 X)−1 X0 y ist offensichtlich linear in den yi .
Einsetzen von y = Xβ + u liefert die Darstellung
βb = (X0 X)−1 X0 y = (X0 X)−1 X0 (Xβ + u)
= (X0 X)−1 (X0 X)β + (X0 X)−1 X0 u = β + (X0 X)−1 X0 u
b unter der Annahme E(u) = 0 folgt daraus sofort E(β)
b = β und damit
von β,
die Erwartungstreue von βb für β.
b von βb erhält man mit der obigen
Für die (Varianz-)Kovarianzmatrix V(β)
Darstellung für βb wegen der Symmetrie von (X0 X)−1 weiter
0 h
0 i
0
−1 0
0
−1 0
b
b
b
b
b
V(β) = E β − E(β) β − E(β)
= E (X X) X u (X X) X u
= E (X0 X)−1 X0 uu0 X(X0 X)−1 = (X0 X)−1 X0 E(uu0 ) X(X0 X)−1
| {z }
=V(u)=σ 2 In
= σ 2 (X0 X)−1 X0 X(X0 X)−1 = σ 2 (X0 X)−1
Ökonometrie (SS 2014)
Folie 198
4 Multiple lineare Regression
Parameterschätzung 4.2
Schätzung im multiplen linearen Modell XII
b enthält alle Varianzen der Parameterschätzer
Die (symmetrische) Matrix V(β)
βb0 , βb1 , . . . , βbK sowie deren paarweise Kovarianzen in der Gestalt

Var(βb0 )
 Cov(βb1 , βb0 )

b
V(β) = 
..

.
Cov(βbK , βb0 )
Cov(βb0 , βb1 ) · · ·
Var(βb1 )
···
..
..
.
.
Cov(βbK , βb1 ) · · ·

Cov(βb0 , βbK )
Cov(βb1 , βbK )

 .
..

.
Var(βbK )
c2 durch
b = σ 2 (X0 X)−1 kann unter Zuhilfenahme von σ
V(β)
geschätzt werden.
c2 (X0 X)−1
b =σ
b β)
V(
Ökonometrie (SS 2014)
Folie 199
4 Multiple lineare Regression
Parameterschätzung 4.2
Schätzung im multiplen linearen Modell XIII
Man erhält so Schätzwerte für die Varianzen der Schätzer βb0 , βb1 , . . . , βbK
sowie deren paarweise Kovarianzen in der Gestalt


b
b
b
b
b
d
d
d
Var(β0 )
Cov(β0 , β1 ) · · · Cov(β0 , βK )
d b b
d βb1 )
d βb1 , βbK )
 Cov(β1 , β0 )

Var(
· · · Cov(
b =
b β)
 .
V(
..
..
..
..


.


.
.
.
d βbK , βb0 ) Cov(
d βbK , βb1 ) · · ·
Cov(
d βbK )
Var(
b
b β),
Die (positiven) Wurzeln der Hauptdiagonalelemente von V(
q
q
q
d βb0 ), σ
d βb1 ), . . . , σ
d βbK ) ,
σ
bβb0 := Var(
bβb1 := Var(
bβbK := Var(
werden wie üblich als Standardfehler der Parameterschätzer βb0 , βb1 , . . . , βbK
bezeichnet.
Ökonometrie (SS 2014)
Folie 200
4 Multiple lineare Regression
Parameterschätzung 4.2
Schätzung im multiplen linearen Modell XIV
Zusammengefasst erhält man unter bisherigen Annahmen an X sowie den
anfangs getroffenen Annahmen
1
2
3
E(ui ) ≡ 0,
Var(ui ) ≡ σ 2 > 0,
Cov(ui , uj ) = 0 für alle i, j mit i 6= j
an die Störgrößen ui , i ∈ {1, . . . , n}, dass
I
I
I
b eine in yi lineare Schätzfunktion ist,
β
b erwartungstreu für β ist,
β
b die Varianz-Kovarianzmatrix V(β)
b = σ 2 (X0 X)−1 besitzt.
β
Der Satz von Gauß-Markov sichert darüberhinaus, dass βb sogar die beste
lineare unverzerrte Schätzfunktion (BLUE) ist.
Unter der zusätzlichen Annahme einer
4
gemeinsamen Normalverteilung der ui
b
erhält man mit der Linearität sofort die Normalverteilungseigenschaft von β,
also βb ∼ N β, σ 2 (X0 X)−1 . Außerdem kann man zeigen, dass βb dann sogar
varianzminial unter allen für β erwartungstreuen Schätzfunktionen ist.
Ökonometrie (SS 2014)
4 Multiple lineare Regression
Folie 201
Parameterschätzung 4.2
Schätzung im multiplen linearen Modell XV
Auch ohne Normalverteilungsannahme für die ui kann man unter gewissen
technischen Voraussetzungen (die hier nicht näher ausgeführt werden) zeigen,
dass die Verteilung von βb bei wachsendem Beobachtungsumfang n gegen
eine (mehrdimensionale) Normalverteilung konvergiert.
In der Praxis bedeutet dies, dass man – auch für endliches n – als geeignete
Näherung der Verteilung von βb häufig eine mehrdimensionale
Normalverteilung mit dem Erwartungswertvektor β und der
Varianz-Kovarianzmatrix σ 2 (X0 X)−1 verwenden kann.
Wie gut“ diese Näherung ist, hängt wieder von vom konkreten
”
Anwendungsfall
ab; insbesondere
I
I
steigt die Qualität der Näherung i.d.R. mit wachsendem n,
ist die Näherung umso besser, je ähnlicher die tatsächliche Verteilung der ui
einer Normalverteilung ist.
In der Praxis beurteilt man die Nähe“ der Verteilung der (unbeobachteten!)
”
Störgrößen ui zu einer Normalverteilung mit Hilfe der (geschätzten!)
bi .
Residuen u
Ökonometrie (SS 2014)
Folie 202
4 Multiple lineare Regression
Konfidenzintervalle und Tests 4.3
Konfidenzintervalle und Tests für einzelne Parameter
Konfidenzintervalle und Tests für einzelne Parameter können ganz analog
zum einfachen linearen Modell konstruiert werden.
Für die Komponenten βbk , k ∈ {0, . . . , K }, des Parameterschätzers βb gilt bei
Normalverteilungsannahme an die ui exakt (sonst ggf. approximativ)
βbk − βk
∼ t(n − (K + 1)),
σ
bβbk
k ∈ {0, . . . , K }
Hieraus ergeben sich für k ∈ {0, . . . , K } unmittelbar die zum einfachen
linearen Modell analogen Formeln“ der (ggf. approximativen)
”
(symmetrischen) Konfidenzintervalle für βk zum Konfidenzniveau 1 − α
bzw. zur Vertrauenswahrscheinlichkeit 1 − α als
h
i
βbk − tn−(K +1);1− α2 · σ
bβbk , βbk + tn−(K +1);1− α2 · σ
bβbk
Ebenfalls analog erhält man t-Tests für die Regressionsparameter
β0 , β1 , . . . , βK .
Ökonometrie (SS 2014)
Folie 203
4 Multiple lineare Regression
Konfidenzintervalle und Tests 4.3
Zusammenfassung: t-Test für den Parameter βk
im multiplen linearen Regressionsmodell
Anwendungsvoraussetzungen
exakt: y = Xβ + u mit u ∼ N(0, σ 2 In ),
approx.: y = Xβ + u mit E(u) = 0, V(u) = σ 2 In ,
σ 2 unbekannt, X deterministisch mit vollem Spaltenrang K + 1,
Realisation y = (y1 , . . . , yn )0 beobachtet
H0 : βk = βk0
H1 : βk 6= βk0
Nullhypothese
Gegenhypothese
H0 : βk ≤ βk0
H1 : βk > βk0
Teststatistik
Verteilung (H0 )
Benötigte Größen
Kritischer Bereich
zum Niveau α
p-Wert
Ökonometrie (SS 2014)
t=
H0 : βk ≥ βk0
H1 : βk < βk0
βbk − βk0
σ
bβbk
t für βk = βk0 (näherungsweise) t(n − (K + 1))-verteilt
q
h
i
0
−1 0
c2 [(X0 X)−1 ]
b
βk = (X X) X y
,σ
bβbk = σ
k+1,k+1 mit
k+1
c2 =
σ
b0 b
u u
,
n−(K +1)
wobei b
u = y − X(X0 X)−1 X0 y
(−∞, −tn−(K +1);1− α2 )
∪(tn−(K +1);1− α2 , ∞)
2 · (1 − Ft(n−(K +1)) (|t|))
(tn−(K +1);1−α , ∞)
(−∞, −tn−(K +1);1−α )
1 − Ft(n−(K +1)) (t)
Ft(n−(K +1)) (t)
Folie 204
4 Multiple lineare Regression
Konfidenzintervalle und Tests 4.3
Beispiel: Multiples Modell/Omitted Variable Bias I
Beispieldatensatz mit Daten zur Lohnhöhe (yi ), zu den Ausbildungsjahren
über den Hauptschulabschluss hinaus (x1i ) sowie zum Alter in Jahren (x2i )
von n = 20 Mitarbeitern eines Betriebs:
i
Lohnhöhe yi
Ausbildung x1i
Alter x2i
1
2
3
4
5
6
7
8
9
10
1250
1
28
1950
9
34
2300
11
55
1350
3
24
1650
2
42
1750
1
43
1550
4
37
1400
1
18
1700
3
63
2000
4
58
11
12
13
14
15
16
17
18
19
20
1350
1
30
1600
2
43
1400
2
23
1500
3
21
2350
6
50
1700
9
64
1350
1
36
2600
7
58
1400
2
35
1550
2
41
i
Lohnhöhe yi
Ausbildung x1i
Alter x2i
(vgl. von Auer, Ludwig: Ökonometrie – Eine Einführung, 6. Aufl., Tabelle 13.1)
Es soll nun angenommen werden, dass das multiple lineare Regressionsmodell
iid
ui ∼ N(0, σ 2 ),
yi = β0 + β1 x1i + β2 x2i + ui ,
i ∈ {1, . . . , 20},
mit den üblichen Annahmen korrekt spezifiziert ist.
Ökonometrie (SS 2014)
Folie 205
4 Multiple lineare Regression
Konfidenzintervalle und Tests 4.3
Beispiel: Multiples Modell/Omitted Variable Bias II
Zunächst wird (fälschlicherweise!) die Variable Alter“ (x2i ) weggelassen und
”
die Lohnhöhe“ (yi ) nur mit der Variable Ausbildung
“ (x1i ) erklärt:
”
”
Call:
lm(formula = Lohnhöhe ~ Ausbildung)
Residuals:
Min
1Q
-458.19 -140.36
Median
-68.94
3Q
87.32
Max
620.37
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1354.66
94.22 14.377 2.62e-11 ***
Ausbildung
89.28
19.82
4.505 0.000274 ***
--Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 264.6 on 18 degrees of freedom
Multiple R-squared: 0.5299, Adjusted R-squared: 0.5038
F-statistic: 20.29 on 1 and 18 DF, p-value: 0.0002742
Ökonometrie (SS 2014)
Folie 206
4 Multiple lineare Regression
Konfidenzintervalle und Tests 4.3
Beispiel: Multiples Modell/Omitted Variable Bias III
Danach wird das korrekte, vollständige Modell geschätzt:
Call:
lm(formula = Lohnhöhe ~ Ausbildung + Alter)
Residuals:
Min
1Q
-569.50 -120.79
Median
-5.14
3Q
73.12
Max
519.26
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1027.806
164.473
6.249 8.81e-06 ***
Ausbildung
62.575
21.191
2.953
0.0089 **
Alter
10.602
4.577
2.317
0.0333 *
--Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 237.4 on 17 degrees of freedom
Multiple R-squared: 0.6427, Adjusted R-squared: 0.6007
F-statistic: 15.29 on 2 and 17 DF, p-value: 0.0001587
Ökonometrie (SS 2014)
Folie 207
4 Multiple lineare Regression
Konfidenzintervalle und Tests 4.3
Beispiel: Multiples Modell/Omitted Variable Bias IV
Geschätzte Regressionsebene mit Residuen
●
●
●
●
●
●
●
●
●
●
●
●
●
70
60
●●
●
●
50
●
Alter x2i
1200 1400 1600 1800 2000 2200 2400 2600
Lohnhöhe yi
●
40
●
30
20
10
0
2
4
6
8
10
12
Ausbildung x1i
Ökonometrie (SS 2014)
Folie 208
4 Multiple lineare Regression
Konfidenzintervalle und Tests 4.3
Beispiel: Multiples Modell/Omitted Variable Bias V
Gegenüberstellung der Schätzergebnisse:
Absolutglied
Ausbildung
Alter
falsches Modell
korrektes Modell
1354.658
94.222
1027.806
164.473
89.282
19.82
62.575
21.191
βb0
σ
bβb0
βb1
σ
bβb1
βb2
σ
bβb2
10.602
4.577
b0 u
b
u
SER
R2
2
R
1260028
264.578
0.5299
0.5038
957698
237.35
0.6427
0.6007
Ökonometrie (SS 2014)
Folie 209
4 Multiple lineare Regression
Konfidenzintervalle und Tests 4.3
Beispiel: Multiples Modell/Omitted Variable Bias VI
Die Regressoren x1i (Ausbildungsjahre) und x2i (Alter) sind positiv korreliert,
es gilt (mit den Bezeichnungen von Folie 191) genauer
s12 = 22.445
bzw.
√
s12
√
s11 s22
=√
22.445
√
= 0.544
8.91 · 191.028
Außerdem hat der Regressor Alter“ (neben dem Regressor Ausbildung“) im
”
”
korrekten Modell einen signifikanten Regressionskoeffizienten.
Im Modell mit ausgelassener Variablen x2i (Alter) spiegelt der geschätzte
Koeffizient zum Regressor Ausbildung“ damit nicht den isolierten“ Effekt der
”
”
Ausbildung wider, sondern einen kombinierten“ Effekt.
”
Wie man zeigen (und im Beispiel leicht nachrechnen) kann, erhält man
(analog zum Resultat von Folie 184) durch
s12 b
22.445
βb1 +
β2 = 62.575 +
· 10.602 = 89.282
s11
8.91
aus den Schätzergebnissen des korrekten Modells den Punktschätzer für β1
im falschen Modell mit ausgelassenem Regressor.
Ökonometrie (SS 2014)
Folie 210
4 Multiple lineare Regression
Konfidenzintervalle und Tests 4.3
Beispiel: Multiples Modell/Omitted Variable Bias VII
Auch die Punkt- und Intervallschätzung von β0 sowie Hypothesentests für die
Regressionsparameter unterliegen im Modell mit ausgelassener Variablen
vergleichbaren Verzerrungen.
Geht man fälschlicherweise davon aus, die Annahmen des linearen
Regressionsmodell im Modell mit ausgelassenem Regressor erfüllt und mit der
Modellschätzung den isolierten Effekt des Regressors Ausbildung“ gemessen
”
zu haben, so führt dies zu
I
I
I
verzerrten Punktschätzern,
verschobenen und in der Breite verzerrten Konfidenzintervallen sowie
wertlosen Hypothesentests
für den isolierten Effekt (da man tatsächlich einen kombinierten Effekt
gemessen hat).
Ökonometrie (SS 2014)
Folie 211
4 Multiple lineare Regression
Punkt- und Intervallprognosen 4.4
Punkt- und Intervallprognosen I
Wie im einfachen linearen Regressionsmodell: Erweiterung der
Modellannahme
yi = β0 + β1 x1i + . . . + βK xKi + ui ,
iid
ui ∼ N(0, σ 2 ),
i ∈ {1, . . . , n}
auf (zumindest) einen weiteren Datenpunkt (y0 , x10 , . . . , xK 0 ), bei dem jedoch
y0 nicht beobachtet wird, sondern lediglich die Werte der Regressoren
x10 , . . . , xK 0 bekannt sind.
Ziel ist wiederum die Prognose von y0 = β0 + β1 x10 + . . . βK xK 0 + u0 bzw.
E(y0 ) = β0 + β1 x10 + . . . βK xK 0 auf Grundlage von x10 , . . . , xK 0 .
Hierzu definiert man wie im einfachen linearen Modell mit
yb0 := βb0 + βb1 x10 + . . . + βbK xK 0
[
b
b
b
bzw. E(y
0 ) := β0 + β1 x10 + . . . + βK xK 0
die (bedingte) Punktprognose yb0 für y0 gegeben x10 , . . . , xK 0 bzw.
[
die (bedingte) Punktprognose E(y
0 ) für E(y0 ) gegeben x10 , . . . , xK 0 .
Ökonometrie (SS 2014)
Folie 212
4 Multiple lineare Regression
Punkt- und Intervallprognosen 4.4
Punkt- und Intervallprognosen II
Die Untersuchung der Eigenschaften der bedingten Punktprognosen
vereinfacht sich durch die Definition des Vektors
0
x0 = 1 x10 · · · xK 0 ,
der (transponiert) analog zu einer Zeile der Regressormatrix X aufgebaut ist.
Für die (bedingte) Punktprognose für y0 bzw. E(y0 ) gegeben x0 erhält man
so die kompakte Darstellung
yb0 = x0 0 βb
bzw.
0b
[
E(y
0 ) = x0 β .
Die Erwartungstreue der (bedingten) Punktprognosen ergibt sich damit
unmittelbar aus der Erwartungstreue von βb für β und E(u0 ) = 0:
b = x0 0 E(β)
b = x0 0 β = E(y0 )
E(x0 0 β)
[ = E(E(y0 )) ]
Ökonometrie (SS 2014)
Folie 213
4 Multiple lineare Regression
Punkt- und Intervallprognosen 4.4
Punkt- und Intervallprognosen III
Wie im einfachen linearen Modell resultiert der Prognosefehler
0b
0
0 b
[
eE := E(y
0 ) − E(y0 ) = x0 β − x0 β = x0 (β − β)
b während
nur aus dem Fehler bei der Schätzung von β durch β,
e0 := yb0 − y0 = x0 0 βb − (x0 0 β + u0 ) = x0 0 (βb − β) − u0
zusätzlich die zufällige Schwankung von u0 ∼ N(0, σ 2 ) enthält.
[
Für die Varianz des Prognosefehlers eE erhält man (da E(E(y
0 ) − E(y0 )) = 0)
σe2E
h
i
0 b
2
[
:= Var(eE ) = Var(E(y0 ) − E(y0 )) = E [x0 (β − β)]
h
i
h
i
(!)
0 b
0 b
0
0 b
0
b
= E (x0 (β − β))(x0 (β − β)) = E x0 (β − β)(β − β) x0
b 0 = σ 2 x0 0 (X0 X)−1 x0 .
= x0 0 V(β)x
Ökonometrie (SS 2014)
Folie 214
4 Multiple lineare Regression
Punkt- und Intervallprognosen 4.4
Punkt- und Intervallprognosen IV
Für die Varianz des Prognosefehlers e0 erhält man (wegen E(b
y0 − y0 ) = 0,
E(βb − β) = 0 und E(u0 ) = 0)
h
i
2
0 b
2
σe0 := Var(e0 ) = Var(b
y0 − y0 ) = E [x0 (β − β) − u0 ]
h
i
0 b
2
0 b
2
= E [x0 (β − β)] − 2x0 (β − β)u0 + u0
h
i
h
i
0
0 b
2
b
= E [x0 (β − β)] −2x0 E (β − β)u0 + E(u02 )
{z
}
{z
} | {z2 }
|
|
=σ 2 x0 0 (X0 X)−1 x0
=σ
b
=Cov(β−β,u
0 )=0
= σ 2 1 + x0 0 (X0 X)−1 x0 .
Ökonometrie (SS 2014)
Folie 215
4 Multiple lineare Regression
Punkt- und Intervallprognosen 4.4
Punkt- und Intervallprognosen V
[
b
Wegen der Linearität von yb0 bzw. E(y
0 ) in β überträgt sich die
[
Normalverteilungseigenschaft von βb auf yb0 bzw. E(y
0 ), es gilt also
yb0 ∼ N y0 , σe20
2
[
E(y
0 ) ∼ N E(y0 ), σeE
bzw.
.
Wie im einfachen linearen Regressionsmodell muss das unbekannte σ 2 durch
c2 geschätzt werden, mit
σ
c2 e := σ
c2 1 + x0 0 (X0 X)−1 x0 σ
0
erhält man mit σ
be0 :=
q
bzw.
c2 e und σ
σ
beE :=
0
yb0 − y0
∼ t(n − (K + 1))
σ
be0
bzw.
q
c2 e := σ
c2 x0 0 (X0 X)−1 x0
σ
E
c2 e die Verteilungsaussagen
σ
E
[
E(y
0 ) − E(y0 )
∼ t(n − (K + 1)) ,
σ
beE
aus denen sich Prognoseintervalle für y0 und E(y0 ) konstruieren lassen.
Ökonometrie (SS 2014)
Folie 216
4 Multiple lineare Regression
Punkt- und Intervallprognosen 4.4
Punkt- und Intervallprognosen VI
Intervallprognosen für y0 zur Vertrauenswahrscheinlichkeit 1 − α erhält man
also in der Form
h
i
yb0 − tn−(K +1);1− α2 · σ
be0 , yb0 + tn−(K +1);1− α2 · σ
be0
h
i
√
√
0 (X0 X)−1 x , x 0 β+t
0 (X0 X)−1 x
b
b
α
α
·b
σ
·b
σ
1+x
1+x
= x0 0 β−t
.
0
0
0
0
0
n−(K +1);1−
n−(K +1);1−
2
2
Intervallprognosen für E(y0 ) zur Vertrauenswahrscheinlichkeit 1 − α (auch
interpretierbar als Konfidenzintervalle zum Konfidenzniveau 1 − α für E(y0 ))
erhält man entsprechend in der Form
h
i
[
[
α
α
E(y0 ) − tn−(K +1);1− 2 · σ
beE , E(y0 ) + tn−(K +1);1− 2 · σ
beE
h
i
√
√
b
b
= x0 0 β−t
σ x0 0 (X0 X)−1 x0 , x0 0 β+t
σ x0 0 (X0 X)−1 x0
n−(K +1);1− α ·b
n−(K +1);1− α ·b
2
2
.
Ökonometrie (SS 2014)
Folie 217
4 Multiple lineare Regression
Punkt- und Intervallprognosen 4.4
Punkt- und Intervallprognosen VII
Eine Punktprognose für die (erwartete) Lohnhöhe eines 38-jährigen
Mitarbeiters, der nach dem Hauptschulabschluss weitere 4 Ausbildungsjahre
absolviert
hat, erh
0 ält man im geschätzten Modell aus Folie 207 mit
x0 = 1 4 38 als
0b
[
yb0 = E(y
0 ) = x0 β = 1
4


1027.806
38  62.575  = 1680.978 .
10.602
Im Beispiel aus Folie 207 gilt weiterhin

0.4801866
0.0081102
0
−1

0.0079709
(X X) = 0.0081102
−0.0114619 −0.0009366
und σ
b = 237.35.
Ökonometrie (SS 2014)

−0.0114619
−0.0009366
0.0003718
Folie 218
4 Multiple lineare Regression
Punkt- und Intervallprognosen 4.4
Punkt- und Intervallprognosen VIII
Mit
x0 0 (X0 X)−1 x0 = 1
4

0.4801866
38  0.0081102
−0.0114619
= 0.0536441
 
−0.0114619
1
−0.0009366  4 
0.0003718
38
0.0081102
0.0079709
−0.0009366
erhält man weiter
p
√
σ
be0 = σ
b 1 + x0 0 (X0 X)−1 x0 = 237.35 · 1 + 0.0536441 = 243.6331
und
σ
beE = σ
b
p
x0 0 (X0 X)−1 x0 = 237.35 ·
√
0.0536441 = 54.9731 .
Ökonometrie (SS 2014)
Folie 219
4 Multiple lineare Regression
Punkt- und Intervallprognosen 4.4
Punkt- und Intervallprognosen IX
Insgesamt erhält man für α = 0.05 schließlich das Prognoseintervall
h
i
yb0 − t20−(2+1);1− 0.05 · σ
be0 , yb0 + t20−(2+1);1− 0.05 · σ
be0
2
2
= [yb0 − t17;0.975 · σ
be0 , yb0 + t17;0.975 · σ
be0 ]
= [1680.978 − 2.1098 · 243.6331 , 1680.978 + 2.1098 · 243.6331]
= [1166.961 , 2194.995]
zur Vertrauenswahrscheinlichkeit 1 − α = 0.95 für y0 gegeben x10 = 4 und
x20 = 38.
Entsprechend erhält man für α = 0.05 das Prognoseintervall
h
i
[
[
E(y0 ) − t20−(2+1);1− 0.05
·σ
beE , E(y0 ) + t20−(2+1);1− 0.05
·σ
beE
2
2
= [1680.978 − 2.1098 · 54.9731 , 1680.978 + 2.1098 · 54.9731]
= [1564.996 , 1796.96]
zur Vertrauenswahrscheinlichkeit 1 − α = 0.95 für E(y0 ) gegeben x10 = 4 und
x20 = 38.
Ökonometrie (SS 2014)
Folie 220
4 Multiple lineare Regression
Tests einzelner linearer Hypothesen 4.5
Tests einzelner linearer Hypothesen I
Neben Tests für einzelne Regressionsparameter sind auch Tests (und
Konfidenzintervalle) für Linearkombinationen von Regressionsparametern
problemlos möglich.
iid
Bei Vorliegen der Normalverteilungseigenschaft ui ∼ N(0, σ 2 ) bzw.
u ∼ N(0, σ 2 In ) gilt bekanntlich
βb ∼ N β, σ 2 (X0 X)−1
,
und auch ohne Normalverteilungsannahme an die ui ist die approximative
Verwendung einer (mehrdimensionalen) Normalverteilung für βb oft sinnvoll.
•
Damit gilt allerdings nicht nur βbk ∼ N(βk , σ 2 ) bzw. βbk ∼ N(βk , σ 2 ) für
k ∈ {0, . . . , K }, sondern darüberhinaus, dass jede beliebige Linearkombination
der Koeffizientenschätzer βb0 , βb1 , . . . , βbK (näherungsweise) normalverteilt ist.
Ökonometrie (SS 2014)
Folie 221
4 Multiple lineare Regression
Tests einzelner linearer Hypothesen 4.5
Tests einzelner linearer Hypothesen II
Tests über einzelne Linearkombinationen von Regressionsparametern lassen
sich mit Hilfe von K + 1 Koeffizienten a0 , a1 , . . . , aK ∈ R für die Parameter
β0 , β1 , . . . , βK sowie einem Skalar c ∈ R in den Varianten
H0 :
K
X
ak βk = c
H0 :
k=0
H1 :
K
X
k=0
K
X
k=0
vs.
ak βk 6= c
H1 :
K
X
ak βk ≤ c
vs.
H1 : a0 β 6= c
ak βk ≥ c
K
X
ak βk < c
k=0
vs.
ak βk > c
H1 :
k=0
vs.
k=0
bzw. in vektorieller Schreibweise mit a := a0
H0 : a0 β = c
H0 :
K
X
a1
···
aK
0
als
H0 : a0 β ≤ c
H0 : a0 β ≥ c
H1 : a0 β > c
H1 : a0 β < c
vs.
vs.
formulieren.
Ökonometrie (SS 2014)
Folie 222
4 Multiple lineare Regression
Tests einzelner linearer Hypothesen 4.5
Tests einzelner linearer Hypothesen III
Mit den bekannten Rechenregeln“ für die Momente von Linearkombinationen
”
eines Zufallsvektors (vgl. Folie 50) erhält man zunächst
a0 βb ∼ N a0 β, σ 2 a0 (X0 X)−1 a
•
bzw. a0 βb ∼ N a0 β, σ 2 a0 (X0 X)−1 a .
Ersetzt man die unbekannte Störgrößenvarianz σ 2 wie üblich durch den
c2 , so erhält man die Verteilungsaussage
(erwartungstreuen) Schätzer σ
a0 βb − a0 β
p
∼ t(n − (K + 1))
σ
b a0 (X0 X)−1 a
bzw.
a0 βb − a0 β
•
p
∼ t(n − (K + 1)) ,
σ
b a0 (X0 X)−1 a
woraus sich in gewohnter Weise Konfidenzintervalle und Tests konstruieren
lassen.
Ökonometrie (SS 2014)
Folie 223
4 Multiple lineare Regression
Tests einzelner linearer Hypothesen 4.5
Zusammenfassung: t-Test für einzelne lineare Hypothesen
im multiplen linearen Regressionsmodell
Anwendungsvoraussetzungen
Nullhypothese
Gegenhypothese
Teststatistik
Verteilung (H0 )
Benötigte Größen
Kritischer Bereich
zum Niveau α
p-Wert
Ökonometrie (SS 2014)
exakt: y = Xβ + u mit u ∼ N(0, σ 2 In ),
approx.: y = Xβ + u mit E(u) = 0, V(u) = σ 2 In ,
σ 2 unbekannt, X deterministisch mit vollem Spaltenrang K + 1,
Realisation y = (y1 , . . . , yn )0 beobachtet
H0 : a0 β = c
H1 : a0 β 6= c
H0 : a0 β ≤ c
H1 : a0 β > c
H0 : a0 β ≥ c
H1 : a0 β < c
b−c
a0 β
p
σ
b a0 (X0 X)−1 a
t für a0 β = c (näherungsweise) t(n − (K + 1))-verteilt
t=
c2 =
b = (X0 X)−1 X0 y, σ
β
(−∞, −tn−(K +1);1− α2 )
∪(tn−(K +1);1− α2 , ∞)
2 · (1 − Ft(n−(K +1)) (|t|))
b
u0 b
u
b
, wobei b
u = y − Xβ
n − (K + 1)
(tn−(K +1);1−α , ∞)
(−∞, −tn−(K +1);1−α )
1 − Ft(n−(K +1)) (t)
Ft(n−(K +1)) (t)
Folie 224
4 Multiple lineare Regression
Tests einzelner linearer Hypothesen 4.5
Beispiel: Test einer einzelnen linearen Hypothese I
Im vorangegangenen Beispiel (Lohnhöhe erklärt durch Ausbildung und Alter)
kann (im korrekt spezifizierten Modell) zum Beispiel getestet werden, ob der
(isolierte) Effekt eines weiteren Ausbildungsjahres mehr als doppelt so groß
wie der (isolierte) Effekt eines zusätzlichen Lebensjahres ist, also ob
β1 > 2 · β2 gilt.
Die passende Hypothesenformulierung lautet in diesem Fall
H0 : β1 − 2 · β2 ≤ 0
gegen
H1 : β1 − 2 · β2 > 0
gegen
H1 : a0 β > c
bzw. in der bisherigen Schreibweise
mit a = 0
1
H0 : a0 β ≤ c
0
−2 und c = 0.
Ökonometrie (SS 2014)
Folie 225
4 Multiple lineare Regression
Tests einzelner linearer Hypothesen 4.5
Beispiel: Test einer einzelnen linearen Hypothese II
Mit (X0 X)−1 und σ
b wie auf Folie 218 angegeben erhält man zunächst

 
0.4801866
0.0081102
−0.0114619
0
0
0
−1
0.0079709 −0.0009366  1 
a (X X) a = 0 1 −2  0.0081102
−0.0114619 −0.0009366 0.0003718
−2
= 0.013204
und mit a0 βb = 0
t=
1


1027.806
−2  62.575  = 41.371 die realisierte Teststatistik
10.602
41.371 − 0
a0 βb − c
p
√
=
= 1.5169 .
237.35 · 0.013204
σ
b a0 (X0 X)−1 a
H0 kann hier zum Signifikanzniveau α = 0.05 nicht abgelehnt werden, da
t = 1.5169 ∈
/ (1.74, ∞) = (t17;0.95 , ∞) = (tn−(K +1);1−α , ∞) = K .
Ökonometrie (SS 2014)
Folie 226
4 Multiple lineare Regression
Konfidenzintervalle für Linearkombinationen 4.6
Konfidenzintervalle für (einzelne) Linearkombinationen
h
Ein (ggf. approximatives) symmetrisches Konfidenzintervall für a0 β zum
Konfidenzniveau 1 − α erhält man auf vergleichbare Art und Weise durch:
a βb − tn−(K +1);1− α2
0
i
p
p
0b
0
0
−1
0
0
−1
·σ
b a (X X) a , a β + tn−(K +1);1− α2 · σ
b a (X X) a
Im vorangegangenen Beispiel erhält
man somit
0 ein Konfidenzintervall für
0
β1 − 2 · β2 , also für a β mit a = 0 1 −2 , zum Konfidenzniveau
1 − α = 0.95 unter Verwendung der bisherigen Zwischenergebnisse sowie von
t17;0.975 = 2.11 durch:
h
i
p
p
0b
0
0
0
−1
0
0
−1
b
a β − tn−(K +1);1− α2 · σ
b a (X X) a , a β + tn−(K +1);1− α2 · σ
b a (X X) a
h
i
√
√
= 41.371 − 2.11 · 237.35 0.013204 , 41.371 + 2.11 · 237.35 0.013204
= [−16.1762 , 98.9182]
Ökonometrie (SS 2014)
Folie 227
4 Multiple lineare Regression
Tests mehrerer linearer Hypothesen 4.7
(Simultane) Tests mehrerer linearer Hypothesen I
Neben einzelnen linearen Hypothesen können auch mehrere lineare
Hypothesen simultan überprüft werden.
Die Nullhypothese H0 solcher Tests enthält L lineare
(Gleichheits-)Restriktionen in der Gestalt
a10 β0 + a11 β1 + . . . + a1K βK = c1
a20 β0 + a21 β1 + . . . + a2K βK = c2
..
..
..
.
.
.
aL0 β0 + aL1 β1 + . . . + aLK βK = cL
bzw.
K
X
k=0
Ökonometrie (SS 2014)
alk βk = cl
für l ∈ {1, . . . , L} .
Folie 228
4 Multiple lineare Regression
Tests mehrerer linearer Hypothesen 4.7
(Simultane) Tests mehrerer linearer Hypothesen II
0
Mit dem L-dimensionalen Vektor c := c1 · · · cL und der
(L × (K + 1))-Matrix


a10 a11 · · · a1K

..
.. 
A :=  ...
.
. 
aL0 aL1 · · · aLK
lässt sich die Nullhypothese auch als Aβ = c schreiben.
H1 ist (wie immer) genau dann erfüllt, wenn H0 verletzt ist, hier also wenn
mindestens eine Gleichheitsrestriktion nicht gilt.
Da Vektoren genau dann übereinstimmen, wenn alle Komponenten gleich
sind, kann das Hypothesenpaar also in der Form
H0 : Aβ = c
gegen
H1 : Aβ 6= c
kompakt notiert werden.
Ökonometrie (SS 2014)
4 Multiple lineare Regression
Folie 229
Tests mehrerer linearer Hypothesen 4.7
(Simultane) Tests mehrerer linearer Hypothesen III
Zur Konstruktion eines Hypothesentests fordert man zunächst, dass A weder
redundante noch zu viele“ Linearkombinationen enthält, dass A also vollen
”
Zeilenrang L besitzt.
Eine geeignete Testgröße zur gemeinsamen Überprüfung der L linearen
Restriktionen aus der Nullhypothese ist dann
.
0
−1 0 −1
0
b
b
(Aβ − c) A(X X) A
(Aβ − c) L
F =
b0 u
b/(n − (K + 1))
u
h
i−1
0 c
0
−1 0
2
b
(Aβ − c) σ A(X X) A
(Aβb − c)
=
.
L
Man kann zeigen, dass F bei Gültigkeit von H0 : Aβ = c unter den
bisherigen Annahmen (einschließlich der Annahme u ∼ N(0, σ 2 In )) einer
sogenannten F -Verteilung mit L Zähler- und n − (K + 1)
Nennerfreiheitsgraden folgt, in Zeichen F ∼ F (L, n − (K + 1)).
Ökonometrie (SS 2014)
Folie 230
4 Multiple lineare Regression
Tests mehrerer linearer Hypothesen 4.7
(Simultane) Tests mehrerer linearer Hypothesen IV
Die F -Statistik aus Folie 230 ist im Wesentlichen eine (positiv definite)
quadratische Form in den empirischen Verletzungen“ Aβb − c der
”
Nullhypothese.
Besonders große Werte der F -Statistik sprechen also gegen die Gültigkeit der
Nullhypothese.
Entsprechend bietet sich als kritischer Bereich zum Signifikanzniveau α
K = (FL,n−(K +1);1−α , ∞)
an, wobei mit Fm,n;p das p-Quantil der F (m, n)-Verteilung (F -Verteilung mit
m Zähler- und n Nennerfreiheitsgraden) bezeichnet ist.
Auch bei Verletzung der Normalverteilungsannahme ist eine approximative
Annahme der F (L, n − (K + 1))-Verteilung (unter H0 !) und damit ein
approximativer Test sinnvoll.
Ökonometrie (SS 2014)
Folie 231
4 Multiple lineare Regression
Tests mehrerer linearer Hypothesen 4.7
Grafische Darstellung einiger F (m, n)-Verteilungen
für m, n ∈ {2, 5, 10}
0.0
0.2
0.4
f(x)
0.6
0.8
1.0
F(2, 2)
F(5, 2)
F(10, 2)
F(2, 5)
F(5, 5)
F(10, 5)
F(2, 10)
F(5, 10)
F(10, 10)
0
1
2
3
4
x
Ökonometrie (SS 2014)
Folie 232
4 Multiple lineare Regression
Tests mehrerer linearer Hypothesen 4.7
0.95-Quantile der F (m, n)-Verteilungen Fm,n;0.95
n\m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
30
40
50
100
150
1
161.448
18.513
10.128
7.709
6.608
5.987
5.591
5.318
5.117
4.965
4.844
4.747
4.667
4.600
4.543
4.494
4.451
4.414
4.381
4.351
4.171
4.085
4.034
3.936
3.904
2
199.500
19.000
9.552
6.944
5.786
5.143
4.737
4.459
4.256
4.103
3.982
3.885
3.806
3.739
3.682
3.634
3.592
3.555
3.522
3.493
3.316
3.232
3.183
3.087
3.056
3
215.707
19.164
9.277
6.591
5.409
4.757
4.347
4.066
3.863
3.708
3.587
3.490
3.411
3.344
3.287
3.239
3.197
3.160
3.127
3.098
2.922
2.839
2.790
2.696
2.665
4
224.583
19.247
9.117
6.388
5.192
4.534
4.120
3.838
3.633
3.478
3.357
3.259
3.179
3.112
3.056
3.007
2.965
2.928
2.895
2.866
2.690
2.606
2.557
2.463
2.432
5
230.162
19.296
9.013
6.256
5.050
4.387
3.972
3.687
3.482
3.326
3.204
3.106
3.025
2.958
2.901
2.852
2.810
2.773
2.740
2.711
2.534
2.449
2.400
2.305
2.274
6
233.986
19.330
8.941
6.163
4.950
4.284
3.866
3.581
3.374
3.217
3.095
2.996
2.915
2.848
2.790
2.741
2.699
2.661
2.628
2.599
2.421
2.336
2.286
2.191
2.160
7
236.768
19.353
8.887
6.094
4.876
4.207
3.787
3.500
3.293
3.135
3.012
2.913
2.832
2.764
2.707
2.657
2.614
2.577
2.544
2.514
2.334
2.249
2.199
2.103
2.071
8
238.883
19.371
8.845
6.041
4.818
4.147
3.726
3.438
3.230
3.072
2.948
2.849
2.767
2.699
2.641
2.591
2.548
2.510
2.477
2.447
2.266
2.180
2.130
2.032
2.001
Ökonometrie (SS 2014)
Folie 233
4 Multiple lineare Regression
Tests mehrerer linearer Hypothesen 4.7
Zusammenfassung: F -Test für L ≥ 1 lineare Restriktionen
im multiplen linearen Regressionsmodell
Anwendungsvoraussetzungen
exakt: y = Xβ + u mit u ∼ N(0, σ 2 In ),
approx.: y = Xβ + u mit E(u) = 0, V(u) = σ 2 In ,
σ 2 unbekannt, X deterministisch mit vollem Spaltenrang K + 1,
Realisation y = (y1 , . . . , yn )0 beobachtet, c ∈ RL ,
(L × (K + 1))-Matrix A mit vollem Zeilenrang L
Nullhypothese
Gegenhypothese
Teststatistik
Verteilung (H0 )
Benötigte Größen
Kritischer Bereich
zum Niveau α
p-Wert
Ökonometrie (SS 2014)
F =
H0 : Aβ = c
H1 : Aβ 6= c
h
i−1
c2 A(X0 X)−1 A0
b − c)0 σ
b − c)
(Aβ
(Aβ
L
F ist (approx.) F (L, n − (K + 1))-verteilt, falls Aβ = c
c2 =
b = (X0 X)−1 X0 y, σ
β
b
u0 b
u
b
, wobei b
u = y − Xβ
n − (K + 1)
(FL,n−(K +1);1−α , ∞)
1 − FF (L,n−(K +1)) (F )
Folie 234
4 Multiple lineare Regression
Tests mehrerer linearer Hypothesen 4.7
Ein spezieller F -Test
auf Signifikanz des Erklärungsansatzes“
”
Eine spezielle, häufig verwendete Ausgestaltung des F -Tests überprüft
(simultan), ob mindestens ein Regressor einen (signifikanten) Effekt auf den
Regressanden hat.
Die Hypothesen lauten also:
H0 : β1 = . . . = βK = 0
gegen H1 : βk 6= 0 für mind. ein k ∈ {1, . . . , K }
Die realisierte Teststatistik zu diesem Test, die Anzahl der (Zähler- und
Nenner-)Freiheitsgrade der (F -)Verteilung unter H0 sowie der p-Wert der
realiserten Teststatistik sind üblicherweise Bestandteil von Regressionsoutputs
zu Schätzungen linearer Modelle mit Statistik-Software.
In der Schätzung des korrekt spezifizierten Modells aus Folie 207 liest man
beispielsweise die realisierte Teststatistik F = 15.29, 2 Zähler- und 17
Nennerfreiheitsgrade der F -Verteilung unter H0 sowie den p-Wert 0.0001587
ab.
Ökonometrie (SS 2014)
Folie 235
4 Multiple lineare Regression
Tests mehrerer linearer Hypothesen 4.7
Alternative Darstellungen der F -Statistik I
Es kann gezeigt werden, dass man unter den getroffenen Annahmen die
realisierte F -Statistik auch berechnen kann, in dem man neben dem
eigentlichen unrestringierten“ Regressionsmodell das sogenannte
”
restringierte“ Regressionsmodell schätzt und die Ergebnisse vergleicht.
”
Die Schätzung des restringierten Modells erfolgt als Lösung des
ursprünglichen KQ-Optimierungsproblems unter der Nebenbedingung
Aβ = c.
Werden mit RSS0 die Summe der quadrierten Residuen bzw. mit R02 das
Bestimmtheitsmaß der restringierten Modellschätzung bezeichnet, lässt sich
die F -Statistik auch als
(RSS0 − RSS)/L
(R 2 − R02 )/L
F =
=
RSS/(n − (K + 1))
(1 − R 2 )/(n − (K + 1))
darstellen, wenn mit RSS, R 2 bzw. K wie üblich die Summe der quadrierten
Residuen, das Bestimmtheitsmaß bzw. die Anzahl der Regressoren des
unrestringierten Modells bezeichnet werden und L die Anzahl der linearen
Restriktionen (Anzahl der Zeilen von A) ist.
Ökonometrie (SS 2014)
Folie 236
4 Multiple lineare Regression
Tests mehrerer linearer Hypothesen 4.7
Alternative Darstellungen der F -Statistik II
Insbesondere wenn die linearen Restriktionen im Ausschluss einiger der
Regressoren bestehen, die Nullhypothese also die Gestalt
für j ∈ J ⊆ {1, . . . , K }
H0 : βj = 0
mit |J| = L
besitzt, kann die Schätzung des restringierten Modells natürlich durch die
Schätzung des entsprechend verkleinerten Regressionsmodells erfolgen.
Im bereits betrachteten Spezialfall J = {1, . . . , K } bzw.
H0 : β1 = . . . = βK = 0
gegen H1 : βk 6= 0 für mind. ein k ∈ {1, . . . , K }
gilt offensichtlich R02 = 0, damit kann die F -Statistik ohne weitere Schätzung
auch durch
R 2 /K
F =
(1 − R 2 )/(n − (K + 1))
ausgewertet werden.
Ökonometrie (SS 2014)
Folie 237
4 Multiple lineare Regression
Konfidenzellipsen 4.8
Konfidenzellipsen für mehrere Parameter I
Konfidenzintervalle für einen Regressionsparameter βk zur
Vertrauenswahrscheinlichkeit 1 − α bestehen aus genau den hypothetischen
Parameterwerten βk0 , zu denen ein (zweiseitiger) Signifikanztest zum
Signifikanzniveau α (mit H0 : βk = βk0 ) die Nullhypothese nicht ablehnt.
Dieses Konzept lässt sich problemlos auf Konfidenzbereiche (simultan) für
mehrere Regressionsparameter erweitern; wegen der resultierenden Gestalt
werden diese Konfidenzellipsen oder ggf. Konfidenzellipsoide genannt.
Für eine Teilmenge J = {j1 , . . . , jL } ⊆ {0, . . . , K } mit |J| = L enthält also ein
Konfidenzbereich für den Parameter(teil)vektor (βj1 , . . . , βjL )0 zum
Konfidenzniveau 1 − α genau die Vektoren (βj01 , . . . , βj0L )0 , für die ein F -Test
zum Signifikanzniveau α mit
H0 : βj1 = βj01 ∧ . . . ∧ βjL = βj0L
diese Nullhypothese nicht verwirft.
Ökonometrie (SS 2014)
Folie 238
4 Multiple lineare Regression
Konfidenzellipsen 4.8
Konfidenzellipsen für mehrere Parameter II
Da der F -Test H0 genau dann nicht verwirft, wenn für die Teststatistik
F =
h
i−1
0 c
0
−1 0
2
b
(Aβ − c) σ A(X X) A
(Aβb − c)
L
≤ FL,n−(K +1);1−α
gilt, wird der Konfidenzbereich zum Niveau 1 − α also durch die Menge
h
i−1
c2 A(X0 X)−1 A0
c ∈ RL (Aβb − c)0 σ
(Aβb − c) ≤ L · FL,n−(K +1);1−α
beschrieben, wobei die Matrix A aus L Zeilen besteht und die Zeile l jeweils
in der (zu βjl gehörenden) (jl + 1)-ten Spalte den Eintrag 1 hat und sonst nur
Nullen beinhaltet.
Konfidenzellipsen bzw. -ellipsoide sind auch für mehrere Linearkombinationen
der Regressionsparameter als Verallgemeinerung der Konfidenzintervalle für
einzelne Linearkombinationen ganz analog konstruierbar, es muss lediglich die
entsprechende (allgemeinere) Matrix A eingesetzt werden.
Ökonometrie (SS 2014)
Folie 239
4 Multiple lineare Regression
Konfidenzellipsen 4.8
Beispiel: Konfidenzellipse für β1 und β2
10
●
0
5
Alter β2
15
20
im korrekt spezifizierten Modell von Folie 207, 1 − α = 0.95
20
40
60
80
100
120
Ausbildung β1
Ökonometrie (SS 2014)
Folie 240
4 Multiple lineare Regression
Multikollinearität 4.9
Multikollinearität
Erinnerung: Unter der (gemäß Modellannahmen ausgeschlossenen) perfekten
Multikollinearität versteht man eine perfekte lineare Abhängigkeit unter den
Regressoren (einschließlich des Absolutglieds“).
”
Bei perfekter Multikollinearität ist eine Schätzung des Modells mit dem
vorgestellten Verfahren nicht möglich.
Im Unterschied zur perfekten Multikollinearität spricht man von imperfekter
Multikollinearität, wenn die Regressoren (einschließlich des Absolutglieds“)
”
beinahe (in einem noch genauer zu spezifizierenden Sinn!) lineare
Abhängigkeiten aufweisen.
Eine (konventionelle) Schätzung des Modells ist dann (abgesehen von
numerischen Schwierigkeiten in sehr extremen Fällen) möglich, die Ergebnisse
können aber (i.d.R. unerwünschte) Besonderheiten aufweisen.
Ökonometrie (SS 2014)
4 Multiple lineare Regression
Folie 241
Multikollinearität 4.9
Perfekte Multikollinearität I
Perfekte Multikollinearität tritt in linearen Modellen mit Absolutglied (wie
hier betrachtet) zum Beispiel dann auf, wenn Modelle mit sog.
Dummy-Variablen falsch spezifiziert werden.
Unter Dummy-Variablen versteht man Regressoren, die nur die Werte 0 und 1
annehmen.
Oft werden nominalskalierte Regressoren mit Hilfe von Dummy-Variablen in
lineare Modelle einbezogen, indem den vorhandenen (!) Ausprägungen
separate Dummy-Variablen zugeordnet werden, die jeweils den Wert 1
annehmen, wenn die entsprechende Ausprägung vorliegt, und 0 sonst.
Wird zu jeder vorhandenen Ausprägung eine solche Dummy-Variable
definiert, hat offensichtlich immer genau eine der Dummy-Variablen den Wert
1, alle anderen den Wert 0.
Damit ist aber offensichtlich die Summe über alle Dummy-Variablen stets
gleich 1 und damit identisch mit dem (und insbesondere linear abhängig zum)
Absolutglied.
Ökonometrie (SS 2014)
Folie 242
4 Multiple lineare Regression
Multikollinearität 4.9
Perfekte Multikollinearität II
Lösung: (Genau) eine Dummy-Variable wird weggelassen.
Damit nimmt die zu dieser Dummy-Variablen gehörende Ausprägung des
Merkmals eine Art Benchmark“ oder Bezugsgröße ein.
”
Die Koeffizienten vor den im Modell verbliebenen Dummy-Variablen zu den
anderen Merkmalsausprägungen sind dann als Änderung gegenüber dieser
Benchmark zu interpretieren, während der Effekt“ der Benchmark selbst im
”
Absolutglied enthalten (und ohnehin nicht separat zu messen) ist.
Beispiel: Einbeziehung des Merkmals Geschlecht“ mit den beiden (auch im
”
Datensatz auftretenden!) Ausprägungen weiblich und männlich mit Hilfe
einer Dummy-Variablen weiblich (oder alternativ männlich) ist korrekt,
während Aufnahme der beiden Variablen weiblich und männlich
zwangsläufig zu perfekter Multikollinearität führt.
Lineare Abhängigkeiten zwischen Regressoren können auch ohne (fehlerhafte)
Verwendung von Dummy-Variablen auftreten.
Ökonometrie (SS 2014)
Folie 243
4 Multiple lineare Regression
Multikollinearität 4.9
Perfekte Multikollinearität III
Beispiel 1: Sind in einem Modell die Regressoren durchschnittl.
”
Monatseinkommen“ (Monat), Jahressonderzahlung“ (Sonderzahlung) und
”
Jahreseinkommen“ (Jahr) enthalten, besteht wegen des Zusammenhangs
”
Jahr = 12 · Monat + Sonderzahlung
offensichtlich perfekte Multikollinearität.
Beispiel 2: Sind gleichzeitig die Regressoren Nettoeinnahmen mit reduz.
”
MWSt.“ (NettoReduziert), Nettoeinnahmen mit regul. MWSt.“
”
(NettoRegulär) und Bruttoeinnahmen“ (Brutto) enthalten, besteht wegen
”
des Zusammenhangs
Brutto = 1.07 · NettoReduziert + 1.19 · NettoRegulär
ebenfalls perfekte Multikollinearität.
Lösung: Eine der Variablen im linearen Zusammenhang weglassen (wird von
Statistik-Software meist automatisch erledigt).
Ökonometrie (SS 2014)
Folie 244
4 Multiple lineare Regression
Multikollinearität 4.9
Beispiel: Imperfekte Multikollinearität I
Imperfekte Multikollinearität kann im Beispiel 1 aus Folie 244 auch nach
Elimination des Regressors Jahr auftreten:
Oft ist die Jahressonderzahlung (mehr oder weniger) linear vom
durchschnittlichen Monatseinkommen abhängig ( 13. Monatsgehalt“). Dies
”
kann zu beinahe“ linearen Abhängigkeiten zwischen den Regressoren führen.
”
In einem (fiktiven) linearen Modell werden die monalichen Ausgaben für
Nahrungs- und Genussmittel in Haushalten (NuG) durch die Anzahl Personen
im Haushalt (Personen), das durchschn. Monatseinkommen (Monat) und die
jährliche Sonderzahlung (Sonderzahlung) erklärt.
Im (ebenfalls fiktiven) Datensatz der Länge n = 25 beträgt die Korrelation
zwischen den Regressoren Monat und Sonderzahlung 0.972, wie auch im
folgenden Plot visualisiert ist.
Ökonometrie (SS 2014)
Folie 245
4 Multiple lineare Regression
Multikollinearität 4.9
Beispiel: Imperfekte Multikollinearität II
Darstellung der Regressoren Monat und Sonderzahlung
5000
Punktwolke der Regressoren Monat und Sonderzahlung
●●
4500
●
●
●
●
●
3500
●
●
3000
●
●
●
●
●
2500
Sonderzahlung x3i
4000
●
●
●
2000
●
●
●
●
1500
●
●
●
●
1500
2000
2500
3000
3500
4000
4500
5000
Monat x2i
Ökonometrie (SS 2014)
Folie 246
4 Multiple lineare Regression
Multikollinearität 4.9
Beispiel: Imperfekte Multikollinearität III
Schätzergebnisse des vollständigen Modells
Call:
lm(formula = NuG ~ Personen + Monat + Sonderzahlung)
Residuals:
Min
1Q
-268.49 -109.97
Median
-0.13
3Q
122.96
Max
248.30
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)
61.44311 124.97001
0.492
0.628
Personen
159.57520
29.13033
5.478 1.96e-05 ***
Monat
0.17848
0.11854
1.506
0.147
Sonderzahlung
0.07205
0.12413
0.580
0.568
--Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 153.3 on 21 degrees of freedom
Multiple R-squared: 0.8242, Adjusted R-squared: 0.7991
F-statistic: 32.82 on 3 and 21 DF, p-value: 4.097e-08
Ökonometrie (SS 2014)
4 Multiple lineare Regression
Folie 247
Multikollinearität 4.9
Beispiel: Imperfekte Multikollinearität IV
In der Schätzung des vollständigen Modells ist nur der Koeffizient des
Regressors Personen signifikant von Null verschieden (zu gängigen
Signifikanzniveaus).
Insbesondere die (geschätzten) Koeffizienten zu den Regressoren Monat und
Sonderzahlung sind zwar (wie zu erwarten) positiv, durch die
vergleichsweise großen Standardfehler jedoch insignifikant.
Es liegt die Vermutung nahe, dass die Schätzung der Koeffizienten deshalb so
ungenau“ ausfällt, weil die Effekte der beiden Regressoren wegen der hohen
”
Korrelation im linearen Modellansatz kaum zu trennen sind.
Die imperfekte, aber große (lineare) Abhängigkeit der beiden Regressoren
Monat und Sonderzahlung überträgt sich auf einen stark ausgeprägten
(negativen!) Zusammenhang der Koeffizientenschätzer zu diesen Regressoren,
was sich auch in Konfidenzellipsen zu den entsprechenden Parametern
widerspiegelt:
Ökonometrie (SS 2014)
Folie 248
4 Multiple lineare Regression
Multikollinearität 4.9
Beispiel: Imperfekte Multikollinearität V
0.1
0.0
●
−0.2
−0.1
Sonderzahlung β3
0.2
0.3
0.4
Konfidenzellipse (1 − α = 0.95) für β2 und β3 im vollständigen Modell
−0.1
0.0
0.1
0.2
0.3
0.4
0.5
Monat β2
Ökonometrie (SS 2014)
Folie 249
4 Multiple lineare Regression
Multikollinearität 4.9
Beispiel: Imperfekte Multikollinearität VI
Bei Betrachtung der Konfidenzellipse fällt auf, dass die Ellipse sehr flach“ ist.
”
Grund hierfür ist die bereits erwähnte starke negative (geschätzte)
Korrelation der Schätzfunktionen βb2 und βb3 , die sich aus der geschätzten
Varianz-Kovarianzmatrix


15617.50443 −2322.95496 −3.52136 0.76131
−2322.95496
848.57606
0.76545 −0.69665
b
b


V(β) = 
−3.52136
0.76545
0.01405 −0.01431
0.76131
−0.69665
−0.01431 0.01541
−0.01431
= −0.973 errechnen lässt.
0.01405 · 0.01541
Fasst man die Regressoren Monat und Sonderzahlung in dem Regressor
d βb2 , βb3 ) = √
als Korr(
Jahr = 12 · Monat + Sonderzahlung
zusammen, erhält man folgende Ergebnisse:
Ökonometrie (SS 2014)
Folie 250
4 Multiple lineare Regression
Multikollinearität 4.9
Beispiel: Imperfekte Multikollinearität VII
Modell mit Regressor Jahr statt Regressoren Monat und Sonderzahlung
Call:
lm(formula = NuG ~ Personen + Jahr)
Residuals:
Min
1Q
-263.159 -109.291
Median
5.702
3Q
121.542
Max
262.347
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 58.0719
122.3825
0.475
0.64
Personen
162.0057
28.0344
5.779 8.18e-06 ***
Jahr
0.0190
0.0021
9.044 7.27e-09 ***
--Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 150.5 on 22 degrees of freedom
Multiple R-squared: 0.8227, Adjusted R-squared: 0.8066
F-statistic: 51.04 on 2 and 22 DF, p-value: 5.449e-09
Ökonometrie (SS 2014)
4 Multiple lineare Regression
Folie 251
Multikollinearität 4.9
Beispiel: Imperfekte Multikollinearität VIII
Nun ist auch der Koeffizient zum (aggregierten) Regressor Jahr (hoch)
signifikant von Null verschieden (und wie zu erwarten positiv).
Trotz der Reduzierung der Zahl der Regressoren bleibt der Anteil der
erklärten Varianz beinahe unverändert, das adjustierte Bestimmtheitsmaß
vergrößert sich sogar.
Nicht wesentlich andere Resultate sind zu beobachten, wenn man einen der
Regressoren Monat oder Sonderzahlung aus dem ursprünglichen Modell
entfernt.
Ist das Weglassen von Regressoren oder eine Umspezifikation des Modells
möglich und sinnvoll, kann man das Problem der (imperfekten)
Multikollinearität also dadurch umgehen.
Ansonsten kann man den bisher dargestellten Folgen von imperfekter
Multikollinearität nur durch einen vergrößerten Stichprobenumfang
entgegenwirken.
Ökonometrie (SS 2014)
Folie 252
4 Multiple lineare Regression
Multikollinearität 4.9
Beispiel: Imperfekte Multikollinearität IX
Modell ohne Regressor Sonderzahlung
Call:
lm(formula = NuG ~ Personen + Monat)
Residuals:
Min
1Q
-261.656 -109.348
Median
7.655
3Q
109.174
Max
267.646
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 57.88292 122.92403
0.471
0.642
Personen
162.83304
28.15048
5.784 8.08e-06 ***
Monat
0.24538
0.02726
9.003 7.88e-09 ***
--Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 151 on 22 degrees of freedom
Multiple R-squared: 0.8214, Adjusted R-squared: 0.8052
F-statistic: 50.59 on 2 and 22 DF, p-value: 5.901e-09
Ökonometrie (SS 2014)
Folie 253
4 Multiple lineare Regression
Multikollinearität 4.9
Beispiel: Imperfekte Multikollinearität X
Modell ohne Regressor Monat
Call:
lm(formula = NuG ~ Personen + Sonderzahlung)
Residuals:
Min
1Q
-299.94 -113.54
Median
25.03
3Q
87.79
Max
293.15
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept)
106.1682
124.8342
0.850
0.404
Personen
149.8531
29.2120
5.130 3.85e-05 ***
Sonderzahlung
0.2538
0.0298
8.515 2.06e-08 ***
--Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 157.7 on 22 degrees of freedom
Multiple R-squared: 0.8052, Adjusted R-squared: 0.7875
F-statistic: 45.48 on 2 and 22 DF, p-value: 1.53e-08
Ökonometrie (SS 2014)
Folie 254
4 Multiple lineare Regression
Multikollinearität 4.9
Beispiel: Imperfekte Multikollinearität XI
Das Vorliegen von imperfekter Multikollinearität bedeutet im Übrigen nicht,
dass die Resultate der Schätzung nicht mehr nützlich oder gar falsch sind,
insbesondere bleiben verwertbare Prognosen meist möglich.
Im vollständigen Modell erhält man außerdem beispielsweise mit dem
Konfidenzintervall zum Konfidenzniveau
1 − α = 0.95 für die Summe
0
0
β2 + β3 , also für a β mit a = 0 0 1 1 , mit
[0.1781, 0.3219]
eine deutlich präzisere Schätzung als für die einzelnen Koeffizienten
β2 (Konfidenzintervall zum Niveau 1 − α = 0.95: [−0.0681, 0.425]) und
β3 (Konfidenzintervall zum Niveau 1 − α = 0.95: [−0.1861, 0.3302]).
Werden die schlecht zu trennenden“ Effekte also (z.B. durch geeignete
”
Linearkombination) zusammengefasst, sind wieder präzisere Schlüsse möglich.
Auch die Frage, ob wenigstens einer der Koeffizienten β2 bzw. β3 signifikant
(α = 0.05) von Null verschieden ist, kann mit einem Blick auf die
Konfidenzellipse auf Folie 249 (oder mit einem passenden F -Test) klar positiv
beantwortet werden.
Ökonometrie (SS 2014)
Folie 255
4 Multiple lineare Regression
Multikollinearität 4.9
Messung von imperfekter Multikollinearität I
Ausstehend ist noch die präzisere Festlegung einer Schwelle für die lineare
Abhängigkeit zwischen den Regressoren, ab der man üblicherweise von
imperfekter Multikollinearität spricht.
Man benötigt zunächst ein Maß für die lineare Abhängigkeit der Regressoren.
Dazu setzt man zunächst jeden der K (echten) Regressoren separat als
abhängige Variable in jeweils ein neues Regressionsmodell ein und verwendet
als unabhängige, erklärende Variablen jeweils alle übrigen Regressoren in der
folgenden Gestalt:
x1i = γ0
+ γ2 x2i + γ3 x3i + . . . + γK −1 x(K −1)i + γK xKi + ui ,
x2i = γ0 + γ1 x1i
..
..
.
.
+ γ3 x3i + . . . + γK −1 x(K −1)i + γK xKi + ui ,
..
..
.
.
x(K −1)i = γ0 + γ1 x1i + γ2 x2i + γ3 x3i + . . .
xKi = γ0 + γ1 x1i + γ2 x2i + γ3 x3i + . . . + γK −1 x(K −1)i
Ökonometrie (SS 2014)
+ γK xKi + ui ,
+ ui .
Folie 256
4 Multiple lineare Regression
Multikollinearität 4.9
Messung von imperfekter Multikollinearität II
Die K resultierenden Bestimmtheitsmaße Rk2 (k ∈ {1, . . . , K }) werden dann
verwendet, um die sogenannten Varianz-Inflations-Faktoren (VIF)
VIFk :=
1
1 − Rk2
zu definieren.
Offensichtlich gilt VIFk ≥ 1, und VIFk wächst mit zunehmendem Rk2
(es gilt genauer VIFk = 1 ⇐⇒ Rk2 = 0 und VIFk → ∞ ⇐⇒ Rk2 → 1).
Sind Regressoren mit einem Varianz-Inflations-Faktor von mehr als 10 im
Modell enthalten, spricht man in der Regel vom Vorliegen von imperfekter
Multikollinearität oder vom Multikollinearitätsproblem, es existieren aber
auch einige andere Faustregeln“.
”
Ökonometrie (SS 2014)
Folie 257
4 Multiple lineare Regression
Multikollinearität 4.9
Messung von imperfekter Multikollinearität III
In der Darstellung (mit den Abkürzung x k und skk aus Folie 191)
d βbk ) =
Var(
c2
c2
σ
σ
· VIFk = Pn
· VIFk
2
n · skk
(x
−
x
)
ki
k
i=1
der geschätzten Varianz der Parameterschätzer βbk ist die Bezeichnung
Varianz-Inflations-Faktor“ selbsterklärend.
”
In der im Beispiel durchgeführten Schätzung des vollständigen Modells
ergeben sich die folgenden Varianz-Inflations-Faktoren:
Regressor
VIF
Personen
Monat
Sonderzahlung
1.062
18.765
18.531
Nach der oben genannten Faustregel“ liegt also ein Multikollinearitätsproblem
”
bei den Regressoren Monat und Sonderzahlung vor.
Ökonometrie (SS 2014)
Folie 258
4 Multiple lineare Regression
Heteroskedastische Störgrößen 4.10
Heteroskedastie der Störgrößen I
Die Annahme 2 an die Störgrößen ui auf Folie 186 lautet Var(ui ) = σ 2 für
alle i ∈ {1, . . . , n}, es wird also die Gleichheit aller Störgrößenvarianzen
gefordert.
Die Gleichheit der Varianz mehrerer Zufallsvariablen wird auch als
Homoskedastie oder Homoskedastizität dieser Zufallsvariablen bezeichnet.
Man spricht bei Erfüllung der Annahme 2 an die Störgrößen damit auch von
homoskedastischen Störgrößen.
Das Gegenteil von Homoskedastie wird mit Heteroskedastie oder
Heteroskedastizität bezeichnet.
Ist Annahme 2 an die Störgrößen verletzt, gilt also (mit σi2 := Var(ui ))
σi2 6= σj2 für mindestens eine Kombination i, j ∈ {1, . . . , n}, so spricht man
von heteroskedastischen Störgrößen.
Ökonometrie (SS 2014)
Folie 259
4 Multiple lineare Regression
Heteroskedastische Störgrößen 4.10
Heteroskedastie der Störgrößen II
Im Folgenden untersuchen wir die Auswirkungen des Vorliegens
heteroskedastischer, aber (nach wie vor) unkorrelierter Störgrößen.
Es gelte also
 2
σ1
0


2
2
V(u) = diag(σ1 , . . . , σn ) :=  ...

0
0
V(u) ist also eine Diagonalmatrix.
0
σ22
0 ···
0 ···
..
.
0
0
0
0
0
0
0
0
···
···
0
0
2
σn−1
0

0
0

..  ,
.

0
σn2
Sind die Störgrößen gemeinsam normalverteilt (gilt also Annahme
sind die ui noch unabhängig, aber nicht mehr identisch verteilt.
Ökonometrie (SS 2014)
4
), so
Folie 260
4 Multiple lineare Regression
Heteroskedastische Störgrößen 4.10
Heteroskedastie der Störgrößen III
Auswirkungen von Heteroskedastie in den Störgrößen
bei Schätzung des Modells mit der OLS-/KQ-Methode
I
I
I
b bleibt unverzerrt für β.
Der Vektor von Schätzfunktionen β
(Die Koeffizientenschätzer bleiben prinzipiell sinnvoll und gut einsetzbar.)
b ist nicht mehr effizient (varianzminimal).
β
(Je nach Situation, insbesondere bei bekannter Struktur der Heteroskedastie, sind
präzisere Schätzfunktionen konstruierbar. Dies wird in dieser Veranstaltung aber
nicht weiter besprochen.)
Konfidenzintervalle und Tests werden in der bisherigen Ausgestaltung
unbrauchbar!
Ursächlich für den letzten (und folgenreichsten) Aspekt ist, dass bei der
b bzw. V(
b regelmäßig die (bei
b β)
Herleitung bzw. Berechnung von V(β)
Heteroskedastie falsche!) Spezifikation V(u) = σ 2 In eingesetzt bzw.
verwendet wurde.
Ökonometrie (SS 2014)
4 Multiple lineare Regression
Folie 261
Heteroskedastische Störgrößen 4.10
b bei Heteroskedastie I
Schätzung von V(β)
b nicht mehr
Bei Vorliegen von Heteroskedastie in den Störgrößen kann V(β)
so stark wie auf Folie 198 vereinfacht werden, man erhält lediglich
0 h
0 i
0
−1 0
0
−1 0
b
b
b
b
b
V(β) = E β − E(β) β − E(β)
= E (X X) X u (X X) X u
= E (X0 X)−1 X0 uu0 X(X0 X)−1 = (X0 X)−1 X0 E(uu0 )X(X0 X)−1
= (X0 X)−1 X0 V(u)X(X0 X)−1 .
Bei unbekannter Form von Heteroskedastie wurde als Schätzer für V(u) von
Halbert White zunächst (Econometrica, 1980) die folgende Funktion
vorgeschlagen:
 2

b1 0 0 · · · 0
u
0
0
0 u
b22 0 · · · 0
0
0



 ..
.
2
2
.
b
.
.
bn ) =  .
Vhc0 (u) := diag(b
u1 , . . . , u

.
.


2
 0 0 0 ··· 0 u
bn−1
0
bn2
0 0 0 ··· 0
0
u
Ökonometrie (SS 2014)
Folie 262
4 Multiple lineare Regression
Heteroskedastische Störgrößen 4.10
b bei Heteroskedastie II
Schätzung von V(β)
Auf dieser Basis wurden weitere Schätzer entwickelt, einer davon ist die (für
bessere Eigenschaften in kleinen Stichproben um Freiheitsgrade korrigierte)
Variante
n
bn2 )
diag(b
u12 , . . . , u
n − (K + 1)
 2
b1 0 0 · · ·
u
0 u
b22 0 · · ·

n
 ..
..
=
.
.
n − (K + 1) 
 0 0 0 ···
0 0 0 ···
b hc1 (u) :=
V
0
0
0
0
0
0
2
bn−1
u
0

0
0

..  .
.

0
bn2
u
b aus Folie 262 liefert dann z.B.
Einsetzen in die Darstellung von V(β)
b := (X0 X)−1 X0 V
b hc1 (β)
b hc1 (u)X(X0 X)−1
V
als (unter moderaten Bedingungen konsistenten) Schätzer für die
b
Varianz-Kovarianz-Matrix V(β).
Ökonometrie (SS 2014)
4 Multiple lineare Regression
Folie 263
Heteroskedastische Störgrößen 4.10
Konfidenz-, Prognoseintervalle und Hypothesentests I
bei heteroskedastischen Störgrößen
Konfidenz- und Prognoseintervalle sowie Hypothesentests müssen nun auf der
Verteilungsaussage
bzw.
βb ∼ N(β, (X0 X)−1 X0 V(u)X(X0 X)−1 )
•
βb ∼ N(β, (X0 X)−1 X0 V(u)X(X0 X)−1 )
aufbauen, die durch eine geeignete Schätzung von V(u) nutzbar gemacht
wird.
b für
b hc (β)
Die Verwendung eines heteroskedastie-konsistenten Schätzers V
b führt dazu, dass viele bei Homoskedastie (zumindest bei gemeinsam
V(β)
normalverteilen Störgrößen) exakt gültigen Verteilungsaussagen nur noch
asymptotisch und damit für endliche Stichprobenumfänge nur noch
näherungsweise (approximativ) gelten (selbst bei gemeinsam normalverteilten
Störgrößen).
Ökonometrie (SS 2014)
Folie 264
4 Multiple lineare Regression
Heteroskedastische Störgrößen 4.10
Konfidenz-, Prognoseintervalle und Hypothesentests II
bei heteroskedastischen Störgrößen
Achtung!
b muss
Bei der Verwendung von heteroskedastie-konsistenten Schätzern für V(β)
unbedingt darauf geachtet werden, keine Formeln“ einzusetzen, die unter
”
Ausnutzung von nur bei Homoskedastie der Störgrößen gültigen
Zusammenhängen hergeleitet wurden.
c2 oder σ
Generell sind ganz offensichtlich alle Formeln“, die σ
b enthalten, also
”
nicht mehr einsetzbar. Dazu zählen einige Darstellungen auf den Folien 204,
217, 224, 227, 230 und 234.
Bei der Berechnung von Konfidenzintervallen (Folie 203) und der
Durchführung von Tests (Folie 204) für einzelne Parameter sind natürlich bei
c2 b bzw. σ
allen Vorkomnissen von σ
bβbk die entsprechenden Diagonaleinträge
βk
b bzw.
b hc (β)
der verwendeten heteroskedastie-konsistenten Schätzmatrix V
deren Wurzeln einzusetzen!
Der t-Test für einzelne lineare Hypothesen hat nun die folgende Darstellung:
Ökonometrie (SS 2014)
Folie 265
4 Multiple lineare Regression
Heteroskedastische Störgrößen 4.10
Zusammenfassung: t-Test für einzelne lineare Hypothesen
im multiplen linearen Regressionsmodell mit heteroskedastischen Störgrößen
Anwendungsvoraussetzungen
Nullhypothese
Gegenhypothese
Teststatistik
Verteilung (H0 )
Benötigte Größen
Kritischer Bereich
zum Niveau α
p-Wert
Ökonometrie (SS 2014)
approx.: y = Xβ + u mit E(u) = 0, V(u) = diag(σ12 , . . . , σn2 ),
σi2 unbekannt, X deterministisch mit vollem Spaltenrang K + 1,
Realisation y = (y1 , . . . , yn )0 beobachtet
H0 : a0 β = c
H1 : a0 β 6= c
H0 : a0 β ≤ c
H1 : a0 β > c
H0 : a0 β ≥ c
H1 : a0 β < c
b−c
a0 β
t= q
b
b hc (β)a
a0 V
t für a0 β = c näherungsweise t(n − (K + 1))-verteilt
b = (X0 X)−1 X0 y, V
b eine heteroskedastie-konsistente Schätzb hc (β)
β
b z.B. V
b = (X0 X)−1 X0 V
b hc1 (β)
b hc1 (u)X(X0 X)−1
funktion für V(β),
n
b
b hc1 (u) =
bn2 ), wobei b
mit V
diag(b
u12 , . . . , u
u = y − Xβ
n−(K +1)
(−∞, −tn−(K +1);1− α2 )
∪(tn−(K +1);1− α2 , ∞)
2 · (1 − Ft(n−(K +1)) (|t|))
(tn−(K +1);1−α , ∞)
(−∞, −tn−(K +1);1−α )
1 − Ft(n−(K +1)) (t)
Ft(n−(K +1)) (t)
Folie 266
4 Multiple lineare Regression
Heteroskedastische Störgrößen 4.10
Konfidenz-, Prognoseintervalle und Hypothesentests III
im multiplen linearen Regressionsmodell mit heteroskedastischen Störgrößen
Auch die alternativen Darstellungen der Statistik des F -Tests von Folie 236f.
verlieren ihre Korrektheit!
Die F -Statistik aus Folie 230 ist durch eine Darstellung der Bauart“
”
i−1
h
0
0
b
b
b
(Aβb − c)
(Aβ − c) AVhc (β)A
F =
L
zu ersetzen, beispielsweise also durch
F =
h
i−1
0
0
−1 0 b
0
−1 0
b
(Aβ − c) A(X X) X Vhc1 (u)X(X X) A
(Aβb − c)
b hc1 (u) =
mit V
L
n
n−(K +1)
bn2 ).
diag(b
u12 , . . . , u
Der F -Test hat also bei heteroskedastischen Störgrößen die folgende Gestalt:
Ökonometrie (SS 2014)
Folie 267
4 Multiple lineare Regression
Heteroskedastische Störgrößen 4.10
Zusammenfassung: F -Test für L ≥ 1 lineare Restriktionen
im multiplen linearen Regressionsmodell mit heteroskedastischen Störgrößen
Anwendungsvoraussetzungen
approx.: y = Xβ + u mit E(u) = 0, V(u) = diag(σ12 , . . . , σn2 ),
σi2 unbekannt, X deterministisch mit vollem Spaltenrang K + 1,
Realisation y = (y1 , . . . , yn )0 beobachtet, c ∈ RL ,
(L × (K + 1))-Matrix A mit vollem Zeilenrang L
Nullhypothese
Gegenhypothese
Teststatistik
Verteilung (H0 )
Benötigte Größen
F =
H0 : Aβ = c
H1 : Aβ 6= c
h
i−1
b − c)0 AV
b 0
b − c)
b hc (β)A
(Aβ
(Aβ
L
F ist approx. F (L, n − (K + 1))-verteilt, falls Aβ = c
b = (X0 X)−1 X0 y, V
b eine heteroskedastie-konsistente Schätzb hc (β)
β
b z.B. V
b = (X0 X)−1 X0 V
b hc1 (β)
b hc1 (u)X(X0 X)−1
funktion für V(β),
n
b
b hc1 (u) =
bn2 ), wobei b
mit V
diag(b
u12 , . . . , u
u = y − Xβ
n−(K +1)
Kritischer Bereich
zum Niveau α
p-Wert
Ökonometrie (SS 2014)
(FL,n−(K +1);1−α , ∞)
1 − FF (L,n−(K +1)) (F )
Folie 268
4 Multiple lineare Regression
Heteroskedastische Störgrößen 4.10
Konfidenz-, Prognoseintervalle und Hypothesentests IV
im multiplen linearen Regressionsmodell mit heteroskedastischen Störgrößen
Ein approximatives symmetrisches Konfidenzintervall für a0 β zum
Konfidenzniveau 1 − α erhält man bei heteroskedastischen Störgrößen durch
q
q
0b
0
b , a βb + tn−(K +1);1− α · a0 V
b
b hc (β)a
b hc (β)a
a β − tn−(K +1);1− α2 · a0 V
2
b
b hc (β).
mit einer geeigneten (heteroskedastie-konsistenten) Schätzmatrix V
Bei der Konstruktion von Konfidenzellipsen bzw. -ellipsoiden ist natürlich
analog eine geeignete Darstellung der F -Statistik (siehe z.B. Folie 267) zu
verwenden, man erhält einen (approximativen) Konfidenzbereich zum
Konfidenzniveau 1 − α also nun (unter Beibehaltung der bisherigen
Bezeichnungen) mit der Menge
h
i−1
b 0
b hc (β)A
c ∈ RL (Aβb − c)0 AV
(Aβb − c) ≤ L · FL,n−(K +1);1−α .
Ökonometrie (SS 2014)
4 Multiple lineare Regression
Folie 269
Heteroskedastische Störgrößen 4.10
Konfidenz-, Prognoseintervalle und Hypothesentests V
im multiplen linearen Regressionsmodell mit heteroskedastischen Störgrößen
(Approximative) Intervallprognosen für E(y0 ) gegeben x0 zur
Vertrauenswahrscheinlichkeit 1 − α (auch interpretierbar als
Konfidenzintervalle zum Konfidenzniveau 1 − α für E(y0 ) gegeben x0 ) erhält
man nun in der Gestalt
q
q
b 0 , x0 0 βb + tn−(K +1);1− α · x0 0 V
b 0
b hc (β)x
b hc (β)x
x0 0 βb − tn−(K +1);1− α2 · x0 0 V
2
b
b hc (β).
mit einer geeigneten (heteroskedastie-konsistenten) Schätzmatrix V
Intervallprognosen von y0 gegeben x0 sind nun nicht mehr sinnvoll
durchführbar, da man keine Informationen mehr über die von u0 verursachte
Schwankung von y0 hat!
Ökonometrie (SS 2014)
Folie 270
4 Multiple lineare Regression
Heteroskedastische Störgrößen 4.10
Robuste Standardfehler“
”
Die Verwendung von heteroskedastie-konsistenten Schätzern für die
Standardabweichungen von βbk (bzw. weitergehender die Verwendung eines
b wird
heteroskedastie-konsistenten Schätzers für die Schätzung von V(β))
auch als Verwendung robuster Standardfehler“ bezeichnet.
”
Gängige Statistik-Software erlaubt die Verwendung robuster Standardfehler,
auch wenn standardmäßig in der Regel von homoskedatischen Störgrößen
ausgegangen wird.
In der Statistik-Software R implementiert beispielsweise die Funktion hccm
( heteroscedasticity-corrected covariance matrix“) im Paket car verschiedene
”
b bei den
Varianten heteroskedastie-konsistenter Schätzungen von V(β)
Auswertungen zu linearen Regressionsmodellen.
Die Verwendung robuster Standardfehler trotz homoskedastischer Störgrößen
ist unkritisch. Moderne Lehrbücher empfehlen zunehmend eine generelle
Verwendung robuster Standardfehler.
Ökonometrie (SS 2014)
4 Multiple lineare Regression
Folie 271
Heteroskedastische Störgrößen 4.10
Beispiel: Robuste Standardfehler I
b und V
b im Beispiel von Folie 207:
b β)
b hc1 (β)
Berechnung von V(
> library(car)
> fit
<- lm(Lohnhöhe ~ Ausbildung + Alter)
> print(vcov(fit),digits=6)
# "standard"
(Intercept) Ausbildung
Alter
(Intercept)
27051.397
456.8888 -645.7068
Ausbildung
456.889
449.0435 -52.7609
Alter
-645.707
-52.7609
20.9445
> Vhhc1 <- hccm(fit, type="hc1")
> print(Vhhc1,digits=6)
# "robust"
(Intercept) Ausbildung
Alter
(Intercept)
23815.318 -1602.3359 -583.2360
Ausbildung
-1602.336
271.0231
26.8099
Alter
-583.236
26.8099
16.1392
Ökonometrie (SS 2014)
Folie 272
4 Multiple lineare Regression
Heteroskedastische Störgrößen 4.10
Beispiel: Robuste Standardfehler II
t-Tests auf Signifikanz der einzelnen Koeffizienten:
> print(coeftest(fit))
# "standard"
t test of coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1027.8058
164.4731 6.2491 8.814e-06 ***
Ausbildung
62.5745
21.1906 2.9529 0.008904 **
Alter
10.6020
4.5765 2.3166 0.033265 *
--Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
> print(coeftest(fit, vcov. = Vhhc1))
# "robust"
t test of coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1027.8058
154.3221 6.6601 4.021e-06 ***
Ausbildung
62.5745
16.4628 3.8010 0.001428 **
Alter
10.6020
4.0174 2.6390 0.017229 *
--Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Ökonometrie (SS 2014)
Folie 273
4 Multiple lineare Regression
Heteroskedastische Störgrößen 4.10
Beispiel: Robuste Standardfehler III
Die Schätzung unter Zulassung heteroskedastischer Störgrößen führt im
Beispiel zu kleineren p-Werten der Tests auf Signifikanz der einzelnen
Parameter.
Insbesondere ist nun der Koeffizient zum Regressor Ausbildung sogar zum
Signifikanzniveau α = 0.001 bzw. der Koeffizient zum Regressor Alter sogar
zum Signifikanzniveau α = 0.01 signifikant positiv!
Der t-Test zum Test der linearen Hypothese
H0 : β1 − 2 · β2 ≤ 0
gegen
H1 : β1 − 2 · β2 > 0
bzw.
H0 : a0 β ≤ c
gegen
H1 : a0 β > c
0
mit a = 0 1 −2 und c = 0 wird im Folgenden statt unter der Annahme
von Homoskedastie der Störgrößen unter Zulassung heteroskedastischer
Störgrößen durchgeführt.
Ökonometrie (SS 2014)
Folie 274
4 Multiple lineare Regression
Heteroskedastische Störgrößen 4.10
Beispiel: Robuste Standardfehler IV
b wie auf Folie 272 angegeben erhält man nun zunächst
b hc1 (β)
Mit V

 
23815.318
−1602.336
−583.236
0
0b
b = 0 1 −2 −1602.336
271.023
26.810   1 
a Vhc1 (β)a
−583.236
26.810
16.139
−2
= 228.3404
und mit a0 βb = 0


1027.806
−2  62.575  = 41.371 die realisierte Teststatistik
10.602
1
t=q
a0 βb − c
41.371 − 0
=√
= 2.7378 .
228.3404
0
b
b
a Vhc1 (β)a
H0 kann nun zum Signifikanzniveau α = 0.05 anders als bei Annahme
homoskedastischer Störgrößen also abgelehnt werden, da
t = 2.7378 ∈ (1.74, ∞) = (t17;0.95 , ∞) = (tn−(K +1);1−α , ∞) = K .
Ökonometrie (SS 2014)
Folie 275
4 Multiple lineare Regression
Heteroskedastische Störgrößen 4.10
Beispiel: Robuste Standardfehler V
[
Mit der (bereits auf Folie 218 berechneten) Punktprognose E(y
0 ) = 1680.982
für die erwartete Lohnhöhe eines 38-jährigen Mitarbeiters, der nach dem
Hauptschulabschluss weitere 4 Ausbildungsjahre absolviert hat (also für
0
x0 = 1 4 38 ), erhält man unter Annahme heteroskedastischer
Störgrößen nun mit
b 0= 1
b hc1 (β)x
x0 0 V
4

23815.318
38 −1602.336
−583.236
−1602.336
271.023
26.810
 
−583.236
1


26.810
4  = 2462.304
16.139
38
das Prognoseintervall
q
q
b 0 , x0 0 βb + tn−(K +1);1− α · x0 0 V
b 0
b hc (β)x
b hc (β)x
x0 0 βb − tn−(K +1);1− α2 · x0 0 V
2
h
i
√
√
= 1680.982 − 2.1098 · 2462.304 , 1680.982 + 2.1098 · 2462.304
= [1576.29 , 1785.674]
zur Vertrauenswahrscheinlichkeit 1 − α = 0.95 für E(y0 ) gegeben x10 = 4 und
x20 = 38. (Intervall bei homoskedastischen Störgrößen: [1565, 1796.964])
Ökonometrie (SS 2014)
Folie 276
4 Multiple lineare Regression
Heteroskedastische Störgrößen 4.10
Beispiel: Robuste“ Konfidenzellipse für β1 und β2
”
Modell von Folie 207, mit bzw. ohne Verwendung robuster Standardfehler, 1 − α = 0.95
10
●
0
5
Alter β2
15
20
^ ^
V(β)
^
^
Vhc1(β)
20
40
60
80
100
120
Ausbildung β1
Ökonometrie (SS 2014)
4 Multiple lineare Regression
Folie 277
Tests auf Heteroskedastie 4.11
Inhaltsverzeichnis
(Ausschnitt)
4
Multiple lineare Regression
Multiples lineares Modell
Parameterschätzung
Konfidenzintervalle und Tests
Punkt- und Intervallprognosen
Tests einzelner linearer Hypothesen
Konfidenzintervalle für Linearkombinationen
Tests mehrerer linearer Hypothesen
Konfidenzellipsen
Multikollinearität
Heteroskedastische Störgrößen
Tests auf Heteroskedastie
Ökonometrie (SS 2014)
Folie 278
4 Multiple lineare Regression
Tests auf Heteroskedastie 4.11
Tests auf Heteroskedastie der Störgrößen
Neben dem Ansatz, generell eine heteroskedastie-konsistente Schätzung von
b zu verwenden, besteht auch die Möglichkeit, das Vorliegen von
V(β)
Heteroskedastizität der Störgrößen statistisch zu untersuchen, um dann bei
”
Bedarf“ einen heteroskedastie-konsistenten Schätzer zu verwenden.
Hierzu existieren verschiedene Hypothesentests, deren
Anwendungsmöglichkeiten zum Beispiel davon abhängen, ob man eine
bestimmte Quelle“ für die Heteroskedastie in den Störgrößen angeben kann
”
bzw. vermutet.
In der vorangegangenen Regression (Lohnhöhe regressiert auf Ausbildung
und Alter) könnte man beispielsweise vermuten, dass die Varianz der
Störgrößen dort groß ist, wo auch die Lohnhöhe groß ist.
Ein Test, der in dieser Situation sehr gut geeignet sein kann, ist der
Goldfeldt-Quandt-Test.
Ökonometrie (SS 2014)
4 Multiple lineare Regression
Folie 279
Tests auf Heteroskedastie 4.11
Goldfeld-Quandt-Test I
Zur (sinnvollen) Anwendung des Goldfeld-Quandt-Tests ist es erforderlich,
dass die Heteroskedastie in den Störgrößen
I
I
von einer beobachteten (und identifizierten) Variablen verursacht wird und
monoton“ in dieser Variablen ist.
”
Die Monotonie“ kann sich auch dahingehend äußern, dass sich bei einem
”
(nur) nominalskalierten Regressor mit zwei Ausprägungen (also z.B. einer
Dummy-Variablen!) die Störgrößenvarianz in der einen Gruppe“ von der in
”
der anderen Gruppe unterscheidet!
Zur Anwendung des Goldfeld-Quandt-Tests ist es bei einer
ordinal-/kardinalskalierten Variablen, die die Störgrößenvarianz monoton“
”
beeinflussen soll, sogar erforderlich, den Datensatz in eine Gruppe von
Beobachtungen mit kleinen“ Ausprägungen und eine weitere Gruppe von
”
Beobachtungen mit großen“ Ausprägungen dieser Variablen aufzuteilen
”
(eventuell unter Auslassung eines Teils der Daten mit mittelgroßen“
”
Ausprägungen dieser Variablen).
Ökonometrie (SS 2014)
Folie 280
4 Multiple lineare Regression
Tests auf Heteroskedastie 4.11
Goldfeld-Quandt-Test II
Das ursprüngliche Regressionsmodell wird dann jeweils getrennt für die
beiden Gruppen A (entspricht ggf. Gruppe mit kleinen“ Ausprägungen) und
”
B (entspricht ggf. Gruppe mit großen“ Ausprägungen) (unter der – für die
”
Durchführung des Tests wenig schädlichen – Annahme von Homoskedastie in
beiden Gruppen) geschätzt.
Die Anwendung des Goldfeld-Quandt-Tests läuft dann auf einen (aus der
Schließenden Statistik bekannten!) F -Test zum Vergleich zweier Varianzen
(unter Normalverteilungsannahme) hinaus.
Unter der Nullhypothese der Homoskedastie sind insbesondere die
Störgrößenvarianzen beider Gruppen, im Folgenden mit σA2 bzw. σB2
bezeichnet, sowohl konstant als auch gleich.
Der Test kann sowohl beidseitig als auch einseitig (links- bzw. rechtsseitig)
durchgeführt werden, so erhält man die folgenden Hypothesenpaare:
H0 : σA2 = σB2
gegen
H1 : σA2 6= σB2
H0 : σA2 ≤ σB2
gegen
H1 : σA2 > σB2
Ökonometrie (SS 2014)
H0 : σA2 ≥ σB2
gegen
H1 : σA2 < σB2
Folie 281
4 Multiple lineare Regression
Tests auf Heteroskedastie 4.11
Goldfeld-Quandt-Test III
bA bzw. u
bB jeweils den Residuenvektor der Schätzung aus
Bezeichnen u
Gruppe A bzw. B, SERA bzw. SERB jeweils den Standard Error of Regression
(residual standard error) der Schätzung aus Gruppe A bzw. B, nA bzw. nB
die Länge des jeweils zur Schätzung verwendeten (Teil-)Datensatzes für
Gruppe A bzw. B sowie K (wie üblich) die Anzahl (echter) Regressoren, so
erhält man die möglichen Darstellungen
b0A u
bA /(nA − (K + 1))
SER2A
u
=
F = 0
bB u
bB /(nB − (K + 1))
u
SER2B
der Teststatistik, die bei Gültigkeit von σA2 = σB2 eine
F (nA − (K + 1), nB − (K + 1))-Verteilung besitzt.
Insgesamt erhält man die folgende Zusammenfassung des
Goldfeld-Quandt-Tests:
Ökonometrie (SS 2014)
Folie 282
4 Multiple lineare Regression
Tests auf Heteroskedastie 4.11
Zusammenfassung: Goldfeld-Quandt-Test (GQ-Test)
auf Heteroskedastizität der Störgrößen
Anwendungsvoraussetzungen
Nullhypothese
Gegenhypothese
exakt: y = Xβ + u mit E(u) = 0, V(u) Diagonalmatrix aus σA2 , σB2 ,
X deterministisch mit vollem Spaltenrang K + 1, Realisation
y = (y1 , . . . , yn )0 beobachtet, Auswahl von zwei Gruppen
A bzw. B vom Umfang nA bzw. nB aus den Beobachtungen
H0 : σA2 = σB2
H1 : σA2 6= σB2
Benötigte Größen
Kritischer Bereich
zum Niveau α
p-Wert
Ökonometrie (SS 2014)
H0 : σA2 ≥ σB2
H1 : σA2 < σB2
b
u0A b
uA /(nA − (K + 1))
SER2A
F = 0
=
b
uB /(nB − (K + 1))
uB b
SER2B
Teststatistik
Verteilung (H0 )
H0 : σA2 ≤ σB2
H1 : σA2 > σB2
F unter H0 für σA2 = σB2 F (nA − (K + 1), nB − (K + 1))-verteilt
Residuenvektoren b
uA bzw. b
uB oder Standard Error of Regression
SERA bzw. SERB aus jeweils separater Modellschätzung
zu den Gruppen A und B
[0, FnA −1,nB −1; α )
2
α
nA −1,nB −1;1− 2
∪(F
, ∞)
2·min FF (nA −1,nB −1) (F ),
1 − FF (nA −1,nB −1) (F )
(FnA −1,nB −1;1−α , ∞)
[0, FnA −1,nB −1;α )
1−FF (nA −1,nB −1) (F )
FF (nA −1,nB −1) (F )
4 Multiple lineare Regression
Folie 283
Tests auf Heteroskedastie 4.11
Beispiel: Goldfeld-Quandt-Test I
Teilt man den Datensatz des Lohnhöhen-Beispiels“ in die beiden Gruppen A“
”
”
zu den 10 höchsten Lohnhöhen und B“ zu den 10 niedrigsten Lohnhöhen auf,
”
so erhält man die folgende Modellschätzung für Gruppe A“:
”
Call:
lm(formula = Lohnhöhe ~ Ausbildung + Alter, subset = Lohnhöhe >
sort(Lohnhöhe)[10])
Residuals:
Min
1Q
-488.33 -154.11
Median
-34.06
3Q
78.62
Max
534.61
Coefficients:
Estimate Std. Error t
(Intercept) 1516.69
561.23
Ausbildung
51.87
32.07
Alter
3.20
11.07
--Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.'
value Pr(>|t|)
2.702
0.0305 *
1.618
0.1498
0.289
0.7809
0.1
' '
1
Residual standard error: 328 on 7 degrees of freedom
Multiple R-squared: 0.3051, Adjusted R-squared: 0.1066
F-statistic: 1.537 on 2 and 7 DF, p-value: 0.2797
Ökonometrie (SS 2014)
Folie 284
4 Multiple lineare Regression
Tests auf Heteroskedastie 4.11
Beispiel: Goldfeld-Quandt-Test II
Die Schätzung für Gruppe B“ liefert:
”
Call:
lm(formula = Lohnhöhe ~ Ausbildung + Alter, subset = Lohnhöhe <=
sort(Lohnhöhe)[10])
Residuals:
Min
1Q
-100.381 -27.528
Median
-2.589
3Q
47.221
Max
101.743
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1198.772
108.647 11.034 1.11e-05 ***
Ausbildung
57.711
24.688
2.338
0.052 .
Alter
3.270
3.359
0.973
0.363
--Signif. codes:
0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 77.72 on 7 degrees of freedom
Multiple R-squared: 0.4967, Adjusted R-squared: 0.3529
F-statistic: 3.454 on 2 and 7 DF, p-value: 0.09045
Ökonometrie (SS 2014)
Folie 285
4 Multiple lineare Regression
Tests auf Heteroskedastie 4.11
Beispiel: Goldfeld-Quandt-Test III
Die Teststatistik des GQ-Tests erhält man also durch
3282
F =
= 17.811 .
77.722
Der rechtsseitige Test zum Signifikanzniveau α = 0.05 lehnt mit
K = (F1−α;nA −(K +1),nB −(K +1) , ∞) = (F0.95;7,7 , ∞) = (3.79, ∞)
wegen F ∈ K die Nullhypothese der Homoskedastie der Störgrößen also ab
und entscheidet sich für eine größere Störgrößenvarianz in der Gruppe, die zu
den größeren Lohnhöhen gehört.
Ökonometrie (SS 2014)
Folie 286
4 Multiple lineare Regression
Tests auf Heteroskedastie 4.11
Beispiel: Goldfeld-Quandt-Test IV
Visualisierung der Abhängigkeit der b
ui2 vom Regressor Lohnhöhe und des GQ-Tests
Punktwolke der abhängigen Variablen und der quadrierten Residuen
SER2B
SER2A
100000 150000 200000 250000 300000
●
●
50000
2
quadrierte Residuen u^i
●
●
●
0
●
1200
●
●
●
●
1400
●
●
●
●
●
1600
●
●
1800
●
2000
2200
2400
2600
Lohnhöhe yi
Ökonometrie (SS 2014)
4 Multiple lineare Regression
Folie 287
Tests auf Heteroskedastie 4.11
Beispiel: Goldfeld-Quandt-Test V
Schneller lässt sich die Fragestellung mit dem Befehl gqtest aus dem Paket
lmtest bearbeiten.
Die Verwendung der Voreinstellung teilt den Datensatz gemäß der Ordnung
einer vorgegebenen Variablen in zwei (möglichst) gleich große Teile und
macht einen einseitigen Test auf positive Abhängigkeit der Störgrößenvarianz
von der vorgegebenen Variablen (wie im Beispiel):
> library(lmtest)
> gqtest(lm(Lohnhöhe~Ausbildung+Alter),order.by=Lohnhöhe)
Goldfeld-Quandt test
data: lm(Lohnhöhe ~ Ausbildung + Alter)
GQ = 17.8168, df1 = 7, df2 = 7, p-value = 0.00058
Ökonometrie (SS 2014)
Folie 288

Zugehörige Unterlagen

Diplomarbeitssthema Logistische Regression zur Schätzung von

Beispiel: Einstiegsgehalt und Gehalt nach 10 Jahren

Okonometrie Organisatorisches I

Zugehörige Unterlagen

Produkte

Unterstützung

Okonometrie Organisatorisches I

Zugehörige Unterlagen

Dieses Dokument Sammlung (en)

Dieses Dokument gespeichert

Schlagen Sie uns vor, wie wir StudyLib verbessern können