Laplace-Transformation

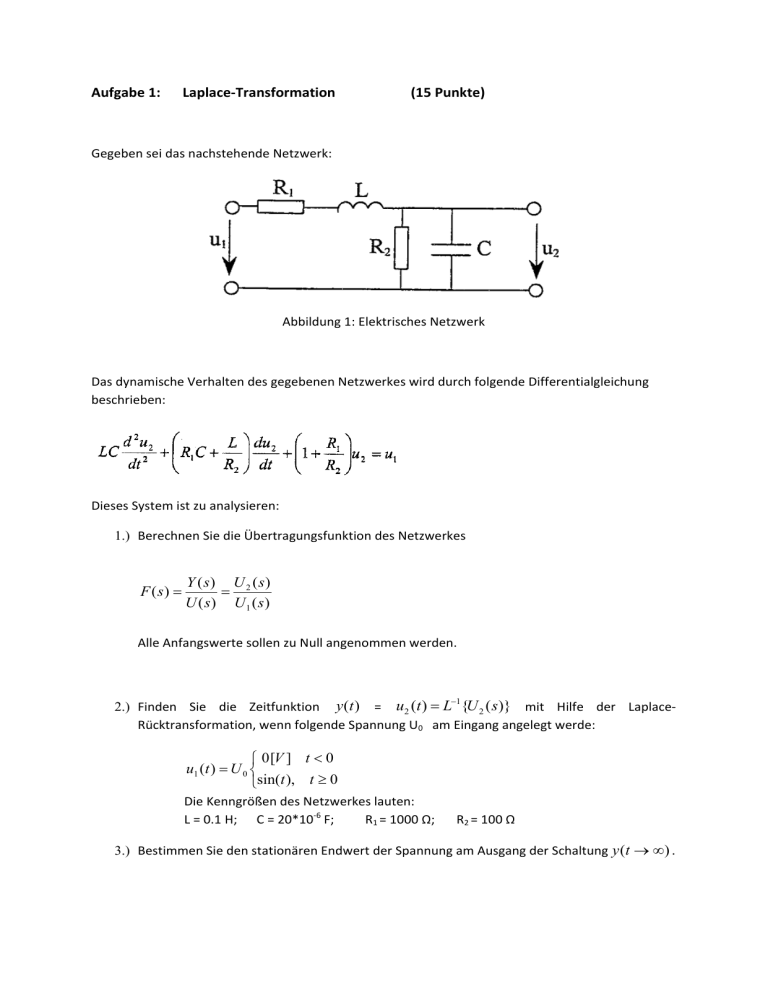
Aufgabe 1: Laplace‐Transformation (15 Punkte) Gegeben sei das nachstehende Netzwerk: Abbildung 1: Elektrisches Netzwerk Das dynamische Verhalten des gegebenen Netzwerkes wird durch folgende Differentialgleichung beschrieben: Dieses System ist zu analysieren: 1.) Berechnen Sie die Übertragungsfunktion des Netzwerkes F ( s) =
Y ( s) U 2 ( s)
=
U ( s ) U 1 ( s ) Alle Anfangswerte sollen zu Null angenommen werden. −1
2.) Finden Sie die Zeitfunktion y (t ) = u2 (t ) = L {U 2 ( s )} mit Hilfe der Laplace‐
Rücktransformation, wenn folgende Spannung U0 am Eingang angelegt werde: ⎧ 0 [V ] t < 0
u1 (t ) = U 0 ⎨
⎩sin(t ), t ≥ 0 Die Kenngrößen des Netzwerkes lauten: L = 0.1 H; C = 20*10‐6 F; R1 = 1000 Ω; R2 = 100 Ω 3.) Bestimmen Sie den stationären Endwert der Spannung am Ausgang der Schaltung y (t → ∞) . Aufgabe 2: Strukturbild‐Reduktion ( 20 Punkte) Gegeben sei das im abgebildeten Strukturbild beschriebene Übertragungssystem: U
G 1(s)
X
G 6(s)
G (s)
4
G2 (s)
G (s)
5
G3 (s)
Abbildung 2: Strukturbild des verkoppelten Gesamtsystems Bestimmen Sie mit Hilfe der grafischen Strukturbild‐Reduktion schrittweise die Gesamtübertragungsfunktion des Systems. Aufgabe 3: Ortskurve und Nyquist‐Stabilität (15 Punkte) Gegeben sind die folgenden drei Übertragungsfunktionen von offenen Regelkreisen: F1 ( s) =
50s 4 + 400s 3 + 5s 2 + 4000s + 1
s 5 − 6 s 4 − 74 s 3 + 684 s 2 − 1655s + 1050 F2 ( s) =
160s 4 − 16s 3 + 3200s 2 + 3200s + 1
s 5 − 6s 4 − 74s 3 + 684s 2 − 1655s + 1050 F3 ( s ) =
100 s 4 + 800 s 3 + 10 s 2 + 9000 s + 1
s 5 − 6 s 4 − 74 s 3 + 684 s 2 − 1655s + 1050 Die charakteristische Gleichung dieser Übertragungsfunktionen hat erkennbar stets dieselben Pole; diese Pole liegen in ‐10, 7, 5, 3, 1. Bestimmen Sie mit Hilfe eines geeigneten Nyquist‐Kriteriums, ob die in den nachfolgenden drei Ortskurven dargestellten Frequenzgänge F1 ( jω ) , F2 ( jω ) und F3 ( jω ) der offenen Kreise auf Stabilität im geschlossenen Regelkreis hinweisen. (Begründung erforderlich!) Abbildung 3a: Ortskurve für F1 ( jω ) . (bitte umblättern!) Abbildung 3b: Ortskurve für F2 ( jω ) . Abbildung 3c: Ortskurve für F3 ( jω ) . Aufgabe 4: Wurzelortskurve ( 25 Punkte) Gegeben ist eine Regelstrecke mit der Übertragungsfunktion: 6
4
10
8
•
•
Skizzieren Sie die WOK des geschlossenen Regelkreises. Die Verzweigungspunkte (falls sie existieren) müssen lediglich skizziert und nicht berechnet werden. Bestimmen Sie den Bereich der Verstärkung K, in welchem der geschlossene Regelkreis stabil arbeitet. Aufgabe 5: Kaskadenregelung ( 25 Punkte) Gegeben sei das folgende kaskadierte Regelungssystem mit den Übertragungsstrecken G1, G2, G3 und den Reglern R1, R2. z
R1 wa ‐
wi R2 G1
+
G2
xi G3 xa ‐
Abbildung 5a: Kaskadenregelung mit innerem und äußerem Regelkreis 1.) Wie lautet die Führungsübertragungsfunktion Fa =
2.) Wie lautet die Störübertragungsfunktion Fz =
xa
der gesamten Regelkaskade? wa
xa
, (wa (t) = 0) der gesamten Regelkaskade? z
Hinweis: Die Lösung dieses Abschnitts ist nicht die Voraussetzung für die Bearbeitung der folgenden Abschnitte 3 und 4. Die Übertragungsstrecken G1, G2, G3 sind wie folgt vorgegeben: z
+
1
1
1
wi xi R1 R2 wa 1 + 10s
1+ s
1 + 0.5s
‐
‐
Abbildung 5b: Kaskadenregelung mit vorgegebenen Regelstrecken 3.) Innerer Regelkreis: Wählen Sie zunächst den Regler R2 (s) den inneren Kreises so, dass die Strecke mit der größten Zeitverzögerung wirkungslos wird und dessen Ausgang xi (t) 63% seines Endwertes in einer Zeit T=0.25 bei einem Eingangssprung von wi(t) erreicht. Geben Sie die Übertragungsfunktion dieses Reglers und die Zahlenwerte seiner Parameter an. Der Regler des äußeren Regelkreises R1(s) sei ein PI‐Regler in der Form K1
1 + sT1
. Seine sT1
Integrationszeit betrage T1=0.5 4.) Bestimmen Sie ‐basierend auf den ermittelten Werten des inneren Kreises‐ die Verstärkung K1 des äußeren Kreises nun so, dass für das schwingfähige Gesamtsystem eine Dämpfung von 0.5 erreicht wird. xa