Baustofflieferanten

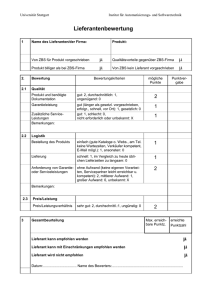
Baustofflieferanten
Anlässlich einer Lieferantenanalyse werden verschiedenen Baustofflieferanten
für vorher festgelegte wichtige Eigenschaften, Punkte vergeben.
Da aber bestimmte Eigenschaften, je nach … unterschiedliche Gewichtungen
haben können, werden die festgelegten Eigenschaften außerdem noch mit
Faktoren belegt.
Nach diesen Vorentscheidungen soll nun der beste Lieferant ermittelt werden
Als Grundlage für die Bewertung der 5 ausgesuchten Baustofflieferanten ( B1,
B2, B3, B4, B5 ) werden folgende Eigenschaften festgelegt: Preishöhe(PH),
Preissicherheit(PS), Zahlungsbedingungen(ZB), Qualität(Q), Lieferzeit(LZ),
Termintreue(TT) und Kundenservice(KS).
Die Ergebnisse der Bewertung (bei einer Punkteskala von 1 bis 10) sind in der
nachstehenden Tabelle zusammengefasst:
B1 B2 B3 B4 B5
PH
3
6
2
5
6
PS
6
5
10
7
6
ZB
5
6
5
3
7
Q
6
7
10
7
8
LZ
8
4
6
4
4
TT
8
5
4
7
9
KS
9
6
2
1
3
Da aber bestimmte Eigenschaften, je nach Schwerpunkt. unterschiedliche
Gewichtung haben können, werden nun die festgelegten Eigenschaften
außerdem noch mit folgenden Faktoren versehen:
PH(Faktor 4), PS(Faktor 5), ZB(Faktor 4), Q(Faktor 5),
LZ(Faktor 1), TT(Faktor 3), KS(Faktor 2).
1. Ermittle den besten Lieferanten nach den oben festgelegten Kriterien!
2. Betrachte die Spaltensummen und interpretiere das Ergebnis!
3. Erläutere, dass ein solcher Test nicht immer sinnvoll ist und finde ein
Beispiel B6 für deine Überlegung!
4. Wie könnte man die Lieferanten noch anders bewerten?
[Quelle: SelMa-Team des Beisenkamp-Gymnasiums, Hamm;
http://www.learn-line.nrw.de/angebote/selma/foyer/projekte/hammproj3/lieferanten_test/index.html]
Lösung
"Baustofflieferant"
Bewertungsmatrix:
1. Der beste Lieferant
Zur Bewertung müssen die Punkte für die verschiedenen Eigenschaften mit dem
zugehörigen Faktor multipliziert und anschließend summiert werden. Das kann man
mit Hilfe der Matrixmultiplikation und eines "Gewichtungsvektors" machen. Da aber
die Spalten und nicht die Zeilen multipliziert werden müssen, kann man nicht von
links multiplizieren! Der Vektor hat sieben Einträge, die Matrix aber nur 5 Spalten!
Daher muss man einen
Zeilenvektor als Gewichtungsvektor nehmen, der dann von rechts multipliziert
werden kann!
Gewichtungsvektor mit den Faktoren für die Eigenschaften:
Multiplikation von links:
Die höchste Punktzahl erhält also der Lieferant 5 mit 159 Punkten!
2. Spaltensummen
Die Spaltensummen geben die Gesamtpunktzahlen der Lieferanten ohne die
Gewichtung an.
Die Spaltensummen lassen sich mit dem CAS berechnen, indem man die Matrix B
mit einem nur aus Einsen
bestehenden Vektor e multipliziert:
Danach hätte Lieferant 1 die höchste Punktzahl, obwohl er nach der Gewichtung erst
an dritter Stelle käme.
3. Kritik
Es könnte vorkommen, dass ein Lieferant in einigen Bereichen die Höchstpunktzahl
bekommt, ansonsten aber sehr
schlecht bewertet wird. Zum Beispiel:
Dieser Lieferant bekäme also die Punktzahl 160 und würde den Auftrag bekommen.
Hier muss man abwägen, ob bei solchen Extrembeispielen diese
Bewertungsmethode noch sinnvoll ist...
4. Alternative Bewertung
Man könnte berücksichtigen, ob die Punkte für die Eigenschaften eines Lieferanten
einigermaßen gleich verteilt
sind. Ein Maß dafür wäre die Streuung um den Mittelwert der Eigenschaftspunkte:
Mit dem CAS kann man statistische Berechnungen, wie Mittelwert,
Standardabweichung usw. anstellen, wenn die Werte in einer Liste geschrieben sind.
Diese Listen für die Baustofflieferanten muss man aber erst aus den Matrixspalten
erstellen.
Der Befehl dafür ist "matToList" (Findet man auch im Aktionsmenü unter "Liste
erstellen").
Liste l1 für Lieferant 1:
(Die 1. Spalte (Lieferant 1) der Matrix B soll als Liste l1 gespeichert werden)
Liste l2 für Lieferant 2:
Die anderen Lieferanten:
Mit den Listen l1 bis l5 kann man nun statistische Berechnungen (im Aktions- bzw.
Interaktionsmenü unter "Liste
berechnen") durchführen.
Z.B. die Summe der Werte von Lieferant 1 (vgl. Aufg. 2)
Jetzt kann man auch einfach die Standardabweichungen ("stdDev") der Lieferanten
berechnen:
Die Standardabweichung ist bei Lieferant 3 am größten und bei Lieferant 2 am
kleinsten.
Für den Lieferanten 6 ergäbe sich folgender Abweichungswert:
Um das mit zu berücksichtigen, könnte man jetzt die gewichteten Punktzahlen der
Lieferanten noch durch die
Abweichungs- bzw. Streuungswerte subtrahieren.
Dann wäre Lieferant 5 wieder besser als Lieferant 6:
Welche Art der Bewertung allerdings am sinnvollsten ist, hängt von den Bedürfnissen
des Unternehmens ab...