Lineare Optimierung

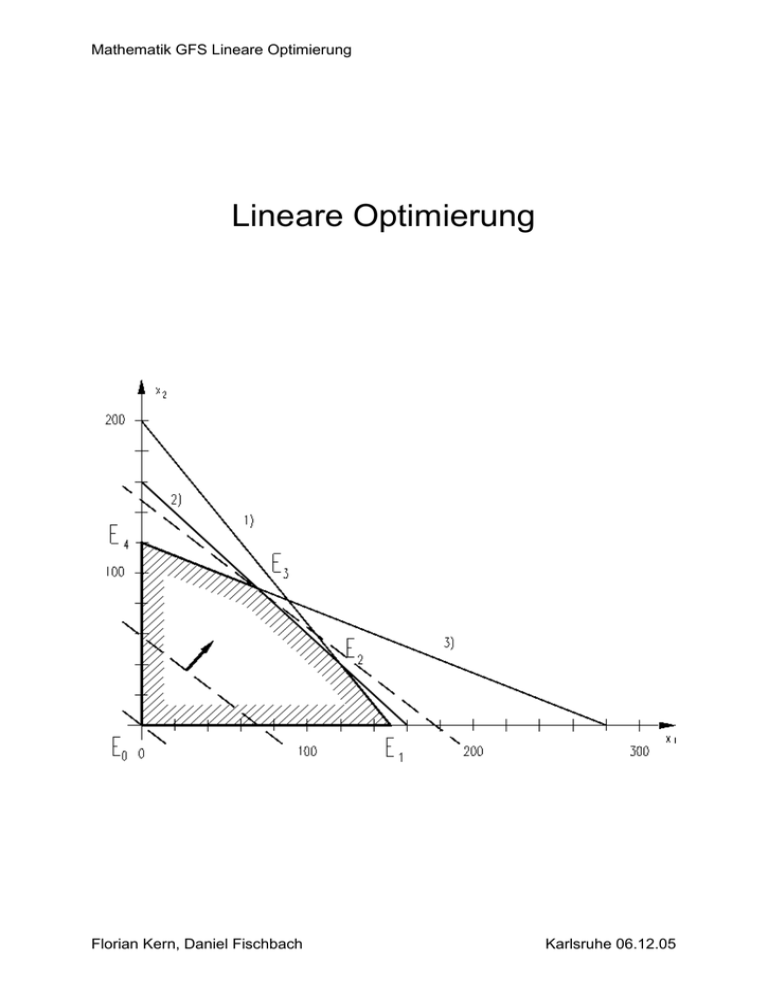
Mathematik GFS Lineare Optimierung
Lineare Optimierung
Florian Kern, Daniel Fischbach
Karlsruhe 06.12.05
Mathematik GFS Lineare Optimierung
Inhaltsverzeichnis
Definition
-
Seite 3
Aufgabe
-
Seite 4
Lösungsverfahren
-
Seite 5 - 8
Lösungsverfahren
-
Seite 9
Florian Kern, Daniel Fischbach
Karlsruhe 06.12.05
Mathematik GFS Lineare Optimierung
Definition:
Die Lineare Optimierung ist eines der Hauptverfahren, eine oder die
optimale Menge zu bestimmen (z.B. maximaler Gewinn oder minimale
Kosten).
Dies geschieht mit Hilfe von linearen Gleichungen, Ungleichungen und
einer Zielfunktion.
Florian Kern, Daniel Fischbach
Karlsruhe 06.12.05
Mathematik GFS Lineare Optimierung
Aufgabe:
Für die Herstellung von zwei Schrankmodellen werden zwei Holzarten
benötigt. Die Herstellung des Modells A erfordert 0,15 E der Holzart I
und 0,2 E der Holzart II. Die Herstellung des Modells B erfordert 0,2 E
der Holzart I und 0,1 E der Holzart II. Von Holzart I stehen 60 E und von
Holzart II 40 E zur Verfügung
Der Gewinn je Schrank beträgt bei Modell A 25€, bei Modell B 20€
Wie viel Stück sind von jedem Modell herzustellen, damit der
Gesamtgewinn möglichst groß wird?
Florian Kern, Daniel Fischbach
Karlsruhe 06.12.05
Mathematik GFS Lineare Optimierung
Lösungsverfahren:
1. Analysieren der Aufgabe und übertragen in eine tabellarische
Form.
Holzart I
Holzart II
Gewinn pro Schrank
Schrankmodell I
Schrankmodell II Max. Einheiten
0,15 E
0,2 E
60 E
0,2 E
0,1 E
40 E
25 €
20 €
2. Zielfunktion.
Annahme:
x = Menge Schrankmodell I
y = Menge Schrankmodell II
Erstellen der Zielfunktion:
max. Gewinn ist:
Menge Schrankmodel mal Gewinn Schrankmodell I
+ Menge Schrankmodel mal Gewinn Schrankmodell II
max. Gewinn = x * 25 € + y * 20 €
Florian Kern, Daniel Fischbach
Karlsruhe 06.12.05
Mathematik GFS Lineare Optimierung
3. Nebenbedingungen
Es stehen nur 60 E von Holzart I und 40 E von Holzart II zur Verfügung. Daher
muss die Nebenbedingung so erstellt werden, dass die Vorraussetzungen erfüllt
werden und nicht mehr als die vorhandenen Einheiten verwendet werden.
Bedingung für Holzart I
Einheiten Holzart I mal Menge Schrank I plus Einheiten Holzart I mal Menge
Schrank II muss kleiner oder gleich 60 E sein.
0,15 * x + 0,2 * y ≤ 60 E
Bedingung für Holzart II
Einheiten Holzart II mal Menge Schrank I plus Einheiten Holzart II mal Menge
Schrank II muss kleiner oder gleich 40 E sein.
0,2 * x + 0,1 * y ≤ 40 E
Eine weitere Bedingung ist, dass x und y größer oder gleich null sein müssen und
dass x und y natürliche Zahlen sein müssen.
x , y ≥ 0 ; x , y E |N
Florian Kern, Daniel Fischbach
Karlsruhe 06.12.05
Mathematik GFS Lineare Optimierung
4. Erstellen des Graphs
Erstellen der drei Funktionen für das Schaubild. Nebenbedingungen auf x und y
auflösen mit geschickt gewählten Wert Null für x und y, ebenso die Zielfunktion auf y
auflösen.
Holzart I
x = 0 => 0,15 * 0 + 0,2 * y ≤ 60 => y = 300
y = 0 => 0,15 * x + 0,2 * 0 ≤ 60 => x = 400
Holzart II
x = 0 => 0,2 * 0 + 0,1 * y ≤ 40 => y = 400
y = 0 => 0,2 * x + 0,1 * 0 ≤ 40 => x = 200
Zielfunktion
max. Gewinn = x * 25 € + y * 20 €
=> y = -5/4x + G/20
Florian Kern, Daniel Fischbach
Karlsruhe 06.12.05
Mathematik GFS Lineare Optimierung
Die berechneten Werte für x und y sind die Schnittpunkte der 2 Geraden von Holzart
I und Holzart II im Koordinatensystem mit der x und y Achse. Die Zielfunktion
einzeichnen.
Der Schnittpunkt der beiden Geraden ( SB x=80 y=240 ) ist der Punkt bei dem der
max. Gewinn erreicht wird. Bei 80 E von Schrankmodell I und 240 E von
Schrankmodell II.
Florian Kern, Daniel Fischbach
Karlsruhe 06.12.05
Mathematik GFS Lineare Optimierung
5. Begriff der Zielfunktion
Florian Kern, Daniel Fischbach
Karlsruhe 06.12.05