Übung Thermodynamik, Serie 2 Aufgabe 2

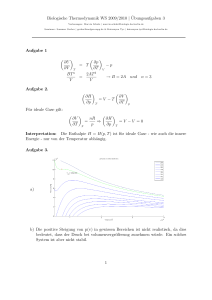
Übung Thermodynamik, Serie 2
Christoph Mahnke, 003200856, Gruppe : Fr . Nettelmann
2nd November 2005
Aufgabe 2)
a) gegebene Gröÿen :
n
T
Prozess
p1
p2
Gas
1
293K
quasistatisch
2 · 106 Pa
1 · 105 Pa
2-atomig, ideal
Table 1: gegebene Werte
folgende Gleichungen können benutzt werden :
pV = nRT
(1)
5
nRT
2
(2)
(ideale Gasgleichung)
U=
(innere Energie)
(3)
dU = δA + δQ
(1. Hauptsatz)
Für einen isothermen Prozess (T = const) kann man mit 1 die Beziehung
V (p) = nRT ·
1
p
(4)
herleiten. Die Arbeit errechnet sich mit W = pV oder dierentiell ∆W = V (p)dp. Die gesamte vom System
geleistete Arbeit errechnet sich durch Integration :
µ ¶
Z p2
p2
W1,2 =
V (p)dp = nRT · ln
p1
p1
Setzt man die gegebenen Werte ein, so erhält man :
µ
∆W1,2 = 1mol · 8, 3 · JK
−1
−1
mol
· 293K · ln
1
105 Pa
2 · 106 Pa
¶
= −7, 3 · 103 J
Dies ist die vom System geleistete Arbeit. Mit 3 kann man nun auch unter Berücksichtigung des isothermen
Prozesses (dU = 0) die zugeführte Wärme zu
δQ = −δA = 7, 3kJ
berechnen.
b) Es soll nun eine adiabatische (δQ = 0) statt wie oben isobare Expansion erfolgen. Hierbei gilt :
T1
=
T2
Mit κ =
5
2
µ
p1
p2
¶ κ−1
κ
(für ein 2 atomiges Gas) ergibt sich so für die Temperatur T2 :
T2 = ³
293K
T1
=
= 34, 5K.
5
´ κ−1
κ
20 7
p1
p2
Die innere Energie hat sich also um
∆U =
5
5
nR(T2 − T1 ) = · 8, 3JK−1 · (−258, 5)K = −5, 4 · 103 J
2
2
geändert. Mit der adiabatischen Zustandsgleichung kann man dann sofort die geleistetete Arbeit ablesen :
dU = δA = −5, 4kJ
2