gleichsinnig geordnete reelle Zahlen: { a1 ≤···≤ an, b1 ≤···≤ bn
Werbung
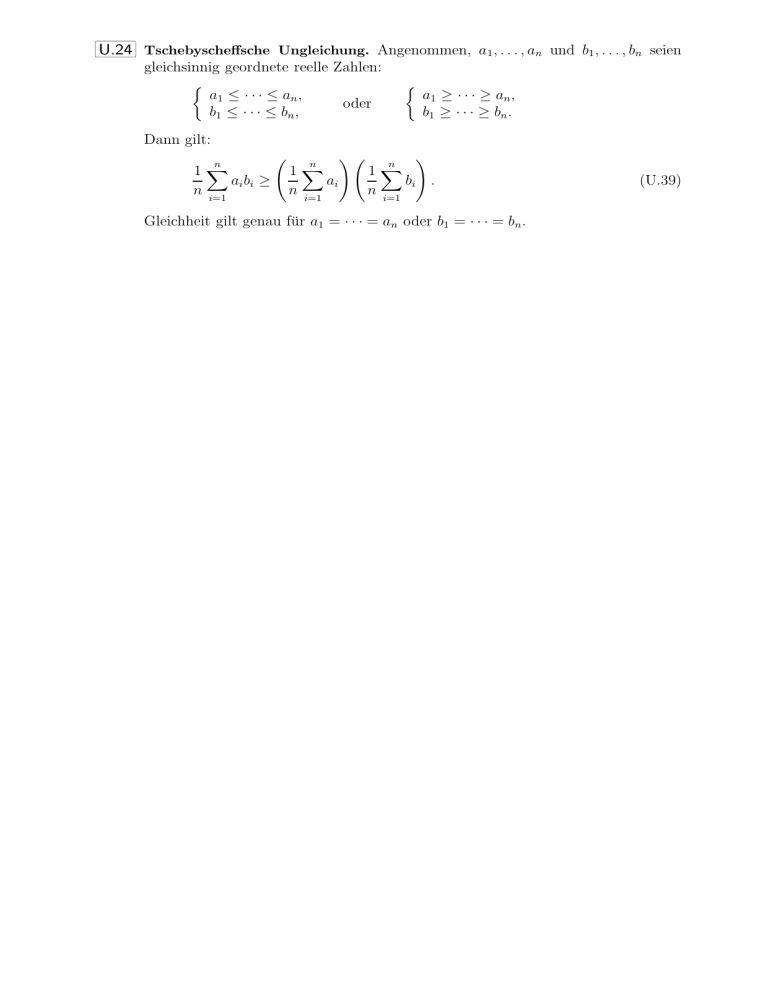
U.24 Tschebyscheffsche Ungleichung. Angenommen, a 1 , . . . , an und b1 , . . . , bn seien gleichsinnig geordnete reelle Zahlen: ½ a1 ≤ · · · ≤ a n , oder b1 ≤ · · · ≤ b n , ½ a1 ≥ · · · ≥ a n , b1 ≥ · · · ≥ b n . Dann gilt: n 1X a i bi ≥ n i=1 Ã n 1X ai n i=1 !Ã n 1X bi n i=1 ! . Gleichheit gilt genau für a1 = · · · = an oder b1 = · · · = bn . (U.39) U.24 Beweis: In beiden Fällen gilt bezüglich der jeweiligen Ordnung der Zahlen a i und bi für jedes Paar (i, j) (ai − aj )(bi − bj ) ≥ 0. (U.113) Summation über beide Indizes und Ausmultiplizieren führt auf die Behauptung: n X n X (ai − aj )(bi − bj ) ≥ 0, i=1 j=1 n X ai bi i=1 2n n X i=1 n X (1) − j=1 ai bi − 2 n X i=1 n X i=1 ai ai n X bj − j=1 n X n X j=1 aj n X i=1 bi + n X j=1 aj bj n X (1) ≥ 0 oder i=1 bi ≥ 0. i=1 Aus (U.113) erkennen wir, daß das Gleichheitszeichen für ai = aj oder bi = bj für alle Paare (i, j), also a1 = · · · = an oder b1 = · · · = bn gilt. ¤








