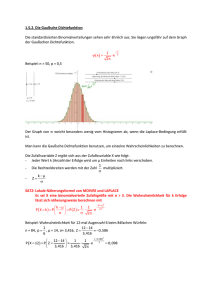
5.2 Multinomiale Wahrscheinlichkeiten Wir betrachten ein zufälliges

5.2 Multinomiale Wahrscheinlichkeiten
Wir betrachten ein zufälliges Experiment mit den Ausgängen
A1, A2, . . . , Al . Wir setzen
pi = P (Ai),
l
X
pi = 1.
i=1
Ein Beispiel ist das folgende Experiment:
Es sei ein Behälter mit k Kugeln in l verschiedenen Farben gegeben, wobei ki Kugeln die Farbe i (i = 1, . . . , l)
besitzen,
l
X
ki = k.
i=1
Es soll die Wahrscheinlichkeit untersucht werden, mit
der eine Kugel einer bestimmten Farbe aus dem Behälter
entnommen wird:
P (Kugel der Farbe i) = pi = kki .
Das Experiment soll nun n–mal wiederholt werden.
95
W.Kössler, Humboldt-Universität zu Berlin
Bn1,n2,...,nl : das Ereignis, daß die Ereignisse A1 n1–mal,
A2 n2–mal, . . ., und Al nl –mal eintreten.
P (Bn1,k2,...,nl ) =
n!
n
· pn1 1 · pn2 2 · . . . · pl l .
n1 ! · n2 ! · . . . · nl !
Derartige Wahrscheinlichkeiten bezeichnen wir auch als
multinomiale Wahrscheinlichkeiten (oder polynomiale Wktn.)
5.3
P OISSON–Wahrscheinlichkeiten
Beispiele, bei denen P OISSON–Wahrscheinlichkeiten auftreten, sind
• die Anzahl von Verkehrsunfällen in einem Ort in einem bestimmten Zeitintervall,
• die Ankünfte von Kunden an einem Schalter oder
• der radioaktive Zerfall von α–Teilchen.
• In einer Telefonzentrale wird ermittelt, wieviel Anrufe in einer bestimmten Zeiteinheit ankommen.
96
W.Kössler, Humboldt-Universität zu Berlin
Elementarereignisse sind hier also zufällige Anzahlen.
Ω = {ω1, ω2, . . . , ωn, . . .} = { 0“, 1“, . . . , n“, . . .}.
” ”
”
Das Ereignis ωi ist z.B. das Ereignis, daß in einer Zeiteinheit genau i Anrufe eintreffen. Die Wahrscheinlichkeit dieses Elementarereignisses ist gegeben durch:
λi −λ
P (ωi) = e .
i!
λ ist dabei ein noch unbestimmter Parameter. Er kann
als mittlere Rate aufgefaßt werden. Diese Wahrscheinlichkeit bezeichnen wir als P OISSON–Wahrscheinlichkeit.
Für die Wahrscheinlichkeit von Ω gilt dann:
P (Ω) =
∞
X
P (ωi) =
i=0
−λ
= e
∞
X
λi −λ
e
i!
i=0
∞
X
λi
i!
=1
|i=0
{z }
=eλ
Wir werden später sehen, daß diese Verteilung “natürlich”
ist.
97
W.Kössler, Humboldt-Universität zu Berlin
98
W.Kössler, Humboldt-Universität zu Berlin
Kapitel 2
Zufallsvariablen
Contents
1 Grundbegriffe . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
2 Eigenschaften der Verteilungsfunktion . 118
3 Diskrete zufällige Variablen
. . . . . . . . . . . . 122
4 Charakteristika von Verteilungsfunktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 142
5 Die Exponentialverteilung
6 Die Normalverteilung
. . . . . . . . . . . . . . 175
. . . . . . . . . . . . . . . . . . . 204
7 Transformation von Zufallsvariablen
. . 219
8 Mehrdimensionale Zufallsvariablen . . . . 229
99
1 Grundbegriffe
Def. 2.1 Es seien (Ω1, E1, P1) und (Ω2, E2, P2) Wahrschein-
lichkeitsräume. Eine Abbildung
X : Ω1 −→ Ω2
heißt E1–E2–meßbar, falls für alle Ereignisse A ∈ E2
gilt:
X −1(A) = {ω ∈ Ω1 : X(ω) ∈ A} ∈ E1.
Bem.: Oftmals wird die Menge B1 der B OREL–Mengen
als Ereignisfeld E2 betrachtet.
100
W.Kössler, Humboldt-Universität zu Berlin
Def. 2.2 Es sei (Ω, E, P ) ein Wahrscheinlichkeitsraum.
Eine E–B1 –meßbare Abbildung X von Ω in R heißt (reellwertige) z
oder Zufallsgröße.
Bem.: (R, B1, P 0) bildet hier den zweiten Wahrschein-
lichkeitsraum, wobei P 0 eine Abbildung von B1 in R ist,
die den KOLMOGOROFF–Axiomen genügt.
Wir betrachten den Wahrscheinlichkeitsraum (Ω, E, P ).
X : Ω −→ R. sei eine zufällige (reellwertige) Variable.
Den zweiten Wahrscheinlichkeitsraum bezeichnen wir
mit (R, B1, PX ). Es sei B ∈ B1 ein zufälliges Ereignis,
für das gilt:
B =] − ∞, x[,
wobei x eine beliebige, fest gewählte reelle Zahl ist. Mit
{X < x} bezeichnen wir das zufällige Ereignis, für das
gilt:
{X < x} := {ω ∈ Ω : X(ω) < x}.
101
W.Kössler, Humboldt-Universität zu Berlin
Dann gilt für die Wahrscheinlichkeit dieses Ereignisses:
P (X < x) = P ({ω : X(ω) < x}) = P ({ω : X(ω) ∈ B})
= P (X −1(B)) =: PX (B)
Für alle zufälligen Ereignisse B ∈ B1 bezeichnen wir
also: PX (B) := P (X −1(B)).
Def. 2.3 Es sei X : Ω −→ R eine zufällige Variable,
(Ω, E, P ) und (R, B1, PX ) seien Wahrscheinlichkeitsräume.
Dann heißt die Funktion
FX (x) := P (X < x) = PX (] − ∞, x[)
Verteilungsfunktion von X.
Bem.: Der Einfachheit halber werden wir die Funktion
FX einfach nur mit F bezeichnen.
Bem.: Manchmal wird die Verteilungsfunktion auch
durch
FX (x) = P (X ≤ x)
definiert (bei SAS z.B.)
102
W.Kössler, Humboldt-Universität zu Berlin
Diskrete Zufallsvariablen
Eine diskrete Zufallsgröße X nimmt höchstens abzählbar viele verschiedene Werte mit positiver Wahrscheinlichkeit an. Das heißt, X ist eine Abbildung der folgenden Form:
X : Ω −→ {xi : i ∈ N} =: W ⊂ R.
Wir notieren das inder Form:

x1 x2 . . . xn . . .
X :

p1 p2 . . . pn . . .
Dabei sind die xi ∈ R die Werte, die die Zufallsgröße
annehmen kann. Die pi sind die Wahrscheinlichkeiten,
mit denen diese Werte angenommen werden. Es gilt:
∞
X
pi = 1,
pi = P (X = xi).
pi ≥ 0,
i=1
Wenn wir Mengen Ai definieren durch
Ai := {ω : X(ω) = xi}, ∀i ∈ N,
so gilt offenbar:
Ai ∩ Aj = ∅,
103
∀i, j ∈ N, i 6= j.
W.Kössler, Humboldt-Universität zu Berlin
Allgemein gilt dann:


 pi, falls x = xi
P (X = x) =

 0, falls x 6= xi
∀xi ∈ W, i ∈ N.
Das bedeutet für die Verteilungsfunktion:
F (x) = P (X
 < x) 
[

= P
Ai
i : xi <x
X
=
P (Ai)
i : xi <x
X
=
pi
i : xi <x
D.h.: Eine diskrete Zufallsgröße, die die Werte {xi : i ∈
N} annimmt, wobei x1 < x2 < x3 < . . . gilt, hat die
folgende Verteilungsfunktion:




0,
falls x ≤ x1
F (x) =
P


 i : x <x pi, falls x1 < x
i
104
W.Kössler, Humboldt-Universität zu Berlin
Betrachten wir eine Menge B ∈ B1, so können wir
feststellen:
PX (B) = P ({ω : X(ω) ∈ B}) =
X
pi .
i : xi ∈B
Bsp. 2.1 Es sei
X:


x1 x2 . . . xn 


1
1
1
... n
n n
Die Zufallsvariable X heißt diskret gleichverteilt auf
der Menge {x1, . . . , xn}.
Bsp. 2.2 Sei Xeine diskrete Zufallsgröße,


0 1 ... n
X: 

p0 p1 . . . pn
mit
n i
P (X = i) = pi =
p ·(1−p)n−i > 0,
i
105
mit 0 < p < 1.
W.Kössler, Humboldt-Universität zu Berlin
Bez. 1
Die Zufallsvariable X heißt binomialverteilt,
bez.: X ∼ B(p, n) oder X ∼ Bi(p, n).
Wir haben oben gesehen, daß
n n
X
X
n i
p (1 − p)n−i = (p + 1 − p)n = 1.
pi =
i
i=0
i=0
Bsp. 2.3 Es sei X eine diskrete Zufallsgröße,


 0 1 . . . n . . .
X: 

p0 p1 . . . pn . . .
mit
λn −λ
P (X = n) = pn = e ,
n!
λ > 0.
Bez. 2 Die Zufallsvariable X heißt P OISSON–verteilt,
bez.: X ∼ P oi(λ).
Wir haben oben gesehen, daß
∞
∞
∞
n
X
X
X
λn −λ
λ
e = e−λ
=1
pn =
n!
n!
n=0
n=0
|n=0{z }
=eλ
106
W.Kössler, Humboldt-Universität zu Berlin
Stetige Zufallsvariablen
Def. 2.4 Eine Funktion f : R −→ R heißt Dichtefunktion,
falls sie die folgenden Eigenschaften hat:
1. Für alle x ∈ R gilt: f (x) ≥ 0.
R
2. Es gilt: f (x) dx = 1.
R
Def. 2.5 Eine zufällige Variable X heißt stetig, falls eine
Dichtefunktion f existiert, so daß gilt:
Zx
P (X < x) = F (x) =
f (t) dt.
−∞
Falls die Funktion f stetig ist, gilt: F 0(x) = f (x).
Bem.: Für die Wahrscheinlichkeit P (X = x) gilt
Zx
P (X = x) = f (t) dt = 0,
x
sogar wenn X den Wert x tatsächlich annehmen kann!
Das heißt jedoch nichts anderes, als daß gilt:
P (X ≤ x) = P (X < x).
107
W.Kössler, Humboldt-Universität zu Berlin
Außerdem gilt:
P (a ≤ X ≤ b) =
Zb
f (t) dt.
a
Veranschaulichung: Es sei X eine stetige Zufallsgröße. Wir teilen den Wertebereich von X in Intervalle Ij ein und beobachten für jeden der Versuche Xi, in
welches der Intervalle Ij der Wert Xi (i = 1, . . . , n)
fällt. Es sei nj = #{Xi ∈ Ij }. Die Länge eines Inter-
valls Ij bezeichnen wir mit ∆(Ij ) = ∆j . Desweiteren sei
∆0 = max{∆j }. Wir definieren nun folgende Funktion:
j
femp.(x) =
nj
n
∆j
, ∀x ∈ Ij .
Dann gilt:
f (x) = n→∞
lim femp.(x).
∆0 →0
Dichtefunktion allg.sas
108
W.Kössler, Humboldt-Universität zu Berlin
Bsp. 2.4 Es sei die Zufallsvariable X auf dem Intervall
[0, 1[ definiert mit der Verteilungsfunktion



0, falls x < 0



F (x) = x, falls 0 ≤ x < 1 .




 1, falls x ≥ 1
Bez. 3 Die Zufallsvariable X heißt auf dem Intervall
[0, 1[ gleichverteilt,
bez. X ∼ R(0, 1) oder X ∼ U (0, 1).
Die Dichtefunktion ist die Funktion f ;



0, falls x < 0



f (x) = 1, falls 0 ≤ x < 1 .




 0, falls x ≥ 1
109
W.Kössler, Humboldt-Universität zu Berlin
Ist X gleichverteilt auf dem Intervall [a, b[, X ∼ R(a, b),
so hat X die Dichtefunktion:



0, falls x < a



1
f (x) = b−a
, falls a ≤ x < b .




 0, falls x ≥ b
Für 0 ≤ a < b < 1 gilt:
P ({ω : X(ω) ∈ [a, b]) = P (a ≤ X ≤ b)
Zb
Z b
1
=
f (x) dx = b−a
dx = 1
a
a
Bsp. 2.5 Die Zufallsvariable X habe die Verteilungsfunktion


 1 − e−λ·x , falls x ≥ 0
.
F (x) =

 0,
falls x < 0
Bez. 4 Die Zufallsvariable X heißt exponentialverteilt,
bez. X ∼ Exp(λ).
110
W.Kössler, Humboldt-Universität zu Berlin
Die Dichtefunktion ist


 λ · e−λ·x , falls x ≥ 0
f (x) = F 0(x) =
.

 0,
falls x < 0
Weiterhin gilt:
lim F (x) = 0,
x→−∞
lim F (x) = 1.
x→+∞
Bsp. 2.6 Sei die Zufallsvariable
X:
(Ω, E, P ) → (R1, B1, PX )
der Meßfehler bei Messung einer physikalischen Konstanten.
Der W.raum (Ω, E, P ) ist ein Modell eines im Hintergrund wirkenden Zufallsmechanismus, der nicht
näher beschrieben werden kann,
Fehler im Meßinstrument
zufällige äußere Einflüsse.
Er enthält alle nicht näher bestimmbaren zufälligen Effekte. Zur Beschreibung dient der Bildraum (R1, B1, PX ).
111
W.Kössler, Humboldt-Universität zu Berlin
Oft kann man annehmen,
PX (B) =
√1
2πσ
Z
− 12 ( t−µ
σ )
e
2
dt.
B
Die Zufallsvariable X mit der Verteilungsfunktion
Zx
1 t−µ 2
−
1
F (x) = √2πσ
e 2 ( σ ) dt.
−∞
heißt normalverteilt mit den Parametern (µ, σ 2),
bez. X ∼ N (µ, σ 2). Die zugehörige Dichtefunktion hat die Form:
f (x) =
1 x−µ
−
1
2( σ )
√
e
2πσ
2
,
σ > 0.
Ist f (x) wirklich eine Dichtefunktion? Offensichtlich ist f (x) ≥ 0 für alle Zahlen x ∈ R und
σ > 0. Es bleibt zu untersuchen, ob gilt:
Z+∞
Z+∞
2
− 12 ( t−µ
1
σ ) dt =
√
lim F (x) =
e
f (t) dt = 1.
2πσ
x→∞
−∞
Wir bezeichnen
Z+∞
1 x−µ
√ 1 e− 2 ( σ )
2πσ
−∞
2
dx =: I.
−∞
112
W.Kössler, Humboldt-Universität zu Berlin
Wir betrachten zunächst:
2

Z+∞
1 x−µ 2
−
2
1

e 2 ( σ ) dx
I = √2πσ
 −∞
  +∞

Z+∞
Z
2
2
− 12 ( x−µ
− 21 ( y−µ
1 
)
)


σ
σ
= 2πσ2
e
dx
e
dy 
=
=
−∞

Z+∞ Z+∞
1
2πσ 2
1
2πσ 2
− 12 ( x−µ
σ )
e

−∞
−∞
Z+∞ Z+∞
− 12 ( x−µ
σ )
e
2
2
−∞
1
dx e− 2 (
− 12 ( y−µ
σ )
y−µ 2
σ
) dy
2
e
dx dy
−∞ −∞
Wir führen nun eine Substitution durch:
s :=
x−µ
σ
t :=
y−µ
.
σ
Dann gilt:
113
x = sσ + µ
y = tσ + µ,
dx = σ ds
dy = σ dt.
W.Kössler, Humboldt-Universität zu Berlin
Wir erhalten damit:
Z+∞ Z+∞
− 12 s2 − 12 t2 2
2
1
e
I = 2πσ2
e
σ ds dt
=
1
2π
−∞ −∞
Z+∞ Z+∞
− 12 (s2+t2 )
e
ds dt
−∞ −∞
Wir führen eine weitere Substitution durch, Polarkoordinaten:
s = r cos ϕ
t = r sin ϕ.
Dann gilt allgemein nach der Substitutionsregel:
Z Z
Z Z
g(s, t) ds dt =
g(r, ϕ) det J dr dϕ,
114
W.Kössler, Humboldt-Universität zu Berlin
det J = |J| = ∂s
∂r
∂t
∂r
∂s cos ϕ −r sin ϕ ∂ϕ =
sin ϕ r cos ϕ ∂t ∂ϕ = r cos2 ϕ + r sin2 ϕ
= r(cos2 ϕ + sin2 ϕ) = r
2
I =
=
=
=
1
2π
1
2π
1
2π
1
2π
Z2π Z∞
0 0
Z2π Z∞
0 0
Z2π 0
Z2π
− 12 (r2 cos2 ϕ+r2 sin2 ϕ)
e
− 12 r2
e
r dr dϕ
−e
∞
dϕ =
1
2π 2π
2
− r2
r dr dϕ
dϕ
(durch Differentiation leicht nachvollziehbar!)
0
=1
0
=⇒
115
I = 1, d.h. f ist eine Dichtefunktion.
W.Kössler, Humboldt-Universität zu Berlin
Zusammenfassung (Zufallsvariable).
Eine (meßbare) Abbildung
X:
Ω −→ R
heißt Zufallsvariable.
Jedem Element ω des Stichprobenraumes Ω wird eine
reelle Zahl zugeordnet.
Def.: Die Zufallsvariable X heißt diskret, wenn X nur
endlich viele oder abzählbar unendlich viele Werte xi annehmen kann. Jeder dieser Werte kann mit
einer gewissen Wkt. pi = P (X = xi) auftreten.
Bsp.: - geografische Lage (N,O,S,W)
- Länge einer Warteschlange
- Anzahl der erreichten Punkte in der Klausur.
116
W.Kössler, Humboldt-Universität zu Berlin
Def.: Die Zufallsvariable X heißt stetig, falls X beliebige Werte in einem Intervall (a, b), [a, b], (a, b], (a, b],
(−∞, a), (b, ∞), (−∞, a], [b, ∞), (−∞, ∞) an-
nehmen kann.
Bem.: Jeder einzelne Wert xi ∈ (a, b) (oder in einem der
anderen Intervalle) hat die Wkt. Null.
Die Verteilungsfunktion F wird dann durch die sogen.
Dichtefunktion f beschrieben,
Z
F (x) = P (X ≤ x) =
x
f (t) dt
−∞
117
W.Kössler, Humboldt-Universität zu Berlin