Festk0203_11 93 4/17/2003 Mit zunehmender Temperatur

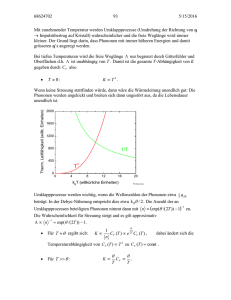
Festk0203_11
93
4/17/2003
Mit zunehmender Temperatur werden Umklappprozesse (Umdrehung der Richtung von q
→ Impulsübertrag auf Kristall) wahrscheinlicher und die freie Weglänge wird immer
kleiner. Der Grund liegt darin, dass Phononen mit immer höheren Energien und damit
grösseren q’s angeregt werden.
Bei tiefen Temperaturen wird die freie Weglänge Λ nur begrenzt durch Gitterfehler und
Oberflächen d.h. Λ ist unabhängig von T . Damit ist die gesamte T-Abhängigkeit von K
gegeben durch CV also
•
T ≈ 0:
K ∝T 3.
Therm. Leitfähigkeit (willk. Einheiten)
Wenn keine Streuung stattfinden würde, dann wäre die Wärmeleitung unendlich gut: Die
Phononen werden angekickt und breiten sich dann ungestört aus, da die Lebensdauer
unendlich ist.
2000
1600
1200
800
1/T
400
T
0
0
4
3
8
12
16
kB T (willkürliche Einheiten)
20
File Gauss.opj
Umklappprozesse werden wichtig, wenn die Wellenzahlen der Phononen etwa 14 q ZB
beträgt. In der Debye-Näherung entspricht dies etwa k Bθ / 2 . Die Anzahl der an
Umklappprozessen beteiligten Phononen nimmt dann mit n ≈ (exp(θ /( 2T )) − 1) zu.
Die Wahrscheinlichkeit für Streuung steigt and es gilt approximativ
−1
Λ ∝ n = exp(θ /( 2T )) − 1 .
−1
•
Für T ≈ θ ergibt sich:
θ
1
2T
K∝
C (T ) ∝ e CV (T ) ,
n V
dabei ändert sich die
Temperaturabhängigkeit von CV (T ) ∝ T 3 zu CV (T ) = const .
•
Für T >> θ :
K∝
θ
θ
CV ∝ .
T
T
Festk0203_11
94
4/17/2003
Λ nimmt mit T 3 zu, durchläuft ein Maximum und nimmt dann zuerst exponentiell und
dann umgekehrt proportional mit der Temperatur ab. Einfache Betrachtungsweise: An
der “heissen” Seite werden Phononen mit dem Wärmeinhalt ∆Q ∝ CV ∆T ausgesandt
und werden dann gestreut. Mit Umklappprozessen besteht dann eine Wahrscheinlichkeit,
dass sich das Phonon wieder in Richtung der heissen Seite bewegt, es bringt also keine
Wärmeenergie zur “kalten” Seite.
In einer Übungsaufgabe wird die freie Weglänge für Diamant ( c ≈ 1000 m/s) abgeschätzt
und man erhält:
•
•
T = 100 K (maximale Leitfähigkeit, K ≈ 100 W/cm/K, CV ≈ 0.1 J/mol/K):
l ≈ 1 mm
T = 300 K: ( K ≈ 0.1 W/cm/K, CV ≈ 10 J/mol/K):
l ≈ 10 nm
3.14. Extrem anharmonische Systeme
Für kristalline Materialien ist die harmonische Approximation eine gute Näherung um
thermische Eigenschaften und Gitterschwingungen von Kristallen zu verstehen.
Insbesondere kann zum Beispiel die Temperaturabhängigkeit von CV ∝ T 3 erklärt
werden. Im Gegensatz dazu beobachtet man in Gläsern bei tiefen Temperaturen CV ∝ T
(wie Elektronen in Metallen bei T ≈ 0 K). CV ist auch viel grösser als in Kristallen.
Festk0203_11
95
4/17/2003
Offenbar sind in Gläsern Freiheitsgrade vorhanden, die man nicht harmonischen
Oszillatoren zuordnen kann. In der Figur ist eine mögliche Struktur für ein SiO 2 -Glas
aufgezeichnet. Das Fehlen der Periodizität kann zu lokalen Anregungen wie angedeutet
führen. Die Positionen x1 und x 2 haben die potentiellen Energien E1 und E2 .
Mit zunehmender Temperatur kann das rote Atom immer leichter zwischen x1 und x 2 hin
und her springen. Wir haben hier das Modell eines Zweiniveau-Systems.
Berechnen wir also im folgenden die spezifische Wärme von N gleichen ZweiniveauSystemen.
Die Niveaux sind immer besetzt:
N1 + N 2 = N = const .
Im thermodynamischen Gleichgewicht ist dann ( E2 − E1 = ε )
N 1 N − N 2 e − E1 /(k BT )
=
= −E2 /( k BT ) = e ( E2 − E1 ) /( kB T ) = e ε /(k BT ) .
N2
N2
e
N
N − N2
N
Man erhält damit über 1 =
⇒
N 2 = ε /( k T )
.
N2
N2
e B +1
Die Energie des ganzen Ensembles beträgt
Festk0203_11
96
4/17/2003
U = N 1E1 + N 2 E2 = ( N − N 2 ) E1 + N 2 E 2 = N 2ε + NE1 =
N
e
ε /( k BT )
+1
ε + const .
Damit erhält man für die spezifische Wärme:
2
 ε 
Nε
e ε /(k BT )
 ∂U 
 ∂ 

CV = 
= Nk B 
.
 =
 ε /(k B T )
ε /( k BT )
+1
+ 1) 2
 ∂T  V  ∂T  e
 k B T  (e
Spezifische Wärme (arb. units)
0.5
0.4
C/(NkB )
0.3
U/(N ε )
0.2
0.1
0.0
0
1
2
3
k BT/ε
•
•
•
4
File Gauss.opj
k BT << ε : CV ≅ 0 , da die Temperatur nicht ausreichend ist, um das obere Niveau
anzuregen.
k BT >> ε : CV ≅ 0 , da beide Energieniveaux mit je N / 2 besetzt sind. Eine
Temperaturerhöhung ändert die Verteilung nicht mehr.
k BT ≈ ε finden die grössten Besetzungszahländerungen statt. CV weisst bei 0.41
einen Buckel auf. Man beobachtet oft eine sogenannte Schottkyanomalie in
Kristallen, die Atome oder Ionen enthalten, die mit einer Energieänderung von
etwa k BT in einen angeregten Zustand gebracht werden können. Die SchottkyAnomalie überlagert sich dann dem normalen Debye’schen Verlauf.
Offensichtlich kann man mit diesem einfachen Modell die spezifische Wärme in Gläsern
nicht beschreiben.
Im nächsten Schritt beachten wir, dass in einem Glas viele verschiedene Konfigurationen
möglich sind und deshalb eine Verteilung von Zweiniveau-Systemen existieren wird. Wir
nehmen an, dass diese Systeme mit einer einfachen Verteilungsfunktion n (ε ) verteilt
sind, die gegeben ist durch n (ε ) = 1 / ε max für 0 ≤ ε ≤ ε max . n (ε ) ist normiert durch die
Bedingung
∫
∞
0
dε / ε max = 1 .
Damit erhalten wir
∞
n (ε )ε
N
U (T ) = N ∫ dε ε /(k BT )
=
e
+ 1 ε max
0
ε max
∫ dε e
0
ε
ε /(k BT )
+1
=
N
ε max
x max
( k BT )
2
∫ dx e
0
x
x
.
+1
Festk0203_11
97
4/17/2003
Der Integrand fällt mit zunehmendem x so schnell ab, dass wir für unsere Abschätzung
x max durch ∞ ersetzen können. Das Integral wird dann 0.822 und man erhält:
•
U (T ) ≈ 0.822 Nk B2T 2 / ε max und
•
CV (T ) ≈ 1.644 Nk B2T / ε max ∝ T .
Es ist klar, dass diese Betrachtungsweise nur für tiefe Temperaturen gilt. Immerhin liefert
das Model einen Mechanismus, der zu einer linearen Zunahme von CV bei tiefen
Temperaturen führt. Es ist klar, dass zum Beispiel in SiO 2 Glas die Atome nicht
unabhängig schwingen, sondern miteinander korrelierte Bewegungen (≈ Phononen)
ausführen werden. In den letzten Jahren wurden grosse Fortschritte im Verständnis von
Gläsern gemacht, insbesondere mit Hilfe von Neutronenstreuung.
Festk0203_11
98
4/17/2003
4. Elektronenzustände in Kristallen
Ungefähr ¾ der Elemente liegen in der metallischen Form vor währendem die Mehrheit
der Verbindungen nicht-metallisch ist. In diesem Kapitel möchten wir verstehen lernen,
warum ein Material metallisch, isolierend, halbleitend oder halbmetallisch sein kann. Es
ist klar, dass die Elektronen für das chemische Verhalten von Substanzen verantwortlich
sind. Aus diesem Grund müsste man im Prinzip die Schrödingergleichung lösen für rund
1023 Elektronen, die sich im Coulombfeld von ca. 1022 Atomkernen bewegen. Um dem
Pauliprinzip zu genügen, müsste man Lösungen finden, die antisymmetrisch sind in
Bezug auf die Vertauschung der Koordinaten. Diese Aufgabe ist unlösbar. Wir werden
uns im wesentlichen mit der Einelektronnäherung beschäftigen, die trotz ihrer
Einfachheit erstaunlich gut funktioniert.
4.1. Klassische Voraussagen
Unter der Annahme, dass sich die Elektronen in einem Material wie ein klassisches Gas
mit der Geschwindigkeit v (gegeben durch die Maxwell-Boltzmann Verteilung)
bewegen, kann man verschiedene Eigenschaften herleiten:
•
spezifische Wärme: Jedes Elektron hat 3 Freiheitsgrade, also wäre CVelekt = 32 k B .
Die Experimente zeigen, dass die Elektronen nicht wesentlich zur spezifischen
Wärme beitragen, ausser in der Nähe von T = 0 , wo CVelekt ∝ T ist.
•
Elektrische Leitfähigkeit: Ohm’sches Gesetz: j = s E
ne 2τ ne 2 Λ
=
.
m
m v
Für klassisches Gas gilt E ∝ v 2 ∝ T . Also σ ∝ T −1 / 2 . Beobachtet wird σ ∝ T −1
bei Raumtemperatur.
σ =
•
Thermische Leitfähigkeit:
K = 13 ρCV vΛ
Wie vorhin: v ∝ T , also K ∝ T 1/ 2 . Beobachtet wird K = const .
•
Wiedemann-Franz Gesetz: W und F beobachteten bei Raumtemperatur, dass
K / σ für verschiedene Metalle ähnlich sind. Lorenz zeigte dann (L = Lorenz
Zahl):
Festk0203_11
99
4/17/2003
2
K
k 
L=
= 3 B  . Erstaunlicherweise stimmte diese Zahl sehr gut mit dem Wert
σT
 e 
2
π 2  kB 
WO
aus der Theorie der freien Elektronen überein: L =
  = 2.45 ⋅10 −8 2 .
3  e 
K
•
Halleffekt: Wenn ein Strom durch einen Leiter fliesst, werden die Elektronen
durch das Magnetfeld abgelenkt. Sie erfahren dabei eine Kraft in die − y Richtung:
e
F = − v ×H .
c
Die Ladung e = 1.602 ⋅ 10 -19 C ist dabei eine positive Zahl. Es entsteht ein
elektrisches Feld
−1
E = RH j x mit der Hallkonstanten RH =
.
ne
z
H
y
v
+++++++++++++++++++++
---------------------
I
x
F
E
Dabei bedeutet n die Zahl der Elektronen pro Volumeneinheit. Wenn pro Atom
ein Elektron zum Ladungstransport beiträgt, entspricht n der Dichte der Atome.
Für einige Metalle, wie Na, K, Ag erhält man aus Hallmessungen Werte für n die
typisch 10-20% grösser sind. Andererseits ändert zum Beispiel für Al die
Hallkonstante sogar das Vorzeichen mit zunehmendem Feld! Be liefert ebenfalls
eine negative Dichte. Diese Ergebnisse sind inkompatibel mit dem klassischen
Modell.
4.2. Einelektron-Näherung
Wir betrachten zuerst ein Atom mit der Kernladung Ze , das von N Elektronen umgeben
ist. Die stationären Zustände erhält man dann durch Lösung der Schrödingergleichung
 N Ze 2
h2
e2

−
∆Ψ( r1 , r2 ,...rN ) + − ∑
+∑
 j =1 r j
2m
i ≠ j r j − ri


Ψ = EΨ .


Festk0203_11
100
4/17/2003
Dieses Problem ist nur analytisch lösbar, wenn man die Wechselwirkung zwischen den
Elektronen vernachlässigt. Man spricht dann von unabhängigen Elektronen. Die Lösung
ist dann ein Produkt von N Einelektron-Wellenfunktionen ψ j (r j ) die Lösungen von
−
h2
Ze 2
∆ψ j (r j ) −
ψ j (r j ) = ε jψ j (r j ) .
2m
rj
N
Die Lösung des Vielteilchenproblems hat den Energieeigenwert E = ∑ ε j und die
j =1
Wellenfunktion Ψ = ψ 1 ⋅ψ 2 ⋅ .... ⋅ψ N . Es ist klar, dass die Vernachlässigung der
Coulombwechselwirkung zwischen den Elektronen sowie des Pauli-Prinzips nicht
zulässig ist.
Eine wesentlich bessere Beschreibung der Atome erhält man mit Hilfe der Hartree-Fock
Näherung. Hartree addierte zur potentiellen Energie der Kerne die potentielle Energie des
Elektrons im Ladungsfeld der übrigen Elektronen:
2
e 2 ψ i ( ri )
h2
Ze 2
−
∆ψ j (r j ) −
ψ j (r j ) + ∑ ∫
dτ i ψ j (r j ) = ε jψ j (r j ) .
2m
rj
r j − ri
i≠ j
Mit Hilfe eines selbstkonsistenten Verfahrens kann man dann die EinelektronWellenfunktionen optimieren. Die antisymmetrische Produktwellenfunktion erhält man
dann durch Bestimmung der Determinanten:
ψ 1 ( r1 ) ψ 1 (r2 )
ψ (r ) ψ 2 (r2 )
Ψ= 2 1
...
...
ψ N (r1 ) ψ 2 (r2 )
... ψ 1 (rN )
... ψ 2 (rN )
.
...
... ψ N (r N )
Im Prinzip kann man auch in einem Kristall die Hartree-Fock Methode zur Berechnung
der Einelektronwellenfunktionen anwenden. Die Wellenfunktionen ψ j wären dann als
Kristallorbitale aufzufassen. Auf dieser Ebene muss man aber nicht anfangen.
Um dies zu verstehen, betrachten wir die Elektronenkonfiguration 1s 2 2 s 2 2 p 6 3s von Na.
Wie in der folgenden Figur gezeigt ist, halten sich die Rumpfelektronen 1s 2 2s 2 2 p 6
(Neon) so nahe am Kern auf, dass sie nicht mit den Orbitalen der benachbarten Na Atome
überlappen. Deshalb verhalten sie sich im wesentlichen wie atomare Orbitale, die man
mit Hartree-Fock Methoden berechnen kann. Die 3s Elektronen hingegen überlappen
sehr stark und halten sich bevorzugt zwischen den Atomrümpfen auf. Sie sind nur
schwach an die einzelnen Atome gebunden, d.h. sie sind frei (= delokalisiert).