3. Medizinische Bilddaten

Bildverarbeitung in der Medizin
am Beispiel der (digitalen) Mammographie
Sommersemester 2002
Susanne Maier
Abgabe am 19.06.2002
Betreuender Dozent
Prof. Dr. N. Link
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
1.
2.
Einführung _____________________________________________________ 4
Das Mammographie-System _______________________________________ 5
2.1. Komponenten _______________________________________________ 5
2.2. Arbeitsablauf _______________________________________________ 5
2.3. Bildentstehung ______________________________________________ 5
2.3.1. Erzeugung von Röntgenstrahlen _____________________________ 5
2.3.2. Entstehung des Strahlenbildes ______________________________ 6
2.3.3. Bildverbesserung durch das Streustrahlenraster ________________ 6
2.3.4. Absorption der Strahlung am Bildempfänger ___________________ 7
2.3.5. Umwandlung der Bildinformation im Detektor ___________________ 7
2.3.6. Bildwiedergabe __________________________________________ 7
2.4. Workstation ________________________________________________ 7
2.5. Bildkommunikation und Archivierung _____________________________ 7
2.6. Software ___________________________________________________ 8
3. Medizinische Bilddaten ___________________________________________ 8
3.1. Das 2D-Bild ________________________________________________ 8
3.2. Das Mammogramm __________________________________________ 8
4. Auswertung der Bilder (allgemein) __________________________________ 9
4.1. Phasen des Erkennungsprozesses ______________________________ 9
4.2. Methoden zur Bewertung der Erkennungsleistung von
Mustererkennungssystemen ________________________________________ 12
4.2.1. Hold-out-Methode _______________________________________ 13
4.2.2. Leaving-one-out-Methode (Spezialfall der Hold-out-Methode) _____ 13
5. Bildanalyse/Mustererkennung (automatisiert) _________________________ 14
5.1. Mögliche Mustererkennungsaufgaben bei Mammogrammen __________ 14
5.2. Texturanalyse zur Detektion gruppierter Mikroverkalkungen bei der
Brustkrebsfrüherkennung __________________________________________ 15
5.2.1. Mustererkennungsaufgabe ________________________________ 15
5.2.2. Klassifikation ___________________________________________ 15
5.2.3. Vorverarbeitung_________________________________________ 15
5.2.4. Merkmalsselektion ______________________________________ 17
5.2.5. Klassifikatorauswahl _____________________________________ 18
5.2.6. Texturanalyse __________________________________________ 18
5.2.7. Test/Ergebnisse ________________________________________ 19
6. Analyse-Werkzeug (Baukasten-System) – Komponentensoftware _________ 20
6.1. Neuronale Netze ___________________________________________ 21
6.2. Fuzzy-Bildverarbeitung_______________________________________ 22
6.3. Editoren __________________________________________________ 24
6.4. Programmierumgebung ______________________________________ 25
6.5. Baukasten-System Zusammenfassung __________________________ 25
7. Anforderungen an Komponentensoftware ____________________________ 26
8. Zusammenfassung _____________________________________________ 27
9. Glossar ______________________________________________________ 28
10.
Literaturverzeichnis ___________________________________________ 31
Seite 2 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
Vorwort
Bildverarbeitung für die Medizin ist ein Workshop, der sich in den letzten Jahren
durch viele erfolgreiche Veranstaltungen als ein interdisziplinäres Forum für die
Präsentation und Diskussion von Methoden, Systemen und Anwendungen im
Bereich der medizinischen Bildverarbeitung einen Namen gemacht hat. Grundlage
meiner Arbeit sind drei im Workshop 2001 vorgestellte Themen, die in der Reihe
Informatik aktuell herausgegeben wurden.



Texturanalyse zur Detektion gruppierter Mikroverkalkungen bei der
Brustkrebsfrüherkennung
Ein Baukasten zur Analyse medizinischer Bilddaten mit Hilfe neuronaler Netze
und Fuzzy-Logik
Konsequenzen des Medizinproduktegesetzes für die Erstellung von
Bildverarbeitungssoftware: Qualitätssicherung gemäß ISO-9001 als
Lösungsansatz
Mitherausgeber von „Bildverarbeitung für die Medizin 2001“ war Heinz Handels vom
Institut für Medizinische Informatik in Lübeck, der gleichzeitig der Autor von
„Medizinische Bildverarbeitung“ ist. Aus diesem Werk stammen auch die
Zusammenfassung, Bilder und Zitate u. a. auch die Vorgehensweise beim
Verarbeiten von medizinischen Bildern (Phasen des Erkennungsprozesses).
Seite 3 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
1.
Einführung
Zur Zeit erkranken in Deutschland etwa 46 000 Frauen jährlich an Brustkrebs und
18000 sterben an dieser Krankheit (Robert Koch Institut, www.rki.de). Damit ist in
Deutschland Brustkrebs die häufigste Krebserkrankung bei Frauen.
Eine Maßnahme, die zur Reduktion der Mortalität beitragen könnte: die zusätzliche
Einführung von Früherkennungsmaßnahmen. Deswegen wird seit einigen Jahren in
Deutschland heftig über die Durchführung von MammographieReihenuntersuchungen (Mammographiescreening) diskutiert. Eine Einführung von
flächendeckenden Screeninguntersuchungen, wie bereits in etlichen Ländern (USA,
Kanada, Niederlande, usw.) erfolgte, sollte nach einem bestimmten „Programm“
durchgeführt werden, um eine einheitliche Qualitätssicherung und Evaluation zu
gewährleisten. Jedoch stehen bereits jetzt – vor Einführung der
Reihenuntersuchungen - Unmengen von röntgenologischen Aufnahmen der
weiblichen Brust zur Befundung an.
Dies erhöht natürlich die Anforderungen an die Auswerter. Ziel ist es, mit so
geringem Kostenaufwand wie möglich eine bestmögliche Diagnosesicherheit zu
erlangen.
Optimal dafür geeignet sind Mammographie-Analysesysteme, die die Probleme der





Bilddatenerzeugung,
Bilddatenaufbereitung,
Bildinterpretation,
Visualisierung und
Archivierung der angefallenen Datenmenge bewältigen können.
Eine rechnergestützte Befunderhebung soll dem Untersucher die Befundung der
Aufnahmen erleichtern bzw. eigenständig mit Hilfe von Interpretationsalgorithmen
eine automatisierte Doppelbeurteilung zur Sicherungen der Auswertequalität
ermöglichen.
Die folgenden Kapitel sollen einen Einblick in ein Mammographie-System
(Komponenten, Bildentstehung) gewähren, wobei das Hauptaugenmerk auf die
Systemkomponenten richten, die für die medizinische Bildverarbeitung notwendig
sind. Es soll die allgemeine Vorgehensweise zur Auswertung von medizinischen
Bilddaten vorgestellt werden. An einem speziellen Beispiel (Detektion von Mikrokalk)
wird das Vorgehen für eine automatisierte Befunderhebung gezeigt. Es folgt noch
eine kurze Beschreibung einer Komponentensoftware für die medizinische
Bildverarbeitung mit Fuzzy-Logik und neuronalen Netzen. Im Anschluss an diese
Themen steht noch ein Hinweis auf die Notwendigkeit der Produktdokumentation (z.
B. mit Hilfe eines Qualitätsmanagement-Systems) um den Vorgaben des
Medizinproduktegesetzes zu entsprechen.
Seite 4 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
2.
Das Mammographie-System
2.1.
Komponenten
Zu den wichtigsten Komponenten eines digitalen Mammographie-Systems gehören:




2.2.
Mammographiegerät
CCD-Kamera
Workstation
Software
Arbeitsablauf
Mittels digitaler Mammographie werden digitale Bilddateien erzeugt und via DICOMDatenaustausch direkt in einen Bildserver übernommen. Für die Digitalisierung
konventioneller Filme werden hoch auflösende Röntgenfilmscanner (10LP/mm, OD
0,03-4,1) angeboten. Anschließend können mit Hilfe von Bildanalyseverfahren die
Bilddateien für die Befundung vorbereitet werden. Die Befundung der Aufnahmen
findet an der Mammographie-Diagnostikworkstation mit den integrierten
Spezialwerkzeugen für die computerassistierte Diagnose bereit.
Zur Archivierung der angefallenen Datenmengen gibt es mehrere Möglichkeiten (je
nach Anforderungen an Zugriffszeiten und Archivierungsdauer) :





2.3.
Bildserver
CD-Juke-Box (zur Ergänzung des Bildservers)
Band/MOD-Roboter
RAID-Systeme
...
Bildentstehung
Da die röntgen-physikalischen Eigenschaften von Gewebe, d. h. die der Absorption
und Streuung bekannt sind, ist es möglich den Prozess der Bildentstehung
vollständig zu beschreiben.
2.3.1. Erzeugung von Röntgenstrahlen
Elektronen werden aus einer beheizten Kathode emittiert und durch Anlegen einer
Spannung (bei Mammographien mit Belichtungsautomatik ca. zwischen 24 und 30
kV) auf die Anode beschleunigt. Beim Auftreffen von Elektronen auf Materie (Anode)
werden diese abgebremst und verlieren Energie. Im wesentlichen unterscheidet
man drei verschiedene Verlust-Prozesse:
Seite 5 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne

"Zusammenstoß" mit äußerem Elektron der Atomhülle
Dabei übergibt das primäre Elektron einen Teil seiner Energie auf eines der
Hüllenelektronen, die wiederum weitere Ionisationen auslösen können. Die
übertragene Energie erscheint schließlich als Wärmeenergie (Anodenkühlung
notwendig).

Übertragung der Energie auf ein kernnahes Elektron.
Für die Ionisation sind hier größere Energiebeträge notwendig. Das erzeugte
"Loch" der Atomhülle ist nicht stabil und wird durch ein anderes Elektron
wieder aufgefüllt --> charakteristische Röntgenstrahlung (Bedeutung bei
manchen Mammographieröhren).

Abgabe der Energie durch Abbremsung im elektrischen Feld des Atomkerns
Diese durch Abbremsung verlorene Energie wird in Form eines einzelnen
Photons, als sog. Röntgenbremsstrahlung emittiert.
Die Höhe der Röhrenspannung, das Anodenmaterial sowie die Art und Dicke des
verwendeten Filtermaterials bestimmen die Transparenz, mit der das darzustellende
Gewebe im Bild wiedergegeben wird. Form und Größe des Brennflecks legen
zusammen mit der Aufnahmegeometrie das mit dem Aufnahmesystem maximal
erreichbare Auflösungsvermögen fest.
2.3.2. Entstehung des Strahlenbildes
Die Möglichkeit, Gewebe im Bild wiederzugeben, liegt in den
Absorptionseigenschaften des Gewebes für Röntgenstrahlung begründet. Die
Intensitätsverteilung der Röntgenstrahlung in der Ebene unmittelbar hinter der
Mamma stellt das Strahlenbild des Gewebes dar. Die von der Röntgenröhre
emittierte Röntgenstrahlung hat bei der Durchdringung des Brustgewebes durch
Absorption und Streuung eine Modulation erfahren. Die aus der Mamma wieder
austretende Strahlung enthält in der Intensitäts- und Richtungsverteilung bereits alle
mit Röntgenstrahlung erzielbaren Informationen über das Gewebe. Auf den weiteren
Weg bis zur Bildwiedergabe kann keine neue Bildinformation mehr gewonnen
werden, sondern nur noch Information bewusst hervorgehoben bzw. unterdrückt
werden.
2.3.3. Bildverbesserung durch das Streustrahlenraster
Die aus der Mamma austretende Strahlung besteht aus Primärstrahlung, die die
gesamte Bildinformation enthält, und aus Streustrahlung (Streuung – das Photon
ändert seine Richtung). Je größer die Dicke des zu durchstrahlenden Objektes, desto
größer ist die Streustrahlung (deshalb Kompression der Brust in der
Mammographie). Die Streustrahlung vermindert vor allem den Strahlenkontrast, da
sie als Schleier über dem Röntgenbild liegt. Bevor die aus der Mamma austretende
Strahlung den Bildempfänger trifft, erfährt sie die erste Modifikation: Die
Streustrahlung wird durch ein Raster teilweise unterdrückt und trifft anschließend auf
den Bildempfänger. Streustrahlenraster bestehen aus einer Anordnung von dünnen
Bleilammellen und einem möglichst wenig absorbierenden Schachtmedium. Die
Durchlässigkeit der Nutzstrahlung hängt von der Dicke der im Raster befindlichen
Bleilamellen und der Durchlässigkeit der Zwischenschichten ab. Die Wirksamkeit des
Rasters wird dagegen vom Schachtverhältnis, d. h. der Höhe der Bleilamellen und
Seite 6 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
deren Abstand, sowie der Dicke der Bleilamellen bestimmt. Die Ausrichtung der
Bleilamellen sind auf einen bestimmten Abstand abgestimmt, „fokussiert“. Bei
Anwendung eines Streustrahlenrasters ist jedoch eine höhere Strahlendosis
notwendig, da auch Nutzstrahlung absorbiert wird.
2.3.4. Absorption der Strahlung am Bildempfänger
Im Bildempfänger werden die einfallenden Röntgenquanten teilweise absorbiert und
die Bildinformation an andere Informationsträger weitergegeben: bei den
Verstärkungsfolien sind dies durch Lumineszenz entstehende Lichtquanten, bei
einigen digitalen Detektoren sind es Elektronen. Je mehr freie Elektronen pro
Röntgenquant (bei den direkt umwandelnden digitalen Detektoren) erzeugt werden,
desto empfindlicher ist das bildgebende System (physikalische Kenngröße zur
Beschreibung des Wirkungsgrads dieser Signalumwandlung: DQE detective
quantum efficiency).
2.3.5. Umwandlung der Bildinformation im Detektor
Die im Detektor erzeugten Lichtquanten bzw. Sekundärelektronen können nicht
direkt zur Bildwiedergabe genutzt werden. Die Information muss an einen weiteren
geeigneten Informationsträger übergeben werden. Es können mehrere Schritte
notwendig sein, bis ein latentes Bild für die Entwicklung im weiteren Sinn zur
Verfügung steht. Das latente Bild (Rohbild) bei der digitalen Bildgebung ist die
Verteilung der Zahlenwerte je Pixel im Speicher des Bildrechners. Die Zahlenwerte
entsprechen der absorbierten Energie pro Pixel bzw. dem daraus resultierenden
Signalwert.
2.3.6. Bildwiedergabe
Das digitale Rohbild befindet sich jetzt im Speicher des Bildrechners und kann dort
auch gesichert werden; bis zur Bildwiedergabe am Monitor werden aber noch weitere
Bildverarbeitungsschritte benötigt. Das digitale Bild kann nach Umsetzung der
Zahlenwerte/Pixel in Grauwerte/Pixel am Monitor oder als Hardcopy auch am
Schaukasten betrachtet werden.
2.4.
Workstation
Speziell für die Mammographie werden Workstations angeboten, die für den Einsatz
in kurativer und Screening-Mammographie optimiert sind. Die Diagnostikworkstation
ist mit hochauflösenden Monitoren für die Monitorbefundung (softcopy-reading)
ausgestattet und besitzt eine für die Mammographie entwickelte Oberfläche.
2.5.
Bildkommunikation und Archivierung
Ziel der Bilddaten-Kommunikation ist es, die Daten jedem, der eine
Zugangsberechtigung hat, überall und jederzeit zur Verfügung zu stellen. In der sog.
Teleradiologie geht es u. a. auch darum, eine Befundung von Bilddaten gemeinsam
mit anderen über die ganze Erde verteilten Experten durchführen zu können. Hierbei
stellen sich natürlich insbesondere die Fragen nach Datensicherheit,
Verschlüsselungstechniken und Zugangsrechten.
Seite 7 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
Moderne Klinikbetriebe verfügen über Picture Archiving and Communication Systems
(PACS), in denen diagnostische Bilddaten archiviert sind. Die aufgenommenen Bilder
werden in den überwiegenden Fällen im DICOM-Format abgespeichert. Der
Datenaustausch zwischen dem PACS und den Aufnahmesystemen, sowie zu den
Bildschirmarbeitsplätzen erfolgt über DICOM-Kommunikationsschnittstellen.
2.6.
Software
Die Workstations können mit Software für die Bildverarbeitung und Bild-/PatientenDatenmanagement ausgerüstet werden. Aufgrund der großen Datenmengen,
besonders im Hinblick auf die Teleradiologie, sind Bildkompressionsverfahren
notwendig.
Eine Möglichkeit, wie eine Komponenten-Software für ein MammographieAnalysesystem konzipiert sein könnte, ist im später noch folgenden Abschnitt
„Analyse-Werkzeug (Baukasten-System) – Komponentensoftware“ beschrieben.
Zunächst jedoch soll Grundsätzliches über die der medizinischen Bilddaten und Ihre
Analyse ausgeführt werden.
3.
Medizinische Bilddaten
3.1.
Das 2D-Bild
Digitale Bilder werden zumeist in einer zweidimensionalen Matrix mit Nx Zeilen und Ny
Spalten dargestellt. Die Bildpunkte werden als Pixel (engl. picture element)
bezeichnet. Die Anzahl der Bildpunkte bestimmt die Auflösung des Bildes. Eine
weitere, wichtige Kenngröße ist die Grauwerttiefe, die angibt, wie fein diskretisiert die
gemessenen Signale in der Bildmatrix repräsentiert werden können. Es können in
der medizinischen Bildverarbeitung drei wichtige Spezialfälle unterschieden werden.
Grauwertbild
Das Grauwertbild mit meistens g = 256 Grauwerten. Abweichend von diesem in der
Bildverarbeitung verbreiteten Standard werden in der medizinischen Anwendung die
gemessenen Signale auch in 12-Bit Tiefe mit g = 4096 Messwertabstufungen erfasst.
(z. B. Computer- und Magnetresonanztomographie).
Parameterbild
Bei einer Vielzahl spezieller Bildanalyse- und Auswerteverfahren können einzelnen
Bildpunkten neue Merkmale bzw. Parameter zugeordnet werden, die in
Parameterbildern (parameter maps) dargestellt werden (z. B. Texturparameter zur
Charakterisierung lokaler Textureigenschaften).
Indexbild
Indexbilder werden z. B. durch Segmentierungs- oder Klassifikationsalgorithmen
generiert. (Spezialfall des Indexbildes imax = 2  das Binärbild).
3.2.
Das Mammogramm
Seite 8 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
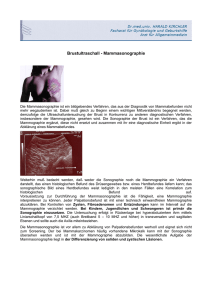
Bei der Mammographie werden Röntgenbilder der Brust angefertigt. Von jeder Brust
werden 2 Aufnahmen von oben (cranio-caudal, cc) und schräg von der Seite
(oblique, obl) erstellt. Das Komprimieren der Mammae ist für eine gute Qualität der
Mammogramme erforderlich. Durch Kompression wird die Brust wesentlich dünner,
so dass sie über ein großes Areal die gleiche Dicke hat. Vorteile in Bezug auf die
Bildauswertung:




Reduzierung der Streustrahlung  besserer Kontrast
Geringere Unschärfe durch günstigere Geometrie
Weniger Überlagerungen
Störungen der Architektur besser sichtbar
Ein Standardmammogramm digitalisiert mit einer Auflösung von 450 dpi hat etwa
eine Ausdehnung von 4000 x 3000 Bildpunkten.
4.
Auswertung der Bilder (allgemein)
4.1.
Phasen des Erkennungsprozesses
Bei der computergestützten Analyse und Interpretation von Mustern in medizinischen
Bilddaten werden folgende Phasen des Analyseprozesses unterschieden:



Bildvorverarbeitung
Bildanalyse
Klassifikation und Bildinterpretation
Die Bildvorverarbeitung ist stark von der Problemstellung und dem zu analysierenden
Bilddatenmaterial abhängig und wird, falls notwendig, zur Verbesserung der Qualität
der Bilddaten im Hinblick auf die nachfolgenden Analyseschritte eingesetzt. Spezielle
Aufgaben der Vorverarbeitung können z. B. die Reduzierung des Rauscheinflusses,
das Entfernen von Artefakten und Störeinflüssen, die Verbesserung des
Bildkontrastes, die Skalierung des Grauwertbereiches oder die Normierung der
Bildgröße sein.
Die Bildanalyse beinhaltet die Segmentierung von Bildobjekten und sorgt für ihre
quantitative Beschreibung. Für die Segmentierung hat sich eine Vielzahl
verschiedener Verfahren herausgebildet, da die Komplexität der Problematik
einerseits, sowie eine starke Abhängigkeit der Bilddaten und den zu extrahierenden
Objekten andererseits, vorliegt. Methodisch können kantenorientierte,
regionenorientierte, clusteranalytische sowie klassifikatorbasierte
Segmentierungsansätze unterschieden werden. Die Segmentierung bildet den ersten
Schritt zu einer weitergehenden Bildinterpretation, da sie den Übergang von
unstrukturierten Pixelmengen zu interpretierbaren Objekten bzw. Segmenten
realisiert.
Für die quantitative Beschreibung segmentierter Bildobjekte und –strukturen können
objektbezogene Bildanalyseverfahren eingesetzt werden. Durch die extrahierten
Merkmale werden charakteristische Objekteigenschaften verdichtet dargestellt.
Seite 9 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
Für die Erkennung und Klassifikation werden die analysierten Muster durch ndimensionale Vektoren
 m1 
 
. 
m   .   WM
 
. 
 
 mn 
beschrieben. Der Merkmalsraum WM beschreibt den Wertebereich der
Merkmalsvektoren. Bei n Merkmalen M1,...,Mn mit den Wertebereichen WM1 ,...,WM n ist
er gegeben durch:
WM  WM1  ...  WM n
Durch numerische Klassifikationsverfahren werden die untersuchten Bildobjekte bzw.
die aus ihnen extrahierten Merkmalsvektoren auf der Basis einer vorklassifizierten
Stichprobe S  m, WM   einer von k vordefinierten Klassen 1 ,...,  k
zugeordnet, die die Menge der möglichen Interpretationen   1 ,...,  k  vollständig
beschreiben. Die Menge  wird Ereignismenge oder Klassenmenge genannt. In
einem medizinischen Bildanalyse- und Erkennungssystem sind die Klassen durch die
medizinische Fragestellung vorgegeben und repräsentieren verschiedene Typen zu
erkennender Bildstrukturen.
Um ein Mustererkennungssystem problemorientiert zu trainieren, wird eine
Lernstichprobe mit vorklassifizierten Merkmalsvektoren benötigt. Dazu müssen aus
ausgewählten Bilddaten Segmente oder Bildobjekte extrahiert werden, die aufgrund
von Vorwissen eindeutig und korrekt einer Klasse zugeordnet werden können. Zur
Abgrenzung der untersuchten Bildobjekte können Segmentierungsverfahren
eingesetzt werden. Diese sind insbesondere bei Problemstellungen von Bedeutung,
bei denen Objekteigenschaften wie z. B. die Morphologie oder Struktur der
Objektberandung beachtet werden sollen.
Ist eine automatische Segmentierung der Bildstrukturen nicht möglich, können ROI’s
(Regions of Interest) zum Aufbau der Stichproben interaktiv bestimmt werden
(zumeist kreisförmige, rechteckige oder durch Polygone begrenzte Flächen). Die
Bildsegmente werden durch Bildanalyseverfahren charakterisiert und anhand von
Merkmalsvektoren m WM beschrieben. Aufgrund medizinischen Vorwissens oder
ergänzender Untersuchungsergebnissen wird eine manuelle Zuordnung des so
erhaltenen Merkmalsvektors m WM zur einer Klasse    vorgenommen und das
Stichprobenelement (m, ) gespeichert. Während der Trainingsphase justiert der
Klassifikator die Grenzen der Klassenbereiche 1, ..., k im Merkmalsraum unter
Ausnutzung des implizit in der Stichprobe dargestellten Wissens. In der darauf
folgenden Klassifikationsphase werden neu hereinkommende Bilddaten zunächst
analysiert und die interessierenden Muster durch Merkmalsvektoren m WM
beschrieben.
Die Abbildung unten zeigt den Zweiklassenfall im zweidimensionalen Merkmalsraum
(k=2, n=2). Die von einem Klassifikator bestimmte Grenze ist durch eine lineare
Seite 10 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
Funktion beschreibbar und trennt die Merkmalsräume in die Klassenbereich 1 und
2.
M2
2
1
M1
Anhand der extrahierten Merkmalsvektoren wird mit dem trainierten Klassifikator eine
Interpretation des Muster durch Zuordnung zu einer der Klassen 1 ,...,  k
vorgenommen. Es erfolgt eine Überprüfung, in welchem Klassenbereich der zu
klassifizierende Merkmalsvektor m liegt. Ist m  1  WM, so wird er der Klasse i
zugeordnet. Mehrdeutigkeiten treten bei der Klassifikation dann nur bei
Merkmalsvektoren aus den Trennflächen der Klassenbereiche auf. Die Eindeutigkeit
der Klassifikation kann hier durch zusätzliche Klassifikationsregeln oder die
Einführung einer Rückweisungsklasse o erzwungen werden. Entscheidend für den
Klassifikationserfolg ist die Extraktion und Auswahl charakteristischer Merkmale, die
eine Abgrenzung der Merkmalsvektoren verschiedener Objektklassen im
Merkmalsraum ermöglichen.
Bildanalyse
Lern- und Trainingsphase
Bildobjekte mit
Merkmalsvektoren m1
Trainierter
Klassifikator
Klassifikation
Lernkomponente
Stichprobe
Klassifizierte Bildobjekte
(m1, 1)
(m2, 2)
(m3, 3)
Seite 11 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
4.2.
Methoden zur Bewertung der Erkennungsleistung von
Mustererkennungssystemen
In der medizinischen Anwendung werden zur Bewertung von
Mustererkennungssystemen – besonders in der Designphase – quantitative
Maßzahlen benötigt. Sie werden zum Vergleich verschiedener
Klassifikationsverfahren, zur Bewertung der Güte der beim Klassifikationsprozess
verwendeten Merkmale oder alternativ durchgeführter Vorverarbeitungsschritte
innerhalb des Analyseprozesses herangezogen.
Die Erkennungsleistung eines Mustererkennungssystems wird durch die
Gesamtfehlerrate charakterisiert, die einen Schätzer für die
Gesamtfehlklassifikationswahrscheinlichkeit (kurz
Fehlklassifikationswahrscheinlichkeit) bildet. Die
Fehlklassifikationswahrscheinlichkeit ist in Abhängigkeit vom verwendeten
Klassifikator Klass definiert durch
k
eKlass  1    p(m |  i ) p( i )dm
i 1 i
k = Anzahl der Klassen , p(i) a priori Wahrscheinlichkeit
p(m|i) klassenbedingte Wahrscheinlichkeitsdichte für die Klasse i
i  WM (i{1,...,k}) durch den Klassifikator ermittelten Klassenbereich der Klasse i
im Merkmalsraum WM
Als komplementäre Maßzahl zu eKlass kann die Trefferwahrscheinlichkeit TKlass, auch
Klassifikationsleistung genannt, verwendet werden:
k
TKlass    p (m |  i ) p ( i )dm  1  eKlass
i 1 i
Zwei Methoden zur Schätzung der Fehlklassifikationswahrscheinlichkeiten auf der
Basis einer Stichprobe sind die Hold-out-Methode und Leaving-one-out-Methode, die
die Bewertung der Generalisierungsleistung eines Mustererkennungssystems
ermöglichen. Sie basieren auf folgender Überlegung:
Werden die Elemente einer s-elementigen Stichprobe S={(mi,)| mi  WM, i = 1,...,s,
 } klassifiziert, so kann unter der Annahme, dass die Merkmalsvektoren
stochastisch unabhängig voneinander sind, die Wahrscheinlichkeit für das Auftreten
von sf Fehlklassifikationen durch die Binomialverteilung beschrieben werden:
s
pe ( s f )  
sf

(eKlass ) s f (1  eKlass ) s s f


Der relative Anteil falsch klassifizierter Stichprobenelemente ist die Gesamtfehlerrate
êKlass:
sf
ê Klass 
s
Seite 12 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
4.2.1. Hold-out-Methode
Dabei wird die Schätzung der Fehlklassifikationswahrscheinlichkeit auf der Basis
einer Teststichprobe T={(mi, )WM  | i = 1,...,t } mit t Mustern vorgenommen, die
zur Lernstichprobe L, mit der der Klassifikator trainiert wird, disjunkt ist. Hierzu wird
die Stichprobe S zumeist vollständig in eine Lern- und eine Teststichprobe zerlegt, so
dass gilt:
T L 
 T L S
Durch die Verwendung der Teststichprobe bei der Fehlerratenschätzung wird
überprüft, ob der Klassifikator aus der Lernstichprobe die Zusammenhänge zwischen
Merkmalsvektoren und Klassenzugehörigkeit generalisieren konnte und somit in der
Lage ist, neue, für den Klassifikator unbekannte Muster zu erkennen.
Zu beachten ist, dass für die Hold-out-Methode relativ umfangreiche Stichproben
benötigt werden. Falls diese nicht zur Verfügung stehen, können, um die
Fehlerratenschätzung zu stabilisieren und zufallsbedingte Einflüsse auf die
Schätzung zu reduzieren, die Fehlerratenbestimmung mehrfach unter Verwendung
verschiedener, zufällig bestimmter Test- und Lernstichproben wiederholt werden.
Hierbei ergibt sich die resultierende Fehlerrate aus dem Mittelwert der geschätzten
Fehlerraten (k-fache Kreuzvalidierung).
4.2.2. Leaving-one-out-Methode (Spezialfall der Hold-out-Methode)
Die Leaving-one-out-Methode wird auch als totale Kreuzvalidierung bezeichnet.
Hierbei besteht die Teststichprobe stets aus t = 1 und die Lernstichprobe aus l = s – 1
Elementen. Das Teststichprobenelement wird solange variiert, bis alle Elemente der
Stichprobe genau einmal als Teststichprobenelement selektiert wurden. Die Anzahl
der zur Fehlerratenschätzung zu trainierenden Klassifikatoren ist daher gleich der
Anzahl der Stichprobenelemente s. Die Fehlerrate ergibt sich als der relative Anteil
der in s Durchläufen falsch klassifizierten Merkmalsvektoren.
Vorteile der Leaving-one-out-Methode:



Robuste und nahezu unverzerrte Schätzung der
Fehlklassifikationswahrscheinlichkeiten
Sowohl für statistische und nicht-parametrische, sowie für neuronale
Klassifikatoren anwendbar
Bewertung und Vergleich der Erkennungsleistung unterschiedlichster
Klassifikatoren
Seite 13 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
5.
Bildanalyse/Mustererkennung (automatisiert)
Medizinische Bildanalysesysteme dienen zur Unterstützung des Arztes in der
Diagnostik und Therapie und werden problemspezifisch zur weitgehend
automatischen Nachverarbeitung medizinischer Bilddaten entwickelt.
5.1.
Mögliche Mustererkennungsaufgaben bei Mammogrammen
Beim Betrachten des Mammogramms ist ein systematisches Vorgehen notwendig,
dass auch den Vergleich mit den Voraufnahmen beinhaltet. Die Hauptziele der
Untersuchungen sind

die Feststellung von Störungen der Architektur und Asymmetrie des
Drüsenkörpers und der Haut

die Charakterisierung von Verdichtungen

und die Analyse von Verkalkungen.
Seite 14 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
Auf der Suche nach den o. g. Veränderungen ist eine Unterstützung des
Untersuchers durch eine rechnergestützte Befunderhebung sehr vorteilhaft. Auch
könnte eine Doppelbeurteilung durch Interpretationsalgorithmen besonders bei
Mammographie-Screeninguntersuchungen (Brustkrebsreihenuntersuchung) nützlich
sein. Zur Auswertung stehen viele unterschiedliche Vorgehensmodelle zur
Verfügung. Einen dieser Ansätze zur automatisierten Beurteilung, inkl. der
detaillierten Darstellung der einzelnen Verarbeitungsschritte, möchte ich hier näher
beschreiben.
5.2.
Texturanalyse zur Detektion gruppierter Mikroverkalkungen bei der
Brustkrebsfrüherkennung
Bei der Untersuchung von Röntgenbildern der Brust dienen Mikroverkalkungen als
erste Hinweise auf einen Tumor. Verkalkungen können überall in der Mamma
vorkommen. Durch die Analyse von Größe (einschließlich Dichte), Anzahl, Form und
Anordnung ist es möglich, einen evtl. malignen Prozess festzustellen. Eine Methode,
mittels Texturanalyse automatisch Merkmale für die Klassifikation zu gewinnen, wird
hier vorgestellt.
5.2.1. Mustererkennungsaufgabe
Eine der bei der Mammographie gesuchten Veränderungen ist das Auftreten
gruppierter Mikroverkalkungen. Eine durchschnittliche Verkalkung hat eine Größe
von etwa 10 Bildpunkten. Gruppierte Mikroverkalkungen können auf Tumore im
Frühstadium mit einer Größe von wenigen Millimetern hinweisen. Gruppierte
Mikroverkalkungen werden von Radiologen manchmal übersehen, da sie aufgrund
geringem Kontrast und überlagertem Gewebe schwer detektierbar sind. Hilfreich ist
dann die Unterstützung durch einen Rechner. Ein Computer kann für eine Region of
Interest (ROI) aus einem Röntgenbild der Brust entscheiden, ob diese
Mikrokalzifikationen enthält.
5.2.2. Klassifikation
Als Klassifikation bezeichnet man die Zuordnung eines Muster zu einer bestimmten
Kategorie. Im Falle der Mammographieuntersuchung wird "überwachtes Lernen" für
die Klassifikation eingesetzt. Dabei wird dem Klassifikationssystem –
Computersystem, dass eine Klassifikation durchführt - eine Anzahl befundeter
Mammogramme als Trainingsdaten übergeben. Nach der Trainingsphase kann das
System selbständig neue, noch unbefundete Mammogramme in Klassen "mit
Mikroverkalkungen" und "ohne Mikroverkalkungen" einordnen.
5.2.3. Vorverarbeitung
Die digitalisierten/digitalen Mammogramme werden durch
Bildverarbeitungsalgorithmen aufbereitet und verbessert. Bei diesem Schritt sollte
das Rauschen entfernt werden und zur Hervorhebung der Mikroverkalkung der lokale
Kontrast verstärkt werden. Die für Mikroverkalkungen charakteristischen Strukturen,
die dem Rauschen sehr ähnlich sind, müssen bei der Rauschunterdrückung erhalten
bleiben (kantenerhaltende Rauschunterdrückung).
Vorgehensweise in diesem Beispiel: lokale Kontrastanpassung und
Rauschunterdrückung mit folgendem Schwellwertverfahren.
Seite 15 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
Die Kontrasterhöhung erfolgt durch eine Grauwertmanipulation. Ausgangspunkt ist
das einkanalige Grauwertbild S = (s(x, y)) mit der Grauwertmenge G = {0, 1,..., 255}.
Eine Grauwertmanipulation ist eine Abbildung f:GG, wobei f die Funktion der
Grauwerttransformation ist, die über G definiert und beschränkt ist (min{f} > -;
max{f} < +).
Beispiel für Grauwerttransformation:
lineare Skalierung der Grauwerte
fn ist (stückweise) linear
0

f n ( x)  255
( x  c )c  c x  c c
1
2
2
1 2

falls c2x + c1c2<0
falls c2x + c1c2<0
sonst
c1 und c2 können mit unterschiedlichen Methoden bestimmt werden. Hier werden sie
aus dem Histogramm des Bildes ermittelt, indem die Bestimmung von min und max,
der minimale und maximale Grauwert des Bildes, durchgeführt wird. Berechnung von
c1 = -min;
c2 = 255/(max-min)
Weitere Grauwerttransformationen



logarithmische und exponentielle Skalierung (nichtlineare Transformation)
Histogrammlinearisierung (Ebnen der Grauwerte – nichtlineare
Transformation),
Kombination einer Grauwertskalierung mit einer Hochpassfilterung.
Geeignet für die Rauschunterdrückung ist ein Glättungsfilter, der die Objektkanten im
gefilterten Bild weitgehend erhält: z. B. der Medianfilter. Der Medianfilter ist ein nichtlinearer Glättungsfilter, bei dem dem betrachteten Pixel (x, y) der Median der in
seiner lokalen Umgebung U(x, y) auftretenden Bildfunktionswerte zugeordnet wird.
Zur Berechnung des Medians werden die in der Umgebung U(x, y) auftretenden
Bildfunktionswerte zunächst aufsteigend sortiert. Der Median ist dann gegeben durch
den in der Sortierung an mittlerer Position stehenden Bildfunktionswert. Der
Medianfilter eliminiert vereinzelte Ausreißer im Bild, d. h. lokale Extrema der
Bildfunktion.
Schwellwertverfahren (Thresholding) gehören zu den Basiswerkzeugen bei der
Verarbeitung von 1-kanaligen 2D-Bildern, die häufig innerhalb umfangreicherer
Abfolgen von Bildverarbeitungsoperationen verwendet werden. Bei der
schwellwertbasierten Segmentierung medizinischer Bildobjekte werden die zu einem
Bildobjekt gehörenden Pixel anhand zweier Schwellwerte tunten und toben in dem Bild
separiert und in einem Binärbild markiert.
Seite 16 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
5.2.4. Merkmalsselektion
Zunächst werden aus den aufbereiteten Bildern alle möglichen Merkmale ohne
Vorwissen und Einschränkung aus den ROI’s extrahiert. Eine Zusammenfassung
aller Merkmale einer ROI wird als Muster bezeichnet. Ein Problem ist, dass unnütze
Merkmale die Abstraktionsfähigkeit des System einschränken und die Gefahr des
Overfitting (Auswendiglernens) besteht. Deshalb werden bei der Merkmalsselektion
die für die Entscheidung wichtigen Merkmale ausgewählt und die Unbedeutenden
verworfen.
Für die Merkmalselektion existieren mehrere Standardalgorithmen. Da aber für die
Bewertung der Texturmerkmale ausreichend ist, eine „gute“ Selektion zu finden, wir
ein „Forward-Select-Verfahren“ (Greedy-Strategie) eingesetzt, bei dem nacheinander
das am besten geeignete Merkmal der selektierten Menge von Merkmalen
hinzugefügt wird.
Greedy-Algorithmen sind polynomiale Algorithmen zur Bestimmung zumeist
suboptimaler Lösungen von Optimierungsproblemen. Die Greedy-Methode kann
allgemein bei Problemen verwendet werden, bei denen aus einer gegebenen Menge
von Eingabewerten eine Teilmenge ermittelt wird, die vorgegebenen
Optimierungskriterien und Bedingungen genügen muss. Die Greedy-Methode kann
auf das Merkmalsauswahlproblem, bei dem maximal m Merkmale aus einer nelementigen Merkmalsmenge selektiert werden sollen, angewandt werden. Dabei
wird iterativ ein Eingabewert nach dem anderen betrachtet und derjenige
ausgewählt, durch dessen Hinzunahme das Gütemaß für die neu gebildete
Teilmenge maximiert wird. Ein Merkmal wird nur dann zur aktuellen Merkmalsmenge
hinzu genommen, falls hierdurch eine Verbesserung des Gütekriteriums erzielt wird.
Gibt es innerhalb eines Iterationsschrittes mehrere Merkmalsteilmengen gleicher
maximaler Güte, so kann in Erweiterung des im unten aufgeführten Pseudocode
angegebenen Grundalgorithmus jede dieser Merkmalsmengen mittels der GreedyStrategie in den nachfolgenden Iterationen erweitert werden.
Pseudocode Greedy-Algorithmus - forward search
Merkmalsmenge M = {M1, ..., Mn}
Gütefunktion G, durch die jeder Merkmalsteilmenge M’ M eine
Güte- oder Bewertungszahl zugeordnet wird.
M’ := Ø; Gmax = 0;
WHILE (|M| > n-m) DO
Selektiere das Merkmal Mi aus M so, dass G(M’{Mi})
maximal wird.
M’ := M’{Mi};
M := M\{Mi};
IF (G(M’)>Gmax THEN Gmax .= G(M’); M’best := M’ END IF
END WHILE
Seite 17 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
5.2.5. Klassifikatorauswahl
Um eine Einteilung in Klassen vornehmen zu können, muss mit Hilfe des
Klassifikators der Merkmalsraum in Unterräume aufgeteilt werden. Es können die
Trennungsgrenzen berechnet werden, wobei z. B. mathematische Formeln die
Trennungsgrenze beschreiben (Annäherungen). Die Annäherung der Klasse im ndimensionalen Merkmalsraum wird je nach Verfahren mehr oder weniger gut sein.
Die Zahl der Klassifikatoren wurde hier auf zwei beschränkt – ein Klassifikator mit
linearer und ein Klassifikator mit quadratischer Funktion. Die ausgewählten
Texturmerkmale wurden aufgrund dieser Klassifikatoren bewertet.
Als Maß für die Abstraktionsfähigkeit eines Klassifikationssystems gilt die
Generalisierung, das Klassifikationsverhalten auf unbekannten Daten. Idealerweise
sollten für die Training- und Testphase ausreichend Daten zur Verfügung stehen, um
eine Klassifikator mit den statistischen Eigenschaften der Merkmale zu trainieren und
um zu testen, wie sich der Klassifikator gegenüber unbekannten Daten verhält. Da
jedoch hier nicht genügend Daten zur Verfügung standen, wurde fast alle
vorhandenen Muster des Datensatzes zum Training benötigt und die
Generalisierungsfähigkeit mit eine vollständigen Kreuzvalidierung geschätzt (siehe
auch Bewertung von Mustererkennungssystemen).
5.2.6. Texturanalyse
Da gruppierte Mikroverkalkungen immer in regelmäßiger Struktur auftreten, liegt es
nahe, automatisch Merkmale aus dieser Regelmäßigkeit zu gewinnen. Die
Regelmäßigkeit wird durch eine gleichmäßige Verteilung von Mikroverkalkungen
innerhalb eines Clusters erzeugt. Diese Eigenschaften spiegeln sich in einer für
Mikroverkalkungen eigenen Textur wider, welche zwar von Gruppe zu Gruppe
unterschiedlich ist, sich aber immer ähnelt.
Der Begriff Textur steht für eine Struktureigenschaft eines Musters oder
Bildbereiches. Typische Texturen sind durch periodisch wiederkehrende Variationen
von Grauwerten bzw. (Teil-)Mustern gekennzeichnet. Methodisch unterscheidet man
statistische und syntaktische bzw. strukturelle Texturanalyseverfahren. In der
medizinischen Bildverarbeitung stehen statistische Texturanalyseverfahren im
Vordergrund, u. a. weil sie den Vorteil haben, auf beliebige Bildmuster anwendbar zu
sein und somit allgemein zur quantitativen Beschreibung medizinischer
Bildstrukturen genutzt werden können.
Eine Methode zur Texturanalyse ist der Einsatz von Cooccurence-Matrizen. Dies ist
eine Möglichkeit eine Charakterisierung von Texturen durch die statistische Analyse
der Auftrittshäufigkeiten von Grauwertübergängen in definierten geometrischen
Anordnungen vorzunehmen. Die relativen Häufigkeiten des Auftretens zweier
Grauwerte in einer festengeometrischen Anordnung werden dann in einer
Cooccurence-Matrix gespeichert.
Beispiel:
B Bildmatrix 6x6  Grauwertmenge G={0,1,2,3}  q=4 verschiedene Grauwerte
K=2q = 16 mögliche Wertekombinationen. Positionsoperator P1,0 (rechte Nachbar
Relation).
Seite 18 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
Betrachtet man - unter Berücksichtigung der rechten Nachbar Relation - die
Wertekombination 00 (K) so findet man in der Bildmatrix B vier Wertepaare 0 0
Der Wert 4 wir dann in der Cooccurence-Matrix an die Position c00 eingetragen. Die
gleiche Vorgehensweise wird für alle Wertekombinationen aus K durchgeführt. Falls
keine entsprechende Werte in B zu finden ist, wird in C 0 eingetragen. Im Bild unten
sind aus Gründen der Übersichtlichkeit die Vorgehensweise für nur 3
Wertekombinationen gezeigt.
Ergebnis C (Cooccurence-Matrix).
00
10
K
20

30
01 02 03 
11 12 13 
21 22 23

31 32 33
0
0
Relation:

Rechter Nachbar 0

B
0
1

2
0 1 1 2 3
0 0 1 2 3 
0 1 2 3 3

1 1 2 3 3
2 2 3 3 3

2 3 3 3 3

4
0
C
0

0
4 0 0
2 5 0
0 2 6

0 0 7
K: mögliche Wertekombinationen
B: Bildmatrix
C: Cooccurencematrix
Da hier nur genau eine Frequenz berücksichtigt wird, bei Mikroverkalkungen jedoch
viele Frequenzen in Form von Kantenanstieg und Abstand voneinander auftreten –
was die Textur ausmacht –, werden Cooccurence-Matrizen einiger möglichen
Abstände gebildet.
Aus der Coocurrence-Matrix können geeignete Maße zur Charakterisierung der
Textur gewonnen werden. Geeignet wären hier z. B. die Entropie (Maß für die
Unordnung):
  cij log( cij )
i
j
bzw. auch das 2. Moment der Elemente-Differenz (Ordnung 2)
 (i  j )
i
k
cij
j
5.2.7. Test/Ergebnisse
Bei der oben beschriebenen Vorgehensweise wurden die verwendeten
Mammogramme digitalisiert mit einer Quantisierung von 256 Graustufen. Die aus
diesen Aufnahmen ausgeschnittenen ROI's wurden in eine Datenbank eingegeben
(256 Einträge), wovon 128 Ausschnitte Mikrokalzifikationen zeigen, die restlichen
128 keine Mikroverkalkungen beinhalten. Diese Datenbank dient als Basis zur
Analyse der entwickelten Algorithmen. Die Größe des ROI beträgt 256x256
Seite 19 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
Gitterpunkte. Zur Bewertung werden jeweils die besten 5, 7, 14, 44 und 275
Merkmale von 4096 durch die Merkmalsselektion ausgewählt und anschließend
durch den linearen und den quadratischen Klassifikator bewertet.
Anzahl
Merkmale
Trainingsfehler Generalisierungsfehler
Linear
Linear
Trainingsfehler Generalisierungsfehler
Quadratisch
Quadratisch
5
7
14
44
275
38 %
32 %
26 %
17 %
3%
28 %
17 %
8%
2%
42 %
33 %
33 %
34 %
38 %
37 %
38 %
41 %
43 %
Ingesamt kommt es durch die Verwendung von mehr Merkmalen wie erwartet zu
einer stetigen Verringerung des Trainingsfehlers. Die Generalisierung nahm bei
größerer Anzahl von Merkmalen entsprechend ab. Der Generalisierungsfehler ist
entsprechend hoch und die statistische Aussagekraft der Muster gering, da eine
verhältnismäßig kleine Stichprobe und eine große Anzahl von extrahierten
Merkmalen vorliegen. Die Ergebnisse entsprachen aber den Erwartungen der
Entwickler. Es wurde auch gezeigt, dass sich automatische Merkmale gewinnen
lassen, die bei der Aufgabe „Detektion von Mikroverkalkungen“ wertvoll sind und das
diese Methode sich auf jeden Fall zur Verbesserung der bestehenden Systeme
eignet.
Wie bereits erwähnt, gibt es auf Grund der Komplexität der Problematik
verschiedene Vorgehensweisen bei der Bildanalyse. Um an ein gewünschtes
„Rezept“ (Standardvorgehen) für eine bestimmte Fragestellung zu kommen, könnte
z. B. ein Analyse-Werkzeug nach dem Baukasten-System genutzt werden.
6.
Analyse-Werkzeug (Baukasten-System) –
Komponentensoftware
Für die Analyse von Bilddaten ist es häufig wichtig, dass ein erfahrener Experte
daran beteiligt ist. Dabei bestehen Probleme, die ein experimentelles Vorgehen mit
verschiedenen bekannten Verfahren erfordern. Mit einem Baukastensystem könnten
verschiedene "intelligente" Methoden genutzt werden und somit schnell zu
Ergebnissen bei der Lösung neuer Aufgabenstellungen führen. So ein Baukasten
besteht aus zwei Teilen: Editoren (Definition und Verwaltung der Wissensinhalte)
und eine Programmierumgebung (mit Befehlen für den Zugriff auf Bilddaten,
Wissensbasen oder neuronale Netze). Zur Verfügung stehen Standardfunktionen,
wie z. B. bei Khoros. Zu diesen Standardfunktionen gehören vordefinierte Filter
(Prewitt, Sobel, Laplace, etc.), ebenso können auch Filter frei definiert werden. Zur
Segmentierung stehen kantenorientierte, bereichsorientierte und auch modellbasierte
Methoden zur Verfügung. Die Verwendung verschiedener Bildformate ist möglich
(RAW-Format, VFF-Format, DICOM-Format), die Bilddaten können sowohl 2D als
auch 3D sein. Die Einsatzmöglichkeiten von „herkömmlichen“ Werkzeugen kann
aber durch die ergänzende Verwendung von so genannten CI-Methoden (FuzzyMethoden, künstliche neuronale Netze) deutlich überstiegen werden.
Seite 20 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
Bevor ich mit der Übersicht des Analysesystems vorfahre, möchte ich noch kurz auf
Neuronale Netze und Fuzzy-Methoden eingehen.
6.1.
Neuronale Netze
Künstliche neuronale Netze sind biologisch inspirierte, mathematische Modelle, die
zur Mustererkennung, Segmentierung und Klassifikation von Bildobjekten,
Bildfilterung, Funktionenapproximation, Lösung von Optimierungsproblemen, sowie
zur Realisierung von Assoziativspeichern oder Simulation biologischer Prozesse
eingesetzt werden können.
Für die verschiedenen Problemfelder haben sich im Laufe der Zeit verschiedene
Typen künstlicher neuronaler Netzwerke herausgebildet. Sie bestehen aus einfachen
Basisbausteinen - Neuronen (Units) –die durch ein komplexes Netzwerke
miteinander verbunden sind. Künstliche neuronale Netze sind sowohl in ihrer
Architektur, als auch in ihren Funktionsprinzipien am biologischen Vorbild orientiert.
Schematische Darstellung eines mathematisch modellierten Neurons:
m1
m2
wi1
wi2
neti
∑
Θ
o = Θ (neti)
...
mn
wn
Die Größen mi, i = 1,...,n sind die Eingabewerte (die Eingangsaktivierungen) des

T
Neurons. Sie werden häufig als Vektor m  m1 , m2 ,..., mn  geschrieben. Jedem

Eingang ist ein (Netz-) Gewicht wi  ( wi1 ,..., win )T zugeordnet. Der durch die Stimuli
hervorgerufene innere Aktivierungszustand des i-ten Neurons wird durch den
Netzinput neti zumeist wie folgt definiert:
n
neti  mT  wi   m j  wij .
j 1
Die nichtlineare Ausgabefunktion Θ, auch Transfer- oder Übertragungsfunktion
genannt, kann als Schwellwertfunktion
0, falls neti  
(neti )  
1, falls neti  
oder sigmoide Fermi-Funktion
  (net i ) 
1
1  exp(   net i )
Seite 21 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
modelliert werden. Die Fermi-Funktion approximiert für große Parameterwerte
   die Schwellwertfunktion. Fermi-Funktionen sind vor allem im Zusammenhang
mit Back-Propagation-Netzwerken von Bedeutung.
Eine wesentliche Eigenschaft neuronaler Netze bildet die Möglichkeit zur Adaption
und problemspezifischen Selbstorganisation in einem Lernprozess. Algorithmisch
wird während des Lernvorganges durch iterative Veränderungen der Gewichte die
Optimierung eines Gütekriteriums angestrebt. Neben den verwendeten
Lernmechanismen sind künstliche neuronale Netzwerke vor allem durch die
Netzwerktopologie charakterisiert, durch die die Anzahl der Gewichte und somit die
Dimensionierung neuronaler Klassifikatoren festgelegt wird.
Im Bereich der medizinischen Mustererkennung und Bilddatenanalyse gehören
Multilayer-Perzeptrons und topologische Merkmalskarten zu den wichtigsten
neuronalen Netzwerktypen.
In Neuro-Fuzzy-Systemen können neuronale Lernmechanismen mit FuzzyOperatoren zur adaptiven Analyse und Erkennung von Mustern kombiniert werden.
6.2.
Fuzzy-Bildverarbeitung
Fuzzy – im Sinne der Fuzzy Logik als ungenau, unscharf oder unpräzise zu
interpretieren. Die Fuzzy Logik ist eine exakte mathematische Theorie, mit der
versucht wird, nicht exakten Begriffen gerecht zu werden. Bei der Verarbeitung eines
Grauwertbildes treten verschieden Arten von Unsicherheiten auf:



Mehrdeutigkeit bei der Grauwertmanipulation
Geometrische Unschärfe
aus Expertenwissen stammend
Ergebnis
Vorlage
Bildaufnaufnahme
Vorverarbeitung
Segmentierung
Darstellung
Beschreibung
Analyse
Interpretation
Erkennung
low-level
intermediate-level
high-level
in den Grauwerten
geeignete
Modellierung:
HistogrammFuzzyfizierung
in der Geometrie
geeignete
Modellierung:
lokale
Fuzzyfizierung
im Expertenwissen
geeignete
Modellierung:
MerkmalFuzzyfizierung
Unsicherheit
Seite 22 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
Unscharfe Bilddefinition
Wie oben bereits erwähnt, wird ein digitales Bild X als eine Matrix mit M Zeilen und N
Spalten repräsentiert, deren Elemente Grauwerte sind. Für eine auf der FuzzyMengenlehre basierende Bilddefinition wird jedem Grauwert ein Grad der
Zugehörigkeit zugeordnet  Array von Fuzzy-Singletons.
Matrizen-Darstellung
 11
g
 11
  21

X   g 21
...

  M1
 g M 1
11
g11
 22
g 22
M 2
gM 2
11
...
...
...

g11 

 2N 
g 2 N 


 MN 
g MN 
wobei gmn die Bildgrauwerte und mn die Zugehörigkeit (Zugehörigkeit wird als
„Grauwert“ interpretiert) darstellen.
Die Zugehörigkeit reflektiert die Helligkeit oder andere Eigenschaften, wie Kantenoder Textur-Zugehörigkeit, die das Bild am besten charakterisieren.
Diese Singletons werden durch die Definition einer lokalen (z. B. für Bildsegmente)
oder globalen Zugehörigkeitsfunktion von Bild zu Bild neu berechnet. Wie die
Zugehörigkeitsfunktion x explizit definiert wird, ist eine aufgabenspezifische Sache
und verlangt eine eingehende Beschäftigung mit der Fuzzy-Bildverarbeitung.
Die Fuzzy-Bildverarbeitung läuft generell in drei Stufen ab



Fuzzyfizierung – Gewinnung von Zugehörigkeiten aus Bildern
Operationen mit den Zugehörigkeiten (linguistische Modifikatoren, Einbindung
in ein Inferenzverfahren, Aggregation untereinander, numerische oder
syntaxorientierte Klassifikation.
Defuzzyfizierung (ansatzabhänig, bei unscharfen Klassen nicht notwendig).
Beipiel:
Die Fuzzyfizierung wird in diesem Beispiel für ein Histogramm durchgeführt, das
einen maximalen Grauwert von 255 aufweist. Die Zugehörigkeit i der Grauwerte gi
wird durch die Vorschrift
g
i  i
255
ermittelt (i = 0, 1, ..., 255). Für die Modifikation in der Zugehörigkeitsebene (  ’)
Seite 23 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
wird der Intensitätsoperator (gehört zu den linguistischen Modifikatoren) eingesetzt:
2

2   i
i '  
2

1  2  (1   i )
falls 0   i  0.5
falls 0.5   i 1
Für die Defuzzyfizierung wird hier die inverse Zugehörigkeitsfunktion benützt:
g i '  255   i '
50 55 63
58 205 210
215 223 230
Originalbild (Ausschnitt)
Fuzzyfizierung
Modifikation
Defuzzyfizierung
18 23 31
25 234 237
242 247 250
Grauwert-Ebene
.19 .21 .25
.23 .80 .82
.84 .87 .90
.07 .09 .12
.10 .92 .93
.95 .97 .98
Ergebnisbild (Ausschnitt)
Zugehörigkeits-Ebene
Grauwert-Ebene
Die unscharfe Bilddefinition soll die Bereitstellung einer neuen Palette von Methoden
für die digitale Bildverarbeitung erleichtern. Der theoretische Zugang zur FuzzyBildverarbeitung wird durch die vielfältigen Aspekte der Fuzzy-Mengenlehre bzw. der
Fuzzy-Logik geschaffen. Der Theorien-Reichtum der Fuzzy-Systeme scheint für die
Entwicklung neuer Methoden für die Mustererkennung und für die Bildverarbeitung
geradezu prädestiniert zu sein. Es ist natürlich nicht möglich, alle Aspekte der FuzzySysteme, in dieser Ausarbeitung aufzunehmen. Es sollte nur erwähnt werden, dass
die Fuzzy-Bildverarbeitung eine Methodik ist, die Möglichkeiten der klassischen
Bildverarbeitung zu erweitern.
Nach diesen Ausführungen möchte ich wieder fortfahren mit der Beschreibung des
Baukasten-Systems. Wie bereits erwähnt, existieren verschiedene Editoren zur
Definition und Verwaltung der einzelnen Wissensinhalte.
6.3.
Editoren
Die angesprochenen Erweiterungen zu bisher existierenden System beziehen sich
auf die umfangreiche Verwendung von unscharfen (Fuzzy-)Methoden und
künstlichen neuronalen Netzen. Dabei werden die Fuzzy-Methoden hauptsächlich
zur Repräsentation des unscharfen Expertenwissens verwendet. Der Experte kann
sein Domänenwissen in Wissensbasen unterschiedlicher Art speichern, etwa zur
Seite 24 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
Beschreibung von Handlungswissen in Form von WENN-DANN-Regeln oder zur
Beschreibung von Faktenwissen in semantischen Netzen. Diese Wissensbasen
werden über eine Komponente des Baukastens verwaltet und können einfach
strukturiert angelegt und gepflegt werden. In den Wissensbasen können
Beschreibungen gesuchter Objekte mit natürlich sprachlichen Begriffen (Termen)
hinterlegt werden, deren Interpretation mittels Fuzzy-Mengen mit Hilfe geeigneter
Werkzeuge des Baukastens definiert werden können.
Die Verwaltung der Interpretationen der verwendeten Sprache (die durch FuzzyMengen hinterlegt sind) erfolgt ebenfalls mit Hilfe des Editors. Der Editor erlaubt es,
die Definition der Interpretationen von den in der Wissensbasis genutzten Termen.
Die Verwendung des Wissens erfolgt kontextabhängig, damit sichergestellt ist, dass
die jeweils gültige Interpretation eines Termes gewählt wird.
Weiterhin wird die Verwendung künstlicher neuronaler FF-Netze durch den
Baukasten unterstützt. Diese können zum einen zur Klassifikation segmentierter
Strukturen verwendet werden, aber auch zur Vorsegmentierung von Bilddaten
eingesetzt werden. Der Baukasten verfügt über einen Editor, der eine Definition der
Struktur, der Gewichte des Netzes sowie der Aktivierungsfunktionen erlaubt. Die
Trainingsdaten für das jeweils konstruierte Netz können in einer Datei hinterlegt
werden, die ggf. auch von anderen Programmen erzeugt wurden (z. B. SNNS –
Stuttgarter Neuronale Netze Simulator). Auch zellulare neuronale Netze können zur
Bildvorverarbeitung eingesetzt werden. Dadurch ist die Schnittstelle zu einer
geplanten Implementierung einer Lernkomponente gewährleistet.
6.4.
Programmierumgebung
Für den Baukasten wurde eine eigens implementierte Programmiersprache
CIM2BA/Prg implementiert. Sie bietet alle vom Baukasten zur Verfügung gestellten
Methoden an. Die Programmiersprache erlaubt das in der Experimentierphase
gefundene „Rezept“ zu hinterlegen und in Form einer Stapelverarbeitung
automatisiert für eine Fülle von Bilddaten anzuwenden, die einer gleichen
Aufgabenstellung unterliegen. Dabei können sowohl die Standardmethoden auf
einen Bilddatensatz angewendet werden, als auch die unscharfen Beschreibungen
der Wissensbasis und die künstlichen neuronalen Netze.
6.5.
Baukasten-System Zusammenfassung
Der Baukasten ist zur Zeit (2001) noch prototypenhaft in C++ implementiert. Er ist
eine Experimentier-Tool, das die Auswertung von Bilddaten mit neuartigen
Aufgabenstellungen erleichtert, aber auch mittels der Programmiersprache eine
spätere Routinenutzung zulässt. Die Implementierung in CIM2BA/Prg weist derzeit
noch den Nachteil auf, dass die Sprache interpretiert wird und dadurch einen
Geschwindigkeitsnachteil gegenüber kompilierter Software aufweist. Jedoch wird
neben einer Erweiterung der Programmiersprache auch über die Entwicklung eines
Compilers nachgedacht.
Seite 25 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
7.
Anforderungen an Komponentensoftware
In der medizinischen Bildverarbeitung hat der Einsatz von Software einen hohen
Stellenwert. Dabei müssen bei der Entwicklung solcher Programme nicht nur die
Schnittstellen zu anderen Informationssystemen berücksichtigt werden, sondern
auch den gesetzlichen Vorgaben entsprochen werden (Medizinproduktegesetz
1995). Die Regelungen der Gesetzgeber sollen zur Sicherheit der Patienten einen
gewissen Mindeststandard gewährleisten. Unter das Gesetz, das besser auf
medizinische Geräte anzuwenden ist, fällt auch Software, die für medizinische
Zwecke eingesetzt werden, sie gilt als Medizinprodukt. Solange nur Forschung
betrieben wird, ist das Gesetz nicht anzuwenden, soll jedoch ein Einsatz am
Menschen erfolgen, sind die entsprechenden Richtlinien einzuhalten. Deshalb ist es
empfehlenswert, die gesetzlichen Vorgaben bereits bei der Entwicklung zu beachten.
Grundlegende Anforderungen werden im Rahmen des
Konformitätsbewertungsverfahren überprüft. Der Nachweis wird erbracht, indem eine
Produktdokumentation erstellt wird, anhand derer gezeigt werden kann, ob die
gesetzlichen Bestimmungen erfüllt wurden. Fällt die Prüfung positiv aus, kann das
Produkt auf den Markt. Es gibt verschiedene Möglichkeiten, die
Konformitätsbewertung durchzuführen – abhängig von den so genannten
Risikoklassen. Es gibt vier Risikoklassen: I, IIa, IIb und III, die einen Anhaltspunkt
dafür geben sollen, wie hoch das Risiko geschätzt wird, das von einem Produkt
ausgeht. Anschließend muss das Produkt mit dem CE-Zeichen versehen werden,
wobei Sonderanfertigungen kein CE-Zeichen tragen. Wenn alle Voraussetzungen
erfüllt sind, muss die zuständige Behörde von der Vermarktung des
Medizinproduktes in Kenntnis gesetzt werden. Weiterhin muss ein Beobachtungsund Meldesystem eingerichtet werden, und es muss im Betrieb des Herstellers ein
Sicherheitsbeauftragter benannt werden (Aufgabe: Meldung an die Behörden, wenn
Patienten oder Anwender zu Schaden gekommen sind).
Es empfiehlt sich der Einsatz eines Qualitätsmanagement-Systems (nach ISO
9000ff), denn die Anforderungen, die das Qualitätsmanagement an die
Produktdokumentation stellt, finden sich auch im Medizinproduktegesetz wieder.
Eine ausführliche Dokumentation hilft dabei, den Qualitätsstandard aufrecht zu
erhalten  „bessere“ Software!
Seite 26 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
8.
Zusammenfassung
„Eines der spannendsten und interessantesten Anwendungsgebiete der Informatik ist
zweifelsohne die digitale Bildverarbeitung.“ (aus Javamagazin der Software &
Support Verlag).
Mit diesem Zitat möchte ich die Erläuterungen aus dem Bereich „Bildverarbeitung in
der Medizin“ beenden. Man sollte einen kleinen Einblick in die Welt der
medizinischen Bilddaten gewonnen haben: von der Entstehung der Bilder, über die
„Bildverbesserung“, zur Bildanalyse und schließlich die Bildinterpretation. Im Rahmen
dieser Seminararbeit kann natürlich auf viele Aspekte nur stichpunktartig
eingegangen werden (bei weitergehenden Interesse – siehe Literaturangaben). Das
gilt besonders für die Themen Fuzzy-Methoden und neuronale Netze, die hier nur als
weiteren Beweis für die Vielfältigkeit der Bildverarbeitung dienen sollen. Ebenso gibt
es allein für die Mammographie noch unzählige Mustererkennungsaufgaben, die
teilweise in einigen Workshop-Arbeiten bereits behandelt wurden. Besonders zu
erwähnen: die Einführung einer neuartigen Methode, um Übereinstimmungen bzw.
Abweichungen beim Vergleich zweier Mammographien eines Patienten zu erzielen
(Landmarkenbasierte Registrierung). Information Processing in Medical Imaging,
2001
Wie breit gefächert die Aufgabenstellungen im Bereich der medizinischen
Bildverarbeitung sind, zeigt auch deutlich die Themenvielfalt des Workshops
„Bildverarbeitung für die Medizin“. Gleichzeitig wird klar, wie wichtig die
Zusammenarbeit von Wissenschaftlern, Herstellern und Anwender aus Medizin,
Technik, Natur- und Ingenieurwissenschaften, sowie der Informatik ist. Weitere
Informationen dazu unter http//:bvm-workshop.org. Bei Interesse können sogar die
Arbeiten vom Workshop 2002 unter http://sunsite.informatik.rwthaachen.de/Publications/CEUR-WS/Vol-56/ herunter geladen werden (pdf/ps-Format).
Seite 27 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
9.
Glossar
Im Glossar finden sich einige Begriffe wieder, die nicht explizit in der Ausarbeitung
erklärt wurden.
Absorption
Unter Absorption versteht man die teilweise oder gänzliche Abgabe von Energie des
einfallenden Photons an das getroffene Material.
Auflösung (Schärfe)
Die Fähigkeit eines Bildempfängers, kleine Details in einem Bild wiederzugeben. Je
besser die Auflösung ist, desto kleiner sind die Details, die noch getrennt
voneinander erkannt werden können.
CCD-Bildsensoren
CCD-(Charge-coupled-device-)Bildsensoren sind über eine Faseroptik an einen
Leuchtstoff angekoppelt. CCD-Detektoren sind matrixförmige Anordnungen von
lichtempfindlichen Halbleiterelementen.
DICOM-Format – Digital Imaging and Communications in Medicine
Der DICOM 3.0-Standard definiert ein Bildformat, das den standardisierten Zugriff
auf Bilddaten und die zugehörigen Bildzusatzinformationen ermöglicht. Darüber
hinaus werden Kommandos und Protokolle spezifiziert, durch die die Kommunikation
und der Bilddatenaustausch zwischen bildgebenden Modalitäten unterschiedlicher
Hersteller auf der Basis von Standard-Netzwerkprotokollen wie TCP/IP möglich wird.
Dies unterstützt insbesondere den Aufbau herstellerunabhäniger, radiologischer
Kommunikations- und Bildarchivsysteme (PACS).
DQE - detective quantum efficiency
DQE dient der Charakterisierung der Rauscheigenschaften eines bildgebenden
Systems. Eine einfache Messung des Rauschens am Ausgang ist nicht geeignet,
das bildgebende System zu bewerten, da das Quantenrauschen ja vorgegeben ist.
Ein geeignetes Maß Für die Qualität eines bildgebenden Systems ist daher die
Angabe, um welchen Faktor das System das Rauschen verschlechtert:
Detective Quantum Efficiency = DQE =
(Signal/Rausch)2 am Ausgang/ (Signal/Rausch)2 am Eingang.
Die beste DQE, die eine System erreichen kann, ist 1  Das System fügt kein
Rauschen hinzu.
Glättungsfilter
Glättungsfilter werden zur Rauschunterdrückung und Bildglättung eingesetzt. Durch
sie werden lokale Variationen der Bildfunktionswerte in den Bilddaten reduziert und
somit eine Homogenisierung der Bildfunktionswerte in verschiedenen Bildregionen
erreicht.
HIS – Hospital Information Systems
Die PACS und RIS werden heute in so genannten HIS eingebettet, in denen nicht
nur alle Patientendaten, sondern auch andere für das Krankenhausmanagement
wichtigen Daten bereitgestellt werden.
Seite 28 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
Histogrammlinearisierung
Eine nichtlineare Transformation der Grauwerte eines Bildes, wobei die Funktion
aber nicht vorgegeben, sondern aus dem zu verarbeitenden Bild berechnet wird und
deshalb auf die gegebene Grauwertverteilung des Bildes abgestimmt ist.
Hochpassfilterung
Hochpassfilter werden eingesetzt, um feine Strukturen in einem Bild zu extrahieren
oder zu verstärken. Ein solcher Filter lässt nur noch die Frequenzen oberhalb eines
Schwellwertes durch und wird deshalb Hochpass genannt.
Logarithmische und exponentielle Skalierung
Falls bei einem Bild der Kontrast im dunklen Bereich stärker angehoben werden soll
als in hellen Bildbereichen, kann dies mit Hilfe einer logarithmischen bzw.
exponentiellen Funktion zur Grauwerttransformation erzielt werden.
Kantenfilter
Kantenfilter (Kantenoperatoren) sind Bildverarbeitungsmethoden, durch die Kanten
im Bild hervorgehoben werden. Sie sind Basiswerkzeuge für die Verarbeitung
medizinischer Bilder, die zur Visualisierung der in einem Bild enthaltenen
Kanteninformationen sowie bei der Segmentierung von Bildobjekten eingesetzt
werden.
Klassifikatoren
Zentrale Bausteine von Mustererkennungssystemen, die sich durch ihre
datengetriebene Lern- und Generalisierungsfähigkeit auszeichnen. In medizinischen
Bildanalyse- und Erkennungssystem werden sie sowohl zur Segmentierung als auch
zur computergestützten Erkennung diagnostisch relevanter Bildstrukturen verwendet.
Kontrast
Die Fähigkeit, kleine Dichteunterschiede im Gewebe in Bildinformation umzusetzen,
wird Kontrastauflösung genannt. Kontrast wird durch unterschiedliche Schwächung
der Röntgenstrahlung im Mammagewebe erzeugt oder durch unterschiedlich dicke
Brustbereiche. Weiterhin wird der Kontrast im Röntgenbild durch das
Röntgenspektrum beeinflusst, welches wiederum durch Röhrenspannung,
Anodenmaterial und Filterung bestimmt wird. Der Kontrast im Strahlenbild enthält alle
mit dem gewählten Röntgenspektrum erzielbaren Informationen. Je größer der
Kontrast ist, desto stärker treten die hellen und dunklen Bildbereiche hervor.
linguistische Modifikatoren
Linguistische Modifikatoren sind solche Operatoren, die die Bedeutung einer
linguistischen Variablen verändern (die Zugehörigkeiten werden manipuliert, indem
die Form der Zugehörigkeitsfunktion verändert wird).
Neuronen, biologische
Die wesentlichen Bestandteile einer Nervenzelle (Neuron) bilden Zellkörper, die
Dendriten und das Axon. Bei der neuronalen Reizübermittlung stellen die Dendriten
die Eingänge, das Axon den Ausgang dar. An den Ausläufern des Axons finden sich
die synaptischen Endköpfe, die die Kontaktstellen zu den Dendriten anderer
Seite 29 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
Neuronen bilden. An den Dendriten eingehende Reize versetzen das Neuron in
einen inneren Aktivierungszustand, der durch die Stärke der synaptischen
Verbindungen beeinflusst wird. Die synaptischen Verbindungen können sowohl
anregende (exzitatorische) als auch hemmende (inhibitorische) Wirkung haben.
Übersteigt die Summe der eingehenden Reize einen Schwellwert, so löst das Neuron
ein Signal aus, das über das Axon an andere Neuronen weitergeleitet wird.
Rauschen
Rauschen ist der Anteil an der optischen Dichte oder Helligkeit im Bild, der keine
Information enthält und die Bildinformation überlagert. Die Zahl der aus dem
Strahlenbild vom Bildempfänger absorbierten Röntgenquanten bestimmt das
Quantenrauschen. Zusätzlich wird das Rauschen noch durch das Systemrauschen,
den statistischen Fluktuationen innerhalb des bildgebenden Systems (beim digitalen
Bildsystem z.B. elektrisches Rauschen) erhöht.
RIS – Radiology Information Systems
Informationssystem in der Medizin, dass bereits komplette Patienten-Mappen mit
Befunden und Abrechnungsunterlagen behandelt.
Segmentierung
Segmentierung medizinischer Bilder ist die Abgrenzung verschiedener diagnostisch
oder therapeutisch relevanter Bildobjekte (z. B. Tumore, Gefäße, ...) von der
Objektumgebung.
Zugehörigkeit
Die Zugehörigkeit eines Elementes zu einer gegebenen Menge wird graduell und
abgestuft definiert, ein Spielraum, um ungenaue und vage Sachverhalte
mathematisch abzubilden. Mögliche Interpretation des Begriff Zugehörigkeit:




Zugehörigkeit als Ähnlichkeit (Grad der Ähnlichkeit der Objekte bezüglich
eines Idealobjektes) z. B. 0,9 für sehr ähnlich, fast identisch
Zugehörigkeit als Wahrscheinlichkeit, mit der ein Objekt einer
Klasse/Segment/Menge zugeordnet wird.
Zugehörigkeit als Intensität, z. B. Helligkeit (sehr hell, fast dunkel usw.)
Zugehörigkeit als Approximation – Zugehörigkeit ist ein Ausdruck der Qualität,
mit der ein Messwert durch einen festgelegten Wert approximiert wird (ebnet
den Weg für statistisches Lernen, das aus vagen Daten den Verlauf der
Zugehörigkeit ermittelt und iterativ verbessert).
Seite 30 von 31
Bildverarbeitung in der Medizin am Beispiel der (digitalen) Mammographie
Maier Susanne
10.
Literaturverzeichnis
1. Bildverarbeitung für die Medizin 2001, H. Handels, A. Horsch, T.Lehmann,
H.-P. Meinzer (Herausgeber),Springer Verlag Berlin Heidelberg, 2001
2. Medizinische Bildverarbeitung, Heinz Handels
B.G. Teubner Stuttgart Leipzig, 2000
3. Praxis der digitalen Bildverarbeitung und Mustererkennung, Peter Haberäcker,
Carl Hanser Verlag München Wien, 1995
4. Graphische Datenverarbeitung Grundzüge und Anwendungen,
R. Zavodnik/H. Kopp, Hanser Verlag München Wien, 1995
5. Fuzzy-Bildverarbeitung, Hamid R. Tizhoosh,
Springer Verlag Berlin Heidelberg, 1998
6. Radiologische Mammadiagnostik, Dronkers, Hendriks, Holland, Rosenbusch,
Georg Thieme Verlag Stuttgart New York, 1999
7. Bildgebende Verfahren in der Medizin, Olaf Dössel,
8. Springer Verlag Berlin Heidelberg, 2000
9. www  hauptsächlich Bilder
10. Javamagazin, Software & Support Verlag GmbH, Frankfurt,
Ausgaben 04/02, 05/02, 06/02
Seite 31 von 31