7 ¨Ubungsblatt

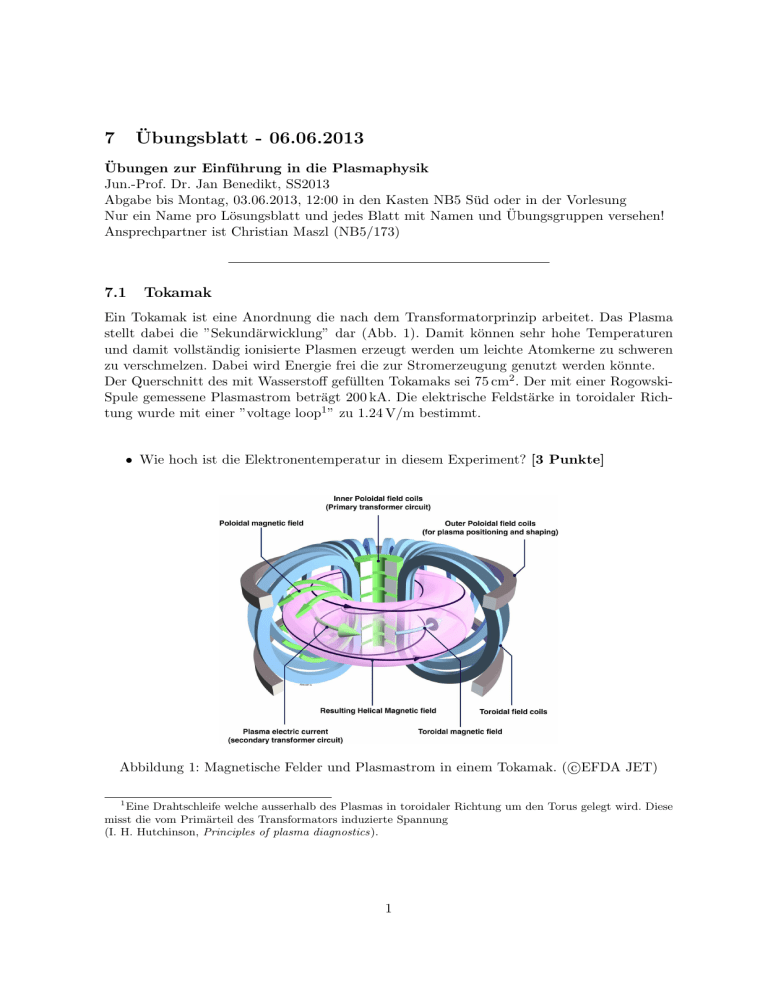
7
Übungsblatt - 06.06.2013
Übungen zur Einführung in die Plasmaphysik
Jun.-Prof. Dr. Jan Benedikt, SS2013
Abgabe bis Montag, 03.06.2013, 12:00 in den Kasten NB5 Süd oder in der Vorlesung
Nur ein Name pro Lösungsblatt und jedes Blatt mit Namen und Übungsgruppen versehen!
Ansprechpartner ist Christian Maszl (NB5/173)
7.1
Tokamak
Ein Tokamak ist eine Anordnung die nach dem Transformatorprinzip arbeitet. Das Plasma
stellt dabei die ”Sekundärwicklung” dar (Abb. 1). Damit können sehr hohe Temperaturen
und damit vollständig ionisierte Plasmen erzeugt werden um leichte Atomkerne zu schweren
zu verschmelzen. Dabei wird Energie frei die zur Stromerzeugung genutzt werden könnte.
Der Querschnitt des mit Wasserstoff gefüllten Tokamaks sei 75 cm2 . Der mit einer RogowskiSpule gemessene Plasmastrom beträgt 200 kA. Die elektrische Feldstärke in toroidaler Richtung wurde mit einer ”voltage loop1 ” zu 1.24 V/m bestimmt.
• Wie hoch ist die Elektronentemperatur in diesem Experiment? [3 Punkte]
c
Abbildung 1: Magnetische Felder und Plasmastrom in einem Tokamak. (EFDA
JET)
1
Eine Drahtschleife welche ausserhalb des Plasmas in toroidaler Richtung um den Torus gelegt wird. Diese
misst die vom Primärteil des Transformators induzierte Spannung
(I. H. Hutchinson, Principles of plasma diagnostics).
1
7.2
Diffusion
Eine RF-Entladung wird zwischen zwei parallelen Elektroden an den Positionen x = ± 2l
gezündet. Die eindimensionale stationäre Diffusionsgleichung
d2 n
+ k2 n = 0
dx2
mit
n(±l/2) = 0
(1)
hat die Lösung n(x) = n0 cos(kx) mit k 2 = νi /Da . νi sei die Elektron-NeutralteilchenIonisationsrate und Da ∝ µi Te der ambipolare Diffusionskoeffizient.
(a) Geben Sie den stationären Teilchenfluß Γ(x), das ambipolare elektrische Feld E(x) und
das Potential Φ(x) an. Skizzieren Sie deren Verläufe für |x| ≤ l/2. [3 Punkte]
(b) Geben Sie ∆n = ni − ne an und skizzieren Sie ∆n(x) und n(x) im selben Graphen für
|x| ≤ l/2. Sind die ambipolaren Lösungen für ∆n(x) > n(x) gültig? Begründen Sie Ihre
Antwort! [3 Punkte]
7.3
Diffusion senkrecht und parallel zum Magnetfeld
Ein zylindrisches Argonplasma brennt in einem Rohr mit Radius R und Länge L bei einem
Druck von 3 Pa. Das Plasma sei magnetisiert mit einem starken Magnetfeld von B0 =0.1 T
entlang der Rohrachse. Es gelte Te Ti und kB Te =9 eV. Die radiale Geschwindigkeit der
Ionen entspricht einer Temperatur von 1 eV.
(a) Bestimmen Sie die freie Weglänge λAr+ von Argonionen entlang B0 unter der Annahme,
daß der Koeffizient für ambipolare Diffusion entlang B0 gleich Da = 130 m2 s−1 Pa/p
ist und die Geschwindigkeit der ambipolaren Ionendrift einer Energie von Ek =10 eV
entspricht. [4 Punkte]
(b) Berechnen Sie den Gyrationsradius der Ionen und D⊥ . [4 Punkte]
(c) Prüfen Sie, ob der radiale Transport im Vergleich zum parallelen Transport bedeutsam
ist. L sei 30 cm und der Radius R sei 10 cm. [3 Punkte]
Der 4. Aggregatszustand
Plasmen werden oft als der 4. Aggregatszustand der Materie bezeichnet. Üblicherweise teilt man Phasenübergänge anhand der thermodynamischen Eigenschaften
gemäß der Klassifikation nach Ehrenfest ein. Bei einem Phasenübergang erster Ordnung (schmelzen, verdampfen, ...) wird die Wärmekapazität Cp bei der
Übergangstemperatur unendlich groß. Bei einer Flüssigkeit bleibt an diesem Punkt
die Temperatur, trotz Wärmezufuhr, konstant bis sie vollständig verdampft ist. Da
dies für Plasmen nicht beobachtet wird, kann man daher streng genommen nicht
vom 4. Aggregatszustand im klassischen Sinne sprechen.
2