Technische Informatik
Werbung

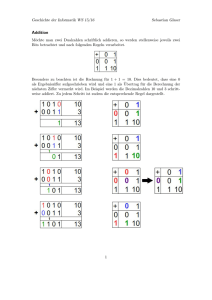
Rechnen mit Binärzahlen An dieser Stelle soll nun auf die wichtigsten Zusammenhänge bezüglich der Lösung arithmetischer Probleme eingegangen werden. Dabei werden sowohl Subtraktion und Division außen vorgelassen, während Addition und Subtraktion die entscheidende Rolle spielen. Außerdem beschränken sich diese Ausführungen auch auf Operationen an reinen Dualzahlen, d.h. die BCD- Codierung, bei der die Ziffern der einzelnen Stellen einer Dezimalzahl in Tetraden (zu je 4 Bit) umgewandelt werden, soll hier nicht näher betrachtet werden. Zur weiteren Erleichterung des Verständnisses dieser Thematik, wird für diesen Abschnitt ein Dualzahlensystem von nur vier Bitstellen verwendet. Somit ist nur ein stark eingeschränkter Zahlenbereich darstellbar, jedoch lassen sich die dabei gewonnenen Einsichten auch ohne größere Schwierigkeiten auf erweiterte Zahlwortbreiten, wie 8 oder 16 Bit, übertragen. Stellenwertschema für eine vierstellige Dualzahl mit Vorzeichenstelle (VZ): VZ Stellenwert Hierbei wird deutlich, das die höchste Bitstelle nicht als Stellenwert, sondern als Vorzeichen definiert wird. Dabei gilt: - 4.1 Vorzeichenbit = 0 entspricht einer positiven Zahl Vorzeichenbit = 1 entspricht einer negativen Zahl Addition Ausgehend von der obigen Festlegung, sollen nun die positiv darstellbaren Zahlen in der folgenden Übersicht aufgezeigt werden: Positive Dualzahlen von null bis sieben: Dezimalzahl 0 +1 +2 +3 +4 +5 +6 +7 Dualzahl 0000 0001 0010 0011 0100 0101 0110 0111 An einigen Beispielen soll nun die Addition mit den oben dargestellten Dualzahlen erläutert werden. Zunächst soll die duale Eins mit der dualen Zwei addiert werden: 1 +2 3 0001 +0010 0011 Es gilt: 1+0 =1 Nun die duale Eins mit der dualen Eins. Der Unterschied zur vorangegangenen Rechnung besteht hierbei darin, das man an der zweiten Stelle einen Übertrag erhält: Übertrag 1 1 +1 2 0001 +0001 0010 Es gilt: 1+1 = 0+Übertrag 1 Am Beispiel der Addition der dualen Drei mit sich selbst soll gezeigt werden, wie drei untereinander stehende Ziffern mit dem Wert eins (1+1+Übertrag) addiert werden. Übertrag 11 3 +3 6 0011 +0011 0110 Es gilt: 1+1+Übertrag 1 = 1+Übertrag 1 Diese Ergebnisse sollen nun verallgemeinert werden. Dazu betrachtet man den Koeffizienten einer betrachteten Bitstelle der ersten Zahl mit an und den Koeffizienten der gleichen Stelle bei der zweiten Zahl mit bn und einen möglichen Übertrag von der vorhergehenden Stelle mit ün-1 . Kombiniert man alle möglichen Wertbelegungen für an, bn und ün-1, so erhält man für die Stellensumme sn und den Übertrag zur nächsten Stelle ün die folgende Zuordnung: Ün-1 0 0 0 0 bn 0 0 1 1 an 0 1 0 1 Sn 0 1 1 0 ün 0 0 0 1 1 1 1 1 0 0 1 1 0 1 0 1 1 0 0 1 0 1 1 1 Aufgabe 1: Lösen Sie nun die folgenden Additionsaufgaben mit Hilfe der gewonnen Erkenntnisse selbst! 1+3 2+4 1+5 Aufgabe 2: Lösen Sie nun die folgenden beiden Aufgaben und vergleichen Sie deren Ergebnisse mit denen der vorangegangenen Aufgabe! 2+6 2+7 4.2 Subtraktion Die Subtraktion könnte nun in ähnlicher Art und Weise eingeführt werden wie die Addition. Dabei würde man entsprechen eine neue Rechenvorschrift erhalten, die ähnlich wie die der Addition aussähe. Für die technische Realisierung müsste man dann anstelle einer Addierstufe (Adder) noch eine Subtrahierstufe aufgebaut werden. Diese Subtrahierstufe kann man jedoch einsparen, wenn man die Subtraktion in eine Addition umwandelt. Aus y= a – b (Minuend a – Subtrahend b )macht man y = a + (-) b ! Man muß also den Subtrahenden in eine negative Zahl verwandeln. Dazu muß die Zahl b durch ihr Zweierkomplement ersetzt werden. Das Zweierkomplement einer Dualzahl wird gebildet, indem man alle Ziffern invertiert (umkehrt), d.h.0 in1 und 1 in0 umschreibt, und anschließend an der niedrigsten Stelle eine Eins addiert. Beispiel : 3 = 0011 Invertieren jeder Stelle Addition einer Eins Zweierkomplement der gegebenen Zahl 1100 + 1 1101 = -3 Beachte: Die duale negative Zahl Drei im Zweierkomplement entsteht nicht einfach dadurch, dass man die duale positive Drei nimmt und im höchstwertigen Bit (in der Vorzeichenstelle) eine Eins setzt! Stellt man nun alle möglichen positiven und negativen Zahlen für eine Breite von 4 Bit zusammen, erhält man folgende duale Werte: Dezimalzahl +7 +6 +5 +4 +3 +2 +1 0 -1 -2 -3 -4 -5 -6 -7 Dualzahl 0111 0110 0101 0100 0011 0010 0001 0000 1111 1110 1101 1100 1011 1010 1001 Welche Ergebnisformen sind nun möglich, wenn man mit dem gesamten, in der vorangegangenen Tabelle definierten Zahlenbereich arbeitet? Addiert man je eine positive und eine negative Zahl dieser Tabelle, entsehen durchweg Ergebnisse, die wiederum im Bereich der Tabellenzahlen liegen müssen, also keine Unregelmäßigkeiten aufweisen dürften. Zur Veranschaulichung sollen nun die folgenden drei Beispiele dienen: 1) 2) 3) Übertrag Übertrag Übertrag 0000 1011 +0100 1111 -5 +4 -1 1111 1011 +0101 0000 - 5 +5 0 1110 1011 +0110 0001 -5 +6 +1 Aus den beiden letzten Beispielen ersieht man, dass doch eine Besonderheit auftritt: Es gibt einen Übertrag über die definierte Zahlwortbreite hinaus. Wertet man jedoch nur die vereinbarten vier Stellen (und davon soll an dieser Stelle ausgegangen werden), so erhält man das richtige Ergebnis. Aufgabe 3: Lösen Sie nun abschließend zur Überprüfung ihrer Kenntnisse aus dem vorangegangenen Abschnitt die folgenden Aufgaben selbständig! 4+2 2-2 3+4 2-7 5+4 -3+5 -1+7