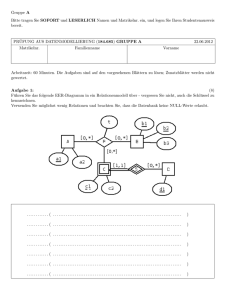
r¢ R£ u¢ X£ v¢ X
Werbung

DEVO 4.1 DEVO Objekttyp der realen Welt Relationenschema R Objektexemplar der realen Welt Tupel t R . Beschränkung der R-Werte auf mögliche Abbilder eines realen Objektes. Einschränkungen (constraints): 4.2 4.5 r R Definition von funktionalen Abhängigkeiten Modellierung mittels Datenabhängigkeiten. Funktionale Abhängigkeiten, Datenabhängigkeiten: Inklusionsabhängigkeiten, http://www.dbai.tuwien.ac.at/staff/slany/ Verbundabhängigkeiten. Wolfgang Slany DEVO 12 PERSONALNR Verkauf Buchhaltung ABTEILUNG 8010 Graz 1030 Wien 1010 Wien ADRESSE 4.3 4.6 TU Wien ADRESSE eine ABTEILUNG ADRESSE nicht erfüllt FDs erfüllt Beispiel 1 F = PERSONALNR ABTEILUNG, ABTEILUNG Menge funktionaler Abhängigkeiten 13 1010 Wien Filiale Buchhaltung 1010 Wien ADRESSE 11 14 Buchhaltung 8010 Graz 1030 Wien ABTEILUNG Verkauf 12 13 5010 Salzburg http://www.dbai.tuwien.ac.at/staff/slany/ Buchhaltung Filiale 14 11 PERSONALNR Wolfgang Slany TU Wien Durch Modellierung von a priori bekannten Constraints: Datenbanksystem übernimmt Teile dieser Aufgaben. Datenbanksysteme sollten Redundanz der Daten minimieren und Verläßlichkeit der Daten maximieren. DEVO Statische Einschränkungen: beschreiben Zustände der Datenbank, vY TU Wien müssen in allen Ausprägungen der DB gültig sein, sind eine spezielle Form von Integritätsbedingungen. z.B. für jeden Piloten muß zu einem Datum und einer Uhrzeit ein Flug eindeutig sein. uY u,v Dynamische Einschränkungen: regeln die Übergänge zwischen zwei Datenbankzuständen, z.B.: “das GEHALT eines Angestellten darf nur zunehmen”. Y , wenn http://www.dbai.tuwien.ac.at/staff/slany/ vY vX Wolfgang Slany uY uX TU Wien DEVO r R Funktionale Abhängigkeiten http://www.dbai.tuwien.ac.at/staff/slany/ 4.4 uv TU Wien X Y Teilmengen von R. Y http://www.dbai.tuwien.ac.at/staff/slany/ Wolfgang Slany Notation vX Relation r R erfüllt die funktionale Abhängigkeit (FD) X gilt: uX X . . . linke Seite (left hand side, LHS), X DEVO , L . . . Attribute, V ,W ,X,Y ,Z . . . Attributmengen, A,B,C, Q,R,S . . . Relationenschemata, Y . . . rechte Seite (right hand side, RHS) von FD. Wolfgang Slany q Q , r R , s S . . . Relationen t, u, v, w . . . Tupel X Y wird geschrieben als XY TU Wien A wird geschrieben als A http://www.dbai.tuwien.ac.at/staff/slany/ Wolfgang Slany X R und A X R X X A R 4.7 TU Wien 4.10 DEVO ADRESSE. ADRESSE eine Ableitungsregeln für funktionale Abhängigkeiten PERSONALNR Beispiel 2 F PERSONALNR ABTEILUNG, ABTEILUNG Menge von funktionalen Abhängigkeiten. F f F f Gültigkeitsbegriff, modelltheoretisch Ableitbarkeitsbegriff, beweistheoretisch http://www.dbai.tuwien.ac.at/staff/slany/ f F f Y X 4.8 Y heißt trivial, wenn Y eine Teilmenge von X ist. 4.11 TU Wien Axiomatisierung: ein System von Ableitungsregeln, mit deren Hilfe alle durch F implizierten funktionalen Abhängigkeiten f abgeleitet werden können ... ... Anmerkung: Wolfgang Slany DEVO F Die Menge aller funktionalen Abhängigkeiten, die von F auf R impliziert werden, heißt die Hülle (closure) von F auf R, FR . Eine funktionale Abhängigkeit X Y trivial DEVO Ableitungsregeln (inference axioms) Armstrong (1974) sind korrekt (sound), d.h. sie leiten von F nur wirklich gültige FDs ab (F f F f ), http://www.dbai.tuwien.ac.at/staff/slany/ Beweis: [Ullman, 1988 Bd. I bzw. Maier, 1983] sind auch vollständig (complete), d.h. sie erzeugen bei wiederholter f F f ). Anwendung alle von F implizierten Abhängigkeiten (F Wolfgang Slany DEVO g4 G g3 g2 g1 ORT ABT ORT ORT ORT ABT Erweiterung Vereinigung Transitivität g5 g2,g4 g2,g3 ORT ABT http://www.dbai.tuwien.ac.at/staff/slany/ g7 g2 Erweiterung Zerlegung ABT ORT ABT PERSONALNR, ABT, ORT ........... PERSONALNR ORT PERSONALNR ORT PERSONALNR ABT PERSONALNR PERSONALNR alle trivialen Abhängigkeiten ABT PERSONALNR PERSONALNR ABT Beispiel 3 Sei G die folgende Menge funktionaler Abhängigkeiten: G G g5 g6 g7 g8 PERSONALNR Wolfgang Slany R Oberschlüssel für R YZ X F DEVO YZ X Z A Unter der Hülle einer Menge von Attributen X R, geschrieben als X , bezüglich F verstehen wir die Menge aller Attribute A, sodaß X A aus F . X R Relationenschema. Y Z Y, X Z A Eine Teilmenge X von Attributen in R ist ein Oberschlüssel für R, genau dann wenn R erfüllt. X die funktionale Abhängigkeit X X XZ X X X TU Wien X A. X Schlüssel für R Ist die Teilmenge X minimal, dh. gilt für jede Teilmenge Y X, daß sie die funktionale Abhängigkeit Y R nicht erfüllt, so ist X ein Schlüssel. X Y Y, X YZ Z Z http://www.dbai.tuwien.ac.at/staff/slany/ X A . . . Mengendifferenz X X Zerlegung (projectivity) X Vereinigung (additivity) X Erweiterung (augmentation) Y Reflexivität (reflexivity) Wolfgang Slany DEVO F1.: F2.: F3.: F4.: Y, Y Transitivität (transitivity) X XW http://www.dbai.tuwien.ac.at/staff/slany/ Wolfgang Slany Pseudotransitivität (pseudotransitivity) Z TU Wien http://www.dbai.tuwien.ac.at/staff/slany/ Y , YW F5.: F6.: X Wolfgang Slany 4.9 TU Wien 4.12 TU Wien DEVO Das Membership-Problem Gegeben eine Menge von funktionalen Abhängigkeiten F. Frage: welche zusätzlichen Abhängigkeiten werden durch F impliziert? Algorithmen: CLOSURE: berechnet die Hülle einer Menge von Attributen. 4.13 TU Wien DEVO X und Z X do http://www.dbai.tuwien.ac.at/staff/slany/ F mit Y Z end INPUT: X Attributmenge, F Menge von FDs Algorithmus CLOSURE OUTPUT: X X : X while (Y Z) X : X return (X ) Wolfgang Slany DEVO 4.14 TU Wien 4.17 DEVO F ABT ORT ABT G, ob F F, ob G ORT ORT f. F G. http://www.dbai.tuwien.ac.at/staff/slany/ F). 4.15 TU Wien 4.18 TU Wien ORT ? Antwort: ja, folgt aus der Transitivität g. Antwort: ja trivialerweise (G g3 g2 http://www.dbai.tuwien.ac.at/staff/slany/ CLOSURE(X,F)) G? ORT PERSONALNR ABT PERSONALNR PERSONALNR ABT Beispiel 4 F DEVO Wolfgang Slany return (Y Algorithmus MEMBER INPUT: X Y FD, F Menge von FDs OUTPUT: true, if F X Y false, if F X Y MEMBER: stellt fest, ob eine funktionale Abhängigkeit in der Hülle enthalten ist. http://www.dbai.tuwien.ac.at/staff/slany/ 4.16 Äquivalenz von Systemen funktionaler Abhängigkeiten Problem: gesucht ist eine möglichst knappe Darstellung für funktionale Abhängigkeiten PERSONALNR ABT PERSONALNR ORT PERSONALNR F, G zwei Mengen funktionaler Abhängigkeiten. G ABT 1. prüfe für alle g 2. prüfe für alle f Frage: gilt G von g2 und g3. Wolfgang Slany DEVO Effiziente Implementierung von CLOSURE (Grundidee): für jedes Attribut: Referenzliste, die angibt, in welchen FDs aus F dieses Attribut auf der linken Seite vorkommt (ATTRLIST) zu jeder FD: Zähler, der angibt, wieviele Attribute der linken Seite noch nicht in X sind (ZÄHLER) G G und F sind äquivalent, G F, wenn sie dieselbe Hülle besitzen. F heißt dann Überdeckung (cover) von G. F wenn der ZÄHLER für eine FD Null wird G Wolfgang Slany die linke Seite von FD im augenblicklichen X enthalten ist F G? g, TU Wien Wann gilt F G, ob F f. 1. prüfe für alle g F, ob G 2. prüfe für alle f http://www.dbai.tuwien.ac.at/staff/slany/ die Attribute der rechten Seite von FD werden zu X hinzugefügt. Wolfgang Slany – Für jedes neue A in X muß dessen ATTRLIST – die angibt, in welchen FDs A in der linken Seite vorkommt – durchgegangen werden. – In diesen FDs muß ZÄHLER um 1 erniedrigt werden, da A in X neu aufgenommen wurde. TU Wien http://www.dbai.tuwien.ac.at/staff/slany/ Wolfgang Slany X A F 4.19 4.23 TU Wien 4.20 DEVO g2 g3 X Y Y F: F F F: Y entferne X Y. Y aus F. http://www.dbai.tuwien.ac.at/staff/slany/ X Y: entferne B aus XB 2. Entfernen überflüssiger Attribute (Ist B in XB Für jede FD XB Y Y 3. Entfernen aller redundanten Abhängigkeiten X X Für jede FD X Wolfgang Slany Inklusionsabhängigkeiten eine weitere besondere Form von statischen Integritätsbedingungen. R, S zwei Relationenschemata, S Y , wenn dienen zur Gewährleistung der referentiellen Integrität. DEVO Y überflüssig): DEVO ABT ORT g1 http://www.dbai.tuwien.ac.at/staff/slany/ PERSONALNR ORT PERSONALNR ABT 1. Zerlegung aller FDs in kanonische. Algorithmus zur Berechnung der minimalen Überdeckung: B ist überflüssig in XBY A bzgl. F F XBY A XY A F Eine Menge funktionaler Abhängigkeiten F heißt linksreduziert, wenn sie keine FD X mit überflüssigen Attributen auf der linken Seite enthält. G 2. Berechnung von G linksreduziert. DEVO Wolfgang Slany Theorem: Zu jeder Menge funktionaler Abhängigkeiten F gibt es eine minimale Überdeckung. (Beweis in [Ullman 1988, Bd I]) Eine Menge funktionaler Abhängigkeiten F heißt minimal, wenn sie kanonisch, nichtredundant und linksreduziert ist. DEVO Zerlegung trivial. F 4.22 Eine Menge funktionaler Abhängigkeiten F heißt kanonisch, wenn für jede FD X F die rechte Seite nur aus einem Attribut besteht. Regel F4 A redundant in F http://www.dbai.tuwien.ac.at/staff/slany/ ABT ORT NAME TU Wien Eine Menge funktionaler Abhängigkeiten F heißt nichtredundant, wenn es keine FD f in F gibt, so daß F f äquivalent zu F ist. X PERSONALNR Wolfgang Slany DEVO Beispiel 5 G ORT PERSONALNR ABT ABT g5 Y πX r πY s NAME SY X, Y Folgen von Attributen von R bzw. S, X RX r R und s S erfüllen die Inklusionsabhängigkeit R X πX r πY s gilt. PERSONALNR ABT ORT PERSONALNR ABT 3. Berechnung von G nichtredundant. G http://www.dbai.tuwien.ac.at/staff/slany/ g1 NAME PERSONALNR 4. Ausgabe der minimalen Überdeckung G g2 g3 g4 Wolfgang Slany ABT ORT NAME PERSONALNR ORT TU Wien http://www.dbai.tuwien.ac.at/staff/slany/ PERSONALNR ABT PERSONALNR ABT Wolfgang Slany TU Wien http://www.dbai.tuwien.ac.at/staff/slany/ 1. Berechnung von G kanonisch. G Wolfgang Slany 4.21 TU Wien 4.24 TU Wien . . . Inklusionsabhängigkeit PNR ist Fremdschlüssel für KINDER. 4.26 TU Wien DEVO R RX RX Yn R Xk Xm S Yk Ym , T Z RX T Z. http://www.dbai.tuwien.ac.at/staff/slany/ Beispielaufgabe n sind Ableitungsregeln für Inklusionsabhängigkeiten Casanova et. al. 1984 X SY ,SY m Folgen von Indizes aus dem Bereich 1 S Y1 Reflexivität Xn wobei k Projektion und Permutation R X1 RX Transitivität I1: I2: I3: Wolfgang Slany Wolfgang Slany F= T U, TS Q, Q TS, PQ R, Q S, U http://www.dbai.tuwien.ac.at/staff/slany/ SU 4.27 TU Wien 4.30 TU Wien Gegeben ist das Relationenschema PQRSTU und die Menge F von funktionalen Abhängigkeiten. Bestimmen Sie eine minimale Überdeckung. DEVO http://www.dbai.tuwien.ac.at/staff/slany/ 4.29 DEVO Wolfgang Slany DEVO 4.25 Beispiel 7 Händler verkaufen Produkte für Firmen, dargestellt im Schema R= HÄNDLER, FIRMA, PRODUKT DEVO Beispiel 6 S Y heißt schlüsselbasiert, wenn Y ein Eine Inklusionsabhängigkeit R X Schlüssel für S ist. Es gilt folgende Wettbewerbsregel: Ein Händler, der ein bestimmtes Produkt verkauft und eine Firma repräsentiert, die dieses Produkt vertreibt, verkauft dieses Produkt für diese Firma. kann zerlegt werden in PERSONEN = PNR, ZUNAME, VORNAME, GEHALT, GESCHLECHT PNR ist für PERSONEN Schlüssel Formal: ( *[HÄNDLER FIRMA, FIRMA PRODUKT, HÄNDLER PRODUKT] ) Schlüsselbasierte Inklusionsabhängigkeiten: Gewährleistung der referentiellen Integrität. TU Wien 4.28 KINDER = PNR, VORNAME, GEBDAT, GESCHLECHT (siehe SQL Teil) http://www.dbai.tuwien.ac.at/staff/slany/ RX S Y schlüsselbasiert, so heißt X Fremdschlüssel und die Inklusionsabhängigkeit Fremdschlüsselbedingung. Wolfgang Slany DEVO Verbundabhängigkeiten statische Integritätsbedingung R Eine Relation r R erfüllt die Verbundabhängigkeit (join dependency) R1 R2 Rn , wenn r R verlustfrei in R1 Rn zerlegbar ist. trivial, wenn ein Ri R1 = HÄNDLER, FIRMA R2 = FIRMA, PRODUKT TU Wien http://www.dbai.tuwien.ac.at/staff/slany/ Wolfgang Slany Y Z und entspricht der TU Wien Sonderfall von Verbundabhängigkeiten: mehrwertige Abhängigkeiten. Eine mehrwertige Abhängigkeit hat die Form X — Verbundabhängigkeit XY XZ . http://www.dbai.tuwien.ac.at/staff/slany/ Wolfgang Slany