Fakultät für Mathematik und Informatik

Fakultät für Mathematik und Informatik
Preprint 2012-07
Melanie Nentwich, Alina Ruziyeva
Aufgabensammlung zur Festigung
der Schulmathematik
ISSN 1433-9307
Melanie Nentwich, Alina Ruziyeva
Aufgabensammlung
zur Festigung der Schulmathematik TU Bergakademie Freiberg
Fakultät für Mathematik und Informatik
Prüferstraße 9
09596 FREIBERG
http://www.mathe.tu-freiberg.de
ISSN 1433 – 9307
Herausgeber:
Dekan der Fakultät für Mathematik und Informatik
Herstellung:
Medienzentrum der TU Bergakademie Freiberg
Aufgabensammlung
zur Festigung der Schulmathematik
Melanie Nentwich, Alina Ruziyeva
17. Oktober 2012
Vorwort
Liebe Studentinnen, liebe Studenten,
zu Beginn möchte ich Sie an der TU Bergakademie Freiberg willkommen heißen, einer kleinen, aber
auf vielen Gebieten (z. B. der Lehre) erstklassigen Universität. Sie werden sie kennen und, so hoffe ich,
auch lieben lernen.
Zunächst steht ein neuer Lebensabschnitt vor Ihnen, Sie werden viel Neues kennen lernen und oft werden Sie vor Problemen stehen, die Sie lösen müssen. Eines der ersten Probleme für viele Studenten
ist die Mathematik; das Fach „(Höhere) Mathematik“ steht im Lehrplan aller an der TU Bergakademie
gelehrten Studienrichtungen in den ersten Semestern. Um es erfolgreich zu absolvieren, müssen manche „lernen lernen“, andere früher Gelerntes auffrischen, wieder andere haben vielleicht keine großen
Schwierigkeiten.
Die Suche nach Bodenschätzen, die sichere Lagerung (für 1 Million Jahre ?) von (radioaktiven) Materialien auf Deponien, die Bestimmung von „besten“ Standorten für Telekommunikationseinrichtungen,
die kostengünstigste Erzeugung und Verarbeitung von Aluminium oder Magnesium und viele andere
Fragestellungen erfordern zur Bearbeitung mathematische Kenntnisse und Hilfsmittel. Im Laufe Ihres
Studiums werden Sie diese kennen und anwenden lernen.
Einige kleine Anwendungsaufgaben, die vielleicht (?) mit Kenntnissen aus dem Gymnasium von Ihnen
gelöst werden können, haben wir in dieser Broschüre zusammengefasst. Beim Lösen ist es sicher an der
einen oder anderen Stelle sinnvoll, mal in das Heft „Mathematische Grundlagen zur Vorbereitung des
Studiums an derTechnischen Universität Bergakademie Freiberg“, das auf derInternetseite
http://www.mathe.tu-freiberg.de/files/page/2012-03-fertig.pdf
gefunden werden kann, hineinzusehen. An einer kleinen Universität wie der TU Bergakademie Freiberg
ist es auch immer möglich, Ansprechpartner zu finden, wenn sich eine mathematische Aufgabenstellung
als hartnäckig herausstellen sollte. Versuchen Sie das, bevor „das Kind in den Brunnen gefallen“ ist.
Ich wünsche Ihnen ein interessantes Studium und immer die Kraft, den „inneren Schweinehund“ zu
besiegen, bevor er Sie am Studieren hindern kann.
Glück Auf,
Prof. Stephan Dempe
Dekan Fakultät für Mathematik und Informatik
i
Bemerkungen
Die folgende Aufgabensammlung stellt eine Ergänzung der Mathe–Fibel dar (http://www.mathe.tufreiberg.de/files/page/2012-03-fertig.pdf, ISSN 1433–9307). Die mit orange markierten Textstellen
sind dynamische Referenzen. In runden Klammern beziehen sie sich auf eine Formel, beginnt diese
nicht mit einer römischen Zahl, dann gehört die Referenz zu einer Formel aus der Fibel.
Die vorgestellten Aufgaben wurden teilweise aus den folgenden Büchern entlehnt:
• Mathematik für Ingenieure und Naturwissenschaftler – Anwendungsbeispiele, Lothar Papula, 5.
Auflage, 2004, Vieweg Verlag
• Mathematik für Wirtschaftswissenschaftler – Basiswissen mit Praxisbezug, Knut Sydsaeter, Peter
Hammond, 2. Auflage, 2006, Pearson Studium
• Mathematik in der Biologie, Annika Eickhoff–Schachtebeck, Anita Schöbel, 2009,
http://optimierung.math.uni-goettingen.de/skripte/bioskript.pdf
• Mathematik für Chemiker, Gerhard Just, Dieter Oelschlägel, 2. Auflage, 1982, Deutscher Verlag
für Grundstoffindustrie
• Übungsbuch Physik – Grundlagen – Kontrollfragen – Beispiele – Aufgaben, Peter Müller, Hilmar
Heinemann, Heinz Krämer, Hellmut Zimmer, 10. Auflage, 2007, Carl Hanser Verlag
ii
I
Aufgaben zu Gleichungen, Ungleichungen und
Systemen
I.1
Stöchiometrie einer chemischen Reaktion
Photosynthese ist die Erzeugung energiereicher Stoffe, wie z. B. Zucker C6 H12 O6 und Sauerstoff O2 , aus
energieärmeren Stoffen, wie z. B. Kohlendioxid CO2 und Wasser H2 O. In welchem Verhältnis stehen die
stöchiometrischen Koeffizienten xi ∈ N zueinander (i = 1, . . . , 4)?
x1 · CO2 + x2 · H2 O −→ x3 · C6 H12 O6 + x4 O2
(I.1.1)
Lösung
Gleichung (I.1.1) kann aus mathematischer Sicht auch geschrieben werden als
x1 · C + 2x1 · O + 2x2 · H + x2 · O = 6x3 · C + 12x3 · H + 6x3 · O + 2x4 · O
Komponentenweise gilt dann
C:
O:
H:
1x1
2x1
+
1x2
2x2
-
6x3
6x3
12x3
-
2x4
=0
=0
=0
Es liegt ein homogenes System aus drei Gleichungen mit vier Unbekannten vor. Daher gibt es unendlich
viele Lösungen (vgl. Abschnitt 3.1.3). Es darf also eine Variable frei gewählt werden. Mit x3 = t folgt:
x1 = x2 = x4 = 6t. Für t = 1 folgt
6 · CO2 + 6 · H2 O −→ C6 H12 O6 + 6O2 .
iii
II
Funktionen
II.1 Federschwingung
Ein Körper mit Masse m durchfällt die Höhe h und trifft zur Zeit t = 0 am Ort z(0) auf eine senkrecht
stehende Schraubenfeder mit Federkonstante k. Nach dem Auftreffen bleibt der Körper mit der Feder
verbunden, sodass eine harmonische Schwingung entsteht. Der Koordinatenursprung z = 0 soll in die
Ruhelage der Schwingung gelegt werden. Die Masse der Feder bleibt unberücksichtigt.
1. Bestimmen Sie den Anfangsort z(0) und die Anfangsgeschwindigkeit vz(0) der harmonischen
Schwingung.
2. Bestimmen Sie für diese Schwingung die in der Ort–Zeit–Funktion z(t) enthaltenen unbekannten
Größen.
3. Welche maximale Geschwindigkeit vz,max tritt bei dieser Schwingung auf?
Lösung
1. Die Federkraft F (z) ist das Produkt aus Federkonstante k und der Auslenkung aus der Ruhelage
(z = 0). Deshalb gilt für die Federkraft
F (z) = −k · (z − z(0)) .
Die Ruhelage z = 0 ist dort, wo Gewichtskraft G und Federkraft F (z) im Gleichgewicht sind:
F (z) = G.
Mit F (0) = k · z(0) und G = m · g folgt
k · z(0) = mg
⇒
z(0) =
mg
.
k
(II.1.1)
Die Anfangsgeschwindigkeit vz(0) dieser Schwingung liefert der Energiesatz, angewandt auf den
freien Fall:
!
m 2
mgh =
· vz(0)
⇒
vz(0) = − 2gh.
2
(Siehe hierzu die Abschnitte 1.2, 1.3 und 3.2.)
Das Vorzeichen wird unter Berücksichtigung der positiven z–Richtung gewählt.
2. Die Ort–Zeit–Funktion der harmonischen Schwingung lautet
z(t) = zmax · cos(ω0 t + α),
(II.1.2)
wobei ω0 = k/m die Kreisfrequenz der Federschwingung ist. Die beiden Unbekannten (Amplitude zmax und Nullphasenwinkel α) müssen aus den Anfangsbedingungen bestimmt werden. Zur
eindeutigen Bestimmung von zwei Unbekannten sind zwei Gleichungen nötig (siehe Abschnitt 3).
Die notwendige zweite Gleichung wird aus Gl. (II.1.2) durch Differenzieren nach der Zeit gewonnen:
vz(t) = −zmax · ω0 · sin(ω0 t + α).
(II.1.3)
!
iv
Zum Zeitpunkt t = 0 resultiert für Gl. (II.1.2) und Gl. (II.1.3)
z(0) = zmax cos α =
vz(0) = −
!
mg
k "
2gh = −zmax
(II.1.4)
k
sin α.
m
(II.1.5)
Zunächst soll zmax ermittelt werden. Dazu ist α zu eliminieren. Das gelingt mit der Beziehung
1 = cos2 α + sin2 α
#
$2
mg
2ghm
1=
+
2
k · zmax
k · zmax
%
2hk
mg
1+
zmax =
.
k
mg
Das gleiche Ergebnis folgt auch mit dem Energiesatz:
mg(h + z(0)) = −mg · zmax +
k
2
(z(0) + zmax ) .
2
Zur Bestimmung von α muss zmax eliminiert werden. Dazu kann Gl. (II.1.5) durch Gl. (II.1.4)
dividiert werden:
%
√
sin α
2hk
k 2gh
!
=
= tan α =
.
cos α
mg
mg k/m
(Siehe hierzu die Abschnitte 3.1.3, 1.3 und 4.)
3. Die Geschwindigkeitsamplitude oder maximale Geschwindigkeit ist der Funktion (II.1.3) zu entnehmen:
vz = −zmax ω0 sin(ω0 t + α)
%
"
2hk k
mg
1+
.
vz,max = zmax ω0 · 1 =
k
mg m
v
II.2 Zerbrochene Scheibe
Beim Beladen eines Autos mit Umzugskartons ist die Heckscheibe zerbrochen. Natürlich hat es sofort
angefangen zu regnen, so dass es durch die schiefe Scheibe (Winkel zur Erdoberfläche beträgt α)
hereinregnen würde. Der schlaue Autofahrer hat erkannt, dass alles im Auto trocken bleibt, wenn er
nur schnell genug fährt. Welche Geschwindigkeit v ist erforderlich, wenn davon ausgegangen wird,
dass der Regen senkrecht mit einer Geschwindigkeit von vR fällt?
Abbildung II.1: Autofahren mit kaputter Heckscheibe im Regen
Lösung
Die Hauptidee ist folgende: der Autofahrer muss so schnell fahren, dass die Verschiebung des Autos
nicht kleiner als die Verschiebung des Tropfens ist.
Betrachte das Dreieck ABC in Abb. II.1:
tan α =
AC
BC
⇒
AC = BC · tan α.
(II.2.1)
Zur Zeit t = 0 befindet sich der Tropfen in Position A und zur Zeit t = τ in C. Also
(II.2.2)
vR · τ = AC.
Das Auto muss schneller als der Tropfen sein, d. h. in derselbe Zeit τ muss das Auto mindestens die
Verschiebung BC durchfahren:
v · τ ≥ BC.
Jetzt wird die Gleichung
vmin · τ = BC
(II.2.3)
vmin
BC
.
=
vR
AC
(II.2.4)
betrachtet, dabei ist vmin die minimale Geschwindigkeit des Autos.
Gleichungen (II.2.2) und (II.2.3) ergeben nun
Durch Kombination der Gleichungen (II.2.4) und (II.2.1) resultiert
1
vmin
BC
=
=
vR
tan α
BC · tan α
vi
(= cot α) ,
d. h.
vmin =
Der Fahrer muss mit einer Geschwindigkeit v ≥
vR
.
tan α
vR
fahren.
tan α
vii
III
Aufgaben zur Vektorrechnung
III.1 Outputvektoren
Ein Unternehmen hat zwei Fabriken, die als Output drei verschiedene Güter produzieren. Die gesamte
Arbeitskraft ist fest. Wenn ein Anteil λ der Arbeitskraft der ersten Fabrik und der Anteil 1 − λ (mit
0 ≤ λ ≤ 1) der zweiten Fabrik zugewiesen wird, so ist der gesamte Output der drei Güter gegeben
durch den Vektor
⎛ ⎞
⎛ ⎞ ⎛
⎞
8
2
6λ + 2
λ · ⎝4⎠ + (1 − λ) ⎝ 6 ⎠ = ⎝−2λ + 6 ⎠ .
4
10
−6λ + 10
1. Ist es dem Unternehmen möglich, einen der zwei Outputvektoren a = (5, 5, 7)T und b = (7, 5, 5)T
zu produzieren, wenn kein Output vernichtet werden darf?
2. Wie ändern sich Ihre Antworten, wenn Output vernichtet werden darf?
3. Wie wird die den Erlös maximierende Wahl des Anteils λ von dem Verkaufspreis (p1 , p2 , p3 ) dieser
drei Güter abhängen? Welche Bedingung müssen die Preise erfüllen, damit beide Fabriken in
Betrieb bleiben sollen?
Lösung
1. Wenn kein Output vernichtet werden darf, kann der Outputvektor a mit λ = 1/2 produziert werden.
Der Outputvektor b ist nicht produzierbar.
2. Wenn Output vernichtet werden darf, ist b trotzdem nicht produzierbar.
3. f (λ) = λ (6p1 − 2p2 − 6p3 ) + 2p1 + 6p2 + 10p3 → max
Die Funktion f (λ) = λ · m + n ist linear. Damit beide Fabriken bestehen bleiben, muss
m = 6p1 − 2p2 − 6p3 = 0
gelten. Für m > 0 läge das Maximum bei λ = 1 und für m < 0 läge das Maximum bei λ = 0.
viii
III.2 Netto–Output–Vektoren
Ein Unternehmen produziert nichtnegative Outputmengen z1 , z2 , . . . , zn von n verschiedenen Gütern
und benutzt als Input die nichtnegativen Mengen x1 , x2 , . . . , xn derselben n Güter.
Konkret produziert das Unternehmen zwei Güter: dabei wird das zweite Gut als Input genutzt und
das erste ist der Output. Sein Netto–Outputvektor y = z − x ist (2, −1). Der Preisvektor p ist (1, 3).
Bestimmen Sie
1. den Outputvektor z und den Inputvektor x,
4. den Wert des Netto–Outputs n,
2. die Kosten k,
5. den Gewinn oder Verlust des Unternehmens.
3. die Einnahmen e,
Lösung
1. Da das erste Gut nur als Output dient und das zweite nur als Input gilt
z = s · (1, 0),
x = t · (0, 1),
s, t ∈ R.
Wegen y = (2, −1) gilt x = (0, 1) und z = (2, 0).
2. Die Kosten ergeben sich als Produkt von Preis der Güter und Anzahl der Inputs
k = (1, 3) · (0, 1)T = 3.
3. Die Einnahmen ergeben sich als Produkt von Preis der Güter und Anzahl der Outputs
e = (1, 3) · (2, 0)T = 2.
4. Der Wert des Netto–Outputs ist das Produkt aus Preisvektor und Netto–Output–Vektor
(1, 3) · (2, −1)T = 2 − 3 = −1.
5. Das Unternehmen macht Verluste, da die Differenz aus Einnahmen und Kosten negativ ist
2 − 3 = −1.
ix
III.3 Bauunternehmen
Ein Bauunternehmen hat einen Auftrag für mehrere Häuser von drei verschiedenen Typen: 5 vom Typ A,
7 vom Typ B und 12 vom Typ C. Schreiben Sie einen 3–dimensionalen Vektor x, dessen Koordinaten
die Anzahl der Häuser von jedem Typ angeben. Nehmen Sie an, dass für Häuser vom Typ A je 20
Einheiten Holz gebraucht werden, für Typ B je 18 Einheiten und für Typ C je 25 Einheiten. Schreiben
Sie einen Vektor u auf, der die verschiedenen Holzmengen angibt, die für je ein Haus von jedem der
drei Typen A, B und C benötigt werden. Bestimmen Sie die Gesamtmenge an Holz, die benötigt wird,
indem Sie das innere Produkt u · x berechnen.
Lösung
x = (5, 7, 12),
u = (20, 18, 25),
u · x = 526
x
III.4 Stabkräfte in einem belasteten Dreibein
In dem in Abb. 4.3 dargestellten Dreibein, dessen Stäbe gelenkig gelagert sind, greift im Gelenk S eine
Gewichtskraft G vom Betrag |G| = 18 kN an. Welche Reaktionskräfte (Zug- bzw. Druckkräfte) FA , FB
und FC treten in den drei Stäben auf?
⎛ ⎞
⎛ ⎞
⎛ ⎞
⎛ ⎞
2
−1
1
0
A = ⎝1⎠ ,
B = ⎝ 1 ⎠,
C = ⎝−2⎠ ,
S = ⎝0⎠
0
0
2
0
Lösungshinweis: Setzen Sie die Reaktionskräfte in der aus Abb. III.1 ersichtlichen Weise zunächst als
Zugkräfte an. Das Eigengewicht der Stäbe bleibt unberücksichtigt.
z
S
FC
G
FB
FA
C
O
x
B
y
A
Abbildung III.1: Dreibein
Lösung
Die Stabkräfte sind Druckkräfte mit (Angaben in kN)
⎛ ⎞
⎛ ⎞
−2
5
FA
= ⎝−1⎠,
FB
= ⎝−5⎠,
2
10
|FA |
=
3,
|FB |
=
12, 25,
xi
FC
=
|FC |
=
⎛ ⎞
−3
⎝ 6⎠,
6
9.
IV
Aufgaben zu Folgen und Reihen
IV.1
Wachstum einer Bakterienkultur
Über eine Bakterienkultur ist bekannt, dass die tägliche Wachstumsrate 6 % beträgt, diese beinhaltet
die Geburten-, sowie die Sterberate. Außerdem sterben täglich je 150 Bakterien durch eine Probenentnahme. Zu Beginn bestand die Kultur aus 2 000 Bakterien. Wieviele Bakterien leben am n–ten Tag nach
Start der Beobachtungen?
Lösung
an+1 = 1, 06 · an − 150,
a0 = 2 000
Es handelt sich hierbei um eine Verknüpfung aus geometrischer und arithmetischer Folge (vgl. Abschnitt 5.1.6, damit folgt im nächsten Schritt)
an+1 = 1, 06n+1 · 2 000 − 150 · (1 + 1, 06 + · · · + 1, 06n )
Der Klammerausdruck beinhatlet nun eine geometrische Reihe (vgl. Abschnitt 5.2.2), diese kann wie
folgt aufgelöst werden
= 1, 06n+1 · 2 000 − 150 ·
xii
1, 06n+1 − 1
1, 06 − 1
IV.2
Geldanlagen mit Zinseszins
1. Als Mr. Barnes starb, erhielt seine Witwe 2/3 seines Vermögens, 1/4 teilten sich seine Kinder und
der Rest, 100 000 e ging an eine wohltätige Organisation. Wie groß war das Vermögen von Mr.
Barnes?
2. Wenn die Witwe ihren Anteil zu 3 % Zinsen mit Zinseszins anlegt, wieviel Geld hat sie dann nach
10 Jahren?
3. Wann erfolgt eine Verdreifachung des eingezahlten Geldes?
Lösung
1. Mr. Barnes hatte insgesamt 1 200 000 e. Der Anteil der Witwe beträgt 800 000 e und die Kinder
bekommen 300 000 e. Siehe Anhang C
2. Die Witwe erhält nach angegebenem Modell nach 10 Jahren 1 075 133, 10 e.
3. Die Verdreifachung erfolgt nach 38 Jahren.
xiii
IV.3
Effektivzinssatz
Ein Kapital K0 werde jährlich mit dem Zinssatz ik , k = 1, . . . , n, verzinst. Der Zinsertrag wird sofort
wieder angelegt. Wie hoch ist der Effektivzinssatz ieff dieser Anlage? Unter welchen Voraussetzungen
stimmt er mit dem arithmetischen Mittel der einzelnen Jahreszinssätze überein?
Lösung
Das Äquivalenzprinzip verlangt die Gleichheit der Endwerte beider Zahlungsreihen nach n Jahren im
entsprechenden Zinsmodell. Eine Zahlungsreihe entsteht durch die jährliche Verzinsung des Startkapitals
K0 mit den Zinssätzen ik (rechte Seite der folgenden Gleichung). Die zweite Zahlungsreihe entsteht,
indem für jedes Jahr der gleiche Zinssatz ieff angenommen wird (linke Seite).
K0 (1 + ieff )n = K0 (1 + i1 ) · · · (1 + in ).
Nach Elimination von K0 und ziehen der n–ten Wurzel (siehe Abschnitt 1.3) folgt
!
1 + ieff = n (1 + i1 ) · · · (1 + in ).
(IV.3.1)
Die rechte Seite der Gleichung stellt ein geometrisches Mittel dar.
Arithmetische und geometrische Mittel über Zahlen ak ≥ 0, k = 0, . . . , n, sind mit folgender Ungleichung verbunden (A. L. Cauchy 1821):
√
a1 + · · · + an
n
a1 · · · an ≤
n
(IV.3.2)
oder in kompakter Form:
*
+ n
n
+1.
n
,
ak
ak ≤
n
k=1
k=1
Gleichheit gilt genau dann, wenn a1 = a2 = . . . = an .
Aus Ungleichung (IV.3.2) und Gleichung (IV.3.1) folgt
(1 + i1 ) + . . . + (1 + in )
n
n
1.
i1 + . . . + in
=
ik
≤
n
n
1 + ieff ≤
ieff
k=1
Der Effektivzinssatz beträgt
ieff =
!
n
(1 + i1 ) · · · (1 + in ) − 1.
Er ist identisch mit dem arithmetischen Mittel der einzelnen Jahreszinssätze, falls diese identisch sind.
xiv
IV.4
Extraktion einer organischen Substanz mit Benzen
Eine bestimmte Menge m0 einer organische Substanz sei in Wasser gelöst und soll mit Benzen extrahiert
werden. Nach Zugabe des Benzens ergibt sich im Gleichgewichtszustand der Verteilungskoeffizient
k = c1/c2 = 0, 653 (c1 Konzentration des Stoffes in Wasser, c2 Konzentration in Benzen).
1. Wie oft muss man 200 ml der wässrigen Lösung mit jeweils 200 ml Benzen extrahieren, um 97 %
der Substanz aus der wässrigen Lösung zu entfernen?
2. Wie oft müsste man mit jeweils 100 ml Benzen extrahieren, um dieselbe Abreicherung zu erhalten?
Lösung
Sei v1 das Volumen der wässrigen Lösung und v2 das Volumen von Benzen, das bei jeder Extraktion
zugegeben wird.
Nach der ersten Zugabe von Benzens verteilt sich die Ausgangsmenge m0 auf Wasser und Benzen wie
folgt:
m0 = v1 c11 + v2 c12 .
Nach der 1. Extraktion verbleibt im Wasser die Substanzmenge
m1 = v1 c11 ,
das Verhältnis zwischen den Anteilen m1 und m0 beträgt
m1
v1 c11
=
1
m0
v1 c1 + v2 c12
1
c1 (v1 · c1/c1 )
= 1 2 1 1 2
c2 (v1 · c1/c2 + v2 )
v1 k
=: α,
=
v1 k + v2
also
m1 = m0 α.
Nach erneuter Zugabe von Benzen verteilt sich die verbleibende Substanzmenge m1 auf Wasser und
Benzen wie folgt:
m1 = v1 c21 + v2 c22 .
Nach der 2. Extraktion verbleibt im Wasser die Substanzmenge
m2 = v1 c21 ,
das Verhältnis zwischen den Anteilen m2 und m1 beträgt
m2
= α,
⇒
m 2 = m1 α = m 0 α 2 .
m1
Es ergibt sich die geometrische Folge {mn } der verbleibenden Substanzmenge mit
mn = m0 α n .
Es soll mehr als 97 % der Substanz entfernt werden, es soll also weniger als 3 % verbleiben
m0 αn ≤ 0, 03m0
αn ≤ 0, 03
| : m0
| ln
ln(αn ) ≤ ln 0, 03
n ln α ≤ ln 0, 03
Um n zu isolieren, muss durch ln α geteilt werden. Da es sich um eine Ungleichung handelt, muss das
Vorzeichen dieses Ausdrucks berücksichtigt werden.
xv
1. α = 0, 395 039 und damit ln α = −0, 928 771 < 0. Also
n≥
ln 0, 03
= 3, 775 483
ln α
Es müssen n = 4 Extraktionen durchgeführt werden.
2. α = 0, 566 348 und damit ln α = −0, 568 547 < 0. Also
n≥
ln 0, 03
= 6, 209 910
ln α
Es müssen n = 7 Extraktionen durchgeführt werden.
xvi
V
Aufgaben zur Differentialrechnung
V.1
Elektronenstrahl–Oszilloskop
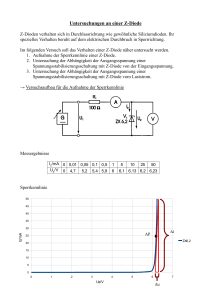
Beim Elektronenstrahl–Oszilloskop werden die von einer Glühkathode ausgesandten Elektronen zunächst auf eine konstante Geschwindigkeit v0 beschleunigt und treten dann senkrecht zu den elektrischen Feldlinien in einen auf die Spannung U aufgeladenen Plattendetektor ein, wo sie aus ihrer
ursprünglichen Richtung abgelenkt werden (vgl. Abb. V.1). (Platten: Abstand d zueinander und Länge l.
Elektronen: Elementarladung e und Ruhemasse m0 )
1. Unter welchem Ablenkwinkel α (gegenüber der Eintrittsrichtung gemessen) verlassen die Elektronen den Kondensator?
2. Im Abstand s hinter dem Kondensator befindet sich ein Auffangschirm für die Elektronen. Wie
groß ist die seitliche Ablenkung b der Elektronen auf diesem Schirm, gemessen gegenüber der
ursprünglichen Flugbahn?
Lösungshinweis: Bestimmen Sie zunächst die Bahnkurve der Elektronen im Plattenkondensator.
y
v0
d
2
+
+
+
C
+
B
b
α
A
m0
x
d
2
E
-
-
-
s
l
Abbildung V.1: Elektronenstrahl–Oszilloskop
Lösung
1. Die Koordinaten (x, y) eines Elektrons zur Zeit t mit einer Beschleunigung a lauten
x = v0 t,
⇒
y=
y=
eU 2
t
2m0 d
1 2
at ,
2
a = (eU )/(m0 d)
t=x/v0
=⇒
y = f (x) =
eU
2m0 d
#
x
v0
$2
.
Im Punkt B verlassen die Elektronen den Kondensator und bewegen sich geradlinig auf der
Bahntangenten weiter auf den Schirm zu. Es gilt:
f ′ (xB) = tan α
⇒
α = arctan
2. Im Auftreffpunkt C = (l + s, b) beträgt die Auslenkung
b=
eU l(l + 2s)
.
2m0 dv02
xvii
eU l
.
m0 dv02
V.2
Wurfparabel eines Wasserstrahls
Abbildung V.2 zeigt einen bis zur Höhe H mit Wasser gefüllten Zylinder. In der Tiefe h (von der als
unveränderlich angenommenen Wasseroberfläche aus gerechnet) befindet sich eine seitliche Öffnung,
aus der das Wasser in waagerechter Richtung mit der nach der Formel
!
v0 = 2gh
berechneten Geschwindigkeit austritt. An welcher Stelle A des Gefäßes muss man dies Öffnung anbringen, damit der seitlich austretende Wasserstrahl den Boden an einer möglichst weit entfernten Stelle B
(in horizontaler Richtung gemessen) trifft?
Lösungshinweis: Die Bewegung des Wasserstrahls kann in guter Näherung als ein waagerecher Wurf
im luftleeren Raum betrachtet werden.
h
v0
A
xW
x
x
y
H
Zylinder
mit
Wasser
H −h
B
xW
y
Abbildung V.2: Parabel eines Wasserstrahls
Lösung
Die Wasserbewegung besteht aus zwei unabhängigen Teilen: Die Bewegung in x–Richtung besitzt die
konstante Geschwindigkeit x = v0 t. In y–Richtung geschieht eine Beschleunigung aufgrund der Gravitation mit der Beschleunigung g, es folgt
1
y = gt2 .
2
Durch Substitution von t folgt
x2
y=
.
4h
Einsetzen des Auftreffpunktes B = (xW , H − h) und Auflösen nach xW :
!
xW = 2 Hh − h2 .
Diese Größe soll maximiert werden, es genügt hierfür
z(h) = Hh − h2
zu maximieren. Der Austrittspunkt A sollte in der Höhe h = H/2 liegen, dann ist xW,max = H.
xviii
V.3
Grenzkosten, Grenzertrag und Grenzgewinn
Ein Unternehmen produziert in einer Zeitperiode x Einheiten einer Ware. Der Gewinn der Produktion
π(x) ist die Differenz aus dem Ertrag R(x) und den Produktionskosten C(x).
Die Grenzkosten C ′ (x) sind definiert als die Ableitung der Kosten C(x). Sie geben die Kosten an, die
durch die Produktion einer zusätzlichen Einheit eines Produktes entstehen. Analog ist der Grenzertrag
R′ (x) die Ableitung des Ertrags R(x), er beschreibt den Ertragszuwachs bei Verkauf einer weiteren
Produktionseinheit. Der Grenzgewinn π ′ (x) ist die Ableitung des Gewinns π(x). Er gibt den erwarteten
Gewinn für eine weitere produzierte Einheit eines Produktes an und kann Aufschluss darüber geben,
wieviele Einheiten produziert werden müssen, um die Gewinnschwelle zu erreichen.
Bestimmen Sie den Grenzertrag, die Grenzkosten und den Grenzgewinn sowie einen Wert x, so dass
der Grenzgewinn Null ist, für
1. R(x) = ax, C(x) = a1 x2 + b1 x + c1 ,
2. R(x) = ax − bx2 , C(x) = a1 x + b1 .
Lösung
1. π(x) = −a1 x2 + (a − b1 )x − c1 ,
R′ (x) = a,
C ′ (x) = 2a1 x + b1 ,
π ′ (x) = −2a1 x + a − b1 ,
a − b1
π ′ (x) = 0 ⇒ x =
2a1
2. π(x) = −bx2 + (a − a1 )x − b1 ,
R′ (x) = a − 2bx,
C ′ (x) = a1 ,
π ′ (x) = −2bx + a − a1 ,
a − a1
π ′ (x) = 0 ⇒ x =
2b
xix
VI
Aufgaben zur Integralrechnung
VI.1 Massenträgheitsmoment eines Rotationskörpers
y
Abbildung VI.1 zeigt einen homogenen Ellipsoiden, also einen Rotationskörper mit elliptischem
Querschnitt. Er entsteht durch Drehung einer Ellipse mit den Halbachsen a und b um die y–Achse.
1. Berechnen Sie das Massenträgheitsmoment
Jy des Ellipsoidstumpfes (hellblau) bezüglich der Rotationsachse in Abhängigkeit vom
Parameter h (2h — Höhe des Rotationskörpers, 0 ≤ h ≤ b). Wie groß ist das Volumen
dieses Körpers?
b
h
2. Welche Werte ergeben sich aus dem ersten
Teil für die Massenträgheitsmomente eines
Rotationsellipsoids und einer Kugel vom Radius R? Wie groß sind die Volumina dieser
Körper?
x
a
Abbildung VI.1: Rotationsellipsoid
Lösung
1. Das Massenträgheitsmoment ist definiert als
/
2
J=
r⊥
ρ(r)dV.
V
Dieses Integral ist in diesem Rahmen zu schwer zu lösen. In Tafelwerken ist jedoch die einfache
Formel für das Trägheitsmoment eines Zylinders mit Radius R und Masse m, bzw. Volumen V =
m/ρ
1
ρ≡1 1
JZylinder = mR2 = V R2
2
2
zu finden. Diese Formel kann genutzt werden, wenn der Rotationskörper in Zylinderscheiben
zerteilt wird, die senkrecht zur y–Achse stehen. Der Radius der Scheiben ist die x–Auslenkung
der begrenzenden Funktion x = R(y). Die Zahl der Scheiben wird vergrößert, sodass sich deren
Höhe H = y und damit auch das Volumen V auf infinitesimale Größe verringert (dy bzw. dV )
V = πR(y)2 y
⇒
dV = πR(y)2 dy.
Es folgt für einen einzelnen Zylinder
JZylinder =
xx
1
πR(y)4 dy.
2
Für den gesamten Rotationskörper wird nun über alle unendlich dünnen Zylinder summiert, es
findet eine Integration im Intervall [−h, h] statt
Jy =
/h
JZylinder =
/h
1
π
πR(y)4 dy =
2
2
−h
−h
/h
R(y)4 dy.
−h
Der Körper ist symmetrisch zur x, z–Ebene, d. h. es genügt eine Hälfte des Körpers zu berechnen
(0 ≤ y ≤ h statt −h ≤ y ≤ h) und den errechneten Wert dann zu verdoppeln
Jy = π ·
/h
R(y)4 dy.
0
Die Formel für x = R(y) resultiert aus der Ellipsengleichung
y2
x2
+
a2
b2
2 0
1
a
x 2 = 2 b2 − y 2
b
|−
1=
y2 2
, ·a
b2
(VI.1.1)
Es folgt für das Massenträgheitsmoment
Jy = πρ ·
/h
0
0
x
1
2 2
$
#
πρ · a4
2 2 3 1 5
4
dy =
· b h− b h + h
b4
3
5
Das Volumen wird mit Hilfe von Gl. (7.4.1) gelöst, der Argumentbereich x = R(y) wird dabei
von y = −h und y = h begrenzt
V =π
/h
(VI.1.1)
x2 dy = π
=π
−h
a2
b2
#
2
2b2 h − h3
3
2. Rotationsellipsoid (h = b):
JEllipsoid =
8
πρa4 b
15
VEllipsoid =
4 2
πa b
3
Kugel mit Radius R (a = b = R):
JKugel =
8
πρR5
15
VKugel =
xxi
4 3
πR
3
$
VI.2 Schlittenfahren
Im Winter will ein kleiner Junge einen glatten Hügel mit Höhe h = 10 m und Länge l = 30 m mit
dem Schlitten hinunter fahren. Der Junge wiegt mJ = 40 kg und sein Schlitten mS = 5 kg. Mit welcher
Geschwindigkeit v wird der Junge das Ende des Hügels (im Punkt A in Abb. VI.2) erreichen, und wie
lange wird seine Abfahrt dauern?
Abbildung VI.2: schematische Darstellung der Kräfte beim Herabfahren eines Hügels
Lösung
Das Zweite Newton’sche Gesetz (Bewegungsgleichung) besagt, dass die Änderung der Bewegung einer Masse proportional zu der einwirkenden Kraft ist. Die hier wirkende Kraft setzt sich aus mehreren
Teilkräften zusammen, daher folgt
.
m·a=
Fi .
i
Die am Schlitten wirkenden Teilkräfte sind die Gewichtskraft FG = m · g, die Hangabtriebskraft FA und
die Reibungskraft FR = µ · FN , mit dem Reibungskoeffizienten µ und der Normalkraft FN . Die Kräfte
wirken, wie in der Skizze vermerkt. Die zwei Dreiecke ABC und N OM sind ähnlich, deshalb sind die
entsprechenden Winkel gleich. Es folgt für die resultierende Kraft
m · a = FA − FR .
(VI.2.1)
Laut Aufgabenstellung ist die Oberfläche ein rutschiger Hügel, d. h. für die Reibungskraft gilt FR = 0.
Daher folgt aus Gl. (VI.2.1)
m · a = FA .
(VI.2.2)
Mit Hilfe der Winkelbeziehungen am rechtwinkligen Dreieck (vgl. Abschnitt 1.5) folgt
m · a = FG · sin α.
Mit Hilfe des Satzes von Pythagoras (1.5.4) lässt sich die Länge von AB bestimmen
!
√
sA := AB = 102 + 302 m = 10 10 m.
(VI.2.3)
(VI.2.4)
Mit Gl. (1.5.2) und Gl. (VI.2.4) folgt
(1.5.2)
sin α =
BC
AB
(VI.2.4)
=
√
1
10 m
10
√
.
=√ =
10
10 10 m
10
(VI.2.5)
Durch Zusammenfassen der Gleichungen (VI.2.2) und (VI.2.5) ergibt sich
g
a= √ .
10
xxii
(VI.2.6)
Offenbar ist die Lösung von der Masse unabhängig, d. h. die Aufgabe enthält überschüssige Daten.
Geschwindigkeit und Beschleunigung sind definiert als erste bzw. zweite Ableitung des Weges nach der
Zeit:
v(t) = s′ (t),
a(t) = v ′ (t) = s′′ (t)
(VI.2.7)
Nach dem Hauptsatz der Differential- und Integralrechnung (7.2.1) kann also die Beschleunigung
integriert werden, um die Geschwindigkeit zu erhalten (vgl. Abschnitt 7). Das Integral über die Geschwindigkeit liefert ferner den Weg:
v=
s=
t=τ
/
t=0
t=τ
/
(VI.2.8)
a dt = a · τ,
v dt =
t=0
t=τ
/
t=0
a · t dt =
1
a · τ 2.
2
(VI.2.9)
Hier ist τ die Fahrtzeit des Jungen den Hügel hinunter, bei Start im Punkt B. Die Aufgabe besteht jetzt
darin, die Zeit τA zu bestimmen, die der Junge braucht um vom Punkt B bis zum Punkt A herunterzufahren. Für die Fahrtzeit τA transformiert sich Gl. (VI.2.9) zu
1
a · τA2
2
sA =
(VI.2.6)
=
g
√ · τA2 .
2 10
(VI.2.10)
% √
%
√
2 10 · 10 10 m
200 s2
=
≈ 4, 5 s
=
9, 81 m/s2
9, 81
(VI.2.11)
Umstellen nach τA ergibt
% √
2 10sA
τA =
g
(VI.2.4)
Wird τ in Formel (VI.2.8) durch τA ersetzt, folgt
v A = a · τA
(VI.2.6)
= g · 4, 5 s =
9, 81 m
· 4, 5 s ≈ 14m/s
s2
Der Junge erreicht den Fuß des Hügels A mit einer Geschwindigkeit vA ≈ 14m/s. Die Fahrt dauert
τA ≈ 4, 5 s.
xxiii
VI.3 Konsumenten– und Produzentenrente
Eine Nachfragefunktion P = f (Q) beschreibt den Zusammenhang von nachgefragter Menge Q und
Preis P . Eine Angebotsfunktion P = g(Q) stellt die Beziehung von angebotener Menge Q und Preis P
dar. Wenn Angebot und Nachfrage gleich sind, wird von einem Gleichgewichtspreis P ∗ gesprochen.
Er tritt bei einer Menge Q∗ ein. Mit Konsumentenrente CS wird der Betrag bezeichnet, der insgesamt
von allen Konsumenten eingespart wird, wenn sie das Gut zu einem Preis kaufen, der unter dem Preis
liegt, den sie maximal zu zahlen bereit sind
CS =
/Q
∗
0
(f (Q) − P ∗ ) dQ.
Die Produzentenrente PS ist der Gesamtbetrag aller Produzenten, die einen höheren Preis erzielen, als
der minimale Preis, zu dem sie ihr Gut verkaufen würden
PS =
/Q
0
∗
(P ∗ − g(Q)) dQ.
Gegeben seien eine Nachfragefunktion f (Q) = 200 − 0, 2 · Q sowie eine Angebotsfunktion g(Q) =
20 + 0, 1 · Q. Bestimmen Sie den Gleichgewichtspreis und berechnen Sie die Konsumenten- und Produzentenrente.
Lösung
Gleichgewichtspreis:
f (Q) = g(Q)
200 − 0, 2 · Q = 20 + 0, 1 · Q
Q∗ = 600
f (600) = P ∗ = 80
Konsumentenrente
CS =
Produzentenrente
/600
(200 − 0, 2 · Q − 80) dQ
/600
(80 − 20 − 0, 1 · Q) dQ
PS =
0
0
= 36 000
= 18 000
xxiv